Hybrid Optimization Based Mathematical Procedure for Dimensional Synthesis of Slider-Crank Linkage
Abstract
:1. Introduction
- Deduction of the equations required for the optimal dimensional synthesis of the slider-crank mechanism, which constitutes an alternative to the hinged four-bar linkage usually used in the literature to solve this type of problem.
- Proposal of an original methodology to solve a non-linear system of equations resulting from the null gradient condition, based on the decoupling of two subsystems of equations. It facilitates the resolution of the system and, in some cases, allows to obtain all the solutions in an analytical way.
- Integration of the local optimization methodology within a hybrid optimization method, which uses a genetic algorithm to search for the best starting approximations. The fitness function has been adapted to solve not only the prescribed timing problem, but also unprescribed timing.
- Solving and comparison of examples proposed by other authors in the literature dealing with the four-bar linkage. Thanks to the effectiveness of the method proposed in this work, the slider-crank mechanism, though being simpler and more limited, is able to provide similar performances (or even better in some cases) in path generation problems.
2. Materials and Methods
2.1. Bases of the Optimum Synthesis Procedure
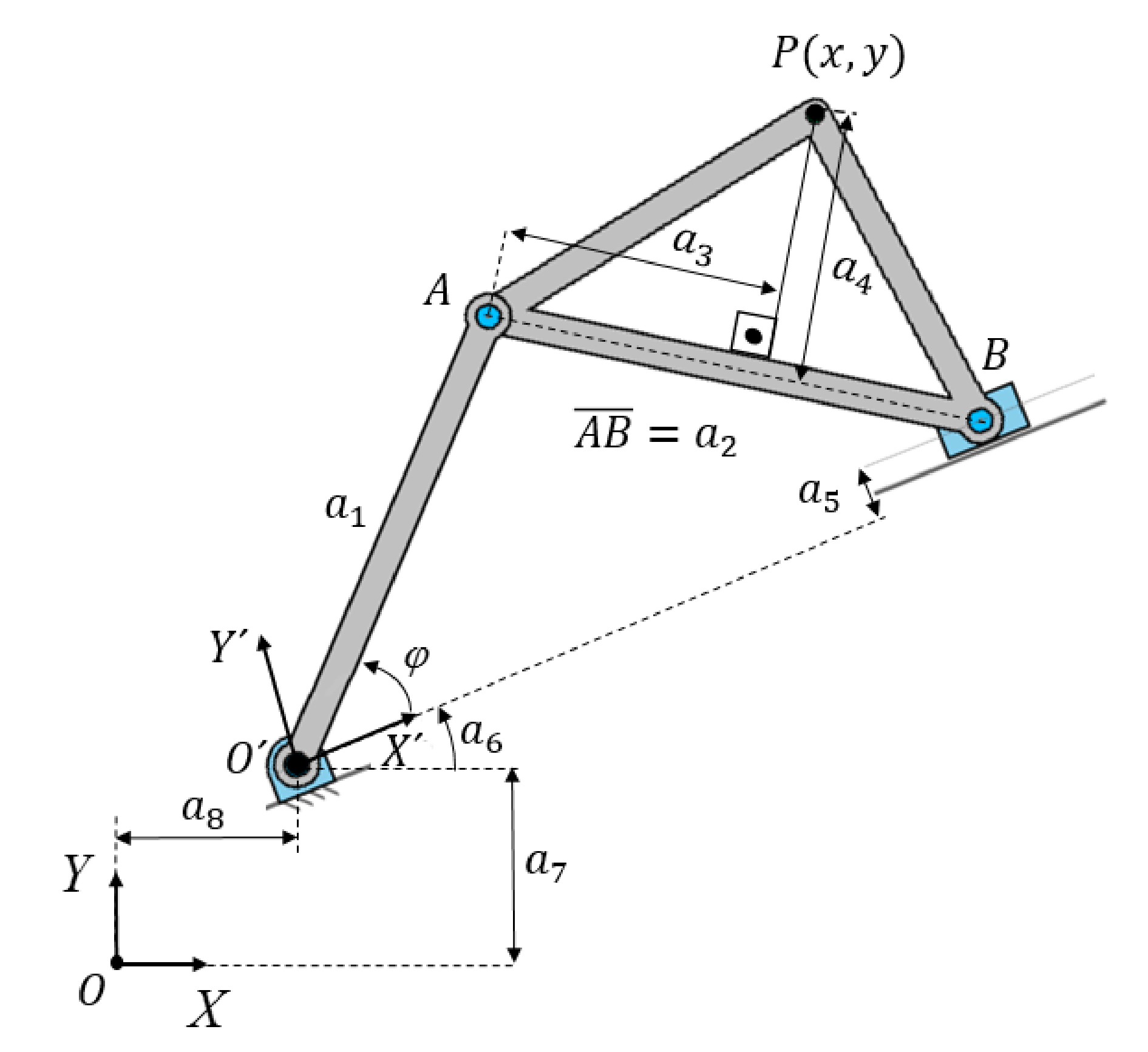
2.1.1. Synthesis Equations for a General Design
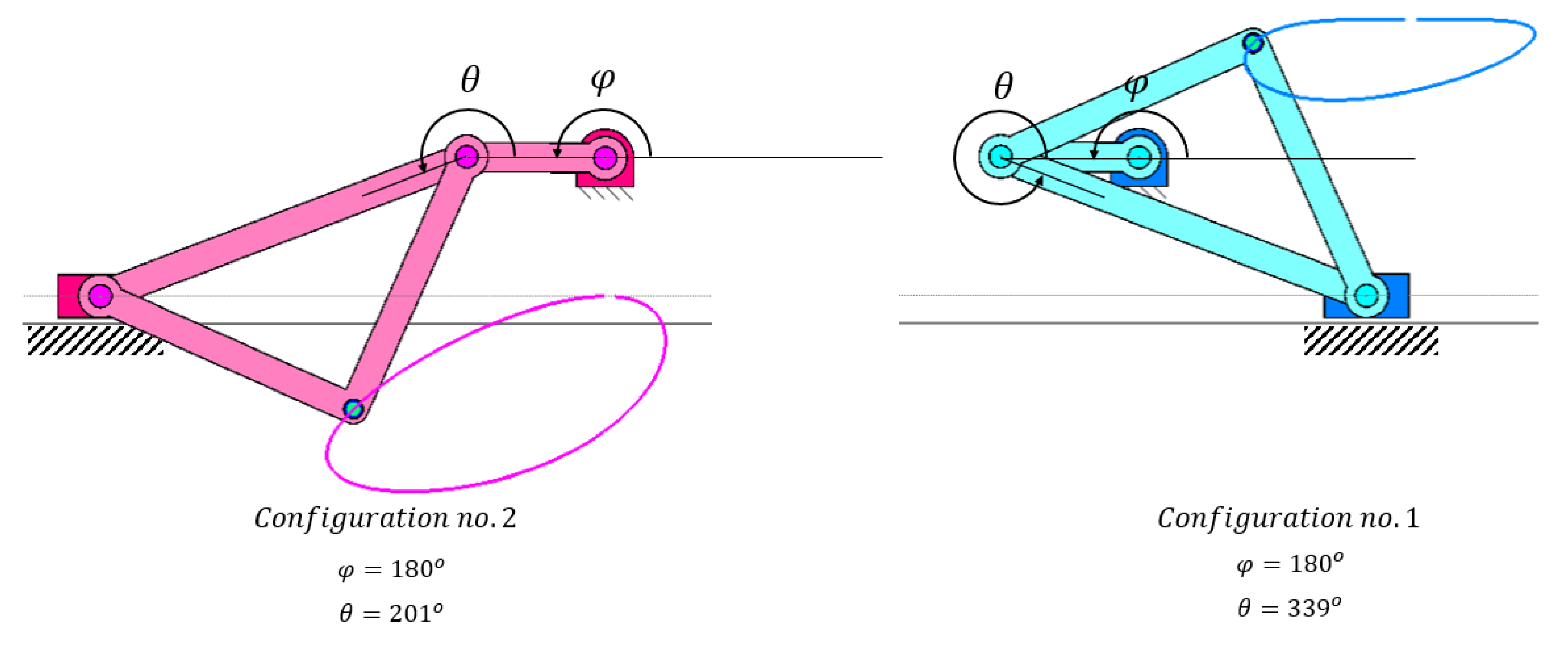
Remark Regarding Branches and Circuits
- Dimensional variables: . These are variables that define the lengths of the bars and the translation or rotation parameters of the studied mechanism.
- Input variable: . This is an independent variable corresponding to the degree of freedom of the mechanism under study.
- Passive variables: . These are not independent variables, but rather depend on the input and the dimensional parameters.
- Output variables or synthesis variables: . These correspond to the coordinates of the coupler point P. In the case of path generation synthesis, these are indeed the synthesis variables.
2.1.2. Optimal Design Based on the Error Function
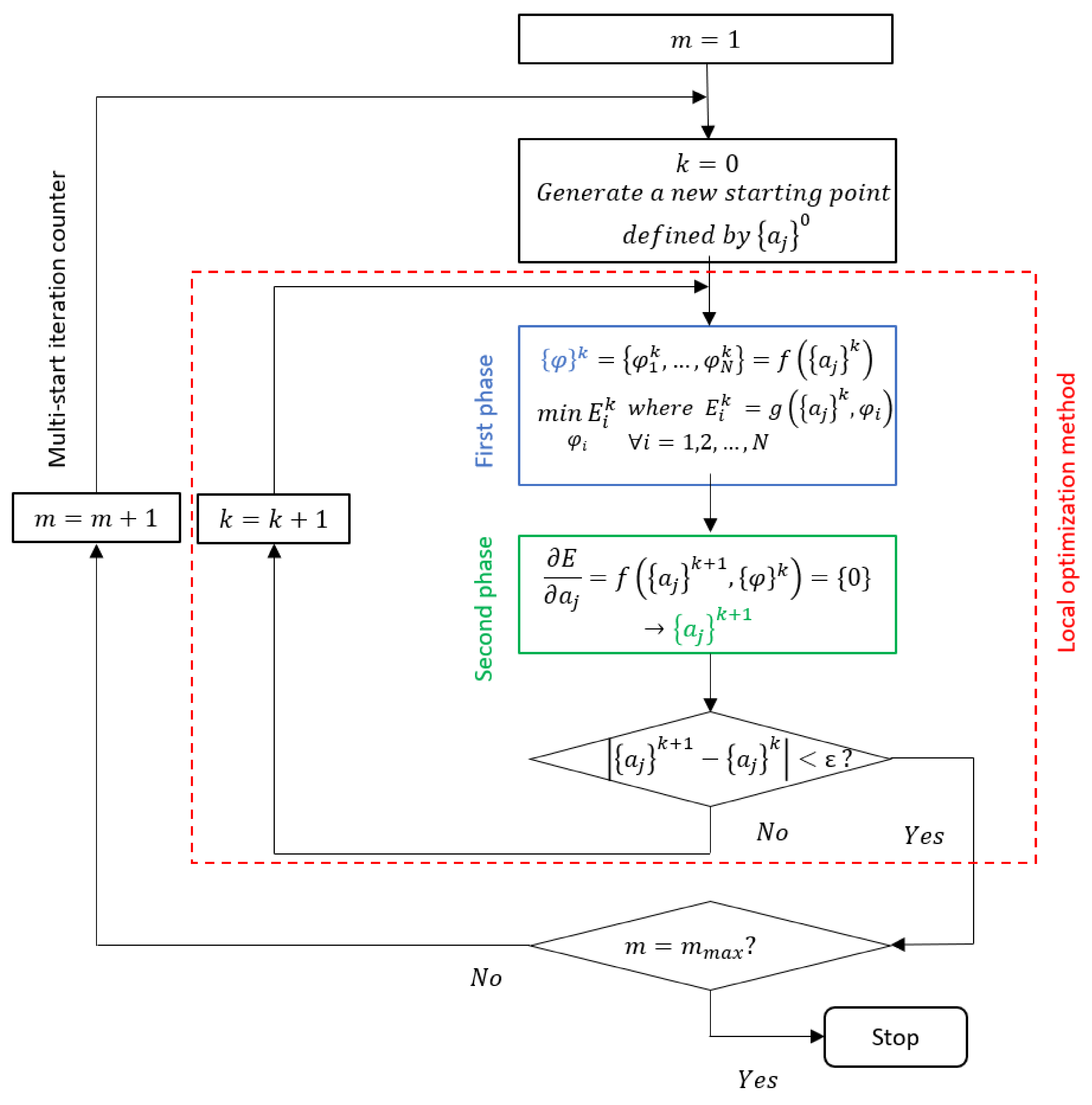
2.2. Hybrid Optimization Procedure
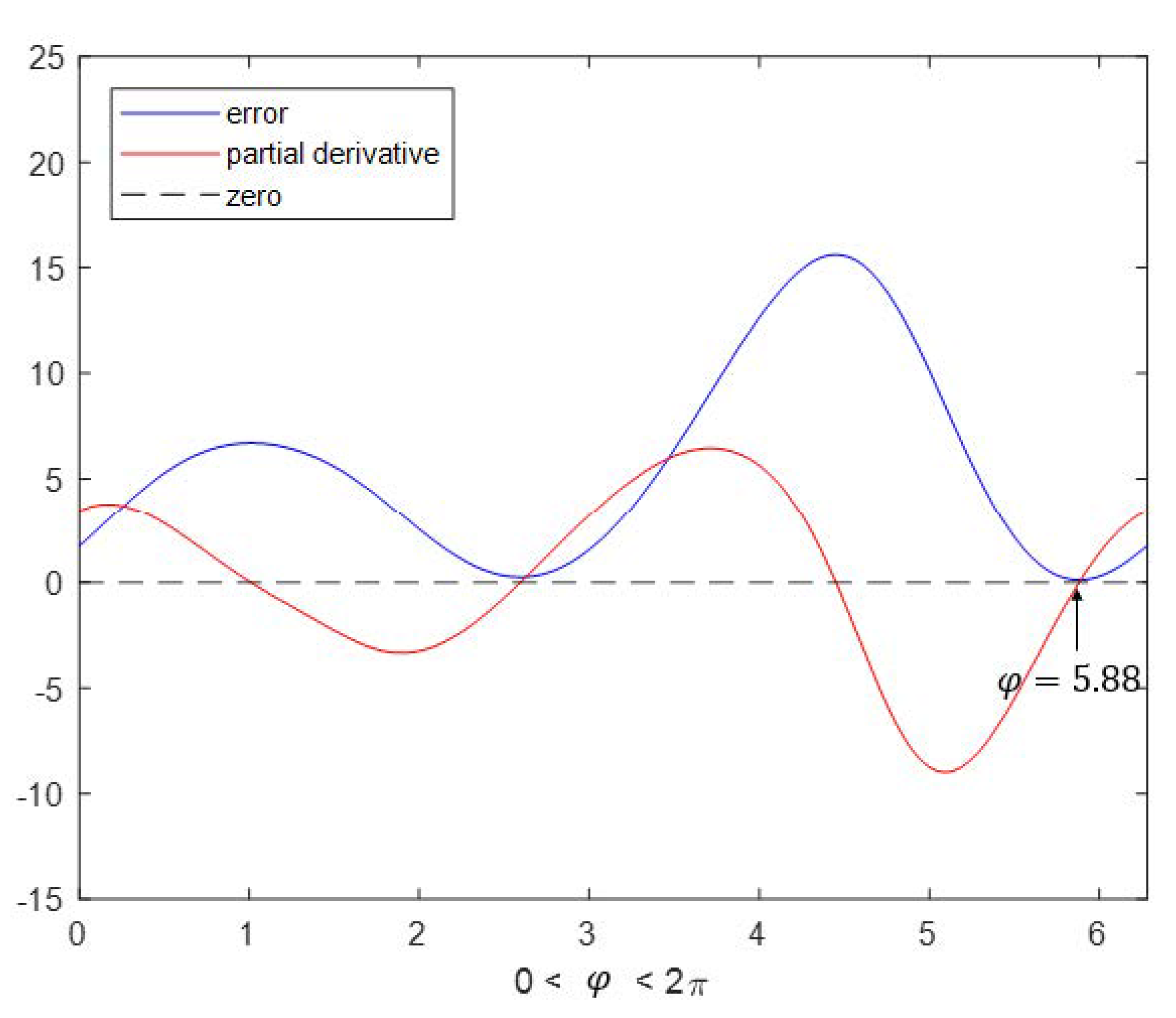
2.2.1. Solving the Equation System for Local Optimization
- First phase:
- Second phase:
- Next steps:
2.2.2. Implementing a Multi-Start Strategy
2.2.3. Incorporation of Design Constraints
3. Results
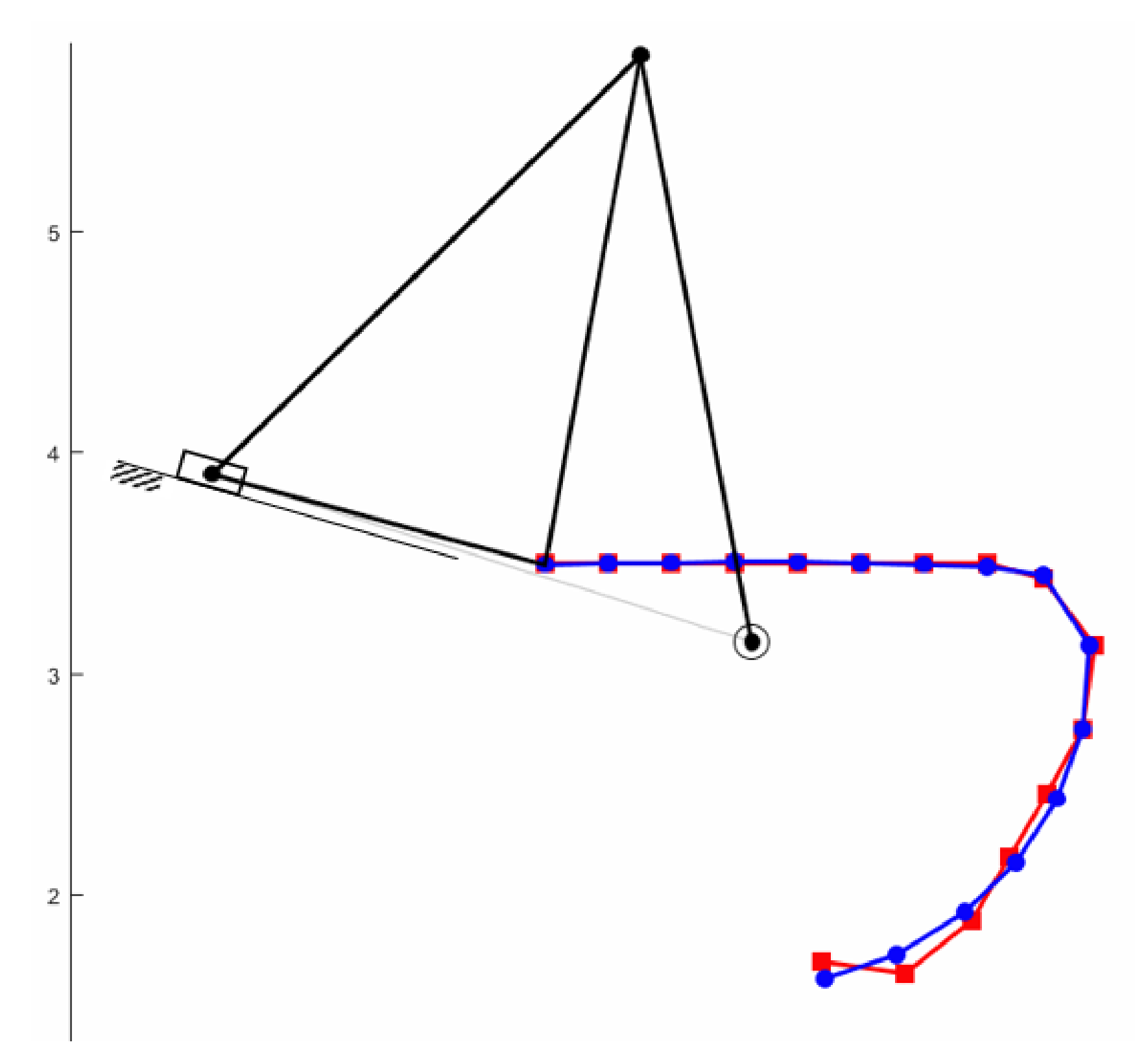
3.1. Demonstrative Example 1
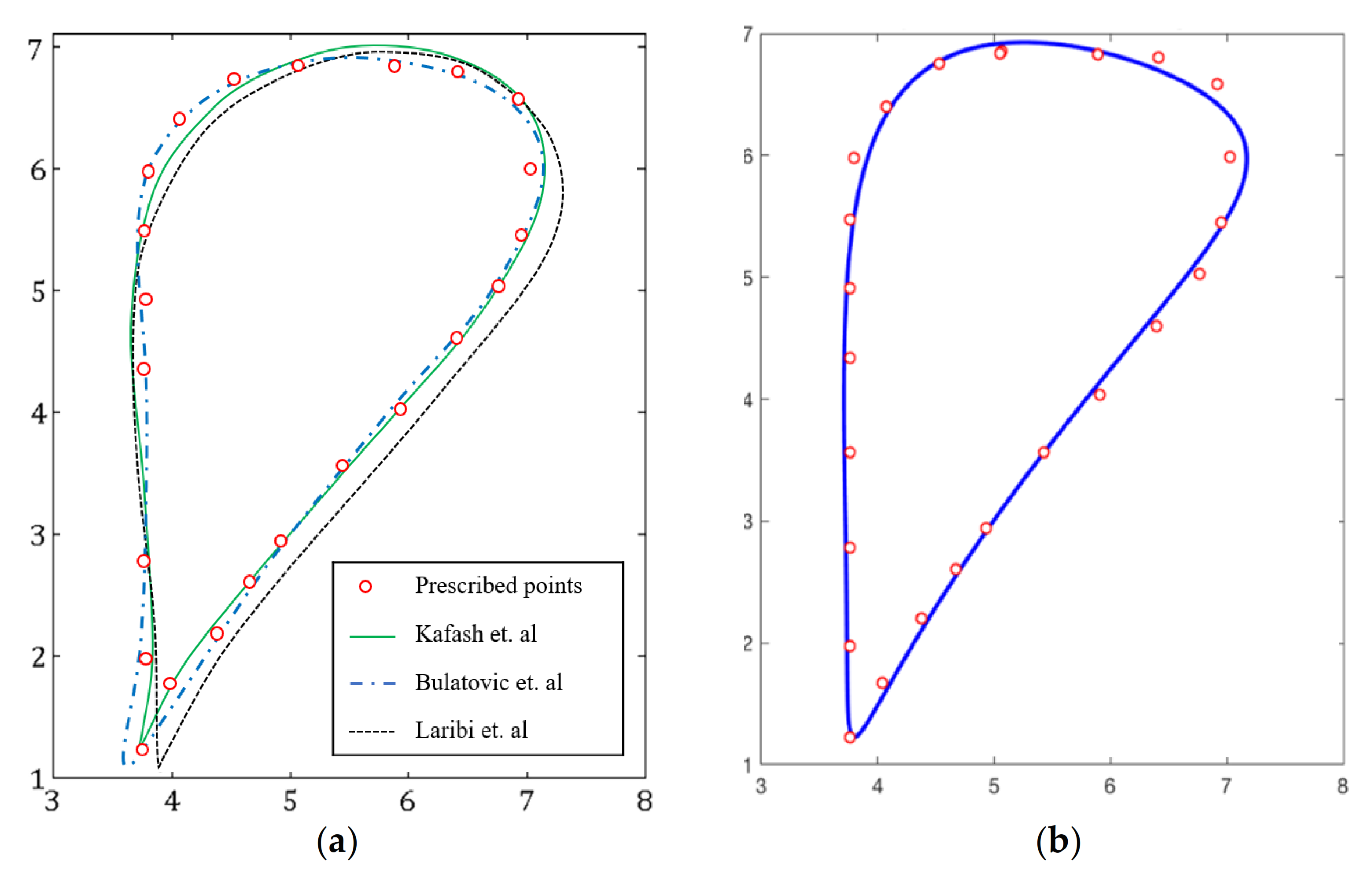
3.2. Demonstrative Example 2
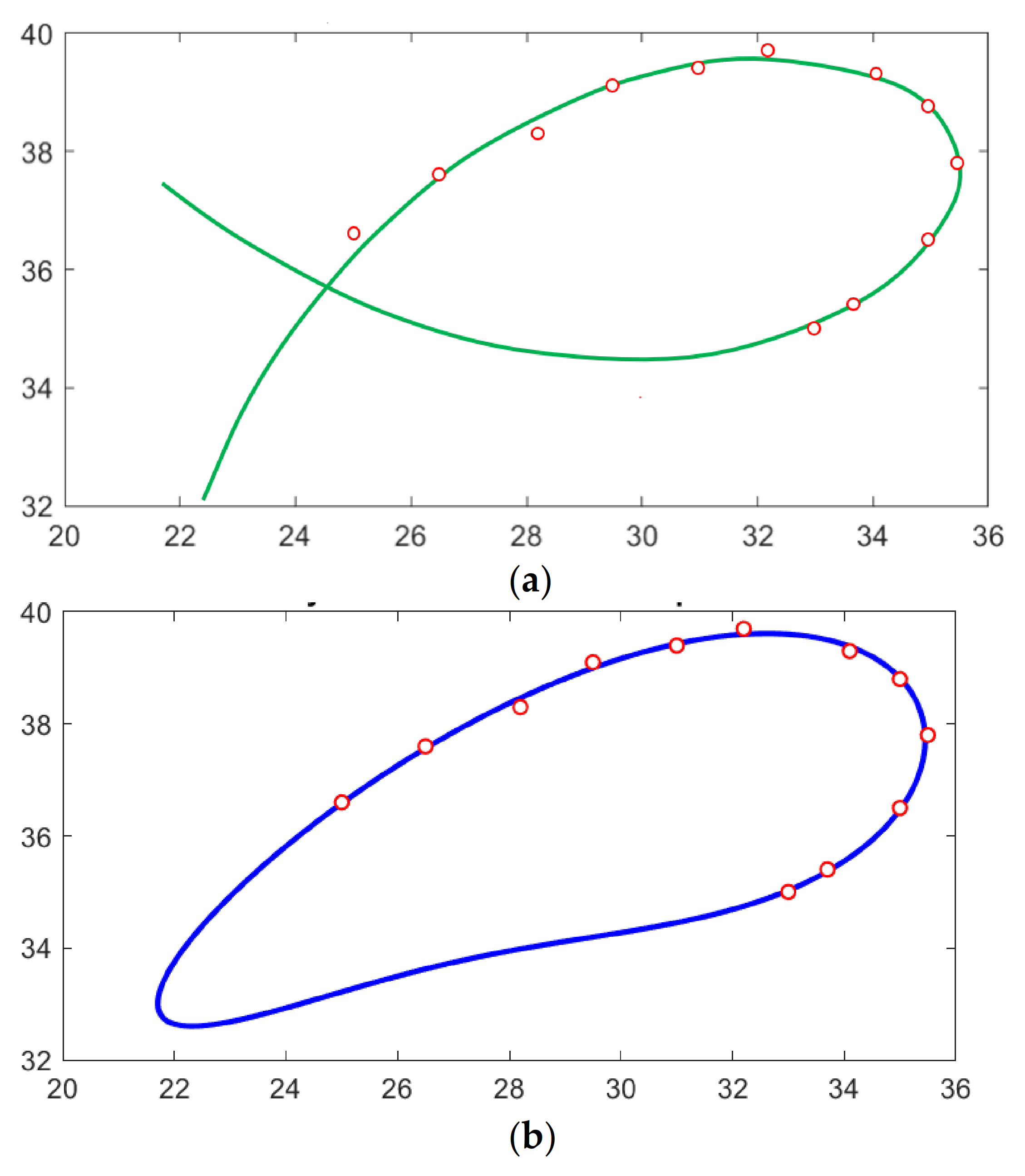
3.3. Demonstrative Example 3
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erdman, A.G.; Sandor, G.N. Mechanism Design: Analysis and Synthesis, 4th ed.; Pearson: London, UK, 2001. [Google Scholar]
- Wampler, C.; Morgan, A.P.; Sommese, A.J. Complete Solution of the Nine-Point Path Synthesis Problem for Four-Bar Linkages. J. Mech. Des. 1992, 114, 153–159. [Google Scholar] [CrossRef]
- Lee, W.-T.; Russell, K. Developments in quantitative dimensional synthesis (1970-present): Four-bar motion generation. Inverse Probl. Sci. Eng. 2017, 26, 133–148. [Google Scholar] [CrossRef]
- Lee, W.-T.; Russell, K. Developments in quantitative dimensional synthesis (1970–present): Four-bar path and function generation. Inverse Probl. Sci. Eng. 2018, 26, 1280–1304. [Google Scholar] [CrossRef]
- Alizade, R.I.; Mohan Rao, A.V.; Sandor, G.N. Optimum Synthesis of Four-Bar and Offset Slider-Crank Planar and Spatial Mechanisms Using the Penalty Function Approach with Inequality and Equality Constraints. J. Eng. Ind. 1975, 97, 785–790. [Google Scholar] [CrossRef]
- Rao, A.C. Optimum synthesis of a slider-crank mechanism using geometric programming. Int. J. Numer. Methods Eng. 1980, 15, 1595–1602. [Google Scholar] [CrossRef]
- Plecnik, M.M.; McCarthy, J.M. Five position synthesis of a slider-crank function generator. In Proceedings of the ASME International Conference IDETC/CIE 2011, Washington, DC, USA, 28–31 August 2011; pp. 317–324. [Google Scholar]
- Almandeel, A.; Murray, A.P.; Myszka, D.H.; Stumph, H.E. A Function Generation Synthesis Methodology for All Defect-Free Slider-Crank Solutions for Four Precision Points. J. Mech. Robot. 2015, 7, 031020–031021. [Google Scholar] [CrossRef]
- Liniecki, A. Synthesis of a slider-crank mechanism with consideration of dynamic effects. J. Mech. 1970, 5, 337–349. [Google Scholar] [CrossRef]
- Davidson, J.K. Analysis and synthesis of a slider-crank mechanism with a flexibly-attached slider. J. Mech. 1970, 5, 239–247. [Google Scholar] [CrossRef]
- Zhou, H.; Ting, K.-L. Adjustable slider–crank linkages for multiple path generation. Mech. Mach. Theory 2002, 37, 499–509. [Google Scholar] [CrossRef]
- Russell, K.; Sodhi, R. On the Design of Slider-Crank Mechanisms. Part I: Multi-Phase Motion Generation. Mech. Mach. Theory 2005, 40, 285–299. [Google Scholar] [CrossRef]
- Russell, K.; Sodhi, R.S. On the design of slider-crank mechanisms. Part II: Multi-phase path and function generation. Mech. Mach. Theory 2005, 40, 301–317. [Google Scholar] [CrossRef]
- Zhou, H. Dimensional synthesis of adjustable path generation linkages using the optimal slider adjustment. Mech. Mach. Theory 2009, 44, 1866–1876. [Google Scholar] [CrossRef]
- Sancibrian, R.; Sarabia, E.G.; Sedano, A.; Blanco, J.M. A general method for the optimal synthesis of mechanisms using prescribed instant center positions. Appl. Math. Model. 2016, 40, 2206–2222. [Google Scholar] [CrossRef]
- Sun, J.; Chu, J. Fourier series representation of the coupler curves of spatial linkages. Appl. Math. Model. 2010, 34, 1396–1403. [Google Scholar] [CrossRef]
- Liu, W.; Sun, J.; Zhang, B.; Chu, J. Wavelet feature parameters representations of open planar curves. Appl. Math. Model. 2018, 57, 614–624. [Google Scholar] [CrossRef]
- Jianwei, S.; Jinkui, C.; Baoyu, S. A unified model of harmonic characteristic parameter method for dimensional synthesis of linkage mechanism. Appl. Math. Model. 2012, 36, 6001–6010. [Google Scholar] [CrossRef]
- Ding, H.; Huang, P.; Zi, B.; Kecskeméthy, A. Automatic synthesis of kinematic structures of mechanisms and robots especially for those with complex structures. Appl. Math. Model. 2012, 36, 6122–6131. [Google Scholar] [CrossRef]
- Chi-Yeh, H. A general method for the optimum design of mechanisms. J. Mech. 1967, 1, 301–313. [Google Scholar] [CrossRef]
- Angeles, J.; Alivizatos, A.; Akhras, A. An unconstrained nonlinear least-square method of optimization of RRRR planar path generators. Mech. Mach. Theory 1988, 23, 343–353. [Google Scholar] [CrossRef]
- Avilés, R.; Navalpotro, S.; Amezua, E.; Hernández, A. An Energy-Based General Method for the Optimum Synthesis of Mecha-nisms. J. Mech. Des. 1994, 116, 127–136. [Google Scholar] [CrossRef]
- Vallejo, J.; Avilés, R.; Hernández, A.; Amezua, E. Nonlinear optimization of planar linkages for kinematic syntheses. Mech. Mach. Theory 1995, 30, 501–518. [Google Scholar] [CrossRef]
- Sancibrian, R.; Viadero, F.; García, P.; Fernández, A. Gradient-based optimization of path synthesis problems in planar mechanisms. Mech. Mach. Theory 2004, 39, 839–856. [Google Scholar] [CrossRef]
- Sancibrian, R.; De Juan, A.; Sedano, A.; Iglesias, M.; García, P.; Viadero, F.; Fernandez, A. Optimal Dimensional Synthesis of Linkages Using Exact Jacobian Determination in the SQP Algorithm. Mech. Based Des. Struct. Mach. 2012, 40, 469–486. [Google Scholar] [CrossRef]
- Mariappan, J.; Krishnamurty, S. A generalized exact gradient method for mechanism synthesis. Mech. Mach. Theory 1996, 31, 413–421. [Google Scholar] [CrossRef]
- Cabrera, J.; Simon, A.; Prado, M. Optimal synthesis of mechanisms with genetic algorithms. Mech. Mach. Theory 2002, 37, 1165–1177. [Google Scholar] [CrossRef] [Green Version]
- Acharyya, S.; Mandal, M. Performance of EAs for four-bar linkage synthesis. Mech. Mach. Theory 2009, 44, 1784–1794. [Google Scholar] [CrossRef]
- Buśkiewicz, J.; Starosta, R.; Walczak, T. On the application of the curve curvature in path synthesis. Mech. Mach. Theory 2009, 44, 1223–1239. [Google Scholar] [CrossRef]
- Kafash, S.H.; Nahvi, A. Optimal synthesis of four-bar path generator linkages using Circular Proximity Function. Mech. Mach. Theory 2017, 115, 18–34. [Google Scholar] [CrossRef]
- Gogate, G.R.; Matekar, S.B. Optimum synthesis of motion generating four-bar mechanisms using alternate error functions. Mech. Mach. Theory 2012, 54, 41–61. [Google Scholar] [CrossRef]
- Bulatović, R.R.; Ðorđević, S.R. Control of the optimum synthesis process of a four-bar linkage whose point on the working member generates the given path. Appl. Math. Comput. 2011, 217, 9765–9778. [Google Scholar] [CrossRef]
- Xiao, R.; Tao, Z. A Swarm Intelligence Approach to Path Synthesis of Mechanism. In Proceedings of the Ninth International Conference on Computer Aided Design and Computer Graphics (CAD-CG’05), Hong Kong, China, 7–10 December 2005; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2005; pp. 451–456. [Google Scholar]
- Bulatovic, R.R.; Miodragovic, G.; Boskovic, M.S. Modified Krill Herd (MKH) algorithm and its application in dimensional syn-thesis of a four-bar linkage. Mech. Mach. Theory 2016, 95, 1–21. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Payvandy, P. Efficient constrained synthesis of path generating four-bar mechanisms based on the heuristic opti-mization algorithms. Mech. Mach. Theory 2015, 85, 189–204. [Google Scholar] [CrossRef]
- Vasiliu, A.; Yannou, B. Dimensional synthesis of planar mechanisms using neural networks: Application to path generator linkages. Mech. Mach. Theory 2001, 36, 299–310. [Google Scholar] [CrossRef] [Green Version]
- Sedano, A.; Sancibrian, R.; De-Juan, A.; Viadero, F.; Egaña, F. Hybrid Optimization Approach for the Design of Mechanisms Using a New Error Estimator. Math. Probl. Eng. 2012, 2012, 1–20. [Google Scholar] [CrossRef]
- Hernández, A.; Muñoyerro, A.; Urízar, M.; Amezua, E. Comprehensive approach for the dimensional synthesis of a four-bar linkage based on path assessment and reformulating the error function. Mech. Mach. Theory 2021, 156, 104126. [Google Scholar] [CrossRef]
- Laribi, M.A.; Mlika, A.; Romdhane, L.; Zeghloul, S. A combined genetic algorithm-fuzzy logic method (GA-FL) in mechanism synthesis. Mech. Mach. Theory 2004, 39, 717–735. [Google Scholar] [CrossRef]
- Smaili, A.; Diab, N. Optimum synthesis of hybrid-task mechanisms using ant-gradient search method. Mech. Mach. Theory 2007, 42, 115–130. [Google Scholar] [CrossRef]
- Fernández-Bustos, I.; Aguirrebeitia, J.; Avilés, R.; Angulo, C. Kinematical synthesis of 1-dof mechanisms using finite elements and genetic algorithms. Finite Elements Anal. Des. 2005, 41, 1441–1463. [Google Scholar] [CrossRef]


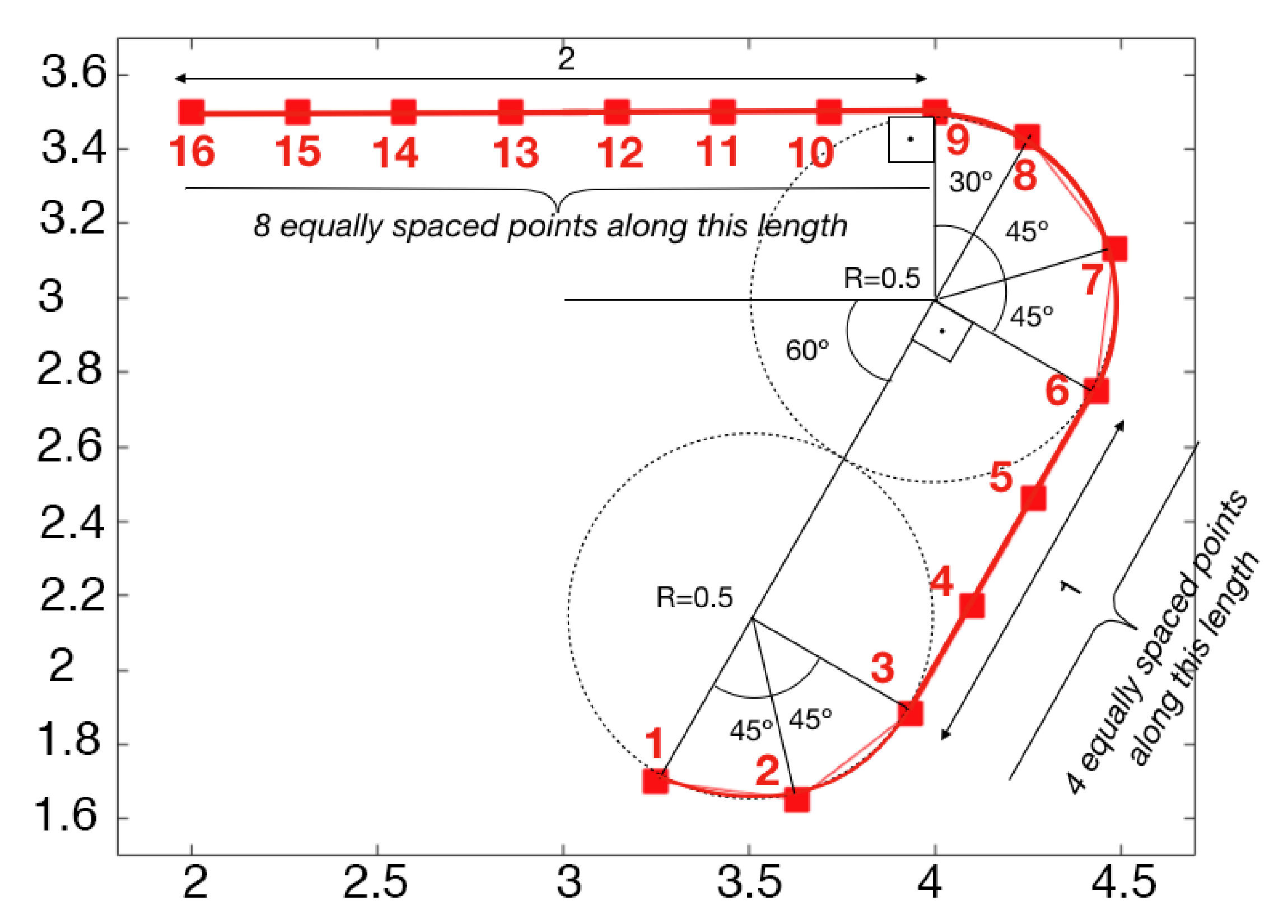

| i | ||
|---|---|---|
| 1 | 3.2500 | 1.7010 |
| 2 | 3.6294 | 1.6510 |
| 3 | 3.9330 | 1.8840 |
| 4 | 4.0995 | 2.1724 |
| 5 | 4.2665 | 2.4616 |
| 6 | 4.4330 | 2.7500 |
| 7 | 4.4829 | 3.1294 |
| 8 | 4.2500 | 3.4330 |
| 9 | 4.0000 | 3.5000 |
| 10 | 3.7143 | 3.5000 |
| 11 | 3.4286 | 3.5000 |
| 12 | 3.1429 | 3.5000 |
| 13 | 2.8571 | 3.5000 |
| 14 | 2.5714 | 3.5000 |
| 15 | 2.2857 | 3.5000 |
| 16 | 2.0000 | 3.5000 |
| Parameters | Inputs | ||||
|---|---|---|---|---|---|
| a1 | 1.292 | φ1 | 4.877 | φ9 | 2.992 |
| a2 | 3.277 | φ2 | 4.568 | φ10 | 2.804 |
| a3 | 1.292 | φ3 | 4.409 | φ11 | 2.634 |
| a4 | 3.875 | φ4 | 4.267 | φ12 | 2.476 |
| a5 | 1.970 | φ5 | 4.104 | φ13 | 2.323 |
| a6 | 3.090 | φ6 | 3.905 | φ14 | 2.171 |
| a7 | 1.356 | φ7 | 3.579 | φ15 | 2.014 |
| a8 | −0.583 | φ8 | 3.192 | φ16 | 1.846 |
| Parameters | Inputs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| a1 | 2.309 | φ1 | 4.703 | φ9 | −0.237 | φ17 | 2.715 | φ25 | 4.451 |
| a2 | 48.819 | φ2 | 4.92 | φ10 | 0.049 | φ18 | 2.933 | ||
| a3 | −3.304 | φ3 | 5.041 | φ11 | 0.672 | φ19 | 3.17 | ||
| a4 | 24.498 | φ4 | 5.181 | φ12 | 1.331 | φ20 | 3.483 | ||
| a5 | 46.315 | φ5 | 5.362 | φ13 | 1.698 | φ21 | 3.762 | ||
| a6 | 4.726 | φ6 | 5.528 | φ14 | 1.996 | φ22 | 3.752 | ||
| a7 | −18.02 | φ7 | 5.745 | φ15 | 2.281 | φ23 | 4.091 | ||
| a8 | 15.293 | φ8 | 5.875 | φ16 | 2.494 | φ24 | 4.265 | ||
| Parameters | Inputs | ||||
|---|---|---|---|---|---|
| a1 | 6.719 | φ1 | 5.580 | φ9 | 3.502 |
| a2 | 15.635 | φ2 | 5.349 | φ10 | 3.101 |
| a3 | 5.217 | φ3 | 5.116 | φ11 | 2.708 |
| a4 | 8.737 | φ4 | 4.918 | φ12 | 2.549 |
| a5 | −6.710 | φ5 | 4.703 | ||
| a6 | −2.924 | φ6 | 4.508 | ||
| a7 | 42.513 | φ7 | 4.124 | ||
| a8 | 35.584 | φ8 | 3.848 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández, A.; Muñoyerro, A.; Urízar, M.; Amezua, E. Hybrid Optimization Based Mathematical Procedure for Dimensional Synthesis of Slider-Crank Linkage. Mathematics 2021, 9, 1581. https://doi.org/10.3390/math9131581
Hernández A, Muñoyerro A, Urízar M, Amezua E. Hybrid Optimization Based Mathematical Procedure for Dimensional Synthesis of Slider-Crank Linkage. Mathematics. 2021; 9(13):1581. https://doi.org/10.3390/math9131581
Chicago/Turabian StyleHernández, Alfonso, Aitor Muñoyerro, Mónica Urízar, and Enrique Amezua. 2021. "Hybrid Optimization Based Mathematical Procedure for Dimensional Synthesis of Slider-Crank Linkage" Mathematics 9, no. 13: 1581. https://doi.org/10.3390/math9131581
APA StyleHernández, A., Muñoyerro, A., Urízar, M., & Amezua, E. (2021). Hybrid Optimization Based Mathematical Procedure for Dimensional Synthesis of Slider-Crank Linkage. Mathematics, 9(13), 1581. https://doi.org/10.3390/math9131581






