An Analytical Solution for Non-Linear Viscoelastic Impact

Abstract

The paper presents an analytical solution for the centric viscoelastic impact of two smooth balls. The contact period has two phases, compression and restitution, delimited by the moment corresponding to maximum deformation. The motion of the system is described by a nonlinear Hunt–Crossley equation that, when compared to the linear model, presents the advantage of a hysteresis loop closing in origin. There is only a single available equation obtained from the theorem of momentum. In order to solve the problem, in the literature, there are accepted different supplementary hypotheses based on energy considerations. In the present paper, the differential equation is written under a convenient form; it is shown that it can be integrated and a first integral is found—this being the main asset of the work. Then, all impact parameters can be calculated. The effect of coefficient of restitution upon all collision characteristics is emphasized, presenting importance for the compliant materials, in the domain of small coefficients of restitution. The results (variations of approach, velocity, force vs. time and hysteresis loop) are compared to two models due to Lankarani and Flores. For quasi-elastic collisions, the results are practically the same for the three models. For smaller values of the coefficient of restitution, the results of the present paper are in good agreement only to the Flores model. The simplified algorithm for the calculus of viscoelastic impact parameters is also presented. This algorithm avoids the large calculus volume required by solving the transcendental equations and definite integrals present in the mathematical model. The method proposed, based on the viscoelastic model given by Hunt and Crossley, can be extended to the elasto–visco–plastic nonlinear impact model.

1. Introduction

The behavior of a mechanical system is described by using ordinary differential equations or differential equations which contain partial derivatives. However, there are few cases for which these equations are linear. Most of the cases involve nonlinear equations, and only the strict local study of the comportment of the system allows the linearization of the equations.

Concerning the domain of dynamics of mechanical systems, the main causes conducting to the occurrence of nonlinearities are as follows:

-

The impact phenomena, characterized by the sudden variation of the kinematical parameters of the system [1];

-

The frictional phenomena: dry friction and rolling friction.

The requirement of precise modeling of the phenomenon of impact for dynamic systems imposed the use of modern mathematical techniques [2,3].

The kinematics discontinuities assume considering the time parameter in order to describe the evolution of the geometrical and kinematical parameters. The sudden variation in time of the geometrical and kinematical parameters of a mechanical system leads to the incidence of forces of considerable intensities. The phenomena characteristic to the sudden variation of geometrical and kinematical parameters have been acknowledged in technical literature as percussions.

Two bodies may act together via two manners: by the interaction of a field and by direct contact. The latter interaction method is especially accustomed in current activities and the good reason for this affirmation is immediate since we can encounter from closing doors and windows to landing of airplanes. However, bringing into contact two bodies intended to interact assumes the existence of relative motion between them. After the two bodies come into contact, the state of relative motion changes. The transition from a kinematical state to another is accomplished during a finite period of time, longer or shorter, and thus leads to the development of interaction forces having greater intensities with the shorter duration of the interaction.

So is explainable the destructive power of the firearms, power which results not from the value of the mass of the projectile, that can be of order of grams, but from the short period of time during which the motion state of the projectile is modified. Consequently, a well-defined category of mechanical phenomena, named percussion, collision or impact, having as common characteristic the development during a very short period of time is accepted. The study of the impact phenomena is particularly contemporary and the numerous treatises, monographs, journals dedicated to the subject sustain this affirmation.

There are two manners to approach the collision mechanics problem [4]. The first manner is by stereo dynamics [5,6,7,8,9,10,11,12,13]. According to this method, the bodies are considered perfectly rigid and the collision is instantaneous. Among the characteristic impact parameters, undoubted the most important is the coefficient of restitution, $c_r$. This is defined as the ratio, with changed sign, between the projections on the normal direction, $n$, of the relative velocities post-impact, $v^{″}$, and pre-impact, $v^{\prime }$ [14,15,16,17].

The requirement of obtaining an almost faithful model imposed the consideration of friction in the contact regions. Keller [18] proposes a model for the study of dry friction collisions but his model is difficult to apply. For the planar collisions with dry friction, the paper of Wang and Mason [10] represents a reference; for the study of dry friction impact the Wang and Mason use the Routh [19] percussion’ plane. Using the Routh’s percussions plane one can explain the paradox reported by Kane [20]. Kane considers a double pendulum subjected to impact with a rough horizontal plane.

To break the deadlock, the hypothesis of rigid colliding bodies hypothesis must be abandoned. Thus, the initial moment $t_i$ of the collision is the instant when the first points belonging to the two bodies come into contact. The moment when the distance between the initial points of contact reaches the maximum value is denoted $t_c$. At this moment $t_c$, the relative velocity between the bodies is zero. After the moment $t_c$, the elastic properties of the two bodies manifest and the effect is a removal till the bodies separate completely. The collision is considered finished at the moment $t_f$, when the last points from the surfaces of the two bodies detach from contact.

The time between the instants $t_i$ and $t_c$ is named compression. The time duration between the moments $t_c$ and $t_f$ is called restitution.

To explain the Kane’s paradox, the kinematical (Newton) definition of the coefficient of restitution must be disregarded and replaced by a new definition, (Poisson) that employs the dynamic concept of percussion, defined as the integral from the interaction force over the period of action of the force [21,22]. The new definition of the coefficient of restitution states that it equals the ratio between the normal percussions corresponding to the restitution and compression phases, respectively [23,24,25].

Wang et al. [26] made a classification of percussions, and concluded that tangential or frictional percussions might exist, which are not caused by normal percussions, as it happens in the case of forces.

One of the main limitations of the model with rigid elements consists in the impossibility of force estimation during the collision process.

A second method of approach considers that during the time of impact the impact forces and the kinematic and dynamic parameters present a continuous and finite variation. It is accepted as an additional hypothesis that, as long as the collision takes place, the configuration of the system remains unaltered.

The evolution of the impact models was a natural one, beginning with the simplest models, consisting of two bodies of simple shape (sphere, cylinder, rod and plate) and between which simple motions exist (mono-axial translation and planar motion), or from small [27] to large deformations [28].

Timoshenko [29] starts from the relation force–deformation for a punctual Hertz contact, Ref. [30] particularized for the contact of two metallic spheres and obtains the expressions for the maximum normal approach, impact time and maximum force. It was experimentally revealed that the Timoshenko model, which accepts the same kinetic energy of the system, even after impact, corresponds to a reduced number of actual cases [31,32].

In chronological order, the second impact model is the impact with internal friction. The damped impact described by using a Kelvin–Voigt model [33,34,35] presents the advantage of hysteresis loop presence, but the weak points are the open hysteresis loop and the fact predicts attraction between the two bodies at the end of the collision, a statement that is different from physical reality.

Dubowski and Freudenstein [36,37] and, later, Hunt and Crossley [38], proved that, in order to obtain a model with the loop closed in origin, the differential equation of the model must be changed, namely the expressions of the coefficients from the Kelvin–Voigt model should be variable and proportional to a power of deformation.

To be remarked that in order to characterize the frictional losses the coefficient of restitution is used.

Next, from the evolution of the damped centric collision models it should be mentioned a reference work due to Lankarani and Nikravesh [39]. Here the authors consider that the entire variation of kinetic energy of the system is retrieved as damping work—the area of the hysteresis loop. Additionally, the hypothesis that the damping work is the same for the two phases of collision is also introduced. Under these conditions, Lankarani and Nikravesh [39] obtained a nonlinear differential equation that after integration leads to the expression of the approach between the balls. The authors mention that the model is applicable only for quasi-elastic collisions $(c_r>0.9)$. Applications of multi-body models are suitable for different domains of engineering, from classical parts of machine elements [40,41], to granular [34,35] and powder materials [42,43] or biomechanics and robotics [44,45,46].

The Lankarani–Nikravesh equation was used nearly for twenty years as the basis for solving numerous multibody problems. Recently, Flores [47] resumed the model proposed by Lankarani and Nikravesh with the adjustment introduced by the hypothesis that in the phase plane, during the two phases of the impact, the characteristic point moves on a quarter of ellipse arch, hypothesis that allows for finding the coefficient of the term characteristic to damping. The Flores equation is similar to the Lankarani–Nikravesh equation with the difference that the numeric coefficient of the damping term is dissimilar. The Flores model eliminates the drawback of the previous model and ensures quasi-equality between the initial coefficient of restitution and the one generated by the proposed model.

A major application in engineering concerns mechanical systems with joint clearances, consequently these were studied by numerous researchers [48,49,50,51]. The most recent research studies concerning the viscoelastic impact phenomenon employ recent results from the theory of differential equations [52,53] validated by experimental results. There are also new theoretical models that simulate the behavior of materials via numerical methods [54], or, some that use for validation experimental data from the classical literature [42,43].

To summarize the above review, in order to apply the Hunt and Crossley equation for the impact model, three coefficients must be known (reduced mass, damping coefficient and contact stiffness), but the viscous damping coefficient it is not known. The actual method is compared to the models proposed by Lankarani and Flores, respectively, who adopt supplementary hypothesis for finding the damping coefficient, but their results do not validate the experimental results for small values of the coefficient of restitution.

Here there are deduced expressions for the next impact parameters: the maximum impact force, the maximum normal deformation and the deformation corresponding to the maximum force that allow for finding the precise values of these; the previous models, for the calculus of these very important parameters in practical applications, give values dependent on the chosen damping characteristic.

The novelty introduced by the present work consists in finding a first integral of the equation that permits the exact finding of damping characteristic and the method is valid for any value of coefficient of restitution, presenting importance for the compliant materials, in the domain of small coefficients of restitution. The proposed model aims to be an instrument for validation of experimental data from impact tests. Additionally, the method proposed, that is based on the viscoelastic model given by Hunt and Crossley, can be extended to the elasto–visco–plastic nonlinear impact model. A simplified algorithm for the calculus of impact parameters is also proposed, based on the remark that for a certain value of the exponent of deformation from the expression of impact force, all normalized contact parameters are invariants with respect to initial impact velocity and stiffness.

2. Materials and Methods

Two manners of approach were highlighted in the study of impact phenomenon. First of these considers an instantaneous impact process between rigid bodies while the second assumes deformable bodies and a finite period of time for impact occurrence.

The first methodology uses simple mathematical tools but unlike the second method, presents the major drawback that the interaction forces during impact cannot be estimated. For the second approaching manner, even for the simplest situations, the mathematical apparatus is much more difficult.

For the simplest impact model, as in Figure 1, the collision initiates when the first points from the two balls come into contact. The bodies are deformable and the regions from vicinity of the contact points distort; the normal approach between the two bodies is defined as the distance between the initial contact points from the un-deformed bodies.

The normal approach x increases from the instant of contact beginning until it reaches a maximum value and afterwards it decreases; the collision ends when the bodies do not have common points any more. The period while the normal approach increases is called the compression phase, and the time elapsed from the moment of maximum approach till the end of impact is called the restitution phase. A parameter that has critical significance for impact process is the coefficient of restitution. It can be defined in kinematical (Newton) or dynamical (Poisson) manner.

In the case of centric collision, the two definitions are equivalent. For this situation, the coefficient of restitution $(c_r$) is defined according to Newton [8] as the ratio with changed sign between the relative velocities corresponding to the end and beginning of collision:

$$c_r=-\frac{{v^{″}}_2-{v^{″}}_1}{{v^{\prime }}_2-{v^{\prime }}_2}=-\frac{{v^{″}}_{21}}{{v^{\prime }}_{21}}$$

(1)

and according to Poisson [9], as the ratio between the percussions from restitution phase and compression phase:

$$c_r=\frac{{{\displaystyle \int }}_{t_c}^{t_f}F\left(t\right)dt}{{{\displaystyle \int }}_0^{t_c}F\left(t\right)dt}$$

(2)

The velocities corresponding to the initiation instant of collision were denoted by $(\prime )$ and the ones corresponding to the ending moment, by $(“)$. The values of coefficient of restitution are situated between two extreme values: $c_r=1$ is characteristic for the perfect elastic collision, and $c_r=0$ is the value related to perfect plastic collision. For the perfect elastic collision between two smooth spheres, Timoshenko accepts that, during impact phenomenon, the variation of impact force is described by the relation of Hertz [38]:

$$F=K{x}^{3/2}$$

(3)

where the $K$ coefficient, is the generalized stiffness parameter that considers the elastic characteristics, $E,\nu$, of the two bodies and the geometry of contact regions, by $r_{1,2}$:

$${\rm K}=\frac{4}{3}\left(\frac{1}{{\sigma }_1+{\sigma }_2}\right)\sqrt{\frac{r_1{r}_2}{r_1+r_2}}$$

(4)

where:

$${\sigma }_i=\frac{1-{\nu }_i^2}{E_i},i=1,2$$

(5)

The exponent of deformation x is 3/2 for the cases when the impacting spheres are made of elastic materials [55,56].

Assuming the above hypotheses, for an imposed value of initial relative velocity, ${v^{\prime }}_r=v_0$, Timoshenko [29] finds the following: the maximum normal approach between the bodies $x_H$, the value of maximum impact force, $F_H$, and values for compression and restitution times, $t_c$ and $t_r$, proving that the two values are equal and that the restitution and compression phases are symmetrical with respect to the moment of reaching maximum normal approach.

Concerning the kinetical energy variation of the system for the case of sub-unitary value of coefficient of restitution, $c_r$, a quantitative characterization a an extremely difficult task. Goldsmith [1] shows that the kinetical energy variation is regained as heat generated by internal friction in the materials of the bodies, work of plastic deformation and energy of the waves traveling through the two bodies.

Allowing for the entire kinetical energy variation to be retrieved as heat generated by internal friction, Hunt and Crossley [38] show that it is inadequate to describe the impact by using a second-order linear homogenous differential equation (the internal friction force being proportional to the deformation rate and to the elastic force), since it leads to a hysteresis loop open in origin, and additionally foreseeing that, at the end of collision, the bodies attract each other instead of rejecting. They prove that, in order to get a hysteresis loop closing in origin when the elastic force is of Hertzian type, it is necessary to adopt a nonlinear viscoelastic model, which ensures zero values of the damping force for the initial and final moments [38], and for which the coefficient of deformation rate should be proportional to deformation. The equation proposed by Hunt and Crossley has the following form:

$$m\frac{d^{2}x}{d{t}^2}=-c\frac{dx}{dt}{x}^{\alpha }-K{x}^{\alpha }$$

(6)

where $\alpha =3/2$, Refs. [1,30,55,56], $c$ is a constant (hysteresis damping factor) and $m$ is the reduced mass of the system:

$$m=\frac{m_1{m}_2}{m_1+m_2}$$

(7)

The relations corresponding to the elastic impact of two spheres can be particularized for the impact between a sphere and a half-space, considering that the mass and radius of one of the spheres tend to infinity [1,56].

By denoting with

$$\gamma =c/m;\chi =K/m,$$

(8)

the characteristic equation of the impact process is as follows:

$$\frac{d^{2}x}{d{t}^2}+\gamma \frac{dx}{dt}{x}^{\alpha }+\chi x^{\alpha }=0$$

(9)

In order to process the Equation (9), the value of the $\gamma$ coefficient should be found. The theorem of kinetic energy in finite form is not practicable, since it cannot be obtained an analytical expression of the work done by internal friction forces.

$$L_a={{\displaystyle \int }}_0^x{F}_{a}dx=-{{\displaystyle \int }}_0^x\gamma \frac{dx}{dt}{x}^{\alpha }dx.$$

(10)

To overcome this difficulty, Lankarani [39] accepts that the work performed by dissipative forces has the same value both for compression and for restitution phase, and, thus, the coefficient $\gamma$ takes the following expression:

$$\gamma =\frac{3\left(1-c_r^2\right)}{4}\frac{K}{v_0}$$

(11)

The limits of the model are underlined even by Lankarani, who highlights that the model is applicable only for quasi-elastic collisions with $c_r>0.9$. For a Hunt–Crossley model, with the damping coefficient given by Relation (11), Ref. [39], a value for the initial velocity $v_0$ and a value for the coefficient of restitution, $c_{r\_in}$, accepted a priori, the equation is integrated, and then the final value of relative velocity is calculated, and the coefficient of restitution, $c_{r\_out}$, can be found. It is noticed that the two values of the coefficient can be considered quasi-equal only for quasi-elastic collisions, $c_r\ge 0.9$.

Recently, Flores retakes the problem of finding a solution for Equation (9). He starts from the observation that, in the case of damped oscillatory motion described by a linear equation, the characteristic point depicts in the phase space an arch from an ellipse, and accepts that for Equation (9) too, in the phase plane, both for compression and for restitution phase the characteristic point describes different quarters of ellipse. Based on this hypothesis, Flores [47] establishes the following expression for $\gamma$ coefficient:

$$\gamma =\frac{8\left(1-c_r\right)}{5c_r}\frac{K}{v_0}$$

(12)

Using Relation (12), Flores finds an analytical expression for maximum approach ($x_m$) and shows that, in the case of damped motion, the maximum impact force is not attained at the end of compression phase, but earlier. The model proposed by Flores satisfies much better the condition of coincidence between the final relative velocity generated by the model and the one established by using the definition of coefficient of restitution.

One considers again Equation (9) in the attempt of applying a numerical integration method, but two impediments are obstructing: the damping coefficient is not known precisely, and the extent of collision time is also unknown. Using Expression (12) given by Flores for damping coefficient, it was noticed that the Runge–Kutta method applied for Equation (9) is inappropriate when, for the impact period, it is specified a greater value than the actual one. Trying to integrate numerically, using the Runge–Kutta IV algorithm, the precise value of the impact time ($t_f$) must be specified, but it is not known in the Flores model. Smaller values for $t_f$ conduct to incomplete solution and greater values for $t_f$ conduct to blocking of the program. To surmount this impediment, the method was applied by starting with small values assumed for the collision period, and following that, the assumed impact time was increased successively till the moment when the method become inappropriate. It was observed that, for small values of coefficient of restitution, $c_r<0.3$, the final value obtained via integration of the equation is greater than the one obtained by using the definition of coefficient of restitution. In Figure 2, we present the plot of impact velocity variation with dimensionless time for the collision between a ball, $r=0.015$, colliding at a velocity $2.8 \mathrm{m}/\mathrm{s}$ an immobile plane, for the coefficient of restitution $c_r=0.2$.

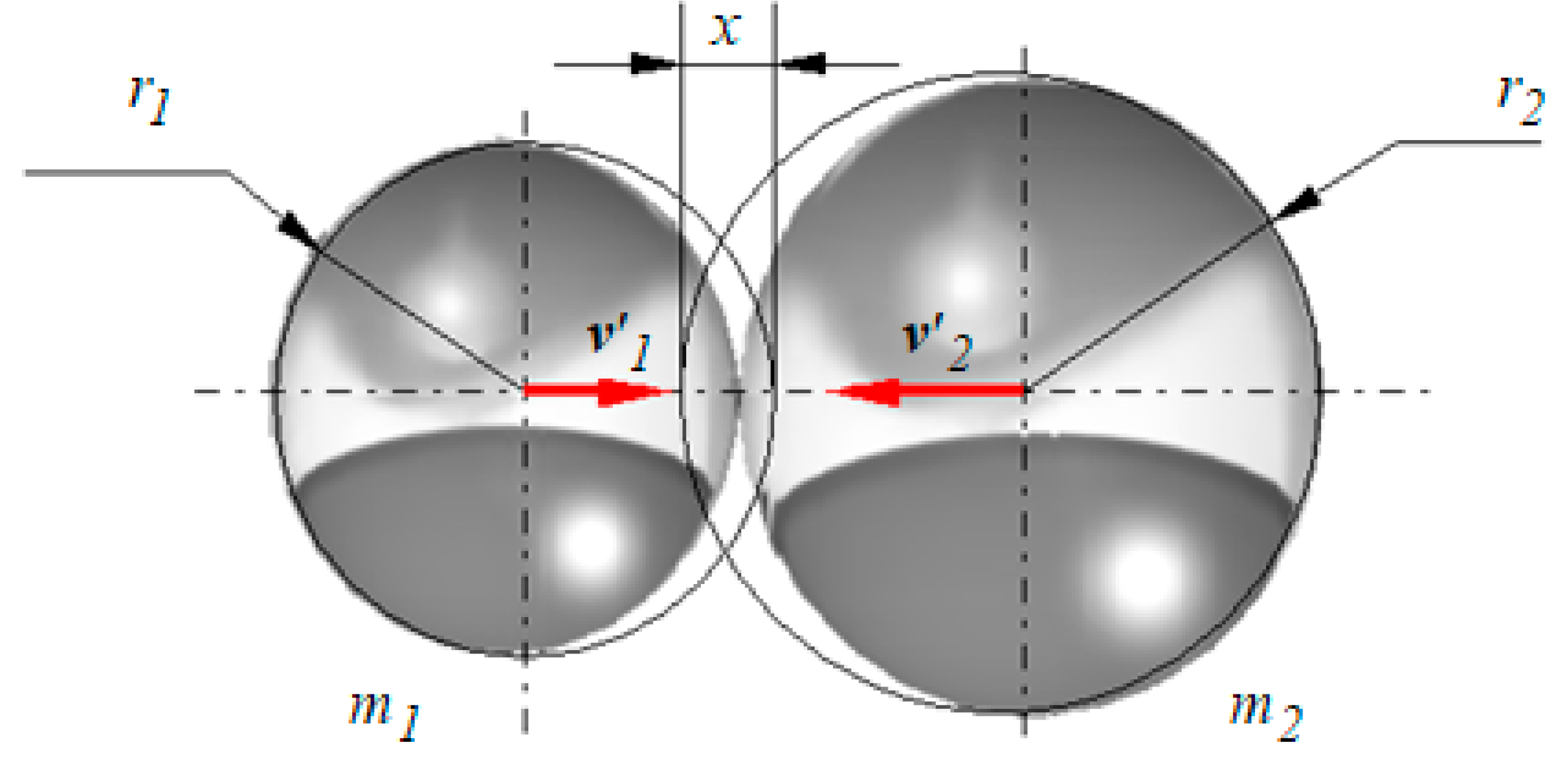
3. Determination of the Viscoelastic Impact Parameters

3.1. Parameters for the Un-Damped Impact

The present paper proposes a method for finding an exact solution of Lankarani–Nikravesh Equation (9). One can notice that, when there is no damping, Equation (9) describes the perfect elastic collision. For exemplification, we consider the next data: the masses of the balls $m_1={10}^9\mathrm{kg}$, $m_2=0.11\mathrm{kg}$; the balls are made of the same material, steel, with $\rho =7800{\mathrm{kg}/\mathrm{m}}^3$, $E=2.1\cdot {10}^{11}\mathrm{Pa}$, $\nu =0.3$; the exponent $\alpha =3/2$ is valid for any pair of elastic materials [1]; the radii of the balls are $r_1=31.28\mathrm{m}$, $r_2=0.015\mathrm{m}$, $r_2/r_1=4.71\cdot {10}^{-4}$ and $r_1>>r_2$; the sphere 1 can be approximated in the vicinity of the contact region to an elastic half-space; the initial velocity $v_0=2.8\mathrm{m}/\mathrm{s}$; and the coefficient of restitution $c_r=0.4$. For this situation, the maximum approach found by Timoshenko by applying the energy theorem for compression period is as follows:

$$x_H={\left(\frac{\alpha +1}{2}\frac{v_0^2}{\chi }\right)}^{\frac{1}{\alpha +1}}=8.00032\cdot {10}^{-5} \mathrm{m}$$

(13)

and it permits us to obtain the maximum impact force, $F_H$:

$$F_H={\rm K}{x}_H^{\alpha }=1.347\cdot {10}^4 \mathrm{N}$$

(14)

Therefore, the work for the compression phase $L_H$ is as follows:

$$L_H={{\displaystyle \int }}_0^{x_H}K{x}^{\alpha }dx=\frac{1}{\alpha +1}K{x}_H^{\alpha +1}=\frac{F_H{x}_H}{\alpha +1}=0.4312 \mathrm{J}$$

(15)

At a certain time (t) when the approach between the bodies is x, the velocity has the following expression:

$$v\left(x\right)=\sqrt{v_0^2-\frac{2\chi }{\alpha +1}{x}^{\alpha +1}}$$

(16)

The duration of the compression and restitution phases is the same, denoted as $t_H$, and the velocity given by Relation (16) is used in finding it:

$$\begin{array}{l}{t}_H={{\displaystyle \int }}_0^{x_H}\frac{dx}{v\left(x\right)}={{\displaystyle \int }}_0^{x_H}\frac{dx}{\sqrt{v_0^2-\frac{2\chi }{\alpha +1}}{x}^{\alpha +1}}\\ =\frac{1}{\alpha +1}\frac{\Gamma \left(\frac{1}{2}\right)\Gamma \left(\frac{1}{\alpha +1}\right)}{\Gamma \left(\frac{1}{2}+\frac{1}{\alpha +1}\right)}\frac{x_H}{v_0}=1.471577\frac{x_H}{v_0}=4.20467\cdot {10}^{-5} \sec \end{array}$$

(17)

In the above expression, $\Gamma \left(x\right)$ is the Eulerian integral of second kind. The values of the parameters $x_H$, $F_H$, $L_H$ and $t_H$ are especially useful because, first, they allow for an estimation of the magnitude of the characteristic parameters of damped impact, and second, they allow for expressing the results by normalized expressions. Moreover, even if in the expression of $t_H$, the denominator is zero for the value of the upper limit of the integral, the integral is convergent, and it is expressed by using the improper integral, $\Gamma \left(x\right)$.

3.2. Finding a First Integral of Nonlinear ODE

The method is based on the remark that we can find a first integral of Equation (9). By multiplying Equation (9) by $\dot{x}$, it can be expressed under the following form:

$$m\frac{d^{2}x}{d{t}^2}\frac{dx}{dt}=-\left(c\frac{dx}{dt}{x}^{\alpha }+K{x}^{\alpha }\right)$$

(18)

and then it is rewritten as follows:

$$\frac{\frac{dx}{dt}}{\gamma \frac{dx}{dt}+\chi }\frac{d^{2}x}{d{t}^2}=-x^{\alpha }\frac{dx}{dt}$$

(19)

By taking into account that

$$v=\frac{dx}{dt}$$

(20)

the following equation with separable variables is obtained:

$$\frac{\nu }{\gamma \nu +\chi }d\nu =-x^{\alpha }dx$$

(21)

A first integral of this equation is as follows:

$$\frac{1}{\gamma }v-\frac{\chi }{{\gamma }^2}\ln (\gamma v+\chi )+\frac{x^{\alpha +1}}{\alpha +1}+C=0$$

(22)

The initial conditions are imposed in order to find the constant of integration:

$$\nu ={\nu }_0, x=0, \mathrm{for} t=0$$

(23)

Moreover, a particular solution of Equation (9) is obtained as follows:

$$\frac{1}{\gamma }\left(v-v_0\right)-\frac{\chi }{{\gamma }^2}\ln \left(\frac{\gamma v+\chi }{\gamma v_0+\chi }\right)+\frac{x^{\alpha +1}}{\alpha +1}=0$$

(24)

Based on this first integral, all the characteristic parameters of the viscoelastic impact can be obtained, and from here, the importance of this expression arises.

To be remarked that the first integral of Timoshenko’s model cannot be obtained directly from Relation (16) by letting $\gamma =0$ as a particular case.

Equation (17) represents the trajectory of the characteristic point from phase plane. Different from Reference [57], where the velocity was expressed as a function of normal approach, requiring numerical solution of the equation with respect to $v$, the present work emphasizes the fact that the equation may be analytically solved with respect to $x$, and therefore substantially reducing the computing time.

$$x\left(\nu \right)={\left[\left(\alpha +1\right)\frac{\left({\nu }_0-\nu \right)+\frac{\chi }{\gamma }ln\left(\frac{\gamma {\nu }_0+\chi }{\gamma \nu +\chi }\right)}{\gamma }\right]}^{\frac{1}{\alpha +1}}$$

(25)

By introducing Expression (25) into Equation (9), we obtain the dependency between relative acceleration (a) and velocity ($v$).

$$a\left(v\right)=-\gamma v\left[x\left(v\right){]}^{\alpha }-\chi \right[x\left(v\right){]}^{\alpha }$$

(26)

Or in explicit manner:

$$a\left(v\right)={\left\{\frac{\alpha +1}{{\gamma }_0}\left[\frac{\chi }{{\gamma }_0}\ln \frac{{\gamma }_{0}v+\chi }{{\gamma }_0{v}_0+\chi }-\left(v-v_0\right)\right]\right\}}^{\frac{\alpha }{\alpha +1}}\left({\gamma }_{0}v+\chi \right)$$

(27)

3.3. Finding the Maximum Approach $x_m$

At the instant the normal approach has reached the maximum value, it results that the derivative $dx/dt=v$ should be zero. By denoting with $x_m$ the value of maximum approach, it can be found from Equation (17) and has the expression:

$$x_m={\left\{\left(\alpha +1\right)\left[\frac{1}{\gamma }{\nu }_0-\frac{\chi }{{\gamma }^2}ln\left(1+\frac{\gamma }{\chi }{\nu }_0\right)\right]\right\}}^{\frac{1}{\alpha +1}}$$

(28)

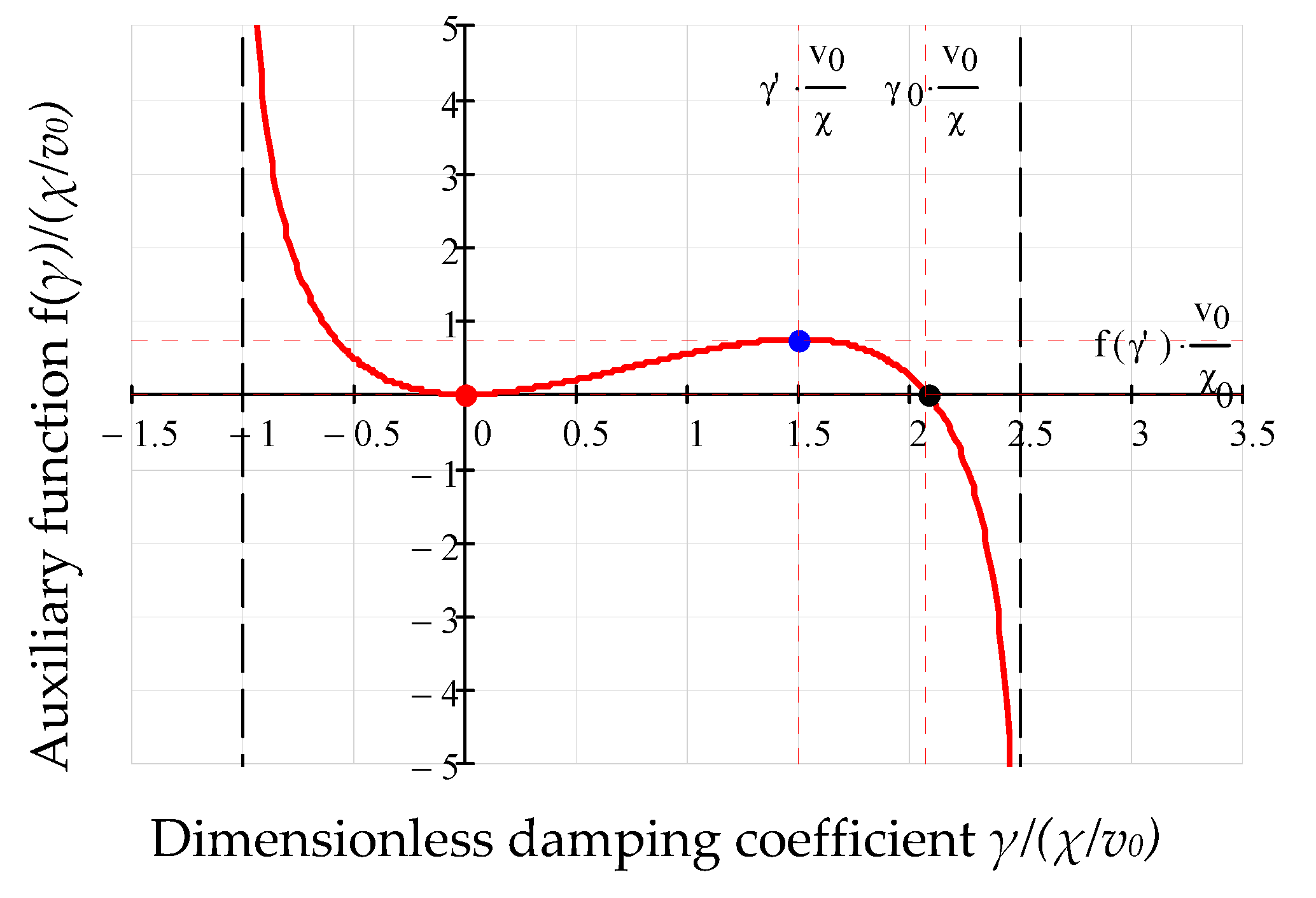
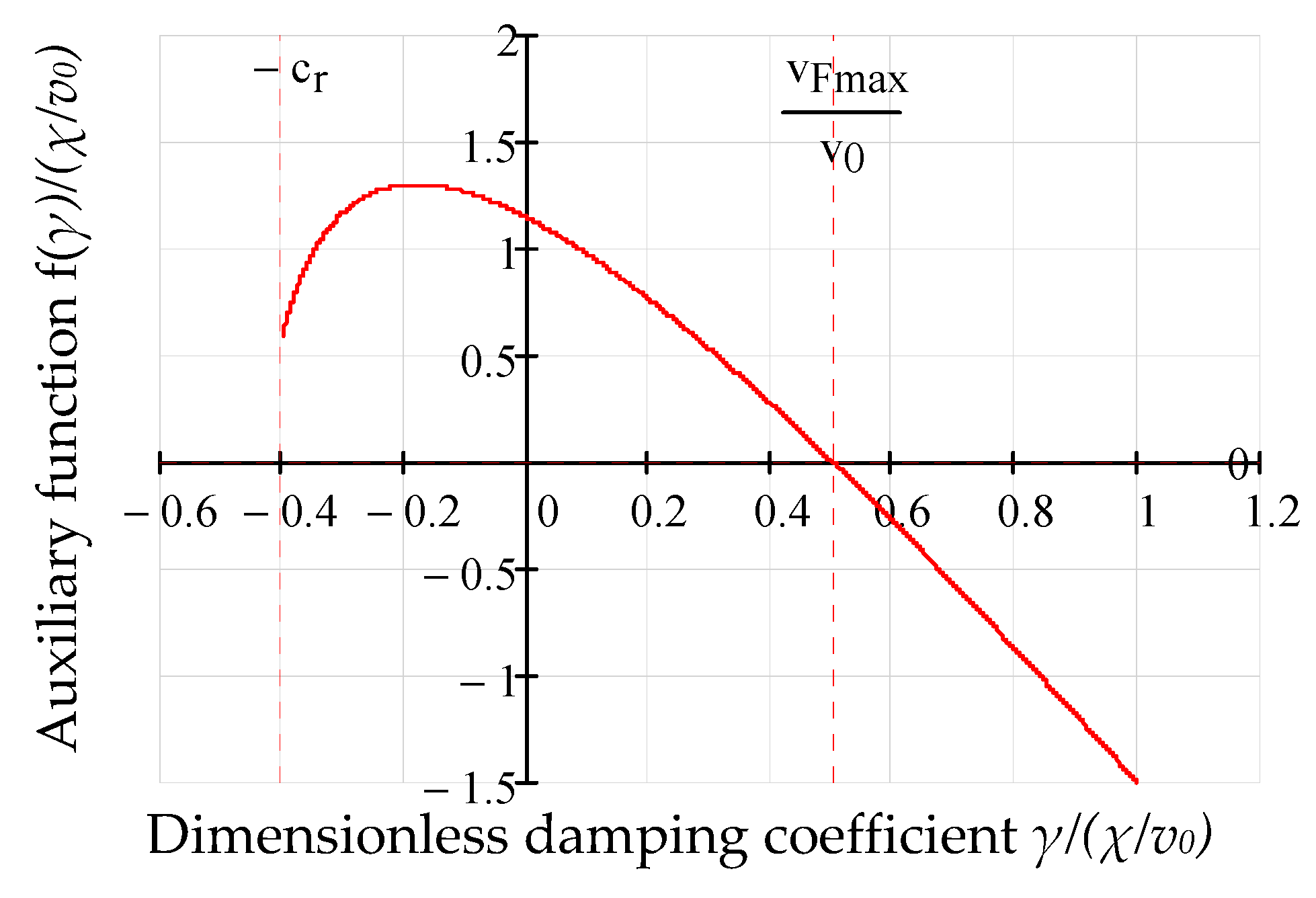
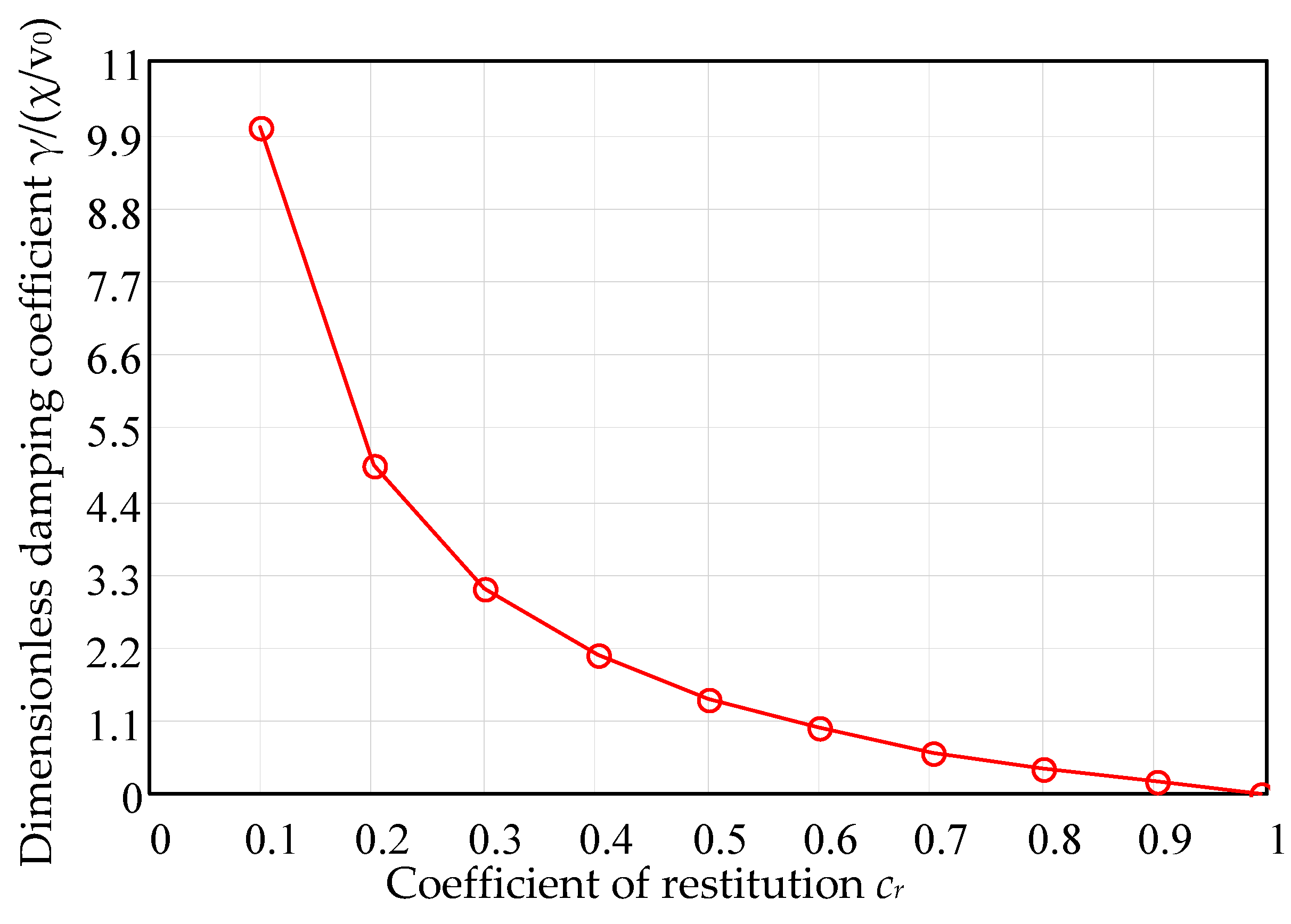
3.4. Obtaining the Coefficient of the Damping Force $\gamma$

Allowing for:

$$v=-c_r{v}_0,x=0,\mathrm{for}t=t_f$$

(29)

It results:

$$\gamma v_0\left(1+c_r\right)+\chi \ln \left(\frac{-\gamma c_r{v}_0+\chi }{\gamma v_0+\chi }\right)=0$$

(30)

Equation (30) allows us to find the exact value of the damping coefficient. The equation is a transcendental one, and solving it requires a numerical procedure.

Denoting by $f\left(\gamma \right)$, the function from the left side of Equation (30), one can easily notice that function is defined on the closed interval $\left[-\chi /v_0,\chi /\left(c_r{v}_0\right)\right]$. The derivative of the function from the left side of the equation has a root:

$${\gamma }^{\prime }=\frac{1-c_r}{c_r} \frac{\chi }{{\nu }_0}$$

(31)

Moreover, in this point, the derivative of the function presents an extremum, specifically as follows:

$$f\left({\gamma }^{\prime }\right)=\frac{1-c_r^2+2c_{r}ln{c}_r}{c_r}\chi$$

(32)

It is seen that $f\left(0\right)=0$. At once, it is shown that, for $0<c_r<1$, $f\left({\gamma }^{\prime }\right)>0$. At the ends of the domain, the function has vertical asymptotes, since we have the following:

$$\underset{\gamma \to -\frac{\chi }{v_0}+\epsilon }{lim}f\left(\gamma \right)=\infty ;\underset{\gamma \to -\frac{\chi }{c_r{v}_0}-\epsilon }{lim}f\left(\gamma \right)=-\infty$$

(33)

From the abovementioned, we draw the conclusion that Equation (30) has one root to be found in the interval $\left(\frac{1-c_r}{c_r}\frac{\chi }{v_0},\frac{\chi }{c_r{v}_0}\right)$. Figure 3 presents the graph of the function $f\left(\gamma \right)$ obtained for the data considered above, and the normalization was made by using the value $\chi /v_0=6.11364\frac{\mathrm{N}\cdot \mathrm{s}}{{\mathrm{m}}^{\mathsf{\alpha }+1}\cdot \mathrm{kg}}$.

In Figure 3, the solution of Equation (19), ${\gamma }_0$ was found by using the bi-partition methodology.

3.5. Finding the Maximum Impact force

The presence of damping leads to a delay between the times when the maximum impact force and maximum approach are reached. In order to obtain the approach corresponding to the maximum force, Relation (5) is used, namely considering the proportionality between the impact force and acceleration. The right member of Equation (27) is differentiated with respect to velocity and from the imposed condition that the expression is zero, the velocity corresponding to maximum force result as solution of the transcendental equation:

$$h\left(v\right)=\left[\frac{\chi }{{\gamma }_0}\ln \frac{{\gamma }_{0}v+\chi }{{\gamma }_0{v}_0}-\left(v-v_0\right)\right]\left(\alpha +1\right)-\alpha v=0$$

(34)

The solution is denoted as $v_{Fmx}$, and, according the physical meanings, it must be contained by the interval $\left[-c_r{v}_0,v_0\right]$. At the end points of the interval, the values of the function $h\left(v\right)$ are as follows:

$$h\left(v_0\right)=-\alpha v_0<0$$

(35)

and

$$h\left(-c_r{v}_0\right)=\left[\frac{\chi }{{\gamma }_0}\ln \frac{-{\gamma }_0{c}_r{v}_0+\chi }{{\gamma }_0{v}_0+\chi }+\left(c_r+1\right)v_0\right]\left(\alpha +1\right)+\alpha c_r{v}_0$$

(36)

Based Relation (24), the logarithm from Relation (36) can be solved, and it results in the following:

$$h\left(-c_r{v}_0\right)=\left[\frac{\chi }{{\gamma }_0}{\gamma }_0{v}_0\left(1+c_r\right)+\left(c_r+1\right)v_0\right]\left(\alpha +1\right)+\alpha c_r{v}_0=\alpha c_r{v}_0>0$$

(37)

The function $h\left(v\right)$ is continuous on the closed interval $\left[-c_r{v}_0,v_0\right]$, and the values with opposite sign for the limits of the interval ensure the existence of at least one root of Equation (34). The derivative of the function $h\left(v\right)$ is as follows:

$$h^{\prime }\left(v\right)=-\frac{\left(2\alpha +1\right){\gamma }_{0}v+\alpha \chi }{{\gamma }_{0}v+\chi }$$

(38)

It has the following roots:

$$v_1=-\frac{\chi }{{\gamma }_0}$$

(39)

and

$$v_2=-\frac{\alpha }{2\alpha +1}\frac{\chi }{{\gamma }_0}$$

(40)

It was shown that ${\gamma }_0<\chi /\left(c_r{v}_0\right)$, and then it results in the following:

$$v_1<-c_r{v}_0$$

(41)

To conclude, in the interval $\left[-c_r{v}_0,v_0\right]$, the derivative $h^{\prime }\left(v\right)$ has maximum one root $v_2$. If the root $v_2$ is outside the interval, $h\left(v\right)$ is monotonous with opposite sign at the ends of the interval (and, then, with a single root inside the interval). If the root $v_2$ is inside the interval, the function $h\left(v\right)$ has an extremum inside the interval, and the root $v_{Fmx}$ is between $v_2$ and the endpoint for which the sign of the function is opposite to the sign of extremum of function. Figure 4 presents the plot of the function $h\left(v\right)$ on the interval $\left[-c_r{v}_0,v_0\right]$ and the found root.

The approach $x_{Fmx}$ corresponding to this velocity is calculated with the following relation:

$$x_{Fmx}=x\left(v_{Fmx}\right)$$

(42)

The maximum force is obtained with the next relation:

$$F_{mx}=m\cdot a\left(v_{Fmx}\right).$$

(43)

3.6. Phase Plane and Hysteresis Loop

With the relations of normal approach and acceleration expressed as functions of velocity, the phase space (Figure 5) and hysteresis loop (Figure 6) were plotted.

In Figure 5, there were also traces of the quarters of ellipses passing through the point that separates the phases and through the points corresponding to impact starting and impact ending. In Figure 6, alongside the hysteresis loop, we traced the loading–unloading curve for un-damped impact.

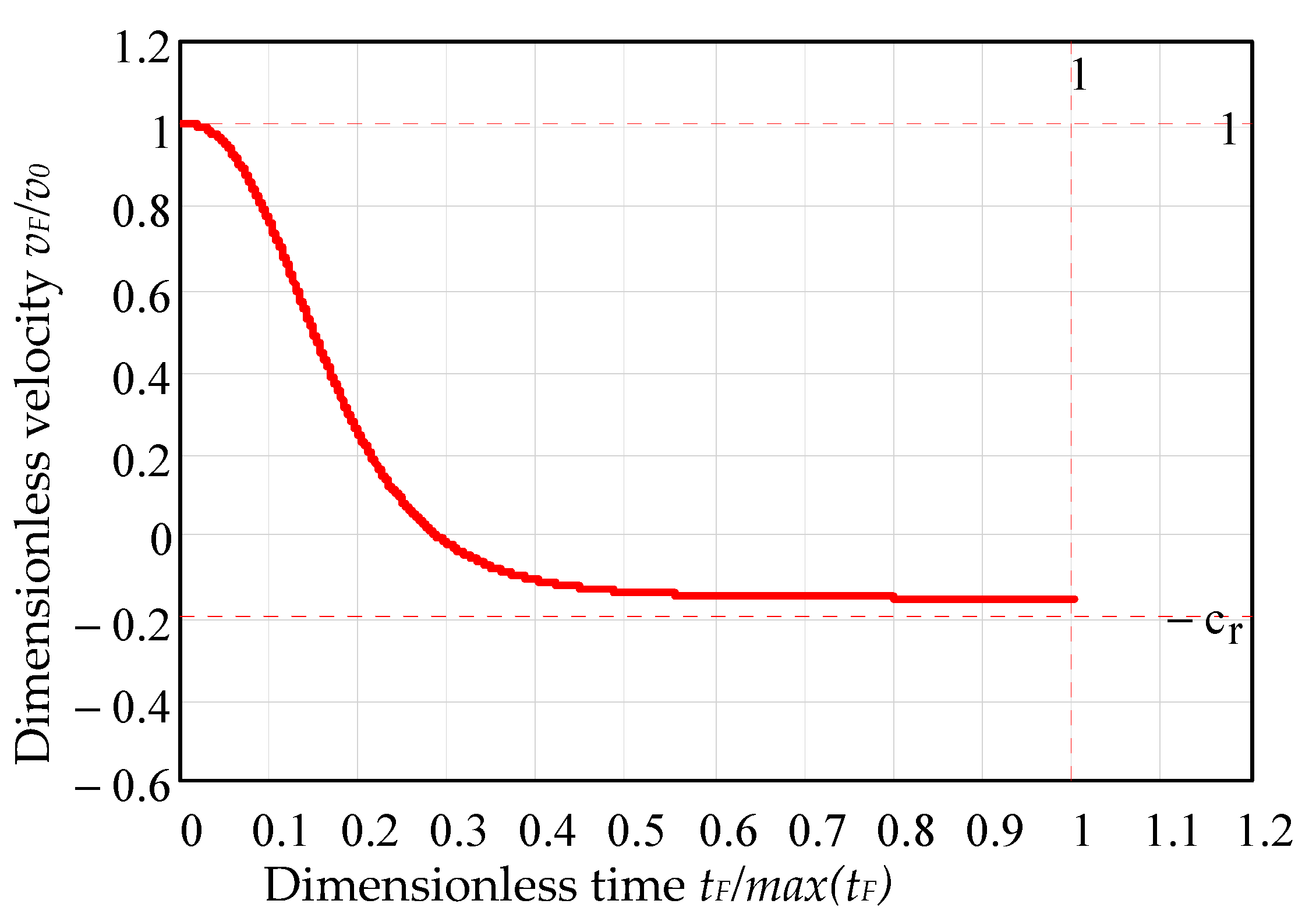
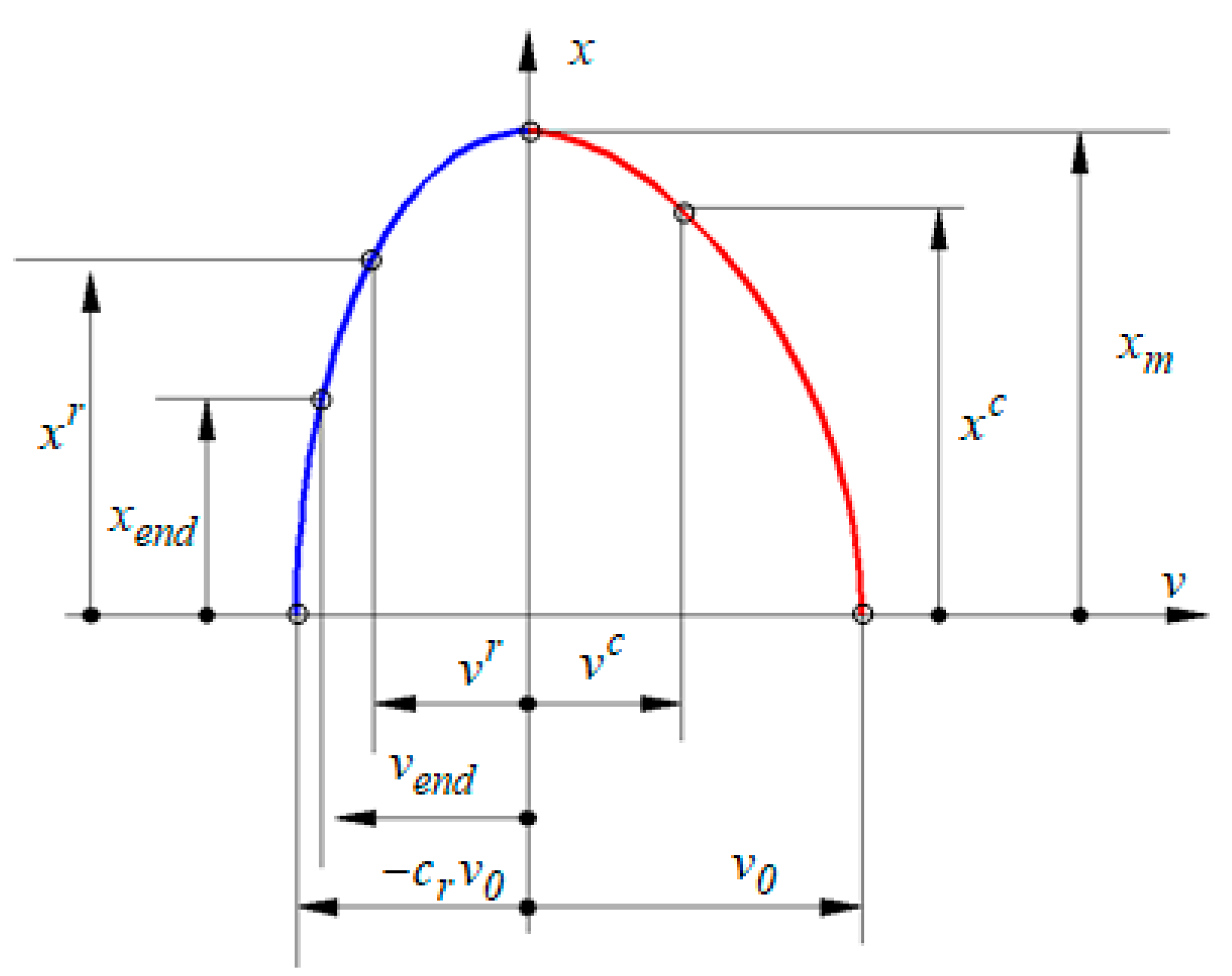
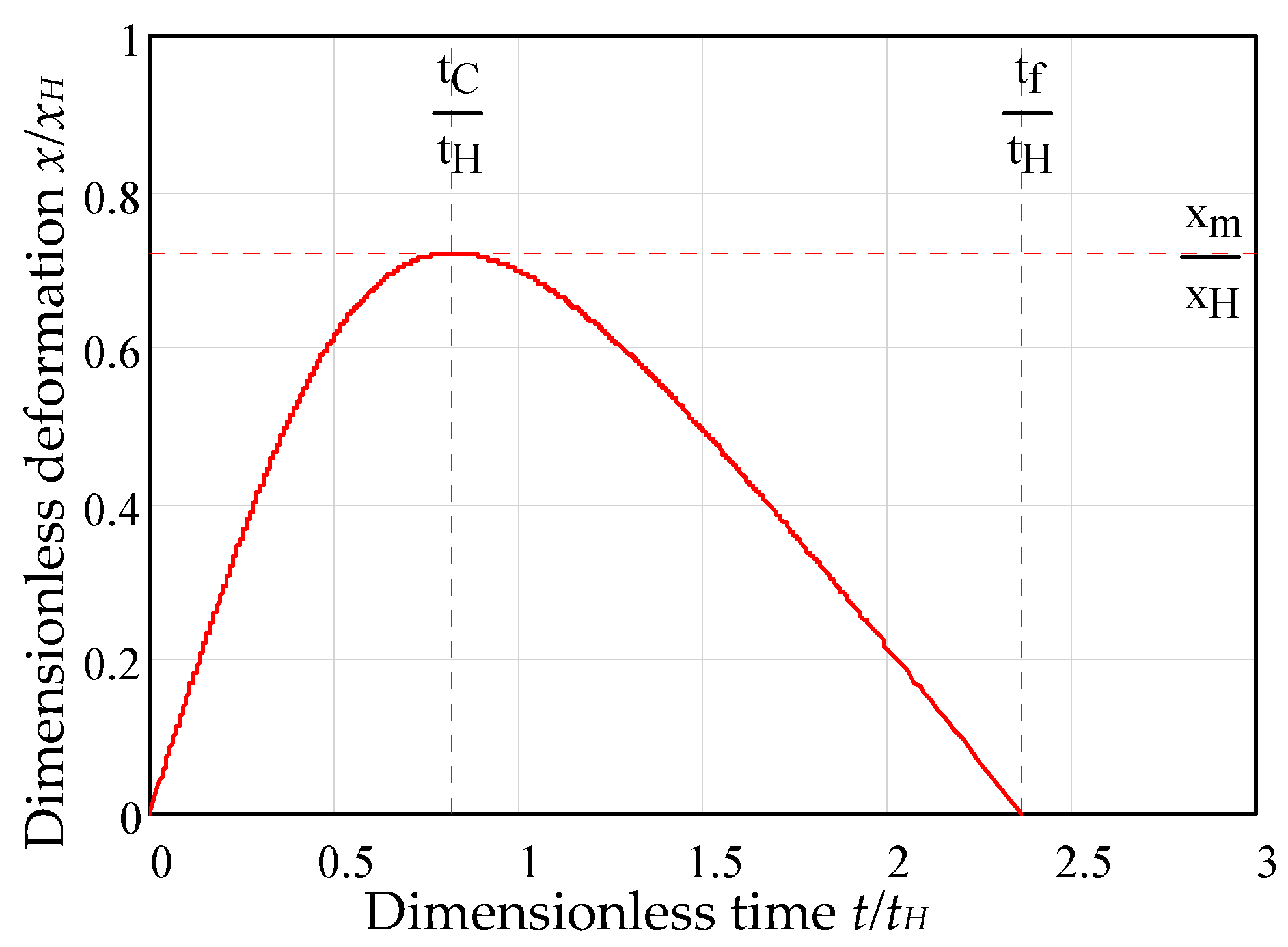
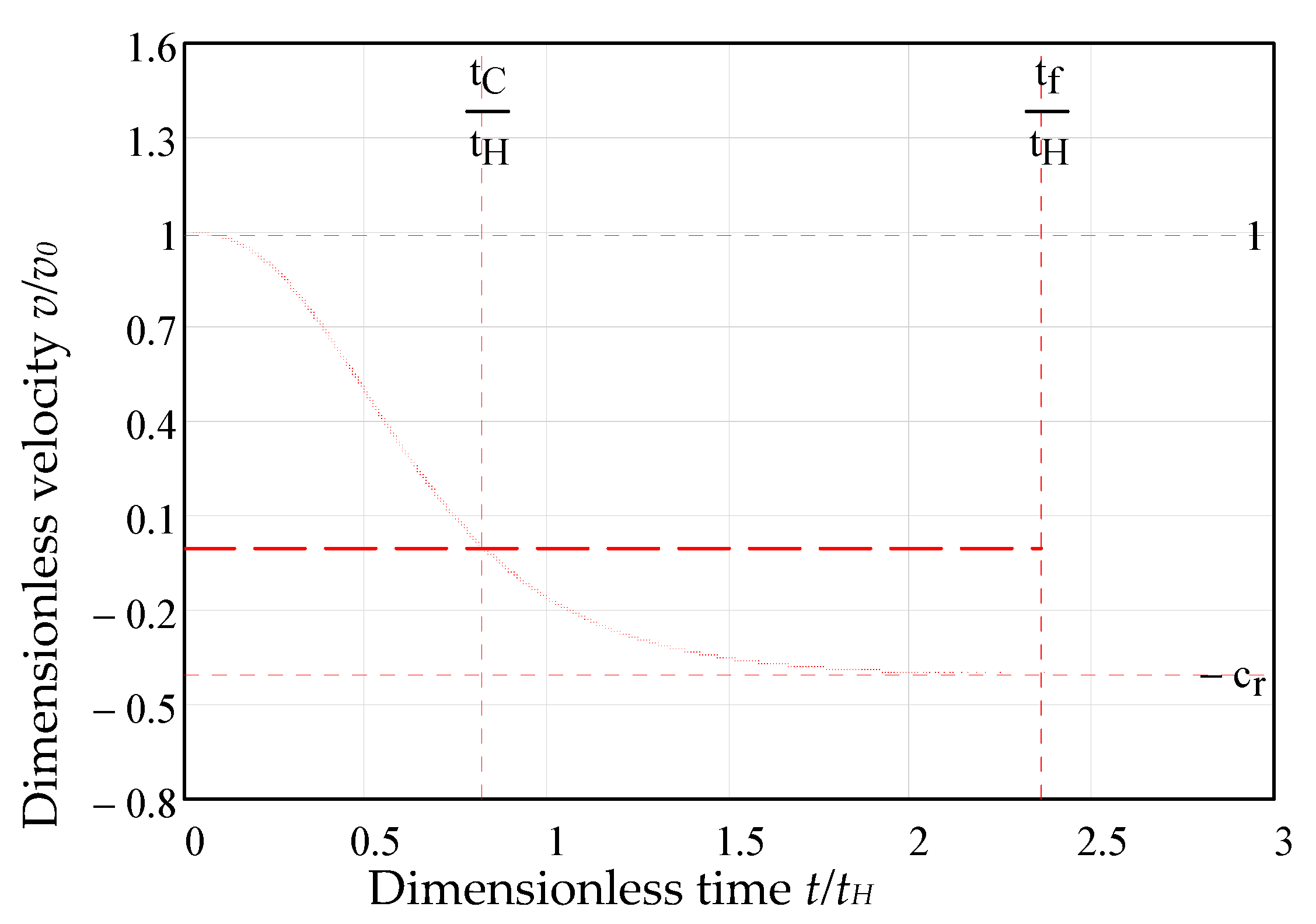
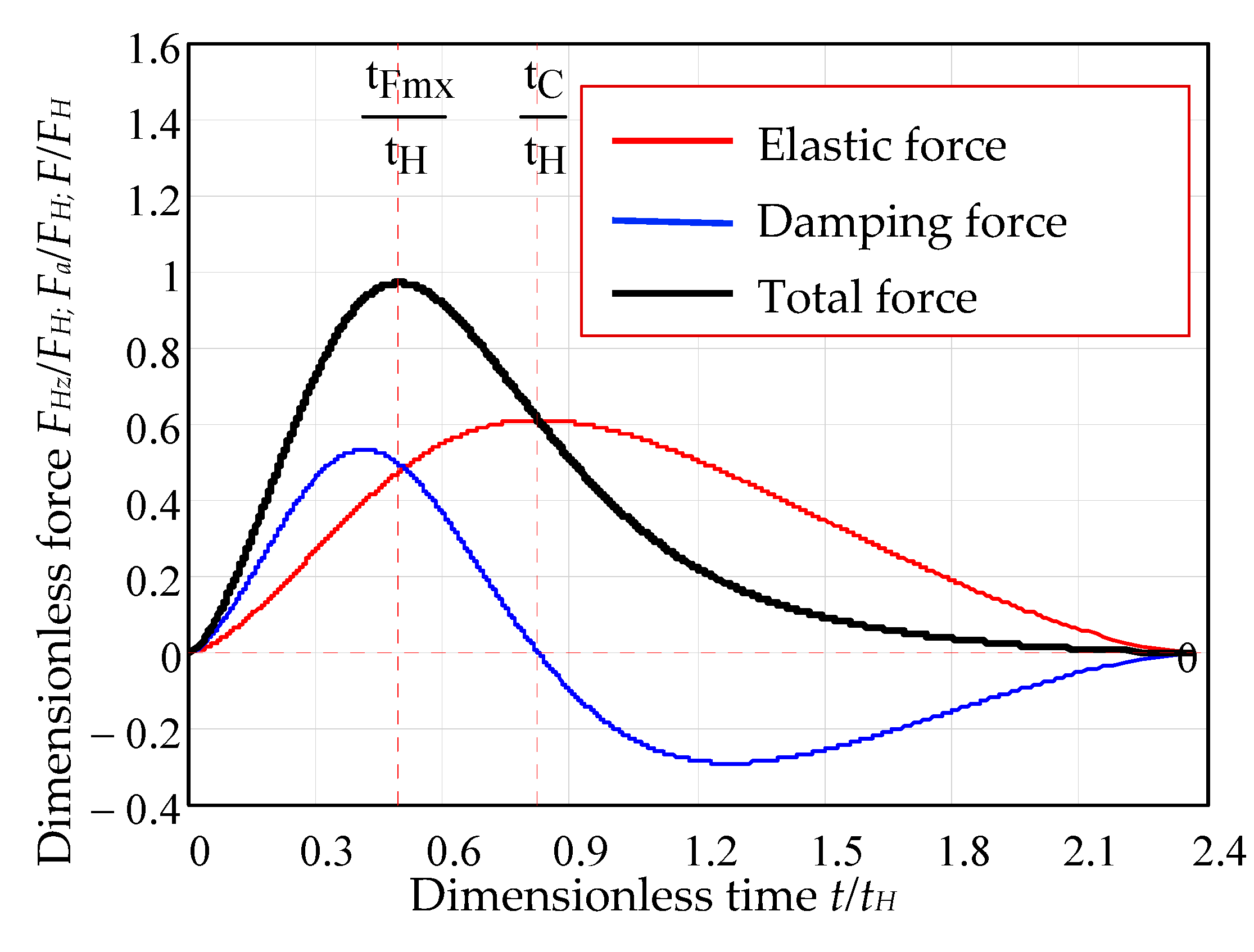
3.7. Impact Parameters as Time Functions

3.7.1. Relations for Finding the Characteristic Periods of Impact

To illustrate the variation with time of the parameters characteristic to collision, the definition relation of the velocity is considered:

$$v=\frac{dx\left(v\right)}{dt}=\frac{dx\left(v\right)}{dv}\frac{dv}{dt}$$

(44)

It results in the following:

$$dt=\frac{1}{v}\frac{dx\left(v\right)}{dv}dv$$

(45)

From the definition of acceleration, we get the following:

$$a=\frac{dv}{dt}$$

(46)

It results in the following:

$$dt=\frac{dv}{a\left(v\right)}$$

(47)

Relations (44)–(47) were written based on the relation $x=x\left(v\right)$ that permits the explicit form of deformation versus velocity. For the general case, the velocity is expressed as follows:

$$v=v\left(x\right)$$

(48)

The following equation must be added to Relations (44) and (46):

$$v=\frac{dx}{dt}$$

(49)

from which it results:

$$dt=\frac{dx}{v\left(x\right)}$$

(50)

Notice that, during the entire impact process, the velocity has a continuous and monotonous variation from $v_0$ to $-c_r{v}_0$, while the approach increases from 0 to $x_m$ during the compression period, and after that, it decreases to zero during the restitution period, and thus, for a given value of deformation, there are two possible values of velocity, $v_{+}$ for compression phase and $v_{-}$ for restitution phase.

$$v\left(x\right)=\{\begin{array}{c}{v}_{+}\left(x\right)\ge 0,0\le t\le t_c\\ v_{-}\left(x\right)<0,t_c<t\le t_f\end{array}$$

(51)

Knowing the variation of normal approach as function of velocity, $x=x\left(v\right)$ (relation 25) and respective $a=a\left(v\right)$ (relation 27) and considering $t=0$ when $v=v_0$ as starting time, the instant at which the velocity $v_{end}$ has an imposed value is given by the following:

$$t={{\displaystyle \int }}_{v_0}^{v_{end}}\frac{1}{v}\frac{dx\left(v\right)}{dv}dv$$

(52)

and:

$$t={{\displaystyle \int }}_{v_0}^{v_{end}}\frac{dv}{a\left(v\right)}$$

(53)

where $dx\left(v\right)/dv$ is the derivative of Relation (25) with respect to velocity and we have the following:

$$t={{\displaystyle \int }}_0^{x_m}\frac{dx}{v_{+}\left(x\right)}+{{\displaystyle \int }}_{x_m}^{x_{end}}\frac{dx}{v_{-}\left(x\right)}$$

(54)

where $v=v\left(x\right)$, respectively, and $x_{end}$ is the deformation corresponding to the instant when the velocity is $v_{end}$.

In order to compute the time of reaching the maximum force, $t_{Fmx}$, the compression time ($t_c$) and the total time ($t_f$), the following relations are used in Equations (52) and (53), where $v_{end}$ takes the values $v_{end}=v_{Fmax}$, $v_{end}=0$ and $v_{end}=-c_r{v}_0$, respectively. It results in the following:

$$t_{F_{mx}}={{\displaystyle \int }}_{v_0}^{v_{Fmx}}\frac{1}{v}\frac{dx\left(v\right)}{dv}dv;t_c={{\displaystyle \int }}_{v_0}^0\frac{1}{v}\frac{dx\left(v\right)}{dv}dv;t_f={{\displaystyle \int }}_{v_0}^{-c{v}_0}\frac{1}{v}\frac{dx\left(v\right)}{dv}dv$$

(55)

and

$$t_{Fmx}={{\displaystyle \int }}_{v_0}^{v_{Fmx}}\frac{1}{a\left(v\right)}dv;t_c={{\displaystyle \int }}_{v_0}^0\frac{1}{a\left(v\right)}dv;t_f={{\displaystyle \int }}_{v_0}^{-c{v}_0}\frac{1}{a\left(v\right)}dv$$

(56)

The same parameters can be obtained by using Relation (54), where $x_{end}$ must be replaced by $x_{Fmx}$, $x_c$ and 0.

$$t_{F_{mx}}={{\displaystyle \int }}_0^{x_{Fmx}}\frac{dx}{v_{+}\left(x\right)};t_c={{\displaystyle \int }}_0^{x_m}\frac{dx}{v_{+}\left(x\right)};t_f={{\displaystyle \int }}_0^{x_m}\frac{dx}{v_{+}\left(x\right)}+{{\displaystyle \int }}_{x_m}^0\frac{dx}{v_{-}\left(x\right)}.$$

(57)

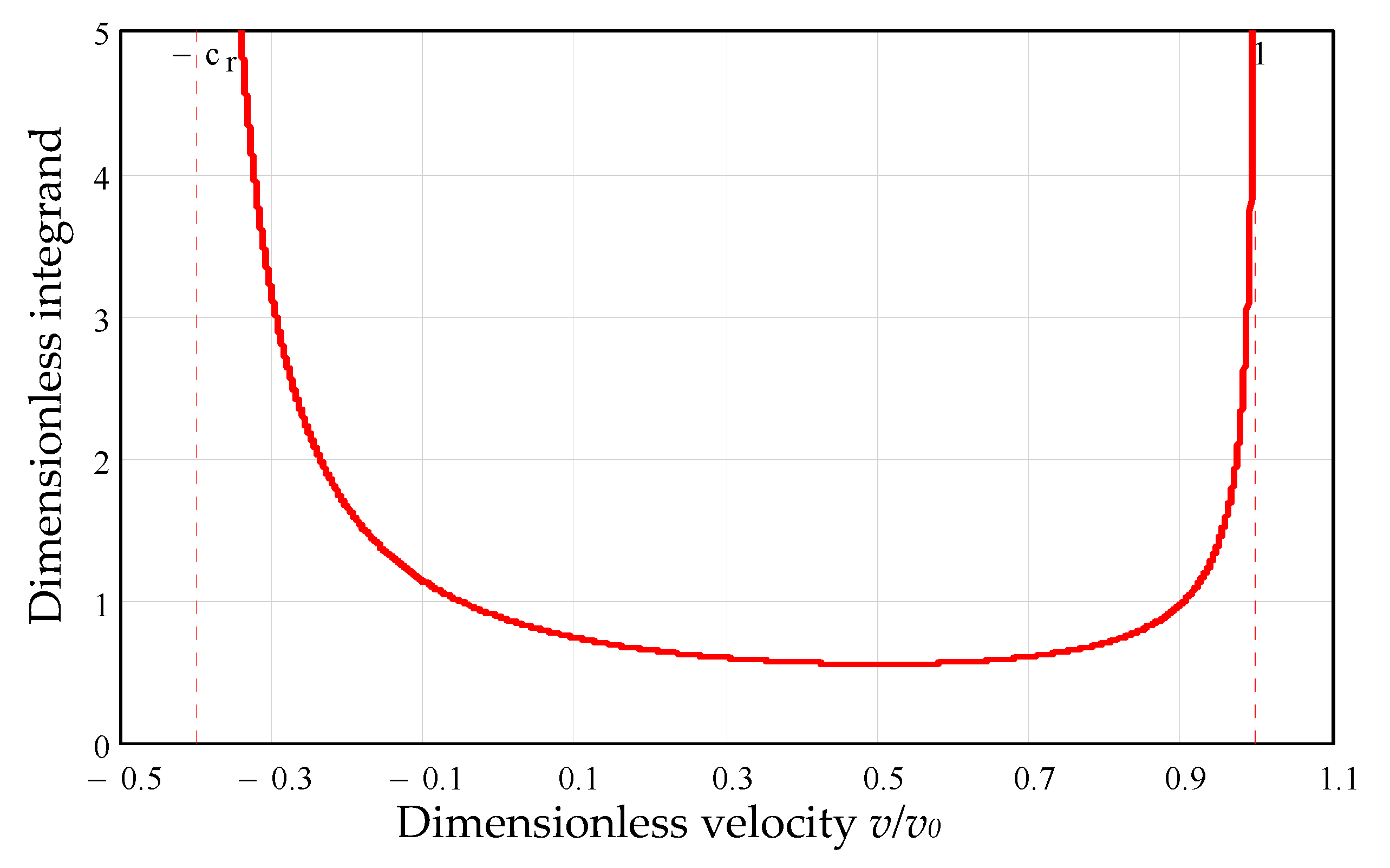
3.7.2. Elimination of Singularities from the Expressions of Impact Periods

The complicate form of the integrands in Relations (55) and (56) cannot allow for closed forms for primitives, and the numerical methods are therefore demanded. Analyzing the integrands from Equations (55) and (56), we see that the integrands tend to infinity for $v=v_0$ and for $v=-c_r{v}_0$ when the entire duration of collision is considered, as presented in Figure 7 and Figure 8.

If the integration is performed with respect to deformation, the integrals from Relation (57) become divergent when the domain contains the time of maximum approach (corresponding to $v=0$). A similar aspect is met for the elastic collision when calculating the approach time with Relation (17), with the integral being expressed with the gamma function $\Gamma \left(x\right)$ and obtaining a finite approach time, $t_H$, which is in agreement with the physical meaning. In order to obtain the value of time $t_{end}$ corresponding to $x_{end}$ and $v_{end}$ (for restitution phase), two values of velocity are considered in the interval of velocity variation $\left[v_0,v_{end}\right]$, denoted $v^c>0$ for compression and $v^r<0$ for restitution, as in Figure 9.

$$v_0\ge v^c>0>v^r>v_{end}\ge -c_r{v}_0$$

(58)

The time $t_{end}$ is obtained with the following relation:

$$t_{end}={{\displaystyle \int }}_0^{x^c}\frac{1}{v_{+}\left(x\right)}dx+{{\displaystyle \int }}_{v^c}^{v^r}\frac{1}{v}\frac{dx\left(v\right)}{dv}dv+{{\displaystyle \int }}_{x^r}^{x_{end}}\frac{1}{v_{-}\left(x\right)}dx$$

(59)

All integrals from Expression (59) are convergent. The difficulty is in the fact that there are no closed forms for the dependencies $v=v_{+}\left(x\right)$ and $v=v_{-}\left(x\right)$, these being obtained by numerical solving of Equation (24), with appreciable calculus volume. Aiming to obtain the values of the characteristic impact parameters for different times, it is considered that the explicit dependency of approach versus velocity $x=x\left(v\right)$ is available by the first integral, Relation (25). Based on this fact, the interval $\left[v_0,v_{end}\right]$ is divided into $n_p$ equal subintervals by $n_p+1$ points. A vector ($v$) is generated with the following elements:

$$v_k=v_0+\frac{v_{end}-v_0}{n_p}k,k=0\dots n_p$$

(60)

Another vector ($x$) is generated, with the following elements:

$$x_k=x\left(v_k\right),k=0\dots n_p$$

(61)

Two values are chosen for the index, $n_{+}$ for the point ($v^c$;$x^c$) from compression phase and $n_{-}$ for the point ($v^r$;$x^r$) from restitution phase. The integrals from Relation (59) are replaced by the attached Darboux sums, with the value of the function calculated for the middle of the subinterval, and it is obtained as follows:

$$t_{end}={\displaystyle \sum }_{k=1}^{n_{+}}\frac{x_k-x_{k-1}}{\frac{v_k+v_{k-1}}{2}}+{\displaystyle \sum }_{k=n_{+}+1}^{n_{-}}\frac{\frac{x_k-x_{k-1}}{v_k-v_{k-1}}}{\frac{v_k+v_{k-1}}{2}}\left(v_k-v_{k-1}\right)+{\displaystyle \sum }_{k=n_{-}+1}^{n_p}\frac{x_k-x_{k-1}}{\frac{v_k+v_{k-1}}{2}}={\displaystyle \sum }_{k=1}^{n_p}\frac{x_k-x_{k-1}}{\frac{v_k+v_{k-1}}{2}}$$

(62)

Based on the relation above, a recurrence formula can be obtained for the moments ($t_k$), and the vector ($t$) is obtained, the vector containing the moments for which the approach and velocity are $x_k$ and $v_k$.

$$t_0=0,t_k=t_{k-1}+\frac{x_k-x_{k-1}}{\left(v_k+v_{k-1}\right)/2}$$

(63)

The last value from the vector (t) corresponds to the moment $t_{end}$. The Figure 10 presents the dependency of the values $t_{Fmx}$, $t_C$ and $t_f$ found by the above algorithm, for a set of increasing values of the number of points, $n_p$. It can be observed that the values of $t_{Fmx}$, $t_C$ and $t_f$ stabilize after a relatively small number of points, $n_p=100$.

For testing the precision of the method, the results of the times $t_C$ and $t_f$ calculated with the above-described methodology are presented next. As shown in Johnson [30] and Popov [56], the Hertzian point contact between two spheres can be considered as an equivalent contact between a sphere and a half-space. Goldsmith [1] also considers the sphere–half-space contact as a particular situation of sphere–sphere contact. Therefore, here it is considered the quasi-elastic impact between a smooth steel ball, radius $r=15 \mathrm{mm}$ that hits with velocity $v_0=2.8 \mathrm{m}/\mathrm{s}$ an immobile smooth steel prismatic block of infinite mass. The coefficient of restitution is adopted, $c_r=0.999$. This value was chosen, since, for the perfect elastic impact of two spheres, the relation for total impact time given by Timoshenko is as follows:

$$c_r=0.999;t_H=4.205\cdot {10}^{-5}s;\frac{t_C}{t_H}=0.99764;\frac{t_f}{t_H}=2.00211$$

(64)

The equation of motion was integrated by using ${\gamma }_0$ and $t_f$ obtained by the presented methodology for two values of the number of discretization points. The results for the approach versus time obtained both by the proposed method and by the Runge–Kutta method are presented comparatively in Figure 11a for $n_p=20$ and in Figure 11b for $n_p=200$. It can be observed that, for the Runge–Kutta algorithm, the points are equidistant with respect to time, but for the present method, the points are congested in the vicinity of the time corresponding to maximum approach, which is also the interval of maximum attention for engineering applications.

In Figure 12, we present the variation of compression and restitution times as functions of index of points.

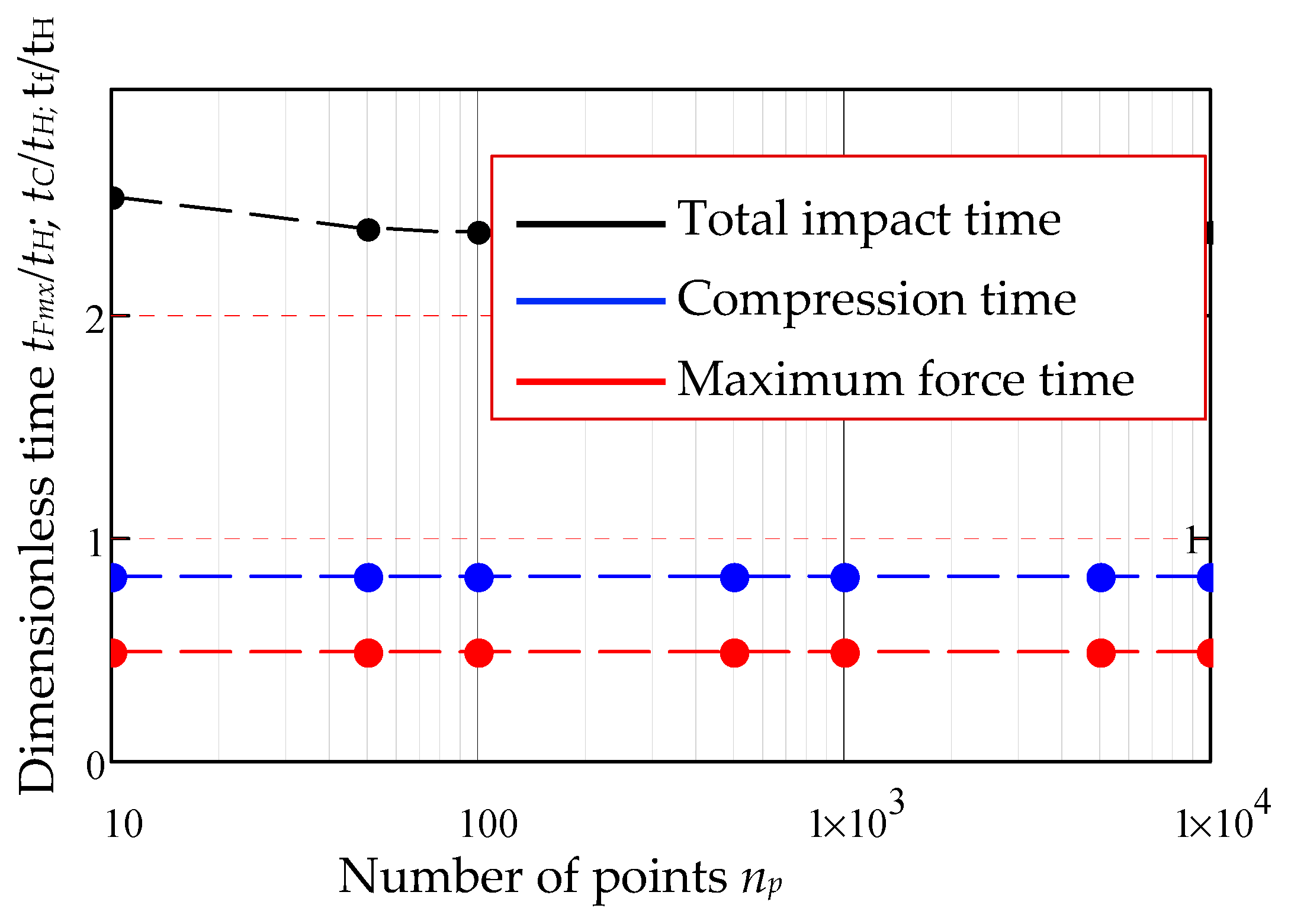
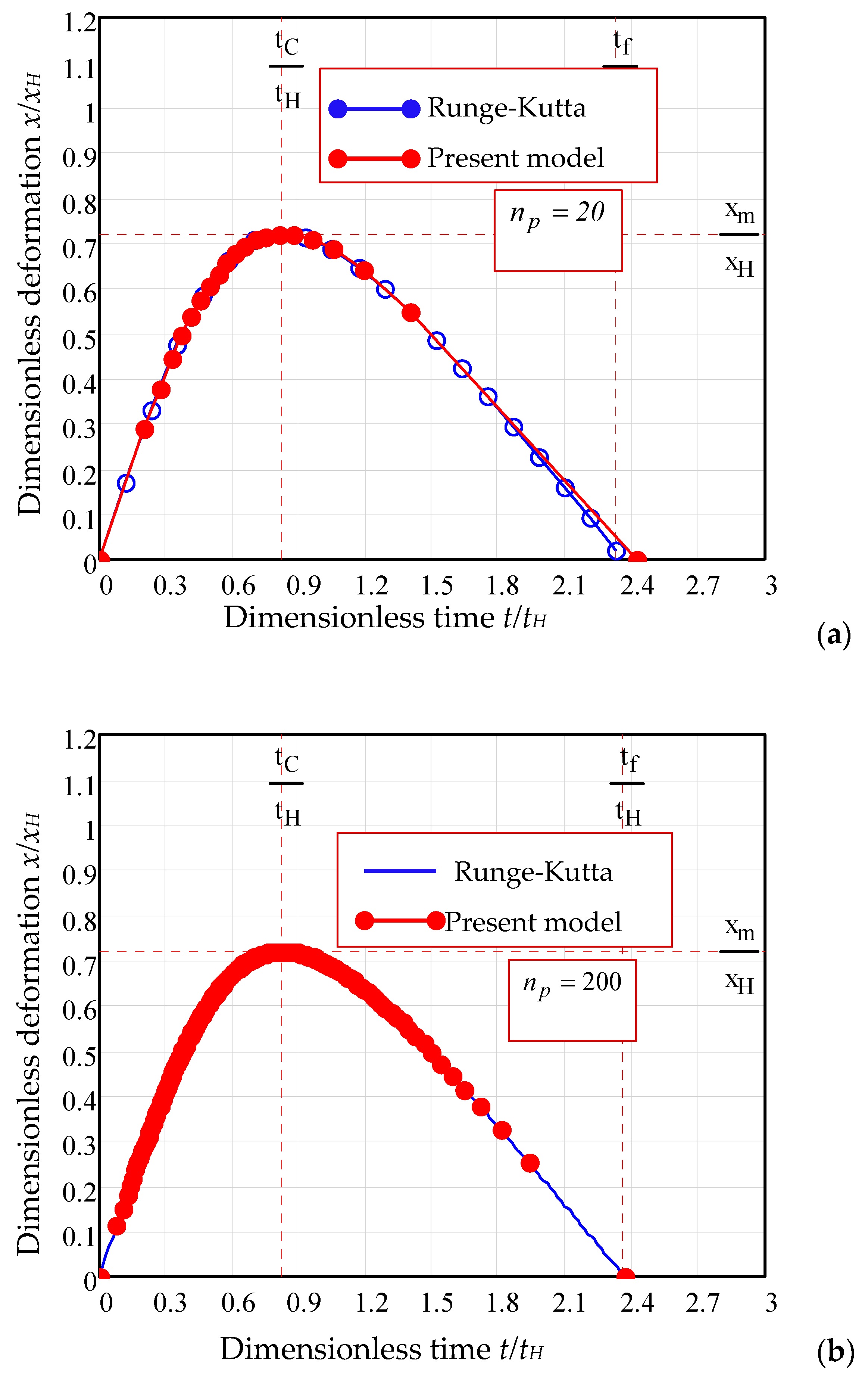
3.8. Graphical Representation of Impact Parameters with Time

At this stage, for a set of equidistant $n_p$ values of velocity, the vectors $x_k$ and $t_k$, corresponding to deformations and times, respectively, are available. The time variations for approach and velocity, for $c_r=0.4$, are presented in Figure 13 and Figure 14, respectively. One can observe that the presence of damping has as consequence a shorter duration of compression compared to restitution. Concerning the velocity, it is observed that, by the present method, the final velocity is precisely $-c_r{v}_0$.

The time variations of forces are represented in Figure 15: the Hertzian (elastic) force, $F_{Hz}$; the damping force, $F_a$; and the total impact force, $F$. The work produced by these forces is represented in Figure 16. Moreover, during the restitution phase, the damping force is negative, and that is an attraction force.

4. Discussions

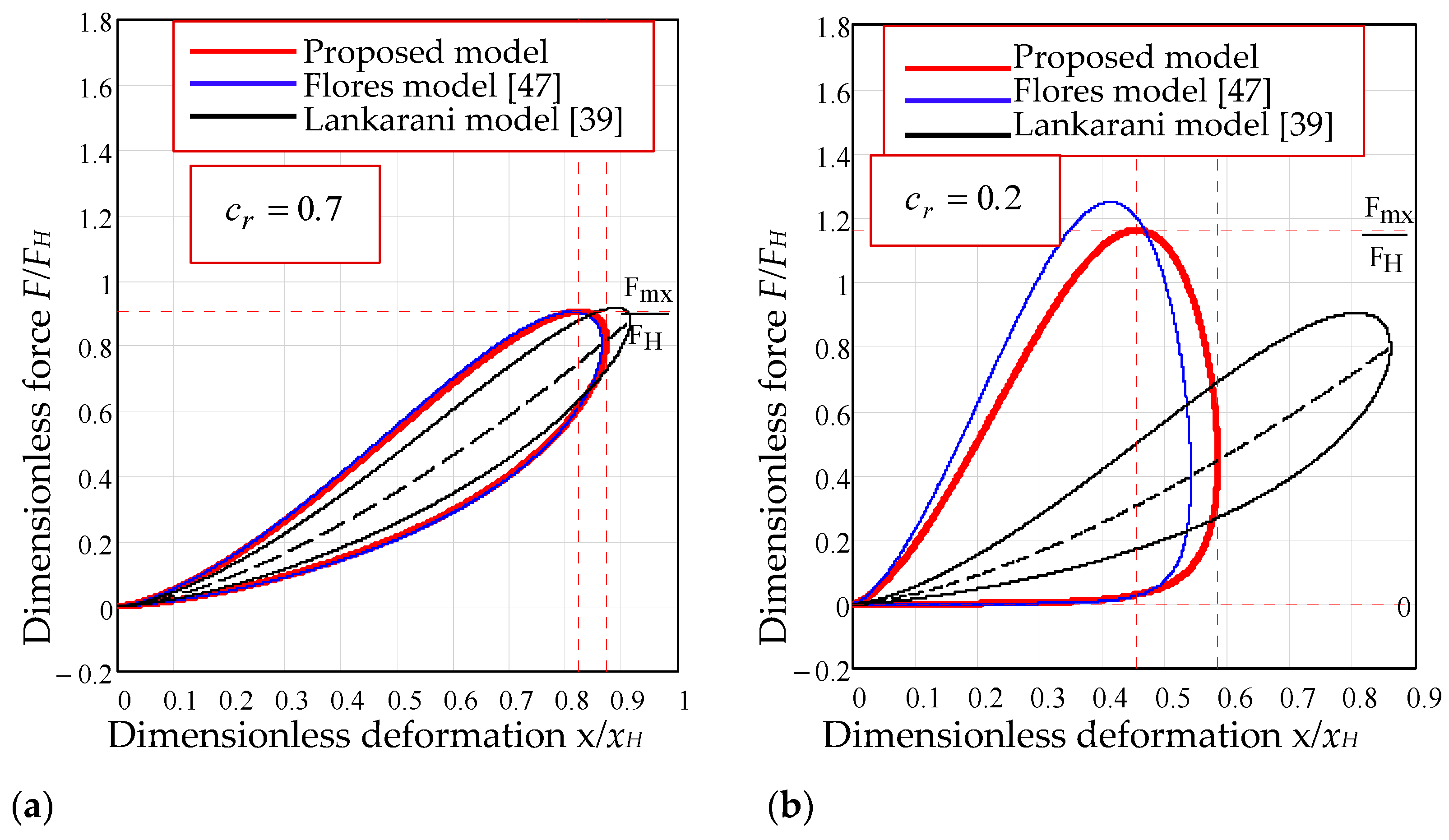
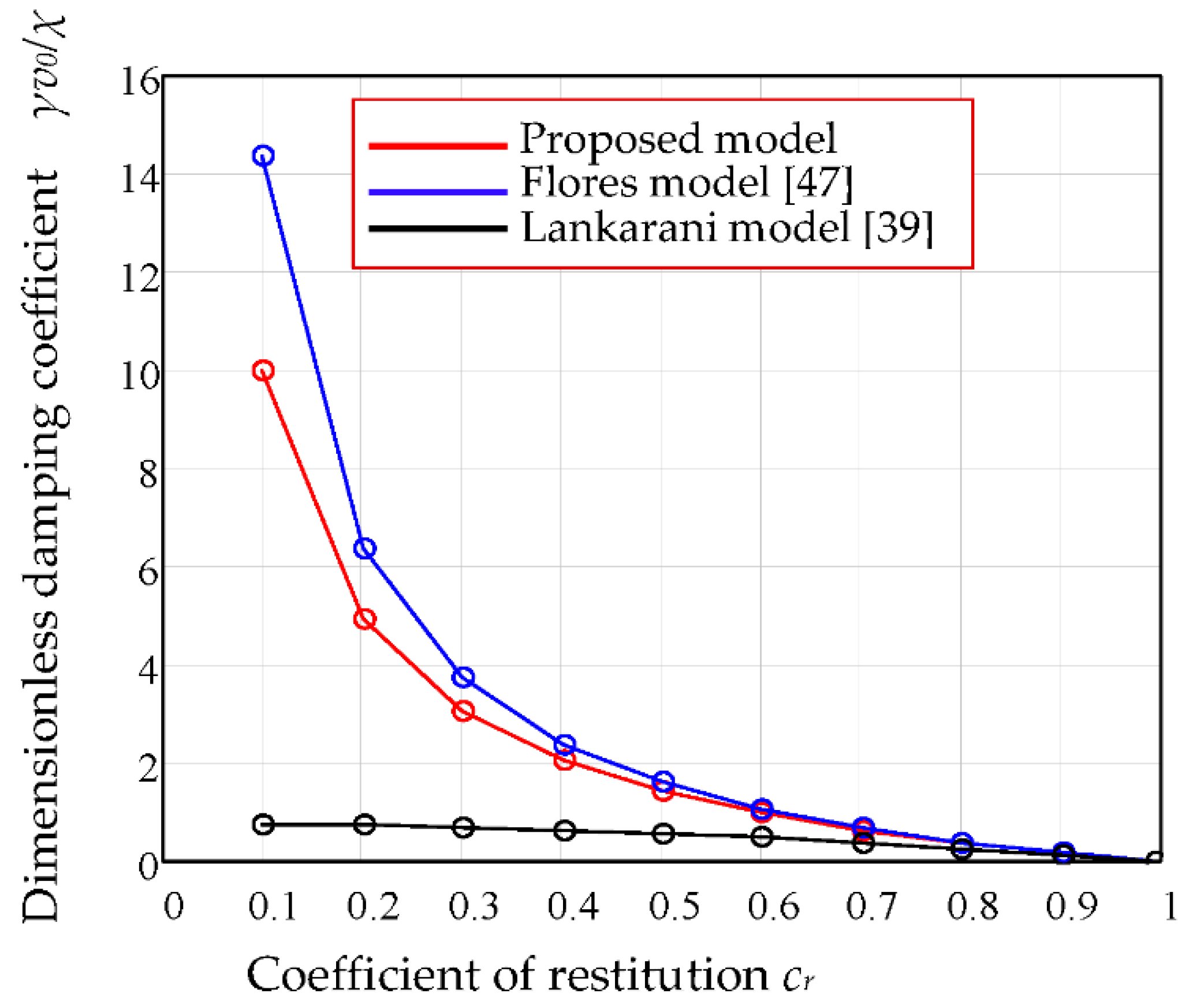
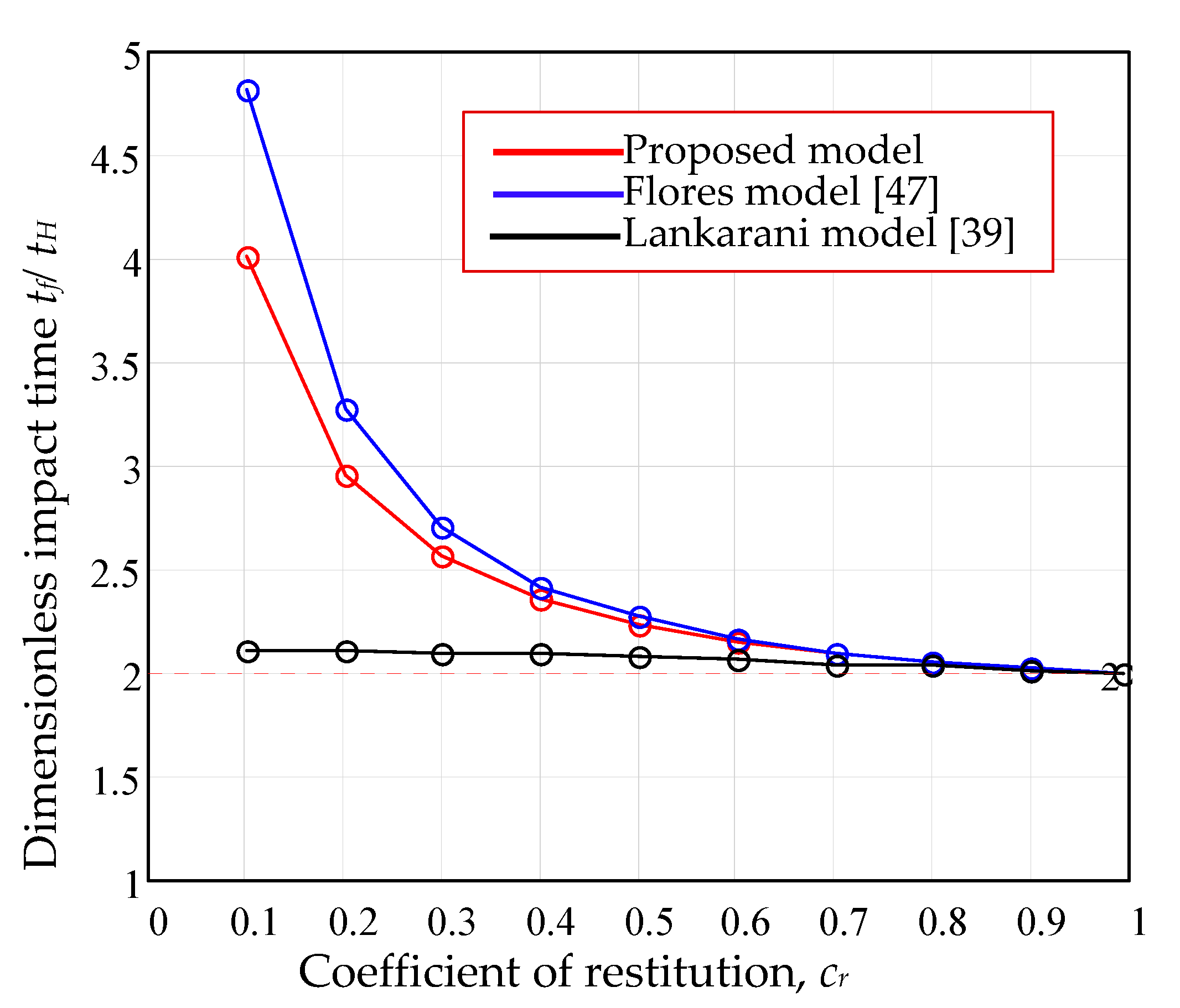
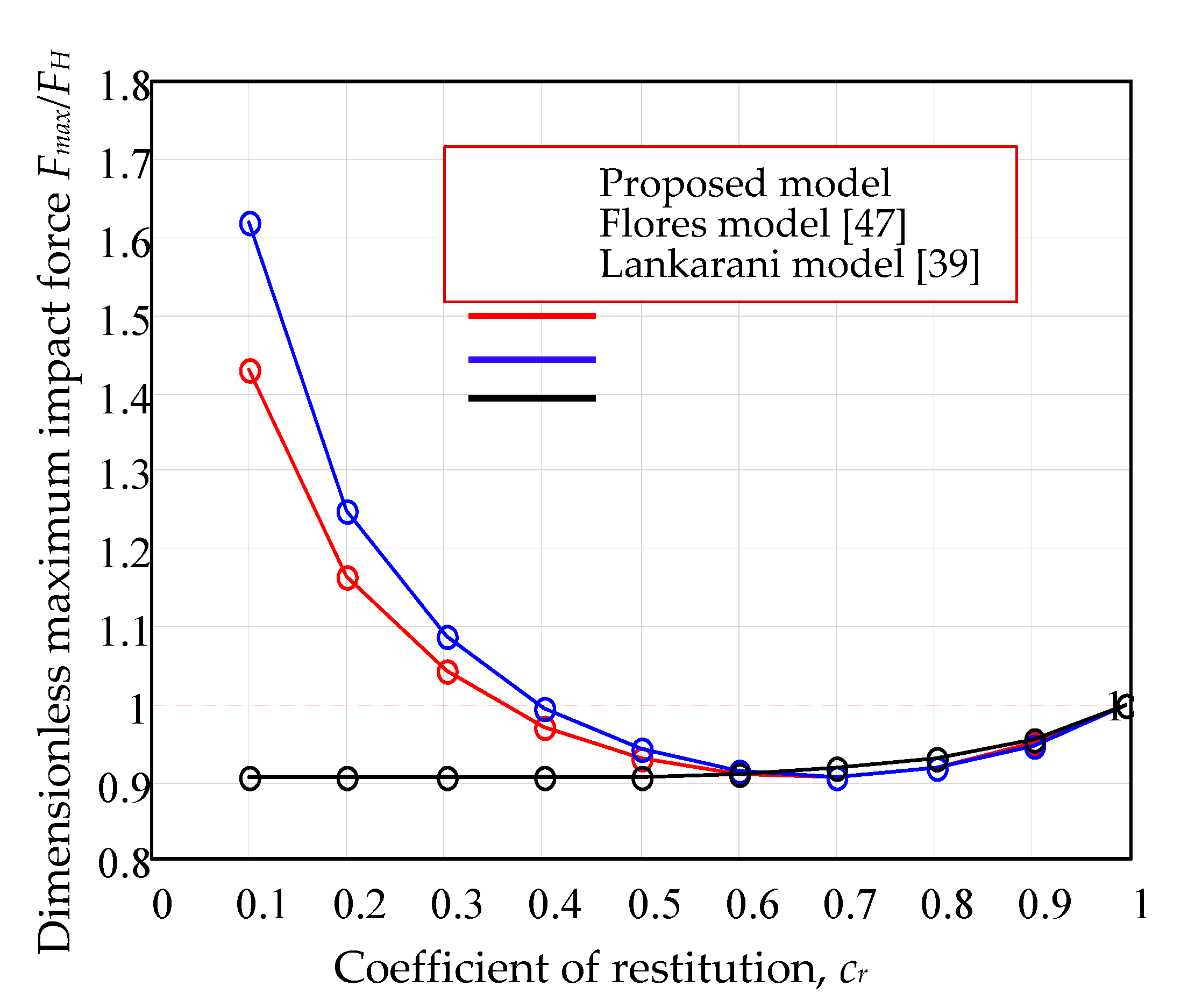
4.1. Comparison of the Proposed Method with the Lankarani and Flores Models

4.1.1. Characteristic Curves

By applying the method detailed above, we estimated the total impact time for the models of Lankarani ($t_{L_f}$) and Flores ($t_{F_f}$) were estimated, and after that, using the values for the coefficients ${\gamma }_L$, ${\gamma }_F$ and ${\gamma }_0$ in Runge–Kutta methodology, the differential equations were integrated for the proposed model and for the Lankarani and Flores models. For two values of the coefficient of restitution, $c_r=0.7$ and $c_r=0.2$, the time dependence of approach, velocity and impact force are presented comparatively in Figure 17, Figure 18 and Figure 19. For the same values of coefficient of restitution, the characteristic curves in the phase plane and the hysteresis loops are plotted in Figure 20 and Figure 21, respectively.

From the presented figures, one can conclude that, for values of coefficient of restitution, $c_r\ge 0.7$, all three models give similar results, while for smaller values, $c_r<0.7$, the current model and the Flores model present close results of the characteristic parameters for impact phenomenon, but the Lankarani model leads to significantly different results.

4.1.2. The Effect of Coefficient of Restitution

In order to describe quantitatively the effect of coefficient of restitution upon the solution of the differential equation of impact, the presented methodology was applied for studying the dependency of the coefficient ($\gamma$), maximum approach ($x_m$), maximum impact force ($F_{max}$) and total impact time ($t_f$). These variations are presented in Figure 22, Figure 23, Figure 24 and Figure 25. All of these plots sustain the previous affirmation, namely that the values of the characteristic impact parameters for the Flores and present model are close for the entire domain of coefficient of restitution variation, but the Lankarani model offers values differing progressively more with the decrease of coefficient of restitution.

4.2. A Simplified Algorithm for Finding the Impact Parameters

As noticed from above, the proposed methodology requires an appreciable volume of numerical calculus for solving the transcendental equations and for evaluations of definite integrals. This drawback is overcome after analyzing the effect of initial impact velocity ($v_0$) and contact stiffness ($\chi$) upon the characteristic parameters of impact phenomenon, when the following remark arises: all normalized contact parameters of impact are invariants with respect to velocity ($v_0$) and stiffness ($\chi$). From here, an important practical consequence is that, for a given value of coefficient of restitution, it is sufficient to solve the equation of the model for a velocity ($v_0$) and a contact stiffness ($\chi$), and after that, for any other values of the two parameters, $v_0$ and $\chi$, all the characteristic parameters of impact can be found by using a much simpler methodology.

For this purpose, for the values of coefficient of restitution are as follows:

$$c_r=0.1\cdot k,k=1\dots 10$$

(65)

We evaluated the values of the main normalized parameters characteristic to impact:

• ${\gamma }_0$, viscous damping coefficient;
• $t_C$, compression time;
• $t_f$, total impact time;
• $v_{Fmx}$, velocity corresponding to the maximum impact force;
• $x_{Fmx}$, approach corresponding to the maximum impact force;
• $x_m$, maximum approach;
• $F_{max}$, maximum impact force;
• $F_{emax}$, elastic force corresponding to maximum approach, $x_m$;
• $F_{amax}$, maximum damping force for compression phase (rejection force);
• $F_{amin}$, maximum damping force for restitution phase (attraction force);
• $L_C$, work done during the compression phase;
• $L_r$, work done during the restitution phase;
• $L_e$, work of elastic force during the compression phase;
• $L_t$, total work.

The calculated values are presented in

Table 1. Normalized impact parameters for a range of values of coefficient of restitution, $c_r$.

${\mathit{c}}_{\mathit{r}}$	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	0.99
$\frac{\chi }{v_0}\gamma$	9.998	4.919	3.087	2.082	1.433	0.975	0.635	0.373	0.166	0.008
$\frac{t_C}{t_H}$	0.638	0.726	0.780	0.823	0.860	0.892	0.922	0.950	0.975	0.999
$\frac{t_f}{t_H}$	4.015	2.965	2.572	2.366	2.240	2.156	2.097	2.055	2.023	2.001
$\frac{v_{Fmx}}{v_0}$	0.596	0.569	0.538	0.502	0.457	0.400	0.327	0.234	0.123	0.006
$\frac{x_{Fmx}}{x_H}$	0.348	0.454	0.535	0.609	0.681	0.753	0.824	0.893	0.953	0.998
$\frac{x_m}{x_H}$	0.471	0.583	0.659	0.721	0.776	0.826	0.873	0.917	0.959	0.998
$\frac{F_{max}}{F_H}$	1.431	1.161	1.041	0.971	0.930	0.908	0.904	0.917	0.949	0.997
$\frac{F_{emax}}{F_H}$	0.323	0.445	0.535	0.612	0.683	0.750	0.815	0.878	0.940	0.997
$\frac{F_{amax}}{F_H}$	1.231	0.869	0.674	0.533	0.419	0.319	0.230	0.148	0.072	0.004
$-\frac{F_{amin}}{F_H}$	0.258	0.299	0.303	0.289	0.263	0.227	0.181	0.128	0.067	0.004
$\frac{L_C}{L_H}$	0.849	0.741	0.649	0.560	0.471	0.381	0.289	0.195	0.099	0.005
$\frac{L_r}{L_H}$	0.090	0.211	0.259	0.279	0.278	0.259	0.220	0.165	0.091	0.005
$\frac{L_e}{L_H}$	0.152	0.260	0.352	0.441	0.530	0.619	0.711	0.805	0.901	0.995
$\frac{L_t}{L_H}$	0.939	0.952	0.907	0.839	0.749	0.640	0.510	0.360	0.190	0.010

.

Based on the results presented in Table 1, the variations of dimensionless parameters versus coefficient of restitution are plotted in Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31.

For a given impact, there must be stipulated the radii of the balls, $r_{1,2}$; the masses, $m_{1,2}$; the elastic parameters, $E_{1,2}$ and ${\nu }_{1,2}$; the exponent, $\alpha =3/2$ for Hertzian contact; the initial impact velocity, $v_0$; and the value of the coefficient of restitution.

Then, the next steps must be followed:

• The elastic constant of the contact (${\rm K}$) and the contact stiffness ($\chi$) are determined;
• The parameters characteristic to Hertzian un-damped impact, $t_H$, $F_H$,$x_H$ and $L_H$, are found;
• The normalized parameters are found by interpolation;
• The actual values of the parameters are found by multiplication of the normalized parameters by the corresponding constants.

5. Conclusions

The main conclusions of the work are as follows:

-

The classical models of damped impact of two smooth spheres are based on the Hunt and Crossley viscoelastic model; the non-linear differential equation cannot be integrated without stipulating three coefficients. The damping coefficient (γ) was chosen by different supplementary hypotheses:

○

Hunt and Crossley considered proportionality between the hysteresis loop area and γ;

○

Lankarani accepts the energy hypothesis of equal work for compression and restitution phase;

○

Flores considers that in the phase plane the characteristic point describes el-liptical arcs.

-

The model proposed in the present work is based on the remark that the differential equation of the motion is an equation with separable variables, both members of the equation admit closed form integrals. A first integral of the equation in analytical form can be obtained. Moreover, this expression of this integral permits an explicit expression of deformation as a function of velocity.

-

The boundary conditions imposed for the first integral for the final moment and for the compression time permit finding the damping coefficient (γ) and the relation of maximum deformation.

-

The expression of deformation as a function of velocity permits finding the instants when a certain velocity and deformation are reached.

-

For the validation of the proposed model, a particular case of quasi-elastic impact of two smooth spheres was considered; the solution is in total agreement to the solution for perfect-elastic impact given by Timoshenko, in analytical form.

-

The impact parameters for the elastic Hertzian point contact, obtained by Timoshenko, were used for obtaining the dimensionless parameters in the actual case, required for the comparison with pervious solutions.

-

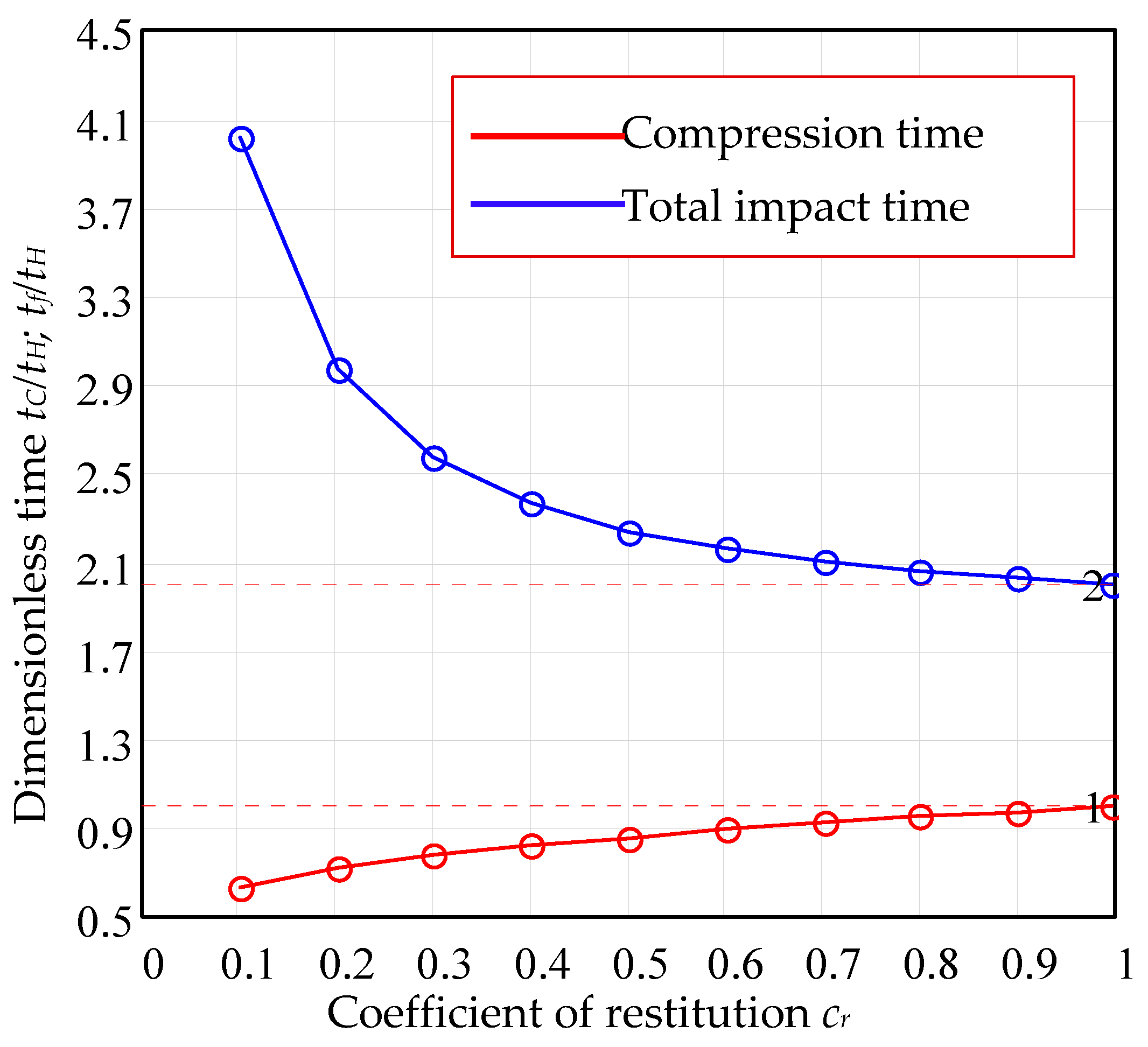
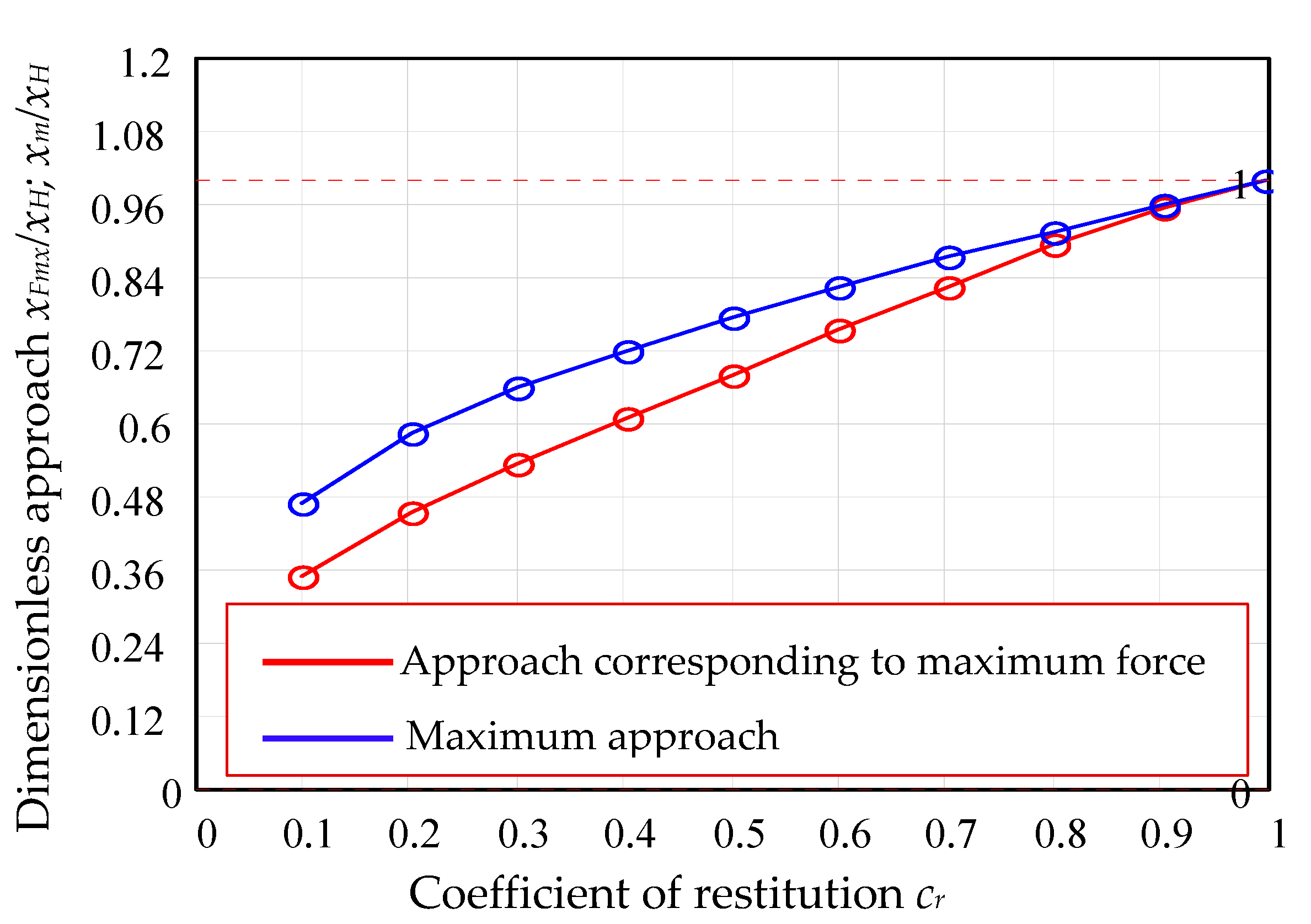
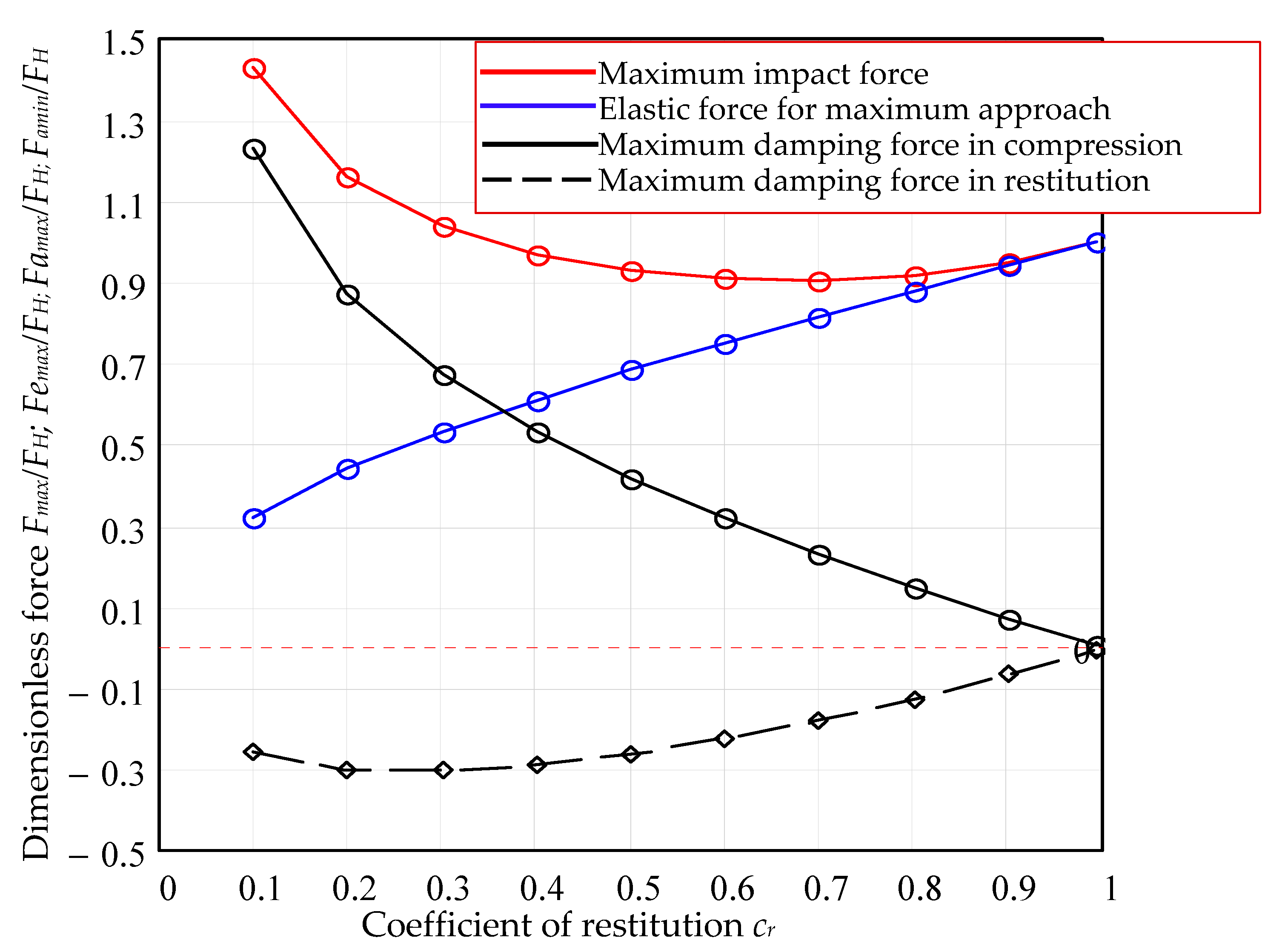
The values of viscous damping coefficient obtained by the actual method were used for integration of the equation of motion for the whole range of coefficients of restitution ($0<c_r<1$). For the same values of coefficients of restitution, the equations of the models Lankarani and Flores were numerically integrated (Runge–Kutta method) and the dimensionless parameters of impact were compared in a graphical manner. The discrepancies between the proposed model and the previous ones are obvious in the range of $0<c_r<0.4$. We emphasize that the present model is applicable for any coefficient of restitution, being especially useful for soft materials.

-

The calculus of the impact parameters can be substantially simplified based on the observation that for a fixed value of α, the exponent of deformation, all dimensionless impact parameters are invariants with respect to initial velocity and stiffness. A table of dimensionless impact parameters is given for rapid interpolation, using the known $c_r$ and the Hertzian impact parameters.

The authors identify, for future research, the following directions:

-

The model can be extended to hyperelastic materials having as force–deformation law a most general expression.

-

The present model can also be employed for modeling the dashpots with large velocities (>50 m/s) when the damping force is proportional to the velocity squared.

-

The model can be extended to model the collision of elasto–visco–plastic nonlinear bodies—which are frequently encountered in concrete dynamical systems. This assertion is based on Johnson’s remark [30] that, only for low-impact velocities, the collision can be regarded as an elastic phenomenon. As an example, Johnson shows that, for steel, the impact velocity must satisfy the condition $v<7.5\mathrm{m}/\mathrm{s}$ This is an aimed future work that can be applied for any domain, from classical industrial dynamical systems to medical devices, food-processing industry, pharmaceutic industry and powder technology.

-

The combined forces (normal and tangential) frequently met in practical applications are an important subject, and, therefore, the issue of tangential impact forces is a task for future research, both for theoretical modeling and for experimental work. The friction forces, which are tangential forces, are a consequence of normal forces, and we meet them in modern but usual applications, for example, the final element of robots—the grasper, the medical prosthesis and the landing gear from aircrafts.