Outer Synchronization of Complex-Variable Networks with Complex Coupling via Impulsive Pinning Control

Abstract

In this paper, outer synchronization of complex-variable networks with complex coupling is considered. Sufficient conditions for achieving outer synchronization using static impulsive pinning controllers are first derived according to the Lyapunov function method and stability theory of impulsive differential equations. From these conditions, the necessary impulsive gains and intervals for given networks can be easily calculated. Further, an adaptive strategy is introduced to design universal controllers and avoid repeated calculations for different networks. Notably, the estimation algorithms of the impulsive gains and intervals are provided. Finally, three numerical examples are performed to verify the effectiveness of the main results.

1. Introduction

Outer synchronization between two networks is an important phenomenon and exists widely in real-world situations [1,2,3,4,5,6,7,8,9,10,11,12]. In [1], authors established a public traffic supernetwork model, which consists in the conventional bus traffic network and the urban rail traffic network. They then studied the impact of the departing frequencies of both types of public traffic vehicles, and the coordinated scheduling in the process of transfer to the supernetwork model’s synchronous ability by using outer synchronization. In [2], authors discussed the applications of outer synchronization of anti-star networks in secure communication. In [3], authors studied the outer synchronization and parameter identification of supply networks with uncertainty. They also used the obtained results for resilient recovery. In [4], authors studied the generalized outer synchronization non-dissipatively with different-dimensional nodes. In [5,6,7,8], authors studied the outer synchronization of fractional-order dynamical networks. In [9], authors studied the outer synchronization of time-varying networks with different node numbers.

Due to the complexities of dynamical networks, outer synchronization between them is difficult and even impossible to achieve without external control. Therefore, many control schemes are adopted to design effective controllers, such as impulsive control [13,14], intermittent control [15,16], pinning control [14,15,16,17], finite-time control [18], and so on. In [14], authors considered the outer synchronization of drive-response networks by combining impulsive and pinning control. It is noted that adaptive strategies are introduced to design universal controllers as well. In [15,16], authors investigated the outer synchronization via intermittent pinning control. In [17], authors considered pinning outer synchronization. In [18], authors considered finite-time outer synchronization and discussed its application in image encryption.

Nevertheless, the above-mentioned results mainly concentrate on dynamical networks coupled with real-variable systems. Alternatively, complex-variable systems are employed to describe physical systems [19,20,21,22,23,24]. In [22], authors used a complex-variable Lorenz system to describe rotating fluid. In [23], authors simulated detuned lasers using a complex-variable Lorenz system. In [19], authors applied complex-valued convolutional neural network in polarimetric SAR image classification. Naturally, dynamical networks coupled with complex-variable systems have drawn increasing attention from researchers and many valuable results have been obtained [25,26,27,28,29,30,31,32,33,34,35,36]. In [35], authors studied the outer synchronization of drive-response networks via intermittent pinning control. In [36], authors considered complex-variable networks with both real and complex coupling, which can better describe the interactions. Until now, there have been few results about outer synchronization of complex-variable networks with complex coupling via impulsive pinning control.

By virtue of the advantages of impulsive and pinning control schemes, in this paper, we investigate the outer synchronization of complex-variable networks with complex coupling through combining impulsive and pinning control. The main contributions are twofold:

(i)

We design the static impulsive pinning controllers and provide the method for choosing pinned nodes based on the norm of synchronization errors. According to the Lyapunov function method and stability theory of impulsive differential equations, we derive the synchronization criteria, from which we can calculate the necessary impulsive gains and intervals for any given networks.

(ii)

We introduce an adaptive strategy to design universal controllers for different networks. The designed controllers can avoid the repeated calculations of the impulsive gains and intervals. That is, the impulsive instants can be adaptively estimated according to the updating laws (see Remark 2).

The rest of this paper is organized as follows. In Section 2, we introduce the network model and some preliminaries. In Section 3, we derive two main results. We perform three numerical examples to illustrate our main results in Section 4. Finally, we conclude this paper in Section 5.

2. Model Description and Preliminaries

Consider a complex-variable dynamical network consisting of N nodes with complex coupling, which is regarded as the drive network and described by

$$\begin{array}{c}\hfill {\dot{x}}_k\left(t\right)=f\left(x_k\left(t\right)\right)+c\sum _{l=1}^N{a}_{kl}{H}_1{x}_l\left(t\right)+c\sum _{l=1}^N{b}_{kl}{H}_2{x}_l\left(t\right),k=1,2,\cdots ,N,\end{array}$$

(1)

where $x_k\left(t\right)={(x_{k1}\left(t\right),\cdots ,x_{k,m+n}\left(t\right))}^T$ is the state variable, ${(x_{k1}\left(t\right),\cdots ,x_{km}\left(t\right))}^T\in C^m$ and ${(x_{k,m+1}\left(t\right),\cdots ,x_{k,m+n}\left(t\right))}^T\in R^n$ are the complex and real components, respectively, f is a continuous and differentiable vector-valued function, $c>0$ is the coupling strength, $H_1=diag(\underset{m}{\underbrace{h_1^1,\cdots ,h_1^m}},\underset{n}{\underbrace{0,\cdots ,0}})$ and $H_2=diag(\underset{m}{\underbrace{0,\cdots ,0}},\underset{n}{\underbrace{h_2^1,\cdots ,h_2^n}})$ denote the inner coupling matrices. $A=\left(a_{kl}\right)\in C^{N\times N}$ and $B=\left(b_{kl}\right)\in R^{N\times N}$ are the zero-row-sum outer coupling matrices. If there exists a connection from node l to node k, then $a_{kl}\ne 0$ and $b_{kl}\ne 0(k\ne l)$, otherwise, $a_{kl}=b_{kl}=0$.

The corresponding response network with impulsive controllers is described by

$$\begin{array}{cc}\hfill & {\dot{y}}_k\left(t\right)=f\left(y_k\left(t\right)\right)+c\sum _{l=1}^N{a}_{kl}{H}_1{y}_l\left(t\right)+c\sum _{l=1}^N{b}_{kl}{H}_2{y}_l\left(t\right),t\ne t_{\sigma },\hfill \\ \hfill & y_k\left(t_{\sigma }^{+}\right)=y_k\left(t_{\sigma }^{-}\right)+b_k\left(t_{\sigma }\right)\left(y_k\left(t_{\sigma }^{-}\right)-x_k\left(t_{\sigma }^{-}\right)\right),t=t_{\sigma },\hfill \end{array}$$

(2)

where $k=1,2,\cdots ,N$, $\sigma =1,2,\cdots$, $y_k\left(t\right)={(y_{k1}\left(t\right),\cdots ,y_{k,m+n}\left(t\right))}^T$ is the response state vector of the node k, ${(y_{k1}\left(t\right),\cdots ,y_{k,m}\left(t\right))}^T\in C^m$ and ${(y_{k,m+1}\left(t\right),\cdots ,y_{k,m+n}\left(t\right))}^T\in R^n$ are the complex and real components, the impulsive instants $t_{\sigma }$ satisfies $0=t_0<t_1<t_2<\cdots <t_{\sigma }<\cdots$, and $t_{\sigma }\to +\infty$ as $\sigma \to +\infty$, $y_k\left(t_{\sigma }^{+}\right)={lim}_{t\to t_{\sigma }^{+}}{y}_k\left(t\right)$ and $y_k\left(t_{\sigma }^{-}\right)={lim}_{t\to t_{\sigma }^{-}}{y}_k\left(t\right)$, $b_k\left(t_{\sigma }\right)$ is the impulsive gain at $t=t_{\sigma }$, and $b_k\left(t\right)=0$ for $t\ne t_{\sigma }$. The solutions of (2) are piecewise left continuous at $t_{\sigma }$, i.e., $y_k\left(t_{\sigma }^{-}\right)=y_k\left(t_{\sigma }\right)$.

Definition 1.

The drive-response networks (1) and (2) are said to achieve outer synchronization if

$$\underset{t\to +\infty }{lim}\parallel y_k\left(t\right)-x_k\left(t\right)\parallel =0,k=1,2,\cdots ,N.$$

Let $e_k\left(t\right)=y_k\left(t\right)-x_k\left(t\right)$ be the synchronization errors, then we have the following error systems:

$$\begin{array}{cc}\hfill & {\dot{e}}_k\left(t\right)=f\left(y_k\left(t\right)\right)-f\left(x_k\left(t\right)\right)+c\sum _{l=1}^N{a}_{kl}{H}_1{e}_l\left(t\right)+c\sum _{l=1}^N{b}_{kl}{H}_2{e}_l\left(t\right),t\ne t_{\sigma },\hfill \\ \hfill & e_k\left(t_{\sigma }^{+}\right)=e_k\left(t_{\sigma }^{-}\right)+b_k\left(t_{\sigma }\right)e_k\left(t_{\sigma }^{-}\right),t=t_{\sigma }.\hfill \end{array}$$

(3)

When $t=t_{\sigma }$, arrange $e_k\left(t\right)$ as

$$\begin{array}{c}\hfill \parallel e_{k_1\left(t\right)}\left(t\right)\parallel \ge \parallel e_{k_2\left(t\right)}\left(t\right)\parallel \ge \cdots \ge \parallel e_{k_p\left(t\right)}\left(t\right)\parallel \ge \parallel e_{k_{p+1}\left(t\right)}\left(t\right)\parallel \ge \cdots \ge \parallel e_{k_N\left(t\right)}\left(t\right)\parallel ,\end{array}$$

(4)

where $k_p\left(t\right)\in \{1,2,\cdots ,N\}$, $p=1,2,\cdots ,N$, and if $p\ne q$, then $k_p\left(t\right)\ne k_q\left(t\right)$. Further, if $\parallel e_{k_p\left(t\right)}\left(t\right)\parallel =\parallel e_{k_{p+1}\left(t\right)}\left(t\right)\parallel$, then $k_p\left(t\right)<k_{p+1}\left(t\right)$. Let $P\left(t_{\sigma }\right)=\{k_1\left(t_{\sigma }\right),k_2\left(t_{\sigma }\right),\cdots ,k_p\left(t_{\sigma }\right)\}$ be a set of p nodes. If $k\in P\left(t_{\sigma }\right)$, then $b_k\left(t_{\sigma }\right)=b\in (-2,-1)\cup (-1,0)$, otherwise, $b_k\left(t_{\sigma }\right)=0$, which means that $P\left(t_{\sigma }\right)$ is the index set of pinned nodes at $t=t_{\sigma }$.

Assumption 1.

Suppose that there exists a positive constant $M>0$ such that the function $f\left(x\right)$ satisfies

$$\begin{array}{c}\hfill \overline{{(y-x)}^T}(f\left(y\right)-f\left(x\right))+\overline{{(f\left(y\right)-f\left(x\right))}^T}(y-x)\le M\overline{{(y-x)}^T}(y-x).\end{array}$$

3. Main Results

Let $e\left(t\right)={\left(e_1^T\left(t\right),\cdots ,e_N^T\left(t\right)\right)}^T$, ${\tau }_{\sigma }=t_{\sigma }-t_{\sigma -1}$ be the impulsive intervals, $\lambda$ be the largest eigenvalue of $c(A\otimes H_1+\overline{A^T}\otimes \overline{H_1})+c(B+B^T)\otimes H_2$, $\beta ={(1+b)}^2$, $\rho \left(t_{\sigma }\right)=1-p(1-\beta )/N$ for $t=t_{\sigma }$ and $\rho \left(t\right)=1$ for $t\ne t_{\sigma }$.

Theorem 1.

Suppose that Assumption 1 holds. If there exists a positive constant ζ such that

$$\begin{array}{c}\hfill ln\rho \left(t_{\sigma }\right)+\zeta +(M+\lambda ){\tau }_{\sigma }<0,\sigma =1,2,\cdots ,\end{array}$$

(5)

holds, then the drive-response networks (1) and (2) achieve the outer synchronization.

Proof. 

Consider the following Lyapunov function:

$$V\left(t\right)=\sum _{k=1}^N\overline{e_k^T\left(t\right)}{e}_k\left(t\right),$$

for $t\in (t_{\sigma -1},t_{\sigma }],\sigma =1,2,\cdots .$

When $t\in (t_{\sigma -1},t_{\sigma })$,

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& \sum _{k=1}^N\overline{e_k^T\left(t\right)}{\dot{e}}_k\left(t\right)+\sum _{k=1}^N\overline{{\dot{e}}_k^T\left(t\right)}{e}_k\left(t\right)\hfill \\ \hfill =& \sum _{k=1}^N\left(\overline{e_k^T\left(t\right)}(f\left(y_k\left(t\right)\right)-f\left(x_k\left(t\right)\right))+\overline{{(f\left(y_k\left(t\right)\right)-f\left(x_k\left(t\right)\right))}^T}{e}_k\left(t\right)\right)\hfill \\ \hfill & +c\sum _{k=1}^N\sum _{l=1}^N(a_{kl}\overline{e_k^T\left(t\right)}{H}_1{e}_l\left(t\right)+\overline{a_{kl}{e}_l^T\left(t\right)H_1}{e}_k\left(t\right)\hfill \\ \hfill & +b_{kl}\overline{e_k^T\left(t\right)}{H}_2{e}_l\left(t\right)+b_{kl}\overline{e_l^T\left(t\right)}{H}_2{e}_k\left(t\right))\hfill \\ \hfill \le & M\sum _{k=1}^N\overline{e_k^T\left(t\right)}{e}_k\left(t\right)+c\overline{e^T\left(t\right)}\left((A\otimes H_1+\overline{A^T}\otimes \overline{H_1})+(B+B^T)\otimes H_2\right)e\left(t\right)\hfill \\ \hfill \le & (M+\lambda )V\left(t\right),\hfill \end{array}$$

which gives

$$\begin{array}{c}\hfill V\left(t\right)\le V\left(t_{\sigma -1}^{+}\right)e^{(M+\lambda )(t-t_{\sigma -1})}.\end{array}$$

(6)

When $t=t_{\sigma }$, one has

$$\begin{array}{cc}\hfill V\left(t_{\sigma }^{+}\right)=& \sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{+}\right)}{e}_k\left(t_{\sigma }^{+}\right)=\sum _{k\in P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{+}\right)}{e}_k\left(t_{\sigma }^{+}\right)+\sum _{k\notin P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{+}\right)}{e}_k\left(t_{\sigma }^{+}\right)\hfill \\ \hfill =& {(1+b)}^2\sum _{k\in P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)+\sum _{k\notin P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)\hfill \\ \hfill =& \beta \sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)+(1-\beta )\sum _{k\notin P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right).\hfill \end{array}$$

According to the definition of $P\left(t_{\sigma }\right)$, one has

$$\begin{array}{c}\hfill \frac{1}{N-p}\sum _{k\notin P\left(t_{\sigma }\right)}\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)\le \frac{1}{N}\sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)\end{array}$$

and

$$\begin{array}{cc}\hfill V\left(t_{\sigma }^{+}\right)\le & \beta \sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)+\frac{(N-p)(1-\beta )}{N}\sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)=\rho \left(t_{\sigma }\right)V\left(t_{\sigma }^{-}\right).\hfill \end{array}$$

(7)

According to mathematical induction, combining inequalities (6) and (7), for any positive integer $\sigma$, the following inequality can be derived:

$$V\left(t_{\sigma }^{+}\right)\le V\left(t_0^{+}\right)\prod _{s=1}^{\sigma }\rho \left(t_{\sigma }\right)e^{(M+\lambda )(t_s-t_{s-1})}.$$

If conditions (5) hold, one has

$$\begin{array}{c}\hfill \rho \left(t_{\sigma }\right)e^{(M+\lambda )(t_s-t_{s-1})}<e^{-\zeta },s=1,2,\dots ,\sigma ,\end{array}$$

and

$$\begin{array}{c}\hfill V\left(t_{\sigma }^{+}\right)\le V\left(t_0^{+}\right)e^{-\sigma \zeta },\end{array}$$

which implies $V\left(t_{\sigma }^{+}\right)\to 0$ as $\sigma \to +\infty$. Then for $t\in (t_{\sigma },t_{\sigma +1})$, one has $V\left(t\right)\le V\left(t_{\sigma }^{+}\right)e^{(M+\lambda ){(t-t_{\sigma })}^{\alpha }}\to 0$ as $t\to +\infty$. which implies that $\parallel e_k\left(t\right)\parallel \to 0$ as $t\to +\infty$, i.e., the outer synchronization of drive-response networks (1) and (2) is achieved. This completes the proof. □

Remark 1.

From conditions (5), the necessary values of impulsive intervals and gains for achieving outer synchronization can be calculated for any given drive-response networks. For other drive-response networks with different system parameters, however, the necessary values must be recalculated. Thus, in the following, we combine adaptive strategy with impulsive control to design unified controllers.

Theorem 2.

Suppose that Assumption 1 holds. If there exists a constant $\zeta >0$ such that

$$\begin{array}{c}\hfill ln\rho \left(t_{\sigma }\right)+\zeta +\widehat{L}\left(t_{\sigma }\right){\tau }_{\sigma }<0,\sigma =1,2,\cdots ,\end{array}$$

(8)

holds, where $\widehat{L}\left(t\right)$ is the estimated value of $M+\lambda$, $\dot{\widehat{L}}\left(t\right)=\eta \overline{e^T\left(t\right)}e\left(t\right)$ and $\eta >0$ is adaptive gain, then the drive-response networks (1) and (2) achieve the outer synchronization.

Proof. 

Consider the following Lyapunov function:

$$\begin{array}{c}\hfill V\left(t\right)=\sum _{k=1}^N\overline{e_k^T\left(t\right)}{e}_k\left(t\right)+\frac{\rho \left(t\right)}{2\eta }{(\widehat{L}\left(t\right)-M-\lambda )}^2.\end{array}$$

for $t\in (t_{\sigma -1},t_{\sigma }],\sigma =1,2,\cdots .$

When $t\in (t_{\sigma -1},t_{\sigma })$, one has

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& \sum _{k=1}^N\overline{e_k^T\left(t\right)}{\dot{e}}_k\left(t\right)+\sum _{k=1}^N\overline{{\dot{e}}_k^T\left(t\right)}{e}_k\left(t\right)+\frac{1}{\eta }\left(\widehat{L}\left(t\right)-M-\lambda \right)\dot{\widehat{L}}\left(t\right)\hfill \\ \hfill =& \sum _{k=1}^N\left(\overline{e_k^T\left(t\right)}(f\left(y_k\left(t\right)\right)-f\left(x_k\left(t\right)\right))+\overline{{(f\left(y_k\left(t\right)\right)-f\left(x_k\left(t\right)\right))}^T}{e}_k\left(t\right)\right)\hfill \\ \hfill & +c\sum _{k=1}^N\sum _{l=1}^N(a_{kl}\overline{e_k^T\left(t\right)}{H}_1{e}_l\left(t\right)+\overline{a_{kl}{e}_l^T\left(t\right)H_1}{e}_k\left(t\right)+b_{kl}\overline{e_k^T\left(t\right)}{H}_2{e}_l\left(t\right)\hfill \\ \hfill & +b_{kl}\overline{e_l^T\left(t\right)}{H}_2{e}_k\left(t\right))+\left(\widehat{L}\left(t\right)-M-\lambda \right)\overline{e^T\left(t\right)}e\left(t\right)\hfill \\ \hfill \le & \widehat{L}\left(t\right)\overline{e^T\left(t\right)}e\left(t\right)\hfill \\ \hfill \le & \widehat{L}\left(t_{\sigma }\right)V\left(t\right),\hfill \end{array}$$

which gives

$$\begin{array}{c}\hfill V\left(t\right)\le V\left(t_{\sigma -1}^{+}\right)e^{\widehat{L}\left(t_{\sigma }\right)(t-t_{\sigma -1})}.\end{array}$$

When $t=t_{\sigma }$,

$$\begin{array}{cc}\hfill V\left(t_{\sigma }^{+}\right)=& \sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{+}\right)}{e}_k\left(t_{\sigma }^{+}\right)+\frac{\rho \left(t_{\sigma }\right)}{2\eta }{(\widehat{L}\left(t_{\sigma }\right)-M-\lambda )}^2\hfill \\ \hfill \le & \rho \left(t_{\sigma }\right)\sum _{k=1}^N\overline{e_k^T\left(t_{\sigma }^{-}\right)}{e}_k\left(t_{\sigma }^{-}\right)+\frac{\rho \left(t_{\sigma }\right)}{2\eta }{(\widehat{L}\left(t_{\sigma }\right)-M-\lambda )}^2\hfill \\ \hfill =& \rho \left(t_{\sigma }\right)V\left(t_{\sigma }^{-}\right).\hfill \end{array}$$

Thus, similar to the proof of Theorem 1, the proof can be completed. □

Remark 2.

From the conditions (8), when p, N, b and ζ are fixed, the impulsive instants $t_{\sigma }$ can be chosen through finding the maximum value of $t_{\sigma }$ subject to $t_{\sigma }<t_{\sigma -1}-(ln\rho \left(t_{\sigma }\right)+\zeta ){\widehat{L}}^{-1}\left(t_{\sigma }\right)$ with $\sigma =1,2,\cdots$.

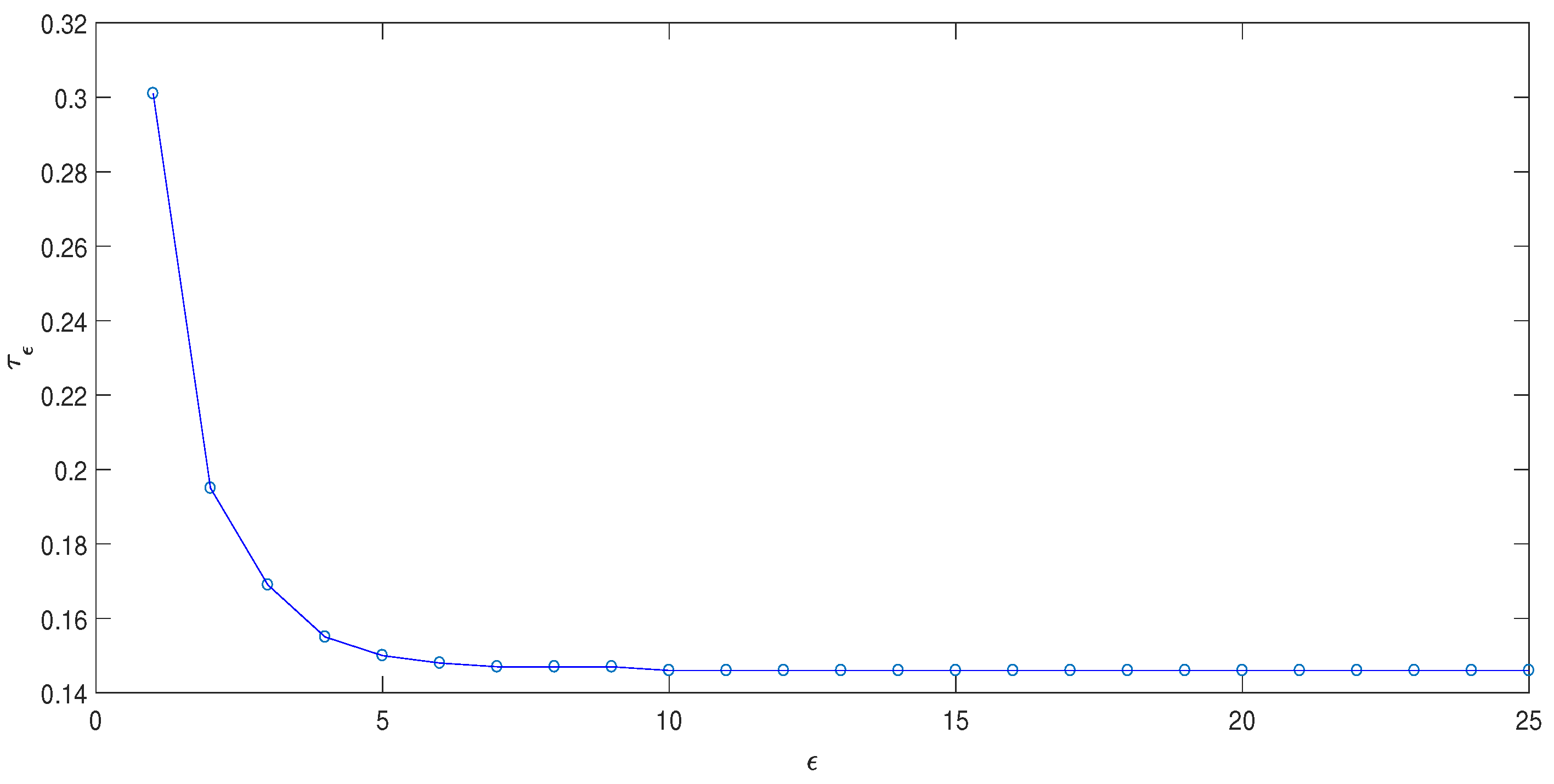
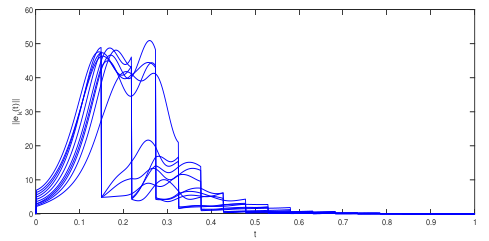
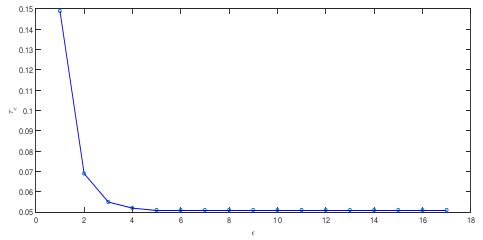
4. Numerical Simulations

Example 1.

Consider drive-response networks coupled with 10 nodes. Choose the node dynamics as a complex-variable Chen system [37]

$$\begin{array}{cc}\hfill {\dot{x}}_{k1}=& 27(x_{k2}-x_{k1}),\hfill \\ \hfill {\dot{x}}_{k2}=& -4x_{k1}+23x_{k2}-x_{k1}{x}_{k3},\hfill \\ \hfill {\dot{x}}_{k3}=& (\overline{x_{k1}}{x}_{k2}+x_{k1}\overline{x_{k2}})/2-x_{k3},\hfill \end{array}$$

where $x_{k1}$ and $x_{k2}$ are complex variables, $x_{k3}$ is the real variable. Refer to [34], choose $M=79$ such that Assumption 1 holds.

Choose $c=1$, $H_1=diag(1,1,0)$, $H_2=diag(0,0,1)$,

$$\begin{array}{c}\hfill A=\left[\begin{array}{cccccccccc}-1-3i& 0& 0& 0& 0& 0& 0& i& 0& 1+2i\\ 1+i& -2-4i& 0& 0& 0& 0& 0& 0& 1+3i& 0\\ 0& 0& -3-2i& 0& 0& 3+2i& 0& 0& 0& 0\\ 0& 0& 2+i& -3-5i& 0& 0& 1+4i& 0& 0& 0\\ 0& 0& 0& 2+2i& -2-2i& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1+i& -1-i& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -1-4i& 0& 0& 1+4i\\ 3+4i& -1-i& 0& 0& 0& 0& 0& -2-3i& 0& 0\\ 0& 5+4i& 0& -1+2i& 0& 0& 0& 0& -4-6i& 0\\ 0& 0& 0& 2+i& 0& 0& 0& 1+2i& 0& -3-3i\end{array}\right],\end{array}$$

$$B=\left[\begin{array}{cccccccccc}-4& 0& 0& 0& 0& 0& 0& 1& 0& 3\\ 1& -3& 0& 0& 0& 0& 1& 0& 2& 0\\ 0& 0& -5& 0& 0& 5& 0& 0& 0& 0\\ 0& 0& 2& -4& 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 3& -3& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 2& -2& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -3& 0& 0& 3\\ 1& 1& 0& 0& 0& 0& 0& -2& 0& 0\\ 0& 5& 0& -1& 0& 0& 0& 0& -4& 0\\ 0& 0& 0& 2& 0& 0& 0& 3& 0& -5\end{array}\right].$$

In numerical simulations, choose $b=-0.9$, $\zeta =0.01$, $p=3$ and ${\tau }_{\sigma }=0.004$ for $\sigma =1,2,\cdots$. By simple calculations, one has $\lambda =2.2253$ and $ln0.703+0.01+(M+\lambda )\times \left(0.004\right)=-0.017499<0$. That is, the conditions (5) in Theorem 1 are satisfied and the outer synchronization can be achieved. Choose the initial values of $x_k\left(0\right)=0.1\times {(2+0.2ki,1+0.5ki,0.1k)}^T$ and $y_k\left(0\right)={(1+0.5ki,2+0.5ki,0.2k)}^T$ with $i=\sqrt{-1}$ for $k=1,2,\cdots ,10$. Figure 1 shows the orbits of the norms of synchronization errors $e_k\left(t\right)$, $k=1,2,\cdots ,10$.

Example 2.

Consider the same network in Example 1 via adaptive impulsive pinning control. In numerical simulations, choose $b=-0.9$, $\eta =0.0002$, $\widehat{L}\left(0\right)=0.1$. The impulsive instants are estimated according to Remark 2. Figure 2 shows the orbits of the norm of synchronization errors. Figure 3 shows the impulsive interval ${\tau }_{\sigma }$ versus σ. From Figure 3, it can be seen that the necessary value of ${\tau }_{\sigma }$ is much larger than the estimated value from conditions (5), i.e., the adaptive impulsive pinning control can reduce control cost.

Example 3.

Consider the outer synchronization of drive-response network consisting of 10 Lü systems [37]

$$\begin{array}{cc}\hfill {\dot{x}}_{k1}=& 40(x_{k2}-x_{k1}),\hfill \\ \hfill {\dot{x}}_{k2}=& -x_{k1}{x}_{k3}+22x_{k2},\hfill \\ \hfill {\dot{x}}_{k3}=& (\overline{x_{k1}}{x}_{k2}+x_{k1}\overline{x_{k2}})/2-5x_{k3},\hfill \end{array}$$

where $x_{k1}$ and $x_{k2}$ are complex variables, $x_{k3}$ is the real variable. In numerical simulations, choose $b=-0.9$, $\eta =0.003$, $\widehat{L}\left(0\right)=0.1$ with the other parameters the same as in Example 1. Figure 4 shows the orbits of the norm of synchronization errors. Figure 5 shows the impulsive interval ${\tau }_{\sigma }$ versus σ.

From Examples 2 and 3, the adaptive impulsive pinning controllers are valid for different networks. That is, the controllers are universal to some extent.

5. Conclusions and Discussions

Both static and adaptive impulsive pinning controllers are designed for achieving the outer synchronization of complex-variable networks with complex coupling. The corresponding synchronization conditions and estimation algorithms with respect to the impulsive gains and intervals are provided as well. Based on the Lyapunov function method and stability theory of impulsive differential equations, the main results are analytically proved. The obtained results are illustrated to be effective by three numerical examples.

On the other hand, synchronization and control of fractional-order dynamical networks attracts increasing attention [5,6,7,8]. As we know, the fractional-order system has a long memory effect from the initial state to the current state. When the impulsive controllers are added at $t=t_k$, the memory effect for $t\in (t_k,t_{k+1})$ needs to be adjusted from $t_k$ to t. That is, the obtained results in this paper cannot be directly extended to the fractional-order dynamical networks. Thus, designing impulsive (or hybrid impulsive) controllers for fractional-order dynamical networks is a challenging and important issue and deserves further studies.