The Initial Algebraic Knowledge of Preservice Teachers

Abstract

Early algebra proposes to incorporate algebra in primary school from the first years of schooling. The success of this incorporation depends, to a large extent, on the training of teachers, so the objective of this article is to study whether the degree of algebraic knowledge of student teachers at the beginning of their training. To conduct this, 106 preservice teachers were given a questionnaire. This survey is based on two daily life situations. They had to propose tasks to develop algebraic reasoning in primary school students. Most of the participants designed tasks in which they assigned specific values to the indeterminate ones and solved them arithmetically. In this way, they transformed open situations and numerous opportunities to promote algebraic thinking in students through the generalization and representation of relationships and functions into closed single-solution problems that do not promote algebraic thinking. We can see from the results that the participants’ algebraic knowledge is insufficient. Therefore, it is necessary to include in their training process the programs and experiences that will allow them to design tasks in order to detect and promote algebraic thinking in their future students. Sequences of tasks are presented to develop both situations by generalizing and representing relationships and functions, which can serve as a starting point for future training programs and experiences.

1. Introduction

The learning of algebra causes in many students, especially in Secondary Education, difficulties that frequently provoke a rejection towards the totality of mathematics [1,2]. In this line, decades ago, Kieran [3] already warned that “algebraic thinking is an area very much needed in mathematical research” (p. 163).

These difficulties are due, in large part, to a simplistic and linear interpretation of Piagetian theory that has taken the reflections on the development of operations too literally [4]. For Piaget [5], the students’ cognitive development occurs in stages, and the stage of development for formal or abstract thinking begins around the age of 11 and is consolidated around the age of 15. In this way, it was considered that Primary school students were not yet ready to move from concrete operational thinking to formal or abstract thinking; for this reason, traditionally, the curricula explicitly postponed the study of algebra until the first years of Secondary Education.

However, in recent decades, researchers in mathematics didactics were against this assessment; for example, Socas [6] considers algebraic thinking to be implicit in Primary school students, and Mason [7] considers that students come to the educational system with natural generalization abilities that allow them to develop algebraic thinking. Other researchers believe that primary school students are able to consider arithmetic operations as functions [8], algebraically symbolize arithmetic relationships [9], work with functional relationships [10] or solve problems using graphs and tables [11].

In response to these observations, in early algebra, it is recommended the introduction of algebraic thinking in primary school through activities with patterns and the study of relationships and their properties. In this way, teachers are encouraged to foster instructional environments in which students, in addition to developing calculus skills, are encouraged to explore, model, make predictions, discuss, argue and test ideas. Based on these recommendations, many countries such as Australia, Chile, Canada, Portugal, Korea, China or the United States, among others, are incorporating the teaching of algebra into their programs from the first years of schooling.

However, research on teachers’ competencies and beliefs about algebraic reasoning has observed that “most elementary school teachers have little experience in the rich and related aspects of elementary algebraic reasoning” [12] (p. 414) and has shown deficiencies regarding their training that could waste the students’ algebraic competencies [12,13].

This incorporation represents a challenge for educational administrations, which must redefine their educational systems, and especially for teachers and teacher educators who must direct their actions in class towards understanding patterns, relationships and functions and analyzing mathematical equations and structures, with progressive use of algebraic symbols [14].

Faced with this challenge, teachers must act as agents of change and offer their students the opportunity to progress in their algebraic reasoning, and researchers and teacher educators must propose new ways of learning and unleash future teachers’ reflection on their own understanding of algebraic thinking and their ability to develop algebraic thinking in their students.

For this reason, researchers such as Castro, Godino and Rivas [15] consider it “pertinent to offer future teachers training experiences on planning and didactic analysis of tasks, which include some aspects of elementary algebraic reasoning in order to initiate them in their identification and promotion” (p. 75).

From this perspective, the purpose of this work is to analyze the algebraic knowledge of student teachers at the beginning of their training and to check if it is sufficient to detect and promote algebraic thinking in Primary school students. This information could help researchers in Mathematical Didactics and teacher educators to propose these new ways of learning algebra and to plan training programs that allow future teachers to design tasks to recognize and promote algebraic thinking in their students.

1.1. Math Teachers’ Knowledge

Shulman [16], contrary to previous trends directed at general aspects of teaching–learning, opened a new line of research in mathematics didactics focused on the characterization of the mathematics teacher’s knowledge. Shulman [17] himself synthesized this line, which is still open, by stating that the teaching process begins when the teacher “understands what has to be learned and how it should be taught” (p. 9). In this way, he established two kinds of knowledge that a teacher must have: content knowledge, in reference to the quantity and structure of the content, and didactic knowledge, in reference to the way of representing and enunciating the contents to make them understandable to the students.

Researchers who have studied the teacher’s knowledge emphasize the importance of both types of knowledge. Thus Grossman, Wilson and Shulman [18] point out that “good teachers not only know their content, but they also know things about their content that make effective instruction possible” (p. 5), and Shulman [17] speaks of “that special amalgam between subject and pedagogy that constitutes an exclusive sphere of teachers” (p. 11).

Other studies on teacher’s knowledge, such as Mathematical Knowledge for Teaching (MKT) [19] and Mathematics Teacher Specialized Knowledge (MTSK) [20], also consider the two aspects of knowledge. In this way, two large knowledge domains are established in the MKT: Subject Matter Knowledge (SMK) and Pedagogical Content Knowledge (PCK); and two similar domains are also established in the MTSK: Mathematical Knowledge (MK) and Pedagogical Content Knowledge (PCK).

Other models that have implicitly established content knowledge and pedagogical knowledge as the knowledge that mathematics teachers should have are “proficiency” in the teaching of mathematics [21] and the “Knowledge Quartet” [22].

Some researchers focus especially on pedagogical knowledge: on the one hand, some speak of the ability to explain the content to students through instructional strategies and methods [23]; on the other hand, others define it as the ability to interpret and transform content into understandable units for students [24]. Using the same approach, Chevallard [25] coined the concept of Didactic Transposition to explain the process by which content is modified to adapt it to teaching.

From the perspective of using the teacher’s knowledge to improve the teaching–learning process of mathematics arose the teaching competence of “professional noticing”, which is conceptualized from three skills [26]: (1) identify relevant aspects in students’ mathematical production, (2) interpret and understand students’ mathematical thinking and (3) make decisions to improve the teaching–learning process. The first skill is related to content knowledge, the second is related to the knowledge of student characteristics and the third is related to didactic knowledge.

This work aims to study the algebraic knowledge of student teachers from both approaches, content and didactic. For this, they will analyze tasks considering two situations of daily life proposed in order to develop the algebraic thinking of primary school students.

1.2. Algebraic Thinking in Primary Education

For Vergel [27], algebraic thinking is a form of mathematical thinking. For Kieran [28], it is an approach to quantitative situations focused on relational aspects. For Radford [29], it is a “very sophisticated type of cultural reflection and action, a way of thinking ”(p. 319).

Algebraic thinking, unlike numerical thinking, deals with indeterminate quantities and operates with them as if they were numbers by expressing them symbolically. In this way, three elements are found in algebraic thinking: (1) the indeterminacy of algebraic objects that allow the substitution of an unknown object for another, (2) the analytical treatment of indeterminate objects and (3) the symbolic expression to designate the objects [30].

Squalli [31], in his integrative model of algebra and algebraic thinking, presents algebra and algebraic thinking as the two complementary and indissoluble sides of the same coin: “algebra appears as a type of mathematical activities and algebraic thinking as a set of intellectual abilities involved in those activities” (p. 277). Algebra activities are (1) the construction and interpretation of algebraic models, (2) the manipulation of algebraic expressions and (3) the elaboration and application of structures and procedures. Additionally, the skills of algebraic thinking are (1) thinking analytically, (2) constructing, interpreting and validating algebraic models of real or mathematical situations; (3) manipulating algebraic expressions; and (4) generalizing and abstracting relationships, rules and algebraic structures of real or mathematical situations

The traditional teaching of mathematics in Primary Education causes difficulties in the teaching of algebra in Secondary Education students. Even if some researchers have attributed these difficulties to limitations in cognitive development [32,33] or to the abstraction of algebra [34], for many others [35,36,37,38,39], these difficulties reflect “the deficiencies of mathematics teaching with an excessive computational focus on arithmetic in primary school” [40] (p. 109).

The teaching of arithmetic is often reduced to teaching the algorithms of operations, ignoring the properties of operations and their meaning; this later makes it difficult for too many students to understand algebraic procedures, many of them based on the properties of operations [40]. By ignoring the algebraic character of arithmetic, students do not develop the skills of generalization, expression and justification, which are a fundamental part of algebra [41]. Furthermore, inadequate teaching of arithmetic produces an artificial separation from algebra, which prevents students from making explicit connections between arithmetic and algebra [42] and causes many of the difficulties of learning algebra.

Schliemn, Carraher and Brizuela [43] argue that arithmetic questions should be treated as concrete examples of more abstract ideas and concepts; consider that this treatment, in addition to improving the understanding of arithmetic, will contribute, later, to meaningful learning of algebra. For this reason, they consider that “the real challenge consists in finding opportunities to highlight the algebraic character of elementary mathematics” (p. 65). Kieran [3] specified the difficulties in learning algebra in three aspects: in the change in conventions regarding the arithmetic referent, in the recognition and use of structures and in the interpretation of letters. Examples of difficulties related to the change in conventions between arithmetic and algebra are:

• The concept of variable;
• The operation signs or the equal sign;
• Examples of difficulties related to the recognition and use of structures are the ordering of elements;
• The hierarchy of operations or the systematic structure that refers to the properties of operations;
• Examples of difficulties related to the interpretation of letters are the different uses of letters made in algebra, sometimes as unknown factors and sometimes as variables or generalized numbers.

To avoid these difficulties and given the evidence that Primary Education students have innate abilities to reason algebraically [5,6,7,8,10], in early algebra, it is proposed to change the teaching of mathematics by integrating algebraic thinking from the first years of schooling.

Various researchers [28,44,45,46,47] proposed different approaches to introduce algebra and algebraic thinking in Primary Education: generalized arithmetic, relationships, functions, equations, generalizations, algebraic language, transformations, modeling, problem solving.

Furthermore, these researchers recommend that school algebra should not focus “on the presentation of ready-made symbolizations called algebraic expressions, but on the organization of classroom activities that actively involve students in mathematical processes, in which algebraic thinking can emerge and be understood” [48] (p. 3). Kieran [2] proposed to start with activities that include the development of ways of thinking such as the analysis of relationships among quantities, the identification of structures, the study of change, generalization, problem solving, modeling, justification, test and prediction. Finally, Carraher and Schliemann [39] consider that the introduction of concepts and representations of algebra can be achieved, from the first years of schooling, through “the analysis of the relations among sets of values or quantities, in particular functional relations” (p. 111). Delving into these ideas, Schoenfeld [40] argues that algebra is the “study of patterns, relationships and functions that uses a variety of representations including verbal, tabular, graphical and symbolic ones” (p. 11). The NCTM [14] argues “that algebra is best learned as a set of concepts and techniques linked to the representation of quantitative relationships and as a style of mathematical thinking to formalize patterns, functions and generalizations” [41] (p. 83).

From this perspective, the NCTM [14] recommends that teaching programs train primary school students to understand patterns, relationships and functions, to represent mathematical situations and structures in a symbolic way, and to analyze the change in various contexts. This way of thinking, described as algebraic, is the heart of mathematics [7] and can be developed by young children [9,42,49,50] and enhanced through activities that involve them in the mathematical processes described above.

The focus of this research to initiate algebra is the functional approach, which refers to the development of experiences of real-life situations in which quantitative relationships can be explained by means of functions or sets of functions [43]. These functions are understood as mathematical relationships between two sets, in which each element of the first set, called the domain, is related to another element of the second set, called the codomain or range.

Functional thinking is a cognitive activity that focuses on “the construction, description, representation and reasoning with and about the functions and the elements that constitute them” [51] (p. 3). Functional thinking includes the establishment and generalization of relationships among varying quantities, the representation of relationships, the use of letters to represent indeterminate quantities (variables or unknowns), the use of tables and graphs, the analysis and prediction of functional behavior.

For Carraher and Schliemann [39], the importance of functions in the introduction of algebra in Primary Education means that:

• Arithmetic operations can be considered functions;
• The domain and range of the functions favor the introduction of variables;
• The representations of the functions are multiple (written or verbal, symbolic or algebraic, tabular, graphic, pictorial, etc.);
• Equations and inequalities can be interpreted as a comparison of functions.

Furthermore, functional thinking in Primary Education contributes to building a solid foundation for learning algebra at higher levels [52,53], fosters the ability to generalize, represent, justify and reason with mathematical relationships [54], and it is a useful tool in problem solving [55].

In order to make the development of algebraic thinking in general, and functional thinking in particular, become the main objectives of mathematics teaching in Primary Education, teachers will have to adapt their beliefs and promote activities that involve the analysis of relationships and functions, the identification of patterns and generalization of functions [39]. Teachers must also find opportunities to highlight the algebraic character of basic mathematics [49], especially by “algebrising” arithmetic problems; that is, transforming arithmetic problems to develop students’ algebraic thinking [56] and by reducing their numerical and computational character.

As a starting point to begin training programs and experiences that promote the ability to find opportunities that highlight the algebraic nature of mathematics, in this paper, we study the algebraic knowledge of student teachers who have not yet started their algebraic training. In this way, the algebraic nature of the student teachers’ proposals is analyzed from two real-life mathematical cases proposed to promote algebraic and functional thinking in Primary Education students.

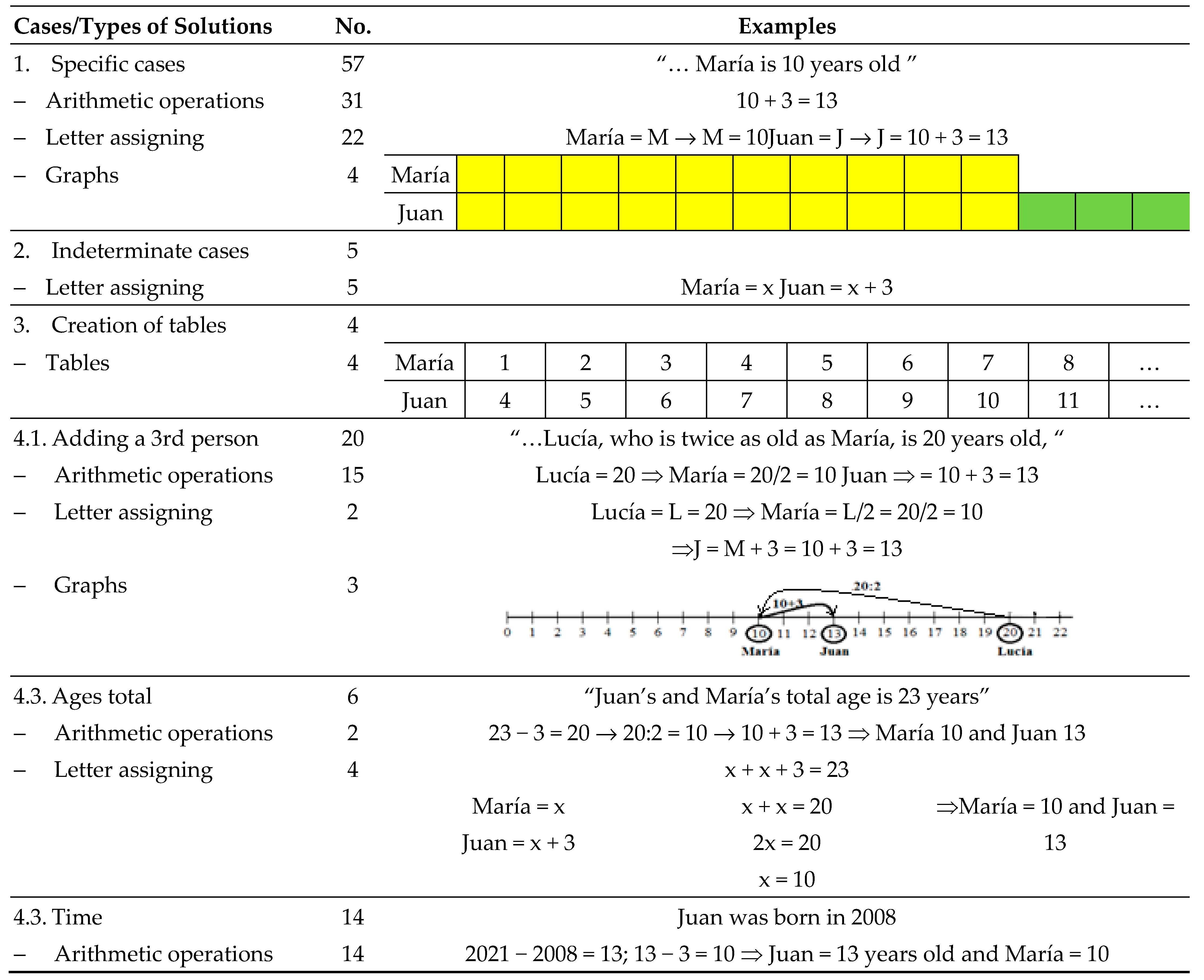
2. Materials and Methods

2.1. Participants

In this study on the algebraic knowledge of students, teachers participated 106 preservice teachers who are students undertaking their 1st year of a degree in Primary Education, within the subject "Mathematics and its Didactics I", whose students had not yet received specific lessons on algebraic thinking.

Eighty of these participants, 75.47%, had studied mathematics in high school until 18 years old (38 from the Science branch and 42 from the Social Sciences itinerary); however, the other 26 students, 24.53%, (22 from the Humanistic itinerary and 4 from the Arts branch) had not taken the subject since 4th year of Secondary Education (16 years old).

The research was carried out at the beginning of the first year of the degree, and the information received was limited to a brief explanation of the relationship and difference between arithmetic, algebra and algebraic thinking in the presentation of the questionnaire.

2.2. Data Collection

The data collection was carried out by means of a questionnaire in which two situations of daily life proposed to enhance the algebraic thinking of Primary Education students are presented. In both cases, the student teachers are asked to design tasks in which the algebraic thinking for Primary Education students must be developed. The proposed cases are adaptations of typical problems that have been used for the introduction of early algebraic thinking [31] and in which the participants can demonstrate their algebraic knowledge, both content and didactic (

Table 1. Algebraic knowledge questionnaire for student teachers.

In the following questionnaire, two cases from everyday life are presented. After carefully analyzing the statements of the cases, you should design tasks to develop algebraic thinking in Primary Education students.

Case 1. Interpretation of variables in relationships − Juan is three years older than María.

Case 2. Solving equations as comparison of functions − Lucas has €8 in his hand and the rest of his money in his wallet. − Aina has 3 times more money in her wallet than Lucas has in his.

).

When analyzing the tasks proposed by the participants, their degree of algebraic knowledge can be inferred since, in order to design adequate tasks adapted to the characteristics of the students, they must have sufficient knowledge of content and didactics.

2.3. Development of Cases and Data Analysis

2.3.1. Case 1. Interpretation of Variables in Relationships

Although the current curriculum promotes the use of letters as unknowns, that is, as unknown values the student must find out, the letters can also represent variables of a relationship defined by the ordered pairs (n, f(n)).

Some teachers think that the ambiguity of letters can confuse students, and therefore, they minimize or even avoid their use, preventing them from progressing algebraically. However, this ambiguity and the discussions among peers allow the teacher to guide the student from the concretion of numbers to the abstraction of letters and promote the creation of algebraic thinking.

In a possible algebraic development of the case proposed, we would start working with specific cases, first with small numbers and then with larger numbers. Later, the case would be generalized with indeterminate cases by using letters as variables; the rule that relates the ages of John and Mary would be expressed, first verbally and then symbolically or algebraically. The sequence of tasks would be completed by making a table with the ages of both and representing the function in a system of axes. We can continue reversing the process of changing the variables so that the independent variable is now Maria’s age and carrying out the same stages (small specific cases, large specific cases, indeterminacy, verbal and algebraic expression of the rule, creation of tables and representation of the function).

2.3.2. Case 2. Equations to Compare Functions

One way to introduce the resolution of equations in Primary Education from functional thinking comes from the comparison of functions. To perform this, two functions are taken from a common independent variable, and then both functions are represented in the same coordinate system.

Faced with case 2, the students sense that they must find out the amount of money each one has. They begin to guess solutions with specific amounts in Lucas’ wallet, first small and then large; later, encouraged by the teacher, they will look for solutions with indeterminate quantities (letters). After that, the rules of the functions that relate the amounts of both with the money in Lucas’ wallet are expressed, verbally and symbolically, which acts as an independent variable; the tables are completed, and the functions are represented, first in different systems and finally in a single system. The solution is determined by the cut-off point, whose x-coordinate corresponds to the independent variable (money in Lucas’ wallet), and the y-coordinate corresponds to the money of each one of them. From the representation, the possible solutions of the cases are analyzed based on the independent variable, that is, from the money in Lucas’ wallet. The development could be completed by performing the reverse process and changing the independent variable. In both cases, the student can work with indeterminate quantities, and we operate with them as if they were numbers and they are expressed symbolically; in other words, the three elements of Radford’s characterization of algebraic thinking [30] are covered: the indeterminacy of algebraic objects, their analytical treatment and their symbolic expression.

In addition, both sequences follow the early algebra proposals to incorporate algebra in the first years of schooling: (1) fundamental aspects of algebraic thinking are included, such as the relationships among quantities, the study of change, generalization, functions, equations, modeling, problem solving, etc.; and, (2) techniques related to the representation of relationships and functions that include verbal, tabular, graphic and symbolic expressions are used [2,14,39,40,45,46,47,48,51].

3. Results

3.1. Case 1

In the tasks proposed by the student teachers for the first situation, 54% of the participants proposed a close problem for a specific case, inventing a piece of information; 5% limited themselves to assigning letters to Juan and María, that is, they worked with indeterminate; 4% proposed to build tables; and 38% introduced new variables in the case. In addition, to solve the task, 58% of the participants performed arithmetic operations, 31% assigned letters to the variables, 5% limited themselves to use tables and 7% used graphs (

Table 2. Tasks and types of solutions in case 1.

Groups			Resolution Strategies				Total
			Arithmetic Operations	Letter Assigning	Tables	Graphs
1.	Specific cases		31	22	-	4	57 (54%)
2	Indeterminate cases		-	5	-	-	5 (5%)
3	Creation of tables		-	-	4	-	4 (4%)
4	Incorporation of variables	3rd person	15	2	-	3	20 (19%)
		Sum of ages	2	4	-	-	6 (6%)
		Time	14	-	-	-	14 (13%)
	Total		61 (58%)	33 (31%)	5 (5%)	7 (7%)	106 (100%)

).

Almost all participants transformed an open situation, with multiple possibilities to promote and develop algebraic thinking, into a closed problem with a single solution, which they mostly solved arithmetically.

Table 3. Examples of resolution for case 1.

shows examples of the resolution of the case following the classification of Table 2.

The 57 participants in the first group, the largest, incorporated María’s age as a datum, thus eliminating the fundamental element of algebraic thinking: indeterminacy. In addition, most of them operated arithmetically to solve the task, other participants limited themselves to writing the initials of María and Juan when assigning letters and four of them responded graphically.

In the responses of the five participants in the second group, we found the element of indeterminacy, but they did not work analytically with the indeterminate and limited themselves to writing that the ages of Juan and María are x and x + 3, respectively.

The four participants in the third group simply completed the table and performed an iterative count

Participants in the other groups introduced new variables: a new person, the sum of ages or time. Most of them solved the task arithmetically; only four participants performed it algebraically, solving an equation that current Primary Education students could hardly solve, and three students used the number line to solve the task.

3.2. Case 2

Following the same procedure as in the previous case, in the tasks proposed by the student teacher, we can see that the majority of the participants, 93%, considered that a datum was missing in the case and incorporated, explicitly or implicitly, a new datum; 5% made use of an indeterminate and 2% made a new statement, which is meaningless. We can also observe that to solve the task they propose, 59% performed arithmetic operations, 30% assigned letters to different variables, 3% completed a table and 8% of them used graphic methods (

Table 4. Tasks posed and types of resolution in case 2.

Groups			Resolution Strategies				Total
			Arithmetic Operations	Letter Assigning	Tables	Graphs
1.	Data incorporation	Lucas’ wallet	30	4	1	4	39 (37%)
		Total Lucas	17	5		3	25 (24%)
		Total Aina	8	2			10 (9%)
		Total from both	6	5		1	12 (11%)
		Both the same		11	2		13 (12%)
2	Use of indeterminate			5			5 (5%)
3	Meaningless statements		2				3 (3%)
	Total		63 (59%)	32 (30%)	3 (3%)	8 (8%)	106 (100%)

).

As in case 1, almost all students transformed an open situation, with multiple possibilities to promote and develop algebraic thinking, into a closed problem with a single solution, and also, for the most part, they solved the problem arithmetically.

Table 5. Tasks posed and types of solutions in case 2.

shows examples of the resolution of the case following the classification of the previous table (groups and types of resolution).

The 98 participants in the first five cases added a new piece of information to the case, which prevented an algebraic approach by eliminating the element of indeterminacy; and most solved the new situations arithmetically, either with arithmetic operations, assigning letters to variables, using tables or graphically

From a total of 16 participants, 5 of them considered the money that both of them had as a new datum, and 11 considered that both of them had the same amount, and they all solved the task by posing an equation. All but two of them solved the equation correctly; one of them algebraically proposed the case as “8 − x”, the second one proposed a meaningless equation “3(x − 8) = 0”.

The five participants who used an indeterminate simply wrote that “Lucas has 8 + x, Aina 3x”, but they did not operate with x as indeterminate.

Two participants wrote sentences that are meaningless, since they contain data that are incompatible with each other.

4. Discussion

From this perspective, the purpose of this work was to analyze whether the algebraic knowledge of preservice teachers, at the beginning of their training, is sufficient to detect and promote algebraic thinking in Primary Education students. To conduct this, 106 preservice teachers were given a questionnaire in which, based on two cases in daily life, they had to propose tasks to develop algebraic reasoning in primary school students.

Most of the participants proposed tasks that reduced the two open situations, which offered multiple opportunities to develop algebraic thinking in Primary school students, to simple closed problems with a single solution that, in addition, they solved arithmetically; this result confirms an excessively computational approach to teaching mathematics [39]. Many participants modified the sentences to make it easier for students to solve tasks numerically, ignoring the algebraic nature of arithmetic [42] and preventing students from establishing connections between arithmetic and algebra [43]. Furthermore, few participants assigned letters to algebraic objects, and most of them were not capable of working analytically with variables and unknowns, ignoring the elements of algebraic thinking established by Radford [30].

In this way, in the initial algebraic training of the student teachers, activities should be incorporated in order to allow them to recognize the possibilities that certain daily situations present to promote the development of algebraic thinking of their future students. The article includes, from the two cases presented to the student teachers, respective sequences of tasks, which can serve as a starting point to start training programs and experiences and as an intervention proposal in the Didactics of Mathematics classes. In both sequences, we can see: (1) functional relationships are recognized from near and far specific cases; (2) they are generalized with indeterminate cases; (3) are expressed verbally and symbolically and are represented tabularly and graphically; moreover, in the sequence of the second situation, the two functional relationships to start the study of equations are compared (

Table 6. Task sequence to promote algebraic thinking from case 1.

Process	Task	Example
Direct process	1.1. Near specific number	− If Juan is 8 years old, how old is María?
	1.2. Far specific number	− If Juan is 52 years old, how old is María?
	1.3. Indeterminate number	− If Juan is n years old, how old is María?
	1.4. Verbal expression of the rule	− State a rule that relates Juan’s and María’s age
	1.5. Algebraic expression of the rule	− Algebraically express the rule [f(n) = n + 3]
	1.6. Using tables	− Complete the table
		Juan	0	1	2	3	4	…	52	…	n
		María
	1.7. Graphical representation	− Represent
Reverse process	2.1. Near specific number	− If María is 8 years old, how old is Juan?
	2.2. Far specific number	− If María is 55 years old, how old is Juan?
	2.3. Indeterminate number	− If María is n years old, how old is Juan?
	2.4. Verbal expression of the rule	− Express a rule to find out the age of Juan knowing the age of María
	2.5. Algebraic expression of the rule	− Algebraically express the reverse rule [f(m) = m – 3]
	2.6. Using tables	− Complete the table
		Juan
		María	3	4	5	6	7	8	…	52	…
	2.7. Graphical representation	− Represent

and

Table 7. Task sequence to promote algebraic thinking from case 2.

Tasks	Examples
Near specific number	− If there are €5 in Lucas’ wallet − How many € does Lucas have? − How many € does Aina have?
2. Far specific number	− If there are €52 in Lucas’ wallet − How many € does Lucas have? − How many € does Aina have?
3. Indeterminate number	− If there are € n in Lucas’ wallet − How many € does Lucas have? − How many € does Aina have?
4. Verbal expression of the rules	− Express a rule that relates the € in Lucas’ wallet with − Lucas’ € − Aina’s €
5. Algebraic expression of the rules	− Algebraically express the rule that relates the € in Lucas’ wallet with − Lucas’ € [f(x) = n + 8] − Aina’s € [f(x) = 3n]
6. Using tables	− Complete the table
	Lucas’ wallet	1	2	3	4	5	…	52	…	n
	€ Lucas
	€ Aina
7. Graphical representation	− Represent the graphs of Lucas and Aina ……
8. Joint representation	− Represent the graphs of Lucas and Aina in a single coordinate system
9. Solution analysis	− Case 1. How many € are there in Lucas’ wallet, if they both have the same amount? − How many € are there in Lucas’ wallet? − How many € do Lucas and Aina have? − Case 2. In which cases does Lucas have more € than Aina? − How many € are there in Lucas’ wallet? − How many € does Lucas have? And Aina? − Case 3. In which cases does Lucas have less € than Aina? − How many € are there in Lucas’ wallet? − How many € does Lucas have? And Aina?

).

Although in the sequence of tasks of the second case, the two dependent variables, Lucas’ money and Aina’s money, are worked together, they could also be treated individually, as in the first case in which there was a single dependent variable. In this case, the tasks would be the same as in case 1 for each function, then adding the last two tasks to be performed together.

The reverse process in the second situation would be worked by choosing other independent variables such as Lucas’ money or Aina’s money; if the independent variable is Lucas’ money, the functions would be f(n) = n − 8 and f(n) = 3·(n − 8), which would correspond, respectively, to the money in Lucas’ wallet and to the money in Aina’s; if the independent variable were Aina’s money, we would work with rationals, since the functions that represent the money in Lucas’ wallet and Lucas’ total money would be f(n) = n/3 and f(n) = n/3 + 8, respectively.

The almost null connection with algebraic concepts that the participants have shown in the approach and resolution of the tasks shows that their algebraic knowledge, both content and didactic, is insufficient to adequately develop the algebraic thinking of Primary Education students.

The low knowledge of algebraic content could derive from the mathematical experiences received in previous stages [35,36,37,38,39,40]. The teaching of algebra they have received in Primary Education was practically null, and that received in Secondary Education was reduced, almost exclusively, to the decontextualized resolution of equations and that received by 75% of the participants in the last two years of high school are focused on solving equations and systems of equations, matrices and polynomials.

5. Conclusions

As possible solutions, and following the guidelines of early algebra, we propose:

• To advance the learning of algebra to the first years of schooling;
• To “algebrise” the entire curriculum, that is, to integrate algebraic thinking both in Primary and Secondary Education, as some educational systems are already undertaking;
• To include in all the branches and itineraries of the high school the subject of mathematics, which should include, in a specific way, the study of algebra and, especially, of functional relationships.

The late introduction of algebra fosters a disconnection with the other blocks of mathematics and, all too often, an absence of meaning. In contrast, it is considered an early integration of algebraic thinking that prioritized the identification and generalization of functional relationships and the use of variables to express them and the transfer between the different ways of representing them (verbal, tabular, graphical and analytical). This would facilitate the transition between Primary and Secondary Education and would promote, in students, a natural evolution in the way of thinking and acting with objects, relationships, structures and mathematical situations.

The results seem to confirm the deficiencies regarding the didactic knowledge of the preservice teachers, and if these deficiencies continue, they will prevent them from taking advantage of the algebraic competencies of their future students [12,13], as the teachers are not able to promote adequate tasks to develop their algebraic thinking adequately [26]. The scarce algebraic knowledge, both content and didactic, of the preservice teachers, shows that there should be a review of the training programs that include “processes of development of mathematical ideas related to the structure, properties or relationships that underlie mathematical ideas” [57] (p. 11). Although Primary Education students are capable of performing certain algebraic tasks [6,7,8,9,10,11], teacher intervention is required to recognize and promote algebraic thinking in them [58].

These programs should offer student teachers the opportunities to design appropriate tasks and analyze them didactically [15] and to expand their algebraic thinking and connect it with the different blocks of mathematics, “algebrising” the curriculum through the recognition of relationships and functions, their generalization and their verbal, tabular, symbolic and graphic representations [1].

In this way, in the initial algebraic training of the student teachers, activities should be incorporated in order to allow them to recognize the possibilities that certain daily situations present to promote the development of algebraic thinking of their future students. The article includes, from the two cases presented to the student teachers, respective sequences of tasks, which can serve as a starting point to start training programs and experiences and as an intervention proposal in the Didactics of Mathematics classes. In both sequences, we can see: (1) functional relationships are recognized from near and far specific cases, (2) they are generalized with indeterminate cases, (3) are expressed verbally and symbolically and are represented tabularly and graphically; moreover, in the sequence of the second situation, are compared the two functional relationships to start the study of equations (Table 6 and Table 7).

The incorporation of algebra in Primary Education and the development of students’ algebraic thinking depend, to a large extent, on the training of teachers and their ability to design algebraic tasks that provide a classroom dynamic that will encourage the recognition and generalization of relationships and functions.