A Parametric Tool for Studying a New Tracheobronchial Silicone Stent Prototype: Toward a Customized 3D Printable Prosthesis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Parametric Geometry of the Tracheobronchial Prosthesis
2.2. Stent Fabrication
2.3. Prosthesis Experimental Testing
2.4. Prosthesis Computational Modelling
3. Results
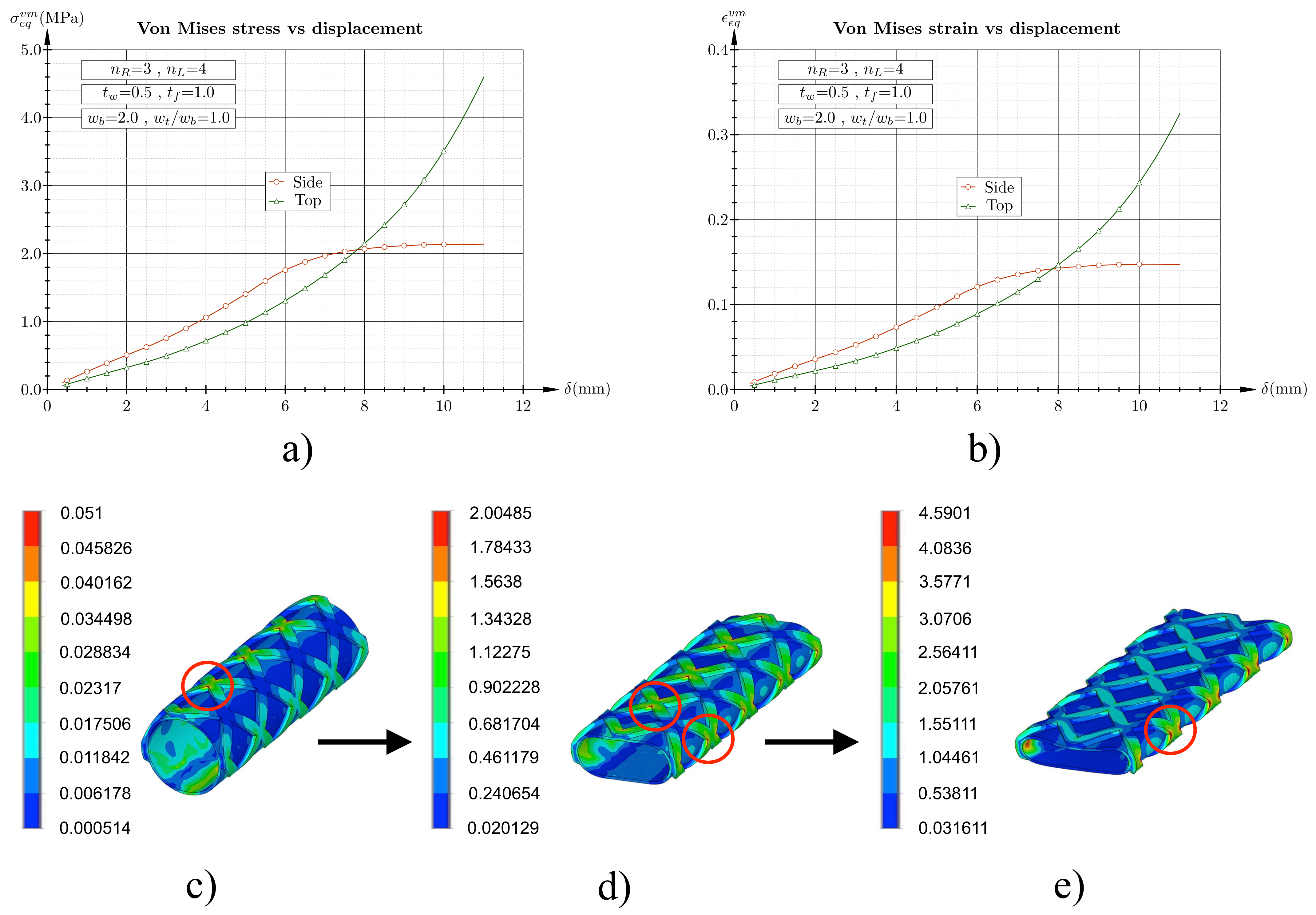
3.1. Flat Plate Test Simulation
3.2. Flat Plate Experimental Testing
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Folch, E.; Keyes, C. Airway stents. Ann. Cardiothorac. Surg. 2018, 7, 273–283. [Google Scholar] [CrossRef] [Green Version]
- Ratnovsky, A.; Regeva, N.; Walda, S.; Naftali, M.K.S. Mechanical properties of different airway stents. Med. Eng. Phys. 2015, 37, 408–415. [Google Scholar] [CrossRef] [PubMed]
- Dumon, J.; Cavaliere, S.; Díaz-Jimenez, J.P.; Vergnon, J.; Venuta, F.; Dumon, M.; Kovitz, K. Seven-Year Experience with the Dumon Prosthesis. J. Bronchol. 1996, 3, 6–10. [Google Scholar] [CrossRef]
- Gaafar, A.H.; Shaaban, A.Y.; Elhadidi, M.S. The use of metallic expandable tracheal stents in the management of inoperable malignant tracheal obstruction. Eur. Arch. Otorhinolaryngol. 2012, 269, 247–253. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Uson, J.; Ezquerra, V.; Crisostomo, V.; Luis, L.; Maynar, M. Endotracheal stenting therapy in dogs with tracheal collapse. Vet. J. 2008, 175, 186–193. [Google Scholar] [CrossRef]
- Charokopos, N.; Foroulis, C.N.; Rouska, E.; Sileli, M.N.; Papadopoulos, N.; Papakonstantinou, C. The management of post-intubation tracheal stenoses with self-expandable stents: Early and long-term results in 11 cases. Eur. J. Cardiothorac. Surg. 2011, 40, 919–925. [Google Scholar] [CrossRef] [Green Version]
- Freitag, L.; Eicker, K.; Donovan, T.J.; Dimov, D. Mechanical properties of airway stents. J. Bronchol. Interv. Pulmonol. 1995, 2, 270–278. [Google Scholar] [CrossRef]
- Food and Drug Administration. FDA Public Health Notification: FDA Recommends Avoiding Use of Metallic Tracheal Stents. Food Drug Adm. 2019. Available online: https://www.medscape.org/viewarticle/510184 (accessed on 15 March 2021).
- Dutau, H.; Breen, D.; Bugalho, A.; Dalar, L.; Daniels, J.; Dooms, C.; Eberhardt, R.; Ek, L.; Encheva, M. Current practice of airway stenting in the adult population in Europe: A survey of the European Association of Bronchology and Interventional Pulmonology (EABIP). Respiration 2018, 95, 44–54. [Google Scholar] [CrossRef] [Green Version]
- Guilbert, N.; Saka, H.; Dutau, H. Airway stenting: Technological advancements and its role in interventional pulmonology. Respirology 2020, 25, 953–962. [Google Scholar] [CrossRef] [Green Version]
- Malvè, M.; Pérez del Palomar, A.; López-Villalobos, J.L.; Ginel, A.; Doblaré, M. FSI Analysis of the Coughing Mechanism in a Human Trachea. Ann. Biomed. Eng. 2010, 38, 1556–1565. [Google Scholar] [CrossRef]
- Malvè, M.; Pérez del Palomar, A.; Mena, A.; Trabelsi, O.; López-Villalobos, J.L.; Ginel, A.; Panadero, F.; Doblaré, M. Numerical modeling of a human stented trachea under different stent designs. Int. Commun. Heat Mass Transf. 2011, 38, 855–862. [Google Scholar] [CrossRef]
- Malvè, M.; Pérez del Palomar, A.; Chandra, S.; López-Villalobos, J.L.; Ginel, E.F.A.; Doblaré, M. FSI Analysis of a Human Trachea Before and After Prosthesis Implantation. J. Biomech. Eng. 2011, 133, 071003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schopf, L.F.; Fraga, J.C.; Porto, R.; Santos, L.A.; Marques, D.R.; Sanchez, P.R.; Meyer, F.S.; Ulbrich, J.M. Experimental use of new absorbable tracheal stent. J. Pediatr. Surg. 2018, 53, 1305–1309. [Google Scholar] [CrossRef] [PubMed]
- Novotny, L.; Crha, M.; Rauser, P.; Hep, A.; Misik, J.; Necas, A.; Vondrys, D. Novel biodegradable polydioxanone stents in a rabbit airway model. J. Thorac. Cardiovasc. Surg. 2012, 143, 437–444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freitag, L.; Gordes, M.; Zarogoulidis, P.; Darwiche, K.; Franzen, D.; Funke, F.; Hohenforst-Schmidt, W.; Dutau, H. Towards individualized tracheobronchial stents: Technical, practical and legal considerations. Respiration 2017, 94, 442–456. [Google Scholar] [CrossRef]
- Xu, J.; Ong, H.X.; Traini, D.; Byrom, M.; Williamson, J.; Young, P.M. The Utility of 3D-Printed Airway Stents to Improve Treatment Strategies for Central Airway Obstructions. Drug Dev. Ind. Pharm. 2019, 45, 1–10. [Google Scholar] [CrossRef]
- Gildea, T.R.; Young, B.P.; Machuzak, M.S. Application of 3D printing for patient-specific silicone stents: 1-year follow-up on 2 patients. Respiration 2018, 96, 488–494. [Google Scholar] [CrossRef]
- Ghosh, S.; Burks, A.C.; Akulian, J.A. Customizable airway stents- personalized medicine reaches the airways. J. Thorac. Dis. 2019, 11, S1129–S1131. [Google Scholar] [CrossRef]
- Food and Drug Administration. 3D Printing of Medical Devices. In Food Drug Adm.; 2018. Available online: https://www.fda.gov/medical-devices/products-and-medical-procedures/3d-printing-medical-devices (accessed on 15 March 2021).
- Nakada, T.; Akiba, T.; Inagaki, T.; Morikawa, T. Thoracoscopic anatomical subsegmentectomy of the right S2b + S3 using a 3D printing model with rapid prototyping. Interact. Cardiovasc. Thorac. Surg. 2014, 19, 696–698. [Google Scholar] [CrossRef]
- Malik, H.H.; Darwood, A.R.; Shaunak, S.; Kulatilake, P.; El-Hilly, A.A.; Mulki, O.; Baskaradas, A. Three-dimensional printing in surgery: A review of current surgical applications. J. Surg. Res. 2015, 199, 512–522. [Google Scholar] [CrossRef]
- Guibert, N.; Moreno, B.; Plat, G.; Didier, A.; Mazieres, J.; Hermant, C. Stenting of complex malignant central-airway obstruction guided by a three-dimensional printed model of the airways. Ann. Thorac. Surg. 2017, 103, e357–e359. [Google Scholar] [CrossRef] [Green Version]
- Miyazaki, T.; Yamasaki, N.; Tsuchiya, T.; Matsumoto, K.; Takagi, K.; Nagayasu, T. Airway stent insertion simulated with a three- dimensional printed airway model. Ann. Thorac. Surg. 2015, 99, e21–e23. [Google Scholar] [CrossRef]
- Cheng, G.Z.; San Jose Estepar, R.; Folch, E.; Onieva, J.; Gangadharan, S.; Majid, A. Three-dimensional printing and 3D slicer: Powerful tools in understanding and treating structural lung disease. Chest 2016, 149, 1136–1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morrison, R.J.; Hollister, S.J.; Niedner, M.F.; Ghadimi Mahani, M.; Park, A.H.; Mehta, D.K.; Ohye, R.G.; Green, G.E. Mitigation of tracheobronchomalacia with 3D-printed personalized medical devices in pediatric patients. Sci. Transl. Med. 2015, 7, 285ra64. [Google Scholar] [CrossRef] [Green Version]
- Debiane, L.; Reitzel, R.; Rosenblatt, J.; Gagea, M.; Chavez, M.A.; Adachi, R.; Grosu, H.B.; Sheshadri, A.; Hill, L.R.; Raad, I.; et al. A Design-Based Stereologic Method to Quantify the Tissue Changes Associated with a Novel Drug- Eluting Tracheobronchial Stent. Respiration 2019, 98, 60–69. [Google Scholar] [CrossRef]
- Melgoza, E.L.; Serenó, L.; Rosell, A.; Ciurana, J. An integrated parameterized tool for designing a customized tracheal stent. Comput.-Aided Des. 2012, 44, 1173–1181. [Google Scholar] [CrossRef]
- Melgoza, E.L.; Vallicrosa, G.; Sereno, L.; Rosell, A.; Rodríguez, C.; Elias, A.; Ciurana, J. Rapid Tooling Using 3D Printing System For Manufacturing Of Customized Tracheal Stent. Rapid Prototyp. J. 2014, 20, 2–12. [Google Scholar] [CrossRef]
- Gastal Xavier, R.; Stefani Sanches, P.R.; Viera de Macedo Neto, A.; Kuhl, G.; Bianchi Vearick, S.; Dall’Orden Michelon, M. Development of a modified Dumon stent for tracheal applications: An experimental study in dogs. J. Bras. Pneumol. 2008, 34, 21–26. [Google Scholar]
- Bianchi Vearick, S.; Bendo Dem´trio, K.; Gastal Xavier, R.; Moreschi, A.H.; Frotta Muller, A.; Stefani Sanches, P.R.; Loureiro dos Santos, L.A. Fiber-reinforced silicone for tracheobronchial stents: An experimental study. J. Mech. Behav. Biomed. Mater. 2018, 77, 494–500. [Google Scholar] [CrossRef]
- Dumon, F. A dedicated tracheobronchial stent. Appl. Sci. 1990, 97, 328–332. [Google Scholar] [CrossRef] [PubMed]
- Park, H.-Y.; Kim, H.; Koh, W.-J.; Suh, G.-Y.; Chung, M.-P.; Kwon, O.-J. Natural stent in the management of post-intubation tracheal stenosis. Respirology 2009, 14, 583–588. [Google Scholar] [CrossRef]
- Lund, M.E.; Force, S. Airway Stenting for Patients With Benign Airway Disease and the Food and Drug Administration Advisory. Chest J. 2007, 132, 1107–1108. [Google Scholar] [CrossRef]
- Food and Drug Administration. Airway stenting for benign tracheal stenosis: What is really behind the choice of the stent? Eur. J. Cardiothorac. Surg. 2011, 40, 924–925. [Google Scholar]
- Guibert, N.; Mhanna, L.; Didier, A.; Moreno, B.; Leyx, P.; Plat, G.; Mazieres, J.; Hermant, C. Integration of 3D printing and additive manufacturing in the interventional pulmonologist’s toolbox. Respir. Med. 2018, 134, 139–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Beule, M.; Van Cauter, S.; Mortier, P.; Van Loob, D.; Van Impe, R.; Verdonck, P.; Verhegghe, B. Virtual optimization of self-expandable braided wire stents. Med. Eng. Phys. 2009, 31, 448–453. [Google Scholar] [CrossRef] [PubMed]
- Gundert, T.J.; Marsden, A.L.; Yang, W.; LaDisa Jr., J. F. Optimization of Cardiovascular Stent Design Using Computational Fluid Dynamics. J. Biomech. Eng. 2012, 134, 011002. [Google Scholar] [CrossRef] [PubMed]
- McGrath, D.J.; O’Brien, B.; Bruzzi, M.; Kelly, N.; Clauser, J.; Steinseifer, U.; McHugh, P.E. Evaluation of cover effects on bare stent mechanical response. J. Mech. Behav. Biomed. Mater. 2016, 61, 567–580. [Google Scholar] [CrossRef]
- Chaure, J.; Serrano, C.; Fernández-Parra, R.; Na, E.P.; Lostalé, F.; De Gregorio, M.A.; Martínez, M.A.; Malvè, M. On Studying the Interaction Between Different Stent Models and Rabbit Tracheal Tissue: Numerical, Endoscopic and Histological Comparison. Ann. Biomed. Eng. 2016, 44, 368–381. [Google Scholar] [CrossRef] [Green Version]

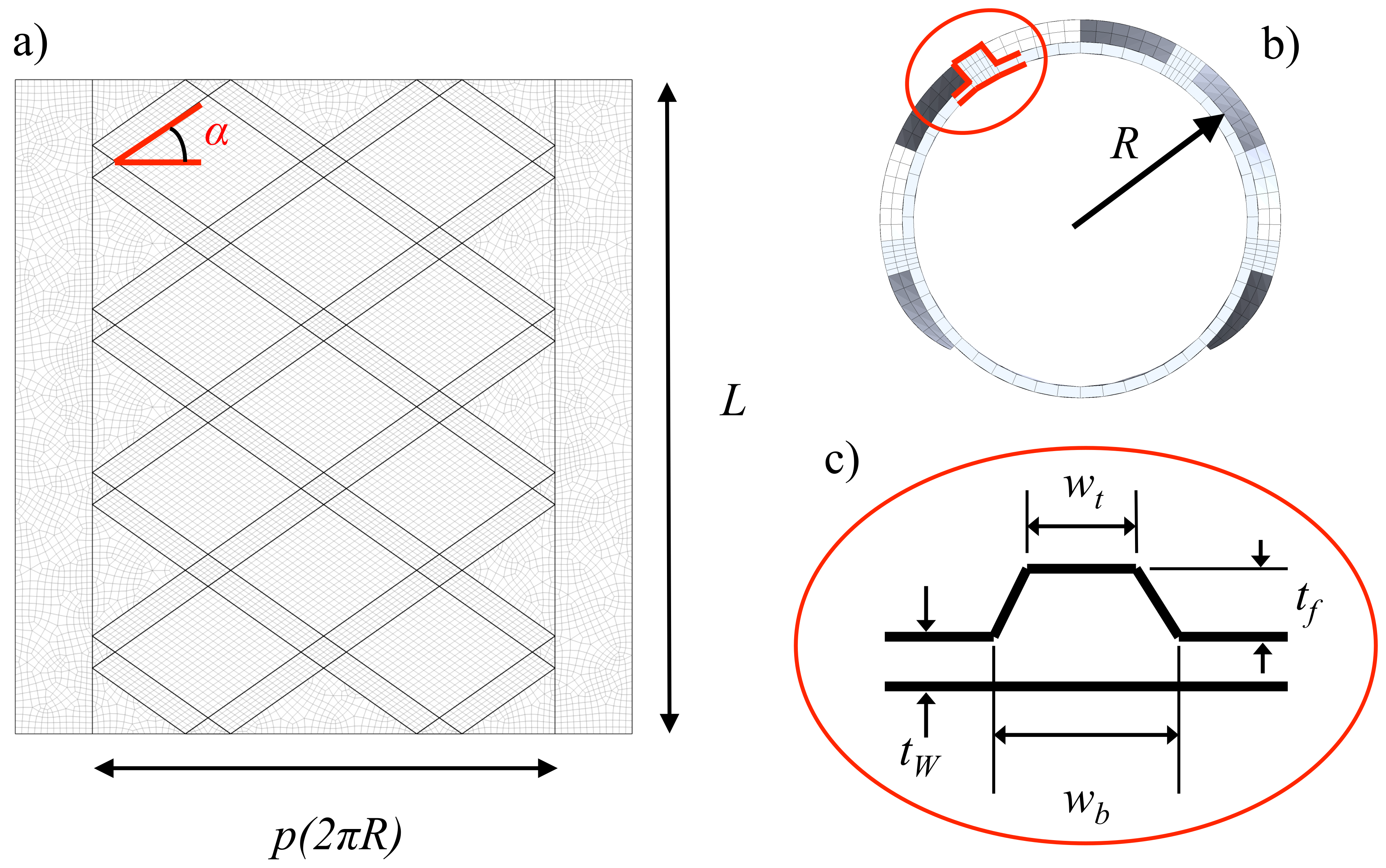












| [mm] | [mm] | L [mm] | p [%] | R [mm] | ||||
|---|---|---|---|---|---|---|---|---|
| 0.5–1 | 1–0.5 | 3–5 | 3–5 | 50 | 0.75 | 9 | 1–4 | 0.5–1 |
| [mm] | [mm] | [] | L [mm] | p [%] | R [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 3 | 5 | 35.27 | 50 | 75 | 0.9 | 1 | |
| 1 | 1 | 4 | 5 | 43.35 | 50 | 75 | 0.9 | 1 | |
| 1 | 1 | 5 | 3 | 63.03 | 50 | 75 | 0.9 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zurita-Gabasa, J.; Sánchez-Matás, C.; Díaz-Jiménez, C.; López-Villalobos, J.L.; Malvè, M. A Parametric Tool for Studying a New Tracheobronchial Silicone Stent Prototype: Toward a Customized 3D Printable Prosthesis. Mathematics 2021, 9, 2118. https://doi.org/10.3390/math9172118
Zurita-Gabasa J, Sánchez-Matás C, Díaz-Jiménez C, López-Villalobos JL, Malvè M. A Parametric Tool for Studying a New Tracheobronchial Silicone Stent Prototype: Toward a Customized 3D Printable Prosthesis. Mathematics. 2021; 9(17):2118. https://doi.org/10.3390/math9172118
Chicago/Turabian StyleZurita-Gabasa, Jesús, Carmen Sánchez-Matás, Cristina Díaz-Jiménez, José Luis López-Villalobos, and Mauro Malvè. 2021. "A Parametric Tool for Studying a New Tracheobronchial Silicone Stent Prototype: Toward a Customized 3D Printable Prosthesis" Mathematics 9, no. 17: 2118. https://doi.org/10.3390/math9172118
APA StyleZurita-Gabasa, J., Sánchez-Matás, C., Díaz-Jiménez, C., López-Villalobos, J. L., & Malvè, M. (2021). A Parametric Tool for Studying a New Tracheobronchial Silicone Stent Prototype: Toward a Customized 3D Printable Prosthesis. Mathematics, 9(17), 2118. https://doi.org/10.3390/math9172118






