Differential Evolution with Estimation of Distribution for Worst-Case Scenario Optimization
Abstract
:1. Introduction
2. Background
2.1. Definition of Classical Optimization Problem
2.2. Definition of Worst Case Scenario Optimization Problem
3. Algorithm Method
3.1. Differential Evolution (DE)
- 1.
- Initialization: A population of individuals is randomly initialized. Each individual is represented by a D dimensional parameter vector, where , , where is the maximum number of generations. Each vector component is subject to upper and lower bounds and . The initial values of the ith individual are generated as:where rand(0,1) is a random integer between 0 and 1.
- 2.
- Mutation: The new individual is generated by adding the weighted difference vector between two randomly selected population members to a third member. This process is expressed as:V is the mutant vector, X is an individual, are randomly chosen integers within the range of and , G corresponds to the current generation, F is the scale factor, usually a positive real number between 0.2 and 0.8. F controls the rate at which the population evolves.
- 3.
- Crossover: After mutation, the binomial crossover operation is applied. The mutant individual is recombined with the parent vector , in order to generate the offspring . The vectors of the offspring are inherited from or depending on a parameter called crossover probability, as follows:where is a uniformly generated number, is a randomly chosen index, which assures that gives at least one element to . denotes the t-th element of the individual’s vector.
- 4.
- Selection: The selection operation is a competition between each individual and its offspring and defines which individual will prevail in the next generation. The winner is the one with the best fitness value. The operation is expressed by the following equation:The above steps of mutation, crossover, and selection are repeated for each generation until a certain set of termination criteria has been met. Figure 2 shows the basic flowchart of the DE.
3.2. Estimation of Distribution Algorithms (EDAs)
- 1.
- Initialization: A population is initialized randomly.
- 2.
- Selection: The most promising individuals from the population , where t is the current generation, are selected.
- 3.
- Estimation of the probabilistic distribution: A probabilistic model is built from .
- 4.
- Generate new individuals: New candidate solutions are generated by sampling from the .
- 5.
- Create new population: The new solutions are incorporated into , and go to the next generation. The procedure ends when the termination criteria are met.
3.3. Proposed Algorithm
- 1.
- Initialization: A population of size is initialized according to the general DE procedure mentioned in the previous section, where the individuals are representing candidate solutions in the design space X.
- 2.
- Evaluation: To evaluate the fitness function, we need to solve the problem in the scenario space. For a fixed candidate UL solution , the LL DE is executed. More detailed steps are given in the next paragraphs. The LL DE returns the solution corresponding to the worst-case scenario for the specific . For each individual, the corresponding best solutions are stored, meaning the solution y that for a fixed x maximizes the objective function.
- 3.
- Building: The individuals in the population are sorted as the ascending of the UL fitness values. The best are selected. From the best individuals, we build the distribution to establish a probabilistic model for the LL solution. The d-dimensional multivariate normal densities to factorize the joint probability density function (pdf) are:where x is the d-dimensional random vector, is the d-dimensional mean vector and is the covariance matrix. The two parameters are estimated from the best of the population, from the stored lower level best solutions. In that way, in each generation, we extract statistical information about the LL solutions of the previous UL population. The parameters are updated accordingly in each generation, following the general schema of an estimation of distribution algorithm.
- 4.
- Evolution: Evolve UL with the steps of the standard DE of mutation, crossover, producing an offspring .
- 5.
- Selection: As mentioned above, the selection operation is a competition between each individual and its offspring . The offspring will be evaluated in the scenario space and sent in LL only if ≤, where corresponds to the worst case vector of the parent individual . In that way, a lot of unneeded LL optimization calls will be avoided, reducing FEs. If the offspring is evaluated in the scenario space, the selection procedure in Equation (6) is applied.
- 6.
- Termination criteria:
- Stop if the maximum number of function evaluations is reached.
- Stop if the improvement of the best objective value of the last generations is below a specific number.
- Stop if the absolute difference of the best and the known true optimal objective value is below a specific number.
- 7.
- Output: the best worst case function value , the solution corresponding to the best worst-case scenario
- 1.
- Setting: Set the parameters of the probability of crossover , the population size , the mutation rate F, the sampling probability .
- 2.
- Initialization: Sample individuals to initialize the population. If , then the individual is sampled from the probabilistic model built in the UL with the Equation (7). The model here is sampled with the built-in function of Matlab, which accepts a mean vector mu and covariance matrix sigma as input and returns a random vector chosen from the multivariate normal distribution with that mean and covariance [23]. Otherwise, it is uniformly sampled in the scenario space according to the Equation (3). Please note that for the first UL generation, is always 0, as no probabilistic model is built yet. For the following generations, can range from (0,1) number, where = 1 means that the population will be sampled only from the probabilistic model. This might lead the algorithm to be stuck in local optima and to converge prematurely. An example of an initial population generated with the aforementioned method with = 0.5 is shown in Figure 5. Magenta asterisk points represent the population generated by the probabilistic model of the previous UL generation. Blue points are samples uniformly distributed in the search space. In Figure 6, the effect of the probabilistic model on the initial population of LL for during the optimization is shown. As the iterations increase, the LL members of the populations sampled from the probabilistic distribution reach the promising area that maximizes the function. In the zoomed subplot in each subfigure, one can see that all such members of the population are close to the global maximum, compared to the randomly distributed members.
- 3.
- Mutation, crossover, and selection as the standard DE.
- 4.
- Termination criteria:
- Stop if the maximum number of generations is reached.
- Stop if the absolute difference between the best and the known true optimal objective value is below a specific number.
- 5.
- Output: the maximum function value , the solution corresponding to the worst-case scenario .
4. Experimental Settings
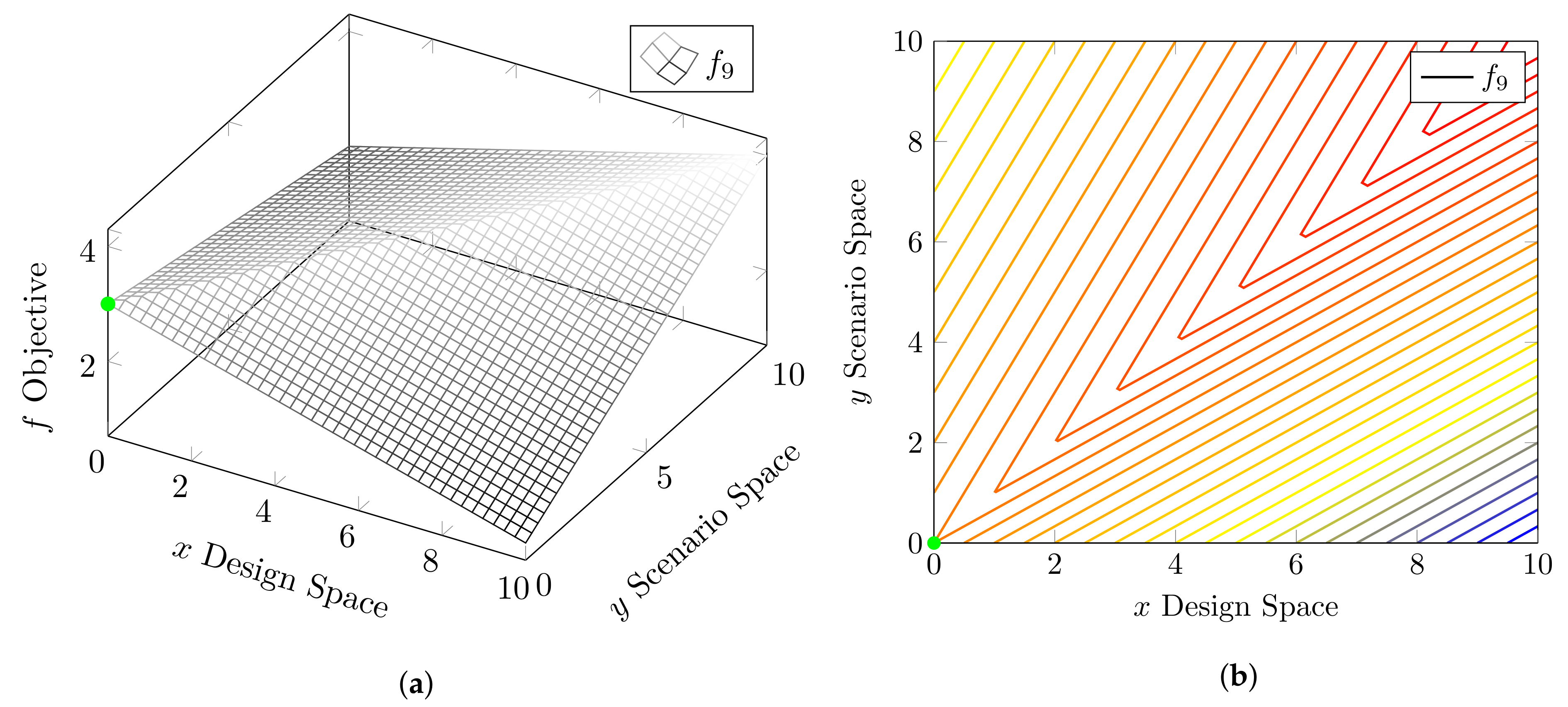
4.1. Test Functions
4.2. Parameter Settings
5. Experimental Results and Discussion
5.1. Effectiveness of the Probabilistic Sharing Mechanism
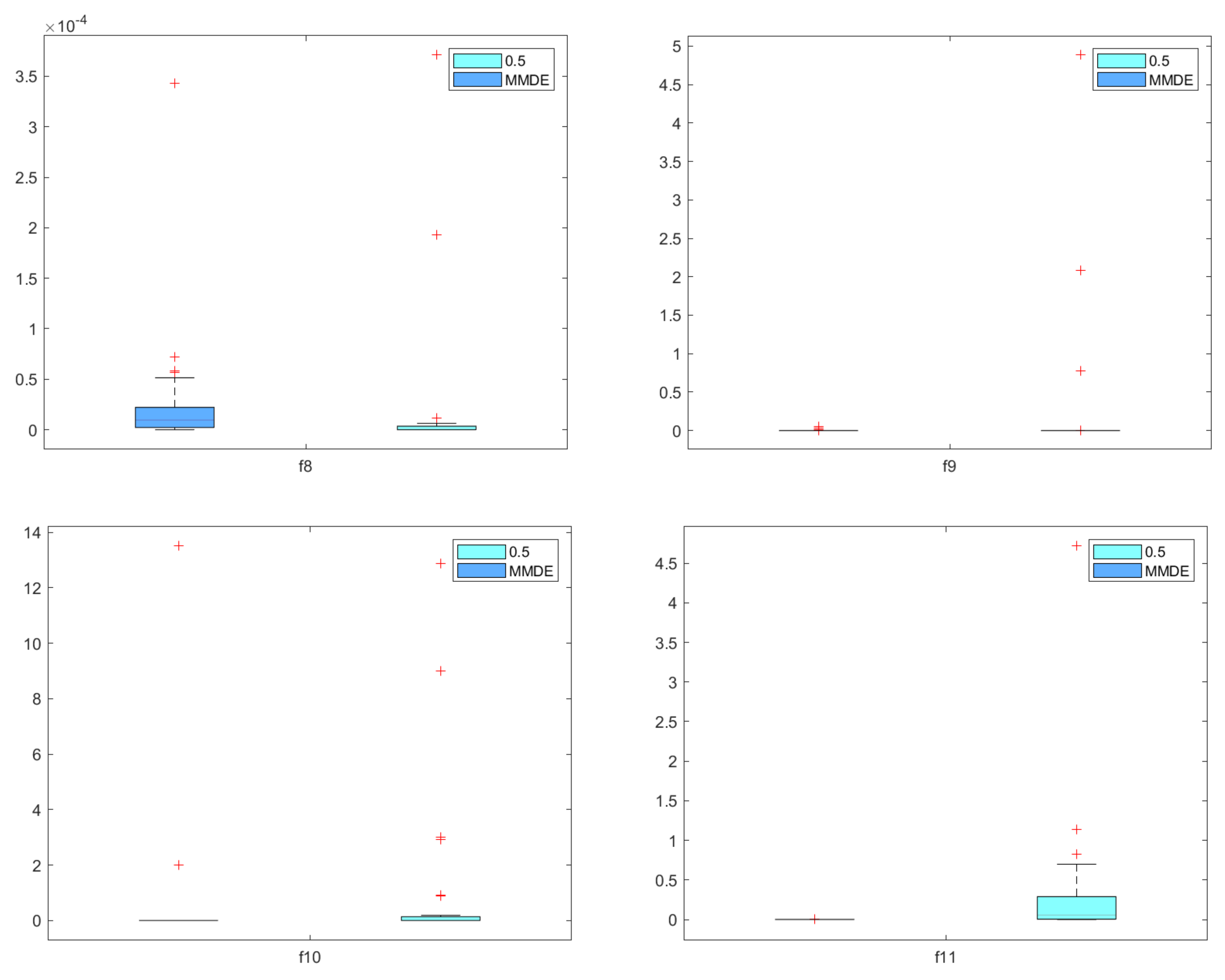
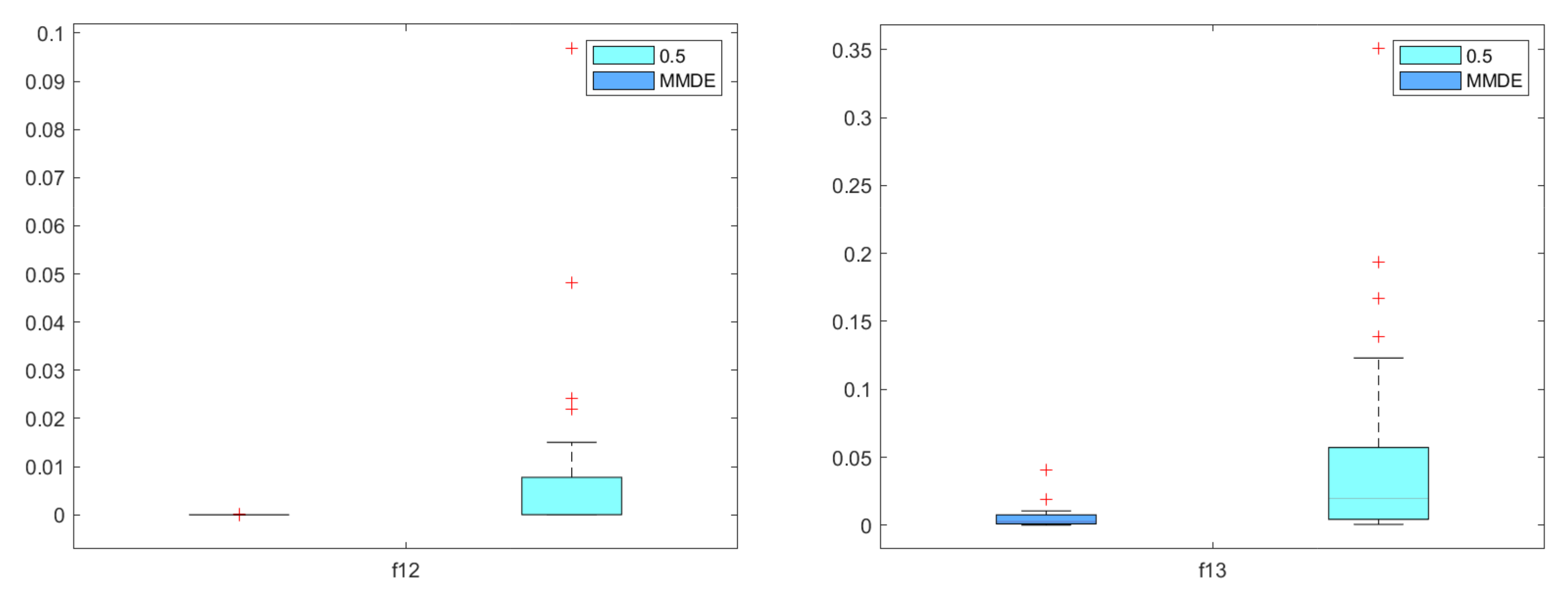
5.2. Comparison with State-of-the-Art Method MMDE
5.3. Engineering Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DE | differential evolution |
| EDA | estimation of distribution algorithm |
| UL | upper level |
| LL | lower level |
| BOP | bilevel optimization problem |
| FEs | function evaluations |
References
- Sinha, A.; Lu, Z.; Deb, K.; Malo, P. Bilevel optimization based on iterative approximation of multiple mappings. J. Heuristics 2017, 26, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, M.; Korošec, P. Multilevel Optimisation. Optimization under Uncertainty with Applications to Aerospace Engineering; Springer: Cham, Switzerland, 2021; pp. 307–331. [Google Scholar]
- Feng, Y.; Hongwei, L.; Shuisheng, Z.; Sanyang, L. A smoothing trust-region Newton-CG method for minimax problem. Appl. Math. Comput. 2008, 199, 581–589. [Google Scholar] [CrossRef]
- Montemanni, R.; Gambardella, L.M.; Donati, A.V. A branch and bound algorithm for the robust shortest path problem with interval data. Oper. Res. Lett. 2004, 32, 225–232. [Google Scholar] [CrossRef]
- Aissi, H.; Bazgan, C.; Vanderpooten, D. Min–max and min–max regret versions of combinatorial optimization problems: A survey. Eur. J. Oper. Res. 2009, 197, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, H.J. A coevolutionary genetic algorithm for constrained optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA; 3, pp. 1605–1611. [Google Scholar]
- Shi, Y.; Krohling, R.A. Co-evolutionary particle swarm optimization to solve min-max problems. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002; IEEE: Piscataway, NJ, USA; Volume 2, pp. 1682–1687. [Google Scholar]
- Vasile, M. On the solution of min-max problems in robust optimization. In Proceedings of the EVOLVE 2014 International Conference, A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computing, Beijing, China, 1–4 July 2014. [Google Scholar]
- Chen, R.B.; Chang, S.P.; Wang, W.; Tung, H.C.; Wong, W.K. Minimax optimal designs via particle swarm optimization methods. Stat. Comput. 2015, 25, 975–988. [Google Scholar] [CrossRef]
- Antoniou, M.; Papa, G. Solving min-max optimisation problems by means of bilevel evolutionary algorithms: A preliminary study. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference Companion, Cancun, Mexico, 8–12 July 2020; pp. 187–188. [Google Scholar]
- Angelo, J.S.; Krempser, E.; Barbosa, H.J. Differential evolution for bilevel programming. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA; pp. 470–477. [Google Scholar]
- He, X.; Zhou, Y.; Chen, Z. Evolutionary bilevel optimization based on covariance matrix adaptation. IEEE Trans. Evol. Comput. 2018, 23, 258–272. [Google Scholar] [CrossRef]
- Qiu, X.; Xu, J.X.; Xu, Y.; Tan, K.C. A new differential evolution algorithm for minimax optimization in robust design. IEEE Trans. Cybern. 2017, 48, 1355–1368. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Zhang, Q. A surrogate-assisted evolutionary algorithm for minimax optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway, NJ, USA; pp. 1–7. [Google Scholar]
- Marzat, J.; Walter, E.; Piet-Lahanier, H. Worst-case global optimization of black-box functions through Kriging and relaxation. J. Glob. Optim. 2013, 55, 707–727. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Feng, L.; Jin, Y.; Doherty, J. Surrogate-Assisted Evolutionary Multitasking for Expensive Minimax Optimization in Multiple Scenarios. IEEE Comput. Intell. Mag. 2021, 16, 34–48. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Larranaga, P. A review on estimation of distribution algorithms. In Estimation of Distribution Algorithms; Springer: Boston, MA, USA, 2002; pp. 57–100. [Google Scholar]
- Zhao, F.; Shao, Z.; Wang, J.; Zhang, C. A hybrid differential evolution and estimation of distribution algorithm based on neighbourhood search for job shop scheduling problems. Int. J. Prod. Res. 2016, 54, 1039–1060. [Google Scholar] [CrossRef]
- Hao, R.; Zhang, J.; Xin, B.; Chen, C.; Dou, L. A hybrid differential evolution and estimation of distribution algorithm for the multi-point dynamic aggregation problem. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 251–252. [Google Scholar]
- Wang, G.; Ma, L. The estimation of particle swarm distribution algorithm with sensitivity analysis for solving nonlinear bilevel programming problems. IEEE Access 2020, 8, 137133–137149. [Google Scholar] [CrossRef]
- Gorissen, B.L.; Yanıkoğlu, İ.; den Hertog, D. A practical guide to robust optimization. Omega 2015, 53, 124–137. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://www.mathworks.com/help/stats/mvnrnd.html (accessed on 3 August 2021).
- Rustem, B.; Howe, M. Algorithms for Worst-Case Design and Applications to Risk Management; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Jensen, M.T. A new look at solving minimax problems with coevolutionary genetic algorithms. In Metaheuristics: Computer Decision-Making; Springer: Boston, MA, USA, 2003; pp. 369–384. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Marzat, J.; Walter, E.; Piet-Lahanier, H. A new expected-improvement algorithm for continuous minimax optimization. J. Glob. Optim. 2016, 64, 785–802. [Google Scholar] [CrossRef]
- Brown, B.; Singh, T. Minimax design of vibration absorbers for linear damped systems. J. Sound Vib. 2011, 330, 2437–2448. [Google Scholar] [CrossRef]











| Upper-Level | Lower-Level | |
|---|---|---|
| Population size | ||
| Crossover | 0.9 | 0.9 |
| Mutation | uniformly (0.2, 0.8) | uniformly (0.2, 0.8) |
| Desired Accuracy | 1 × 10−5 | 1 × 10−5 |
| Maximum Number of Generations | - | 10 |
| Maximum Number of Function Evaluations | 5000 | - |
| Maximum Number of Improvement Generations | 30 | - |
| Least Improvement | 1 × 10−5 | - |
| Problems | = 0 | = 0.5 | = 0.8 | |
|---|---|---|---|---|
| Mean | 3.45 × 10 | 2.77 × 10 | 2.29 × 10 | |
| Median | 9.49 × 10 | 3.33 × 10 | 3.33 × 10 | |
| Std | 6.55 × 10 | 3.43 × 10 | 1.53 × 10 | |
| p-value | ≤0.05 | NA | >0.05 | |
| Median FEs | 20,115 | 28,300 | 46,535 | |
| Mean | 1.11 × 10 | 1.25 × 10 | 1.28 × 10 | |
| Median | 4.96 × 10 | 5.53 × 10 | 5.79 × 10 | |
| Std | 5.38 × 10 | 4.27 × 10 | 5.43 × 10 | |
| p-value | ≤0.05 | NA | >0.05 | |
| Median FEs | 20,665 | 16,180 | 17,140 | |
| Mean | 1.64 × 10 | 2.27 × 10 | 2.35 × 10 | |
| Median | 9.51 × 10 | 1.86 × 10 | 2.47 × 10 | |
| Std | 2.29 × 10 | 1.30 × 10 | 8.35 × 10 | |
| p-value | ≤0.05 | NA | >0.05 | |
| Median FEs | 27,535 | 39,830 | 46,785 | |
| Mean | 3.49 × 10 | 2.93 × 10 | 1.64 × 10 | |
| Median | 2.27 × 10 | 2.03 × 10 | 3.39 × 10 | |
| Std | 4.49 × 10 | 4.41 × 10 | 8.88 × 10 | |
| p-value | ≤0.05 | NA | >0.05 | |
| Median FEs | 19,940 | 26,478 | 40,516 | |
| Mean | 6.23 × 10 | 9.95 × 10 | 8.43 × 10 | |
| Median | 2.63 × 10 | 2.99 × 10 | 8.55 × 10 | |
| Std | 1.05 × 10 | 4.18 × 10 | 5.08 × 10 | |
| p-value | ≤0.05 | >0.05 | NA | |
| Median FEs | 38,694 | 78,444 | 97,506 | |
| Mean | 2.16 × 10 | 1.96 × 10 | 1.19 × 10 | |
| Median | 1.62 × 10 | 7.86 × 10 | 6.33 × 10 | |
| Std | 2.67 × 10 | 6.74 × 10 | 6.50 × 10 | |
| p-value | ≤0.05 | >0.05 | NA | |
| Median FEs | 55,740 | 69,798 | 77,356 | |
| Mean | 5.57 × 10 | 7.90 × 10 | 7.90 × 10 | |
| Median | 4.76 × 10 | 7.90 × 10 | 7.90 × 10 | |
| Std | 3.75 × 10 | 1.34 × 10 | 9.54 × 10 | |
| p-value | ≤0.05 | NA | ≤0.05 | |
| Median FEs | 143,580 | 360,460 | 541,940 | |
| Mean | 9.27 × 10 | 3.03 × 10 | 3.34 × 10 | |
| Median | 6.16 × 10 | 1.17 × 10 | 2.12 × 10 | |
| Std | 1.99 × 10 | 3.24 × 10 | 3.23 × 10 | |
| p-value | ≤0.05 | NA | >0.05 | |
| Median FEs | 9120 | 8150 | 8070 | |
| Mean | 0.00 × 10 | 0.00 × 10 | 2.96 × 10 | |
| Median | 0.00 × 10 | 0.00 × 10 | 0.00 × 10 | |
| Std | 0.00 × 10 | 0.00 × 10 | 1.62 × 10 | |
| p-value | NaN | NA | >0.05 | |
| Median FEs | 3435 | 3935 | 3715 | |
| Mean | 7.54 × 10 | 8.03 × 10 | 8.74 × 10 | |
| Median | 2.86 × 10 | 2.98 × 10 | 2.95 × 10 | |
| Std | 3.60 × 10 | 4.96 × 10 | 4.79 × 10 | |
| p-value | NA | >0.05 | >0.05 | |
| FEs | 4435 | 3995 | 3880 | |
| Mean | 5.11 × 10 | 3.62 × 10 | 1.43 × 10 | |
| Median | 1.79 × 10 | 2.95 × 10 | 1.14 × 10 | |
| Std | 7.44 × 10 | 8.06 × 10 | 1.25 × 10 | |
| p-value | >0.05 | NA | ≤0.05 | |
| FEs | 21,965 | 30,480 | 33,485 | |
| Mean | 3.72 × 10 | 5.21 × 10 | 7.05 × 10 | |
| Median | 2.25 × 10 | 4.77 × 10 | 7.43 × 10 | |
| Std | 5.98 × 10 | 5.23 × 10 | 1.42 × 10 | |
| p-value | NA | ≤0.05 | ≤0.05 | |
| Median FEs | 14,945 | 15,795 | 28,210 | |
| Mean | 3.99 × 10 | 2.42 × 10 | 1.98 × 10 | |
| Median | 6.51 × 10 | 1.82 × 10 | 1.07 × 10 | |
| Std | 7.29 × 10 | 1.21 × 10 | 1.04 × 10 | |
| p-value | ≤0.05 | >0.05 | NA | |
| Median FEs | 22,430 | 56,880 | 61525 |
| Problems | = 0.5 | MMDE | |
|---|---|---|---|
| Mean | 2.0234 × 10 | 2.6618 × 10 | |
| Median | 1.8269 × 10 | 9.5487 × 10 | |
| Std | 7.5060 × 10 | 6.1841 × 10 | |
| p-value | NA | ≤0.05 | |
| Mean | 2.5849 × 10 | 3.3719 × 10 | |
| Median | 0.0000 × 10 | 0.0000 × 10 | |
| Std | 9.6251 × 10 | 1.1081 × 10 | |
| p-value | NA | >0.05 | |
| Mean | 1.0029 × 10 | 5.1712 × 10 | |
| Median | 0.0000 × 10 | 0.0000 × 10 | |
| Std | 2.8499 × 10 | 2.4408 × 10 | |
| p-value | NA | ≤0.05 | |
| Mean | 3.3428 × 10 | 7.9495 × 10 | |
| Median | 5.5485 × 10 | 8.8027 × 10 | |
| Std | 8.7588 × 10 | 1.4876 × 10 | |
| p-value | ≤0.05 | NA | |
| Mean | 8.1786 × 10 | 1.1339 × 10 | |
| Median | 9.6258 × 10 | 2.1344 × 10 | |
| Std | 1.9804 × 10 | 3.2300 × 10 | |
| p-value | ≤0.05 | NA | |
| Mean | 5.0537 × 10 | 5.5425 × 10 | |
| Median | 1.9716 × 10 | 2.7037 × 10 | |
| Std | 7.7093 × 10 | 7.7943 × 10 | |
| p-value | ≤0.05 | NA |
| Problems | = 0.5 | MMDE | |
|---|---|---|---|
| Mean | 1.7100 × 10 | 1.0472 × 10 | |
| Median | 6.4784 × 10 | 9.9247 × 10 | |
| Std | 2.6084 × 10 | 6.0458 × 10 | |
| p-value | NA | >0.05 | |
| Mean | 1.4668 × 10 | 7.6533 × 10 | |
| Median | 6.4275 × 10 | 3.6815 × 10 | |
| Std | 5.1909 × 10 | 7.6206 × 10 | |
| p-value | >0.05 | NA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoniou, M.; Papa, G. Differential Evolution with Estimation of Distribution for Worst-Case Scenario Optimization. Mathematics 2021, 9, 2137. https://doi.org/10.3390/math9172137
Antoniou M, Papa G. Differential Evolution with Estimation of Distribution for Worst-Case Scenario Optimization. Mathematics. 2021; 9(17):2137. https://doi.org/10.3390/math9172137
Chicago/Turabian StyleAntoniou, Margarita, and Gregor Papa. 2021. "Differential Evolution with Estimation of Distribution for Worst-Case Scenario Optimization" Mathematics 9, no. 17: 2137. https://doi.org/10.3390/math9172137
APA StyleAntoniou, M., & Papa, G. (2021). Differential Evolution with Estimation of Distribution for Worst-Case Scenario Optimization. Mathematics, 9(17), 2137. https://doi.org/10.3390/math9172137






