A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-Physical System-ORIENTED
Abstract
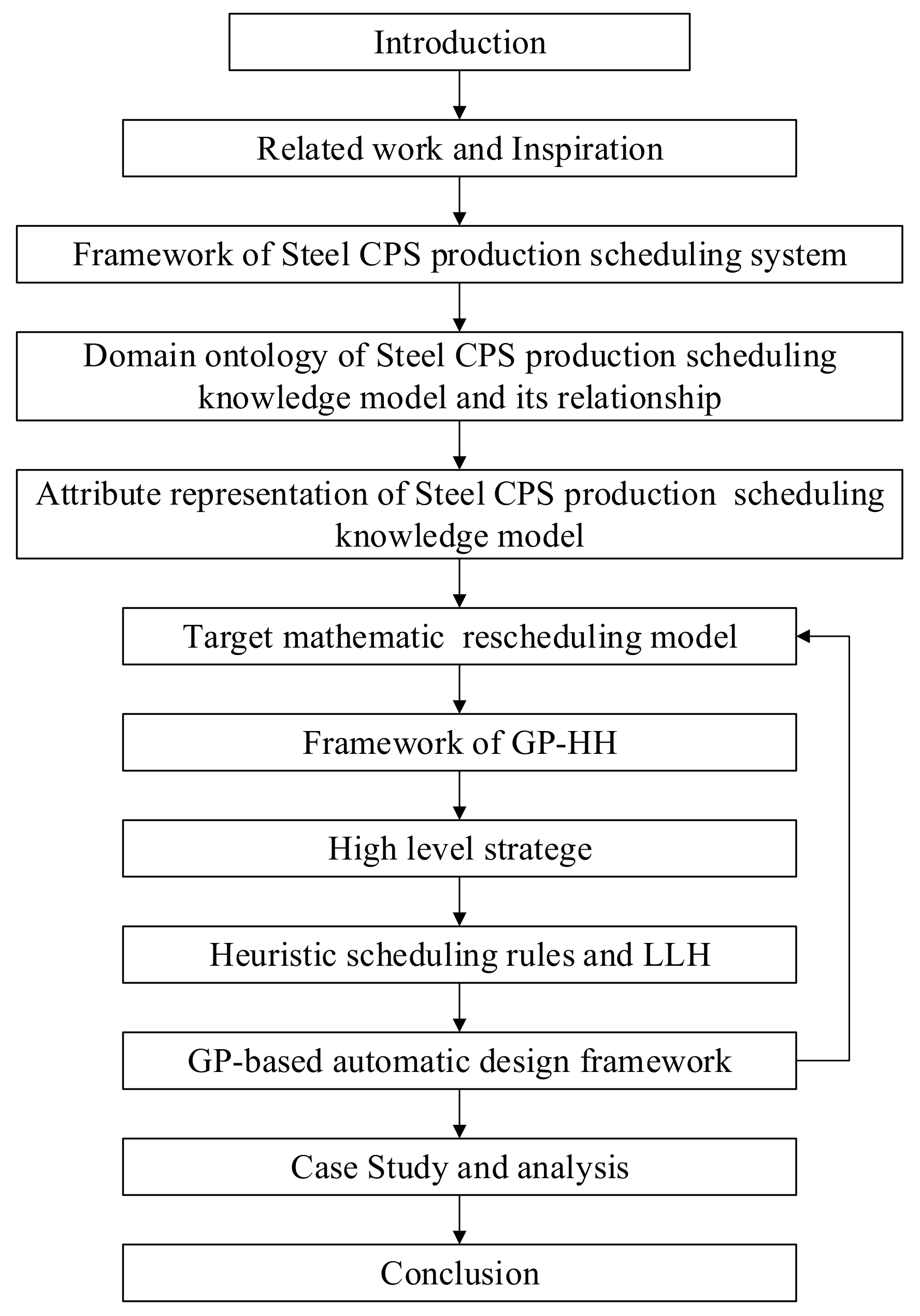
:1. Introduction
2. Related Work
2.1. CPS
2.2. Knowledge-Based of Steel Production Scheduling
2.3. Hyper-Heuristic Algorithm
2.4. Inspiration
3. Ontology-Based Steel CPS-Oriented Production Scheduling Knowledge Model
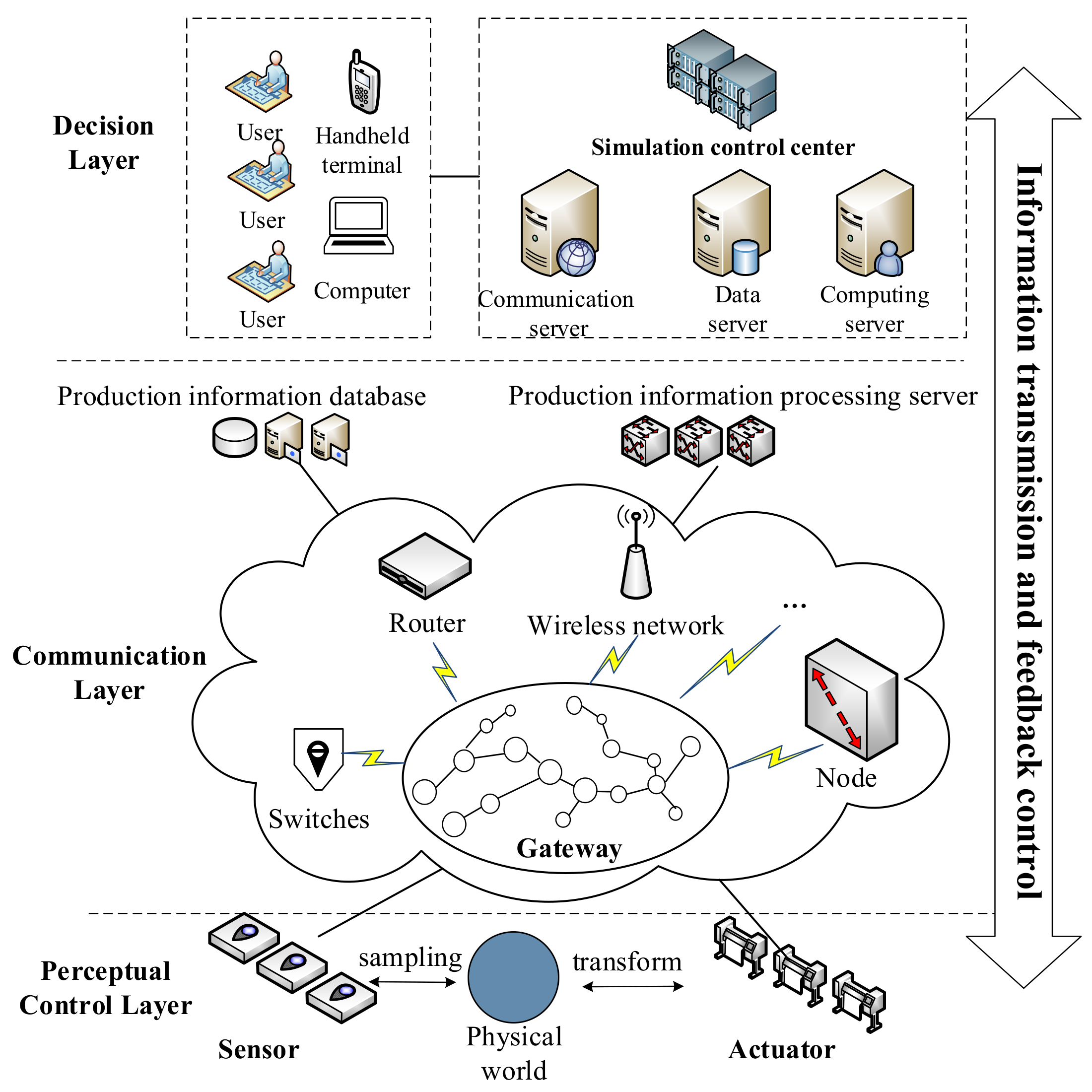
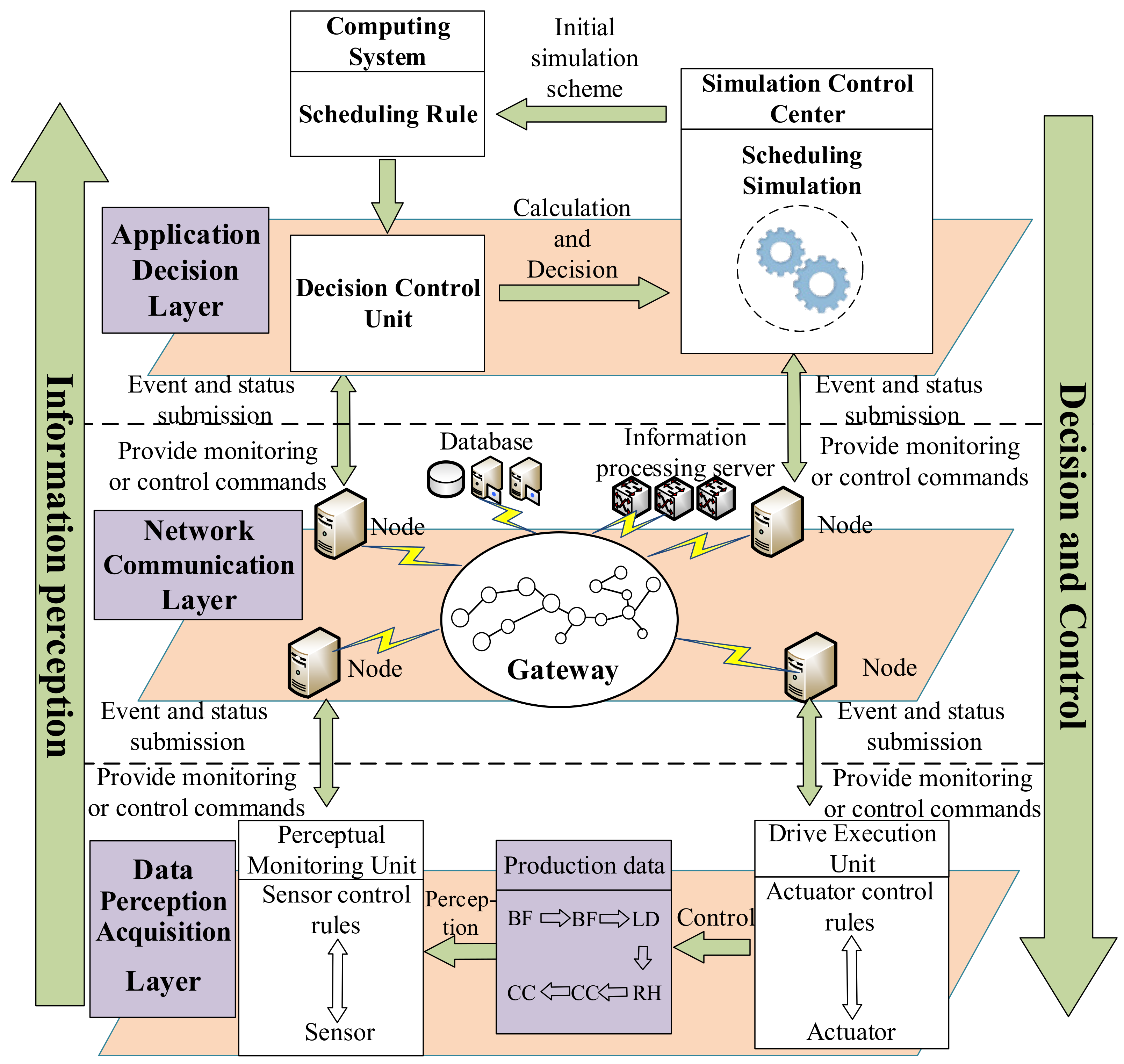
3.1. Framework of Steel CPS-Oriented Production Scheduling System
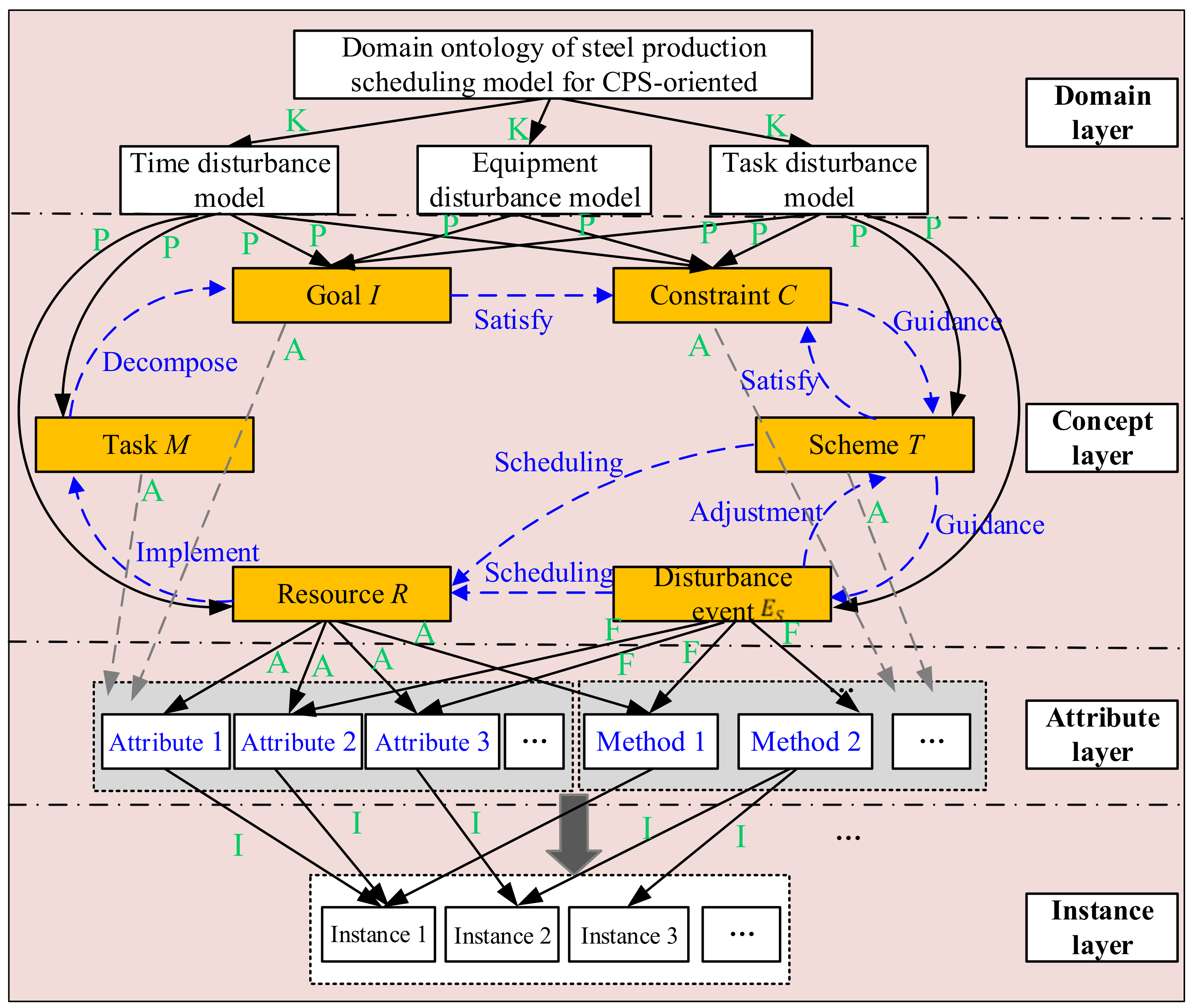
3.2. Definition of Domain Ontology of Steel CPS Production Scheduling Knowledge Model
3.3. Attribute Representation of Steel CPS Production Scheduling Knowledge Model
4. Hyper-Heuristic Algorithm Based on Genetic Programming for Steel CPS
4.1. Target Mathematical Model
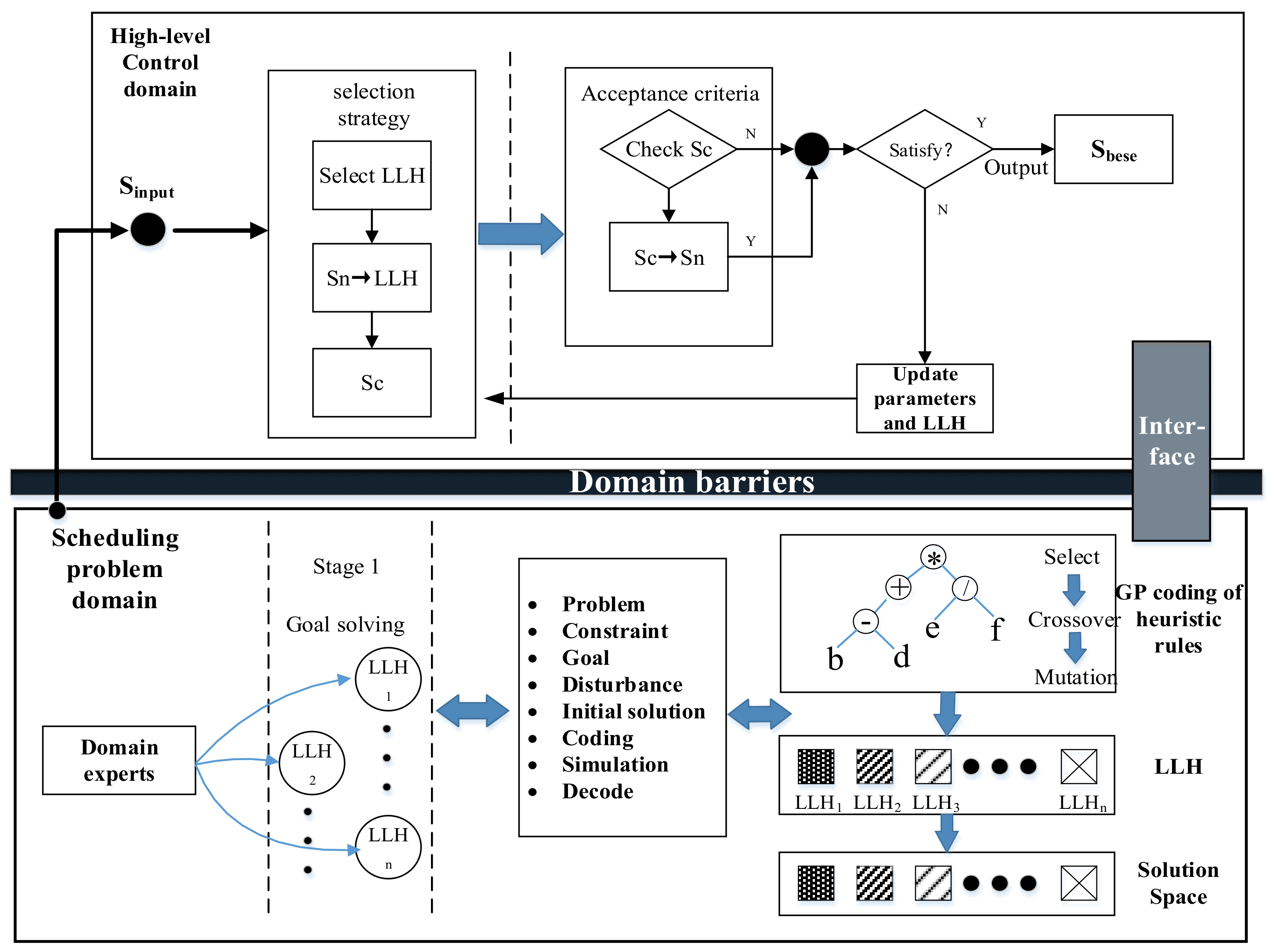
4.2. Hyper-Heuristic Algorithm Framework Based on Genetic Programming
4.3. High-Level Strategy
4.4. Heuristic Scheduling Rules and LLH
4.5. GP Based Heuristic Scheduling Rule Automatic Design Framework
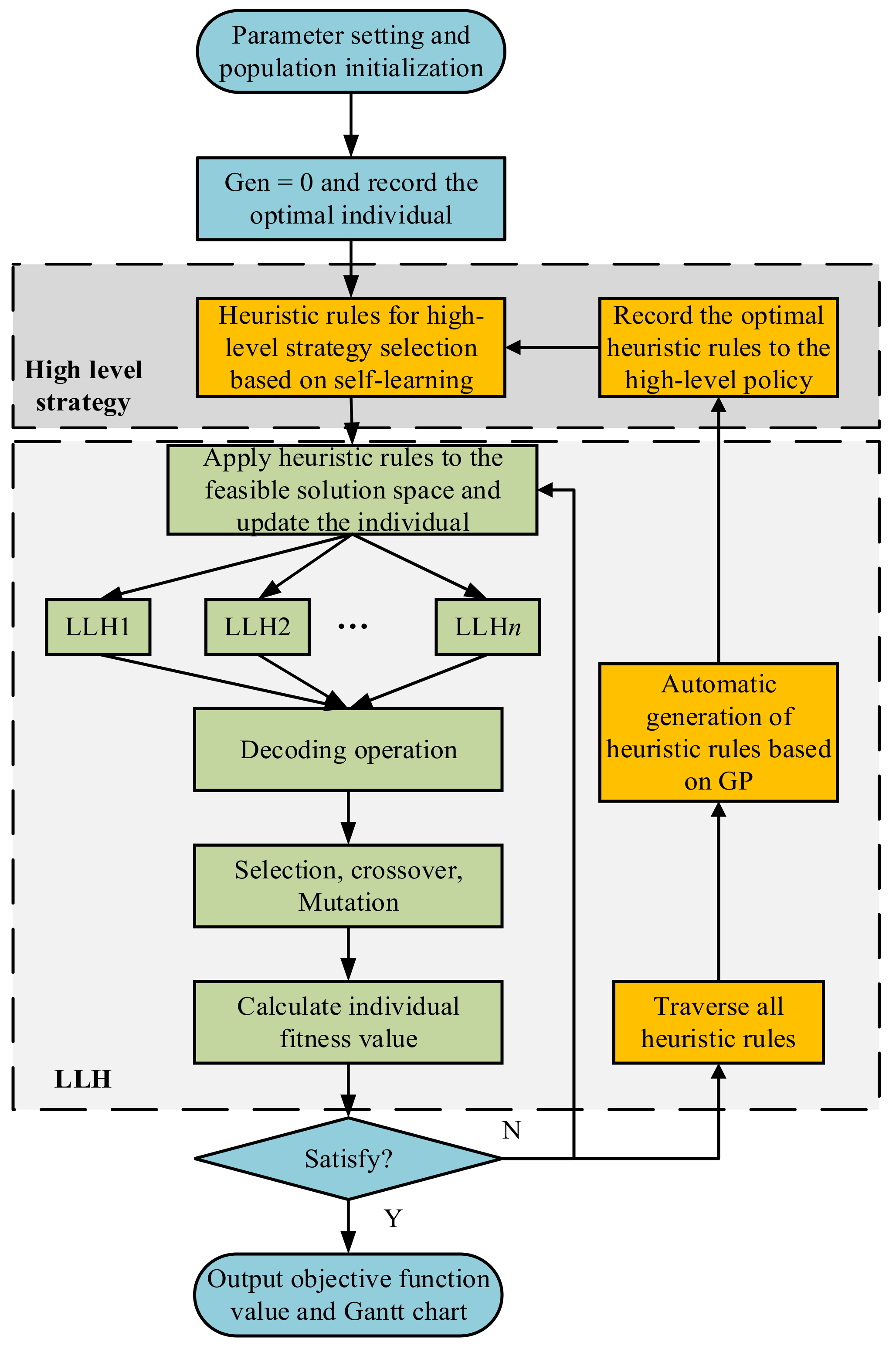
4.6. The Solution Process Based on GP-HH
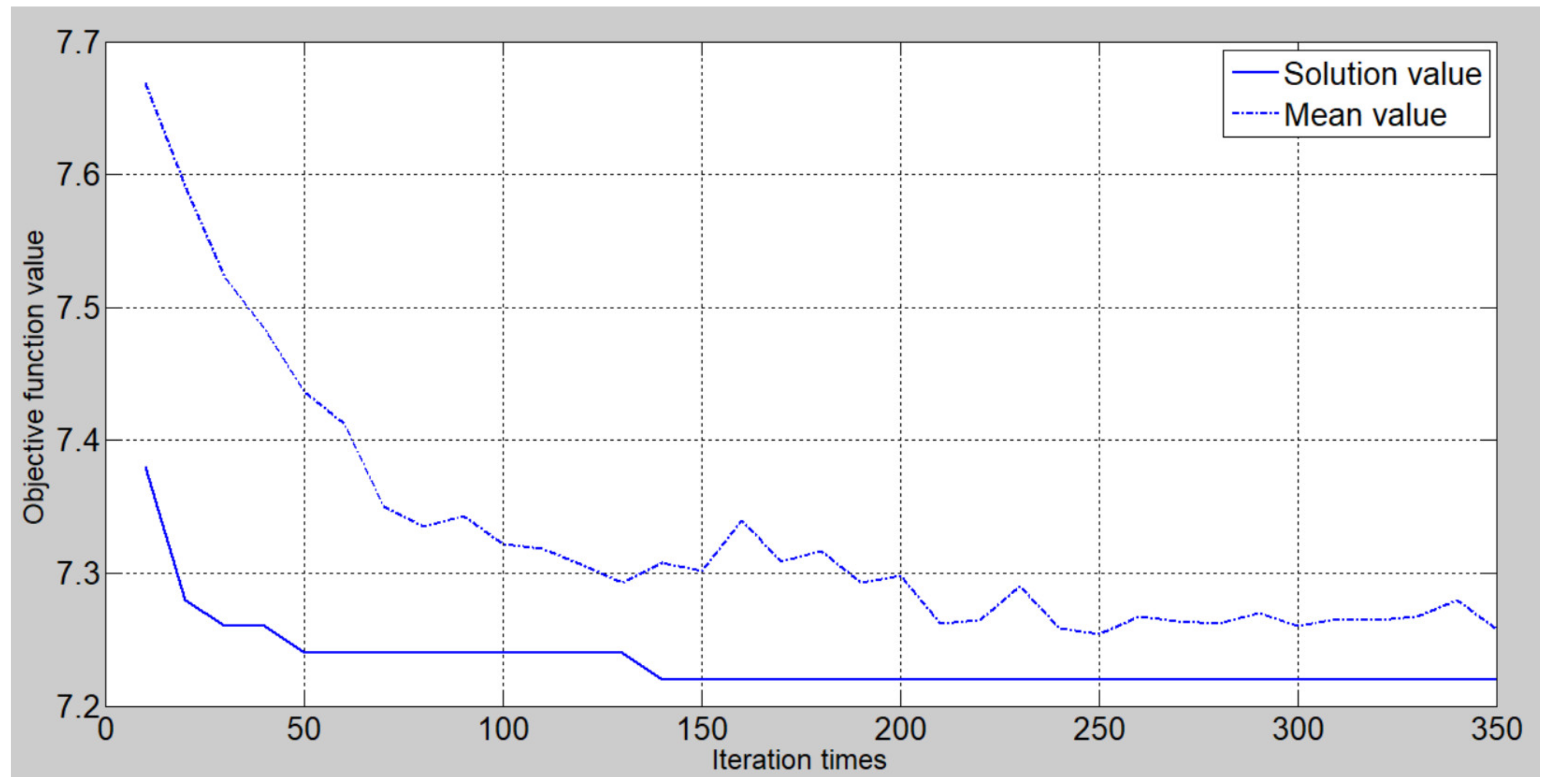
5. Case Study
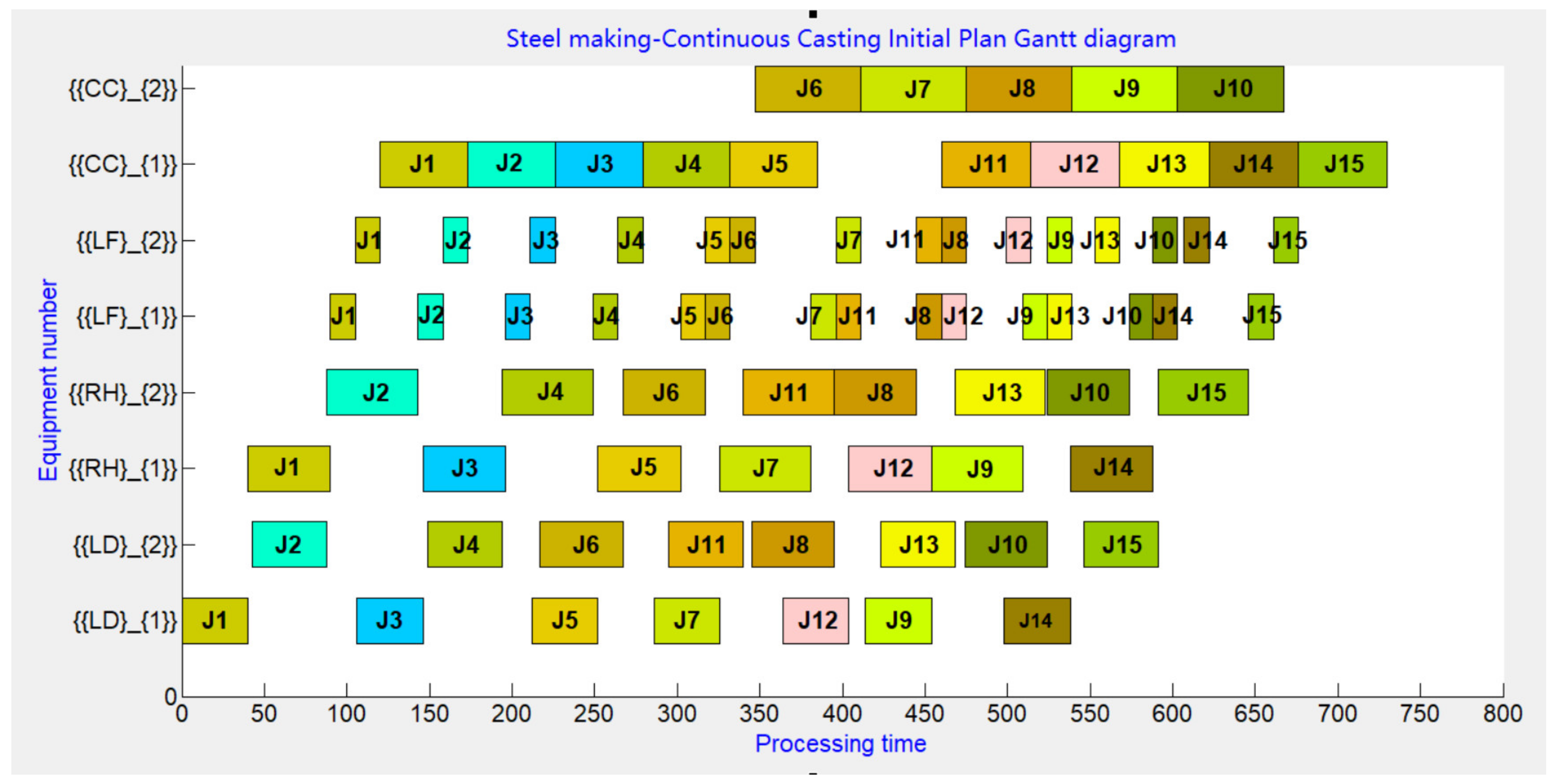
5.1. Original Steel Production Plan
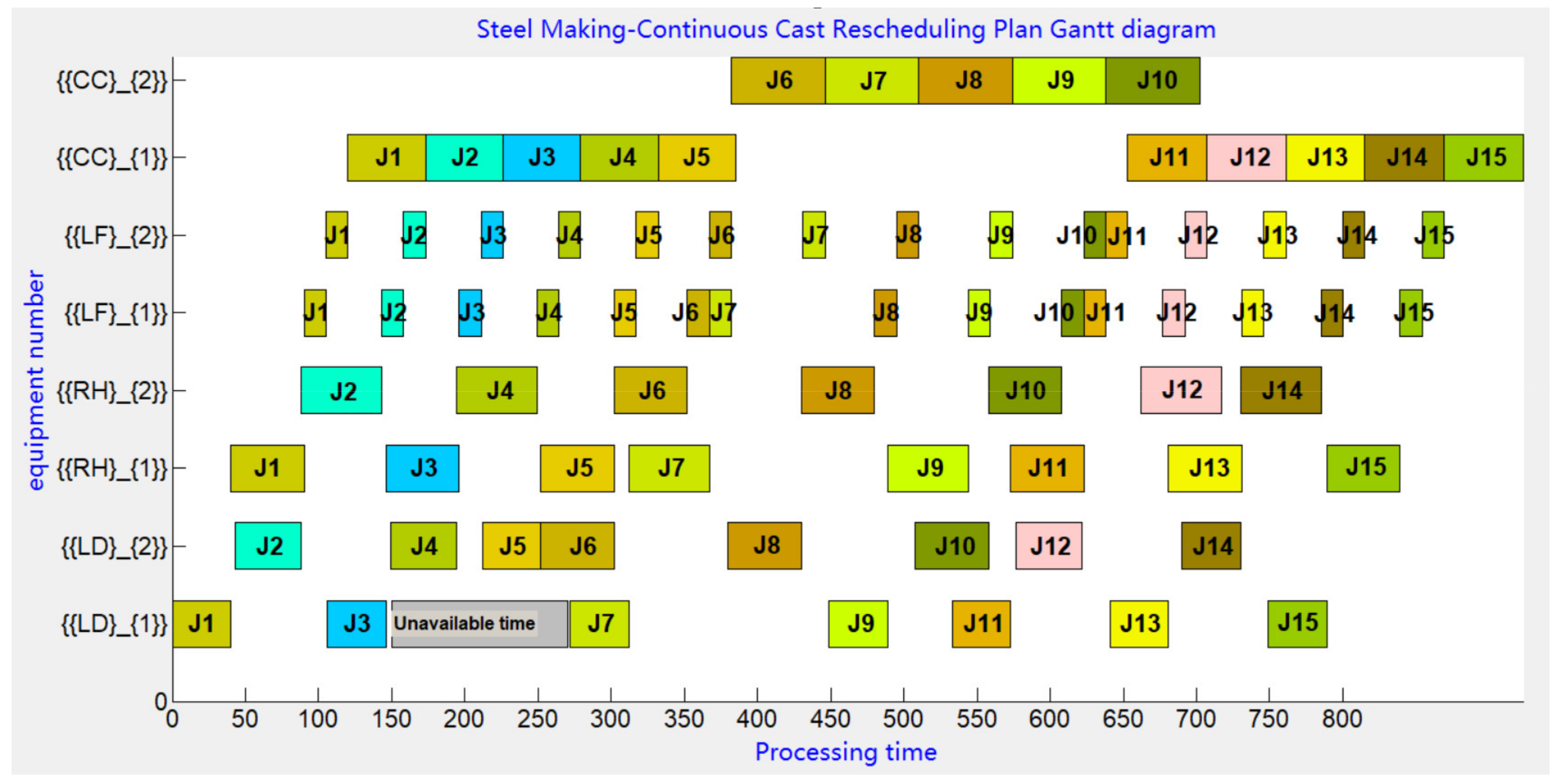
5.2. Case Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Reference Number | Year of Publication and Domain | Main Contribution | Enhancement Requirement/Disadvantage | Similarity with Proposed Work | Possible Research Gap |
|---|---|---|---|---|---|
| [6] | 2019/Engineering | Exposes a spectrum of existing CPS definitions and models. | The application of double loop learning in CPS proposed in this paper is not deep enough. | The architecture of CPS. | Architecture of CPS and its application in engineering practice. |
| [8] | 2018/Computer Science | Study the effect on the quality of Pareto fronts when a biological mathematical model was incorporated into the CPS for a multi objective optimization. | The complexity of the CPS may affect the utility of incorporating biological models. Further research in these areas is suggested. | Research and development of CPS in system performance. | Application of CPS in different fields. |
| [9] | 2019/Computer Science | Presented BPMN4CPS: a preliminary extension of BPMN 2.0 modelling Language to handle CPS process features. | Apply a dynamic (at run time) verification to analyse the temporal consistency still a challenge. | Cyber-physical systems are characterized by a multitude of physical and software. | BPMN4CPS is not widely used, and its specific performance needs to be further verified. |
| [11] | 2016/Computer Science | Introduced ModelPlex, a method ensuring that verification results about models apply to CPS implementations. | The ModelPlex can be extending, so the synthesize prediction monitors from differential equations without polynomial solutions. | Formal method of CPS modeling. | The mapping between virtual model and real model of CPS is not accurate enough. |
| [12] | 2016/Computer Science | Presents a methodology to design and verify CPS using multi-objective evolutionary optimization and software tools. | Improve the performance of verification methods is important. | Optimization of CPS. | Extensions to probabilistic model checking and verifying distributed CPS are difficult. |
| [13] | 2014/Computer Science | The paper propose a co-simulation framework that can facilitate time-triggered automotive CPS design. | The three CPS design layers of Virtual prototyping of automotive control system are simplified. | The architecture of CPS. | The complex network physical interaction makes the security maintenance of the system more important. |
Appendix B
| Reference Number | Year of Publication and Domain | Main Contribution | Enhancement Requirement/Disadvantage | Similarity with Proposed Work | Possible Research Gap |
|---|---|---|---|---|---|
| [16] | 2016/Engineering | Propose a self-evolutionary scheduling algorithm for knowledgeable manufacturing System for flow shop scheduling. | For small-scale scheduling problems, the applicability of the algorithm is not strong and the training time is too long. | Knowledge based scheduling. | How to improve the evolutionary ability of the proposed algorithm is the research gap. |
| [19] | 2020/Computer Science | A new knowledgeable encapsulation method of steel production scheduling model. | Knowledge mapping needs to be studied in the future. | Knowledge scheduling | Research on the large-scale dynamic scheduling algorithm. |
| [20] | 2017/ Physics | Ontology-based modular multi-granularity hierarchical model was built based on modular ontology technology. | The method and application of ontology based modeling are not deep enough. | Ontology based modeling. | The problems of real-time updating of knowledge, automatic generation of new knowledge and knowledge push still need to be solved. |
Appendix C
| Reference Number | Year of Publication and Domain | Main Contribution | Enhancement Requirement/Disadvantage | Similarity with Proposed Work | Possible Research Gap |
|---|---|---|---|---|---|
| [21] | 2019/Computer Science | This overview proposes a unified framework for the algorithmic techniques at the confluence between evolutionary computation and reinforcement learning. | There is no performance comparison experiment of the algorithm. | Discussion on the generality of the algorithm. | More algorithms are waiting to be discussed and verified. |
| [22] | 2020/Logistics Managem | Hyper-heuristic algorithm based on tabu search for time-dependent simultaneous pick-up and delivery vehicle routing problem. | The relationship between vehicle travel speed and customer satisfaction, distribution cost, energy consumption and driving path under variable vehicle speed can be further optimized. | Hyper heuristic algorithm study. | There are still some improvements in the combination of hyper-heuristic algorithm and other strategies. |
| [24] | 2018/Computer Science | This paper proposes a method to automatically design the high-level heuristic of a hyper-heuristic model by utilizing a reinforcement learning technique. | It is necessary to consider the combination of Q-learning based hyper-heuristic and multi-point search strategy to improve the performance of the algorithm. | Hyper heuristic algorithm design. | How to choose single point strategy or multi-point strategy to improve the ability of algorithm is a challenge. |
| [26] | 2020/Computer Science | A genetic programming hyper-heuristic algorithm was proposed for the multi-skill resource constrained project scheduling problem. | To extend the multi-skill resource constrained project scheduling problem to model the realistic environment. | Genetic programming hyper heuristic algorithm. | The fitness landscape analysis will be the promising technique which can be employed to guide the design of some problem-specific low-level heuristics in the hyper-heuristic scheme. |
| [35] | 2014/Computer Science | Different hyper-heuristics combining different selection and move acceptance methods are implemented as search methodologies to solve the constraint magic square problem. | The performance of RP’s hyper heuristic algorithm is compared with other heuristic algorithms. | Hyper heuristic algorithm design. | Choosing different mobile strategies and receiving criteria has a great impact on the performance of super heuristic algorithm. |
References
- Long, J.Y.; Zheng, Z.; Gao, X.Q. Dynamic scheduling in steelmaking-continuous casting production for continuous caster breakdown. Int. J. Prod. Res. 2017, 55, 3197–3216. [Google Scholar] [CrossRef]
- Tang, L.; Meng, Y.; Chen, Z.-L.; Liu, J. Coil batching to improve productivity and energy utilization in steel production. MSom-Manuf. Serv. Oper. Manag. 2016, 18, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Lin, D.Y.; Huang, T.Y. A Hybrid Metaheuristic for the Unrelated Parallel Machine Scheduling Problem. Mathematics 2021, 9, 768. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y.; Wang, B.; Yao, S.; Liu, Z. Review on cyber-physical systems. IEEE/CAA J. Autom. Sin. 2017, 4, 27–40. [Google Scholar] [CrossRef]
- Guan, X.; Yang, B.; Chen, C.; Dai, W.; Wang, Y. A comprehensive overview of cyber-physical systems: From perspective of feedback system. IEEE/CAA J. Autom. Sin. 2016, 3, 1–14. [Google Scholar]
- Putnik, G.D.; Ferreira, L.; Lopes, N.; Putnik, Z. What is a cyber-physical system: Definitions and models spectrum. Fme Trans. 2019, 47, 663–674. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, Y.; Wang, B.; Zang, J. Human Cyber Physical Systems (HCPSs) in the context of new-generation intelligent manufacturing. Engineering 2019, 4, 624–636. [Google Scholar] [CrossRef]
- Keller, K.L. Leveraging biologically inspired models for cyber-physical systems analysis. IEEE Syst. J. 2018, 12, 3597–3607. [Google Scholar] [CrossRef]
- Graja, I.; Kallel, S.; Guermouche, N.; Cheikhrouhou, S.; Kacem, A.H. Modelling and verifying time-aware processes for cyber-physical environments. IET Softw. 2019, 13, 36–48. [Google Scholar] [CrossRef]
- Fu, Y.G.; Zhu, J.M.; Gao, S. CPS information security risk evaluation based on block chain and big data. Teh. Vjesn. Tech. Gaz. 2018, 25, 1843–1850. [Google Scholar]
- Mitsch, S.; Platzer, A. ModelPlex: Verified runtime validation of verified cyber-physical system models. Form. Methods Syst. Des. 2016, 49, 33–74. [Google Scholar] [CrossRef] [Green Version]
- Balasubramaniyan, S.; Srinivasan, S.; Buonopane, F.; Subathra, B.; Vain, J.; Ramaswamy, S. Design and verification of Cyber-Physical Systems using TrueTime evolutionary optimization and UPPAAL. Microprocess. Microsyst. 2016, 42, 37–48. [Google Scholar] [CrossRef]
- Zhang, Z.; Eyisi, E.; Koutsoukos, X.; Porter, J.; Karsai, G.; Sztipanovits, J. A co-simulation framework for design of time-triggered automotive cyber physical systems. Simul. Model. Pract. Theory 2014, 43, 16–33. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Martín, A.; Mateos, A.; Hernández, J.Z. Aluminium parts casting scheduling based on simulated annealing. Mathematics 2021, 9, 741. [Google Scholar] [CrossRef]
- Wang, H.-X.; Yan, H.-S. An interoperable adaptive scheduling strategy for knowledgeable manufacturing based on SMGWQ-learning. J. Intell. Manuf. 2016, 27, 1085–1095. [Google Scholar] [CrossRef]
- Yan, H.-S.; Li, W.-C. A scheduling procedure for a flow shop-like knowledgeable manufacturing cell with self-evolutionary features. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2016, 230, 2296–2306. [Google Scholar] [CrossRef]
- Yan, H.-S.; Yang, H.-B. Deadlock-free scheduling of knowledgeable manufacturing cell with multiple machines and products. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2015, 229, 1834–1847. [Google Scholar] [CrossRef]
- Jiang, G.; Chen, X.; Li, X.; Xiang, F.; Li, G. Model knowledge matching algorithm for steelmaking casting scheduling. Int. J. Wirel. Mob. Comput. 2018, 15, 215–222. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, G.; Li, G.; Zuo, Y.; Xiang, F. A new knowledgeable encapsulation method of steel production scheduling model. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1673–1685. [Google Scholar] [CrossRef]
- Xu, B.Z.; Wang, Y.; Ji, Z.C. Knowledge network model of the energy consumption in discrete manufacturing system. Mod. Phys. Lett. B 2017, 31, 19–21. [Google Scholar] [CrossRef] [Green Version]
- Drugan, M.M. Reinforcement learning versus evolutionary computation: A survey on hybrid algorithms. Swarm Evol. Comput. 2019, 44, 228–246. [Google Scholar] [CrossRef]
- Zhang, J.L.; Liu, J.L.; Zhao, Y.W.; Wang, H.W.; Leng, L.L.; Feng, Q.B. Hyper-heuristic for time-dependent VRP with simultaneous delivery and pick-up. Comput. Integr. Manuf. Syst. 2020, 26, 1905–1917. [Google Scholar]
- Asta, S.; Ozcan, E.; Curtois, T. A tensor based hyper-heuristic for nurse rostering. Knowl. Based Syst. 2016, 98, 185–199. [Google Scholar] [CrossRef] [Green Version]
- Choong, S.S.; Wong, L.P.; Lim, C.P. Automatic design of hyper-heuristic based on reinforcement learning. Inf. Sci. 2018, 436, 89–107. [Google Scholar] [CrossRef]
- Nasser RSabar, M.A.; Graham, K. A dynamic multi-armed bandit-gene expression programming hyper-heuristic for combinatorial optimization problems. IEEE Trans. Cybern. 2015, 45, 217–227. [Google Scholar]
- Lin, J.; Zhu, L.; Gao, K. A genetic programming hyper-heuristic approach for the multi-skill resource constrained project scheduling problem. Expert Syst. Appl. 2020, 140, 112915. [Google Scholar] [CrossRef]
- Kheiri, A.; Ozcan, E. Constructing constrained-version of magic squares using selection hyper-heuristics. Comput. J. 2014, 57, 469–479. [Google Scholar] [CrossRef] [Green Version]
- Yu, L.; Ma, H.; Wang, C. Research on construction of equipment phm knowledge ontology and semantic reasoning method. J. Ordnance Equip. Eng. 2019, 40, 126–130. [Google Scholar]
- Xiong, T.; Zhou, C.G.; Wang, M.Q. Rapid fire weapon technology knowledge push method based on manufacturing situation. J. Ordnance Equip. Eng. 2019, 40, 230–235. [Google Scholar]
- Yu, S.B.; Li, X.M.; Liu, D.; Cheng, J.B.; Li, Y.C. Study on equipment knowledge formalization description model based on extension theory. J. Ordnance Equip. Eng. 2016, 8, 23–28. [Google Scholar]
- Wang, J.H.; Chen, Y. Data-driven Job Shop production scheduling knowledge mining and optimization. Comput. Eng. Appl. 2018, 54, 264–270. [Google Scholar]
- Li, X.B.; Zhuang, P.J.; Yin, C. A metadata based manufacturing resource ontology modeling in cloud manufacturing systems. J. Ambient Intell. Humaniz. Comput. 2019, 10, 1039–1047. [Google Scholar] [CrossRef]
- Marko, D.; Domagoj, J.; Karlo, K. Adaptive scheduling on unrelated machines with genetic programming. Appl. Soft Comput. 2016, 48, 419–430. [Google Scholar]
- Nguyen, S.; Mei, Y.; Zhang, M. Genetic programming for production scheduling: A survey with a unified framework. Complex Intell Syst 2017, 3, 41–66. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.P.; Chai, T.Y. Heuristic scheduling method for steelmaking and continuous casting production process. Control Theory Appl. 2016, 33, 1413–1421. [Google Scholar]


| Reference Number/Publication Year | CPS Modeling and Verification | Scheduling Algorithm | Knowledge Scheduling | Hyper-Heuristic | Knowledge-Based Steel CPS Production Scheduling and Algorithm |
|---|---|---|---|---|---|
| [6]/2019 | ✓ | ||||
| [7]/2019 | ✓ | ||||
| [8]/2018 | ✓ | ||||
| [9]/2019 | ✓ | ||||
| [10]/2018 | ✓ | ||||
| [14]/2021 | ✓ | ||||
| [15]/2016 | ✓ | ||||
| [16]/2016 | ✓ | ✓ | |||
| [18]/2018 | ✓ | ||||
| [19]/2020 | ✓ | ||||
| [20]/2017 | ✓ | ||||
| [21]/2019 | ✓ | ||||
| [22]/2020 | ✓ | ✓ | |||
| [23]/2016 | ✓ | ✓ | |||
| [24]/2018 | ✓ | ||||
| [25]/2015 | ✓ | ✓ | |||
| [26]/2020 | ✓ | ✓ |
| Number | Sequence | Rules | Heuristic Method |
|---|---|---|---|
| 1 | Sq1 | ||
| 2 | Sq1 | ||
| 3 | Sq1 | ||
| 4 | Sq1 | ||
| 5 | Sq2 | ||
| 6 | Sq2 | ||
| 7 | Sq2 | ||
| 8 | Sq2 |
| Casting | Charge | Processing Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LD1 | LD2 | RH1 | RH2 | LF1 | LF2 | CC1 | CC2 | ||
| 1 | 5 | 40 | 45 | 50 | 55 | 15 | 15 | 53 | 61 |
| 2 | 5 | 40 | 50 | 55 | 50 | 15 | 15 | 57 | 64 |
| 3 | 5 | 40 | 45 | 50 | 55 | 15 | 15 | 54 | 63 |
| LD1 | LD2 | RH1 | RH2 | LF1 | LF2 | CC1 | CC2 | |
|---|---|---|---|---|---|---|---|---|
| 1–1 | [0,40] | [40,90] | [90,105] | [105,120] | [125,173] | |||
| 1–2 | [43,88] | [88,143] | [143,158] | [158,173] | [173,226] | |||
| 1–3 | [106,146] | [146,196] | [196,211] | [211,226] | [226,279] | |||
| 1–4 | [149,194] | [194,249] | [249,264] | [264,279] | [279,332] | |||
| 1–5 | [212,252] | [252,302] | [302,317] | [317,332] | [332,385] | |||
| 2–6 | [217,267] | [267,317] | [317,332] | [332,347] | [347,411] | |||
| 2–7 | [286,326] | [326,381] | [381,396] | [396,411] | [411,475] | |||
| 2–8 | [345,395] | [395,445] | [445,460] | [460,475] | [475,539] | |||
| 2–8 | [414,454] | [454,509] | [509,524] | [524,539] | [539,603] | |||
| 2–10 | [474,524] | [524,574] | [574,588] | [588,603] | [603,667] | |||
| 3–11 | [295,340] | [340,395] | [396,445] | [445,460] | [460,514] | |||
| 3–12 | [364,404] | [404,454] | [460,499] | [499,514] | [514,568] | |||
| 3–13 | [423,468] | [468,523] | [524,553] | [553,568] | [568,622] | |||
| 3–14 | [498,538] | [538,588] | [588,607] | [607,622] | [622,676] | |||
| 3–15 | [546,591] | [591,646] | [646,661] | [661,676] | [676,730] |
| Equipment | Disturbance | Start Time/Min | End Time/Min | Failure Time/Min |
|---|---|---|---|---|
| LD1 | Equipment failure | 150 | 270 | 120 |
| LD1 | LD2 | RH1 | RH2 | LF1 | LF2 | CC1 | CC2 | |
|---|---|---|---|---|---|---|---|---|
| 1–1 | [0,40] | [40,90] | [90,105] | [105,120] | [125,173] | |||
| 1–2 | [43,88] | [88,143] | [143,158] | [158,173] | [173,226] | |||
| 1–3 | [106,146] | [146,196] | [196,211] | [211,226] | [226,279] | |||
| 1–4 | [149,194] | [194,249] | [249,264] | [264,279] | [279,332] | |||
| 1–5 | [212,252] | [252,302] | [302,317] | [317,332] | [332,385] | |||
| 2–6 | [252,302] | [302,352] | [352,367] | [367,382] | [382,446] | |||
| 2–7 | [272,312] | [312,367] | [367,431] | [431,446] | [446,510] | |||
| 2–8 | [380,430] | [430,480] | [480,495] | [495,510] | [510,574] | |||
| 2–9 | [449,489] | [489,544] | [544,579] | [559,574] | [574,638] | |||
| 2–10 | [508,558] | [558,608] | [608,623] | [623,638] | [638,702] | |||
| 3–11 | [533,573] | [573,623] | [623,638] | [638,653] | [653,707] | |||
| 3–12 | [577,622] | [622,677] | [677,692] | [692,707] | [707,761] | |||
| 3–13 | [641,731] | [681,731] | [731,746] | [746,761] | [761,815] | |||
| 3–14 | [690,730] | [730,785] | [785,800] | [800,815] | [815,869] | |||
| 3–15 | [749,789] | [789,839] | [839,854] | [854,869] | [869,923] |
| Case | Casting | Charge | GP-HH | |
|---|---|---|---|---|
| Optimal Solution | Mean Value | |||
| 1 | 3 | 15 | 3.693 | 3.696 |
| 2 | 8 | 26 | 6.153 | 6.158 |
| 3 | 13 | 57 | 7.238 | 7.239 |
| 4 | 18 | 68 | 7.605 | 7.606 |
| 5 | 22 | 83 | 7.884 | 7.885 |
| 6 | 28 | 120 | 7.849 | 7.851 |
| 7 | 35 | 147 | 7.953 | 7.955 |
| 8 | 46 | 212 | 7.962 | 7.965 |
| 9 | 55 | 282 | 7.863 | 7.866 |
| Case | Casting | Charge | Heuristic Scheduling Method | GP-HH | ||||
|---|---|---|---|---|---|---|---|---|
| Optimal Solution | Mean Value | CUP Time/s | Optimal Solution | Mean Value | CUP Time/s | |||
| 1 | 3 | 15 | 3.672 | 3.677 | 2.8 | 3.693 | 3.696 | 9.1 |
| 2 | 8 | 26 | 6.132 | 6.136 | 5.1 | 6.153 | 6.158 | 14.6 |
| 3 | 18 | 68 | 7.605 | 7.611 | 6.4 | 7.605 | 7.606 | 16.8 |
| 4 | 22 | 83 | 7.891 | 7.897 | 6.9 | 7.884 | 7.885 | 17.2 |
| 5 | 28 | 120 | 7.893 | 7.899 | 7.1 | 7.849 | 7.851 | 17.9 |
| 6 | 46 | 212 | 7.985 | 7.990 | 7.2 | 7.962 | 7.965 | 18.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Jiang, G.; Xiao, Y.; Li, G.; Xiang, F. A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-Physical System-ORIENTED. Mathematics 2021, 9, 2256. https://doi.org/10.3390/math9182256
Chen X, Jiang G, Xiao Y, Li G, Xiang F. A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-Physical System-ORIENTED. Mathematics. 2021; 9(18):2256. https://doi.org/10.3390/math9182256
Chicago/Turabian StyleChen, Xiaowu, Guozhang Jiang, Yongmao Xiao, Gongfa Li, and Feng Xiang. 2021. "A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-Physical System-ORIENTED" Mathematics 9, no. 18: 2256. https://doi.org/10.3390/math9182256
APA StyleChen, X., Jiang, G., Xiao, Y., Li, G., & Xiang, F. (2021). A Hyper Heuristic Algorithm Based Genetic Programming for Steel Production Scheduling of Cyber-Physical System-ORIENTED. Mathematics, 9(18), 2256. https://doi.org/10.3390/math9182256






