Stability Analysis of Unsteady MHD Rear Stagnation Point Flow of Hybrid Nanofluid
Abstract
:1. Introduction
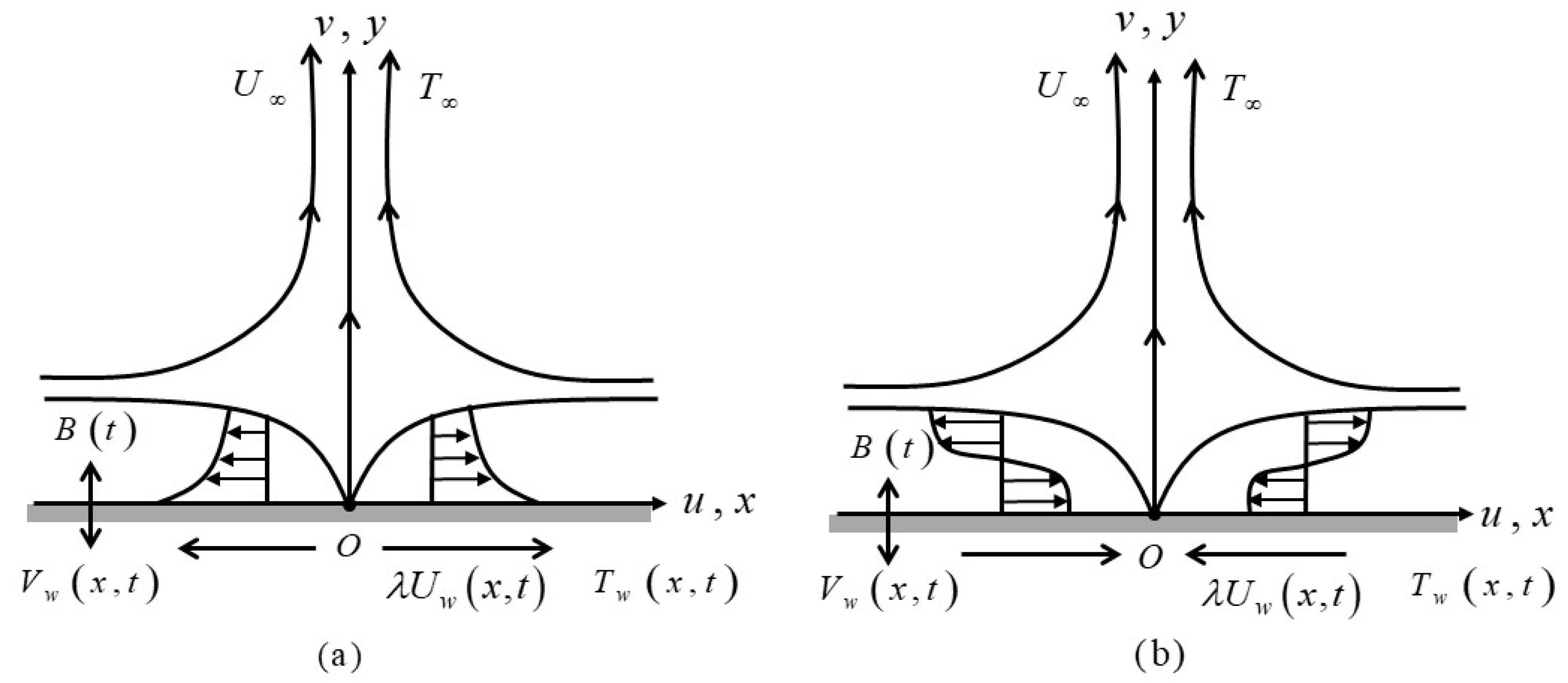
2. Mathematical Modeling
3. Stability Analysis
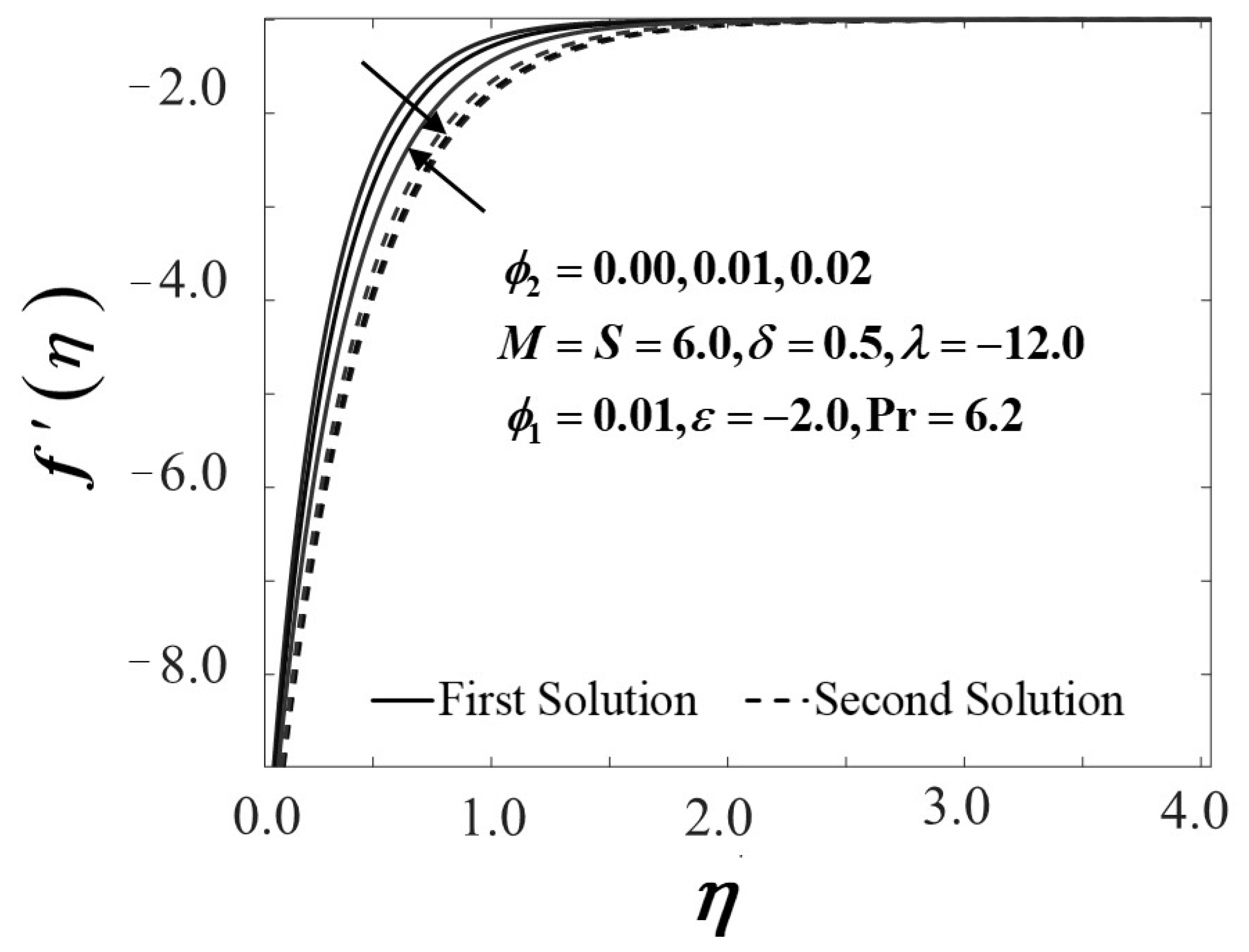
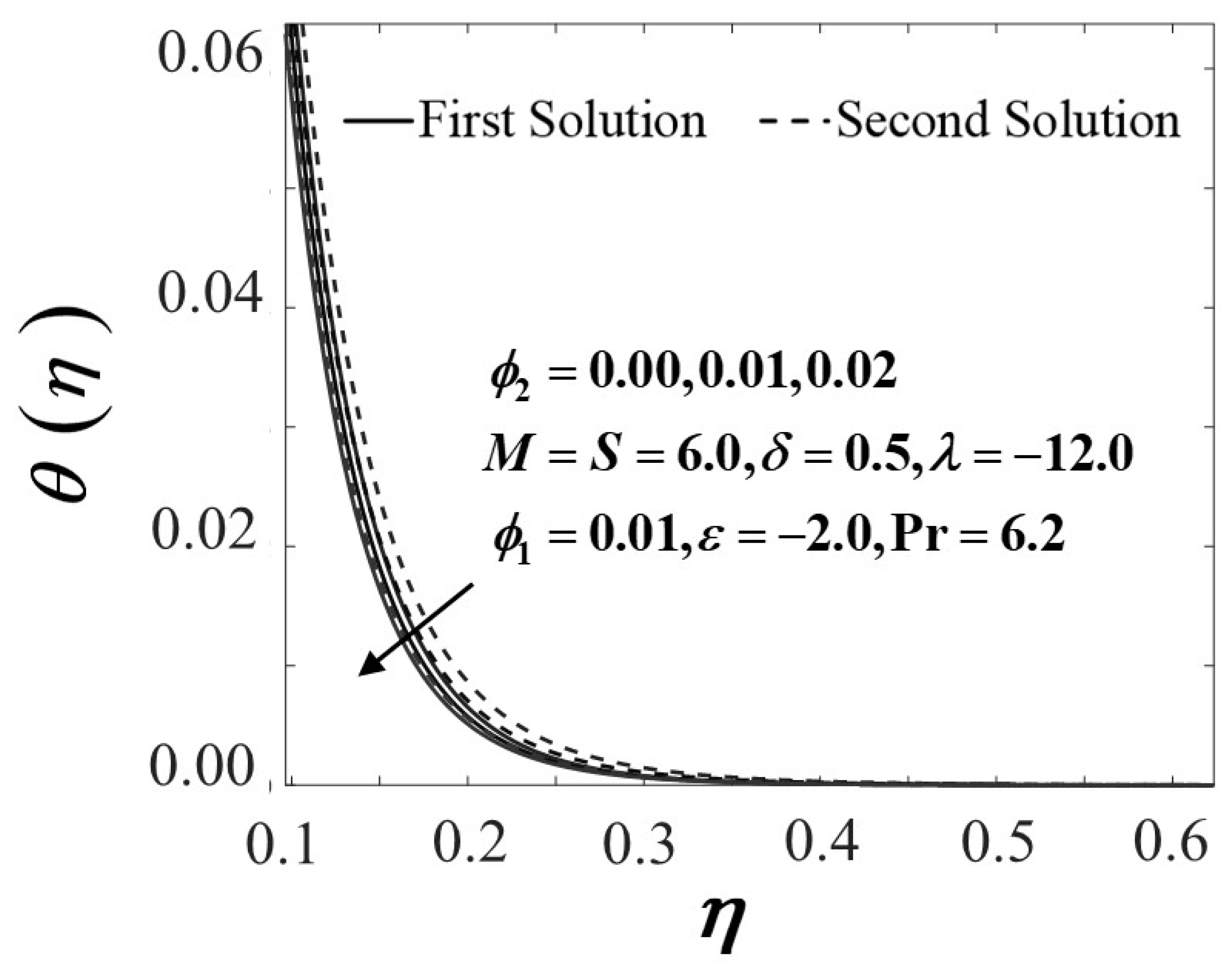
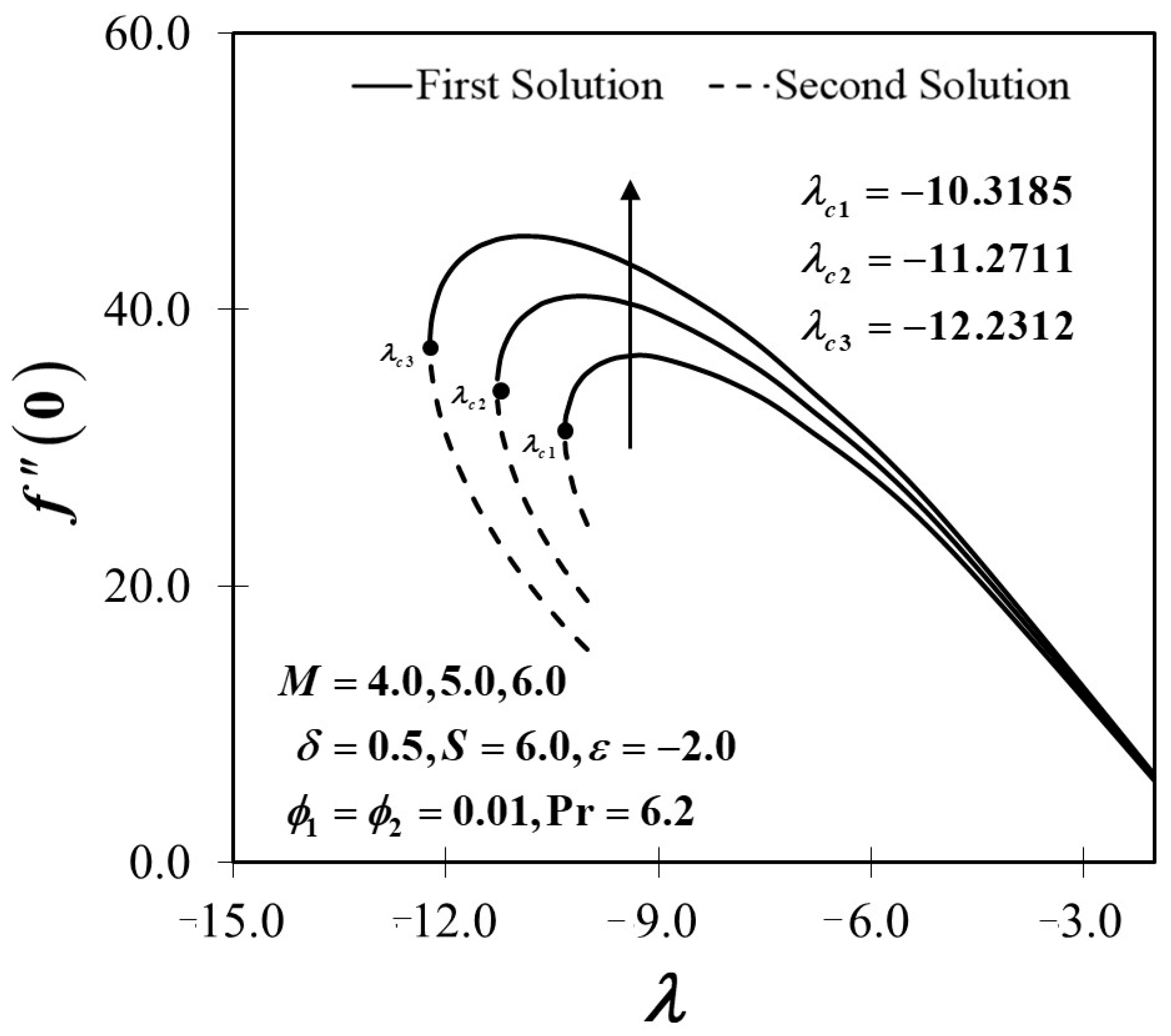
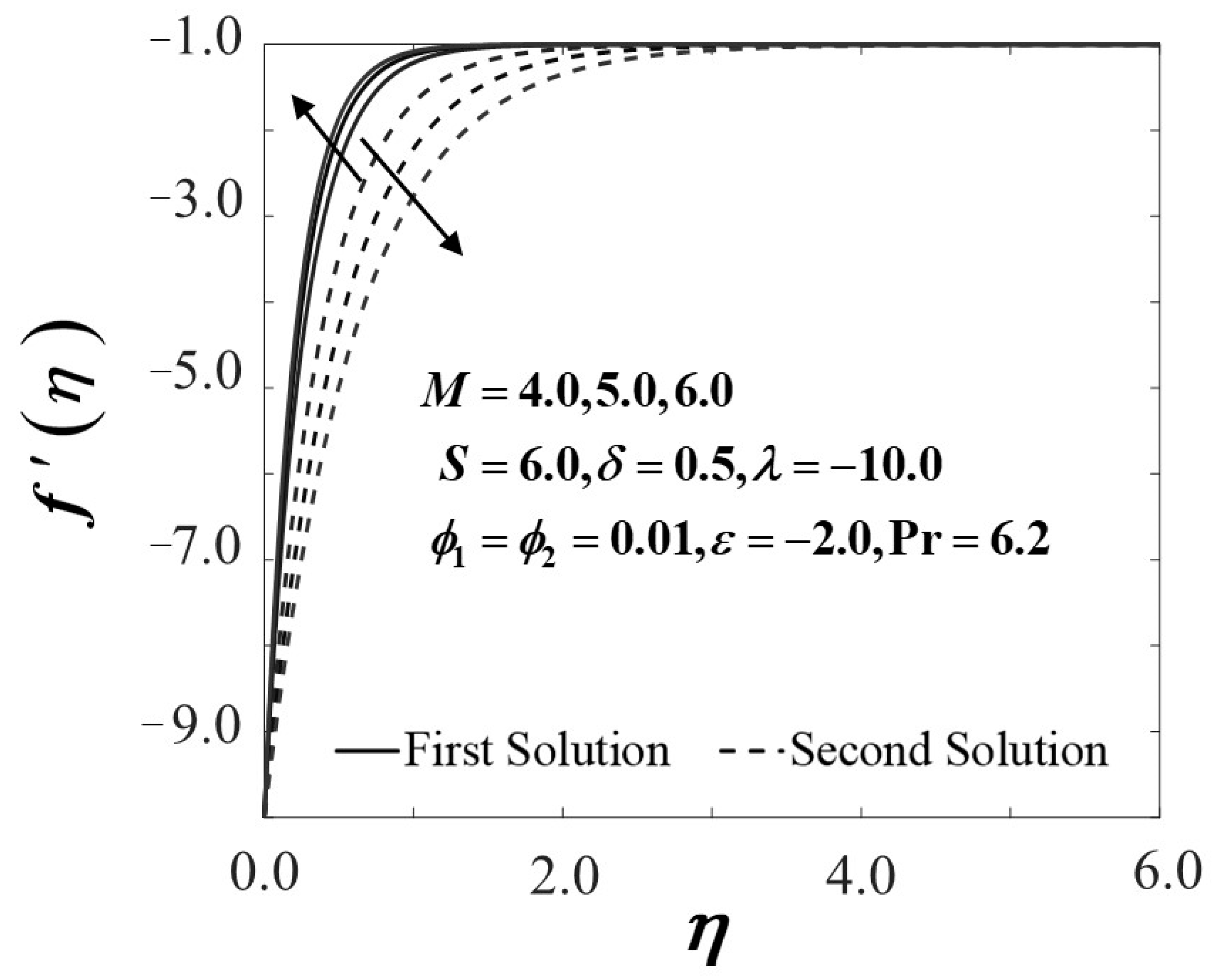
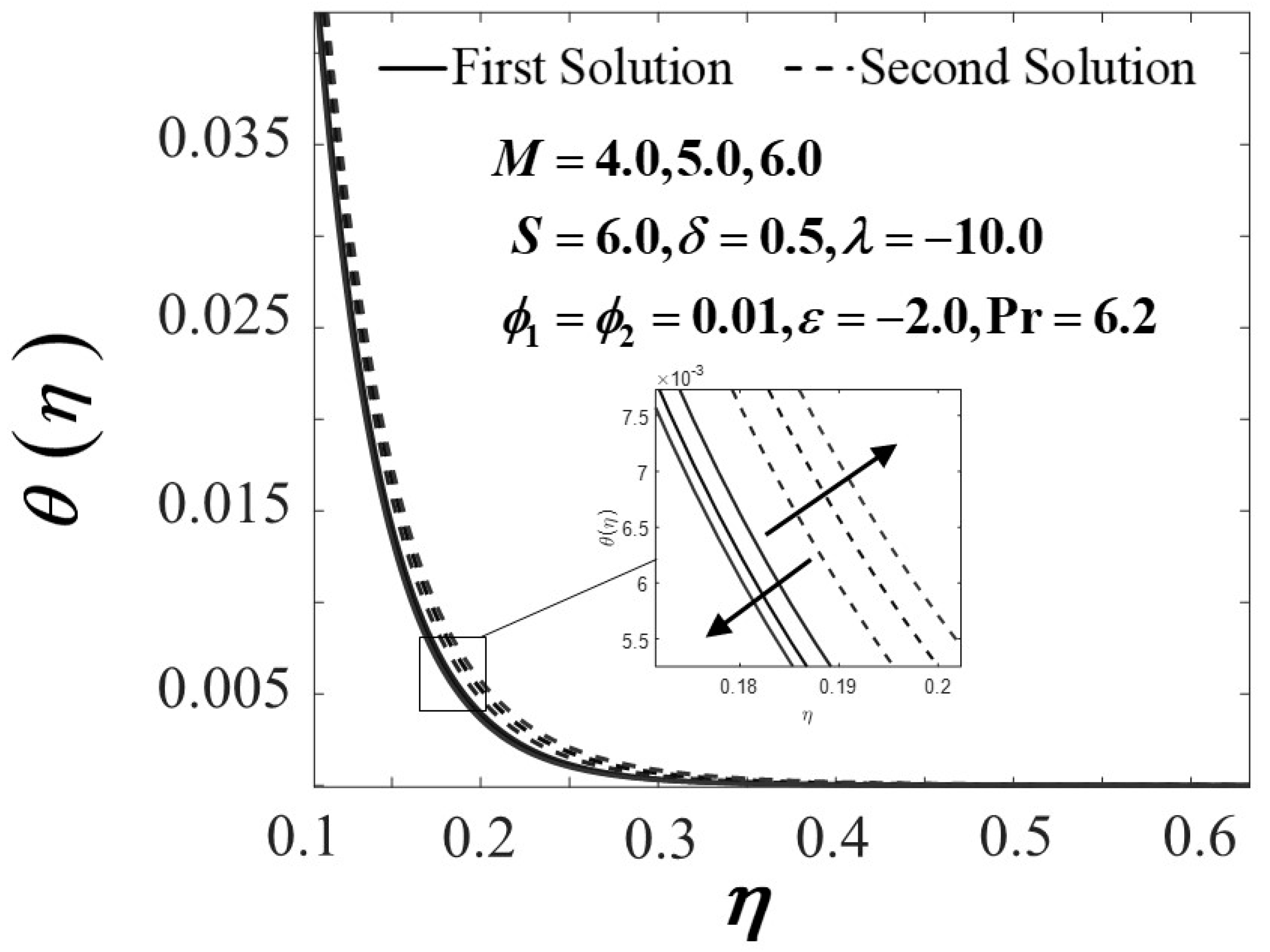
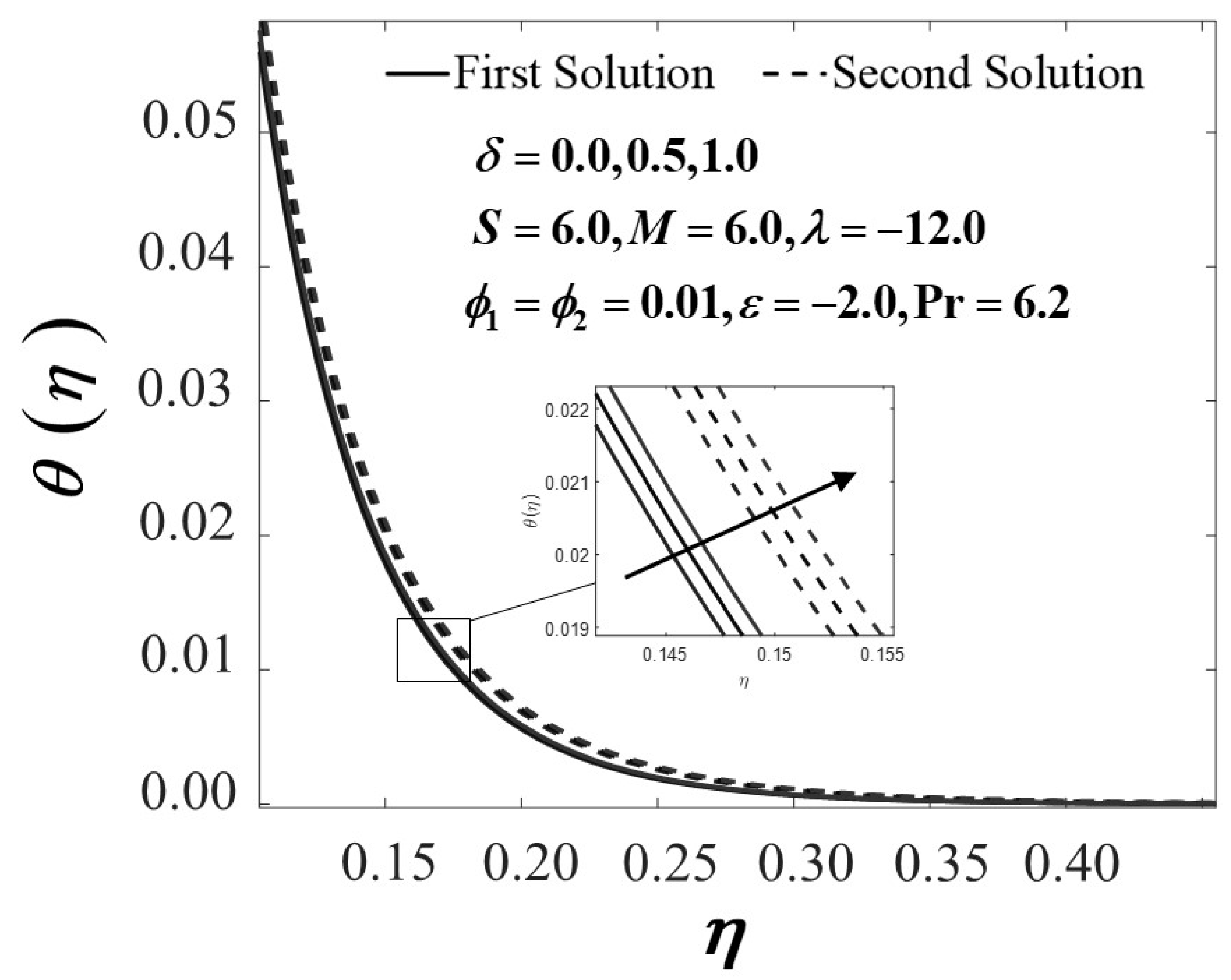
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katagiri, M. On the separation of magnetohydrodynamic flow near the rear stagnation point. J. Phys. Soc. Jpn. 1969, 27, 1045–1050. [Google Scholar] [CrossRef]
- Mitrishkin, Y.V.; Korenev, P.S.; Kartsev, N.M.; Kuznetsov, E.A.; Prokhorov, A.A.; Patrov, M.I. Plasma magnetic cascade multiloop control system design methodology in a tokamak. Control Eng. Pract. 2019, 87, 97–110. [Google Scholar] [CrossRef]
- Mitryushkin, Y.V.; Korenev, P.S.; Prokhorov, A.A.; Kartsev, N.M.; Patrov, M.I. Plasma Control in Tokamaks. Part 1. Adv. Syst. Sci. Appl. 2018, 18, 26–52. [Google Scholar]
- De Tommasi, G. Plasma magnetic control in tokamak devices. J. Fusion Energy 2019, 38, 406–436. [Google Scholar] [CrossRef]
- Hartmann, J. Hg-Dynamics I: Theory of the laminar conductive liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat. Fys. Medd. 1937, 15, 1–28. [Google Scholar]
- Leibovich, S. Magnetohydrodynamic flow at a rear stagnation point. J. Fluid Mech. 1967, 29, 401–413. [Google Scholar] [CrossRef]
- Pavlov, K.B. Magnetohydrodynamic flow of an incompressible viscous fluid caused by deformation of a plane surface. Magn. Gidrodin. 1974, 4, 146–147. [Google Scholar]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady MHD stagnation point flow-induced stretching/shrinking sheet of hybrid nanofluid by exponentially permeable. Eng. Sci. Technol. Int. J. 2021, 24, 1201–1210. [Google Scholar]
- Versaci, M.; Cutrupi, A.; Palumbo, A. A magneto-thermo-static study of a magneto-rheological fluid damper: A finite element analysis. IEEE Trans. Magn. 2020, 57, 1–10. [Google Scholar] [CrossRef]
- Seth, G.S.; Bhattacharyya, A.; Kumar, R.; Chamkha, A.J. Entropy generation in hydromagnetic nanofluid flow over a non-linear stretching sheet with Navier’s velocity slip and convective heat transfer. Phys. Fluids 2018, 30, 122003. [Google Scholar] [CrossRef]
- Aslani, Κ.E.; Sarris, I.E. Effect of micromagnetorotation on magnetohydrodynamic Poiseuille micropolar flow: Analytical solutions and stability analysis. J. Fluid Mech. 2021, 920, A25. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichförmingen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech J. 1911, 326, 321–324. [Google Scholar]
- Homann, F. Der Einfluss grosser Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 1936, 16, 153–164. [Google Scholar] [CrossRef]
- Rauwendaal, C. Polymer Extrusion; Hanser Publications: Cincinnati, OH, USA, 1985. [Google Scholar]
- Fisher, E.G. Extrusion of Plastics; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Proudman, I.; Johnson, K. Boundary-layer growth near a rear stagnation point. J. Fluid Mech. 1961, 12, 161–168. [Google Scholar] [CrossRef]
- Robins, A.; Howarth, J.A. Boundary-layer development at a two-dimensional rear stagnation point. J. Fluid Mech. 1972, 56, 161–171. [Google Scholar] [CrossRef]
- Howarth, J.A. A note on boundary-layer growth at a three-dimensional rear stagnation point. J. Fluid Mech. 1973, 59, 769–773. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Naganthran, K.; Pop, I. Unsteady MHD rear stagnation point flow over off-centred deformable surfaces. Int. J. Numer. Methods Heat Fluid Flow. 2017, 27, 1554–1570. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Hafidzuddin, E.H.; Arifin, N.M.; Wahi, N. Stagnation point flow of hybrid nanofluid over a permeable vertical stretching/shrinking cylinder with thermal stratification effect. CFD Lett. 2020, 12, 80–94. [Google Scholar]
- Khashi’ie, N.S.; Arifin, N.M.; Merkin, J.H.; Yahaya, R.I.; Pop, I. Mixed convective stagnation point flow of a hybrid nanofluid toward a vertical cylinder. Int. J. Numer. Methods Heat Fluid Flow. 2021, in press. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady EMHD stagnation point flow over a stretching/shrinking sheet in a hybrid Al2O3-Cu/H2O nanofluid. Int. Commun. Heat Mass Transf. 2021, 123, 105205. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady MHD mixed convection flow in hybrid nanofluid at three-dimensional stagnation point. Mathematics 2021, 9, 549. [Google Scholar] [CrossRef]
- Smith, F.T. Steady and unsteady boundary layer separation. Annu. Rev. Fluid Mech. 1986, 18, 197–220. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow, 2nd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- McCroskey, W.J. Some current research in unsteady fluid dynamics—The 1976 Freeman Scholar Lecture, Trans. ASME. J. Fluid Eng. 1977, 99, 8–39. [Google Scholar] [CrossRef]
- Benson, R.S.; Garg, R.D.; Woollatt, D. A numerical solution of unsteady flow problems. Int. J. Mech. Sci. 1964, 6, 117–144. [Google Scholar] [CrossRef]
- Sears, W.R.; Telionis, D.P. Boundary-layer separation in unsteady flow. SIAM J. Appl. Math. 1975, 28, 215–235. [Google Scholar] [CrossRef]
- Hayat, T.; Imtiaz, M.; Alsaedi, A. Unsteady flow of nanofluid with double stratification and magnetohydrodynamics. Int. J. Heat Mass Transf. 2016, 92, 100–109. [Google Scholar] [CrossRef]
- Jahan, S.; Sakidin, H.; Nazar, R.; Pop, I. Unsteady flow and heat transfer past a permeable stretching/shrinking sheet in a nanofluid: A revised model with stability and regression analyses. J. Mol. Liq. 2018, 261, 550–564. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD non-axisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Hafidzuddin, M.E.H.; Nazar, R.; Arifin, N.M.; Pop, I. Unsteady flow and heat transfer over a permeable stretching/shrinking sheet with generalised slip velocity. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1457–1470. [Google Scholar] [CrossRef]
- Subhani, S.M. Nadeem, Numerical investigation of unsteady MHD flow of micropolar hybrid nanofluid in porous medium. Phys. Scr. 2019, 94, 105220. [Google Scholar] [CrossRef]
- Khan, U.; Waini, I.; Ishak, A.; Pop, I. Unsteady hybrid nanofluid flow over a radially permeable shrinking/stretching surface. J. Mol. Liq. 2021, 331, 115752. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady hybrid nanofluid flow on a stagnation point of a permeable rigid surface. ZAMM—J. Appl. Math. Mech./Z. Angew. Math. Mech. 2020, 101, e202000193. [Google Scholar]
- Rahman, M.M.; Sattar, M.A. Magnetohydrodynamic convective flow of a micropolar fluid past a continuously moving vertical porous plate in the presence of heat generation/absorption. J. Heat Transf. 2006, 128, 142–152. [Google Scholar] [CrossRef]
- Vajravelu, K.; Hadjinicolaou, A. Heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation. Int. Commun. Heat Mass Transf. 1993, 20, 417–430. [Google Scholar] [CrossRef]
- Alsaedi, A.; Awais, M.; Hayat, T. Effects of heat generation/absorption on stagnation point flow of nanofluid over a surface with convective boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4210–4223. [Google Scholar] [CrossRef]
- Soomro, F.A.; Haq, R.U.; Al-Mdallal, Q.M.; Zhang, Q. Heat generation/absorption and nonlinear radiation effects on stagnation point flow of nanofluid along a moving surface. Results Phys. 2018, 8, 404–414. [Google Scholar] [CrossRef]
- Jo, E.; Park, J.H.; Park, J.; Hwang, J.; Chung, K.Y.; Nam, K.W.; Kim, S.M.; Chang, W. Different thermal degradation mechanisms: Role of aluminum in Ni-rich layered cathode materials. Nano Energy 2020, 78, 105367. [Google Scholar] [CrossRef]
- Berni, F.; Fontanesi, S. A 3D-CFD methodology to investigate boundary layers and assess the applicability of wall functions in actual industrial problems: A focus on in-cylinder simulations. Appl. Therm. Eng. 2020, 174, 115320. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilising nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Ros, N.C.; Ros, A.V.; Pop, I. Mixed convection and stability analysis of stagnation-point boundary layer flow and heat transfer of hybrid nanofluids over a vertical plate. Int. J. Numer. Methods Heat Fluid Flow. 2019, 30, 3737–3754. [Google Scholar] [CrossRef]
- Babu, J.R.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E.; Akbar, T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 2017, 114, 1054–1066. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Devi, S.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Heat generation/absorption effect on MHD flow of hybrid Nnanofluid over bidirectional exponential stretching/shrinking sheet. Chin. J. Phys. 2021, 69, 118–133. [Google Scholar] [CrossRef]
- Abu-Nada, E.; Oztop, H.F. Effects of inclination angle on natural convection in enclosures filled with Cu-water nanofluid. Int. J. Heat Fluid Flow. 2009, 30, 669–678. [Google Scholar] [CrossRef]
- Fang, T.; Jing, W. Closed-form analytical solutions of flow and heat transfer for an unsteady rear stagnation-point flow. Int. J. Heat Mass Transf. 2013, 62, 55–62. [Google Scholar] [CrossRef]
- Merkin, J.H. Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Eng. Math. 1980, 14, 301–313. [Google Scholar] [CrossRef]
- Merrill, K.; Beauchesne, M.; Previte, J.; Paullet, J.; Weidman, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. Int. J. Heat Mass Transf. 2006, 49, 4681–4686. [Google Scholar] [CrossRef] [Green Version]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability analysis of MHD hybrid nanofluid flow over a stretching/shrinking sheet with quadratic velocity. Alex. Eng. J. 2020, 60, 915–926. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2011, 38, 917–922. [Google Scholar] [CrossRef]
- Arifin, N.M.; Nazar, R.; Pop, I. Non-Isobaric Marangoni boundary layer flow for Cu, Al2O3 and TiO2 nanoparticles in a water-based fluid. Meccanica 2011, 46, 833–843. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P. Synthesis, characterisation of Al2O3-Cu nanocomposite powder and water-based nanofluids. Adv. Mater. Res. 2011, 328, 1560–1567. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]



| Physical Properties | |||
|---|---|---|---|
| H2O | 0.613 | 997.1 | 4179 |
| Al2O3 | 40 | 3970 | 765 |
| Cu | 400 | 8933 | 385 |
| Properties | Al2O3–Cu/H2O |
|---|---|
| Density | |
| Dynamic viscosity | |
| Thermal capacity | |
| Thermal conductivity | |
| Electrical conductivity |
| λ | Present Result | Turkyilmazoglu et al. [19] | Bhattacharyya [57] | |||
|---|---|---|---|---|---|---|
| First Solution | Second Solution | First Solution | Second Solution | First Solution | Second Solution | |
| −0.25 | 1.4022408 | - | 1.4022408 | - | 1.4022405 | - |
| −0.50 | 1.4956698 | - | 1.4956670 | - | 1.4956697 | - |
| −0.75 | 1.4892982 | - | 1.4892982 | - | 1.4892981 | - |
| −1.00 | 1.3288169 | 0.0000000 | 1.3288168 | 0.0000000 | 1.3288169 | 0.0000000 |
| −1.15 | 1.0822312 | 0.1167021 | 1.0822312 | 0.1167021 | 1.0822316 | 0.1167023 |
| −1.20 | 0.9324733 | 0.2336497 | 0.9324733 | 0.2336497 | 0.9324728 | 0.2336491 |
| −1.2465 | 0.5842817 | 0.5542962 | 0.5842813 | 0.5542947 | 0.5842915 | 0.5542856 |
| −1.24657 | 0.5745257 | 0.5640125 | 0.5774525 | 0.5640081 | 0.5745268 | 0.5639987 |
| Al2O3–Cu/Water Hybrid Nanofluid | ||||
|---|---|---|---|---|
| 0.00 | 6.0 | 0.5 | 41.0286336560 | 33.2812323540 |
| 0.01 | 44.4794570250 | 33.1259684480 | ||
| 0.02 | 47.9973405430 | 32.9737922260 | ||
| 0.01 | 4.0 | 35.4463147500 | 33.0027615510 | |
| 5.0 | 40.9347604490 | 33.0792778990 | ||
| 6.0 | 44.4794570250 | 33.1259684480 | ||
| 0.0 | - | 33.2417593770 | ||
| 0.5 | - | 33.1259684480 | ||
| 1.0 | - | 33.0091507970 | ||
| First Solution ω1 | Second Solution ω1 | |
|---|---|---|
| −10 | 2.0570 | −1.8571 |
| −10.3 | 0.4956 | −0.4836 |
| −10.31 | 0.3416 | −0.3359 |
| −10.318 | 0.2560 | −0.2527 |
| −10.3183 | 0.2001 | −0.1981 |
| −10.3185 | 0.1210 | −0.1203 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability Analysis of Unsteady MHD Rear Stagnation Point Flow of Hybrid Nanofluid. Mathematics 2021, 9, 2428. https://doi.org/10.3390/math9192428
Zainal NA, Nazar R, Naganthran K, Pop I. Stability Analysis of Unsteady MHD Rear Stagnation Point Flow of Hybrid Nanofluid. Mathematics. 2021; 9(19):2428. https://doi.org/10.3390/math9192428
Chicago/Turabian StyleZainal, Nurul Amira, Roslinda Nazar, Kohilavani Naganthran, and Ioan Pop. 2021. "Stability Analysis of Unsteady MHD Rear Stagnation Point Flow of Hybrid Nanofluid" Mathematics 9, no. 19: 2428. https://doi.org/10.3390/math9192428
APA StyleZainal, N. A., Nazar, R., Naganthran, K., & Pop, I. (2021). Stability Analysis of Unsteady MHD Rear Stagnation Point Flow of Hybrid Nanofluid. Mathematics, 9(19), 2428. https://doi.org/10.3390/math9192428







