Third Grade Students’ Use of Relational Thinking

Abstract

Current mathematics curricula have as one of their fundamental objectives the development of number sense. This is understood as a set of skills. Some of them have an algebraic nature such as acquiring an abstract understanding of relations between numbers, developing awareness of properties and of the structure of the decimal number system and using it in a strategic manner. In this framework, the term relational thinking directs attention towards a way of working with arithmetic expressions that promotes relations between their terms and the use of properties. A teaching experiment has allowed to characterize the way in which third grade students use this type of thinking for solving number equalities by distinguishing four profiles of use. These profiles inform about how students employ relations and arithmetic properties to solve the equalities. They also ease the description of the evolution of the use of relational thinking along the sessions in the classroom. Uses of relational thinking of different sophistication are distinguished depending on whether a general known rule is applied, or relations and properties are used in a flexible way. Results contribute to understanding the process of developing the algebraic component of number sense.

1. Introduction

In the first levels of education, one of the main objectives of mathematics teaching is to develop students’ number sense. The number sense construct is complex, with multiple components. It refers to a broad and well-organized conceptual network related to numbers and operations, their relations and properties, which allows solving number problems in flexible and creative ways [1]. Following a recent literature review, [2] distinguished between three dimensions of number sense: an elementary one which includes aspects such as number recognition, understanding the meanings of numbers, recognizing their relative size and skills related to counting; a second one related to conventional arithmetic focused on calculation and solving story problems; and a third algebraic one. The latter encompasses an abstract understanding of the relations between numbers which entails awareness of the properties and structures of the decimal number system and its strategic use.

The third dimension mentioned connects to current education proposals which demand greater integration of arithmetic and algebra from the earliest school levels [3,4]. These proposals strive to promote mindsets that address the underlying structure of mathematics. The intention is to enrich the teaching of mathematics during the early stages and contribute to later learning of formal algebra during secondary education [5]. Specifically, it is purported that algebraic thinking should be a cross-functional axis of mathematical thinking throughout all the school stages [6], allowing students to participate in algebraic ways of thinking that are age-appropriate, based on their natural intuition about structure and relations [7].

This view assumes a multidimensional conception of school algebra including generalized arithmetic with a focus on perceiving structure [4], the study of functional relations [8,9], the study of patterns [10] and the representational nature of algebra [11]. In addition, it directs attention to mathematical practices such as generalizing, representing, justifying, and reasoning [12]. This rich and interconnected view of school algebra give space for the development of arithmetic reasoning as well as quantitative reasoning [13]. Both approaches to arithmetic differ on the meaning given to numbers: an analytical meaning, defined by the number system, or an extrinsic, representational meaning, in which numbers are signs for quantities or for relations between quantities. The representational meaning is the one connected to problem solving. International examinations such as PISA place the focus in the later by assessing mathematics competence through problem solving. In this paper, however, we focus on the approach to arithmetic in which numbers are given an analytical meaning. Students need to be able to apply their mathematical knowledge in real life contexts but they also need to develop sophisticated mathematical ways of thinking, such as analytical reasoning, as a way to enrich their understanding of arithmetic and increase their opportunities for success in mathematics in secondary grades [2,4,14].

1.1. Relational Thinking

Through relational thinking, this paper focuses on the algebraic view of learning of arithmetic above described and the analytical meaning of numbers. This type of thinking refers to the recognition and use of relations between elements in arithmetic (or algebraic) expression and the essential properties of operations [5,15,16]. Using relational thinking implies considering these expressions globally, from a structural perspective, instead of as processes to be conducted step by step. It requires recognizing certain characteristics and relations between the terms of the expressions and using them to design a strategy applying arithmetic properties [5].

This type of thinking is considered associated to a good understanding of numbers and operations and calculation fluency [17], and it is necessary for algebra-specific activities such as solving equations [16]. It has been observed that becoming proficient in tasks that require relational thinking, in various settings, enhances performance in algebra [18].

The work conducted to date on this subject matter evidence the use of relational thinking by students in situations such as computation through individual strategies [17], the distinction between true and false numerical equalities (e.g., $3 \times 8 = 2 \times 8 + 8;15 + 8=8 + 12$) [19], solving incomplete numerical equalities (e.g., $3 + 5=[ ] + 3$) [8,9,12] and solving equations [20]. It has been found that it develops naturally based on students’ experiences with arithmetic and is manifest at the end of primary education and the beginning of secondary. However, it tends to be limited. If this has not been explicitly worked on in the classroom some students will never manifest it [21]; most tend to use computational methods [22].

The studies mentioned identify difficulties such as an operational interpretation of the equal sign and of arithmetic expressions, the need to close expressions (that is, the need for them to contain their numeric value or result), not respecting the structure of equalities, considering each member of the equality independently, as well as the inability to distinguish between transformation that are invariant and those that are not, and to transfer them from one situation to another.

Teaching has a positive effect on relational thinking when it is linked to promoting the understanding of the equal sign as a representation of equivalence [7,23]. The authors cited distinguished between different levels of sophistication in the use of relational thinking according to its lesser or greater connection to calculation. The cases in which students use calculation and recognize the relations between the terms of equalities, are considered intermediate levels.

The context of numerical equalities based on arithmetic properties has been highlighted for its potential to promote this type of thinking [7,15,19]. There is a positive influence in the presence of large numbers and the consideration of equalities with operations in both members. Both are factors that favor overall observation of equalities, according to [24].

1.2. Research Aim

A teaching experiment is described here, aimed at promoting among third-grade students, who are accustomed to traditional teaching of arithmetic, the use of arithmetic relations and properties when working with numerical equalities. This research seeks to characterize relational thinking evidenced by students in terms of the arithmetic relations and properties they use, and to study how this evolves with their classroom work. Unlike prior studies, it analyzes said use separately from understanding of the equal sign as an expression of equivalence, and without focusing on the presence or not of calculation. Profiles using relational thinking are described, as well as patterns in the evolution of said thinking among students, which contribute to a better understanding of the development of the algebraic component of number sense. This information is useful for the instructional design of practices aimed at promoting a structural view of arithmetic.

2. Materials and Methods

A teaching experiment was conducted within the framework of the design research paradigm [25] that aimed to enhance understanding of the use and development of relational thinking in primary education students. This type of research stands out for its potential to develop theories on the teaching/learning process of specific contents, in a way that is sensitive to the complexity and systemic nature of said process. One of the distinctive features of this potential is the cyclical conjugation of two analyses: of the learning process and of the instructional design elements said learning is based on [26].

The context of numerical equalities based on arithmetic properties was chosen because of its utility, according to previous studies [15,19], to promote the use of relational thinking. One of the distinctive features of the work conducted in the classroom is the consideration, in the design of equalities, of all the arithmetic properties corresponding to the additive structure of natural numbers. The intention is to explore how students use different relations and properties.

2.1. Subjects

Participants were a group of 26 third grade students (12 male and 14 females) from a state school in the region of Granada (Spain). This group was selected given its availability to participate in the study and the suitability of the education level they were in to address our objectives. The participating students were familiar with the meaning of the equal sign in equalities with operations in both members as an indicator of equivalence. Prior to the experiment they had not received any specific teaching on the use of relational thinking. They had worked on arithmetic properties linked to the additive structure from a traditional perspective, that is: theoretically as axioms to be applied when executing a sequence of calculations and as tricks to use for mental calculation. Students were used to a traditional way of teaching mathematics: lessons were based on an explanation from the teacher followed by routine and computational activities where students, individually, had to apply the ideas presented by the teacher. Arithmetic was taught as a set of fixed methods to be applied for solving computations. The students’ discovery and use of personal strategies for solving tasks was not promoted.

2.2. Design of Classroom Intervention

Classroom intervention was carried out in six sessions, with deliberate timing, except for holiday periods, with the aim of (a) favoring a prolonged effect of our intervention, (b) diminishing the probability of evaluating rote learning, and (c) having enough time to analyze the results of each session and make decisions about the next one (as pertains to teaching experiments). During the sessions, students worked individually solving the written tasks, followed by a group discussion of the work done. Interventions were led by one of the researchers, with the official teacher present in the classroom. We also conducted individual structured interviews with some students. The sessions were audio and video recorded.

Table 1. General Characteristics of the Classroom Experiment.

Date	Duration	N	Activities	Type of Equalities	Data Collection Instruments
					Recording	Student Sheets	Observation Notes
23 Nov	30′	26	Written activity Discussion	Open	X (video)	X	X
24 Jan	1 h	21	Written activity Discussion	Open	X (video)	X	X
			Written activity Discussion	Closed
3 Feb	1 h	22	Discussion	Closed	X (video)	X	X
16 Feb	1 h	25	Written activity	Closed		X	X
2 Mar	1 h 50′ (13 × 8′)	13	Individual interviews	Closed	X (audio)	X	X
16 Nov	1 h	25	Written activity	Closed		X	X

Note: N was not always 26 due to absence of some students.

shows the general characteristics of each session.

During the first session we analyzed the initial understanding shown by students of the equalities proposed, and we identified the strategies they used to solve them. The next sessions were designed with the objective of promoting the use of diverse strategies to solve equalities, in particular those using relational thinking. To this end, during the group discussions, students were asked to try to solve the equalities without doing all the calculations. The researcher-teacher did not propose any specific strategies. Her intervention consisted in requesting explanations on different ways of solving equalities and emphasizing those establishing relations. The specific equalities considered during the work sessions with the whole group are shown in

Table 2. Equalities used in sessions 1, 2, 3, 4, and 6.

Session 1	Session 2	Session 3	Sessions 4 and 6
$8+4=[ ]+5$ $[ ]=25-12$ $14+[ ]=13+4$ $13-7=[ ]-6$ $[ ]+4=5+7$ $12+7=7+[ ]$	$12-4=13-[ ]$ $9-4=[ ]-3$ $[ ]-6=15-7$ $14-9=[ ]-10$ $17-[ ]=18-8$	$72=56-14$ $78-16=78-10-6$ $24-15=24-10-5$ $78-45=77-44$ $100+94-94=100$ $27-14+14=26$ $231+48=231+40+8$ $13-5+5=13$ $51+51=50+52$ $15-6=6-15$ $27-14+14=26$ $93=93$ $24-24=0$ $7+7+9=14+9$ $10-7=10-4$ $7+3=10+3$ $62-13+13=65$ $19-3=18-2$ $13+11=12+12$ $10+4=4+10$ $0+325=326$ $37+22=300$ $125-0=125$ $7=12$ $100-100=1$	$18-7=7-18$ $75-14=340$ $17-12=16-11$ $122+35-35=122$ $6+4+18=10+18$ $75+23=23+75$ $7+15=8+15$ $53+41=54+40$ $16+14-14=36$ $257-34=257-30-4$

.

There were two distinct parts in the second session: we began working with given open equalities and then students proposed their own true or false closed equalities. In the third session, all equalities were worked on as a group to enhance student learning of strategies from each other. During the fourth and sixth session we used the same equalities to detect the effect of the passing of time in the use of relational thinking by students. During the fifth session we conducted individual structured interviews with thirteen students. We selected students who had evidenced use of relational thinking at a different rate and in different types of equalities. We proposed between 4 and 7 true or false equalities like those in sessions 3, 4, and 6, selected in each case according to the relational thinking made manifest earlier by the student.

We chose the context of number equalities because it can be a context very rich in patterns which allows working on arithmetic from an algebraic approach as it implies horizontal language, the relational meaning of the equal sign and conceiving expressions as wholes which can be compared, ordered, made equal, transformed, and therefore, the acceptance of lack of closure (i.e., working with expressions without knowing their numeric value or not having it expressed in the equality).

Students had to complete open equalities and indicate whether the given closed equalities were true or false, justifying their answers in both cases and providing corrections to false equalities. This paper uses the term “solving equalities” to refer to either action. Based on the results of our previous study [17], we expected that closed equalities would be essential to halt the computational trend of students and promote relational thinking, and open equalities would help evaluate students’ understanding of equalities.

The design of the equalities proposed was based on several task variables: (a) magnitude of the terms (all below 20 or some above 20); (b) arithmetic properties of the additive structure of the set of natural numbers (see

Table 3. Properties considered in the design of equalities.

Property	Example of Closed Equality (True or False)
Commutativity of the addition	$10+4=4+10$
No commutativity of the subtraction	$15-6=6-15$
Complementarity of addition and subtraction	$100+94-94=100$
Compensation	$13+11=12+12$; $78-45=77-44$
Zero as a neutral element	$0+325=326$; $125-0=125$
Opposite element	$100-100=1$
Associativity of addition	$7+7+9=14+9$
Pseudo-associativity of subtraction	$78-16=78-10-6$
Effect of addition or subtraction in the magnitude of terms	$37+22=300$; $72=56-14$

); (c) type of equality: open (containing unknown quantities to be found) vs. closed (without unknown quantities); and (d) structure of equality: action (all operational symbols in one of its members) vs. no action (with operational symbols in both members). The property considered in the design conditioned whether it was an action or a non-action equality, with the member where the operation symbols were placed (right vs. left) being randomly changed.

2.3. Data Analysis

The data analysis conducted was qualitative. In order to carry it out, we compiled the students’ worksheets and transcribed the recordings of the work sessions in the classroom and the interviews. With this written material, we coded the students’ explanations (oral and written). We used the video and audio recordings to consider pauses and speech intonation. The different profiles presented below were categories formulated on the grounds of an inductive analysis of the data collected. Initially, we identified interventions or productions that evidenced some use of relational thinking. Next, we distinguished between relations (sameness, order relation or quantitative relation) and arithmetic properties used by students in each equality (see Table 3).

3. Findings

This section is divided in two parts. We first distinguish different profiles evidenced in students’ use of relational thinking. Secondly, using those profiles, we analyze students’ individual development of this type of thinking along the various sessions of the teaching experiment.

3.1. Profiles of Use of Relational Thinking

An analysis of the six sessions shows that in total 1 out of 26 (session 1), 6 out of 21 (session 2), 14 out of 22 (session 3), 19 out of 24 (session 4), 11 out 13 (session 5), and 17 out of 24 (session 6) students evidenced having used relational thinking. When we looked at each student’s answers jointly, we identified four profiles of use of relational thinking:

• Absence (A): student did not show use in any of the equalities answered. All their answers were based on the calculation of expressions shown in the equalities (e.g., for equality $122 + 35 - 35 = 122$ they explained, “True because $122 + 35$ is 157 minus 35 is 122”, for equality $7 + 15 = 8+15$ they explained, “False because seven and fifteen is 22 and eight plus fifteen is 23”) and they built equalities such as $19 - 6 = 7+6$^T and $38 - 33 = 33 - 31$^F.
• Simple (S): in some equalities the student applied an arithmetic law or principle which they knew, after having noted the relations or specific characteristics of the equality. This generally known fact allowed them to conclude the truthfulness or falseness of the equality. Specifically, they used the properties of zero as neutral in the addition and the subtraction on the right, restrictions of the definition domain of the subtraction and the property (e.g., in $125 - 0 = 125$ they explained, “I thought that if you take away zero, since zero is nothing, you end up with the two one hundred and twenty-five. One hundred and twenty-five is equal to one hundred and twenty-five”, in $15 - 6 = 6 - 15$ they stated, “False […] Because fifteen minus six is eleven and you can’t take fifteen away from six”, in $125 - 125 = 14$ they explained, “Because one hundred and twenty-five, if we take away one hundred and twenty-five, is zero. [How do you know this so quickly?] Because one hundred and twenty-five, if, if, if you take away all the numbers”. They built equalities such as $5 - 5 = 0$^T and $1000 - 1000 = 3000 + 4000$^F.
• Sameness (M): student evidenced relational thinking in some equalities based on the observation of sameness or “lack of sameness” among the elements comprising the equalities (e.g., in the equality $18 - 7 = 7 - 18$ they stated, “True because seven is equal to seven and eighteen is equal to eighteen”; in the equality $75 + 23 = 23 + 75$ they explained, “True because the two numbers are equal”). This implies applying the reflexive property of equality, the commutativity of addition or, even, an assumed commutativity of subtraction. Some students also used an over-generalization of the reflexive property of equality, ignoring the relative position of the terms or their position in relation to the equal sign (e.g., in $122 + 35 - 35 = 122$ they explained, “True because the numbers and the quantities are the same”, in $6 + 4+8 = 10 + 8$ they stated, “False because it would be $6 + 4$ and then $4 + 6$”). They built equalities such as $10 + 4=4 + 10$^T or even $8 - 1 = 1+8$^T.
• Structural: the student showed recognition of quantitative relations or order relations in some of the expressions given and used them to solve the equalities applying arithmetic properties (in $75 - 14 = 340$ they stated, “False because if we take away $75 - 14$ we get a lower number than 340”, in $257 - 34 = 257 - 30 - 4$ they stated, “True because it is the same, there are just more numbers to subtract”). They built equalities such as $12 + 4=13 + 3$^T and $4 + 6=204 + 6$^F. In this profile we can distinguish two cases, depending on the frequency of use of relational thinking shown: in only one type of equality (Structural-specific profile, P) or in more than one type (Structural-varied profile, V).

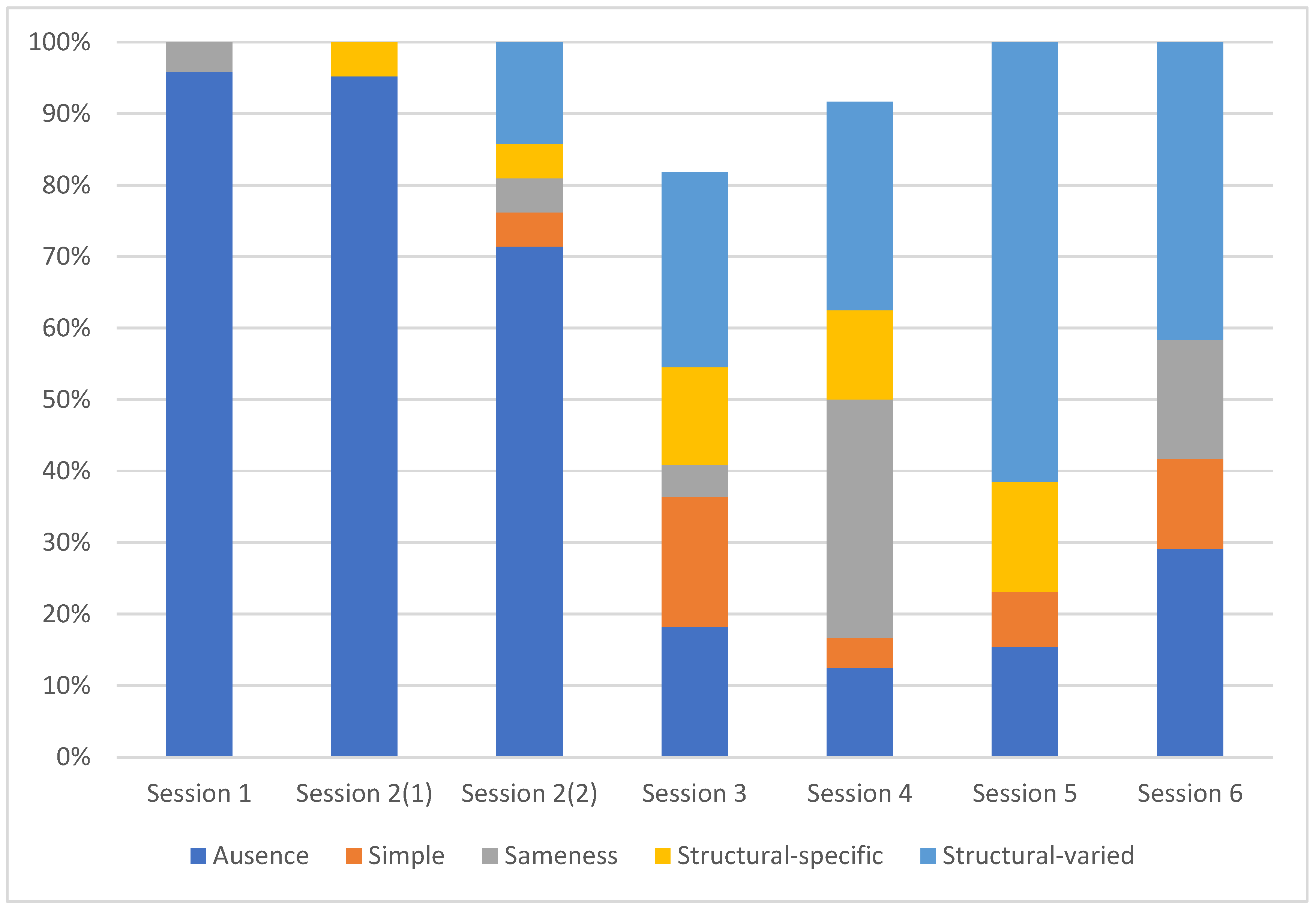
The chart in Figure 1 shows, by percentage, the presence of each profile in the various sessions. In session 1 and in the first part of session 2, most students showed the Absence profile. We only detected the use of relational thinking on two occasions: by student MT in equality $12 + 7=7 + [ ]$during session 1 and by CH in equality $12 - 4 = 13 - [ ]$ during session 2. These students used the commutative properties of addition and subtraction compensation, respectively, evidencing the Sameness and Structural-specific profiles.

During the second part of session 2, when students built their own true or false equalities, we started seeing a greater use of relational thinking. However, it was in session 3 when the change in the profiles being shown was more remarkable. More students and more frequently showed use of this type of thinking after this session. Nonetheless, in all sessions there was a percentage above 10% showing the Absence profile, with a greater presence of this profile in the first two sessions and the last one.

In sessions 3 and 4 we found all the profiles of use of relational thinking. In session 4, the Sameness and Structural-varied profiles were predominant. The interviews underscored the high percentage of students who showed the Structured-varied profile. The Sameness and Structural-specific profiles were absent in sessions 5 and 6, respectively.

3.2. Individual Development of Relational Thinking

Looking at each student individually (see

Table 4. Students’ profiles per session.

	Session
	1	2(1)	2(2)	3	4	5	6
Student	n = 24	n = 21	n = 21	n = 22	n = 24	n = 13	n = 24
CH	A	P	V	V	V	V	V
DL	A			V	P	V	V
EF	A	A	S	V	V	V	V
FM	A	A	A	V	V	V	V
JM	A	A	A	V	V	V	V
MR	A	A	P	P	V	V	V
MT	M	A	A		V		V
RB	A	A	A	A	A	V	V
RL	A			A	V		V
CA	A	A	A	S	P		V
CL	A	A	A	P	M	V	A
CY	A	A	M	S	?		M
EV	A	A	A	S	M	P
FB	A	A	V	P	M	P	M
JQ	A	A	A	V	M		S
MA	A	A	A	-	P		S
MP	A	A	V	A	S	A	M
MAG	A	A	A		M		A
MB	A	A	A	M	M		M
MG	A				M		A
NM	A	A	A	-	M	S	A
BR	A	A	A	-	A	S	A
RT	A			A			S
VS	A	A	A	S	A		A

Note: The empty cells indicate students who did not attend that session, the hyphen marks those who attended but did not participate in session 3 and the question mark those who did not clearly evidence a profile due to ambiguous or too-brief answers. The profiles are indicated as follows: A = Absence, S = Simple, M = Sameness, P = Structural specific and V = Structural varied.

), we described their development throughout the teaching experiment. We distinguished four different types of evolution based on their use of relational thinking: (a) varied consolidated, (b) occasional not consolidated, (c) based on sameness, and (e) limited and simple. The differences between these four types were mainly detected after, and including, the third session. A student was excluded from this classification (BI), as she did not show use of relational thinking in any of the sessions. This student was not interviewed, which leaves the question of whether in a more intimate context such as an interview, she would have provided evidence of this type of thinking. The distinction of these different groups of students in terms of the evolution of their use of relational thinking along the teaching experiment is based on the profiles evidenced. Our analysis of the whole body of data available (written answers, verbal participation in discussions and interviews) clarifies the characteristics defining each group and the differences between them.

3.2.1. Varied Consolidated Use

We identify a group of 9 students who evidenced a varied and consolidated use of relational thinking. These group includes 7 students (CH, DL, EF, FM, JM, MR, and MT) who showed the Structural profile, primarily varied, in most of the last four sessions (see Table 4) and another two (RB and RL) who took longer to establish relations and once they did, also showed the Structural-varied profile. For example, RB did not evidence use of relational thinking in the sessions prior to the interview. He used it during the interview when providing the following explanations for equalities $13 + 5 = 5 + 13$ and $26 - 8 = 100$: “[true] because it’s the same, just the other way around”; “false… because if it were… it’s twenty-six minus eight and it is equal to one hundred so as it is less, it is taking away, and it has to be up to one hundred. Because one hundred is greater than…than that, than that subtraction”. In the last session he once again showed the Structural-varied profile.

The interviewed students within this group (CH, DL, EF, FM, JM, MR, and RB) performed most of the computations mentally making an occasional use of their fingers to count. They evidenced a good fluency in computation. Some noticed relations within the equalities at first sight and used them in their solving strategy, while others required from the interviewer to ask them about other ways to solve the equalities without having to do all the operations. These students proved to have access to two schemas: one operational and another relational. In the rest of the sessions, the nine students within this group evidenced a good computational proficiency and understanding of two- and three-digit numbers.

Therefore, students in this group had a good previous arithmetic knowledge and competence. During the work in the identities, they noticed order, quantitative and sameness relations and evidenced awareness of the arithmetic properties used in the design of the equalities. The results suggest that the work done in the classroom was enough to trigger relational thinking in them. They even maintained their varied and consolidated use of relational thinking several months after the first five sessions of classroom work. It should be noted that this group included the two students who in the first two sessions showed evidence of this type of thinking.

3.2.2. Occasional Not Consolidated Use

Another group of students composed of eight students (CA, CL, CY, EV, FB, JQ, MA, and MP) evidenced an occasional and not consolidated use of relational thinking (see Table 4). They presented various profiles of use of relational thinking: in some sessions, six of them showed the Simple profile, another six the Sameness profile and seven the Structural profile. The students in this group have in common that their performance in some of the equalities provides evidences of noticing order or quantitative relations. Some of them did also use sameness relations in some occasions but this use what not a characteristic of this group. They use relations and arithmetic properties only in some of their solving strategies and, within the interviews (to CL, EV, FB, and MP) we observed that the application of other properties was not accessible to them. The interviewer guided them to notice relations, but they did not recognize any possible use of those relations in solving the equality. We conjectured that these students had not enough awareness of all the addition and subtraction properties implicit in the equalities, and it limited their possibilities of using relational thinking.

3.2.3. Use Based on Sameness

Another group of four students (MAG, MB, MG, and NM) evidenced a used of relational thinking based on the relation sameness (see Table 4). Particularly notable is the case of MB who showed the Sameness profile in the four last sessions. In most cases, she compared the numeric values (“results”) of both members, but in the equalities with equal terms ($75+23=23+75$, $7+15=8+15$ and $18-7=7-18$) she showed appreciation of the sameness or difference of the terms.

These students attended to the regularities in the equalities, but the only relation expressed by them was sameness. They evidenced a low computational fluency, making frequent mistakes when computing, and some difficulties in handling three-digit numbers. Their lower arithmetic competence may have hindered their capacity to perceive order and quantitative relations within the equalities. It can be conjectured that their attention was so occupied by computations that they could only notice the easiest relations: samenesss and lack of sameness.

NM was the only of the four students in this group to be interviewed. She was proposed the following equalities and in any of them showed having noticed any relation: $9 + 4 - 4 = 9$, $10 - 7 = 100$, $8 + 6=4 + 4+6$, $125 - 125 = 14$, $9 - 9 = 3$, $8 - 0 = 9$ and 11 + 7 = 10 + 8. She affirmed not to how of any other way to solve the equalities different to computing the result of the given operations. She did so by counting on her fingers and using the standard algorithm in the case of $125 - 125 = 14$.

3.2.4. Limited and Simple Use

A group of three students (BR, RT, and VS) showed a simple, limited and occasional use of relational thinking (see Table 4). They evidenced only in one session the Simple profile and the Absence profile in all the other ones. These three students showed computational difficulties along the sessions and a strong attachment to the use of the standard algorithms when the numbers in the equality were higher. Their use of relational thinking is not alike the others. They just applied memorized facts, either the restrictions of the definition domain of the subtraction (a memorized fact) or a number fact based on adding or subtracting 0 or subtracting a number to itself. They applied this later fact only in equalities with numbers lower than 10. When encountering higher numbers, they resorted to the use of the vertical standard algorithms. We can affirm that these students had only one strategy for solving the equalities: getting the numeric value of each member. Their competence in arithmetic was too low to be able to engage in noticing relations and applying properties.

BR was the only of the three of them who was interviewed in session 5. The analysis of her responses in the interview confirmed the previous conclusions. At first sight she claimed the equalities $7 + 5=5 + 7$ and $9 + 4 - 4 = 9$ to be false. She applied a computational approach in those two equalities as well as in $10 - 7 = 100$, $4 + 6=300$, $8 + 6=4 + 4+6$, and $5 + 5=5 + 5$. Only in the equalities $9 - 9 = 3$and $8 - 0 = 8$ she did not compute. She claimed to be applying a known fact (“I know it by hearth… my mother taught it to me”).

4. Discussion

The results from session 1 and the first part of session 2 support the findings of previous studies [21] on the evidence of the use of relational thinking (although limited), even when not directly addressed in teaching, suggesting that it develops naturally based on arithmetic learning experiences. In this study we detected it in even younger students than those considered by [21].

We confirmed the results of previous studies regarding the positive effect of teaching in the manifestation and development of this type of thinking, although we detected the need for longer work in the classroom. In the results presented, only one student showed no evidence whatsoever of relational thinking. Over a third showed a varied consolidated use and another third, an occasional use. Slightly less than a third did not show a structural profile, limiting the use of relational thinking to the relations of sameness or the direct application of a law of arithmetic. These differences seem to be due to various factors related to students’ arithmetic competence: knowledge/awareness of arithmetic properties, computational fluency and conception of numbers. All of these are components of number sense considering [2]’s definition. Students’ with a stronger number sense evidenced a more sophisticated and more consolidated use of relational thinking although in the first sessions all the students tended to proceed operationally. This result goes in line with research findings that suggest a positive connection between a strong number sense and getting benefit from mathematics teaching in the elementary grades [27,28]. In addition, this finding is in accord with several other studies [29,30] suggesting that arithmetic might serve as a basis for early algebra and help students move from arithmetic to algebra as attending to relations and using properties is at the base of using the structure shared by arithmetic and algebra.

We distinguished relational thinking uses of varying levels of sophistication depending on whether it was based on the direct application of a general known law (Simple profile) or it required a flexible use of arithmetic relations and properties (Sameness and Structural profiles). In the first instance, there was a use of properties linked to zero and the opposite element or restrictions in the domain to define the subtraction. In the second instance, the equality did not match, in general, with a previous schema of the students about this type of arithmetic tasks. They had to note the peculiarities of the equality, appreciate relations and features of their terms and relate them, using arithmetic knowledge that leads to articulating what has been found, in order to solve the equality. This second way evidence a flexible use of arithmetic knowledge, a characteristic strongly valued in students’ approaches to computation either mental or with notation [31]. In the particular context of number equalities, we promoted this flexibility of thinking by directing students’ attention to relations and restraining their computational tendency, rather than teaching them a set of strategies which have proven to have a negative impact on the development of flexibility in other contexts [32].

The various profiles evidenced that, in general, as a result of prior arithmetic learning, most students had accessible knowledge of some arithmetic properties related to addition and subtraction. Some students’ lack of knowledge or of accessibility to it may explain why they did not evidence a Structural profile. On one hand, the simple appreciation of relations is not enough to be able to use them to solve equalities. Students need to recognize the equality or part of it as an exemplification of a property. On the other hand, knowledge is not enough, it interacts with noticing in the process of solving the given equalities [33]. Noticing as well depend on the students’ conception of numbers and computational fluency as they condition the cognitive load of the task for the student leaving more or less attention available to perceive the relations between the operating terms or between them and the other ones included in the equality.

We noted the different nature of the sameness relations versus order or quantitative relations involved in the equalities provided to the students. At times, the sameness relation led to wrong answers when there was an over-generalization of the commutative property of the addition to the subtraction operation or even an over-generalization of the reflexive property of equality. In the second instance, some students stated that the equalities were equal because they had the same numbers, without considering the operation symbols or the position of the terms and their relation with the equal sign. This behavior has been noted in previous studies [34], when students from higher education levels worked with numeric patterns: students detected patterns but could not identify which ones were useful in a given situation. The sameness relation, possibly more easily detected, was the one used in these cases. The students considered it was important to look at the relations, but they lacked certain arithmetic knowledge or understanding of the task to know how to articulate these relations in order to give the right answer.

In the Absence profile, the student showed not having perceived characteristics or relations between the elements of the equality, beyond the numbers comprising it, the operation symbols articulating it and the presence of the equal sign. This type of behavior suggests the dependence of knowing the numeric values of the members of the equality to determine their truthfulness or falseness. A limitation of the tasks proposed, and at the same time one of its educational strengths, is that they can be solved with various strategies. The task of completing numerical equalities or determining the truthfulness of true or false equalities allows both computational strategies and the use of relational thinking. Therefore, it is possible that students can solve them using relational thinking but choose a computational approach. In the case of the participating students, we found that at times this was so (for example, when they showed a greater use of relational thinking in the interviews than during the classroom sessions). Conceptualization of arithmetic expressions as operating procedures, given by the students’ prior experience and knowledge, favors the use of computational strategies. This conceptualization hinders, in this case, the use of relational thinking [35]. The trend to follow a computational approach enhanced by traditional teaching of arithmetic together with the confidence developed by students in arithmetic procedures, leads to reduced attention to detect relations. From this standpoint, a stronger calculation skill might be counterproductive given the resistance to change shown by most students [36]. Prior knowledge can inhibit the use of more efficient strategies such as the use of relational thinking in this case, given the specific design of equalities.

Our classroom intervention sought to generate a different classroom culture by means of the thorough design of equalities together with class discussions, favoring pooling of diverse strategies for the same equality and highlighting those using relational thinking. If we choose algebraic arithmetic tasks, in line with the idea of the number sense of [2] and the new curricular proposals, it is to be expected that students’ preference for computational approaches will diminish. The objective of teaching should be to make accessible for them both computational/operational thinking and relational thinking. In order for perception and use of relations to become a habit, it is essential to change the classroom culture, together with considering relation-rich tasks involving equalities varied in structure (action and no action, open and closed) and in the relations perceptible between their terms. A fact to be leveraged in teaching plans is that there is greater ease to use relations to build equalities than to solve given equalities, especially when these are open, as detected in session 2.

To end this discussion, we enumerate several ways in which the instructional design considered in this study can be extended or enriched within the same approach to algebra or a different one. First, one way is attending and promoting the generalization and representation of the regularities detected in the equalities, two of the mathematical practices at the core of school algebra [12]. Second, in this study two of the big ideas of generalized arithmetic [37] has been addressed: equivalence and expressions. The other two, equations and inequalities could go next. Third, the instructional approach considered in the teaching experiment focus on the approach to algebra named generalized arithmetic and on the analytical meaning of algebra. Nevertheless, it can be integrated with other tasks implying quantitative reasoning and related to other approaches to algebra. This is the case of words problems where students are asked to study and represent the relations between the quantities in the story (e.g., [38]). Once students have identified the relations and have arrived to an arithmetic representation of them, different representations can be compared, and questions of equivalence can be formulated. In this way attention can be moved from the representational meaning of numbers to the analytical one. Finally, according to research developed in this [39] and other contexts [40,41], incorporating other representations of numbers and of the equality concept such as visuals, gestures, and manipulatives would be a way to help students and raise achievement. In this case it may help students with lower relational thinking to develop their understanding and awareness of arithmetic properties and, widely speaking, increase their number sense. Later symbolic arithmetic (horizontal) representations can be recuperated as a vehicle towards the later introduction of algebraic symbolism.

5. Conclusions

In order to characterize the use of relational thinking evidenced by third-grade students based on arithmetic relations and properties at play, in this study we distinguished among profiles of use of the above type of thinking. These profiles, unlike the approach chosen in previous studies [7,23], did not address the role of calculation. They refer to four different ways in which students show this type of thinking when working with a set of equalities based on diverse arithmetic properties. It is useful to identify them to support instructional design seeking to promote adequate and full development of relational thinking, given the importance it has been awarded by previous studies (e.g., [16,18,23]. Likewise, these profiles are of interest to track students’ development regarding the use of relational thinking, allowing detection of teaching areas to work on, complementing or modifying the teaching proposal described herein.

The variety of profiles and of their frequency detected in each session and the way the use of relational thinking evolves in each student suggest that, as number sense [42] or due to its dependence to it, relational thinking use is highly personal. Students do not develop or manifest it in similar ways as result of their arithmetic teaching and our interventions. We understand this by considering relational thinking, at least partially, as an indirect result of previous arithmetic experience.

Through the individual analysis of each students’ responses we have identified components of number sense that conditioned the evolution of their relational thinking: knowledge/awareness of arithmetic properties, computational fluency and conception of numbers. The first one is related to the algebraic component of number sense.

Finally, we would like to point out some limitations of this study that identified future lines of research on the use and development of relational thinking. The sample was small and not representative. Further research is required to be able to confirm the results presented. More studies are necessary for the definition of profiles of the use of relational thinking to become established, as well as to extend them considering equalities that include multiplication operations and properties. Further, to investigate the effects of longer classroom work as well as the possible uses of this mode of thinking in other types of tasks.

While the duration of the experiment conducted was not long enough to obtain long-term conclusions, it did provide promising and useful results on the viability and potential of an algebraic approach to arithmetic which contributes, at the same time, to the development of number sense among primary school students and to useful ways of thinking for the later study of algebra in higher grades.