Effects of Surface Rotation on the Phase Change Process in a 3D Complex-Shaped Cylindrical Cavity with Ventilation Ports and Installed PCM Packed Bed System during Hybrid Nanofluid Convection
Abstract
:1. Introduction
2. Computational Details of PCM–PB Integrated System
3. Results and Discussion
4. Conclusions
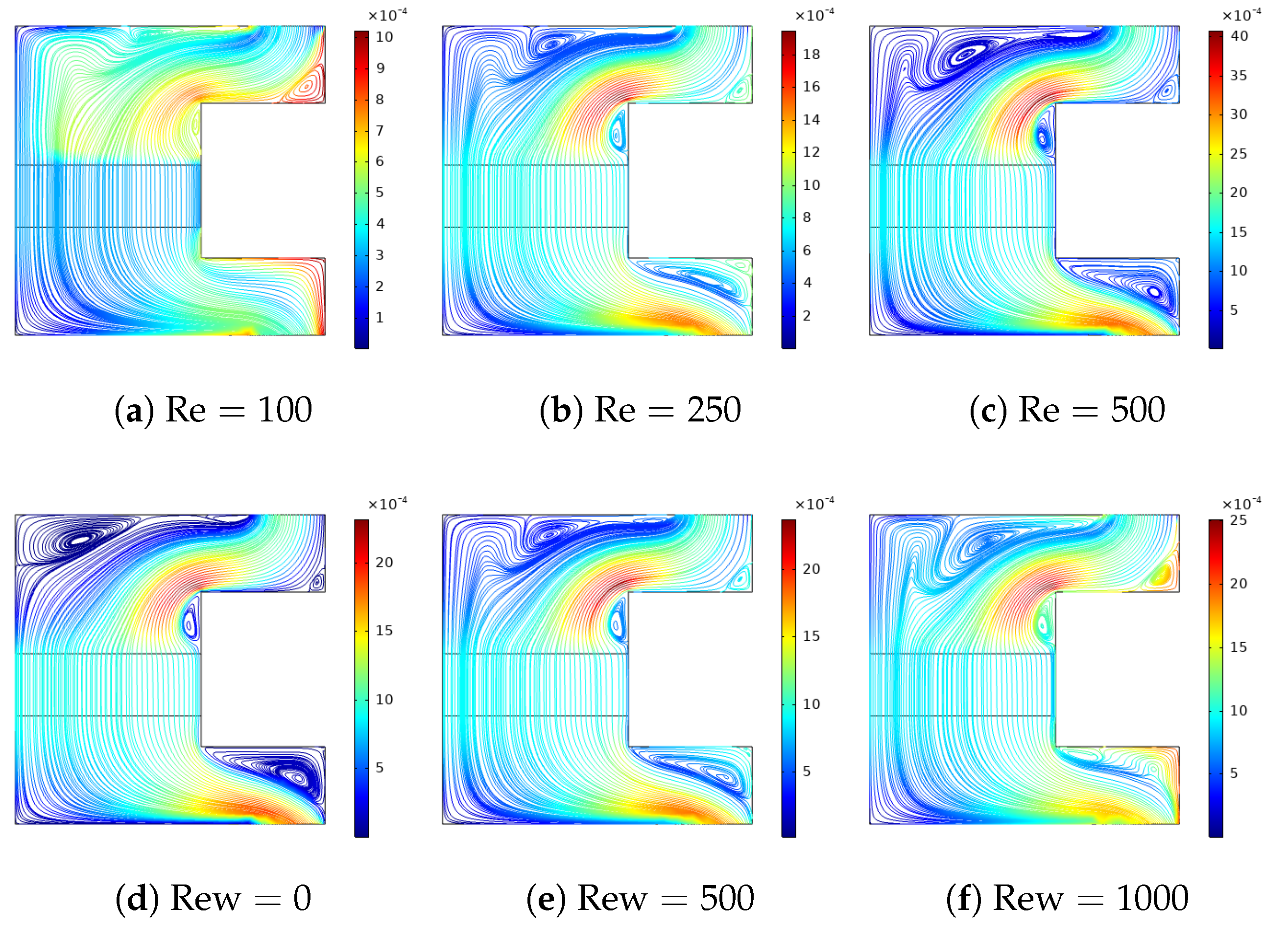
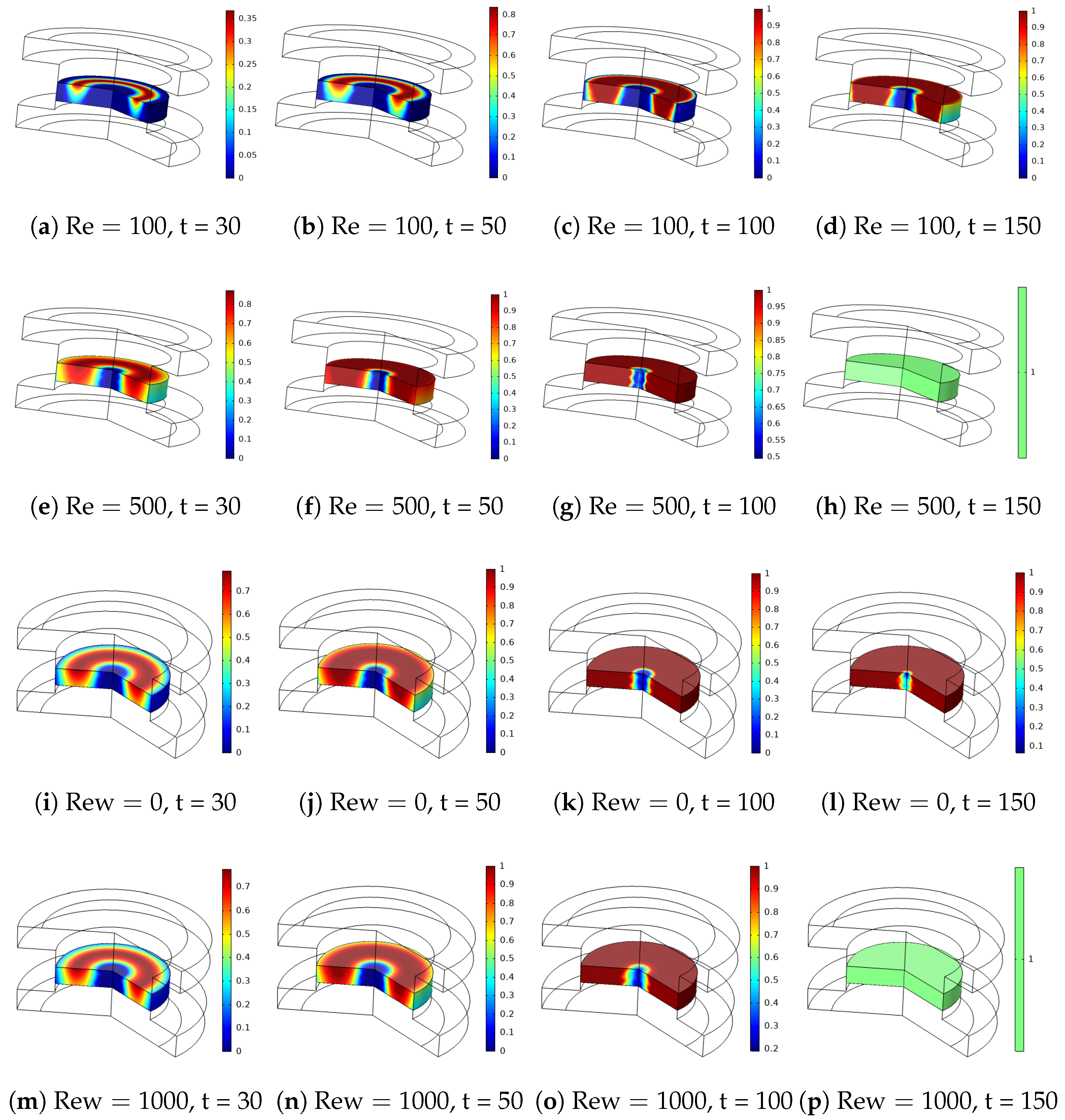
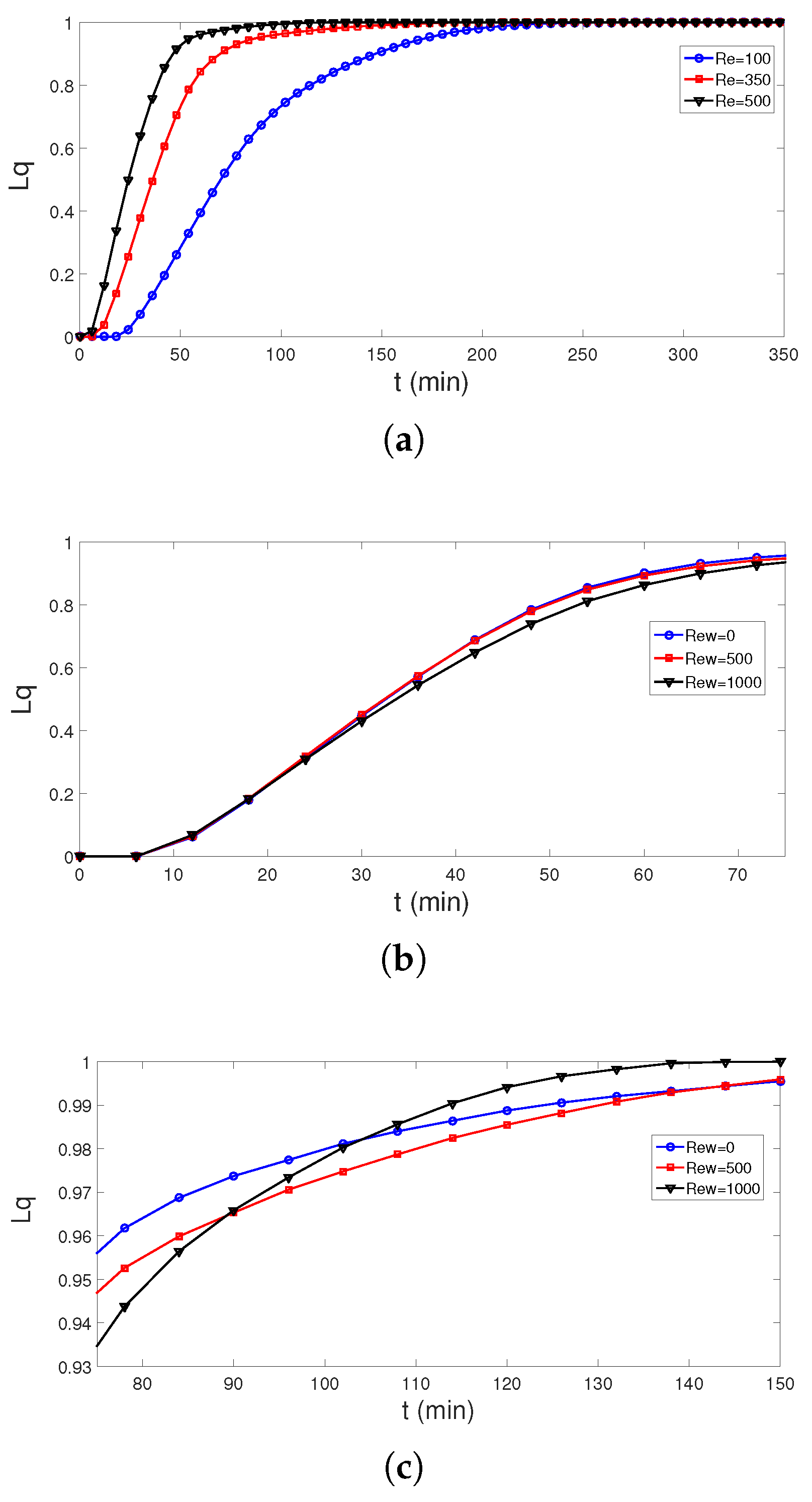
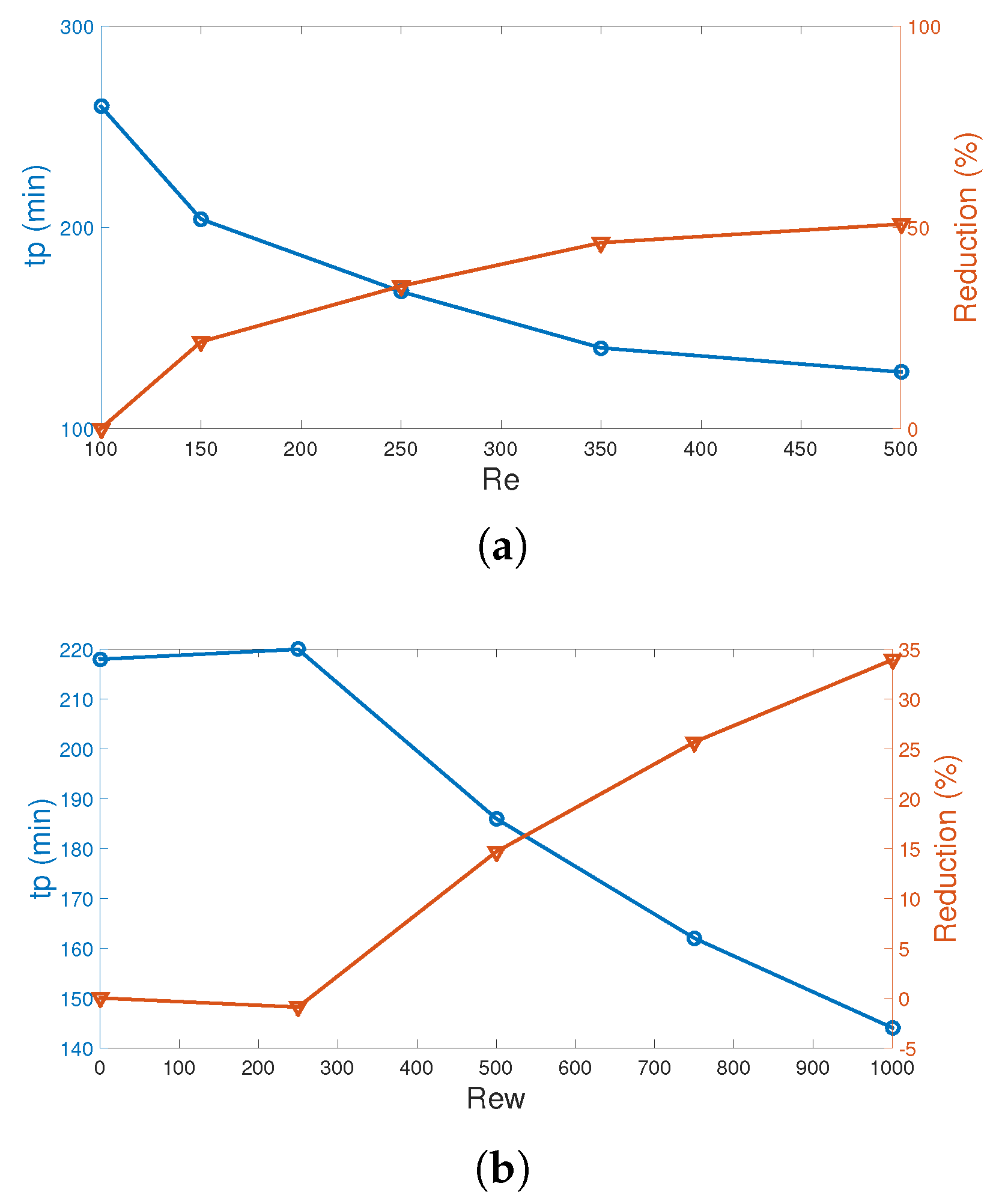
- The impacts of surface rotation on the phase change become effective for lower values of fluid stream Re numbers.
- At the highest rotational speed of the surface, a 39.8% and 24.5% reduction in the phase transition time (tp) were achieved at Re = 100 and Re = 500.
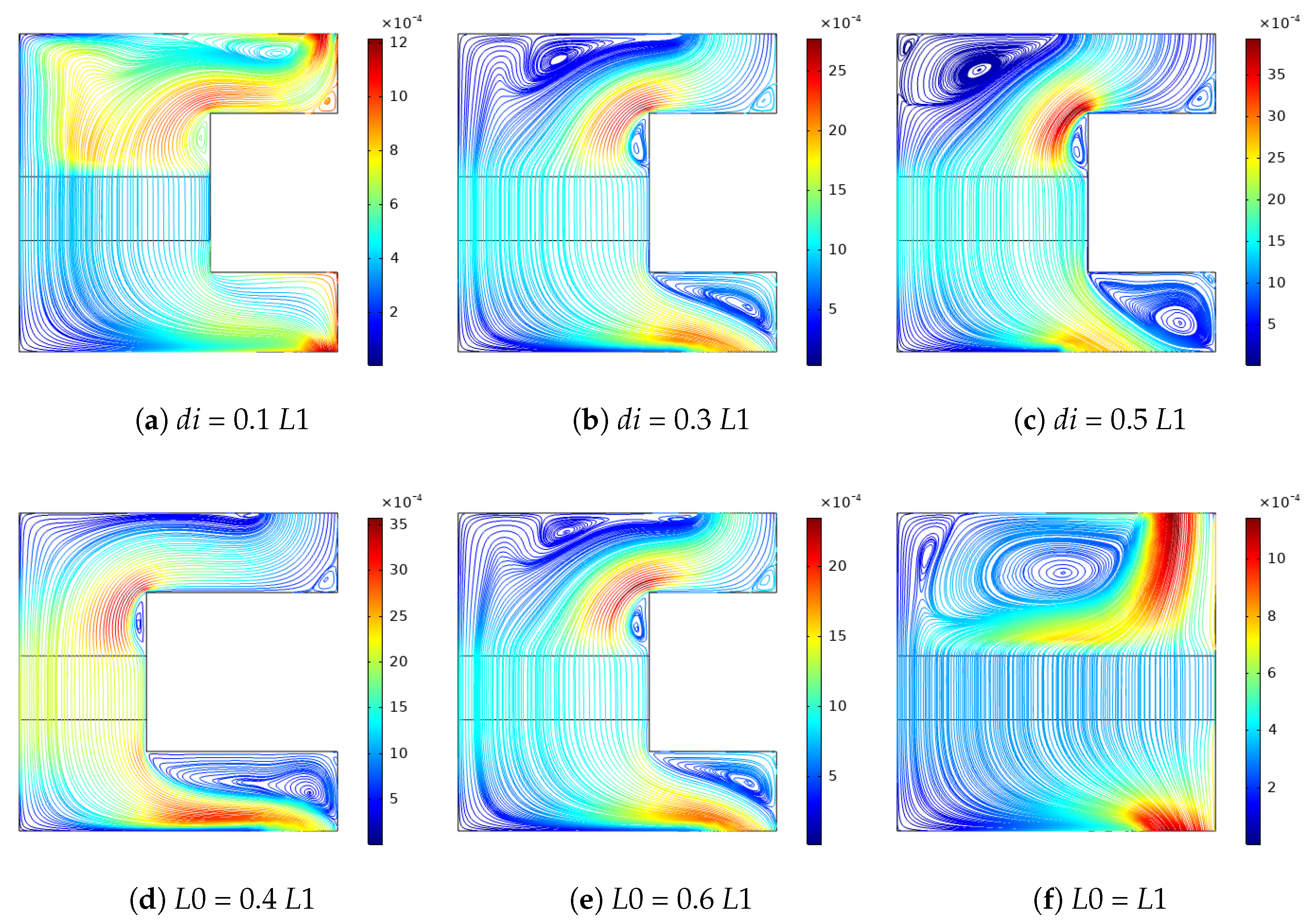
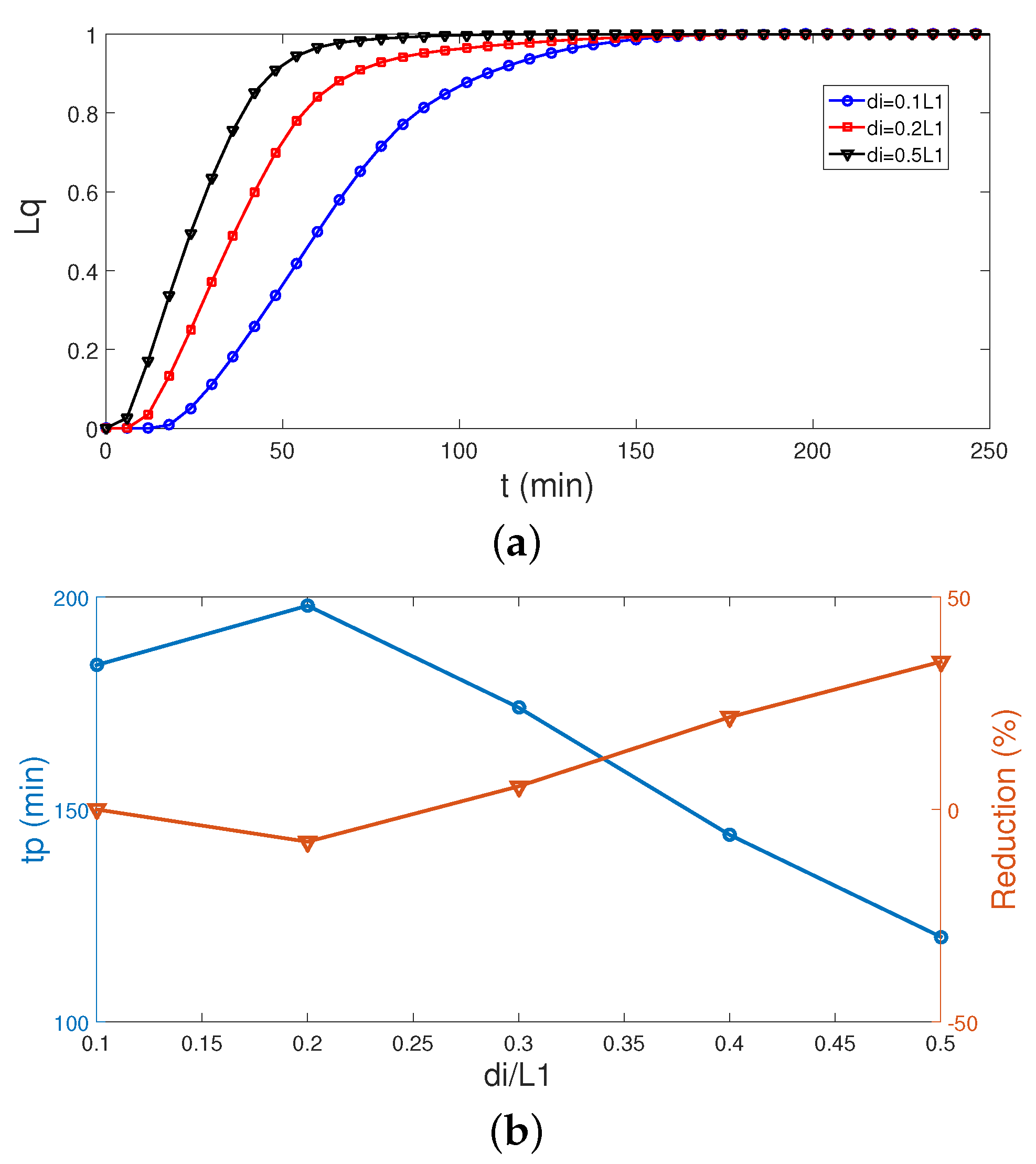
- Flow recirculation, especially near the ports, are affected by the port sizes, while a larger port size accelerates the phase change process. When configurations with the smallest and largest port sizes are compared, a 34.8% reduction in tp is obtained.
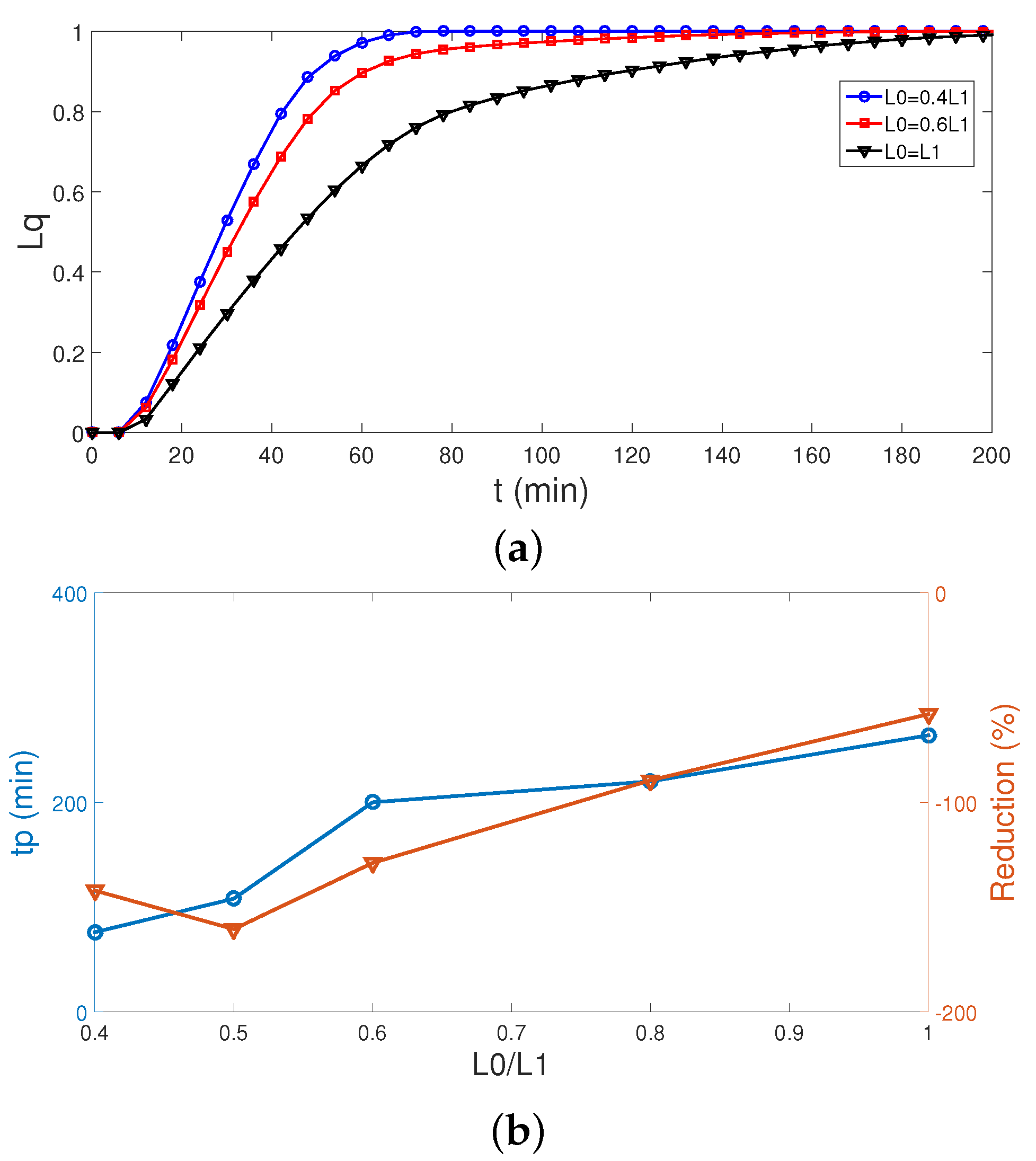
- The size and vertical location of the PCM–PB system shows opposite behavior on the phase change dynamics. When the zone is closer to the inlet port, phase change accelerates. The reduction and increment in the tp are obtained as 20% and 58% for the largest yp and length of the PCM zone.
- Inclusion of hybrid nanoparticles in the base HT fluid accelerates the phase transition and a tp reduction of about 9.5% is achieved at the highest nanoparticle loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| di | port size |
| Lq | liquid fraction |
| k | thermal conductivity |
| H | cavity height |
| hpc | PCM–PB height |
| L | radius of cylinder |
| L0 | PCM–PB radius |
| L | latent heat of fusion |
| n | unit normal vector |
| Nu | Nusselt number |
| p | pressure |
| Pr | Prandtl number |
| Re | Reynolds number |
| R | residual |
| Rew | rotational Reynolds number |
| t | time |
| tp | full phase transition time |
| T | temperature |
| T | melting temperature |
| u, v, w | velocity components |
| W | weight function |
| r, z | cylindrical coordinates |
| ypc | distance of PCM–PB from lower cavity |
| Greek Characters | |
| kinematic viscosity | |
| density of the fluid | |
| permeability | |
| porosity | |
| angular rotational speed | |
| Subscripts | |
| c | cold |
| h | hot |
| m | average |
| nf | nanofluid |
| p | solid particle |
References
- Javadi, F.; Metselaar, H.; Ganesan, P. Performance improvement of solar thermal systems integrated with phase change materials (PCM), a review. Sol. Energy 2020, 206, 330–352. [Google Scholar] [CrossRef]
- Pomianowski, M.; Heiselberg, P.; Zhang, Y. Review of thermal energy storage technologies based on PCM application in buildings. Energy Build. 2013, 67, 56–69. [Google Scholar] [CrossRef]
- Khan, M.M.A.; Ibrahim, N.I.; Mahbubul, I.; Ali, H.M.; Saidur, R.; Al-Sulaiman, F.A. Evaluation of solar collector designs with integrated latent heat thermal energy storage: A review. Sol. Energy 2018, 166, 334–350. [Google Scholar] [CrossRef]
- Shon, J.; Kim, H.; Lee, K. Improved heat storage rate for an automobile coolant waste heat recovery system using phase-change material in a fin–tube heat exchanger. Appl. Energy 2014, 113, 680–689. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, W.; Tian, Y. Heat transfer enhancement for thermal energy storage using metal foams embedded within phase change materials (PCMs). Sol. Energy 2010, 84, 1402–1412. [Google Scholar] [CrossRef] [Green Version]
- Mat, S.; Al-Abidi, A.A.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Enhance heat transfer for PCM melting in triplex tube with internal–external fins. Energy Convers. Manag. 2013, 74, 223–236. [Google Scholar] [CrossRef]
- Mahian, O.; Ghafarian, S.; Sarrafha, H.; Kasaeian, A.; Yousefi, H.; Yan, W.M. Phase change materials in solar photovoltaics applied in buildings: An overview. Sol. Energy 2021, 224, 569–592. [Google Scholar] [CrossRef]
- Hajizadeh, M.R.; Selimefendigil, F.; Muhammad, T.; Ramzan, M.; Babazadeh, H.; Li, Z. Solidification of PCM with nano powders inside a heat exchanger. J. Mol. Liq. 2020, 306, 112892. [Google Scholar] [CrossRef]
- Safaei, M.R.; Goshayeshi, H.R.; Chaer, I. Solar still efficiency enhancement by using graphene oxide/paraffin nano-PCM. Energies 2019, 12, 2002. [Google Scholar] [CrossRef] [Green Version]
- Singh, H.; Saini, R.; Saini, J. A review on packed bed solar energy storage systems. Renew. Sustain. Energy Rev. 2010, 14, 1059–1069. [Google Scholar] [CrossRef]
- de Gracia, A.; Cabeza, L.F. Numerical simulation of a PCM packed bed system: A review. Renew. Sustain. Energy Rev. 2017, 69, 1055–1063. [Google Scholar] [CrossRef] [Green Version]
- Selimefendigil, F.; Öztop, H.F. Analysis of hybrid nanofluid and surface corrugation in the laminar convective flow through an encapsulated PCM filled vertical cylinder and POD-based modeling. Int. J. Heat Mass Transf. 2021, 178, 121623. [Google Scholar] [CrossRef]
- Saeidi, S.; Khodadadi, J. Forced convection in a square cavity with inlet and outlet ports. Int. J. Heat Mass Transf. 2006, 49, 1896–1906. [Google Scholar] [CrossRef]
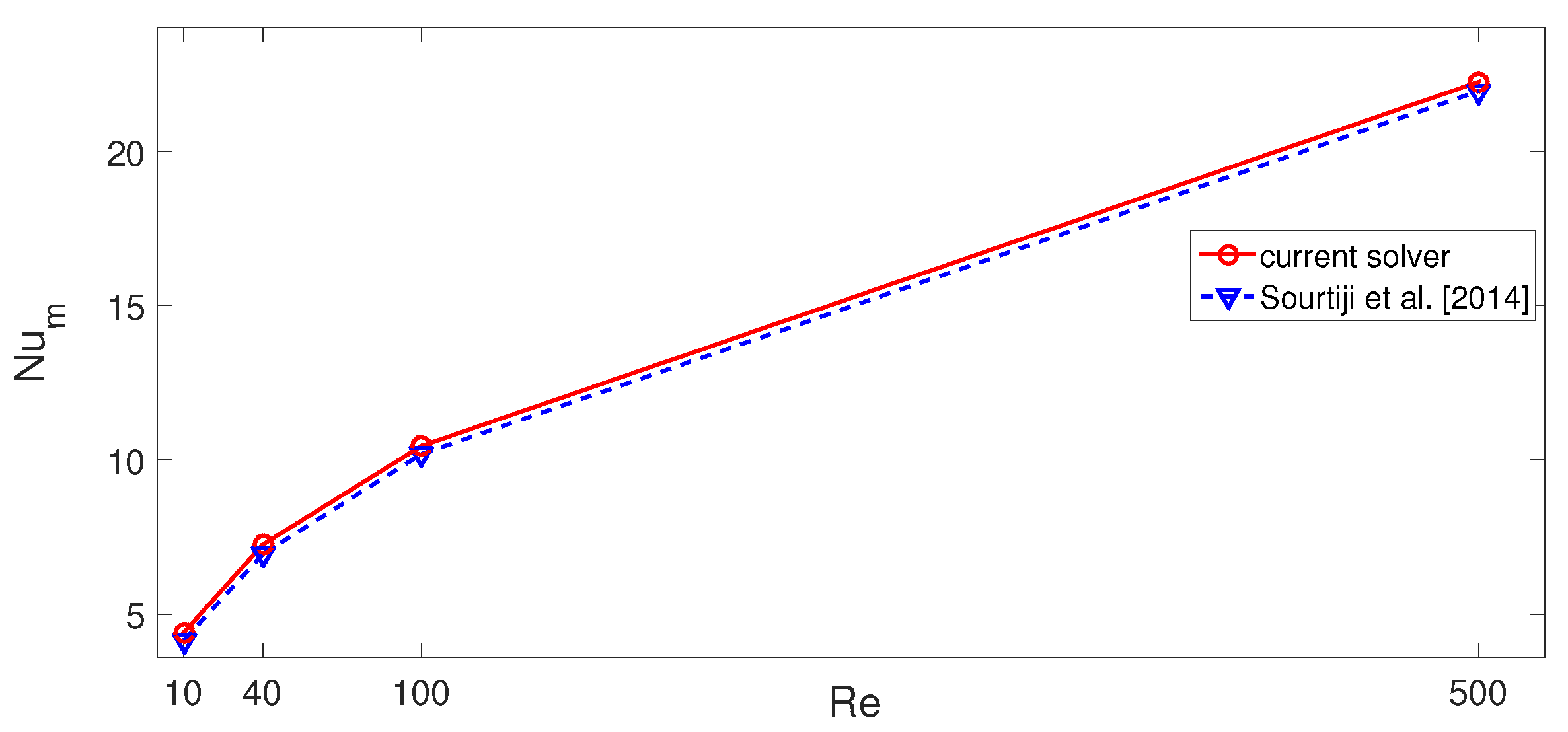
- Sourtiji, E.; Gorji-Bandpy, M.; Ganji, D.; Hosseinizadeh, S. Numerical analysis of mixed convection heat transfer of Al2O3-water nanofluid in a ventilated cavity considering different positions of the outlet port. Powder Technol. 2014, 262, 71–81. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Fluid-solid interaction of elastic-step type corrugation effects on the mixed convection of nanofluid in a vented cavity with magnetic field. Int. J. Mech. Sci. 2019, 152, 185–197. [Google Scholar] [CrossRef]
- Kherroubi, S.; Benkahla, Y.K.; Boutra, A.; Bensaci, A. Two-and three-dimensional comparative study of heat transfer and pressure drop characteristics of nanofluids flow through a ventilated cubic cavity (part II: Non-Newtonian nanofluids under the influence of a magnetic field). J. Therm. Anal. Calorim. 2020, 1–28. [Google Scholar] [CrossRef]
- Ezzouhri, R.; Joubert, P.; Penot, F.; Mergui, S. Large Eddy simulation of turbulent mixed convection in a 3D ventilated cavity: Comparison with existing data. Int. J. Therm. Sci. 2009, 48, 2017–2024. [Google Scholar] [CrossRef]
- Lariani, A.; Nesreddine, H.; Galanis, N. Numerical and experimental study of 3D turbulent airflow in a full scale heated ventilated room. Eng. Appl. Comput. Fluid Mech. 2009, 3, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Selimefendigil, F.; Öztop, H.F. Impact of a rotating cone on forced convection of Ag–MgO/water hybrid nanofluid in a 3D multiple vented T-shaped cavity considering magnetic field effects. J. Therm. Anal. Calorim. 2021, 143, 1485–1501. [Google Scholar] [CrossRef]
- Khan, Z.; Hamid, M.; Khan, W.; Sun, L.; Liu, H. Thermal non-equilibrium natural convection in a trapezoidal porous cavity with heated cylindrical obstacles. Int. Commun. Heat Mass Transf. 2021, 126, 105460. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Abu-Hamdeh, N. Impacts of conductive inner L-shaped obstacle and elastic bottom wall on MHD forced convection of a nanofluid in vented cavity. J. Therm. Anal. Calorim. 2020, 141, 465–482. [Google Scholar] [CrossRef]
- Aly, A.M. Mixing between solid and fluid particles during natural convection flow of a nanofluid-filled H-shaped cavity with three center gates using ISPH method. Int. J. Heat Mass Transf. 2020, 157, 119803. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A.; Sheremet, M.; Hamid, M.; Du, M. Irreversibilities in natural convection inside a right-angled trapezoidal cavity with sinusoidal wall temperature. Phys. Fluids 2021, 33, 083612. [Google Scholar] [CrossRef]
- Mehrizi, A.A.; Farhadi, M.; Afroozi, H.H.; Sedighi, K.; Darz, A.R. Mixed convection heat transfer in a ventilated cavity with hot obstacle: Effect of nanofluid and outlet port location. Int. Commun. Heat Mass Transf. 2012, 39, 1000–1008. [Google Scholar] [CrossRef]
- Hussain, S.; Jamal, M.; Geridonmez, B.P. Impact of fins and inclined magnetic field in double lid-driven cavity with Cu–water nanofluid. Int. J. Therm. Sci. 2021, 161, 106707. [Google Scholar] [CrossRef]
- Shih, Y.C.; Khodadadi, J.; Nien, S.W.; Zeng, Y.; Huang, X.L. Impact of an oscillating guide vane on the thermo-hydraulic fields in a square cavity with single inlet and outlet ports. Int. J. Heat Mass Transf. 2019, 128, 1184–1200. [Google Scholar] [CrossRef]
- Jasim, L.M.; Hamzah, H.; Canpolat, C.; Sahin, B. Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int. Commun. Heat Mass Transf. 2021, 121, 105086. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Estimation of the mixed convection heat transfer of a rotating cylinder in a vented cavity subjected to nanofluid by using generalized neural networks. Numer. Heat Transf. Part A Appl. 2014, 65, 165–185. [Google Scholar] [CrossRef]
- Velazquez, A.; Arias, J.; Montanes, J. Pulsating flow and convective heat transfer in a cavity with inlet and outlet sections. Int. J. Heat Mass Transf. 2009, 52, 647–654. [Google Scholar] [CrossRef] [Green Version]
- Chamkha, A.J.; Selimefendigil, F.; Oztop, H.F. Pulsating flow of CNT—Water nanofluid mixed convection in a vented trapezoidal cavity with an inner conductive T-shaped object and magnetic field effects. Energies 2020, 13, 848. [Google Scholar] [CrossRef] [Green Version]
- Benzema, M.; Benkahla, Y.K.; Labsi, N.; Ouyahia, S.E.; El Ganaoui, M. Second law analysis of MHD mixed convection heat transfer in a vented irregular cavity filled with Ag–MgO/water hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 137, 1113–1132. [Google Scholar] [CrossRef]
- Ismael, M.A.; Jasim, H.F. Role of the fluid-structure interaction in mixed convection in a vented cavity. Int. J. Mech. Sci. 2018, 135, 190–202. [Google Scholar] [CrossRef]
- Ahmed, S.E. Caputo fractional convective flow in an inclined wavy vented cavity filled with a porous medium using Al2O3-Cu hybrid nanofluids. Int. Commun. Heat Mass Transf. 2020, 116, 104690. [Google Scholar] [CrossRef]
- Hamid, M.; Khan, Z.; Khan, W.; Haq, R. Natural convection of water-based carbon nanotubes in a partially heated rectangular fin-shaped cavity with an inner cylindrical obstacle. Phys. Fluids 2019, 31, 103607. [Google Scholar] [CrossRef]
- Shirvan, K.M.; Öztop, H.F.; Al-Salem, K. Mixed magnetohydrodynamic convection in a Cu-water-nanofluid-filled ventilated square cavity using the Taguchi method: A numerical investigation and optimization. Eur. Phys. J. Plus 2017, 132, 204. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, W.; Hamid, M.; Liu, H. Finite element analysis of hybrid nanofluid flow and heat transfer in a split lid-driven square cavity with Y-shaped obstacle. Phys. Fluids 2020, 32, 093609. [Google Scholar] [CrossRef]
- Benzema, M.; Benkahla, Y.K.; Boudiaf, A.; Ouyahia, S.E.; El Ganaoui, M. Magnetic field impact on nanofluid convective flow in a vented trapezoidal cavity using Buongiorno’s mathematical model. Eur. Phys. J. Appl. Phys. 2019, 88, 11101. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Said, Z.; Alsabery, A.I.; Babazadeh, H.; Shafee, A. Modification for helical turbulator to augment heat transfer behavior of nanomaterial via numerical approach. Appl. Therm. Eng. 2020, 182, 115935. [Google Scholar] [CrossRef]
- Nallusamy, N.; Sampath, S.; Velraj, R. Experimental investigation on a combined sensible and latent heat storage system integrated with constant/varying (solar) heat sources. Renew. Energy 2007, 32, 1206–1227. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Mcgraw-Hill Book Company: New York, NY, USA, 1980. [Google Scholar]
- Mohammadnejad, F.; Hossainpour, S. A CFD modeling and investigation of a packed bed of high temperature phase change materials (PCMs) with different layer configurations. J. Energy Storage 2020, 28, 101209. [Google Scholar] [CrossRef]
- Cimpean, D.; Sheremet, M.; Pop, I. Mixed convection of hybrid nanofluid in a porous trapezoidal chamber. Int. Commun. Heat Mass Transf. 2020, 116, 104627. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Nooruddin, H.A.; Hossain, M.E. Modified Kozeny—Carmen correlation for enhanced hydraulic flow unit characterization. J. Pet. Sci. Eng. 2011, 80, 107–115. [Google Scholar] [CrossRef]
- Siavashi, M.; Bahrami, H.R.T.; Saffari, H. Numerical investigation of flow characteristics, heat transfer and entropy generation of nanofluid flow inside an annular pipe partially or completely filled with porous media using two-phase mixture model. Energy 2015, 93, 2451–2466. [Google Scholar] [CrossRef]
- Nield, D.; Bejan, A. Convection in Porous Media, in Convection Heat Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wakao, N.; Kaguei, S.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid heat transfer coefficients in packed beds: Correlation of Nusselt numbers. Chem. Eng. Sci. 1979, 34, 325–336. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.M.; Yang, Z. MHD convective heat transfer of Ag-MgO/water hybrid nanofluid in a channel with active heaters and coolers. Int. J. Heat Mass Transf. 2019, 137, 714–726. [Google Scholar] [CrossRef]
- Esfe, M.H.; Arani, A.A.A.; Rezaie, M.; Yan, W.M.; Karimipour, A. Experimental determination of thermal conductivity and dynamic viscosity of Ag-MgO/water hybrid nanofluid. Int. Commun. Heat Mass Transf. 2015, 66, 189–195. [Google Scholar] [CrossRef]
- Reddy, J.N. Introduction to the Finite Element Method; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Lewis, R.W.; Nithiarasu, P.; Seetharamu, K.N. Fundamentals of the Finite Element Method for Heat and Fluid Flow; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Heinrich, J.C.; Pepper, D.W. Intermediate Finite Element Method: Fluid Flow and Heat Transfer Applications; Routledge: London, UK, 2017. [Google Scholar]
- Reddy, J.N.; Gartling, D.K. The Finite Element Method in Heat Transfer and Fluid Dynamics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis Second Edition: With Applications to Heat Transfer, Fluid Mechanics, and Solid Mechanics; OUP: Oxford, UK, 2014. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P.; Zhu, J. The Finite Element Method; McGraw-hill: London, UK, 1977; Volume 3. [Google Scholar]
- Curtiss, C.F.; Hirschfelder, J.O. Integration of stiff equations. Proc. Natl. Acad. Sci. USA 1952, 38, 235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Ascher, U.M.; Petzold, L.R. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; SIAM: Philadelphia, PA, USA, 1998; Volume 61. [Google Scholar]
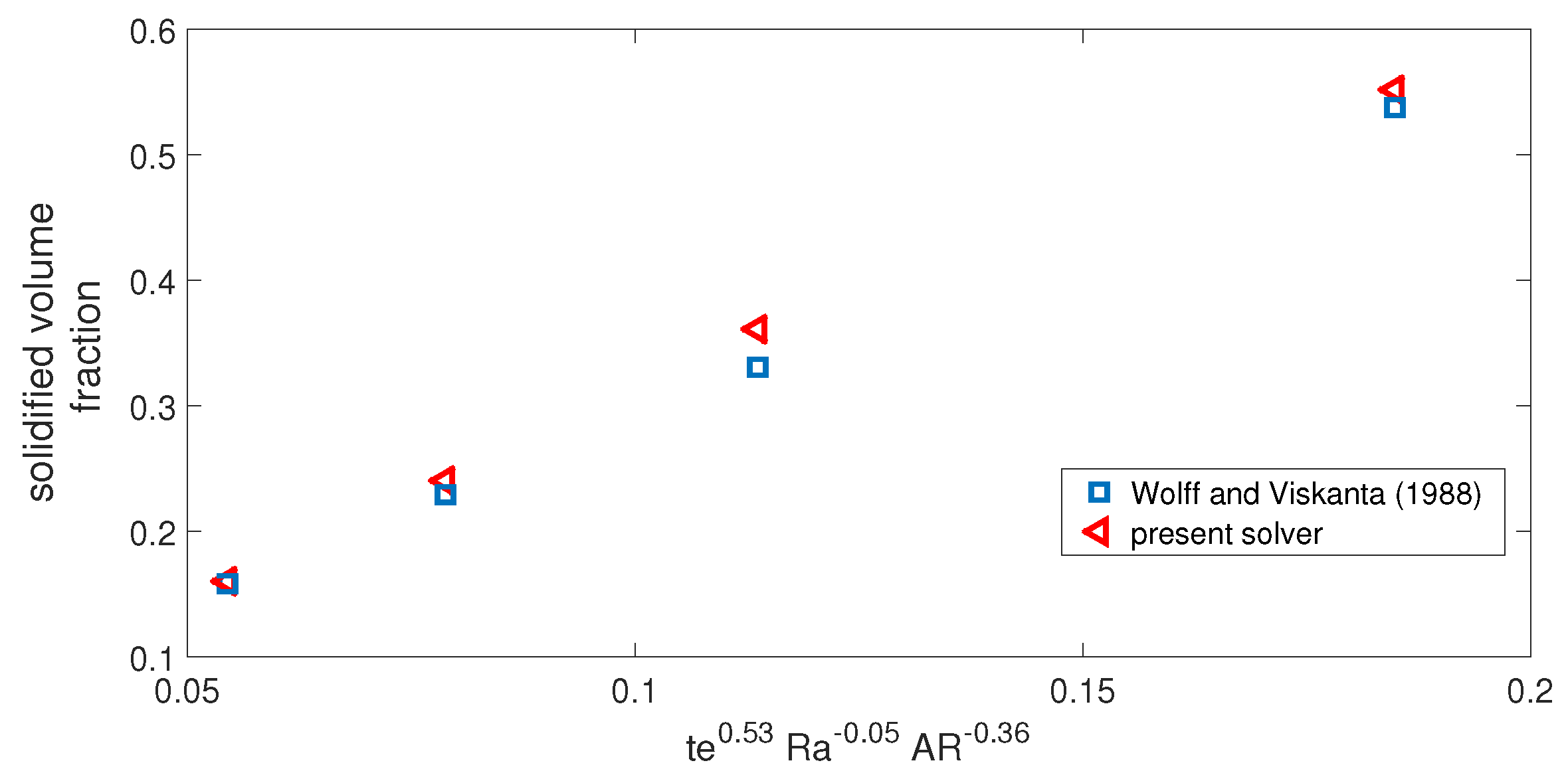
- Wolff, F.; Viskanta, R. Solidification of a pure metal at a vertical wall in the presence of liquid superheat. Int. J. Heat Mass Transf. 1988, 31, 1735–1744. [Google Scholar] [CrossRef]




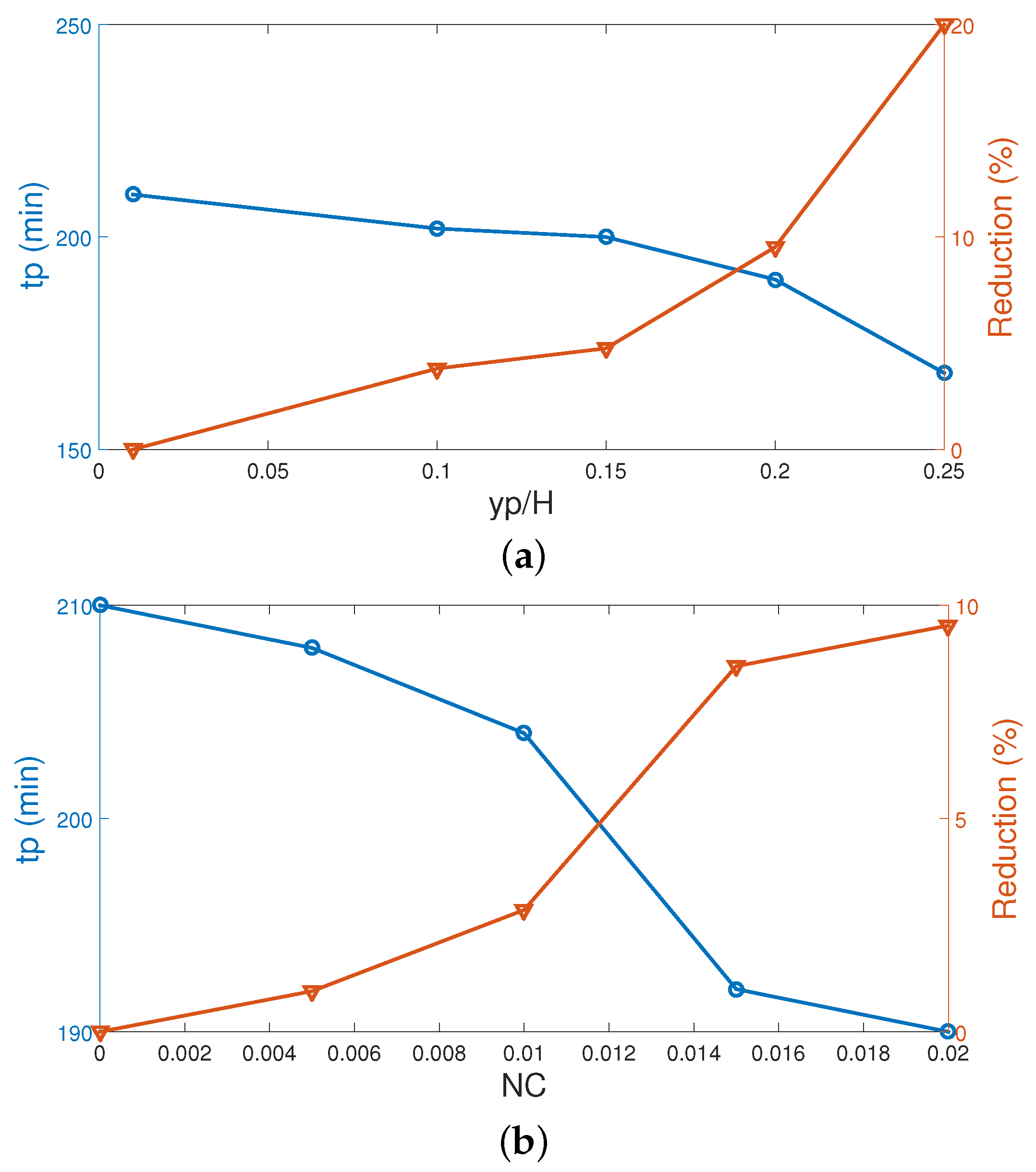
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolsi, L.; Selimefendigil, F.; Omri, M. Effects of Surface Rotation on the Phase Change Process in a 3D Complex-Shaped Cylindrical Cavity with Ventilation Ports and Installed PCM Packed Bed System during Hybrid Nanofluid Convection. Mathematics 2021, 9, 2566. https://doi.org/10.3390/math9202566
Kolsi L, Selimefendigil F, Omri M. Effects of Surface Rotation on the Phase Change Process in a 3D Complex-Shaped Cylindrical Cavity with Ventilation Ports and Installed PCM Packed Bed System during Hybrid Nanofluid Convection. Mathematics. 2021; 9(20):2566. https://doi.org/10.3390/math9202566
Chicago/Turabian StyleKolsi, Lioua, Fatih Selimefendigil, and Mohamed Omri. 2021. "Effects of Surface Rotation on the Phase Change Process in a 3D Complex-Shaped Cylindrical Cavity with Ventilation Ports and Installed PCM Packed Bed System during Hybrid Nanofluid Convection" Mathematics 9, no. 20: 2566. https://doi.org/10.3390/math9202566
APA StyleKolsi, L., Selimefendigil, F., & Omri, M. (2021). Effects of Surface Rotation on the Phase Change Process in a 3D Complex-Shaped Cylindrical Cavity with Ventilation Ports and Installed PCM Packed Bed System during Hybrid Nanofluid Convection. Mathematics, 9(20), 2566. https://doi.org/10.3390/math9202566







