Detecting Jump Risk and Jump-Diffusion Model for Bitcoin Options Pricing and Hedging
Abstract
:1. Introduction
2. Methodology
2.1. Jump Detection Methodology
2.2. The Bitcoin and Its Options Market Model
2.3. Fourier Transform and Moments of Bitcoin’s Returns Dynamic
2.4. Pricing Contingent Claims of Bitcoin under Jump-Diffusion
- X: the strike price of Bitcoin; : the underlying price of Bitcoin at time t.
- : Volatility of the price variation based on no jump.
- risk-free rate, and b are as before.
3. Option Hedging for Bitcoin Market
3.1. Option Hedging for Bitcoin Derivatives and Computation of Greeks
- 1.
- Delta (Δ)
- 2.
- Gamma ()
- 3.
- Theta ()
- 4.
- Vega (ν)
- 5.
3.2. Derivation of Sensitivity for Bitcoin Options Respective with Exercise Price
4. Numerical Application
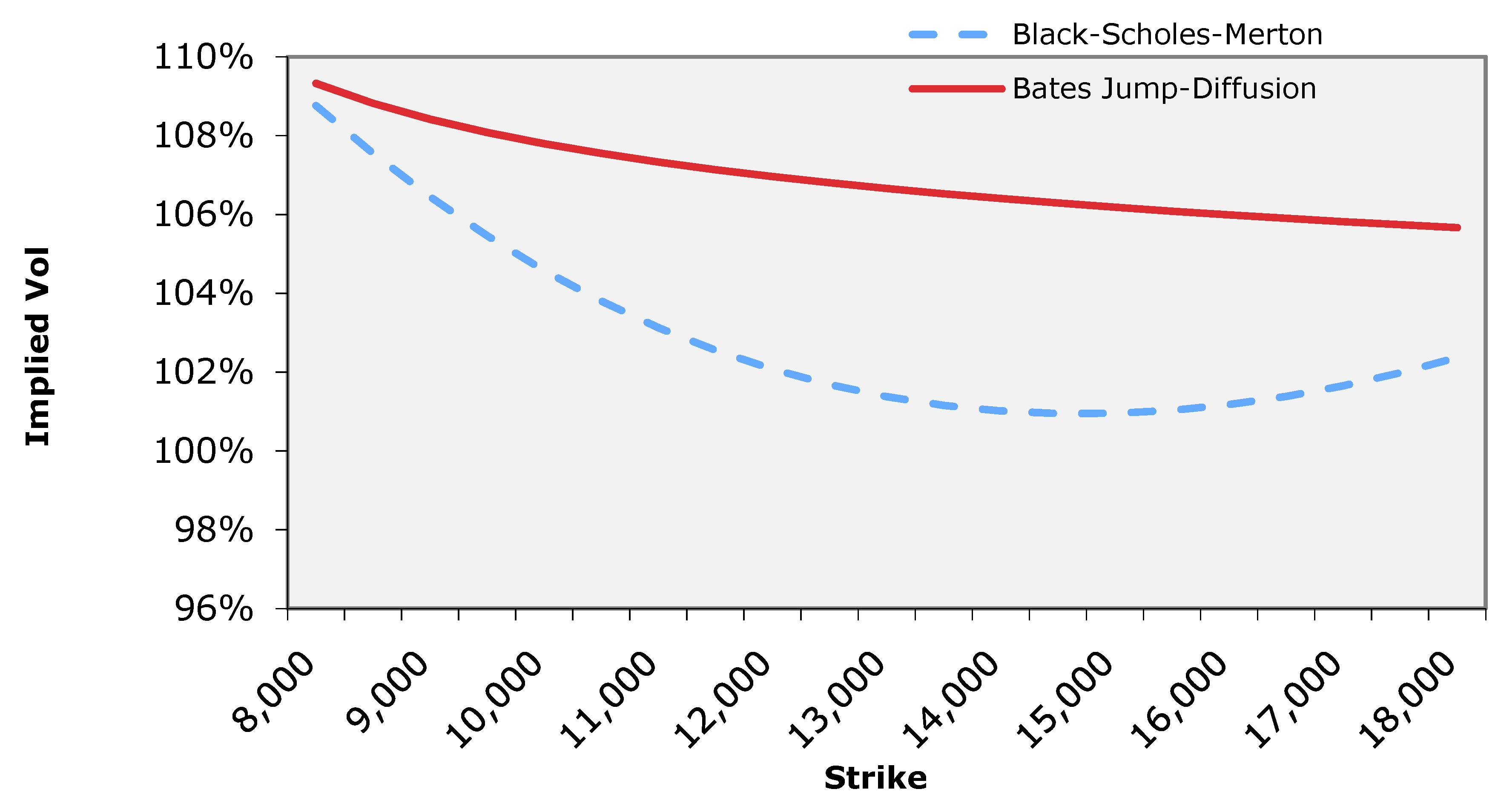
Stability across Strikes
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B. Risk Metrics of the Model of Bates (1991)
Appendix B.1. Derivation of Delta for Different Kinds of Bitcoin Derivatives
Appendix B.2. Derivation of Gamma for Different Kinds of Bitcoin Options
Appendix B.3. Derivation Process of Vega for Different Kinds of Bitcoin Options
Appendix B.4. Derivation Process of Rho for Different Kinds of Bitcoin Options
Appendix B.5. Derivation of Theta for Different Kinds of Bitcoin Options
References
- Dupire, B. Pricing with a smile. Risk 1994, 7, 18–20. [Google Scholar]
- Andersen, L.; Andreasen, J. Jump-diffusion processes: Volatility smile fitting and numerical methods for option pricing. Rev. Deriv. Res. 2000, 4, 231–262. [Google Scholar] [CrossRef]
- Ma, Y.; Shrestha, K.; Xu, W. Pricing vulnerable options with jump clustering. J. Futur. Mark. 2017, 37, 1155–1178. [Google Scholar] [CrossRef] [Green Version]
- He, C.; Kennedy, J.S.; Coleman, T.F.; Forsyth, P.A.; Li, Y.; Vetzal, K.R. Calibration and hedging under jump diffusion. Rev. Deriv. Res. 2006, 9, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Merton, R. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 124–144. [Google Scholar] [CrossRef] [Green Version]
- Bates, D.S. The crash of ’87: Was it expected? The evidence from options markets. J. Financ. 1991, 46, 1009–1044. [Google Scholar] [CrossRef]
- Cont, R.; Tankov, P. Non-Parametric calibration of jump-diffusion option pricing models. J. Comput. Financ. 2004, 7, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Valle, L.; Martínez-Rodríguez, J. Including jumps in the stochastic valuation of freight derivatives. Mathematics 2021, 9, 154. [Google Scholar] [CrossRef]
- Luther, W.J.; White, L.H. Can Bitcoin become a major currency? Cayman Financ. Rev. 2014, 36, 78–79. [Google Scholar] [CrossRef]
- Yermack, M. Is Bitcoin a Real Currency? An Economic Appraisal; NBER Working Paper 19747; National Bureau of Economic Research: Cambridge, MA, USA, 2013. [Google Scholar]
- Dowd, K.; Hutchinson, M. Bitcoin will bite the dust. Cato J. 2015, 35, 357–382. [Google Scholar]
- Ardia, D.; Bluteau, K.; Rüede, M. Regime changes in bitcoin GARCH volatility dynamics. Financ. Res. Lett. 2019, 29, 266–271. [Google Scholar] [CrossRef]
- Fang, L.; Bouri, E.; Gupta, R.; Roubaud, D. Does global economic uncertainty matter for the volatility and hedging effectiveness of Bitcoin? Int. Rev. Financ. Anal. 2019, 61, 29–36. [Google Scholar] [CrossRef]
- Bouri, E.; Roubaud, D.; Shahzad, S.J.H. Do Bitcoin and other cryptocurrencies jump together? Q. Rev. Econ. Financ. 2020, 76, 396–409. [Google Scholar] [CrossRef]
- Bouri, E.; Gkillas, K.; Gupta, R.; Pierdzioch, C. Forecasting Realized Volatility of Bitcoin: The Role of the Trade War. Comput. Econ. 2021, 57, 29–53. [Google Scholar] [CrossRef]
- Cao, M.; Celik, B. Valuation of bitcoin options. J. Futur. Mark. 2021, 41, 1007–1026. [Google Scholar] [CrossRef]
- Scaillet, O.; Treccani, A.; Trevisan, C. High-frequency jump analysis of the Bitcoin market. J. Financ. Econ. 2020, 18, 209–232. [Google Scholar]
- Siu, T.K.; Elliott, R.J. Bitcoin option pricing with a SETAR-GARCH model. Eur. J. Financ. 2021, 27, 564–595. [Google Scholar] [CrossRef]
- Jalan, A.; Matkovskyy, R.; Saqib, A. The Bitcoin options market: A first look at pricing and risk. Appl. Econ. 2021, 53, 2026–2041. [Google Scholar] [CrossRef]
- Hilliard, J.E.; Reis, J.A. Jump processes in commodity futures prices and options pricing. Am. J. Agric. Econ. 1999, 81, 273–286. [Google Scholar] [CrossRef]
- Kapetanios, G.; Konstantinidi, E.; Neumann, M.; Skiadopoulos, G. Jumps in option prices and their determinants: Real-time evidence from the E-mini S&P 500 option market. J. Financ. Mark. 2019, 46, 100506. [Google Scholar]
- Qiao, G.; Yang, J.; Li, W. VIX forecasting based on GARCH-type model with observable dynamic jumps: A new perspective. N. Am. J. Econ. Financ. 2020, 53, 101186. [Google Scholar] [CrossRef]
- Lee, S.S.; Mykland, P.A. Jumps in financial markets: A new nonparametric test and jump dynamics. Rev. Financ. Stud. 2008, 21, 2535–2563. [Google Scholar] [CrossRef]
- Dumitru, A.-M.; Urga, G. Identifying Jumps in Financial Assets: A Comparison Between Nonparametric Jump Tests. J. Bus. Econ. Stat. 2012, 30, 242–255. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Tauchen, G. The relative contribution of jumps to total price variance. J. Financ. Econ. 2005, 3, 456–499. [Google Scholar] [CrossRef]
- Cheang, G.H.L.; Chiarella, C. A Modern View on Mertons Jump-Diffusion Model; Research paper No. 287; University of Technology Sydney, Quantitative Finance Research Centre: Sidney, Australia, 2011. [Google Scholar]
- Geman, H.; EI Karoui, N.; Rochet, J.C. Changes of numeraire, changes of probability measure and option pricing. J. Appl. Probab. 1995, 32, 443–458. [Google Scholar] [CrossRef]
- Bannör, F.K.; Scherer, M. Capturing parameter uncertainty with convex risk measures. Eur. Actuar. J. 2013, 3, 97–132. [Google Scholar] [CrossRef]
- Haug, E.G. The Complete Guide to Option Pricing Formulas, 2nd ed.; McGraw–Hill: New York, NY, USA, 2007. [Google Scholar]
- Beckers, S. A note on estimating the parameters of the diffusion–jump model of stock returns. J. Financ. Quant. Anal. 1981, 16, 127–140. [Google Scholar] [CrossRef]
- Ball, C.A.; Torous, W.N. A simplified jump process for common stock returns. J. Financ. Quant. Anal. 1983, 18, 53–65. [Google Scholar] [CrossRef]
- Duan, J.C.; Ritchken, P.H.; Sun, Z. Jump Starting GARCH Pricing and Hedging Option with Jumps in Returns and Volatilities; Working Paper; National University of Singapore: Singapore, 2007. [Google Scholar]
- Cretarola, A.; Figà-Talamanca, G.; Patacca, M. Market attention and Bitcoin price modeling: Theory, estimation and option pricing. Decis. Econ. Financ. 2020, 43, 187–228. [Google Scholar] [CrossRef] [Green Version]
- Tankov, P.; Voltchkova, E. Pricing, Hedging, and Calibration in Jump-Diffusion Models. In Frontiers in Quantitative Finance; Cont, R., Ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Mijatović, A.; Tankov, P. A new look at short-term implied volatility in asset price models with jumps. Math. Financ. 2016, 26, 149–183. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.G. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef] [Green Version]
- Tauchen, G.; Zhou, H. Realized jumps on financial markets and predicting credit spreads. J. Econ. 2011, 160, 102–118. [Google Scholar] [CrossRef] [Green Version]
- Chan, W.H.; Maheu, J.M. Conditional Jump Dynamics in Stock Market Returns. J. Bus. Econ. Stat. 2002, 20, 377–389. [Google Scholar] [CrossRef]
- Duan, J.-C.; Ritchken, P.; Sun, Z. Approximating GARCH-jump models, jump-diffusion processes, and option pricing. Math. Financ. 2006, 16, 21–52. [Google Scholar] [CrossRef]
- Gronwald, M. Is Bitcoin a Commodity? On price jumps, demand shocks, and certainty of supply. J. Int. Money Financ. 2019, 97, 86–92. [Google Scholar] [CrossRef]
- Chen, K.-S. Research on Equity Release Mortgage Risk Diversification with financial innovation: Reinsurance Usage. J. Risk Model Valid. 2016, 10, 35–55. [Google Scholar] [CrossRef]
- Chen, H.Y.; Lee, C.F.; Shih, W.K. Derivation and application of Greek letters: Review and integration. In Handbook of Quantitative Finance and Risk Management, Part III; Springer: Berlin/Heidelberg, Germany, 2010; pp. 491–503. [Google Scholar]
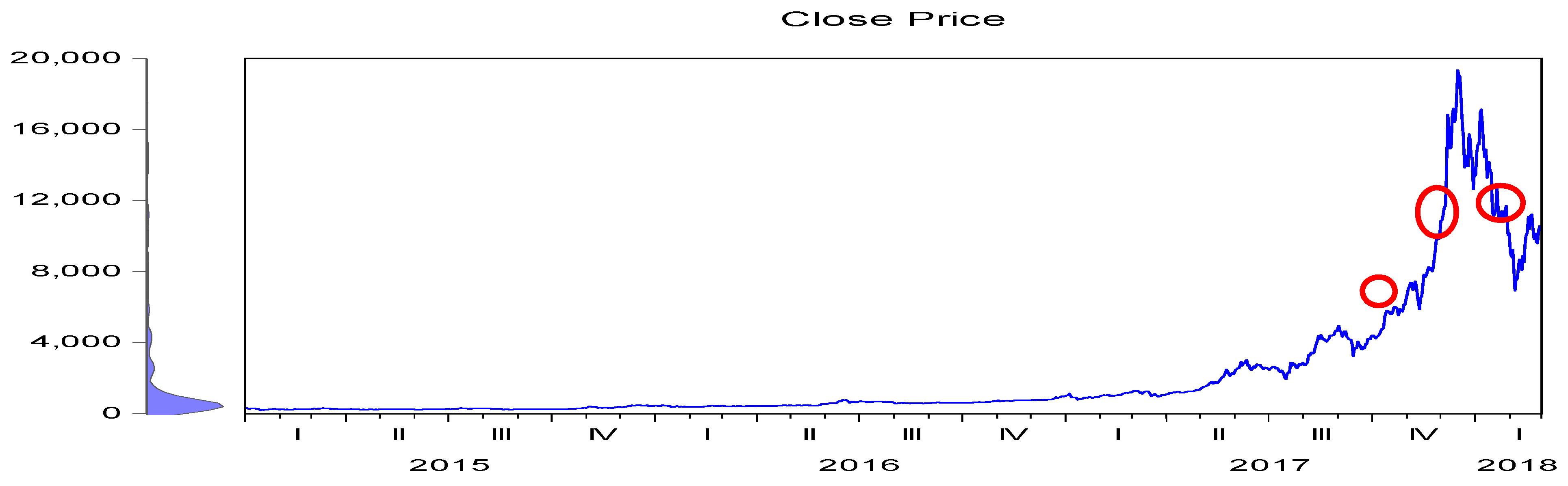
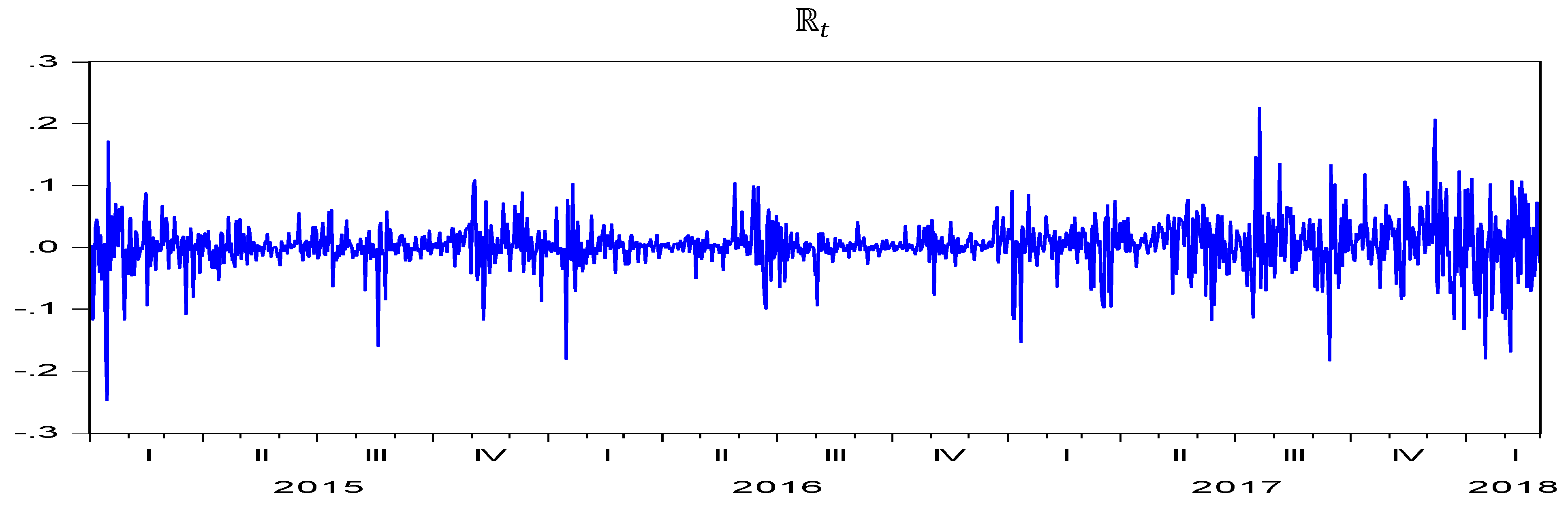
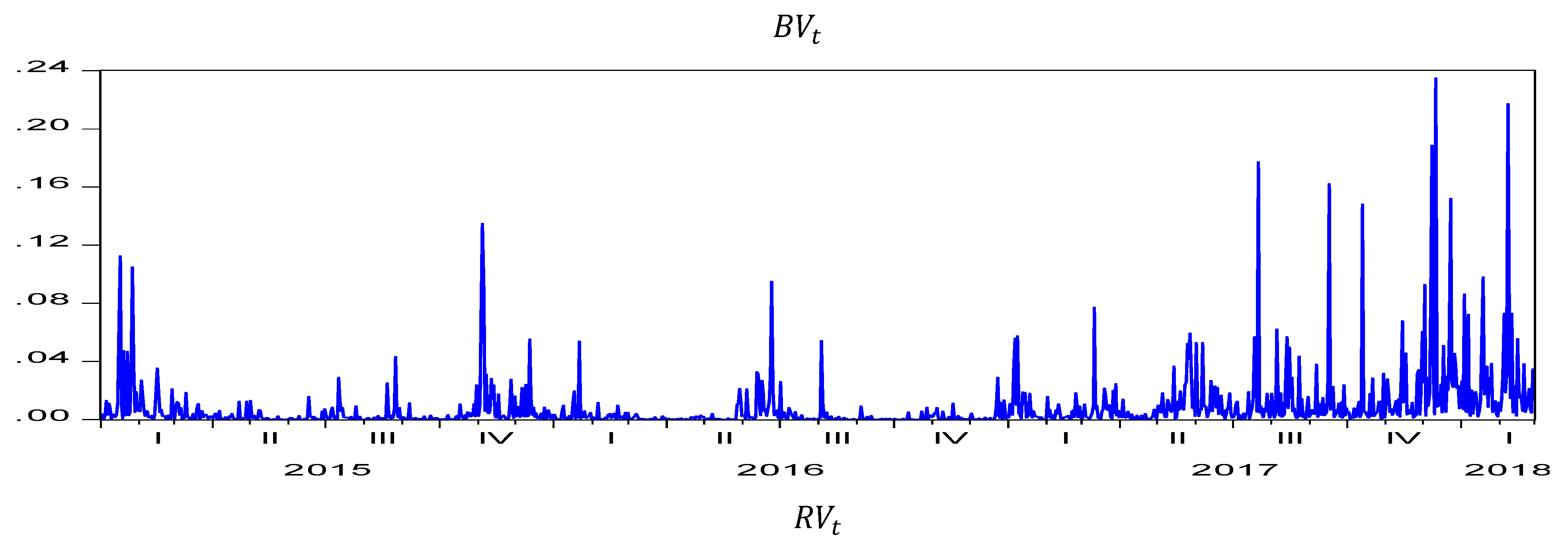
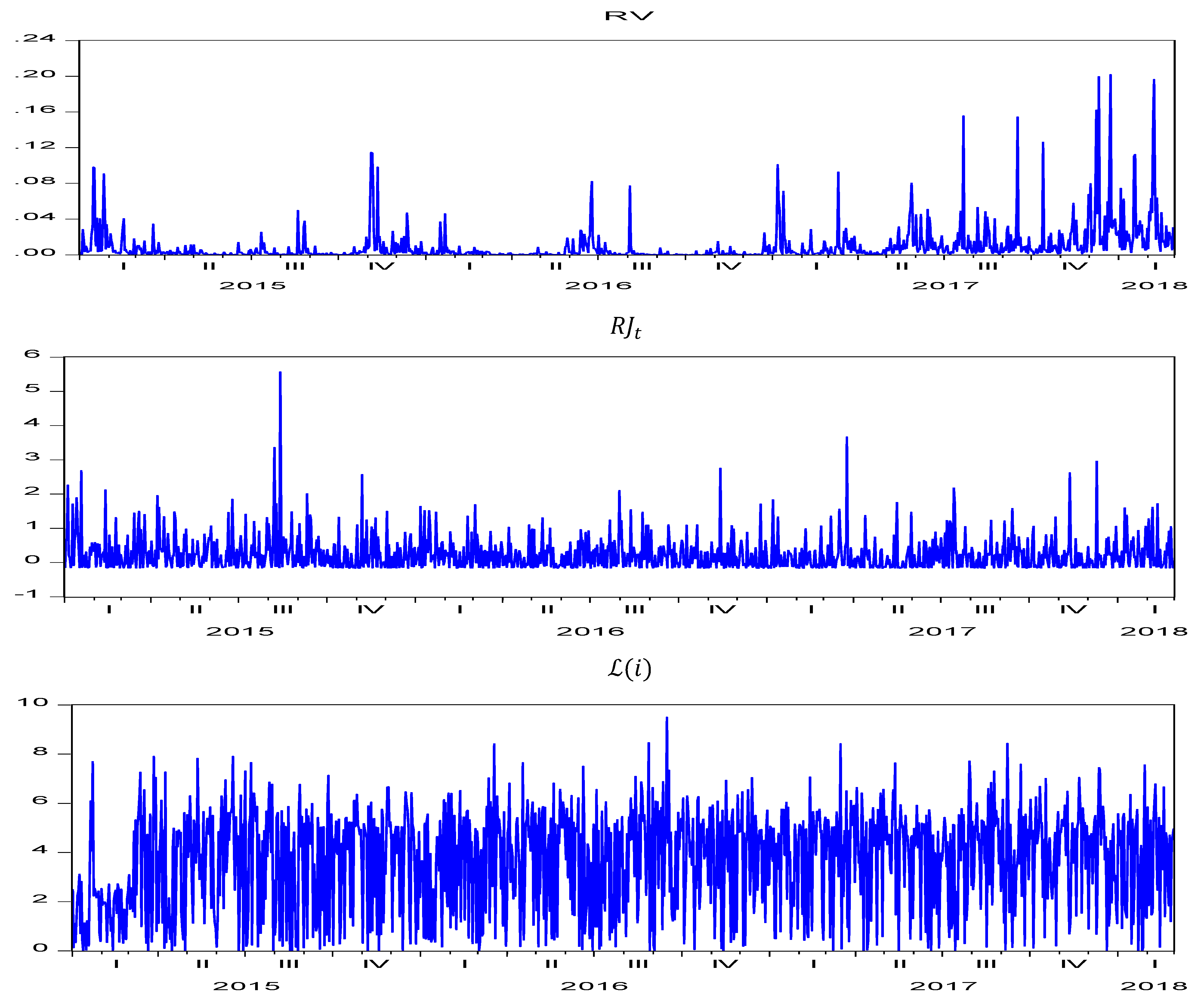

| Q1 | Q2 | Q3 | Q4 | |||||
|---|---|---|---|---|---|---|---|---|
| No. of Jumps | P(Jump freq.) | No. of Jumps | P(Jump freq.) | No. of Jumps | P(Jump freq.) | No. of Jumps | P(Jump freq.) | |
| 2015 | 45 | 0.125 | 52 | 0.1429 | 61 | 0.1685 | 44 | 0.1196 |
| # Observations | 360 | 364 | 368 | 368 | ||||
| 2016 | 45 | 0.1236 | 42 | 0.1154 | 47 | 0.1291 | 37 | 0.1016 |
| # Observations | 364 | 364 | 368 | 368 | ||||
| 2017 | 38 | 0.1056 | 36 | 0.0989 | 50 | 0.1359 | 41 | 0.1114 |
| # Observations | 360 | 364 | 368 | 368 | ||||
| 2018 | 35 | 0.1483 | ||||||
| # Observations | 236 | |||||||
| # jumps | 573 | |||||||
| (Mean) (Std. dev.) (Total Obs. | (0.124) | |||||||
| (0.02) | ||||||||
| 4,620 | ||||||||
| σB2 Strike | (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Time to Maturity | Time to Maturity | Time to Maturity | ||||||||
| 1M | 3M | 6M | 1M | 3M | 6M | 1M | 3M | 6M | ||
| 9000 | 2014.78 | 2044.27 | 2088.59 | 2014.79 | 2044.28 | 2088.58 | 2014.80 | 2044.29 | 2088.57 | |
| 10,000 | 1016.44 | 1053.38 | 1119.73 | 1016.43 | 1053.37 | 1119.72 | 1016.45 | 1053.39 | 1119.74 | |
| 0.1 | 11,000 | 134.84 | 245.47 | 363.59 | 134.83 | 245.45 | 363.58 | 134.85 | 245.49 | 363.57 |
| 12,000 | 0.13 | 11.66 | 55.22 | 0.14 | 11.67 | 55.23 | 0.12 | 11.68 | 55.24 | |
| 13,000 | 0.01 | 0.08 | 3.65 | 0.01 | 0.07 | 3.66 | 0.01 | 0.06 | 3.64 | |
| 9,000 | 2015.28 | 2069.29 | 2185.76 | 2015.27 | 2069.28 | 2185.76 | 2015.28 | 2069.30 | 2185.76 | |
| 10,000 | 1046.95 | 1203.09 | 1407.02 | 1046.94 | 1203.08 | 1407.02 | 1046.95 | 1203.07 | 1407.02 | |
| 0.25 | 11,000 | 323.31 | 570.56 | 820.85 | 323.30 | 570.57 | 820.85 | 323.31 | 570.57 | 820.85 |
| 12,000 | 46.99 | 216.75 | 434.98 | 46.99 | 216.74 | 434.97 | 46.99 | 216.76 | 434.98 | |
| 13,000 | 3.06 | 66.48 | 211.10 | 3.05 | 66.49 | 211.11 | 3.06 | 66.58 | 211.10 | |
| 9000 | 2065.65 | 2324.81 | 2670.25 | 2065.64 | 2324.80 | 2670.26 | 2065.65 | 2324.831 | 2670.27 | |
| 10,000 | 1239.45 | 1642.23 | 2069.64 | 1239.46 | 1642.24 | 2069.63 | 1239.45 | 1642.25 | 2069.65 | |
| 0.5 | 11,000 | 637.06 | 1111.34 | 1580.02 | 637.07 | 1111.33 | 1580.03 | 637.06 | 1111.37 | 1580.04 |
| 12,000 | 279.18 | 723.76 | 1191.25 | 279.17 | 723.77 | 1191.26 | 279.18 | 723.78 | 1191.27 | |
| 13,000 | 105.35 | 455.94 | 889.10 | 105.36 | 455.92 | 889.11 | 105.35 | 455.95 | 889.15 | |
| (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Time to Maturity | Time to Maturity | Time to Maturity | ||||||||
| 1M | 3M | 6M | 1M | 3M | 6M | 1M | 3M | 6M | ||
| 9000 | 2050.00 | 2187.91 | 2410.51 | 2057.83 | 2227.12 | 2488.79 | 2065.43 | 2259.81 | 2550.17 | |
| 10,000 | 1114.09 | 1350.15 | 1646.38 | 1146.09 | 1426.31 | 1764.11 | 1171.19 | 1482.95 | 1850.13 | |
| 0.1 | 11,000 | 381.98 | 704.14 | 1040.01 | 447.37 | 806.26 | 1183.55 | 489.41 | 878.62 | 1285.27 |
| 12,000 | 49.05 | 295.50 | 603.86 | 89.59 | 392.93 | 750.66 | 121.84 | 463.55 | 855.31 | |
| 13,000 | 0.32 | 94.32 | 320.94 | 3.76 | 161.27 | 450.09 | 11.37 | 215.11 | 545.86 | |
| 9000 | 2060.35 | 2249.91 | 2539.11 | 2071.18 | 2292.66 | 2615.41 | 2080.69 | 2326.57 | 2674.05 | |
| 10,000 | 1161.11 | 1472.97 | 1840.52 | 1193.35 | 1541.26 | 1941.94 | 1218.07 | 1592.42 | 2017.41 | |
| 0.25 | 11,000 | 486.37 | 874.77 | 1280.33 | 534.45 | 957.44 | 1396.49 | 569.87 | 1018.31 | 1481.99 |
| 12,000 | 113.63 | 468.59 | 856.52 | 169.57 | 548.11 | 974.78 | 197.93 | 607.68 | 1062.35 | |
| 13,000 | 21.77 | 226.28 | 552.67 | 35.06 | 289.33 | 662.17 | 47.64 | 338.81 | 744.89 | |
| 9000 | 2128.68 | 2495.99 | 2961.99 | 2143.91 | 2535.12 | 3022.75 | 2156.08 | 2565.66 | 3069.84 | |
| 10,000 | 1332.08 | 1834.29 | 2375.33 | 1358.67 | 1883.84 | 2446.11 | 1379.26 | 1922.06 | 2500.62 | |
| 0.5 | 11,000 | 737.67 | 1306.54 | 1886.12 | 769.45 | 1361.35 | 1962.91 | 793.95 | 1403.54 | 2021.95 |
| 12,000 | 359.96 | 905.03 | 1485.66 | 387.99 | 959.66 | 1564.53 | 409.98 | 1001.94 | 1625.31 | |
| 13,000 | 164.43 | 611.86 | 1,162.73 | 174.89 | 662.07 | 1,240.36 | 190.58 | 701.33 | 1,300.48 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-S.; Huang, Y.-C. Detecting Jump Risk and Jump-Diffusion Model for Bitcoin Options Pricing and Hedging. Mathematics 2021, 9, 2567. https://doi.org/10.3390/math9202567
Chen K-S, Huang Y-C. Detecting Jump Risk and Jump-Diffusion Model for Bitcoin Options Pricing and Hedging. Mathematics. 2021; 9(20):2567. https://doi.org/10.3390/math9202567
Chicago/Turabian StyleChen, Kuo-Shing, and Yu-Chuan Huang. 2021. "Detecting Jump Risk and Jump-Diffusion Model for Bitcoin Options Pricing and Hedging" Mathematics 9, no. 20: 2567. https://doi.org/10.3390/math9202567
APA StyleChen, K.-S., & Huang, Y.-C. (2021). Detecting Jump Risk and Jump-Diffusion Model for Bitcoin Options Pricing and Hedging. Mathematics, 9(20), 2567. https://doi.org/10.3390/math9202567





