A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications
Abstract
:1. Introduction
2. Fractional Order Preliminaries
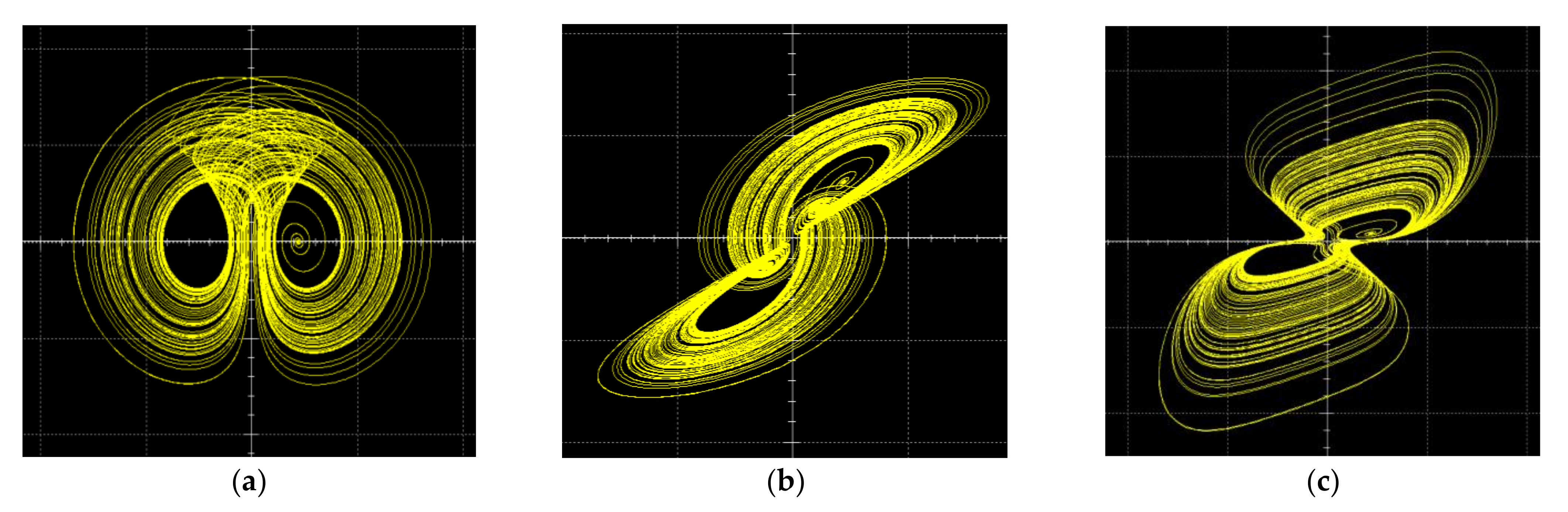
3. New Fractional-Order Chaotic System
4. The Dynamical Analysis
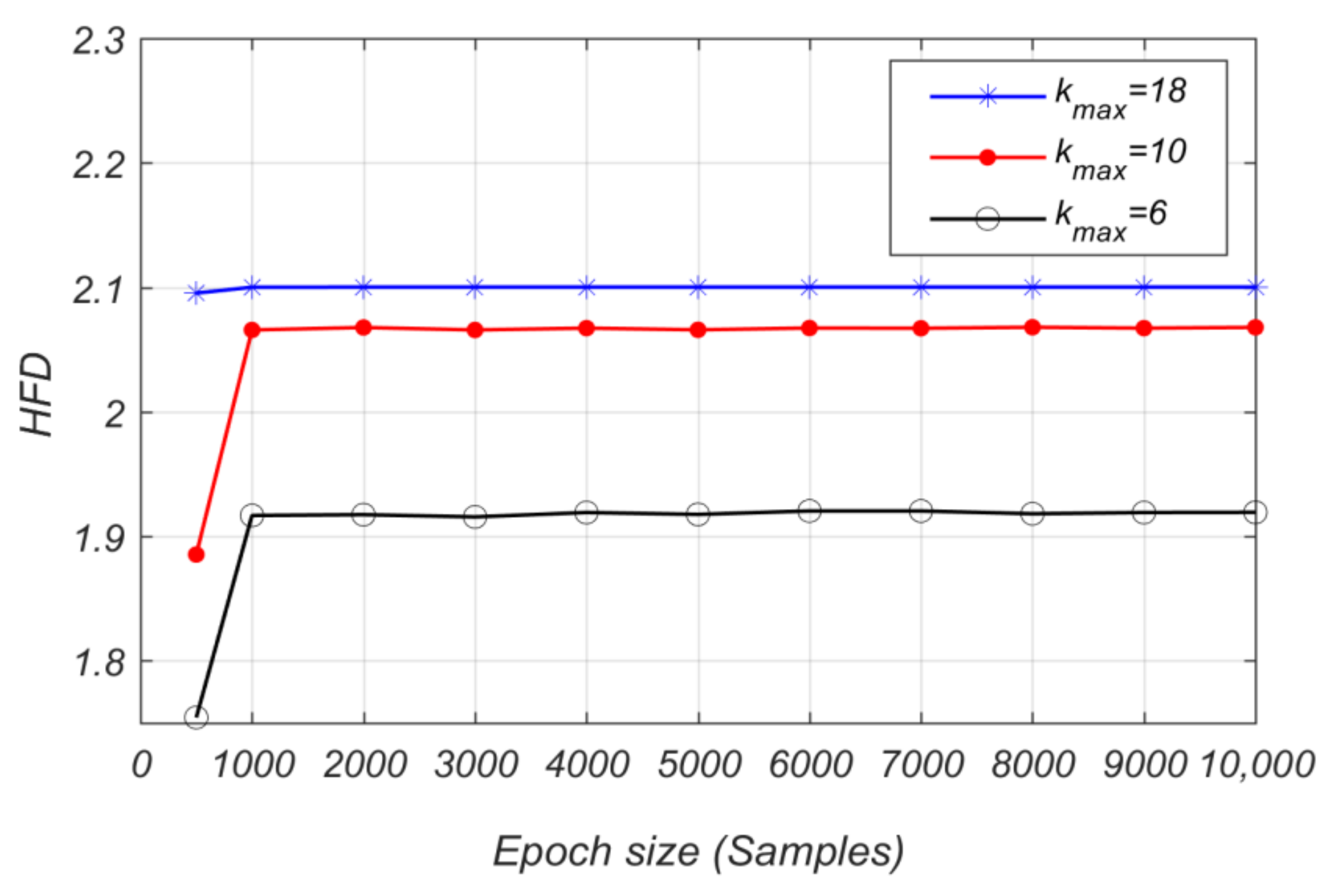
4.1. Fractal Dimension
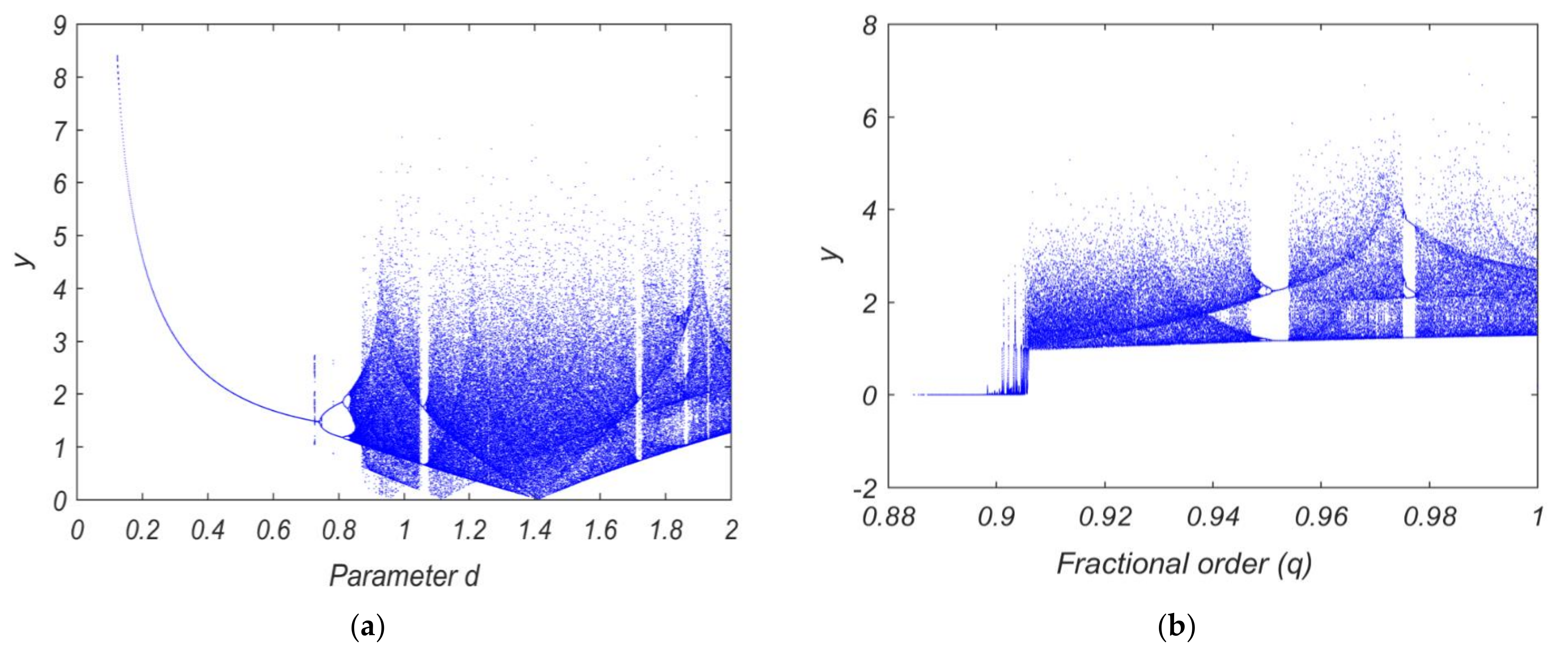
4.2. Bifurcation Diagrams
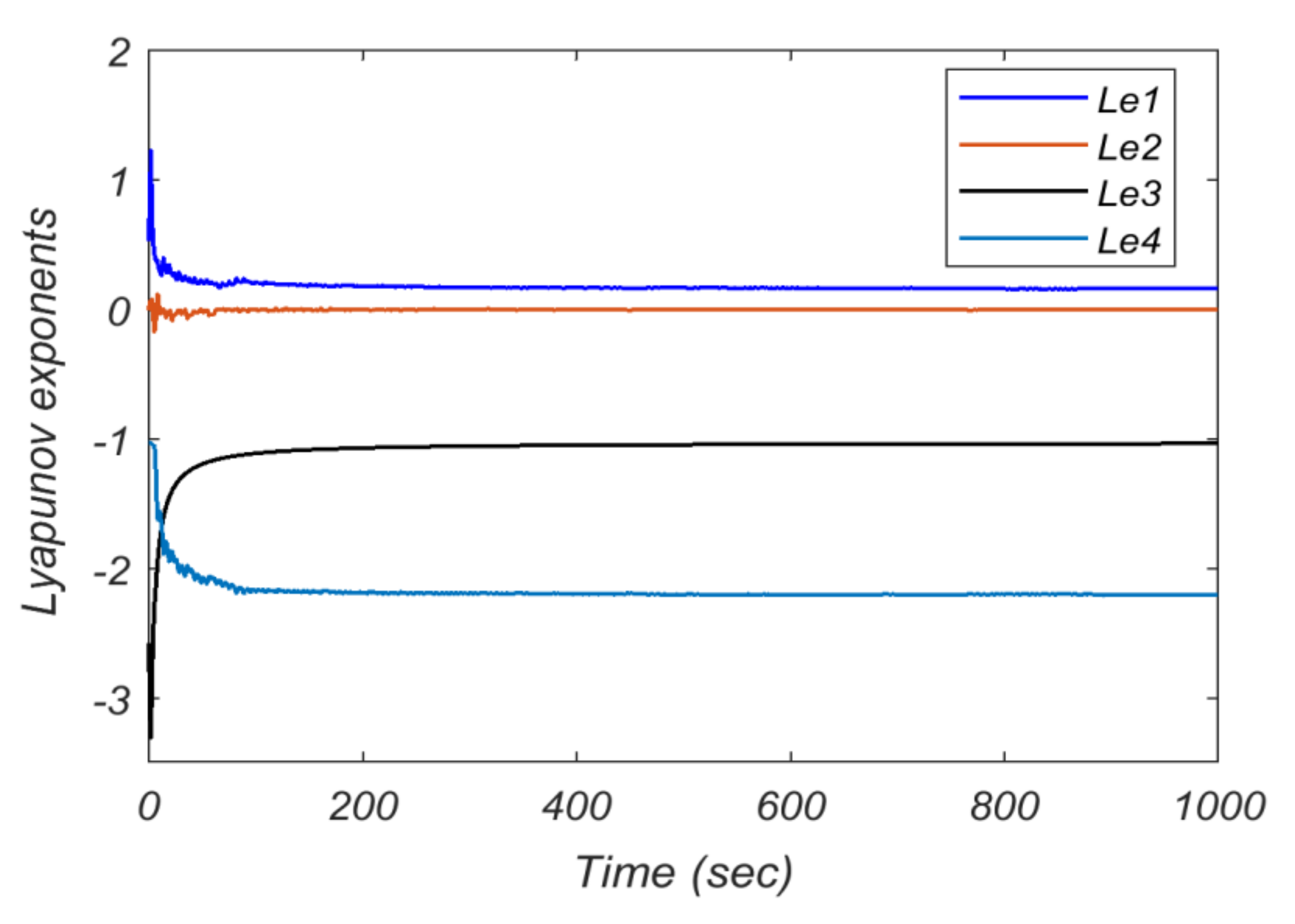
4.3. Lyapunov Exponents
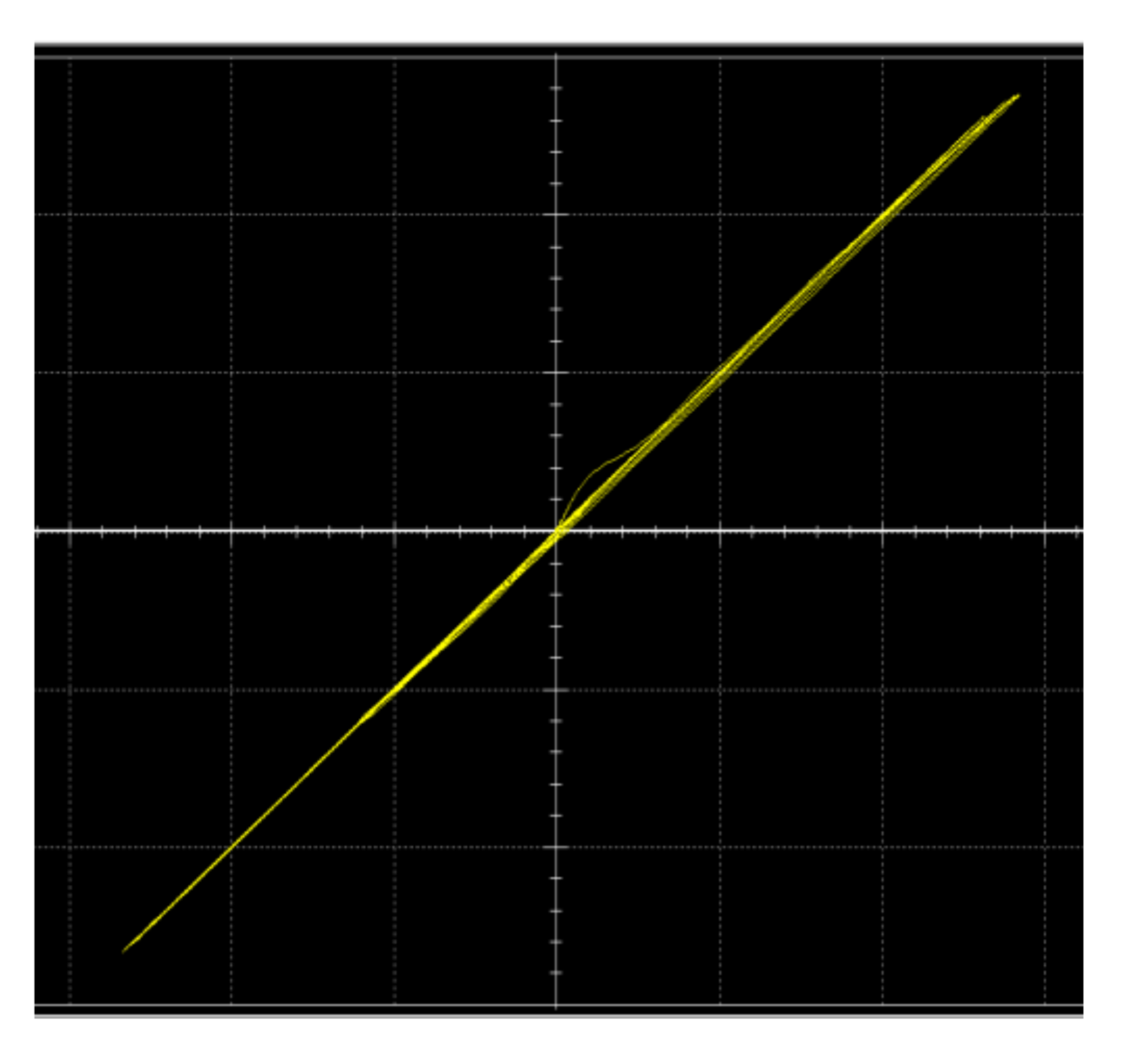
5. Adaptive Synchronization
5.1. Adaptive Control Law Design
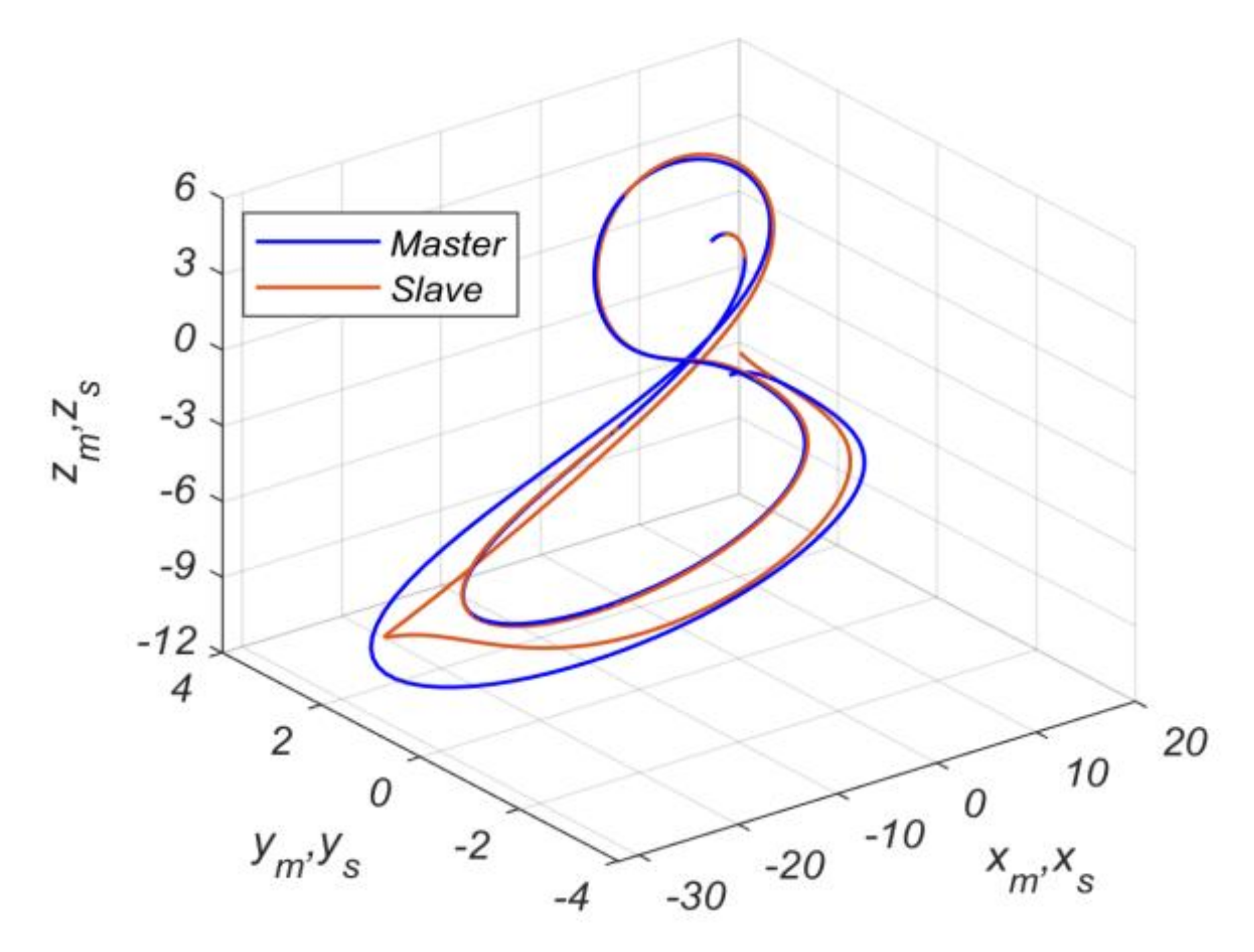
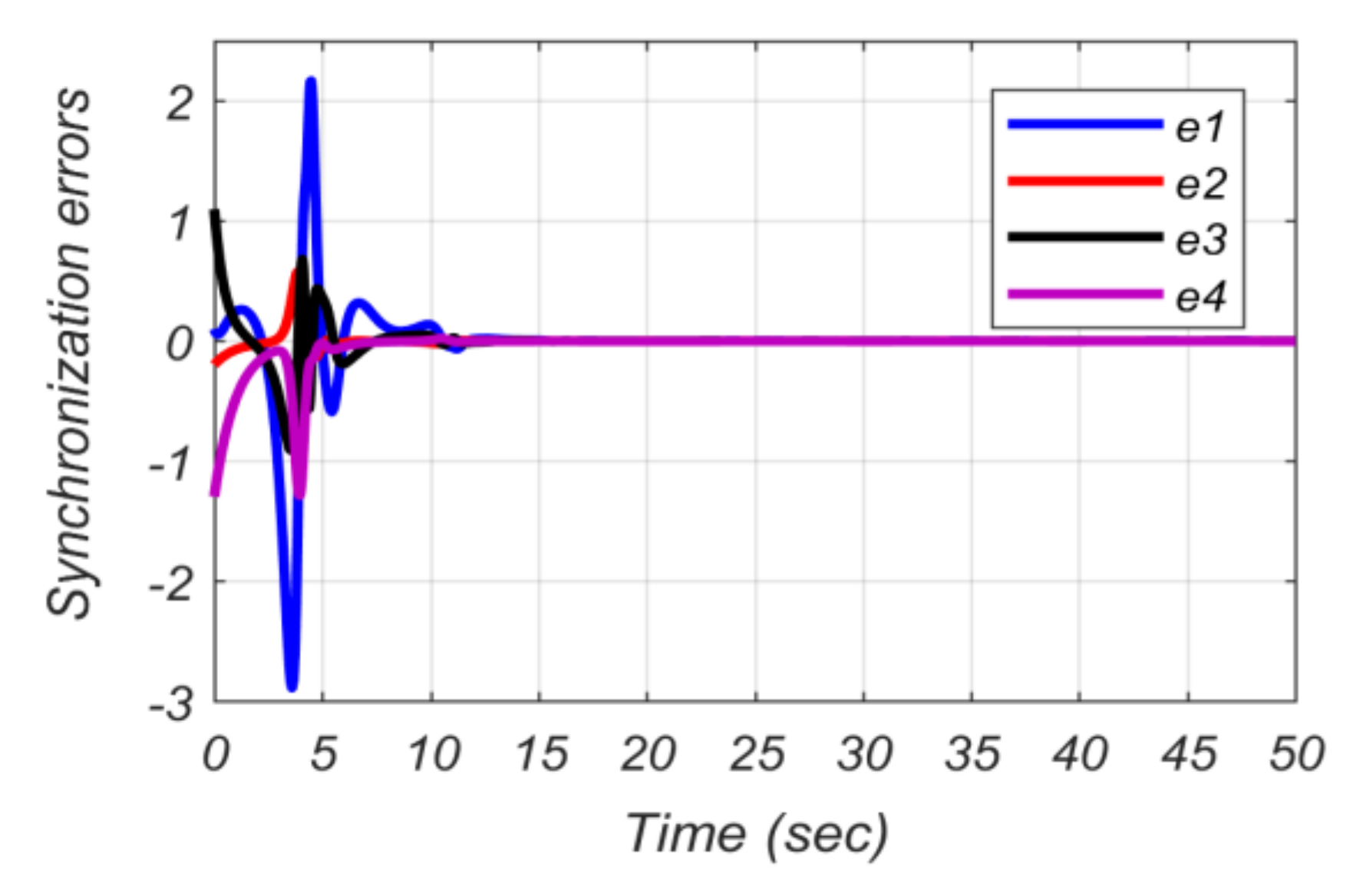
5.2. Numerical Simulation
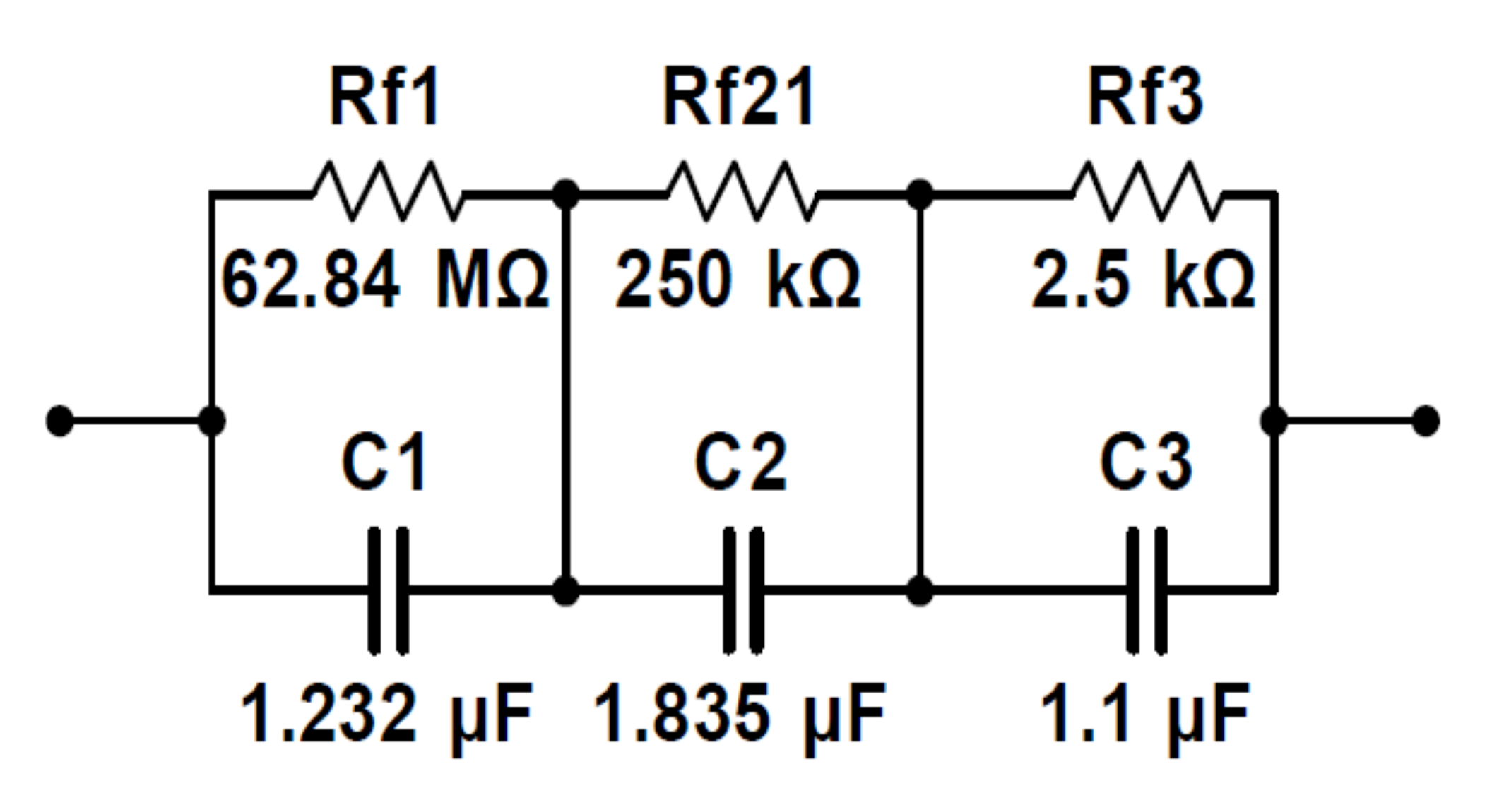
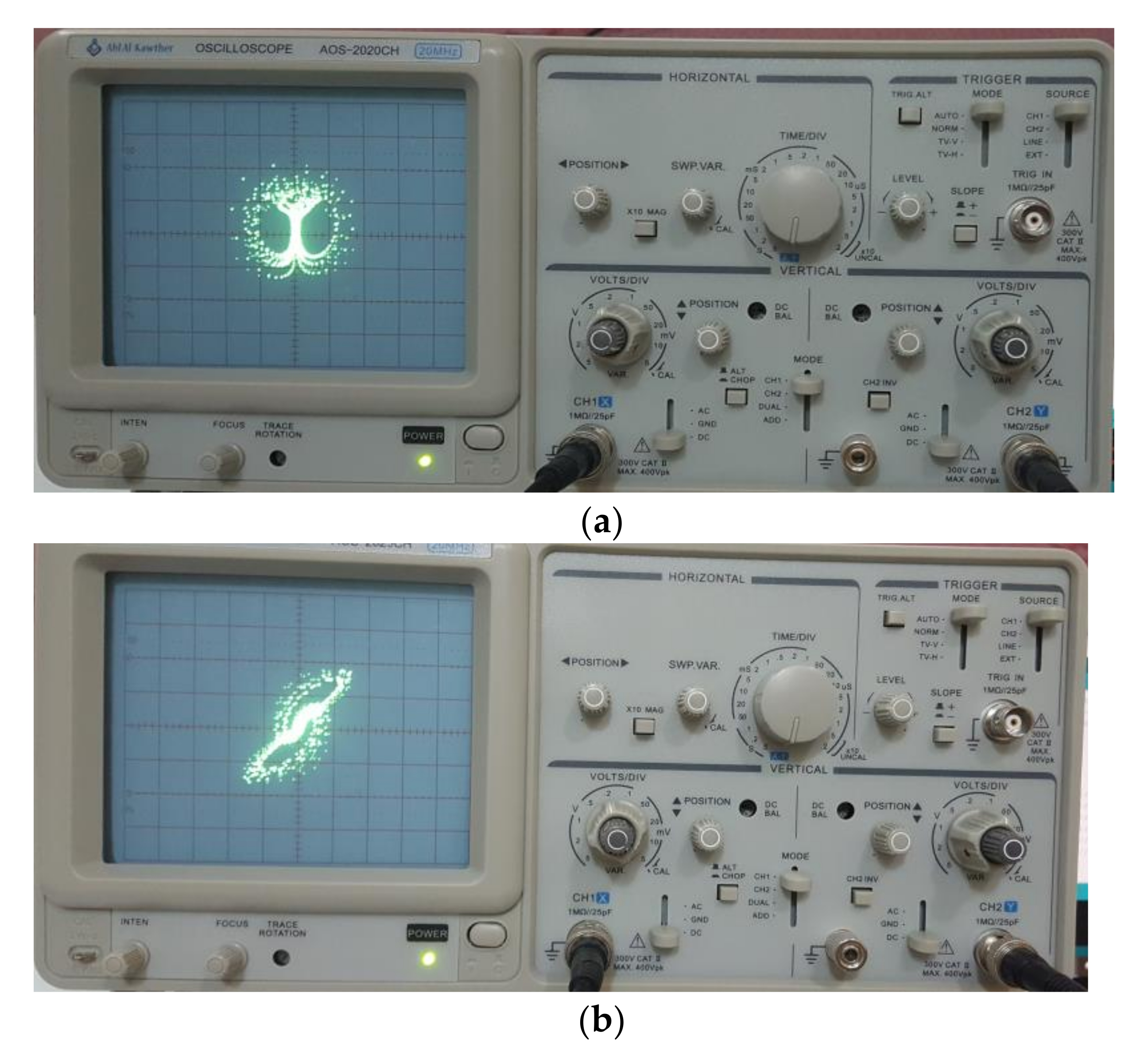
6. Electronic Circuit Realization
7. Microcontroller Implementation
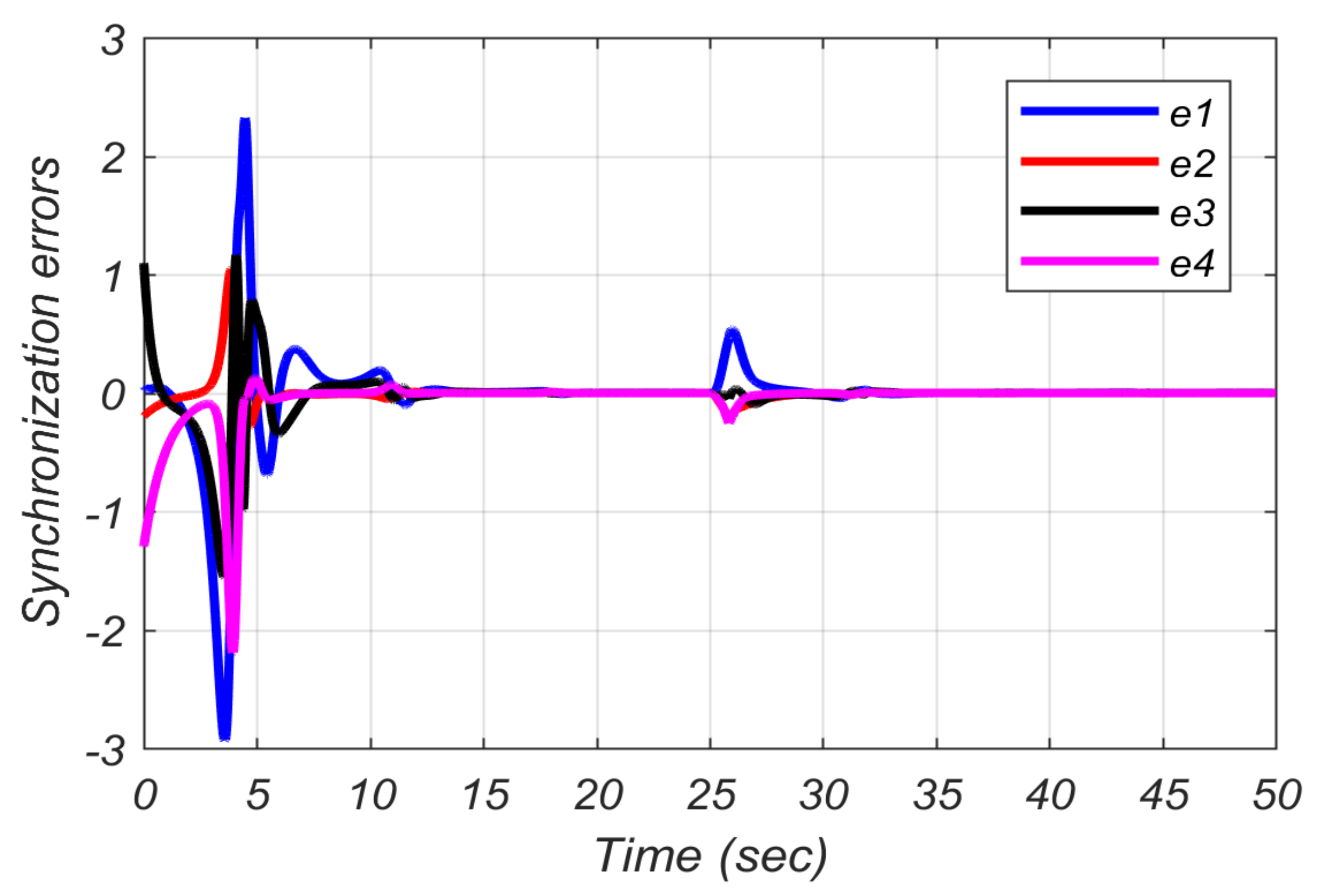
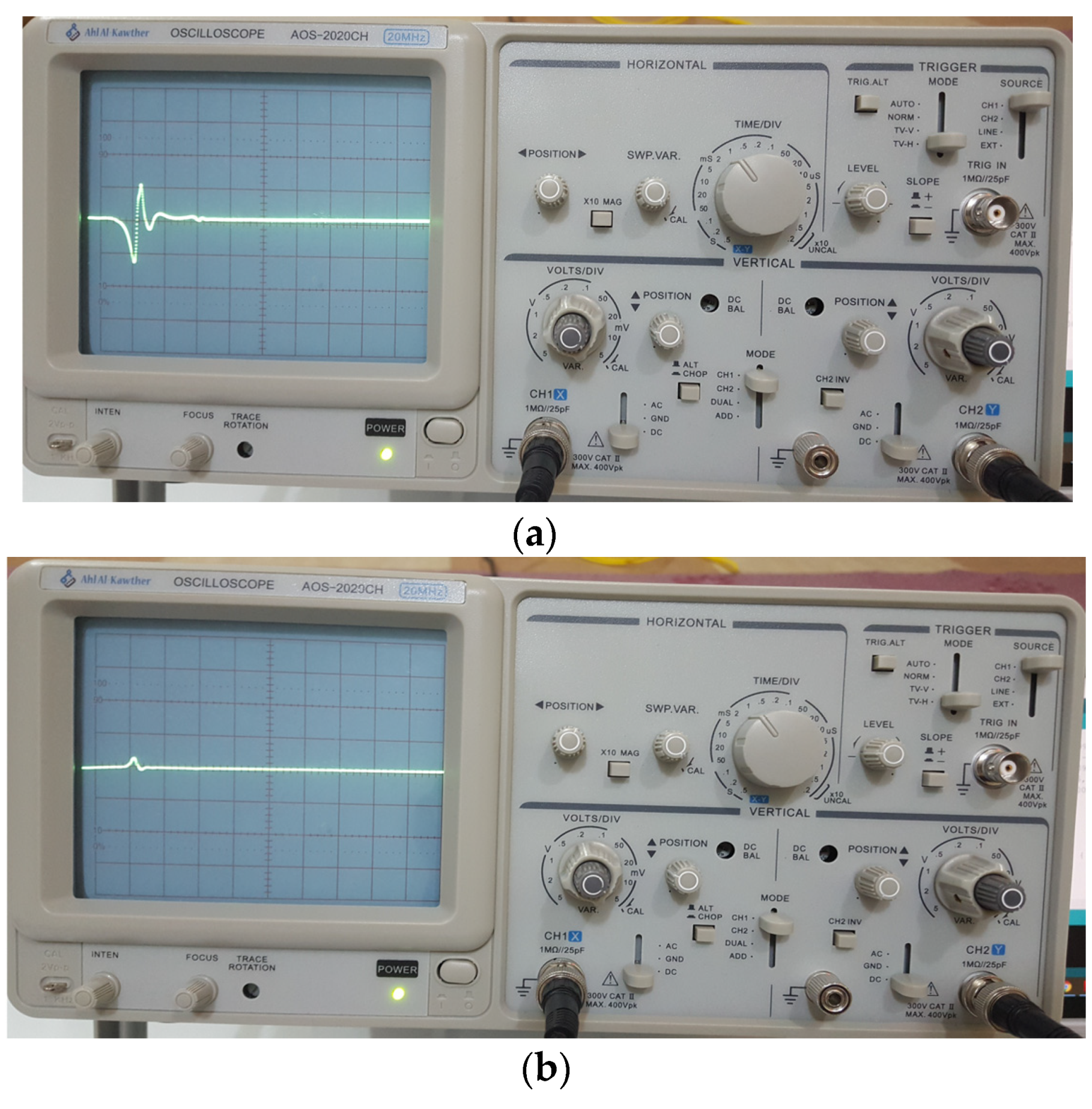
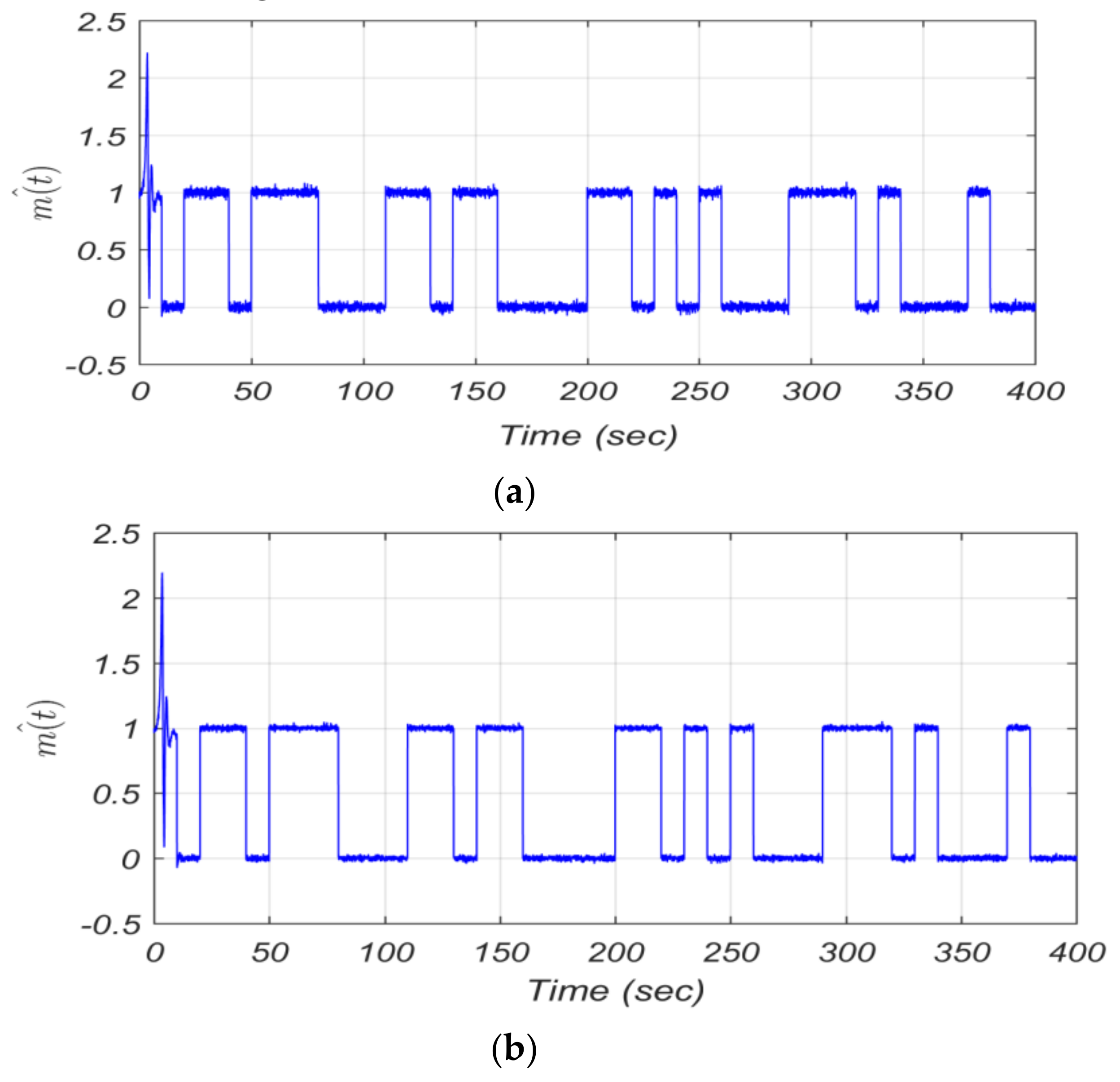
8. Application in Secure Communication
9. Security Analysis
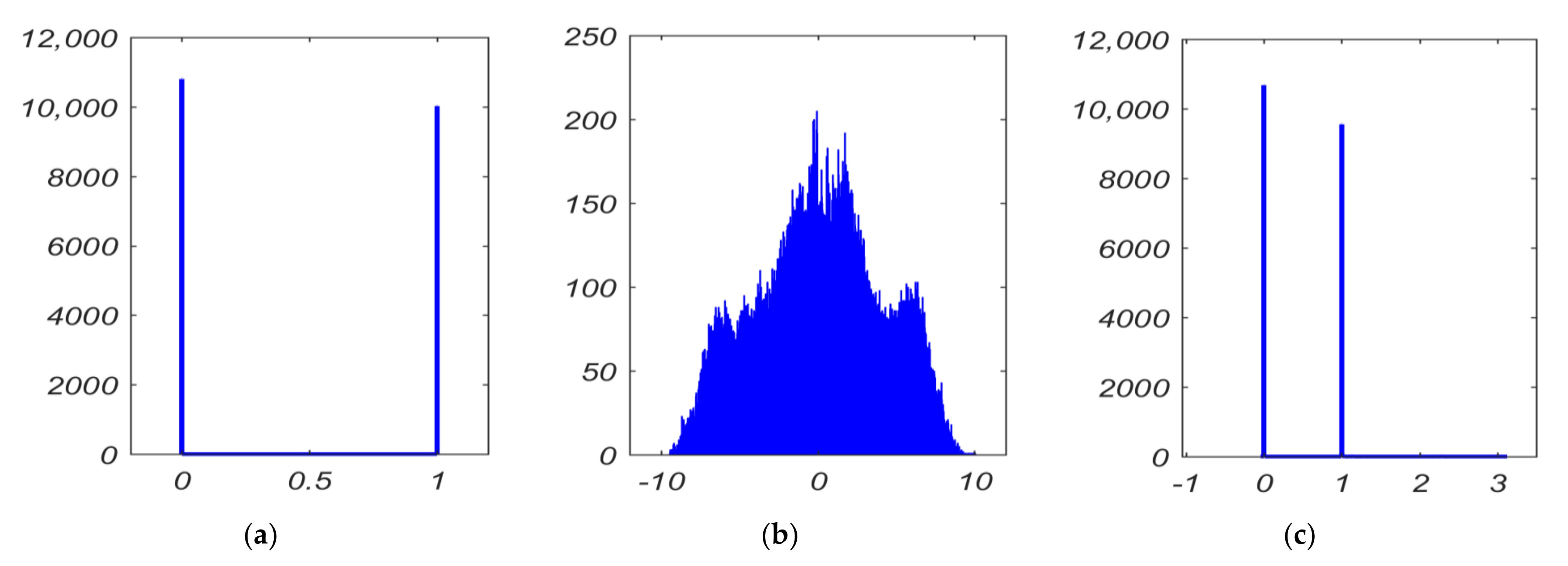
9.1. Histogram Analysis
9.2. Spectrogram Analysis
10. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, Y. Chaotic synchronization based on fractional order calculus financial system. Chaos Solitons Fractals 2020, 130, 109410. [Google Scholar] [CrossRef]
- Ewees, A.A.; Elaziz, M.A. Performance analysis of chaotic multi-verse harris hawks optimization: A case study on solving engineering problems. Eng. Appl. Artif. Intell. 2020, 88, 103370. [Google Scholar] [CrossRef]
- Zhang, Z.; Kundu, S.; Tripathi, J.P.; Bugalia, S. Stability and Hopf bifurcation analysis of an SVEIR epidemic model with vaccination and multiple time delays. Chaos Solitons Fractals 2020, 131, 109483. [Google Scholar] [CrossRef]
- Chen, H.-C.; Liau, B.-Y.; Hou, Y.-Y. Hardware implementation of Lorenz circuit systems for secure chaotic communication applications. Sensors 2013, 13, 2494–2505. [Google Scholar] [CrossRef] [PubMed]
- Al-Hussein, A.-B.A.; Tahir, F.R.; Boubaker, O. Chaos Elimination in Power System Using Synergetic Control Theory. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 340–345. [Google Scholar]
- Solano, J.; Balibrea, F.; Moreno, J.A. Applications of the Network Simulation Method to Differential Equations with Singularities and Chaotic Behaviour. Mathematics 2021, 9, 1442. [Google Scholar] [CrossRef]
- Walleczek, J. Self-Organized Biological Dynamics and Nonlinear Control: Toward Understanding Complexity, Chaos and Emergent Function in Living Systems; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Babajans, R.; Cirjulina, D.; Grizans, J.; Aboltins, A.; Pikulins, D.; Zeltins, M.; Litvinenko, A. Impact of the Chaotic Synchronization’s Stability on the Performance of QCPSK Communication System. Electronics 2021, 10, 640. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, K.; Wang, Y.; Zheng, H. Adaptive PID controller for cloud smart city system stability control based on chaotic neural network. Clust. Comput. 2019, 22, 13067–13075. [Google Scholar] [CrossRef]
- Eisencraft, M.; Attux, R.; Suyama, R. Chaotic Signals in Digital Communications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Tlelo-Cuautle, E.; Díaz-Muñoz, J.D.; González-Zapata, A.M.; Li, R.; León-Salas, W.D.; Fernández, F.V.; Guillén-Fernández, O.; Cruz-Vega, I. Chaotic image encryption using hopfield and hindmarsh–rose neurons implemented on FPGA. Sensors 2020, 20, 1326. [Google Scholar] [CrossRef] [Green Version]
- Curiac, D.-I.; Banias, O.; Volosencu, C.; Curiac, C.-D. Novel bioinspired approach based on chaotic dynamics for robot patrolling missions with adversaries. Entropy 2018, 20, 378. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Singh, S.N. Adaptive control of chaos in Lorenz system. Dyn. Control. 1997, 7, 143–154. [Google Scholar] [CrossRef]
- Javan, A.A.K.; Shoeibi, A.; Zare, A.; Izadi, N.H.; Jafari, M.; Alizadehsani, R.; Moridian, P.; Mosavi, A.; Acharya, U.R.; Nahavandi, S. Design of Adaptive-Robust Controller for Multi-State Synchronization of Chaotic Systems with Unknown and Time-Varying Delays and Its Application in Secure Communication. Sensors 2021, 21, 254. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Shi, B.; Zeng, X.; Ji, W.; Pan, T. Sliding mode control of the fractional-order unified chaotic system. Abstr. Appl. Anal. 2013, 2013, 397504. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Bhalekar, S. Chaos in fractional ordered Liu system. Comput. Math. Appl. 2010, 59, 1117–1127. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Chen, G.; Li, C.; Kurths, J. Chaos synchronization in fractional differential systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120155. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 34101. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yu, W.; Wang, J.; Wang, J.; Chen, Y.; He, X.; Jiang, D. Dynamic analysis of seven-dimensional fractional-order chaotic system and its application in encrypted communication. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 5399–5417. [Google Scholar] [CrossRef]
- Agarwal, P.; Chand, M.; Baleanu, D.; O’Regan, D.; Jain, S. On the solutions of certain fractional kinetic Equations involving k-Mittag-Leffler function. Adv. Differ. Equ. 2018, 2018, 249. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Pham, V.-T.; Kingni, S.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A simple three-dimensional fractional-order chaotic system without equilibrium: Dynamics, circuitry implementation, chaos control and synchronization. AEU-Int. J. Electron. Commun. 2017, 78, 220–227. [Google Scholar] [CrossRef]
- Seifert, R.; Hofmann, W. Highly Dynamic Thrust Bearing Control Based on a Fractional-Order Flux Estimator. IEEE Trans. Ind. Appl. 2021, 57, 1–11. [Google Scholar] [CrossRef]
- Boubaker, O.; Jafari, S. Recent Advances in Chaotic Systems and Synchronization: From Theory to Real World Applications; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Ray, S.S.; Atangana, A.; Noutchie, S.C.; Kurulay, M.; Bildik, N.; Kilicman, A. Fractional Calculus and Its Applications in Applied Mathematics and Other Sciences; Hindawi: London, UK, 2014. [Google Scholar]
- Tarasov, V.E. Mathematical Economics: Application of Fractional Calcu-lus. Mathematics 2020, 8, 660. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New No Equilibrium Fractional Order Chaotic System, Dynamical Investigation, Synchronization, and Its Digital Implementation. Inventions 2021, 6, 49. [Google Scholar] [CrossRef]
- Mobini, M.; Kaddoum, G. Deep chaos synchronization. IEEE Open J. Commun. Soc. 2020, 1, 1571–1582. [Google Scholar] [CrossRef]
- Karthikeyan, A.; Rajagopal, K. FPGA implementation of fractional-order discrete memristor chaotic system and its commensurate and incommensurate synchronisations. Pramana 2018, 90, 14. [Google Scholar] [CrossRef]
- Hu, J.; Liu, B.; Yu, M. A Novel Method of Realizing Stochastic Chaotic Secure Communication by Synchrosqueezed Wavelet Transform: The Finite-time Case. IEEE Access 2021, 9, 1. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H.; Mei, X.; Sun, Y. Generalized synchronization of fractional-order hyperchaotic systems and its DSP implementation. Nonlinear Dyn. 2018, 92, 85–96. [Google Scholar] [CrossRef]
- Rahman, Z.-A.S.A.; Al-Kashoash, H.A.A.; Ramadhan, S.M.; Al-Yasir, Y.I.A. Adaptive Control Synchronization of a Novel Memristive Chaotic System for Secure Communication Applications. Inventions 2019, 4, 30. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-M.; Pham, D.-H.; Huynh, T.-T. Synchronization of Chaotic System Using a Brain-Imitated Neural Network Controller and Its Applications for Secure Communications. IEEE Access 2021, 9, 75923–75944. [Google Scholar] [CrossRef]
- Velamore, A.A.; Hegde, A.; Khan, A.A.; Deb, S. Dual cascaded Fractional-order Chaotic Synchronization for Secure Communication with Analog Circuit Realisation. In Proceedings of the 2021 IEEE Second International Conference on Control, Measurement and Instrumentation (CMI), Kolkata, India, 8–10 January 2021; pp. 30–35. [Google Scholar]
- Jasim, B.H.; Hassan, K.H.; Omran, K.M. A new 4-D hyperchaotic hidden attractor system: Its dynamics, coexisting attractors, synchronization and microcontroller implementation. Int J. Electr. Comput. Eng. 2021, 11, 2068–2078. [Google Scholar]
- Jasim, B.H.; Mjily, A.H.; AL-Aaragee, A.M.J. A novel 4 dimensional hyperchaotic system with its control, synchronization and implementation. Int. J. Electr. Comput. Eng. 2021, 11, 2974–2985. [Google Scholar]
- Fujisaka, H.; Yamada, T. Stability theory of synchronized motion in coupled-oscillator systems. Prog. Theor. Phys. 1983, 69, 32–47. [Google Scholar] [CrossRef]
- Da-Wei, D.; Fang-Fang, L.; Hui, C.; Nian, W.; Dong, L. Sliding Mode Control of Fractional-Order Delayed Memristive Chaotic System with Uncertainty and Disturbance. Commun. Theor. Phys. 2017, 68, 741. [Google Scholar]
- Hou, J.; Xi, R.; Liu, P.; Liu, T. The switching fractional order chaotic system and its application to image encryption. IEEE/CAA J. Autom. Sin. 2016, 4, 381–388. [Google Scholar] [CrossRef]
- Dutta, M.; Roy, B.K. A new fractional-order system displaying coexisting multiwing attractors; its synchronisation and circuit simulation. Chaos Solitons Fractals 2020, 130, 109414. [Google Scholar] [CrossRef]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos, Solitons Fractals X 2020, 5, 100042. [Google Scholar] [CrossRef]
- Ahmad, M.; Shamsi, U.; Khan, I.R. An enhanced image encryption algorithm using fractional chaotic systems. Procedia Comput. Sci. 2015, 57, 852–859. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Guerra, R.; Gómez-Cortés, G.C.; Pérez-Pinacho, C.A. Synchronization of integral and fractional order chaotic systems. In A Differential Algebraic and Differential Geometric Approach with Selected Applications in Real-Time; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Martínez-Guerra, R.; Pérez-Pinacho, C.A. Advances in Synchronization of Coupled Fractional Order Systems: Fundamentals and Methods; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Kharel, R. Design and Implementation of Secure Chaotic Communication Systems. Ph.D. Thesis, Northumbria University, Newcastle upon Tyne, UK, 2011. [Google Scholar]
- Gonzalez, E.A.; Petráš, I. Advances in fractional calculus: Control and signal processing applications. In Proceedings of the 2015 16th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 27–30 May 2015; pp. 147–152. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Sene, N. Analysis of a fractional-order chaotic system in the context of the Caputo fractional derivative via bifurcation and Lyapunov exponents. J. King Saud Univ. 2021, 33, 101275. [Google Scholar] [CrossRef]
- Li, H.-L.; Zhang, L.; Hu, C.; Jiang, Y.-L.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
- Godinho, C.F.D.L.; Panza, N.; Weberszpil, J.; Helayël-Neto, J.A. Variational procedure for higher-derivative mechanical models in a fractional integral. EPL (Europhysics Lett.) 2020, 129, 60001. [Google Scholar] [CrossRef]
- Li, H.-L.; Jiang, H.; Cao, J. Global synchronization of fractional-order quaternion-valued neural networks with leakage and discrete delays. Neurocomputing 2020, 385, 211–219. [Google Scholar] [CrossRef]
- Jalalinejad, H.; Tavakoli, A.; Zarmehi, F. A simple and flexible modification of Grünwald–Letnikov fractional derivative in image processing. Math. Sci. 2018, 12, 205–210. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Liu, J.; Yang, F.; Yan, H.; Zhao, X. Coexistence of multiple attractors for an incommensurate fractional-order chaotic system. Eur. Phys. J. Plus 2020, 135, 95. [Google Scholar] [CrossRef]
- Liu, T.; Yan, H.; Banerjee, S.; Mou, J. A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation. Chaos Solitons Fractals 2021, 145, 110791. [Google Scholar] [CrossRef]
- Gong, L.; Wu, R.; Zhou, N. A New 4D Chaotic system with coexisting hidden chaotic attractors. Int. J. Bifurc. Chaos 2020, 30, 2050142. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, C.; Xu, D.; Chen, C. Dynamic analysis and synchronisation control of a novel chaotic system with coexisting attractors. Pramana 2020, 94, 19. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K.; Fotsin, H. Coexisting attractors, circuit implementation and synchronization control of a new chaotic system evolved from the simplest memristor chaotic circuit. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105341. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical Solution of Fractional Differential Equations: A Survey and a Software Tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, G.; Iu, H.H.-C.; Shen, Y.; Zhou, W. A nonvolatile fractional order memristor model and its complex dynamics. Entropy 2019, 21, 955. [Google Scholar] [CrossRef] [Green Version]
- Dellnitz, M.; Field, M.; Golubitsky, M.; Hohmann, A.; Ma, J. Cycling chaos. IEEE Trans. Circuits Syst. I Fundam Theory Appl. 1995, 42, 821–823. [Google Scholar] [CrossRef]
- Eshaghi, S.; Ghaziani, R.K.; Ansari, A. Hopf bifurcation, chaos control and synchronization of a chaotic fractional-order system with chaos entanglement function. Math. Comput. Simul. 2020, 172, 321–340. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Zhou, X. Bifurcation analysis of a first time-delay chaotic system. Adv. Differ. Equ. 2019, 2019, 78. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Collantoni, E.; Madan, C.R.; Meneguzzo, P.; Chiappini, I.; Tenconi, E.; Manara, R.; Favaro, A. Cortical complexity in anorexia nervosa: A fractal dimension analysis. J. Clin. Med. 2020, 9, 833. [Google Scholar] [CrossRef] [Green Version]
- Mayor, D.; Panday, D.; Kandel, H.K.; Steffert, T.; Banks, D. CEPS: An Open Access MATLAB Graphical User Interface (GUI) for the Analysis of Complexity and Entropy in Physiological Signals. Entropy 2021, 23, 321. [Google Scholar] [CrossRef]
- Shamsi, E.; Ahmadi-Pajouh, M.A.; Ala, T.S. Higuchi fractal dimension: An efficient approach to detection of brain entrainment to theta binaural beats. Biomed. Signal. Process Control 2021, 68, 102580. [Google Scholar] [CrossRef]
- Kesić, S.; Spasić, S.Z. Application of Higuchi’s fractal dimension from basic to clinical neurophysiology: A review. Comput. Methods Programs Biomed. 2016, 133, 55–70. [Google Scholar] [CrossRef]
- Gatfaoui, H.; De Peretti, P. Testing for non-chaoticity under noisy dynamics using the largest Lyapunov exponent. Soft Comput. 2019, 24, 8617–8626. [Google Scholar] [CrossRef]
- Jasim, B.H.; Rashid, M.T.; Omran, K.M. Synchronization and tracking control of a novel 3 dimensional chaotic system. Iraqi J. Electr. Electron. Eng. Basrah University. 3RD. 2020, 1, 1–6. [Google Scholar]
- Rahman, Z.-A.S.A.; Jassim, B.H.; Al-Yasir, Y.I.A. New Fractional Order Chaotic System: Analysis, Synchronization, and it’s Application. Iraqi J. Electr. Electron. Eng. 2021, 17, 1–9. [Google Scholar] [CrossRef]
- Kaddoum, G. Wireless chaos-based communication systems: A comprehensive survey. IEEE Access 2016, 4, 2621–2648. [Google Scholar] [CrossRef]
- Tahir, F.R.; Jafari, S.; Pham, V.-T.; Volos, C.; Wang, X. A novel no-equilibrium chaotic system with multiwing butterfly attractors. Int. J. Bifurc. Chaos 2015, 25, 1550056. [Google Scholar] [CrossRef]
- Tahir, S.A. The synchronization of identical Memristors systems via Lyapunov direct method. Appl. Comput. Math. 2013, 6, 130–136. [Google Scholar] [CrossRef]
- Guo, R. A simple adaptive controller for chaos and hyperchaos synchronization. Phys. Lett. A 2008, 372, 5593–5597. [Google Scholar] [CrossRef]
- Peng, R.; Jiang, C.; Guo, R. Stabilization of a class of fractional order systems with both uncertainty and disturbance. IEEE Access 2021, 9, 42697–42706. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Z. A Fuzzy Lyapunov Function Method to Stability Analysis of Fractional Order T-S Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2021, 29, 1–9. [Google Scholar]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef] [Green Version]
- Pu, Y.-F. Measurement units and physical dimensions of fractance-part I: Position of purely ideal fractor in Chua’s axiomatic circuit element system and fractional-order reactance of fractor in its natural implementation. IEEE Access 2016, 4, 3379–3397. [Google Scholar] [CrossRef]
- Hammouch, Z.; Mekkaoui, T. Circuit design and simulation for the fractional-order chaotic behavior in a new dynamical system. Complex Intell. Syst. 2018, 4, 251–260. [Google Scholar] [CrossRef]
- Sánchez-López, C. An experimental synthesis methodology of fractional-order chaotic attractors. Nonlinear Dyn. 2020, 100, 3907–3923. [Google Scholar] [CrossRef]
- Due, A. Core ARM. Arduino Due. Retrieved 2017, 9, 2019. [Google Scholar]
- Çiçek, S.; Ferikoğlu, A.; Pehlivan, İ. A new 3D chaotic system: Dynamical analysis, electronic circuit design, active control synchronization and chaotic masking communication application. Optik 2016, 127, 4024–4030. [Google Scholar] [CrossRef]
- Hashemi, S.; Pourmina, M.A.; Mobayen, S.; Alagheband, M.R. Design of a secure communication system between base transmitter station and mobile equipment based on finite-time chaos synchronisation. Int. J. Syst. Sci. 2020, 51, 1969–1986. [Google Scholar] [CrossRef]
- Alanazi, A.S.; Munir, N.; Khan, M.; Asif, M.; Hussain, I. Cryptanalysis of Novel Image Encryption Scheme Based on Multiple Chaotic Substitution Boxes. IEEE Access 2021, 9, 93795–93802. [Google Scholar] [CrossRef]
- Yasser, I.; Mohamed, M.A.; Samra, A.S.; Khalifa, F. A chaotic-based encryption/decryption framework for secure multimedia communications. Entropy 2020, 22, 1253. [Google Scholar] [CrossRef] [PubMed]
- Kacha, A.; Grenez, F.; Orozco-Arroyave, J.R.; Schoentgen, J. Principal component analysis of the spectrogram of the speech signal: Interpretation and application to dysarthric speech. Comput. Speech Lang. 2020, 59, 114–122. [Google Scholar] [CrossRef]
- Bruni, V.; Tartaglione, M.; Vitulano, D. A pde-Based Analysis of the Spectrogram Image for Instantaneous Frequency Estimation. Mathematics 2021, 9, 247. [Google Scholar] [CrossRef]
- Karimov, T.; Rybin, V.; Kolev, G.; Rodionova, E.; Butusov, D. Chaotic Communication System with Symmetry-Based Modulation. Appl. Sci. 2021, 11, 3698. [Google Scholar] [CrossRef]
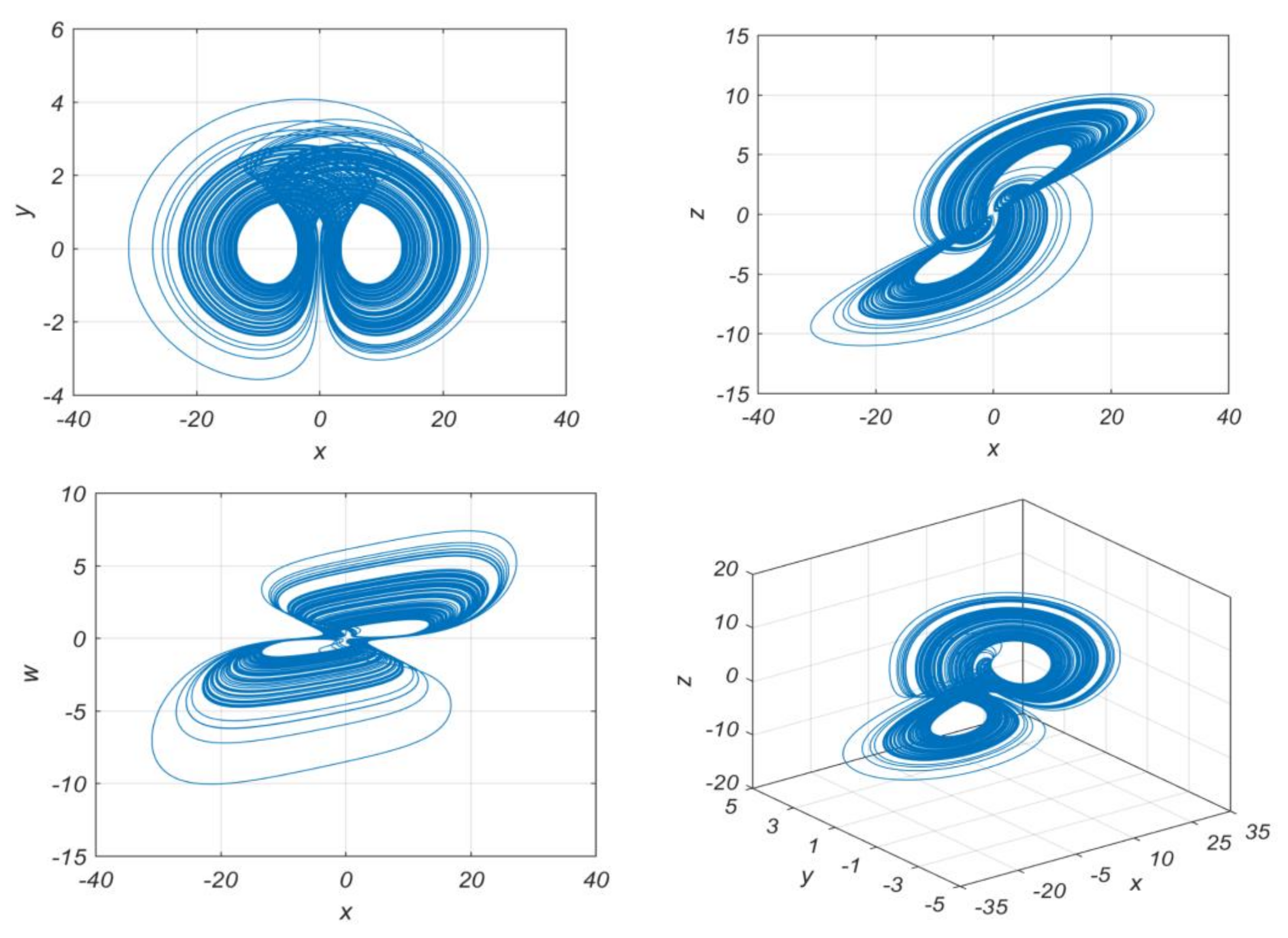






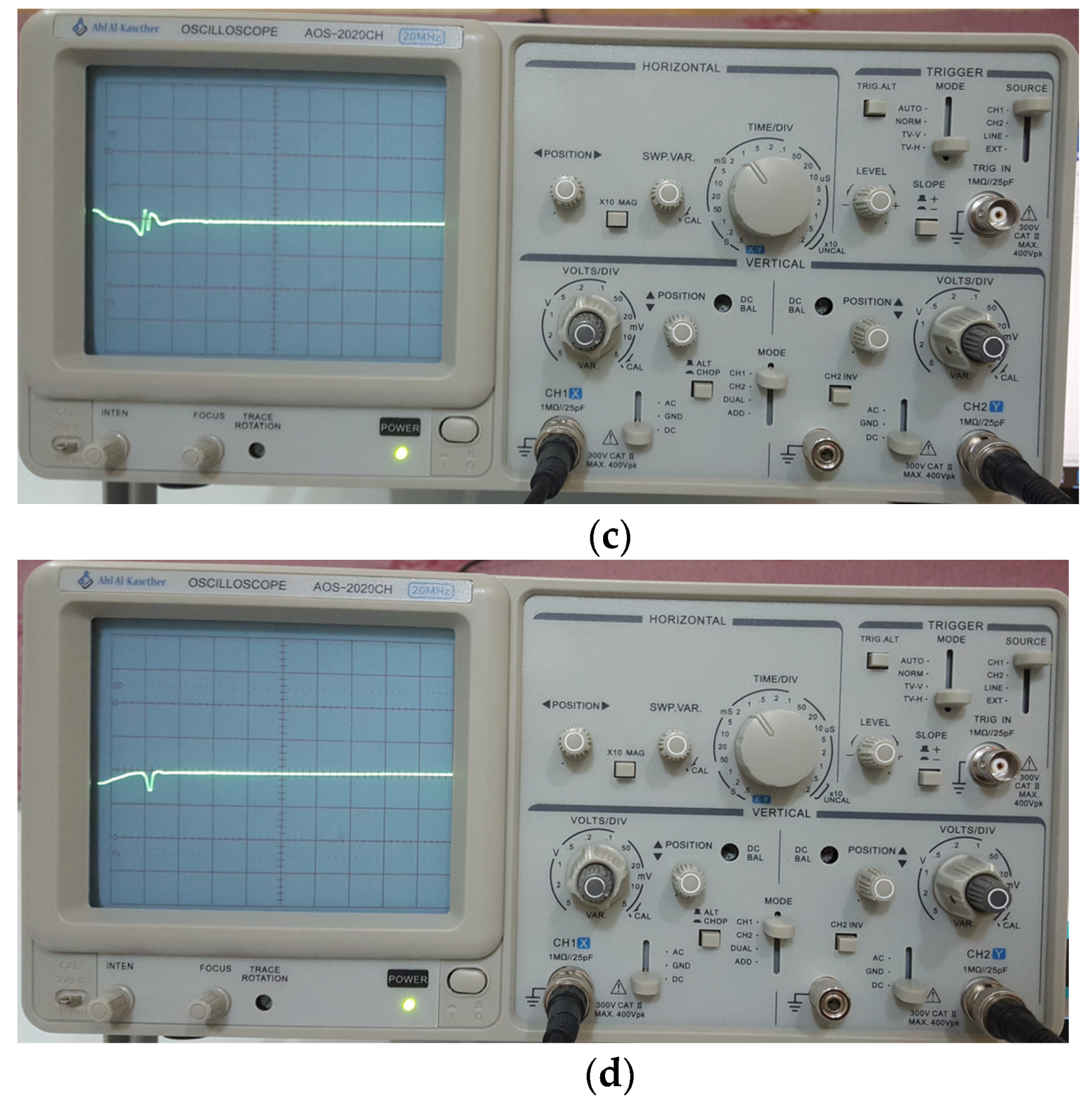




| No. | Equilibrium Point | Eigenvalues | Equilibria Classification |
|---|---|---|---|
| 1 | (6.9282, 0, 3.4641, 0.3326) | (−1, 0.2052 + 1.5643i, 0.2052 − 1.5643i, −2.4104) | Saddle focus |
| 2 | (−6.9282, 0, −3.4641, −0.3326) | (−1, 0.2052 + 1.5643i, 0.2052 − 1.5643i, −2.4104) | Saddle focus |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, Z.-A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.-F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications. Mathematics 2021, 9, 2593. https://doi.org/10.3390/math9202593
Rahman Z-ASA, Jasim BH, Al-Yasir YIA, Hu Y-F, Abd-Alhameed RA, Alhasnawi BN. A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications. Mathematics. 2021; 9(20):2593. https://doi.org/10.3390/math9202593
Chicago/Turabian StyleRahman, Zain-Aldeen S. A., Basil H. Jasim, Yasir I. A. Al-Yasir, Yim-Fun Hu, Raed A. Abd-Alhameed, and Bilal Naji Alhasnawi. 2021. "A New Fractional-Order Chaotic System with Its Analysis, Synchronization, and Circuit Realization for Secure Communication Applications" Mathematics 9, no. 20: 2593. https://doi.org/10.3390/math9202593










