The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (
Abstract
:1. Introduction
2. Modified Riemann–Liouville Derivative and Properties
3. Wave Equation for S-FS-KS Equation
4. The Exact Solutions of the S-FS-KS Equation
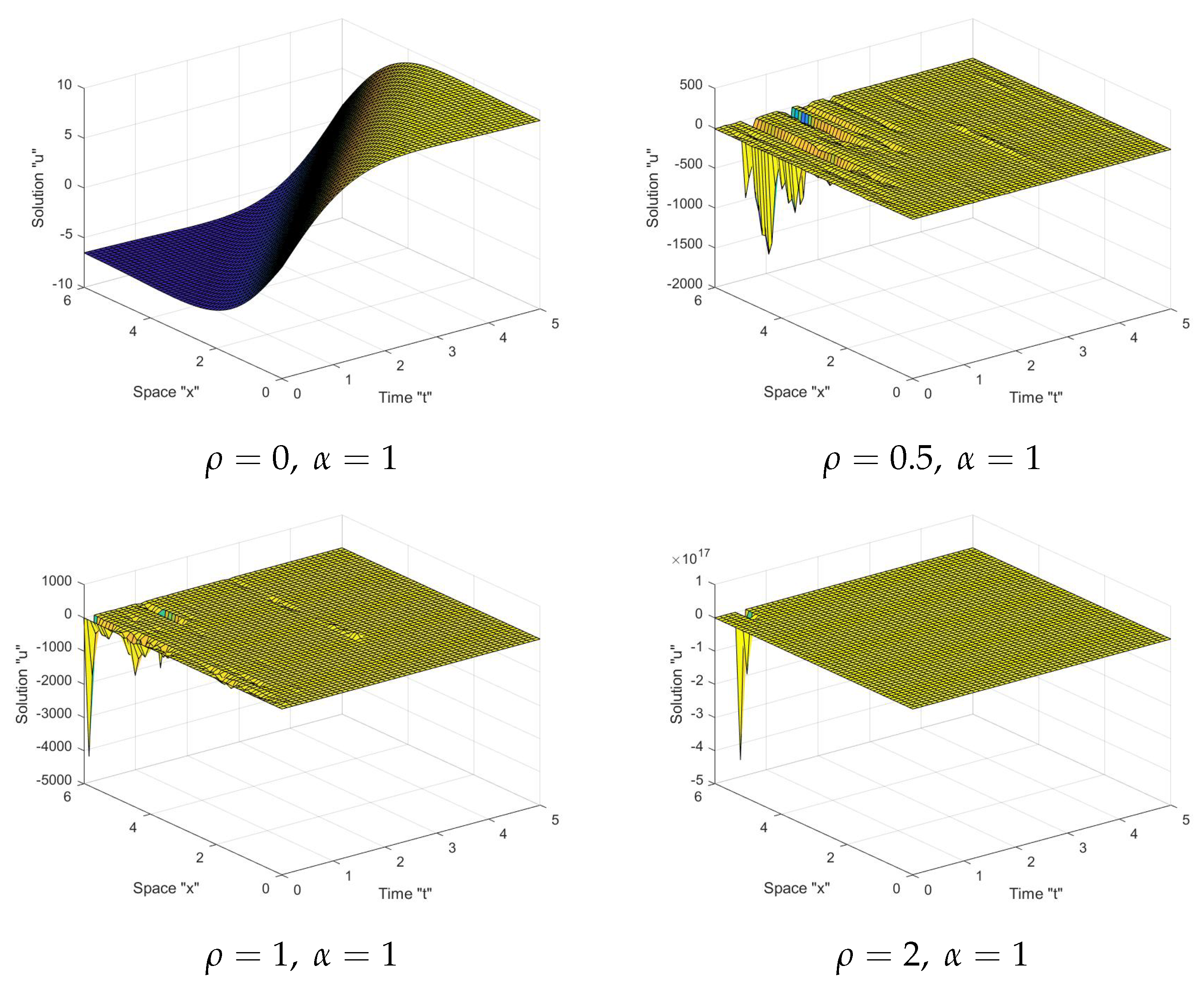
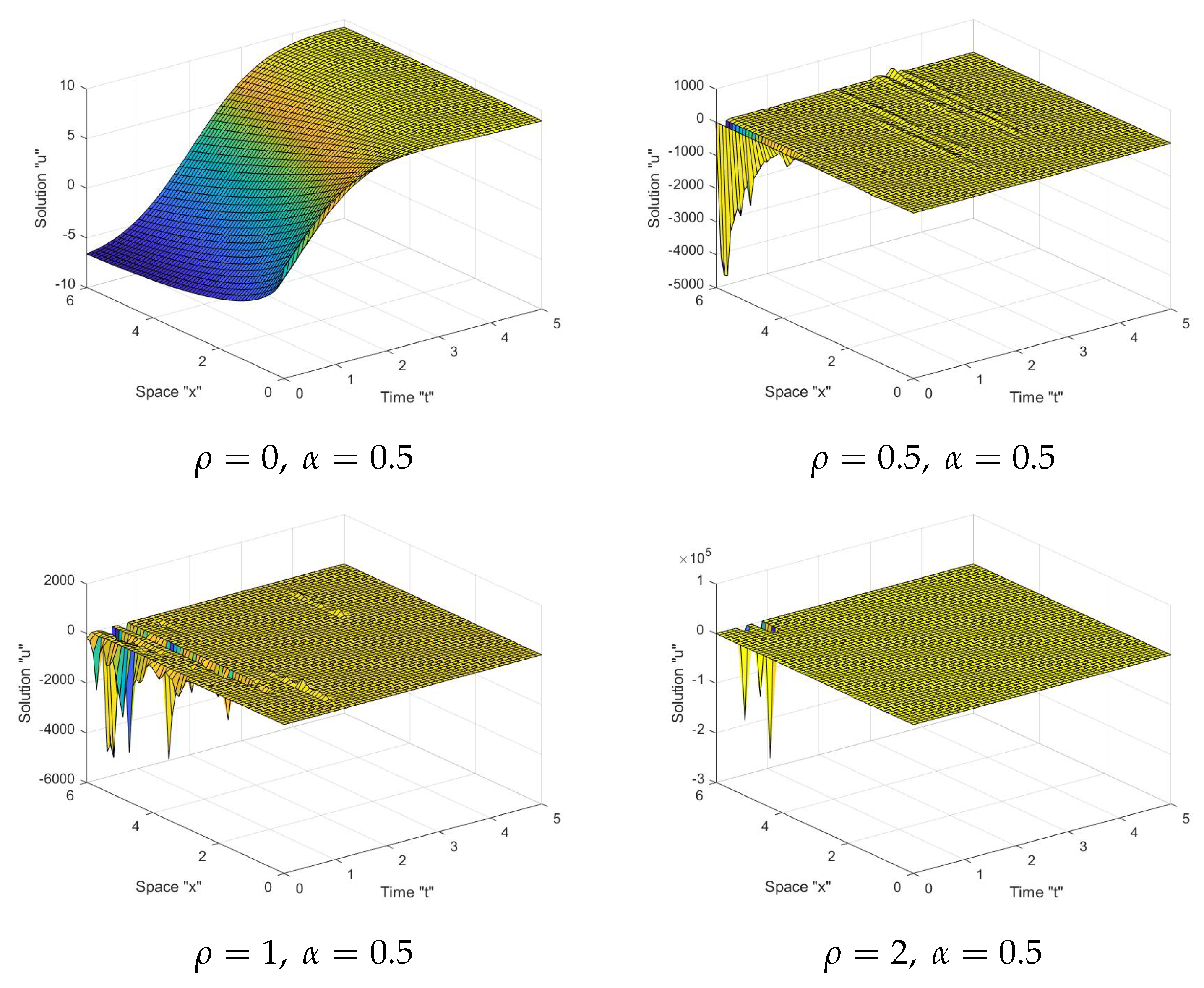
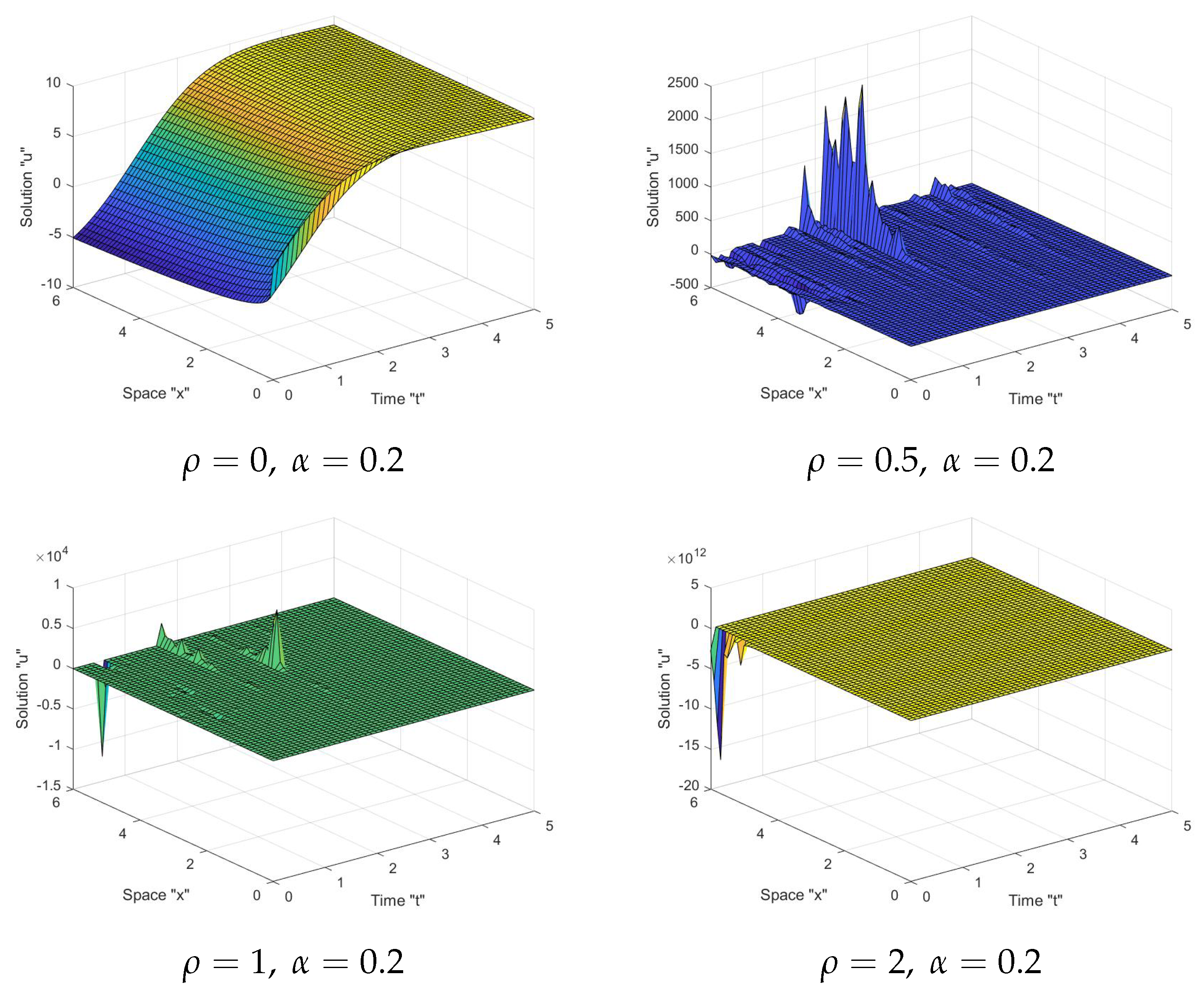
5. The Influence of Noise on the S-FS-KS Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gorenflo, R.; Mainardi, F. Random walk models for space—Fractional diffusion processes. Fract. Calc. Appl. Anal. 1998, 1, 167–191. [Google Scholar]
- Raberto, M.; Scalas, E.; Mainardi, F. Waiting-times and returns in high-frequency financial data: An empirical study. Phys. A Stat. Mech. Appl. 2002, 314, 749–755. [Google Scholar] [CrossRef] [Green Version]
- Wyss, W. The fractional Black—Scholes equation. Fract. Calc. Appl. Anal. 2000, 3, 51–61. [Google Scholar]
- Yuste, S.B.; Lindenberg, K. Subdiffusion-limited A+A reactions. Phys. Rev. Lett. 2001, 87, 118301. [Google Scholar] [CrossRef] [Green Version]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker—Planck equation. Phys. Rev. E 2000, 61, 132–138. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Saichev, A.I.; Zaslavsky, G.M. Fractional kinetic equations: Solutions and applications. Chaos 1997, 7, 753–764. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaslavsky, G.M. Chaos, fractional kinetics and anomalous transport. Phys. Rep. 2002, 6, 461–580. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ahmad, H. Thermodynamic modeling of viscoelastic thin rotating microbeam based on non-Fourier heat conduction. Appl. Math. Model. 2021, 91, 973–988. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abouelregal, A.E. Effect of harmonically varying heat on FG nanobeams in the context of a nonlocal two-temperature thermoelasticity theory. Eur. J. Comput. Mech. 2014, 23, 1–14. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. Res. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Liu, F.; Anh, V.; Turner, I. Numerical solution of the space fractional Fokker—Planck equation. J. Comput. Appl. Math. 2004, 166, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Yuste, S.B.; Acedo, L.; Lindenberg, K. Reaction front in an A+B→C reaction—Subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Taheri, Z.; Javadi, S.; Babolian, E. Numerical solution of stochastic fractional integro-differential equation by the spectral collocation method. J. Comput. Appl. Math. 2017, 321, 336–347. [Google Scholar] [CrossRef]
- Zou, G. Galerkin finite element method for time-fractional stochastic diffusion equations. Comput. Appl. Math. 2018, 37, 4877–4898. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Iqbal, N. Effect of the Same Degenerate Additive Noise on a Coupled System of Fractional-Space Diffusion Equations. Fractals. Accepted.
- Iqbal, N.; Wu, R.; Mohammed, W.W. Pattern formation induced by fractional cross-diffusion in a 3-species food chain model with harvesting. Math. Comput. Simul. 2021, 188, 102–119. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solutions for stochastic time-fractional reaction—Diffusion equations with multiplicative noise. Math. Methods Appl. Sci. 2021, 44, 2140–2157. [Google Scholar] [CrossRef]
- Kamrani, M. Numerical solution of stochastic fractional differential equations. Numer. Algorithms 2015, 68, 81–93. [Google Scholar] [CrossRef]
- Li, X.; Yang, X. Error estimates of finite element methods for stochastic fractional differential equations. J. Comput. Math. 2017, 35, 346–362. [Google Scholar]
- Liu, J.; Yan, L. Solving a nonlinear fractional stochastic partial differential equation with fractional noise. J. Theor. Probab. 2016, 29, 307–347. [Google Scholar] [CrossRef]
- Wazzan, L. A modified tanh-coth method for solving the general Burgers-Fisher and Kuramoto-Sivashinsky Equations. Commun. Nonlinear Sci. Numer. Simulat. 2009, 14, 2642–2652. [Google Scholar] [CrossRef]
- Wazwaz, A.M. New solitary wave solutions to the Kuramoto-Sivashinsky and the Kawahara equations. Appl. Math. Comput. 2006, 182, 1642–1650. [Google Scholar] [CrossRef]
- Abbasbandy, S. Solitary wave solutions to the Kuramoto—Sivashinsky equation by means of the homotopy analysis method. Nonlinear Dyn. 2008, 52, 35–40. [Google Scholar] [CrossRef]
- Kheiri, H.; Jabbari, A. Application of the (G′/G)-expansion method for two nonlinear evolution equations. Int. Nonlinear Dyn. Eng. Sci. 2010, 2, 57–67. [Google Scholar]
- Mohammed, W.W. Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. B 2018, 39, 145–162. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of the generalized kuramoto-sivashinsky equation. Phys. Lett. A 1990, 147, 287–291. [Google Scholar] [CrossRef]
- Kudryashov, N.A. On types of nonlinear nonintegrable equations with exact solutions. Phys. Lett. A 1991, 155, 269–275. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Soukharev, M.B. Popular ansatz methods and solitary wave solutions of the Kuramoto-Sivashinsky equation. Regul. Chaotic Dyn. 2009, 14, 407–409. [Google Scholar] [CrossRef]
- Peng, Y.Z. A polynomial expansion method and new general solitary wave solutions to KS equation. Comm. Theor. Phys. 2003, 39, 641–642. [Google Scholar]
- Kudryashov, N.A. Solitary and periodic solutions of the generalized kuramoto-sivashinsky equation. Regul. Chaotic Dyn. 2008, 13, 234–238. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact soliton solutions of the generalized evolution equation of wave dynamics. J. Appl. Math. Mech. 1988, 52, 361–365. [Google Scholar] [CrossRef]
- Khalique, C.M. Exact Solutions of the Generalized Kuramoto-Sivashinsky Equation. Casp. J. Math. Sci. 2012, 1, 109–116. [Google Scholar]
- Zhang, S. New Exact Solutions of the KdV–Burgers–Kuramoto Equation. Phys. Lett. A 2006, 358, 414–420. [Google Scholar] [CrossRef]
- Blomker, D.; Mohammed, W.W. Amplitude equation for spdes with quadratic nonlinearities. Electron. J. Probab. 2009, 14, 2527–2550. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, S.; Liu, S. New Exact Solutions to the KdV–Burgers–Kuramoto Equation. Chaos Solitons Fractals 2005, 23, 609–616. [Google Scholar] [CrossRef]
- Jumarie, G. Modified Riemann–Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51, 1367–1376. [Google Scholar] [CrossRef] [Green Version]
- He, J.H.; Elegan, S.K.; Li, Z.B. Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 2012, 376, 257–259. [Google Scholar] [CrossRef]
- Aksoy, E.; Kaplan, M.; Bekir, A. Exponential rational function method for space–time fractional differential equations. Waves Random Complex Media 2016, 26, 142–151. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W.; Alesemi, M.; Albosaily, S.; Iqbal, N.; El-Morshedy, M.
The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (
Mohammed WW, Alesemi M, Albosaily S, Iqbal N, El-Morshedy M.
The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (
Mohammed, Wael W., Meshari Alesemi, Sahar Albosaily, Naveed Iqbal, and M. El-Morshedy.
2021. "The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (
Mohammed, W. W., Alesemi, M., Albosaily, S., Iqbal, N., & El-Morshedy, M.
(2021). The Exact Solutions of Stochastic Fractional-Space Kuramoto-Sivashinsky Equation by Using (







