3. Diophantine Equation xyz = F(x + y + z): Parametric Solutions
We shall establish three families of parametric solutions for
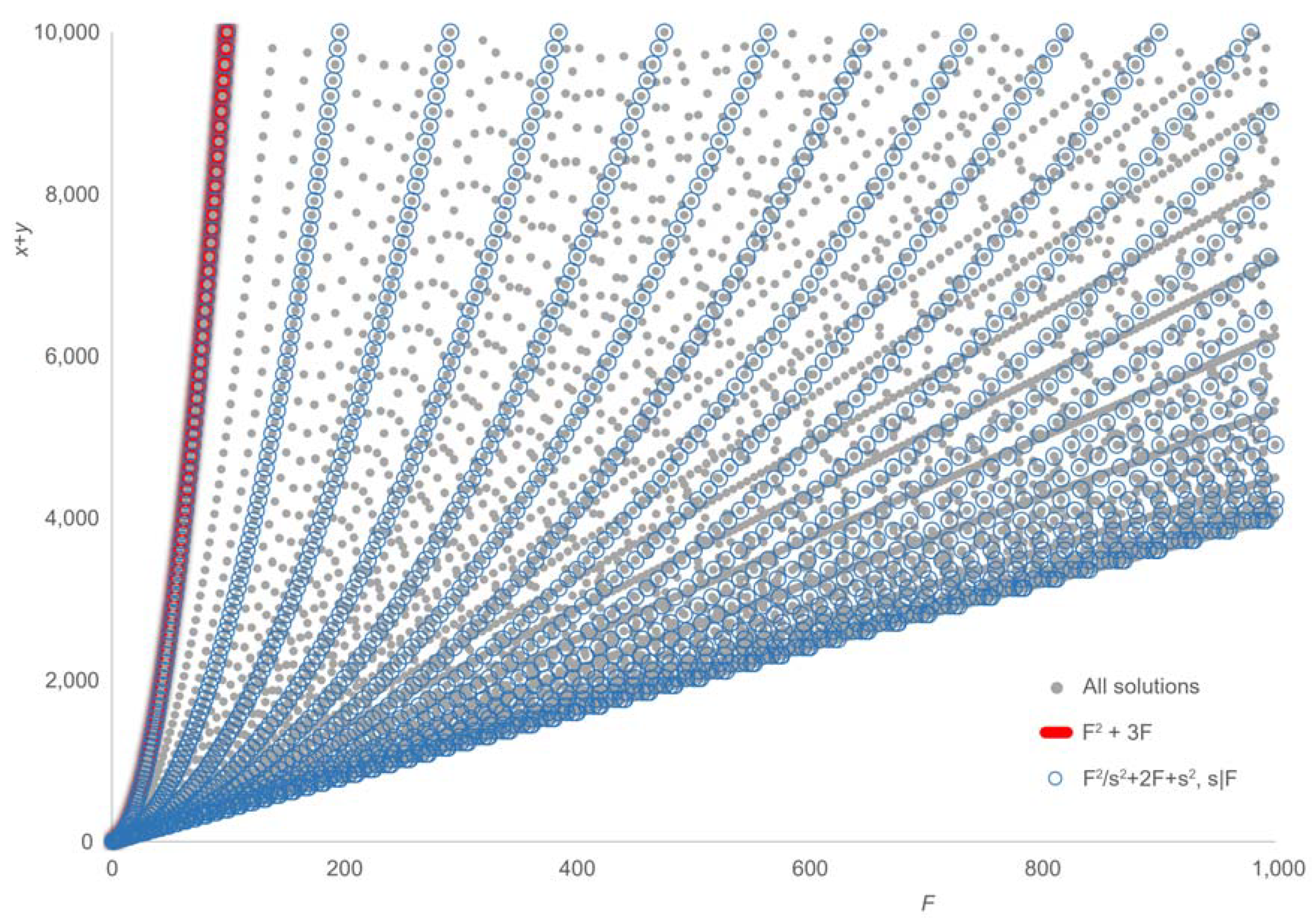
The first family of parametric solutions depends on the divisors of (
F + 1):
A proof is obtained by substituting (9) into (8). These terms generate solutions for any
F. The number of these solutions is
For example, for
xyz = 21(
x +
y +
z),
F + 1 has four divisors and (9) generates two solutions (up to order of terms):
A second set of parametric terms generates solutions of (8) with even
F, depending on the divisors of (
F + 4):
A proof is obtained by substituting (10) into (8). For the equation
xyz = 22(
x +
y +
z), the terms generate two solutions (up to order of terms):
A third family of parametric solutions relies on the divisors of 3
F under the condition that both the divisor
d and 3
F/
d are either even or odd:
A proof is obtained by substituting (11) into (8). For example, (11) generates three solutions (up to order of terms) of the equation
xyz = 21(
x +
y +
z):
The 1002 distinct sums of solution terms for all 627,514 solutions of (8) with
F ≤ 200 and (
x +
y +
z) ≤ 200 are plotted in
Figure 2. Examination of the figure suggests that pairs (
F,
x +
y +
z) corresponding to the solutions generated by the first (9) and second (10) parametric terms are disjoint but this is not true. For instance, 16 is the sum of solutions terms generated by (9) for the equation
xyz = 8(
x +
y +
z), and the sum of solution terms for one of the solutions generated by (10) for the same equation. As the figure shows, pairs (
F,
x +
y +
z) corresponding to solutions generated by the third set of parametric term (11) overlap with pairs generated by (9) and (10). Thus, the sets of pairs (
F,
x +
y +
z) generated by any two families of parametric terms described in
Section 3 overlap.
4. Diophantine Equations xy = F(x + y) and xyz = F(x + y + z): Primality of F and the Number of Solutions
Upper bounds for the solution terms or their sum are needed for computational enumeration. In 2015, Tony Crilly and Colin Fletcher found that the maximum semiperimeter of an integer-sided triangle tightly wrapping a circle of a radius
r is (
r2 + 1)(
r2 + 2) [
23]. The semiperimeter in their calculation equaled the sum of solution terms of the Diophantine Equation (8) with
F =
r2; thus, they established an upper bound for the sum of solution terms of (8) to be (
F + 1)(
F + 2). In 2016, Stan Dolan published a new proof of their result [
22]. We demonstrated his method in
Section 2.2. The upper bounds for sums of solution terms of (1) for
n = 2 and
n = 3 make it possible to count solutions for any
F by computation.
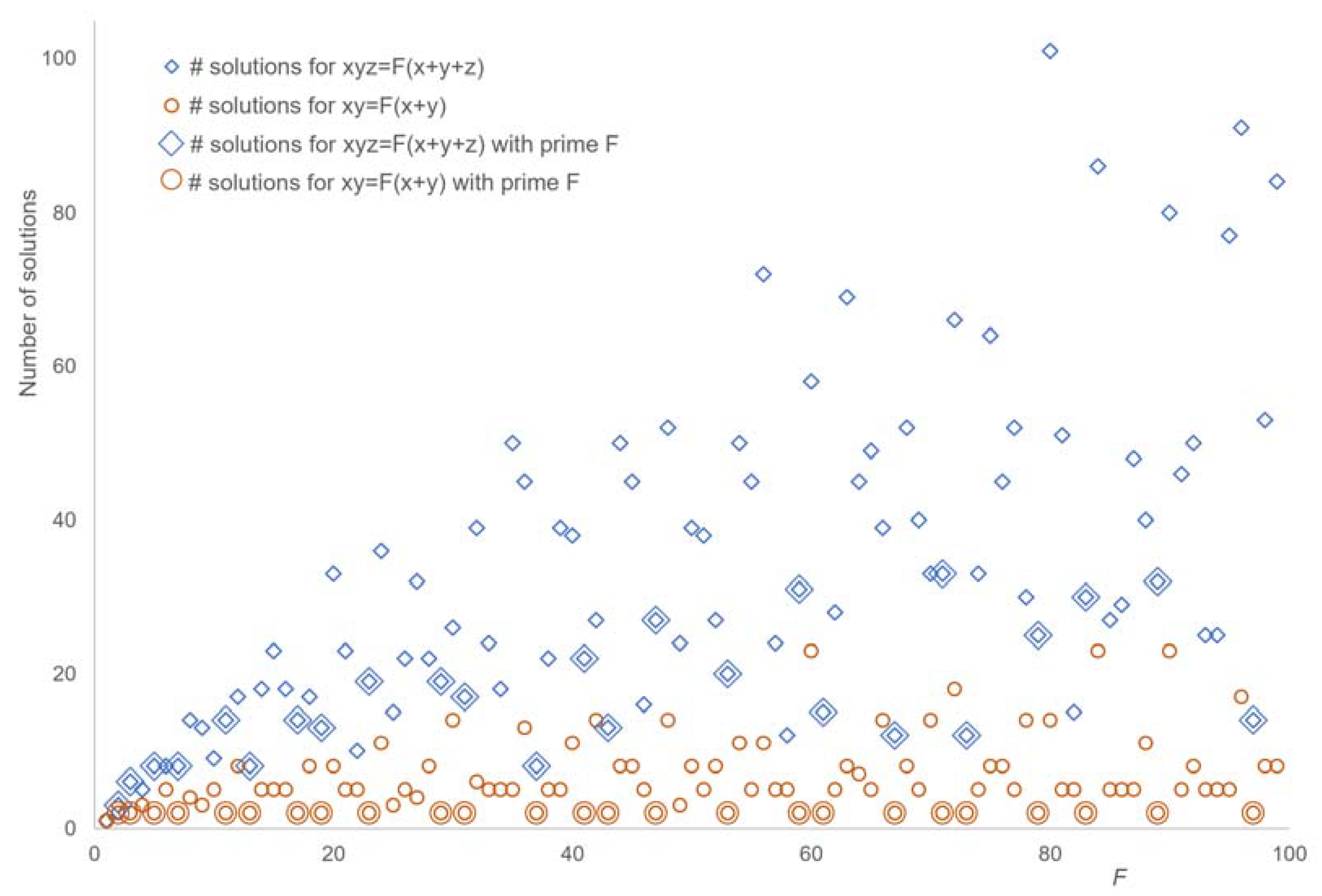
Figure 3 shows such an enumeration for 0 <
F < 100. A total of 634 and 3212 solutions were found for
n = 2 and
n = 3, respectively.
Figure 3 indicates that both equations with any
F are solvable. This is proved by the existence of parametric terms (3)–(5) for
xy =
F(
x +
y), and (9) for
xyz =
F(
x +
y +
z) because these terms generate solutions for any
F. For
n = 3,
Figure 3 appears to indicate that the number of solutions for prime
F is lower than for composite
F. In particular, it seems that the number of solutions for
F =
p with
p being a prime is lower than the number of solutions for
F =
p − 1 and
F =
p + 1. The impression is however misleading: for instance,
xyz =
F(
x +
y +
z) with
F = 59 has 31 solutions but with
F = 58 only 12 solutions.
The plot at
Figure 3 reveals that if
F < 100 is a prime,
xy =
F(
x +
y) has exactly two solutions. Theorem 3 shows that this is true for any
F, and it provides closed forms for both solutions.
Theorem 3. Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ+. If F is a prime, then the equation has exactly two solutions, and these solutions are (2F, 2F) and (F + 1, F(F + 1)).
Proof. According to Theorem 1, any solution of the equation can be written as (F2/r + F, F + r) with r evenly dividing F2. If F is a prime, then the only divisors of F2 are 1, F, and F2. Substituting F for r into (F2/r + F, F + r) leads to the solution (2F, 2F). Substituting 1 or F2 into (F2/r + F, F + r) leads to the solution (F + 1, F(F + 1)). Thus, (2F, 2F) and (F + 1, F(F + 1)) are the only solutions of the equation for any prime F. □
It is easy to show that the equation has exactly three solutions if
F is a square of a prime. If the converse of Theorem 3 is true, counting solutions of (2) could serve as a primality test. This would require that the equation has a single solution or more than two solutions for any composite
F.
Figure 3 shows that this holds true for
F < 100. Theorem 4 shows that the converse of Theorem 3 holds for any
F.
Theorem 4. Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ+. If F is composite, the equation has more than two solutions.
Proof. Assuming that F is composite, F = uv with u, v ∈ ℤ+ and u, v > 1. According to Theorem 1, any solution of the equation can be written as (F2/r + F, F + r) with r evenly dividing F2. Substituting u for r generates the solution (F(v + 1), F + u), which we label #1. Substituting F and 1 for r generates the solutions (2F, 2F) and (F + 1, F(F + 1)), which we label #2 and #3, respectively. Solution #1 is different from solution #2 because neither of the elements of #1 equals 2F. Solution #1 is also different from solution #3 because neither of its elements equals (F + 1). Therefore, the equation has at least three distinct solutions. □
Testing primality by counting solutions of a Diophantine equation is obviously not practical. Showing that a given number is composite based on Theorem 4, however, might be interesting because identification of any solution different from (2
F, 2
F) and (
F + 1,
F(
F + 1)) would be sufficient to prove that
F is composite. The parametric forms derived in
Section 2 are not suitable for this purpose because (3) generates (
F + 1,
F(
F + 1)), which also solves the equation with
F that are primes, and (4) and (5) require prior knowledge of the divisors of
F or
F2, respectively. We conjecture that no parametric solution of the equation
xy =
F(
x +
y) suitable for testing the primality of
F can be found:
Conjecture 1. Any parametric solution of Diophantine equation xy = F(x + y) with x, y, F ∈ ℤ+ generating a solution different from (2F, 2F) and (F + 1, F(F + 1)) is a function of the divisors of F or its powers.
5. Diophantine Equation with n > 3: Universal Parametric Solution
As shown above, (1) with
n ∈ (2,3) and any
F is solvable. It has not been known whether (1) with
n > 3 is solvable for any
F. Parametric solutions may help answering questions about solvability but there is no general method for finding parametric solutions of a Diophantine equation. The strategy that proved helpful here was inspired by the construction of solutions of (1) for a special case
F = 1 by Ecker [
13], by the approach used by Zhang and Cai [
24] to study the equation
in rational numbers, and by M. Ulas [
25] in his study of elementary symmetric functions. The strategy relies on setting all but a few terms of solution
n-tuples to 1.
Terms that equal 1 would collapse in the product on the LHS of (1). The sum of these terms, which equals their count, appears on the RHS. Therefore, the number of terms must be part of at least one solution term in order to also appear on the LHS.
F acting as a multiplier on the RHS cancels out if it also appears on the LHS as a factor in one of solution terms. Furthermore, after
F on both sides cancels out, the sum of terms on the RHS remains “naked” (not multiplied by
F). This sum consists of all terms larger than 1 and the number of terms equaling 1; therefore, a “naked” number of terms should also be part of the result of multiplication on the LHS. Based on this reasoning, the following parametric solution of (1) with any
n ≥ 3 and
F ∈ ℤ
+ was found:
A proof is readily obtained by substituting the terms into (1). Thus, (1) with any
n > 3 and
is solvable. For
n = 2, these terms generate the solution (
F + 1,
F(
F + 1)) derived in the previous section. For
n = 3, the solution (1,
F + 1,
F(
F + 2)) is obtained, which is not covered by any of parametric families presented in
Section 3.
6. Diophantine Equation : A Lower Bound for the Sum of Solution Terms Is
Finding solutions of (1) minimizing the sum of solution terms is a constraint optimization problem. To be able to use calculus, we release the integrality constraint, defining an objective function
and a constraint function
Both
f(
X) and
g(
X) have continuous first partial derivatives; therefore, the method of
Lagrange multiplier is applicable. The
Lagrange function is
with
λ being a multiplication constant. Critical points of
f(
X) under the constraint
g(
X) can be found by setting the
Lagrangian to zero:
Thus, we have a system of (
n + 1) equations:
Partial differentiation leads to
Substituting
from the last equation for each
xi into the first
n equations, followed by multiplying both sides of each
i-th equation with
xi, we obtain
Summing the left sides yields
which implies
. Substituting
for
λ into (12) leads to
Thus, all terms of the critical point of
f(X) constrained by
g(
X) are equal. Restoring integrality, we designate the solution of (1) at the critical point
Am = (
am,
am,
...,
am):
The Diophantine Equation (14) is solvable when
nF is an (
n − 1)-power, which is true for
with
m ∈ ℤ
+. Computational results for selected values of
n and
F are shown in
Table 1. The results illustrate that the sum of solution terms of (1) is bounded from below by (15). When
is an integer, it equals the sum of terms of the solution with the lowest sum of terms.
The inspection of computational results confirmed that solutions with the sum of terms given exactly by
consisted of equal terms. This is reminiscent of the fact that among
n-tuples with the same product of terms,
n-tuples consisting of equal terms have the lowest sum of terms, as can be proved by the AM-GM inequality [
26]. Thus, the constraint has not affected the minimum of the objective function. The situation is different regarding the upper bound, as will be shown in the next section.
The lower bound in
Table 1 increased with
n for
F ≤ 3, while it decreased with
n for
F ≥ 16. We assumed that
has a minimum below 3 for
F ≤ 3 and above 5 for
F ≥ 16. The first-derivative test for
n, F ∈ ℝ leads to
The critical point implicitly defined by is indeed a minimum, as computation shows: switching back to integers, the minimum for F = 16 occurs at n = 5, for F = 27 at n = 6, and for F = 2000 at n = 11. Past the minimum, the lower bound for the sum of solution terms grows with n but the growth is very slow. For instance, the lower bound for the sum of solutions terms of is 35 but for it is only 113.
7. Diophantine Equation : Un Upper Bound for the Sum of Solution Terms Is
An upper bound for the sum of terms of solutions of
is known to be (
F + 1)(
F + 2) [
22,
23]. In
Section 2, an upper bound for the sum of solution terms of
was shown to be
F2 + 2
F + 1 (Theorem 2). In the following, we shall establish an upper bound for the sum of the solution terms of (1) for any
n, based on the parametric solution established in
Section 5 and Lemma 1 about a special kind of variable mixing.
Lemma 1. Let A be an n-tuple of positive rational numbers and aj, ak two of its terms satisfying the inequalities 1 < aj ≤ ak. Let B be an n-tuple of positive rational numbers with bi = ai for 1 ≤ i ≤ n, i ≠ j, i ≠ k. If bj < aj, bk > ak, and , then .
Proof. We set
ak = aj + r with
r ∈ ℚ
+,
bj = (aj − α) with
α ∈ ℚ
+ and
α < aj, and
bk = aj + r + β with
β ∈ ℚ
+. Equating the quotients of products and sums of
A and
B, we have
Multiplying by the denominators, factoring, and substituting
for
leads to
Because the LHS is positive,
β >
α, and therefore
The lemma is proved. □
Now, we prove an upper bound for the sum of solution terms of (1).
Theorem 5. Let be a Diophantine equation with . The sum of terms of any solution is bounded from above by Proof. The
n-tuple
solves the equation because
We shall show that any solution with ci ∈ ℤ+ and at most (n − 3) terms equaling 1 can be converted into A via a series of n-tuples such that the sum of terms of each n-tuple is larger than the sum of terms of the previous n-tuple. The n-tuple is re-ordered ascendingly; one of cj such that 1 ≤ j ≤ (n − 2) and cj > 1 is replaced with 1; and cn−1 is increased in such a way that the quotient of the product and sum of terms remains F. According to Lemma 1, the sum of terms increased.
If any cj with 1 ≤ j ≤ (n − 2) is larger than 1, the process is repeated. If all cj with 1 ≤ j ≤ (n − 2) equal 1, the conversion is completed. According to the new value of cn−1, we now distinguish two cases.
Case 1:. Because the first (n − 2) terms equal 1 and the quotient of product and sum of terms equals F, cn must equal . Therefore, the n-tuple is identical with A and the sum of its terms equals Because in each step of the conversion the sum of terms increased, the sum of terms of any solution of (1) is smaller than or equal to
Case 2: Then, cn-1 is replaced with (F + 1) and cn is increased to keep the quotient of product and sum of terms equal to F, which implies that cn becomes . According to Lemma 1, the sum of terms increased. The conversion is completed. Further reasoning of Case 1 applies.
It remains to be shown that
cn−1 cannot be smaller than (
F + 1). Re-arranging the Equation (1) as
shows that
Because
cn−1 is an integer, it cannot be smaller than (
F + 1). □
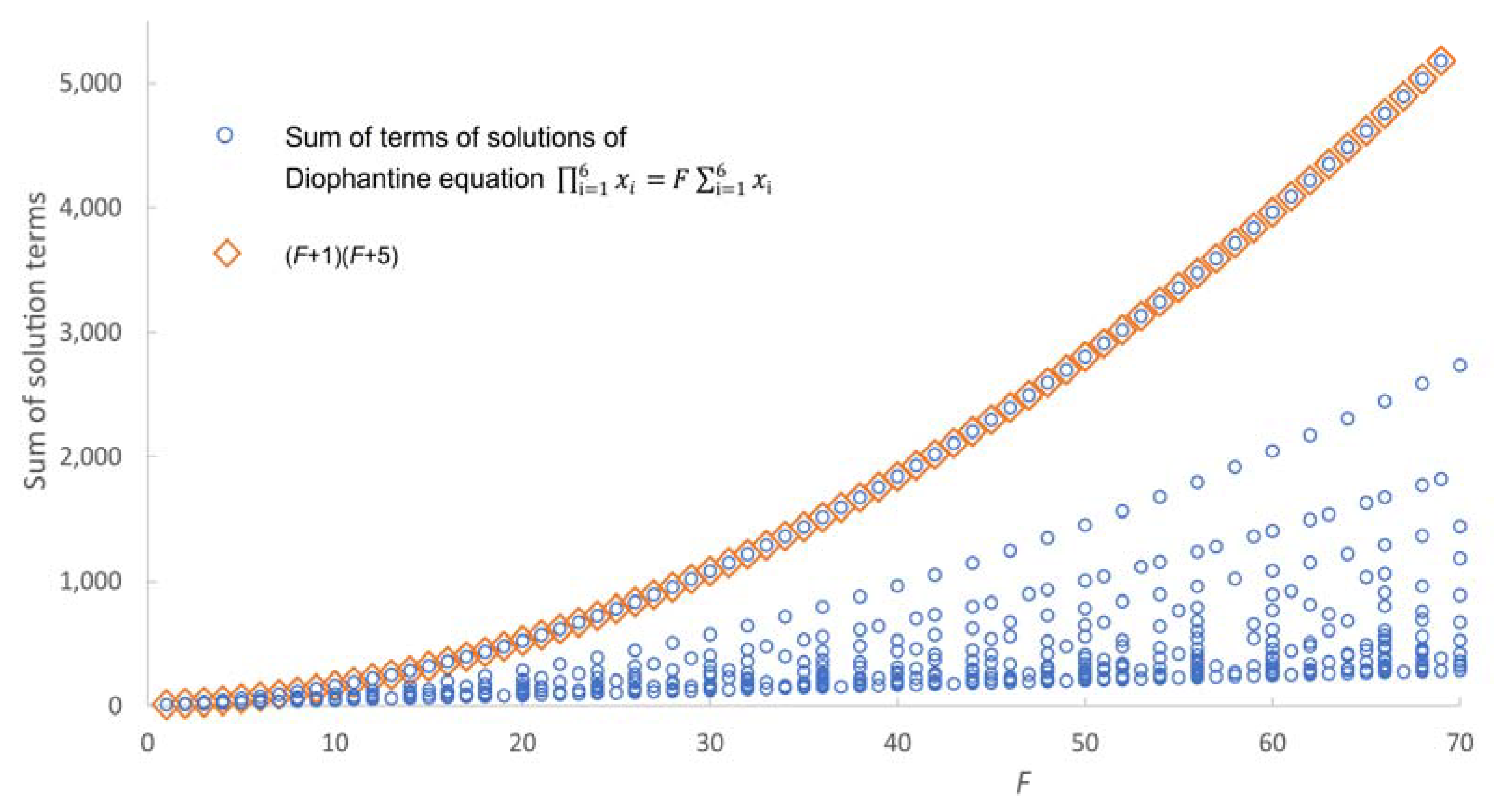
All experimentally determined largest sums of solution terms shown in
Table 1 equal the upper bounds for the sum of solutions terms of (1) according to (16).
Figure 4 shows the sums of solution terms of all 3070 solutions of (1) with
n = 6 and
F ≤ 70 together with the upper bound. The figure illustrates that for any
F, a solution with the sum of terms equal to the upper bound (16) exists.
8. Diophantine Equation with n ≥ 4 and Distinct Terms: Solvability
The upper bound derived in the previous section is based on solutions with the first (
n − 2) terms equal to 1. Such
n-tuples have been used in constructive proofs because they simplify handling products and sums [
13,
24,
25]. However, they are special, and one may argue that they do not represent solutions of (1) adequately. Therefore, in the following we shall consider solutions consisting of distinct terms. Without loss of generality, the terms of such solutions can be ordered ascendingly:
The solutions are totally ordered sets of cardinality n. Because (17) is a special case of (1), the sum of solution terms is bounded from above, and the number of solutions is finite. It is not known whether (17) is solvable for any F; if yes, how many solutions exist; and whether a stronger upper bound than (16) for the sum of solution terms can be found.
Parametric solutions help to answer questions about solvability. We found the following family of parametric solutions of (17) with
n = 4 and any
F > 2:
A proof is readily obtained by substituting the terms into (17). Thus, the equation with n = 4 and any F > 2 is solvable. Inspection of all 19,787 solutions of (17) with n = 4 and F ≤ 300 revealed a single solution for F = 3 and more than one solution for 3 < F ≤ 300.
In contrast to n = 4, is not solvable in distinct terms for all values of F. An inspection of all solutions of the equations with 7 < F ≤ 95, computed within the bounds for (1), showed that no solution in distinct terms exists for F equal to 10, 11, 13, 17, 26, 31, and 43. Similarly, the equations with n ∈ (6, 7, 8, 9) and certain values of F are not solvable in distinct positive integers (data not shown). A question arises whether for any n there exists a threshold M such that the Equation (17) with any F > M is solvable.
Because
is not solvable in distinct terms for all
F, a general parametric solution cannot exist. With the help of computation (see also
Section 10.1), parametric solutions for
F satisfying certain conditions can, however, be found. The following parametric solution for
F such that (
F + 9) is evenly divided by 23 is an example:
A proof is readily obtained by substituting into (17). The recipe also works with k ∈ (2, 3, 4), but the terms of these solutions are not distinct.
9. Diophantine Equation with n ≥ 4 and Distinct Terms: Upper Bound
Solutions of (1) in distinct terms are a subset of all solutions of (1); therefore, the sum of their terms is bounded from above by . In the following, we provide a stronger upper bound.
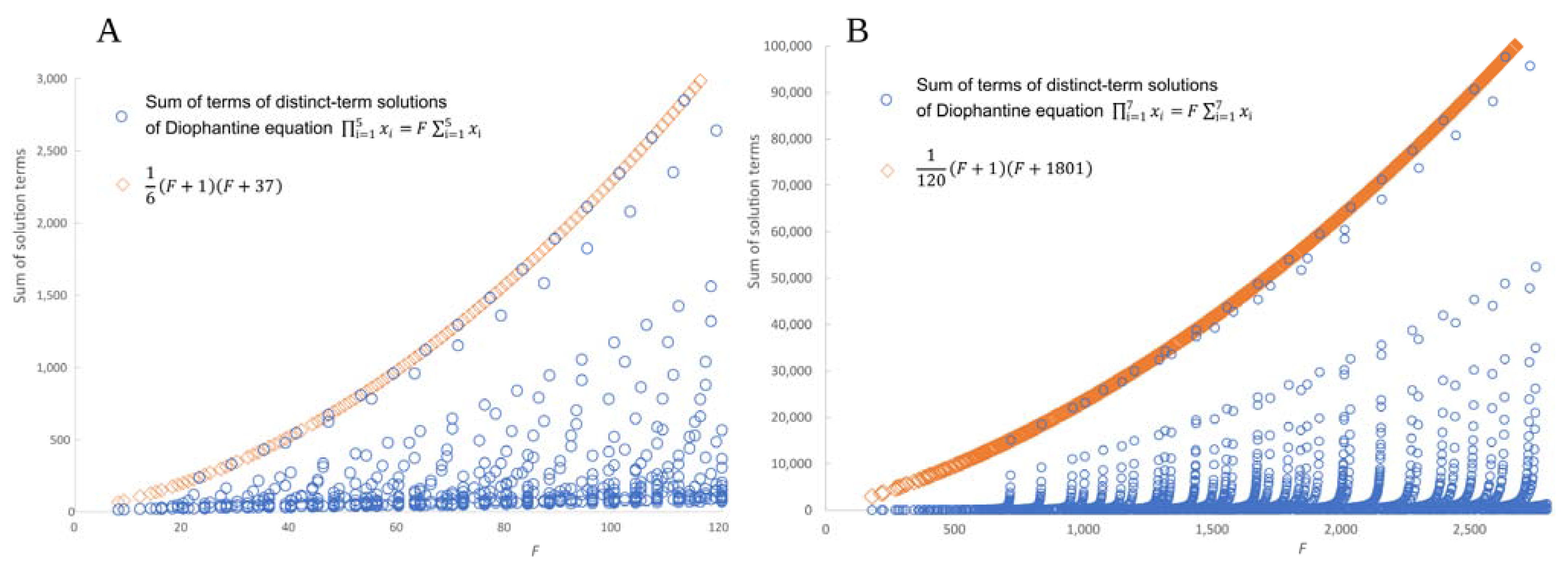
Conjecture 2. Letbe a Diophantine equation with. The sum of terms of solutions consisting of distinct terms is bounded from above by We do not have a proof, but the conjecture is strongly supported by computation. Selected results are shown in
Figure 5.
Figure 5 shows that for certain values of
F, the conjectured upper bound matches the maximum sum of solution terms. These values of
F satisfy the following conditions:
Conjecture 3. Letbe a Diophantine equation with. The upper bound (18) for the sum of solution terms of distinct-term solutions equals the largest sum of terms of distinct-term solutions if and only if A computational example for
n = 8 and
k ≤ 6 is shown in the upper part of
Figure 6. For (17) with
F not satisfying (19), the upper bound (18) is weak. When the constant term in (19) is replaced with divisors of (
n +
k − 2)(
n − 2)! larger than 1, the formula generates
F such that data points in the Cartesian systems with
F on the abscissa and sum of solution terms on the ordinate form strings extending from their highest point downwards, as shown at
Figure 6. This pattern is also apparent at
Figure 5B, but the points are better separated when the vertical axis is scaled logarithmically as in
Figure 7.
The smallest value of parameter
F such that the sum of solution terms of (17) equals the upper bound (18) is obtained from (19) for
k = 1, which leads to
.
Table 2 shows such values of
F for selected
n together with the corresponding solutions with the largest sums of terms, revealing a monotonous structure of such solutions. Remark: because solutions consisting of consecutive numbers 1 to
n have the lowest ratio of product and sum of terms among all distinct-term solutions,
is a lower bound for
F. In other words (17),
F <
is not solvable in distinct integers.