Diophantine Equations Relating Sums and Products of Positive Integers: Computation-Aided Study of Parametric Solutions, Bounds, and Distinct-Term Solutions

Abstract

Diophantine equations ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ with $x_i,F\in {\mathbb{Z}}^{+}$ associate the products and sums of n natural numbers. Only special cases have been studied so far. Here, we provide new parametric solutions depending on F and the divisors of F or F². One of these solutions shows that the equation of any degree with any F is solvable. For n = 2, exactly two solutions exist if and only if F is a prime. These solutions are (2F, 2F) and (F + 1, F(F + 1)). We generalize an upper bound for the sum of solution terms from n = 3 established by Crilly and Fletcher in 2015 to any n to be $\left(F+1\right)\left(F+n-1\right)$ and determine a lower bound to be $\sqrt[n-1]{n^{n}F}$. Confining the solutions to n-tuples consisting of distinct terms, equations of the 4th degree with any F are solvable but equations of the 5th to 9th degree are not. An upper bound for the sum of terms of distinct-term solutions is conjectured to be $\left(F+1\right)\left[F+\left(n-2\right)\left(n-1\right)!/2+1\right]/\left(n-2\right)!$. The conjecture is supported by computation, which also indicates that the upper bound equals the largest sum of solution terms if and only if $F=\left(n+k-2\right)\left(n-2\right)!-1, k\in {\mathbb{Z}}^{+}$. Computation provides further insights into the relationships between F and the sum of terms of distinct-term solutions.

1. Introduction

1.1. Background

Sums and products of integers are common terms in Diophantine equations. The relationship between two products of integers is reflected by type I multiplicative Diophantine equations

$${\displaystyle \prod }_{i=1}^n{x}_i={\displaystyle \prod }_{i=1}^n{y}_i \mathrm{with} x_i,y_i\in \mathbb{Z} \mathrm{and} n>1.$$

In 1930, Eric Temple Bell established a complete parametrized solution by means of his reciprocal array algorithm [1]. Simple and extended multiplicative Diophantine equations and systems of such equations were studied in 1930 and 1940 [2,3,4,5,6] but have attracted limited attention since [7,8].

The equality of sums of integers can be regarded as a special case of the Prouhet–Tarry–Escott problem of equal sums of like powers [9]

$${\displaystyle \sum }_{i=1}^n{x}_i^k={\displaystyle \sum }_{i=1}^n{y}_i^k \mathrm{with} k\in \mathbb{Z}.$$

Solutions of the equation of degree 1 are trivial because all x_i and y_i except one can be chosen deliberately.

The relationship between sums and products of n integers has not been studied in general, but several special cases have been investigated. A product of positive integers larger than 2 is larger than their sum; therefore, an additive or multiplicative compensatory factor is required. This work is concerned with Diophantine equations with a multiplicative compensation factor

$${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i \mathrm{with} x_i,F\in {\mathbb{Z}}^{+}.$$

(1)

F is a fixed parameter; thus, (1) represents a family of equations, yet it is conventionally addressed as a Diophantine equation. In its generality, (1) has not been addressed. A related equation with an additive compensation factor

$${\displaystyle \prod }_{i=1}^n{x}_i=F+{\displaystyle \sum }_{i=1}^n{x}_i \mathrm{with} x_i,F\in {\mathbb{Z}}^{+}$$

was studied mainly for F = 0 [10,11]. For an arbitrary F, Viola [12] determined an upper bound En (N) for the number of positive integers smaller than N for which the equation is not solvable.

A special case of (1) with F = 1 and arbitrary n was studied by Ecker [13] and Kurdlanchik and Nowicki [14]. n-tuples that solve (1) for n > 2 and F = 1 necessarily contain terms equal to 1. The number of these terms grows with n; for instance, all solutions with n > 10 contain at least 8 terms equal to 1 [13]. Furthermore, every n-tuple of positive integers that does not solve the equation can be “padded” into an (n + m)-tuple by adding m terms equal to 1 in such a way that the resulting (n + m)-tuple solves the equation [13].

For F = 1 and n = 3, (1) becomes xyz = x + y + z. A special case of this equation is

$${\displaystyle \prod }_{i=1}^3{x}_i={\displaystyle \sum }_{i=1}^3{x}_i=1,$$

which does not have any solution in ℤ, but it can be solved in other domains. Charles Small [14] studied this equation in rings of integers modulo m and in finite fields 𝔽q, q = pⁿ with prime p and n ≥ 1. The equation was also studied in quadratic [15] and quartic fields [16,17].

Computing has been used in mathematics mainly for four purposes, at an increasing level of sophistication: (i) to disprove or support conjectures by brute-force computation [18]; (ii) provide insight and inspiration by revealing patterns and relationships; (iii) generate new conjectures [19]; and (iv) provide formal proofs [20]. While testing conjectures dominated computing in number theory after the advent of machine computing, automatic conjecturing and theorem proving are subjects of vigorous current research. The second application mentioned, in which computing inspires rather than generates conjectures, is elusive and rarely discussed. It may vaguely be described as a pattern-guided trial-and-error approach. In this work, apart from exhaustive enumeration of solutions to support conjectures and to show that certain equations are not solvable in distinct terms, we repeatedly use computing as a discovery tool.

1.2. Scope of the Work and Main Theorems

Fragmentary results on (1) for n = 2 and n = 3 are scattered through literature. They have often been obtained as side-products of research on other problems. In Section 2, Section 3 and Section 4, we extend these results, providing new parametric solutions, including a set of parametric terms generating all solutions for n = 2, and enumerate solutions for selected n and F computationally. In Section 5, Section 6 and Section 7, we study the solvability of (1) of any degree, and upper and lower bounds for the sum of solution terms. In Section 8 and Section 9, we study solutions of (1) consisting of distinct terms, upper bounds for the sum of terms of these solutions, and the relationship between F and the sum of solution terms.

The main theorems provide the following results. Equation (1) of any degree with any F has a solution (1, 1, …, F + 1, F(F + n − 1)). Equation of the 2nd degree has exactly two solutions if and only F is a prime, and an upper bound for the sum of solution terms is (F² + 2F + 1). Lower and upper bounds for the sum of solution terms of (1) of any degree with any F are $\sqrt[n-1]{n^{n}F}$ and $\left(F+1\right)\left(F+n-1\right)$, respectively. Equations of the 4th degree with any F are solvable in distinct terms, but equations of the 5th to 9th degree are not.

2. Diophantine Equation xy = F(x + y): Parametric Solutions and an Upper Bound for the Sum of Solution Terms

2.1. Parametric Solutions

In the following, we establish three families of parametric solutions for the equation

$$xy=F\left(x+y\right); x,y,F\in {\mathbb{Z}}^{+}.$$

(2)

The first family depends on F as the only parameter:

$$x=F+1, y=F\left(F+1\right).$$

(3)

A proof is obtained by substituting (3) into (2). For example, for the equation xy = 21(x + y), we obtain the solution (22,462).

The second family of parametric solutions depends on the divisors of F, which we designate s:

$$x=\frac{F^2}{s^2}+F, y=F+s^2; s\mid F.$$

(4)

A proof is obtained by substituting (4) into (2). Two solutions (up to order of terms) generated by (4) for the example equation xy = 21(x + y) as above are

$$\left(x,y\right)\in \left\{\left(22,462\right),\left(30,70\right)\right\}.$$

The third family of parametric solutions is obtained by re-arranging (2) as x(y − F) = Fy and substituting r > 0 for (y − F), which leads to x = F²/r + F. Because x is an integer, r must evenly divide F². Parametric solutions are generated from divisors of F², designated r:

$$x=\frac{F^2}{r}+F , y=F+r; r\mid F^2.$$

(5)

Divisors of F² can be partitioned into pairs symmetric with respect to (F² + 1)/2; therefore, the number of solutions generated by (5) (up to order of terms) is

$$\lceil \frac{{{\displaystyle \sum }}_{r\mid F^2}1}{2}\rceil .$$

For the equation xy = 21(x + y) as above, the number of positive divisors of 21² is 9; therefore, (5) generates $\lceil \frac{9}{2}\rceil =5$ solutions:

$$\left(x,y\right)\in \left\{\left(22,462\right),\left(24,168\right),\left(28,84\right),\left(30,70\right),\left(42,42\right)\right\}.$$

These solutions encompass all solutions obtained with (3) and (4). Indeed, Theorem 1 shows that (5) generates all solutions of (2) for a particular F. This is a rare and fortunate situation, which allows us to establish an upper bound for the sum of solution terms (Section 2.2) and study the relationship between the number of solutions of (2) and the primality of F (Section 4).

Theorem 1.

Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ⁺. For any solution (u, v), there exist r ∈ ℤ⁺ such that

$$u=\frac{F^2}{r}+F, v=F+r; r\mid F^2.$$

Proof. 

Let (u, v) be a particular but arbitrarily chosen solution. Because the equation can be rearranged as x(y − F) = Fy and as y(x − F) = Fx, both solution terms must be larger than F. Therefore, we write u = F + a and v = F + b with a, b ∈ ℤ⁺. Substituting F + a and F + b for x and y into the Diophantine equation yields F² = ab; hence, b is a divisor of F² and the statement v = F + r with r|F² is proved. Substituting F²/b for a into u = F + a leads to u = F²/b + F with b|F². The theorem is proved. □

2.2. Upper Bound for the Sum of Solution Terms of xy = F(x + y) with x, y, F ∈ ℤ⁺

Upper bounds for x and y or their sum are needed for computational enumeration of solutions of (2). In 2011, Abdullahi Umar and Rajai Alassar [21], assuming x ≥ y, derived the following bounds for solution terms:

$$2F\le x\le F\left(F+1\right), F<y\le 2F.$$

The sum both upper bounds (F² + 3F) is an upper bound for the sum of solution terms, but because of mutual constraints between the terms, it is likely to be a weak bound. For instance, in the equation x + y = F with $x,y,F\in {\mathbb{Z}}_0^{+}$, the sum of the least upper bounds for x and y is twice the least upper bound for (x + y). Application of the method of Stan Dolan [22] led to an upper bound (2F² + 2), which is even weaker than the upper bound derived from bounds for both terms according to [21]. With growing F, the ratio of the two bounds approaches 2:

$$\underset{F\to \infty }{\lim }\frac{2F^2+2}{F^2+3F}=2.$$

A stronger upper bound for the sum of solution terms of (2), which turns out to be the least upper bound, is proved in Theorem 2.

Theorem 2.

Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ⁺, and A(F) = {(a, b) | ab = F(a + b); a, b ∈ ℤ⁺} a set of solutions for a particular arbitrarily chosen F. Let S(F) = {s | s = a + b, (a, b) ∈ A(F)} be a set of sums of terms of the elements of A(F). Then the least upper bound of S(F) is

$$\sup S\left(F\right)=F^2+2F+1.$$

Proof. 

According to Theorem 1, the sum solution terms of any solution of the Diophantine equation can be expressed as

$$x+y=\frac{F^2}{r}+2F+r , r\mid F^2.$$

(6)

The smallest and largest positive divisors of F² are 1 and F², respectively. Substituting any of these divisors into (6) leads to

$$x+y=F^2+2F+1.$$

(7)

Let a, b be any pair of divisors of F² such that 1 < a, b < F² and ab = F². Substituting ab for F² and a for r into (6) and applying the inequality ab + 1 ≥ a + b, which holds for a, b ∈ ℤ⁺, we have

$$\begin{gathered} x+y=\frac{ab}{a}+2F+a=a+b+2F \\ \le ab+2F+1=F^2+2F+1. \end{gathered}$$

Hence, the sum of solution terms generated by (6) for any divisor of F² larger than 1 and smaller than F² is at most as large as the sum of solution terms generated by (6) for the divisors 1 and F². Therefore, F² + 2F + 1 is larger than or equal to the sum of terms of any solution and thus the supremum of the sum of solution terms. □

With growing F, the sum of the least upper bounds of both solution terms converges to the least upper bound of the sum of solution terms:

$$\underset{F\to \infty }{\lim }\frac{F^2+3F}{F^2+2F+1}=1.$$

Figure 1 shows a computational enumeration of solutions of (2). The sums of terms of 7031 solutions for F ≤ 1000 and (x + y) ≤ 10,000 are plotted. Parametric solutions according to (4) cover part of the results, including solutions with the sums of terms apparently approaching F² + 3F. Because of the scale of the F axis, it appears as if the upper bound F² + 3F were strong.

3. Diophantine Equation xyz = F(x + y + z): Parametric Solutions

We shall establish three families of parametric solutions for

$$xyz=F\left(x+y+z\right);x,y,z,F\in {\mathbb{Z}}^{+}.$$

(8)

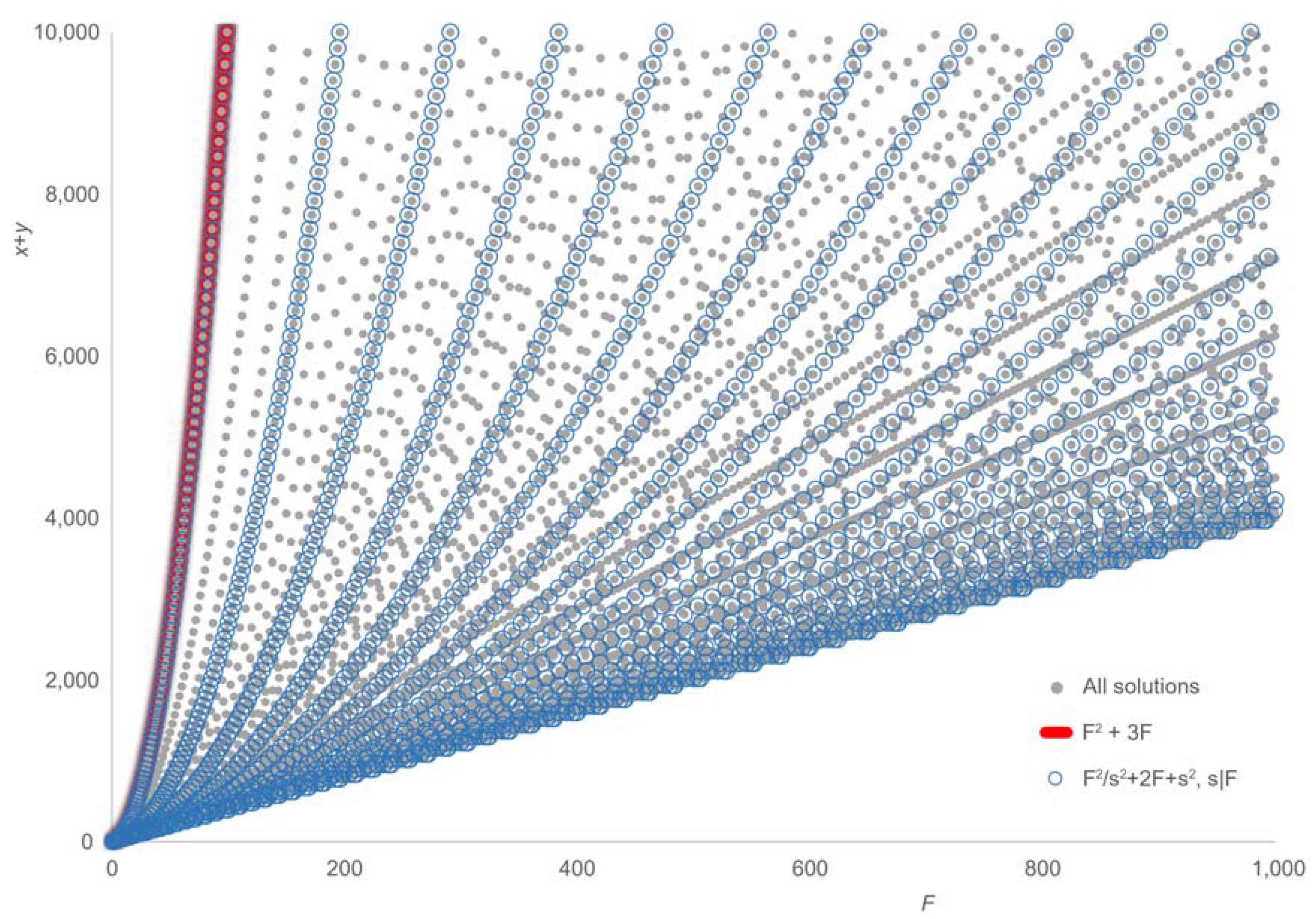
The first family of parametric solutions depends on the divisors of (F + 1):

$$x=d+1 , y=\frac{F+1}{d}+1 , z=F ; d\mid \left(F+1\right).$$

(9)

A proof is obtained by substituting (9) into (8). These terms generate solutions for any F. The number of these solutions is $\lceil \left({\displaystyle \sum }_{r\mid \left(F+1\right)}1\right)/2\rceil .$ For example, for xyz = 21(x + y + z), F + 1 has four divisors and (9) generates two solutions (up to order of terms):

$$\left(x,y,z\right)\in \left\{\left(2,21,23\right),\left(3,12,21\right)\right\}.$$

A second set of parametric terms generates solutions of (8) with even F, depending on the divisors of (F + 4):

$$x=\frac{F}{2}, y=d+2, z=\frac{F+4}{d}+2; F=2k, k\in {\mathbb{Z}}^{+}, d\mid \left(F+4\right).$$

(10)

A proof is obtained by substituting (10) into (8). For the equation xyz = 22(x + y + z), the terms generate two solutions (up to order of terms):

$$\left(x,y,z\right)\in \left\{\left(3,11,28\right),\left(4,11,15\right)\right\}.$$

A third family of parametric solutions relies on the divisors of 3F under the condition that both the divisor d and 3F/d are either even or odd:

$$x=d, y=d+\frac{3F-d^2}{2d}, z=d+\frac{3F-d^2}{d}; d\mid 3F, 2\mid \left(\frac{3F}{d}-d\right).$$

(11)

A proof is obtained by substituting (11) into (8). For example, (11) generates three solutions (up to order of terms) of the equation xyz = 21(x + y + z):

$$\left(x,y,z\right)\in \left\{\left(1,32,63\right),\left(3,12,21\right),\left(7,8,9\right)\right\}.$$

The 1002 distinct sums of solution terms for all 627,514 solutions of (8) with F ≤ 200 and (x + y + z) ≤ 200 are plotted in Figure 2. Examination of the figure suggests that pairs (F, x + y + z) corresponding to the solutions generated by the first (9) and second (10) parametric terms are disjoint but this is not true. For instance, 16 is the sum of solutions terms generated by (9) for the equation xyz = 8(x + y + z), and the sum of solution terms for one of the solutions generated by (10) for the same equation. As the figure shows, pairs (F, x + y + z) corresponding to solutions generated by the third set of parametric term (11) overlap with pairs generated by (9) and (10). Thus, the sets of pairs (F, x + y + z) generated by any two families of parametric terms described in Section 3 overlap.

4. Diophantine Equations xy = F(x + y) and xyz = F(x + y + z): Primality of F and the Number of Solutions

Upper bounds for the solution terms or their sum are needed for computational enumeration. In 2015, Tony Crilly and Colin Fletcher found that the maximum semiperimeter of an integer-sided triangle tightly wrapping a circle of a radius r is (r² + 1)(r² + 2) [23]. The semiperimeter in their calculation equaled the sum of solution terms of the Diophantine Equation (8) with F = r²; thus, they established an upper bound for the sum of solution terms of (8) to be (F + 1)(F + 2). In 2016, Stan Dolan published a new proof of their result [22]. We demonstrated his method in Section 2.2. The upper bounds for sums of solution terms of (1) for n = 2 and n = 3 make it possible to count solutions for any F by computation. 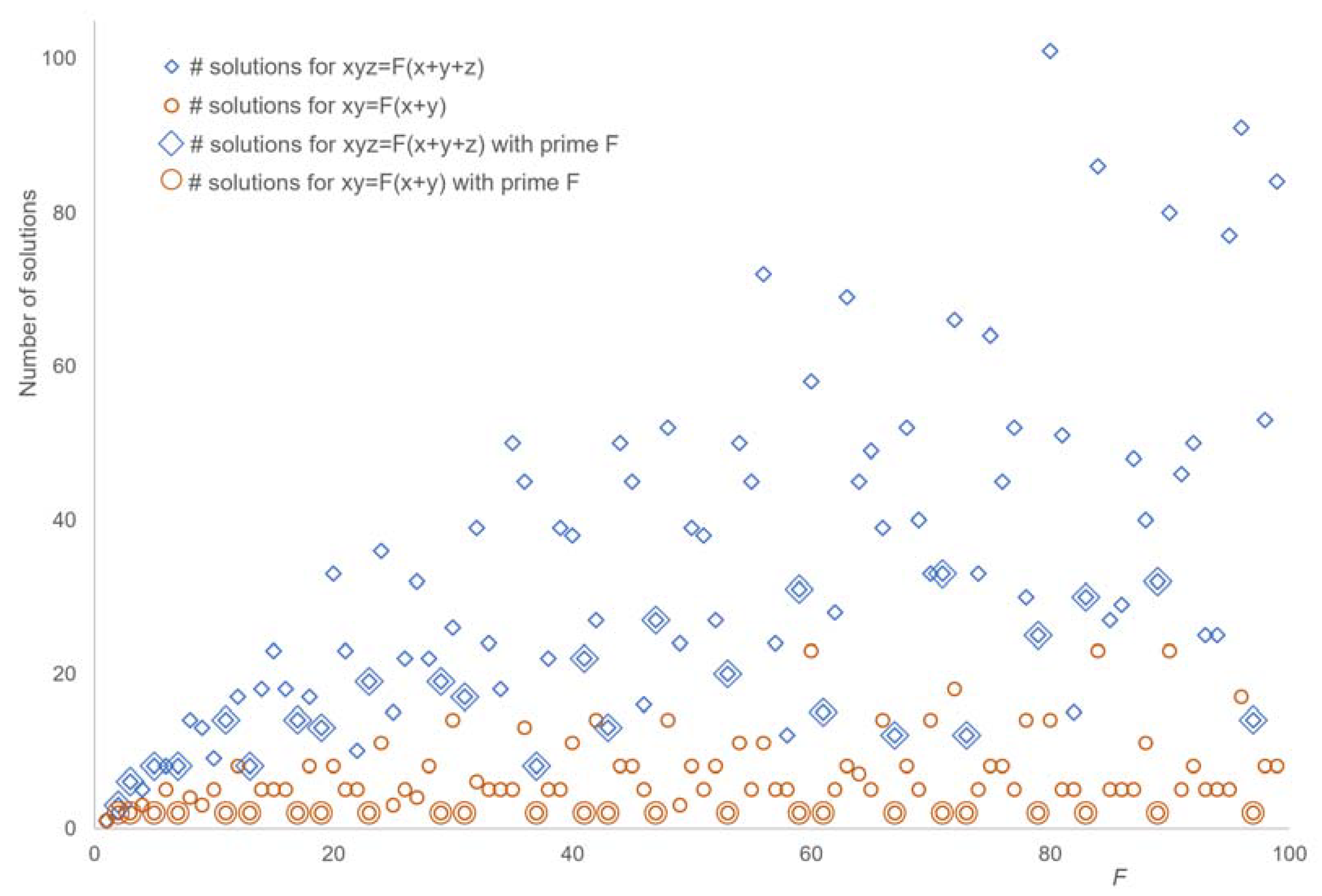Figure 3 shows such an enumeration for 0 < F < 100. A total of 634 and 3212 solutions were found for n = 2 and n = 3, respectively.

Figure 3 indicates that both equations with any F are solvable. This is proved by the existence of parametric terms (3)–(5) for xy = F(x + y), and (9) for xyz = F(x + y + z) because these terms generate solutions for any F. For n = 3, Figure 3 appears to indicate that the number of solutions for prime F is lower than for composite F. In particular, it seems that the number of solutions for F = p with p being a prime is lower than the number of solutions for F = p − 1 and F = p + 1. The impression is however misleading: for instance, xyz = F(x + y + z) with F = 59 has 31 solutions but with F = 58 only 12 solutions.

The plot at Figure 3 reveals that if F < 100 is a prime, xy = F(x + y) has exactly two solutions. Theorem 3 shows that this is true for any F, and it provides closed forms for both solutions.

Theorem 3.

Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ⁺. If F is a prime, then the equation has exactly two solutions, and these solutions are (2F, 2F) and (F + 1, F(F + 1)).

Proof. 

According to Theorem 1, any solution of the equation can be written as (F²/r + F, F + r) with r evenly dividing F². If F is a prime, then the only divisors of F² are 1, F, and F². Substituting F for r into (F²/r + F, F + r) leads to the solution (2F, 2F). Substituting 1 or F² into (F²/r + F, F + r) leads to the solution (F + 1, F(F + 1)). Thus, (2F, 2F) and (F + 1, F(F + 1)) are the only solutions of the equation for any prime F. □

It is easy to show that the equation has exactly three solutions if F is a square of a prime. If the converse of Theorem 3 is true, counting solutions of (2) could serve as a primality test. This would require that the equation has a single solution or more than two solutions for any composite F. Figure 3 shows that this holds true for F < 100. Theorem 4 shows that the converse of Theorem 3 holds for any F.

Theorem 4.

Let xy = F(x + y) be a Diophantine equation with x, y, F ∈ ℤ⁺. If F is composite, the equation has more than two solutions.

Proof. 

Assuming that F is composite, F = uv with u, v ∈ ℤ⁺ and u, v > 1. According to Theorem 1, any solution of the equation can be written as (F²/r + F, F + r) with r evenly dividing F². Substituting u for r generates the solution (F(v + 1), F + u), which we label #1. Substituting F and 1 for r generates the solutions (2F, 2F) and (F + 1, F(F + 1)), which we label #2 and #3, respectively. Solution #1 is different from solution #2 because neither of the elements of #1 equals 2F. Solution #1 is also different from solution #3 because neither of its elements equals (F + 1). Therefore, the equation has at least three distinct solutions. □

Testing primality by counting solutions of a Diophantine equation is obviously not practical. Showing that a given number is composite based on Theorem 4, however, might be interesting because identification of any solution different from (2F, 2F) and (F + 1, F(F + 1)) would be sufficient to prove that F is composite. The parametric forms derived in Section 2 are not suitable for this purpose because (3) generates (F + 1, F(F + 1)), which also solves the equation with F that are primes, and (4) and (5) require prior knowledge of the divisors of F or F², respectively. We conjecture that no parametric solution of the equation xy = F(x + y) suitable for testing the primality of F can be found:

Conjecture 1.

Any parametric solution of Diophantine equation xy = F(x + y) with x, y, F ∈ ℤ⁺ generating a solution different from (2F, 2F) and (F + 1, F(F + 1)) is a function of the divisors of F or its powers.

5. Diophantine Equation ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ with $F\in {\mathbb{Z}}^{+},$ n > 3: Universal Parametric Solution

As shown above, (1) with n ∈ (2,3) and any F is solvable. It has not been known whether (1) with n > 3 is solvable for any F. Parametric solutions may help answering questions about solvability but there is no general method for finding parametric solutions of a Diophantine equation. The strategy that proved helpful here was inspired by the construction of solutions of (1) for a special case F = 1 by Ecker [13], by the approach used by Zhang and Cai [24] to study the equation ${\displaystyle \sum }_{i=1}^n{x}_i={\displaystyle \prod }_{i=1}^n{x}_i=2n$ in rational numbers, and by M. Ulas [25] in his study of elementary symmetric functions. The strategy relies on setting all but a few terms of solution n-tuples to 1.

Terms that equal 1 would collapse in the product on the LHS of (1). The sum of these terms, which equals their count, appears on the RHS. Therefore, the number of terms must be part of at least one solution term in order to also appear on the LHS. F acting as a multiplier on the RHS cancels out if it also appears on the LHS as a factor in one of solution terms. Furthermore, after F on both sides cancels out, the sum of terms on the RHS remains “naked” (not multiplied by F). This sum consists of all terms larger than 1 and the number of terms equaling 1; therefore, a “naked” number of terms should also be part of the result of multiplication on the LHS. Based on this reasoning, the following parametric solution of (1) with any n ≥ 3 and F ∈ ℤ⁺ was found:

$$\begin{gathered} x_1=1, \\ \dots \\ {x}_{n-2}=1, \\ {x}_{n-1}=F+1, \\ {x}_n=F\left(F+n-1\right). \end{gathered}$$

A proof is readily obtained by substituting the terms into (1). Thus, (1) with any n > 3 and $F\in {\mathbb{Z}}^{+}$ is solvable. For n = 2, these terms generate the solution (F + 1, F(F + 1)) derived in the previous section. For n = 3, the solution (1, F + 1, F(F + 2)) is obtained, which is not covered by any of parametric families presented in Section 3.

6. Diophantine Equation ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$: A Lower Bound for the Sum of Solution Terms Is $\sqrt[n-1]{n^{n}F}$

Finding solutions of (1) minimizing the sum of solution terms is a constraint optimization problem. To be able to use calculus, we release the integrality constraint, defining an objective function $f\left(X\right)={\displaystyle \sum }_{i=1}^n{x}_i, x_i\in {ℝ}^{+}$ and a constraint function $g\left(X\right)={\displaystyle \prod }_{i=1}^n{x}_i-F{\displaystyle \sum }_{i=1}^n{x}_i=0, x_i\in {ℝ}^{+}, F\in {\mathbb{Z}}^{+}.$ Both f(X) and g(X) have continuous first partial derivatives; therefore, the method of Lagrange multiplier is applicable. The Lagrange function is $ℒ=f\left(X\right)-\lambda g\left(X\right)$ with λ being a multiplication constant. Critical points of f(X) under the constraint g(X) can be found by setting the Lagrangian to zero:

$${\nabla }_{\left(X,\lambda \right)}\left(f\left(X\right)-\lambda g\left(X\right)\right)=0.$$

Thus, we have a system of (n + 1) equations:

$$\begin{gathered} \frac{\delta }{\delta x_1}\left({{\displaystyle \sum }}_{i=1}^n{x}_i-\lambda \left({{\displaystyle \prod }}_{i=1}^n{x}_i-F{{\displaystyle \sum }}_{i=1}^n{x}_i\right)\right)=0, \\ \frac{\delta }{\delta x_2}\left({{\displaystyle \sum }}_{i=1}^n{x}_i-\lambda \left({{\displaystyle \prod }}_{i=1}^n{x}_i-F{{\displaystyle \sum }}_{i=1}^n{x}_i\right)\right)=0, \\ \dots \\ \frac{\delta }{\delta \lambda }\left({{\displaystyle \sum }}_{i=1}^n{x}_i-\lambda \left({{\displaystyle \prod }}_{i=1}^n{x}_i-F{{\displaystyle \sum }}_{i=1}^n{x}_i\right)\right)=0. \end{gathered}$$

Partial differentiation leads to

$$\begin{gathered} 1-\lambda {{\displaystyle \prod }}_{i=2}^n{x}_i+\lambda F=0, \\ 1-\lambda {{\displaystyle \prod }}_{i=1,\mathrm{i}\ne 2}^n{x}_i+\lambda F=0, \\ \dots \\ 1-\lambda {{\displaystyle \prod }}_{i=1}^{n-1}{x}_i+\lambda F=0, \\ {{\displaystyle \prod }}_{i=1}^n{x}_i-F{{\displaystyle \sum }}_{i=1}^n{x}_i=0. \end{gathered}$$

Substituting ${{\displaystyle \prod }}_{i=1,i\ne j}^n{x}_i=\frac{F}{x_j}{{\displaystyle \sum }}_{i=1}^n{x}_i$ from the last equation for each x_i into the first n equations, followed by multiplying both sides of each i-th equation with x_i, we obtain

$$\begin{array}{c}{x}_1-\lambda F{{\displaystyle \sum }}_{i=1}^n{x}_i+\lambda F{x}_1=0,\\ x_2-\lambda F{{\displaystyle \sum }}_{i=1}^n{x}_i+\lambda F{x}_2=0,\\ \dots \\ x_n-\lambda F{{\displaystyle \sum }}_{i=1}^n{x}_i+\lambda F{x}_n=0.\end{array}\}$$

(12)

Summing the left sides yields

$${{\displaystyle \sum }}_{i=1}^n{x}_i-n\lambda F{{\displaystyle \sum }}_{i=1}^n{x}_i+\lambda F{{\displaystyle \sum }}_{i=1}^n{x}_i=0,$$

which implies $\lambda =1/F\left(n-1\right)$. Substituting $\frac{1}{F\left(n-1\right)}$ for λ into (12) leads to

$$x_1=x_2=\dots =x_n=\frac{{{\displaystyle \sum }}_{i=1}^n{x}_i}{n}.$$

(13)

Thus, all terms of the critical point of f(X) constrained by g(X) are equal. Restoring integrality, we designate the solution of (1) at the critical point A_m = (a_m, a_m, ..., a_m):

$$\begin{gathered} {{\displaystyle \prod }}_{i=1}^n{a}_m=F{{\displaystyle \sum }}_{i=1}^n{a}_m, a_m\in {\mathbb{Z}}^{+}, \\ {\left(a_m\right)}^{n-1}=nF, \end{gathered}$$

(14)

$${\displaystyle \sum }_{i=1}^n{a}_m=\sqrt[n-1]{n^{n}F}.$$

(15)

The Diophantine Equation (14) is solvable when nF is an (n − 1)-power, which is true for $F=n^{n-2}{m}^{n-1}$ with m ∈ ℤ⁺. Computational results for selected values of n and F are shown in

Table 1. Sum of solution terms of ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i; x_i,F\in {\mathbb{Z}}^{+}$ for selected n and F.

n	F	$\sqrt[\mathit{n}-1]{{\mathit{n}}^{\mathit{n}}\mathit{F}}$	No. of Solutions	Smallest Sum of Solution Terms	Largest Sum of Solution Terms
3	2	7.348...	3	8	12
3	3	9	6	9	20
3	16	20.784...	18	21	306
3	27	27	32	27	812
3	54	38.183...	50	40	3080
3	125	58.094...	71	60	16,002
3	2000	232.370...	624	238	4,006,002
4	2	8	5	8	15
4	3	9.158...	4	12	24
4	16	16	30	16	323
4	27	19.048...	27	20	840
4	54	24	108	24	3135
4	125	31.748...	47	36	16,128
4	2000	80	1223	80	4,008,003
5	2	8.891...	3	12	18
5	3	9.839...	6	12	28
5	16	14.953...	35	16	340
5	27	17.043...	50	18	868
5	54	20.268...	77	24	3190
5	125	25	92	25	16,254
5	2000	50	1476	50	4,010,004

. The results illustrate that the sum of solution terms of (1) is bounded from below by (15). When $\sqrt[n-1]{n^{n}F}$ is an integer, it equals the sum of terms of the solution with the lowest sum of terms.

The inspection of computational results confirmed that solutions with the sum of terms given exactly by $\sqrt[n-1]{n^{n}F}$ consisted of equal terms. This is reminiscent of the fact that among n-tuples with the same product of terms, n-tuples consisting of equal terms have the lowest sum of terms, as can be proved by the AM-GM inequality [26]. Thus, the constraint has not affected the minimum of the objective function. The situation is different regarding the upper bound, as will be shown in the next section.

The lower bound in Table 1 increased with n for F ≤ 3, while it decreased with n for F ≥ 16. We assumed that $\sqrt[n-1]{n^{n}F}$ has a minimum below 3 for F ≤ 3 and above 5 for F ≥ 16. The first-derivative test for n, F ∈ ℝ leads to

$$\frac{\partial }{\partial n}\left(\sqrt[n-1]{n^{n}F}\right)=\frac{\sqrt[n-1]{n^{n}F}\cdot \left(\ln \left(n\right)-n+\ln \left(F\right)+1\right)}{{\left(n-1\right)}^2}=0.$$

The critical point implicitly defined by $\left(n-\ln \left(n\right)\right)=\left(\ln \left(F\right)+1\right)$ is indeed a minimum, as computation shows: switching back to integers, the minimum for F = 16 occurs at n = 5, for F = 27 at n = 6, and for F = 2000 at n = 11. Past the minimum, the lower bound for the sum of solution terms grows with n but the growth is very slow. For instance, the lower bound for the sum of solutions terms of ${\displaystyle \prod }_{i=1}^{20}{x}_i=2000\cdot {\displaystyle \sum }_{i=1}^{20}{x}_i$ is 35 but for ${\displaystyle \prod }_{i=1}^{100}{x}_i=2000\cdot {\displaystyle \sum }_{i=1}^{100}{x}_i$ it is only 113.

7. Diophantine Equation ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$: Un Upper Bound for the Sum of Solution Terms Is $\left(F+1\right)\left(F+n-1\right)$

An upper bound for the sum of terms of solutions of ${\displaystyle \prod }_{i=1}^3{x}_i=F{\displaystyle \sum }_{i=1}^3{x}_i$ is known to be (F + 1)(F + 2) [22,23]. In Section 2, an upper bound for the sum of solution terms of ${\displaystyle \prod }_{i=1}^2{x}_i=F{\displaystyle \sum }_{i=1}^2{x}_i$ was shown to be F² + 2F + 1 (Theorem 2). In the following, we shall establish an upper bound for the sum of the solution terms of (1) for any n, based on the parametric solution established in Section 5 and Lemma 1 about a special kind of variable mixing.

Lemma 1.

Let A be an n-tuple of positive rational numbers and a_j, a_k two of its terms satisfying the inequalities 1 < a_j ≤ a_k. Let B be an n-tuple of positive rational numbers with b_i = a_i for 1 ≤ i ≤ n, i ≠ j, i ≠ k. If b_j < a_j, b_k > a_k, and $\frac{{{\displaystyle \prod }}_{i=1}^n{b}_i}{{{\displaystyle \sum }}_{i=1}^n{b}_i}=\frac{{{\displaystyle \prod }}_{i=1}^n{a}_i}{{{\displaystyle \sum }}_{i=1}^n{a}_i}$, then ${\displaystyle \sum }_{i=1}^n{b}_i>{\displaystyle \sum }_{i=1}^n{a}_i$.

Proof. 

We set a_k = a_j + r with r ∈ ℚ⁺, b_j = (a_j − α) with α ∈ ℚ⁺ and α < a_j, and b_k = a_j + r + β with β ∈ ℚ⁺. Equating the quotients of products and sums of A and B, we have

$$\frac{a_j\left(a_j+r\right){{\displaystyle \prod }}_{i=1,i\ne j,i\ne k}^n{a}_i}{{{\displaystyle \sum }}_{i=1}^n{a}_i}=\frac{\left(a_j-\alpha \right)\left(a_j+r+\beta \right){{\displaystyle \prod }}_{i=1,i\ne j,i\ne k}^n{a}_i}{{{\displaystyle \sum }}_{i=1}^n{a}_i-\alpha +\beta }.$$

Multiplying by the denominators, factoring, and substituting ${\displaystyle \sum }_{i=1}^n{a}_i-\left(a_j+r\right)$ for ${\displaystyle \sum }_{i=1,i\ne k}^n{a}_i$ leads to

$$\alpha \left(r+\beta \right){\displaystyle \sum }_{i=1}^n{a}_i=a_j\left(\beta -\alpha \right){\displaystyle \sum }_{i=1,i\ne k}^n{a}_i.$$

Because the LHS is positive, β > α, and therefore

$${\displaystyle \sum }_{i=1}^n{b}_i={\displaystyle \sum }_{i=1}^n{a}_i-\alpha +\beta >{\displaystyle \sum }_{i=1}^n{a}_i.$$

The lemma is proved. □

Now, we prove an upper bound for the sum of solution terms of (1).

Theorem 5.

Let${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ be a Diophantine equation with $F,x_i\in {\mathbb{Z}}^{+}$. The sum of terms of any solution $A=\left(a_1,a_2,\dots ,a_n\right)$is bounded from above by

$${\displaystyle \sum }_{i=1}^n{a}_i\le \left(F+1\right)\left(F+n-1\right).$$

(16)

Proof. 

The n-tuple $A=\left(1,1,\dots ,1,\left(F+1\right),F\left(F+n-1\right)\right)$ solves the equation because

$$\begin{gathered} {\displaystyle \prod }_{i=1}^n{a}_i=\left({\displaystyle \prod }_{i=1}^{n-2}1\right)\cdot \left(F+1\right)\cdot F\left(F+n-1\right) \\ =F\left[n-2+\left(F+1\right)+F\left(F+n-1\right)\right]=F{\displaystyle \sum }_{i=1}^n{a}_i. \end{gathered}$$

The sum of terms of A is

$$\begin{array}{l}{\displaystyle {\displaystyle \sum }_{i=1}^n}{a}_i=n-2+\left(F+1\right)+F\left(F+n-1\right)=\left(F+n-1\right)+F\left(F+n-1\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\left(F+1\right)\left(F+n-1\right).\end{array}$$

We shall show that any solution $C=\left(c_1,c_2,\dots ,c_n\right)$ with c_i ∈ ℤ⁺ and at most (n − 3) terms equaling 1 can be converted into A via a series of n-tuples such that the sum of terms of each n-tuple is larger than the sum of terms of the previous n-tuple. The n-tuple is re-ordered ascendingly; one of c_j such that 1 ≤ j ≤ (n − 2) and c_j > 1 is replaced with 1; and c_n−1 is increased in such a way that the quotient of the product and sum of terms remains F. According to Lemma 1, the sum of terms increased.

If any c_j with 1 ≤ j ≤ (n − 2) is larger than 1, the process is repeated. If all c_j with 1 ≤ j ≤ (n − 2) equal 1, the conversion is completed. According to the new value of c_n−1, we now distinguish two cases.

• Case 1:${\mathrm{c}}_{n-1}=\left(F+1\right)$. Because the first (n − 2) terms equal 1 and the quotient of product and sum of terms equals F, c_n must equal $F\left(F+n-1\right)$. Therefore, the n-tuple is identical with A and the sum of its terms equals $\left(F+1\right)\left(F+n-1\right).$ Because in each step of the conversion the sum of terms increased, the sum of terms of any solution of (1) is smaller than or equal to $\left(F+1\right)\left(F+n-1\right).$
• Case 2:$c_{n-1}>\left(\mathrm{F}+1\right).$ Then, c_n-1 is replaced with (F + 1) and c_n is increased to keep the quotient of product and sum of terms equal to F, which implies that c_n becomes $F\left(F+n-1\right)$. According to Lemma 1, the sum of terms increased. The conversion is completed. Further reasoning of Case 1 applies.

It remains to be shown that c_n−1 cannot be smaller than (F + 1). Re-arranging the Equation (1) as

$$c_n\left({{\displaystyle \prod }}_{i=1}^{n-1}{c}_i-F\right)=F{{\displaystyle \sum }}_{i=1}^{n-1}{c}_i$$

shows that

$$\begin{gathered} {{\displaystyle \prod }}_{i=1}^{n-1}{c}_i>F, \\ {c}_{n-1}\cdot {{\displaystyle \prod }}_{i=1}^{n-2}1=c_{n-1}>F. \end{gathered}$$

Because c_n−1 is an integer, it cannot be smaller than (F + 1). □

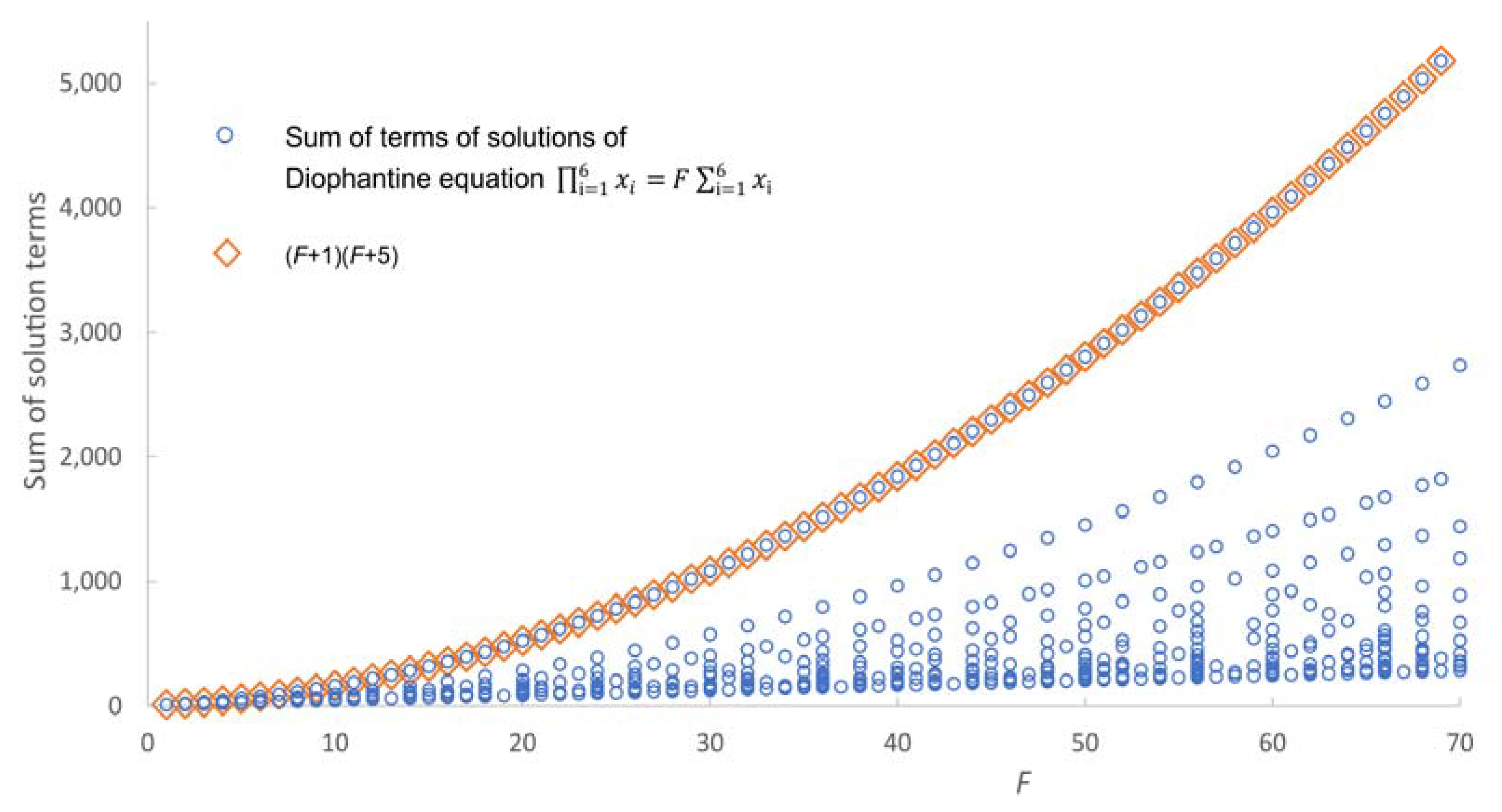
All experimentally determined largest sums of solution terms shown in Table 1 equal the upper bounds for the sum of solutions terms of (1) according to (16). Figure 4 shows the sums of solution terms of all 3070 solutions of (1) with n = 6 and F ≤ 70 together with the upper bound. The figure illustrates that for any F, a solution with the sum of terms equal to the upper bound (16) exists.

8. Diophantine Equation ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ with n ≥ 4 and Distinct Terms: Solvability

The upper bound derived in the previous section is based on solutions with the first (n − 2) terms equal to 1. Such n-tuples have been used in constructive proofs because they simplify handling products and sums [13,24,25]. However, they are special, and one may argue that they do not represent solutions of (1) adequately. Therefore, in the following we shall consider solutions consisting of distinct terms. Without loss of generality, the terms of such solutions can be ordered ascendingly:

$${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i, x_i,F\in {\mathbb{Z}}^{+}, n\ge 4, x_1<x_2<\dots <x_n.$$

(17)

The solutions are totally ordered sets of cardinality n. Because (17) is a special case of (1), the sum of solution terms is bounded from above, and the number of solutions is finite. It is not known whether (17) is solvable for any F; if yes, how many solutions exist; and whether a stronger upper bound than (16) for the sum of solution terms can be found.

Parametric solutions help to answer questions about solvability. We found the following family of parametric solutions of (17) with n = 4 and any F > 2:

$$X=\left\{1,2,F,F+3\right\}.$$

A proof is readily obtained by substituting the terms into (17). Thus, the equation with n = 4 and any F > 2 is solvable. Inspection of all 19,787 solutions of (17) with n = 4 and F ≤ 300 revealed a single solution for F = 3 and more than one solution for 3 < F ≤ 300.

In contrast to n = 4, ${\displaystyle \prod }_{i=1}^5{x}_i=F{\displaystyle \sum }_{i=1}^5{x}_i$ is not solvable in distinct terms for all values of F. An inspection of all solutions of the equations with 7 < F ≤ 95, computed within the bounds for (1), showed that no solution in distinct terms exists for F equal to 10, 11, 13, 17, 26, 31, and 43. Similarly, the equations with n ∈ (6, 7, 8, 9) and certain values of F are not solvable in distinct positive integers (data not shown). A question arises whether for any n there exists a threshold M such that the Equation (17) with any F > M is solvable.

Because ${\displaystyle \prod }_{i=1}^5{x}_i=F{\displaystyle \sum }_{i=1}^5{x}_i$ is not solvable in distinct terms for all F, a general parametric solution cannot exist. With the help of computation (see also Section 10.1), parametric solutions for F satisfying certain conditions can, however, be found. The following parametric solution for F such that (F + 9) is evenly divided by 23 is an example:

$$X=\left\{2,3,4,\frac{F+9}{23},F\right\}, F+9=23k, k\ge 5.$$

A proof is readily obtained by substituting into (17). The recipe also works with k ∈ (2, 3, 4), but the terms of these solutions are not distinct.

9. Diophantine Equation ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ with n ≥ 4 and Distinct Terms: Upper Bound

Solutions of (1) in distinct terms are a subset of all solutions of (1); therefore, the sum of their terms is bounded from above by $\left(F+1\right)\left(F+n-1\right)$. In the following, we provide a stronger upper bound.

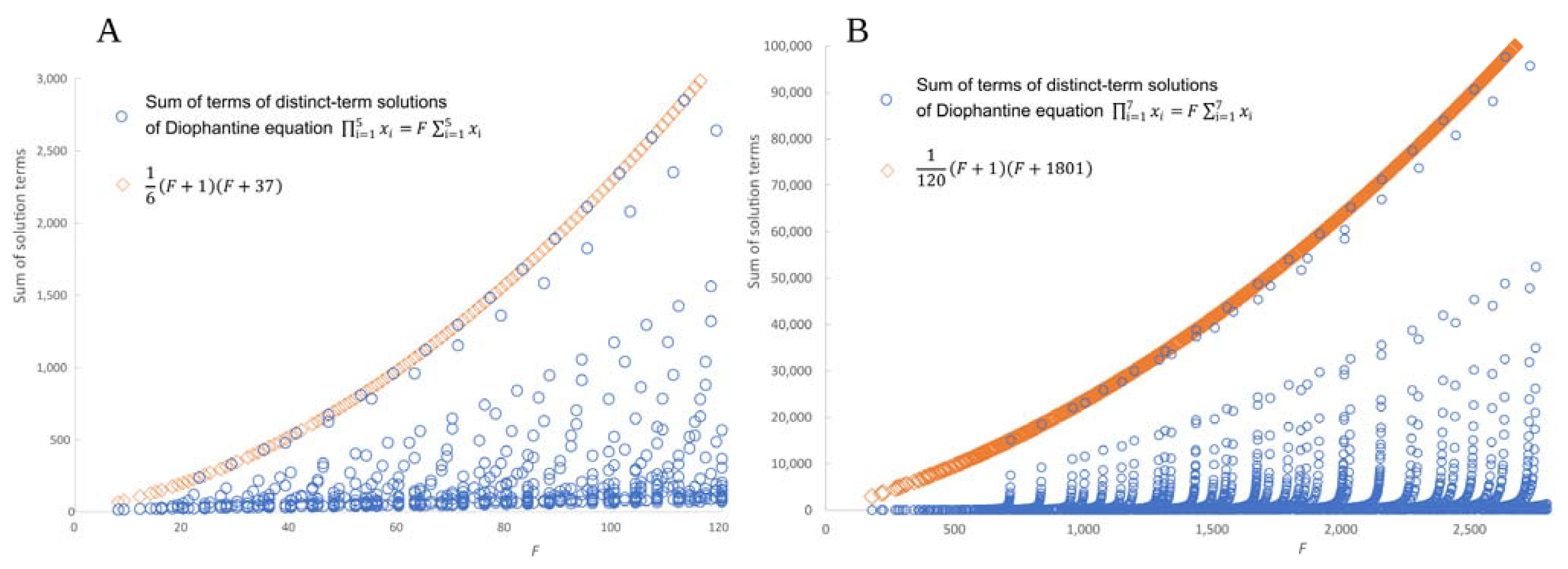
Conjecture 2.

Let${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$be a Diophantine equation with$x_i,F\in {\mathbb{Z}}^{+}$. The sum of terms of solutions consisting of distinct terms is bounded from above by

$$\frac{1}{\left(n-2\right)!}\left(F+1\right)\left(F+\frac{\left(n-2\right)\left(n-1\right)!}{2}+1\right).$$

(18)

We do not have a proof, but the conjecture is strongly supported by computation. Selected results are shown in Figure 5.

Figure 5 shows that for certain values of F, the conjectured upper bound matches the maximum sum of solution terms. These values of F satisfy the following conditions:

Conjecture 3.

Let${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$be a Diophantine equation with$x_i,F\in {\mathbb{Z}}^{+}$. The upper bound (18) for the sum of solution terms of distinct-term solutions equals the largest sum of terms of distinct-term solutions if and only if

$$F=\left(n+k-2\right)\left(n-2\right)!-1, k\in {\mathbb{Z}}^{+}.$$

(19)

A computational example for n = 8 and k ≤ 6 is shown in the upper part of Figure 6. For (17) with F not satisfying (19), the upper bound (18) is weak. When the constant term in (19) is replaced with divisors of (n + k − 2)(n − 2)! larger than 1, the formula generates F such that data points in the Cartesian systems with F on the abscissa and sum of solution terms on the ordinate form strings extending from their highest point downwards, as shown at Figure 6. This pattern is also apparent at Figure 5B, but the points are better separated when the vertical axis is scaled logarithmically as in Figure 7.

The smallest value of parameter F such that the sum of solution terms of (17) equals the upper bound (18) is obtained from (19) for k = 1, which leads to $F=\left(n-1\right)!-1$.

Table 2. Smallest sums of terms of distinct-term solutions of ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ for selected n and F such that ${\displaystyle \sum }_{i=1}^n{x}_i$ matches the upper bound (18).

n	$\mathit{F}=\left(\mathit{n}-\mathbf{1}\right)\mathbf{!}-\mathbf{1}$	Solution Matching the Upper Bound (18) *
4	5	(1, 2, 3, 30)
5	23	(1, 2, 3, 4, 230)
6	119	(1, 2, 3, 4, 5, 1.785)
7	719	(1, 2, 3, 4, 5, 6, 15.099)
8	5039	(1, 2, 3, 4, 5, 6, 7, 141.092)
9	40,319	(1, 2, 3, 4, 5, 6, 7, 8, 1.451.484)

* Period is used as a thousands-separator here because comma separates the terms.

shows such values of F for selected n together with the corresponding solutions with the largest sums of terms, revealing a monotonous structure of such solutions. Remark: because solutions consisting of consecutive numbers 1 to n have the lowest ratio of product and sum of terms among all distinct-term solutions, $2\frac{\left(n-1\right)!}{n+1}$ is a lower bound for F. In other words (17), F < $2\frac{\left(n-1\right)!}{n+1}$ is not solvable in distinct integers.

10. Discussion

10.1. Computational Enumeration of Solutions as a Discovery Tool

Search for parametric solutions has been an important task in research on Diophantine equations. That no general recipe for finding such solutions exists has deep roots. Such a recipe would make it possible to decide whether any Diophantine equation is solvable, which is impossible, as Matiyasevich–Robinson–Davis–Putnam theorem [27] proved. In search for parametric solutions, difficulty of discovery contrasts with ease of obtaining a proof, which is reminiscent of solving logical puzzles [28,29].

Computation was instrumental in the discovery of a parametric solution of ${\displaystyle \prod }_{i=1}^5{x}_i=F{\displaystyle \sum }_{i=1}^5{x}_i$ for F such that (F − 9) is a multiple of 23. This condition appears mysterious at first, but parametric solutions often depend on divisors, e.g., [30]. (In Conjecture 1, we suggest that certain parametric solutions of xy = F(x + y) must depend on the divisors of F or its powers.) We found it difficult to describe the process of computation-aided discovery. Even explaining the genesis of universal parametric solutions in Section 5 was difficult, though it was based on heuristic reasoning. We were not be able to reconstruct the computation-aided discovery of the distinct-term parametric solution of ${\displaystyle \prod }_{i=1}^5{x}_i=F{\displaystyle \sum }_{i=1}^5{x}_i$ described in Section 8, which is trivial to prove, nor could we retrace the genesis of the intriguing upper bound $\frac{1}{\left(n-2\right)!}\left(F+1\right)\left(F+\frac{\left(n-2\right)\left(n-1\right)!}{2}+1\right)$ for the sum of terms of distinct-term solutions (Section 9), which we were unable to prove. Computation was instrumental in both. Another example of a computation-aided discovery is the relationship between the number of solutions of xy = F(x + y) and the primality of F, which was exposed by inspection of computational results shown in Figure 3. The relation was subsequently proved in Theorems 3 and 4.

Computation that led to Conjecture 3 and its extensions at the bottom part of Figure 6 indicates that further treasures wait for discovery in the trove of distinct-term solutions of ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$.

10.2. Connection between Additive and Multiplicative Properties of Natural Numbers

The relationship between additive and multiplicative features is pivotal to understanding natural numbers. Diophantine Equation (1) connect the sums and products of n positive integers in a fundamentally simple way. A prominent system connecting the additive and multiplicative properties of integers is the Erdös–Szemerédi grid [31]. The authors counted distinct pairwise sums and products of a subset A ∈ ℕ with itself (designated sum set and product set) and studied upper bounds for the cardinalities ∣A + A∣ and ∣A⋅A∣. The system still attracts number theorists today. We wondered whether solutions of (17) generated interesting sum sets and product sets. Preliminary results indicate that ∣A⋅A∣ and ∣A + A∣ are statistically undistinguishable from the cardinalities of product sets and sum sets of randomly selected natural numbers within relevant boundaries (unpublished data).

10.3. Open Questions

Diophantine equations of higher degrees with many variables investigated so far were almost exclusively homogeneous equations or equation systems. Best-studied examples include equations consisting of sums of equal powers and systems of such equations (e.g., Prouhet-Tarry-Escott system, [9]), sums of equal powers with additional constraints [32], and many polynomial Diophantine equations (e.g., [33,34,35]). Several tools used to study Diophantine equations with many variables only work with homogeneous equations or require a number of variables vastly exceeding the degree. This may partly explain why only a few special cases of (1) have been studied so far (see Section 1). The existence of a universal parametric solution of (1) (Section 5), which happens to generate solutions with the largest sums of terms (Section 7), guarantees that (1) is solvable for any n and F. Noting is known about the number of solutions. Since an upper bound for the sum of solution terms is known, exhaustive enumeration of solutions by computation is possible. Limited data shown in Table 1 indicate that the number of solutions grows only moderately fast with n, contrary to expectations. Can we obtain an estimate of the mean number of solutions as a function of n and F? A possible strategy is to construct sets of n-tuples satisfying certain conditions implied by (1) using enumerative combinatorics and estimate the cardinality of their overlap. These sets could be sets of n-tuples (i) with sums of terms not exceeding the upper bound (16); (ii) such that the product of their terms is bounded from above by the upper bound for the sum of terms multiplied by F; and (iii) such that the product of terms is evenly divided by F.

Restricting (1) to solutions with distinct terms (a_j ≠ a_k for 1 ≤ j,k ≤ n and j ≠ k) opens new avenues and raises new questions. The equations of the 4th degree with any F are solvable, as proved by parametric solutions (1, 2, F, and F + 3). Equations of the 5th to 9th degree with some F, however, are not solvable in distinct positive integers (Section 8). Is there a positive integer M and a discrete function N = f(n) such that all equations ${\displaystyle \prod }_{i=1}^n{x}_i=F{\displaystyle \sum }_{i=1}^n{x}_i$ with n > M and F > N are solvable in distinct positive integers? Because the number of solutions grows with the degree of the equation (Table 1), it is even conceivable that there is an integer W such that all equations of a degree higher than W with F ≥ $2\frac{\left(n-1\right)!}{n+1}$ (a lower bound for F, see Section 9) are solvable in distinct positive integers. On the other hand, inspection of solutions indicates that with growing n, the gaps between F for which the equations are solvable are growing. For instance, (17) of the 6th degree with 225 ≤ F ≤ 269 has 267 solutions in distinct terms, while the equations of the 7th degree with any F from the same interval have no solution. (Remark: the smallest F for which the equation of the 7th degree is solvable is 180, which equals the lower bound for F, see Section 9). Thus, the relationship between n, F, and the number of solutions in distinct terms is unclear, and it is a promising topic for future research. The fact that the upper bound for the sum of terms of distinct-term solutions has not been proved and a lower bound is unknown will not hinder computational studies because weak bounds for the sum of non-distinct solution terms can be used instead.

The sums of terms of distinct-term solutions possess intriguing properties, as illustrated at Figure 6 and reflected by Conjectures 2 and 3. These conjectures are waiting for proofs. We suggest that examination of solutions found experimentally may provide hints leading to proofs. Furthermore, we conjecture that closed-form expressions for the sum of terms of distinct-term solutions based solely of n, F, and some free parameters can be found. Such expressions would allow one to draw structures similar to the one depicted in Figure 7 without actually solving the equations. Conjectures 2 and 3 and the parametric formula at the bottom of Figure 6, after they are proved, may serve as starting points to derive such expressions.