A Smart Helmet-Based PLS-BPNN Error Compensation Model for Infrared Body Temperature Measurement of Construction Workers during COVID-19
Abstract
:1. Introduction
2. Smart Helmet Development and Data Collection
2.1. Smart Helmet Temperature Measurement System
2.2. Influence Factors of Temperature Measurement Error
2.3. Smart Helmet Temperature Measurement Experiment
- The experimenter wore a smart helmet and held a digital anemometer. The experimenter pressed the storage function of the digital anemometer to save the real-time ambient wind speed (Figure 4).
- The experimenter used the ear temperature gun to measure his or her ear canal temperature, and then the recorder took a reading and recorded the value.
- At the same time, the recorder quickly recorded the measured temperature displayed on the helmet, the temperature and humidity inside helmet, the wind speed displayed on the anemometer, and the ambient temperature and humidity displayed on the ambient thermometer and hygrometer.
- In each recording, the true body temperature was recorded once. The helmet-measured temperature was recorded three times as measured temperature 1, measured temperature 2, and measured temperature 3. The average value was taken as the final measured temperature (MT) of the infrared temperature sensor to reduce the random error. The difference between the measured temperature and the true body temperature was recorded as the temperature error.
- The above steps were repeated, and data were recorded every 5 min. Each experiment lasted for 4 h. During the experiment, the experimenter was required to continuously walk around appropriately and wear the smart helmet continuously without removing the helmet until the end of the experiment. In order to simulate the different environments of indoor and outdoor construction, the experiment was divided into indoor and outdoor parts. The data categories and experiment durations were the same in both indoor and outdoor experiments for comparison purposes. The number of samples in each part was 245 sets, with a total of 490 sets. Figure 5 shows the distribution of the measured temperature and the true value of body temperature.
3. Modeling and Data Analysis
3.1. Modeling Method
3.2. Multicollinearity Analysis
3.3. Extraction of Principal Components
3.4. Fitting by BP Neural Network Model
4. Modeling and Data Analysis
4.1. Multicollinearity Analysis
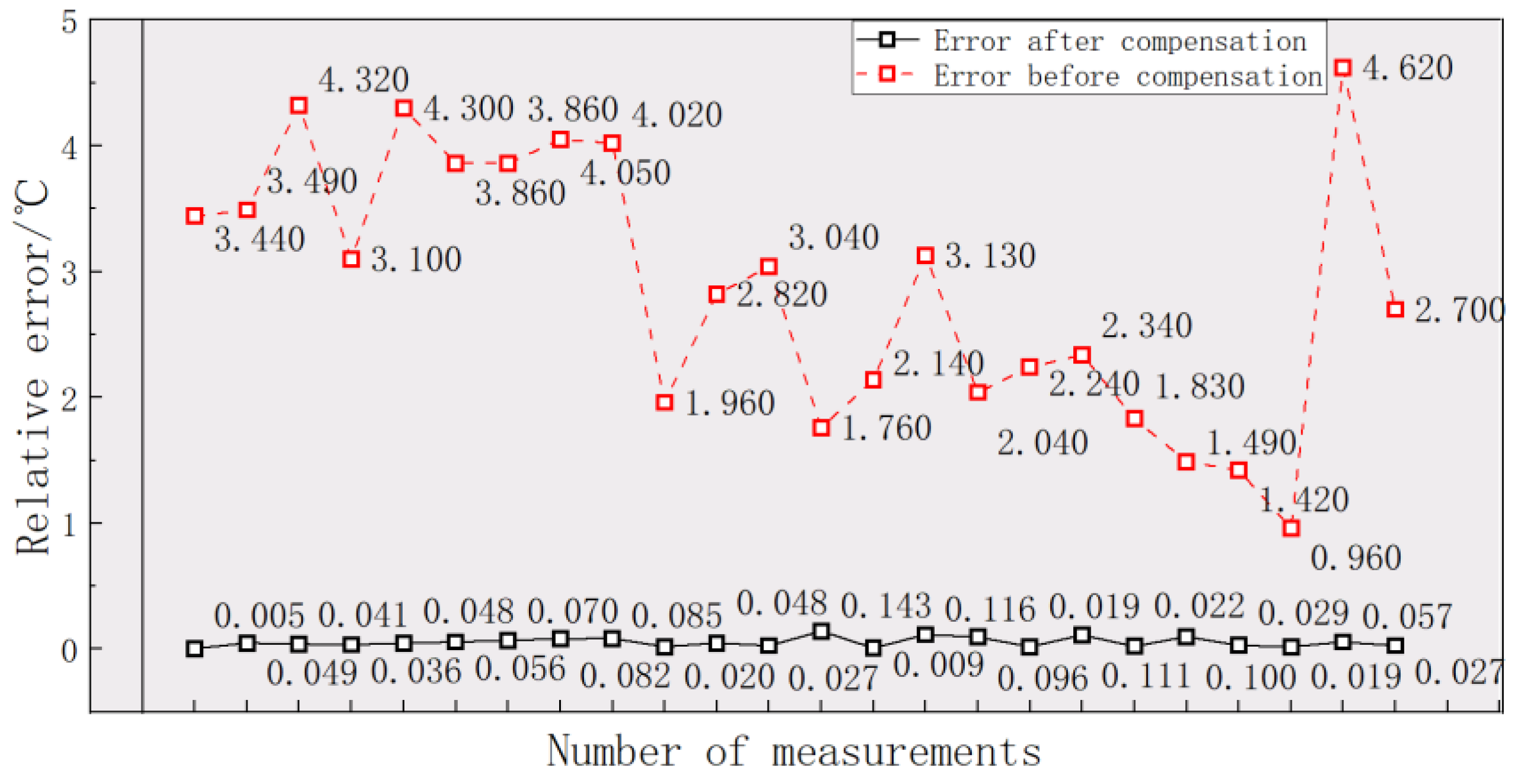
4.2. Infrared Temperature Measurement Compensation Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paules, C.I.; Marston, H.D.; Fauci, A.S. Coronavirus Infections—More Than Just the Common Cold. J. Am. Med Assoc. 2020, 323, 707–708. [Google Scholar] [CrossRef] [Green Version]
- Lippi, G.; Sanchis-Gomar, F.; Henry, B.M. COVID-19: Unravelling the clinical progression of nature’s virtually perfect biological weapon. Ann. Transl. Med. 2020, 8, 693. [Google Scholar] [CrossRef] [PubMed]
- Viswanathan, M.; Kahwati, L.; Jahn, B.; Giger, K.; Gartlehner, G. Universal screening for SARS-CoV-2 infection: A rapid review. Cochrane Database Syst. Rev. Online 2020, 9. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Zhu, B. Fever screening methods in public places during the COVID-19 pandemic. J. Hosp. Infect. 2021, 109, 123–124. [Google Scholar] [CrossRef] [PubMed]
- Lippi, G.; Mattiuzzi, C.; Henry, B. Is Body Temperature Mass Screening a Reliable and Safe Option for Preventing COVID-19 Spread? SSRN Electron. J. 2021. [Google Scholar] [CrossRef]
- Kodam, S.; Bharathgoud, N.; Ramachandran, H. A review on smart wearable devices for soldier safety during battlefield using WSN technology. Mater. Today Proc. 2020, 33, 4578–4585. [Google Scholar] [CrossRef]
- Sawant, P.; Godse, S.; Thigale, V.; Kasar, K. Arduino Based Smart Helmet for Coal Mine Safety. In Proceedings of the 2nd International Conference on Communication & Information Processing (ICCIP) 2020, Pune, India, 8 July 2020. [Google Scholar]
- Yong, J.A.; Kang, M.; Lee, T.G. Study on Remedies of Convergence Design for Personalized Fire Helmets. J. Korean Soc. Precis. Eng. 2016, 33, 371–376. [Google Scholar]
- Altamura, A.; Inchingolo, F.; Mevoli, G.; Boccadoro, P. SAFE: Smart helmet for Advanced Factory Environment. Internet Technol. Lett. 2019, 2, e86. [Google Scholar] [CrossRef] [Green Version]
- Aliyev, A.; Zhou, B.P. HeadgearX: A connected smart helmet for construction sites. In Proceedings of the 2020 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2020 ACM International Symposium on Wearable Computers, New York, NY, USA, 14 September 2020. [Google Scholar]
- Dell’Isola, G.B.; Cosentini, E.; Canale, L.; Ficco, G.; Dell’Isola, M. Noncontact Body Temperature Measurement: Uncertainty Evaluation and Screening Decision Rule to Prevent the Spread of COVID-19. Sensors 2021, 21, 346. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Matsunaga, D.; Tajima, T.; Seyama, M. Skin-attachable Sensor for Core Body Temperature Monitoring. IEEE Sens. J. 2021, 14, 1. [Google Scholar]
- Xu, K.; Zhao, L.; Yuan, Y. Measurement error analysis and compensation experiment research for medicinal infrared thermometer. Electron. Meas. Technol. 2014, 37, 104–118. [Google Scholar]
- Guo, Z.; Dai, S.; Liu, Z.; You, C.; Cheng, Y.; Yu, L. Research on application of polynomial fitting technique in rotary kiln infrared temperature measurement system. Infrared Phys. Technol. 2016, 79, 160–164. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Qin, W.; Han, L.; Cheng, F. The research on compensation algorithm of infrared temperature measurement based on intelligent sensors. Clust. Comput. 2019, 22, 6091–6100. [Google Scholar] [CrossRef]
- Shajkofci, A. Correction of human forehead temperature variations measured by non-contact infrared thermometer. IEEE Sens. J. 2021, 99, 1. [Google Scholar] [CrossRef]
- Ai, H.; Hu, M.; Liu, H.; Yu, H.; Wang, G.; Wang, W. Development of ear cavity infrared thermometer based on thermal radiation. Sens. Microsyst. 2020, 39, 94–96. [Google Scholar]
- Pan, D.; Jiang, Z.; Maldague, X.; Gui, W. Research on the Influence of Multiple Interference Factors on Infrared Temperature Measurement. IEEE Sens. J. 2021, 21, 10546–10555. [Google Scholar]
- Ning, B.; Wu, Y. Research on Non-Contact Infrared Temperature Measurement. In Proceedings of the 2010 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 10–12 December 2010. [Google Scholar]
- Shu, Q.; Dai, S.; Nie, H.; Yi, W. Dynamic temperature compensation model based on nonuniform temperature field change. Infrared Phys. Technol. 2019, 101, 25–31. [Google Scholar] [CrossRef]
- Church, J.S.; Hegadoren, P.R.; Paetkau, M.J.; Miller, C.C.; Regev-Shoshani, G.; Schaefer, A.L.; Schwartzkopf-Genswein, K.S. Influence of environmental factors on infrared eye temperature measurements in cattle. Res. Vet. Sci. 2014, 96, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Kamada, Y.; Miyamoto, N.; Yamakage, M.; Tsujiguchi, N.; Namiki, A. Utility of an infrared ear thermometer as an intraoperative core temperature monitor. Masui Jpn. J. Anesthesiol. 1999, 48, 1121. [Google Scholar]
- Gonzalez, A.J.; Teller, C.; Andersen, S.L.; Jensen, F.B. Influence of body temperature on the development of fatigue during prolonged exercise in the heat. J. Appl. Physiol. 1999, 86, 1032–1039. [Google Scholar] [CrossRef] [Green Version]
- Campa, F.; Gatterer, H.; Lukaski, H.; Toselli, S. Stabilizing Bioimpedance-Vector-Analysis Measures With a 10-Minute Cold Shower After Running Exercise to Enable Assessment of Body Hydration. Int. J. Sports Physiol. Perform. 2019, 14, 1006–1009. [Google Scholar] [CrossRef]
- Emerson, D.M.; Chen, S.C.; Kelly, M.R.; Parnell, B. Non-steroidal anti-inflammatory drugs on core body temperature during exercise: A systematic review. J. Exerc. Sci. Fit. JESF 2021, 19, 127–133. [Google Scholar] [CrossRef]
- Werth, J.; Sigman, M.S. Linear Regression Model Development for Analysis of Asymmetric Copper Bisoxazoline Catalysis. ACS Catal. 2021, 11, 3916–3922. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J. Residential land leasing and price under public land ownership. J. Urban Plan. Dev. 2021, 147, 05021009. [Google Scholar] [CrossRef]
- Cheng, J. Analysis of commercial land leasing of the district governments of Beijing in China. Land Use Policy 2021, 100, 104881. [Google Scholar] [CrossRef]
- Cheng, J. Data analysis of the factors influencing the industrial land leasing in Shanghai based on mathematical models. Math. Probl. Eng. 2020, 2020, 9346863. [Google Scholar] [CrossRef] [Green Version]
- Cheng, J. Mathematical Models and Data Analysis of Residential Land Leasing Behavior of District Governments of Beijing in China. Mathematics 2021, 9, 2314. [Google Scholar] [CrossRef]
- Mancini, M.; Taavitsainen, V.; Toscano, G. Comparative study between Partial Least Squares and Rational function Ridge Regression models for the prediction of moisture content of woodchip samples using a handheld spectrophotometer. J. Chemom. 2021, 35, e3337. [Google Scholar] [CrossRef]
- Panzone, L.; Ulph, A.; Areal, F.; Grippo, V. A ridge regression approach to estimate the relationship between landfill taxation and waste collection and disposal in England. Waste Manag. 2021, 129, 95–110. [Google Scholar] [CrossRef] [PubMed]
- Ataman, M.G.; Saryer, G. Predicting waiting and treatment times in emergency departments using ordinal logistic regression models. Am. J. Emerg. Med. 2021, 46, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J. Analyzing the factors influencing the choice of the government on leasing different types of land uses: Evidence from Shanghai of China. Land Use Policy 2020, 90, 104303. [Google Scholar] [CrossRef]
- He, S.; Wang, Y. A Modified APLS for Key Performance Indicator-Related Diagnosis in Case of Outliers. In Proceedings of the Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017. [Google Scholar]
- Zhang, J.; Lou, Y. Water Level Prediction Based on Improved Grey RBF Neural Network Model. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016. [Google Scholar]
- Herawati, N.; Nisa, K.; Setiawan, E. Regularized Multiple Regression Methods to Deal with Severe Multicollinearity. Int. J. Stat. Appl. 2018, 8, 167–172. [Google Scholar]
- Evans, M. A partial least squares solution to the problem of multicollinearity when predicting the high temperature properties of 1Cr–1Mo–0.25V steel using parametric models. J. Mater. Sci. 2012, 47, 2712–2724. [Google Scholar] [CrossRef]
- Cai, T.; Ju, C.; Yang, X. Comparison of Ridge Regression and Partial Least Squares Regression for Estimating Above-Ground Biomass with Landsat Images and Terrain Data in Mu Us Sandy Land, China. Arid. Land Res. Manag. 2009, 23, 248–261. [Google Scholar] [CrossRef]
- Polat, E.; Gunay, S. The comparison of partial least squares regression, principal component regression and ridge regression with multiple linear regression for predicting pm10 concentration level based on meteorological parameters. J. Data Ence 2015, 13, 663–692. [Google Scholar]
- Fita, K.; Arief, W. Principal Component Analysis (PCA) untuk Mengatasi Multikolinieritas terhadap Faktor Angka Kejadian Pneumonia Balita di Jawa Timur Tahun 2014. J. Biom. Dan Kependud. 2018, 6, 89. [Google Scholar]
- Khedhe, L.; Ramirez, J.; Gorriz, J.M.; Brahim, A.; Segovia, F. Early diagnosis of Alzheimers disease based on partialleast squares, principal component analysis and support vector machine using segmented MRI images. Neurocomputing 2015, 151, 139–150. [Google Scholar] [CrossRef]
- Li, M.; Verma, B. An Improved RBF Neural Network Approach to Nonlinear Curve Fitting. Adv. Comput. Intell. 2015, 9095, 262–275. [Google Scholar]
- Wang, G.; Wu, J.; Yin, S.; Yu, L.; Wang, J. Comparison between BP Neural Network and Multiple Linear Regression Method. In Proceedings of the Information Computing and Applications—First International Conference, ICICA 2010, Tangshan, China, 15–18 October 2010. [Google Scholar]
- An, Y.; Wang, X.; Qu, Z.; Liao, T.; Wu, L.; Nan, Z. Stable temperature calibration method of fiber Bragg grating based on radial basis function neural network. Opt. Eng. 2019, 58, 1. [Google Scholar] [CrossRef]
- Wu, W.; Wang, J.; Cheng, M.; Li, Z. Convergence analysis of online gradient method for BP neural networks. Neural Netw. 2019, 24, 91–98. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, H. The Forecasting Method for the Furnace Bottom Temperature and Carbon Content of Submerged Arc Furnace Based on Improved BP Neural Network. In Proceedings of the International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010. [Google Scholar]
- Qiu, J.W.; Liu, Z.G.; Zhou, L.; Qin, R.X. Prediction Model of Gas Quantity Emitted from Coal Face Based on PCA-GA-BP Neural Network and Its Application. J. Power Technol. 2017, 97, 169–178. [Google Scholar]
- Habshah, M.; Saroje, S.; Sohel, R. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar]
- Aylin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77, 33–42. [Google Scholar] [CrossRef]
- Gilbert, C.L. The Diagnosis of Multicollinearity. Oxf. Bull. Econ. Stat. 2010, 40, 87–91. [Google Scholar] [CrossRef]
- O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M. Lennart Eriksson, PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Buscema, M. Back Propagation Neural Networks. Subst. Use Misuse 1998, 33, 233–270. [Google Scholar] [CrossRef]
- Torrontegui, E.; Garcia-Ripoll, J. Universal quantum perceptron as efficient unitary approximators. Europhys. Lett. 2018, 125, 30004. [Google Scholar] [CrossRef] [Green Version]
- Ilunga, M.; Stephenson, D. Infilling streamflow data using feed-forward back-propagation (BP) artificial neural networks: Application of standard BP and pseudo Mac Laurin power series BP techniques. Water SA 2005, 31, 171–176. [Google Scholar] [CrossRef] [Green Version]
- Langer, S. Approximating smooth functions by deep neural networks with sigmoid activation function. J. Multivar. Anal. 2021, 182, 104696. [Google Scholar] [CrossRef]










| Variable | Tolerance | VIF |
|---|---|---|
| Measured temperature | 0.271 | 3.684 |
| Ambient temperature | 0.280 | 3.577 |
| Ambient humidity | 0.118 | 8.468 |
| Temperature inside helmet | 0.191 | 5.234 |
| Humidity inside helmet | 0.171 | 5.845 |
| Wind speed | 0.663 | 1.509 |
| Model | Number of Components | RMSE | Relative Error/Count | |||
|---|---|---|---|---|---|---|
| <0.1 °C | 0.1 °C~0.3 °C | >0.3 °C | ||||
| LSR | 6 | 0.96079 | 0.242418341 | 162 | 221 | 107 |
| PLSR | 3 | 0.97542 | 0.192571607 | 180 | 264 | 46 |
| BPNN | 6 | 0.98915 | 0.129683998 | 272 | 208 | 10 |
| PLS-BPNN | 3 | 0.99377 | 0.092084235 | 372 | 116 | 2 |
| Measured Temperature (°C) | Ambient Temperature (°C) | Ambient Humidity (%) | Temperature Inside Helmet (°C) | Humidity Inside Helmet (%) | Wind Speed (m/s) | Temperature Error (°C) |
|---|---|---|---|---|---|---|
| 33.05 | 26.41 | 71.75 | 28.79 | 70.86 | 3.65 | 3.44 |
| 33.12 | 26.35 | 42.95 | 24.04 | 49.26 | 1.45 | 3.49 |
| 32.47 | 27.70 | 47.09 | 24.22 | 44.09 | 1.99 | 4.32 |
| 33.51 | 29.07 | 46.55 | 28.79 | 48.14 | 0.38 | 3.10 |
| 32.32 | 28.14 | 40.6 | 24.81 | 48.55 | 1.34 | 4.30 |
| 32.71 | 26.98 | 42.69 | 24.20 | 50.00 | 1.01 | 3.86 |
| 32.74 | 27.55 | 42.69 | 24.58 | 50.00 | 2.71 | 3.86 |
| 32.75 | 27.03 | 46.78 | 24.39 | 46.3 | 2.75 | 4.05 |
| 32.77 | 27.46 | 46.94 | 24.44 | 47.16 | 3.11 | 4.02 |
| 34.92 | 23.56 | 60.39 | 28.97 | 53.82 | 0 | 1.96 |
| 33.66 | 25.80 | 71.26 | 29.05 | 71.56 | 2.99 | 2.82 |
| 33.73 | 26.46 | 68.73 | 27.52 | 68.64 | 0 | 3.04 |
| 34.65 | 24.76 | 78.36 | 27.83 | 70.49 | 0 | 1.76 |
| 34.66 | 32.94 | 56.11 | 30.69 | 67.29 | 1.46 | 2.14 |
| 33.67 | 26.46 | 48.72 | 27.36 | 46.05 | 2.83 | 3.13 |
| 34.66 | 24.49 | 58.48 | 29.79 | 57.46 | 1.39 | 2.04 |
| 34.63 | 23.71 | 60.16 | 28.22 | 53.56 | 0 | 2.24 |
| 34.65 | 32.01 | 56.23 | 30.63 | 63.02 | 0.19 | 2.34 |
| 34.67 | 24.67 | 74.39 | 27.87 | 73.96 | 0 | 1.83 |
| 35.12 | 24.35 | 81.18 | 28.35 | 70.19 | 0 | 1.49 |
| 35.54 | 24.56 | 59.59 | 29.50 | 56.59 | 0 | 1.42 |
| 36.24 | 34.79 | 40.16 | 32.48 | 36.00 | 1.90 | 0.96 |
| 31.88 | 27.49 | 44.32 | 24.58 | 51.26 | 2.88 | 4.62 |
| 33.80 | 25.27 | 81.39 | 27.40 | 73.73 | 0 | 2.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Yu, J.; Cheng, H.; Peng, M. A Smart Helmet-Based PLS-BPNN Error Compensation Model for Infrared Body Temperature Measurement of Construction Workers during COVID-19. Mathematics 2021, 9, 2808. https://doi.org/10.3390/math9212808
Li L, Yu J, Cheng H, Peng M. A Smart Helmet-Based PLS-BPNN Error Compensation Model for Infrared Body Temperature Measurement of Construction Workers during COVID-19. Mathematics. 2021; 9(21):2808. https://doi.org/10.3390/math9212808
Chicago/Turabian StyleLi, Li, Jiahui Yu, Hang Cheng, and Miaojuan Peng. 2021. "A Smart Helmet-Based PLS-BPNN Error Compensation Model for Infrared Body Temperature Measurement of Construction Workers during COVID-19" Mathematics 9, no. 21: 2808. https://doi.org/10.3390/math9212808
APA StyleLi, L., Yu, J., Cheng, H., & Peng, M. (2021). A Smart Helmet-Based PLS-BPNN Error Compensation Model for Infrared Body Temperature Measurement of Construction Workers during COVID-19. Mathematics, 9(21), 2808. https://doi.org/10.3390/math9212808







