SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission
Abstract
1. Introduction
2. Materials and Methods
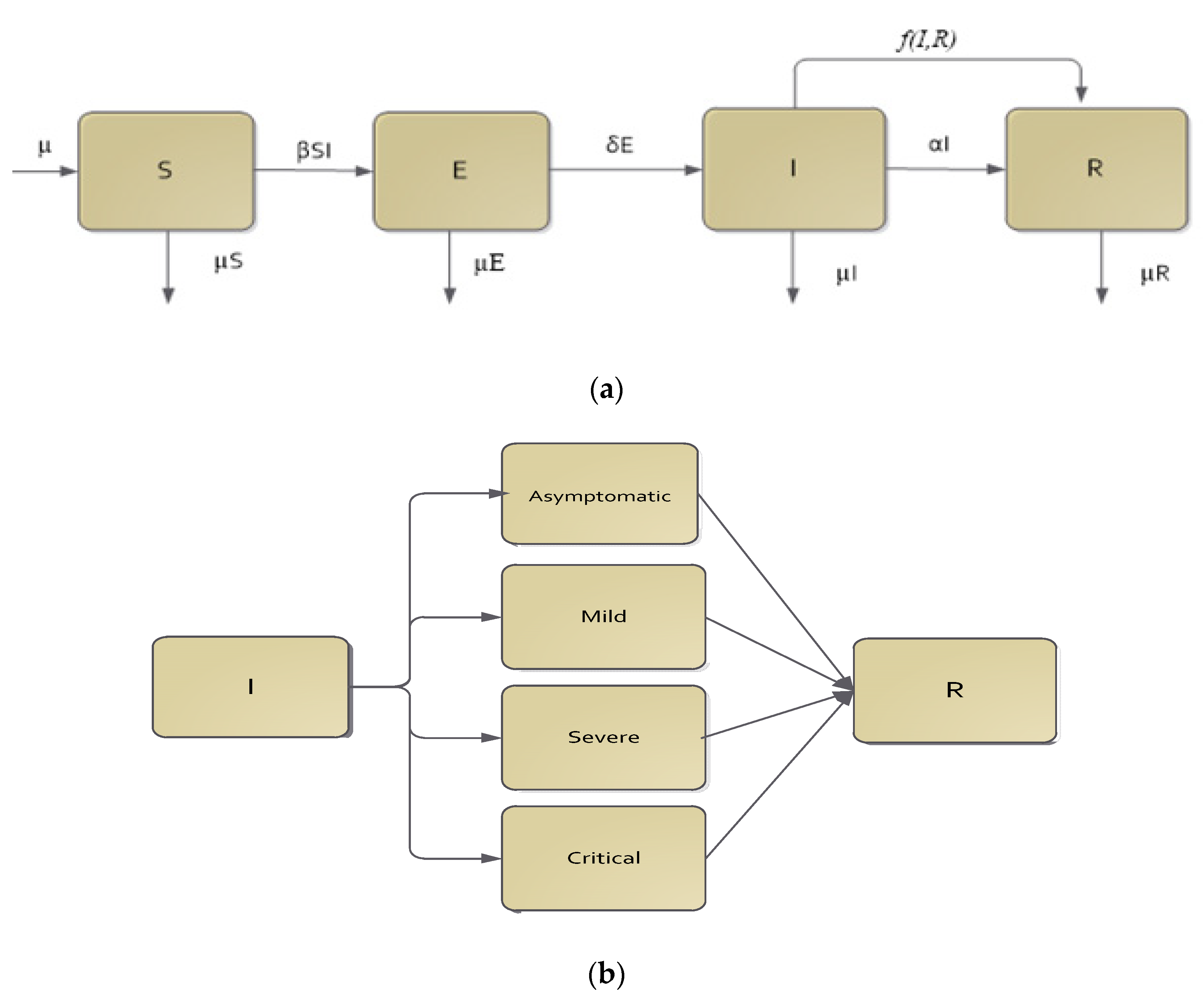
Mathematical Model
| β | Transmission rate; |
| δ | Transition rate from exposed class to infective class; |
| α | Recovery rate; |
| μ | Demographic rate (birth and death); |
| f(I,R) | Functional form, which together with ε, acts as the CPT intervention rate. |
3. Results and Discussions
3.1. The SEIR Continuous Model with CPT Proportional to Infective Class
- (a)
- A non-endemic equilibrium always exists, given by;
- (b)
- The endemic equilibrium is given by with:,,,.
- (c)
- There is a threshold, , such that an endemic equilibrium exists only if; otherwise, an endemic equilibrium does not exist.
- (a)
- is a non-endemic equilibrium, since all of the infected classes (E and I) are zero;
- (b)
- could be an endemic equilibrium, since all of the infected classes (E and I) could be positive for some parameter choices;
- (c)
- To prove this part of the theorem, we looked for a threshold number, so that , , , and . Note that by using some algebraic manipulation, it is easy to show that the components of the equilibrium can be re-written in the following forms:, , , and , with . Hence, it is clear that if , then and . □
- (a)
- The effective reproduction number;
- (b)
- The basic reproduction number.
- (a)
- Following the method in [24], with reference to Equations (5)–(8), we have the rate of appearance of new infections vector and the rate of transfer of individuals vector :and .
- (b)
- It is clear from (a) that when , then , which is the basic reproduction number of the model in Equations (5)–(8).
- (c)
- In addition, comparing the results to Theorem 1, obviously, we have , and consequently , which completes the proof. □
- ⇨
- ⇨
- ⇨
- ⇨
- .
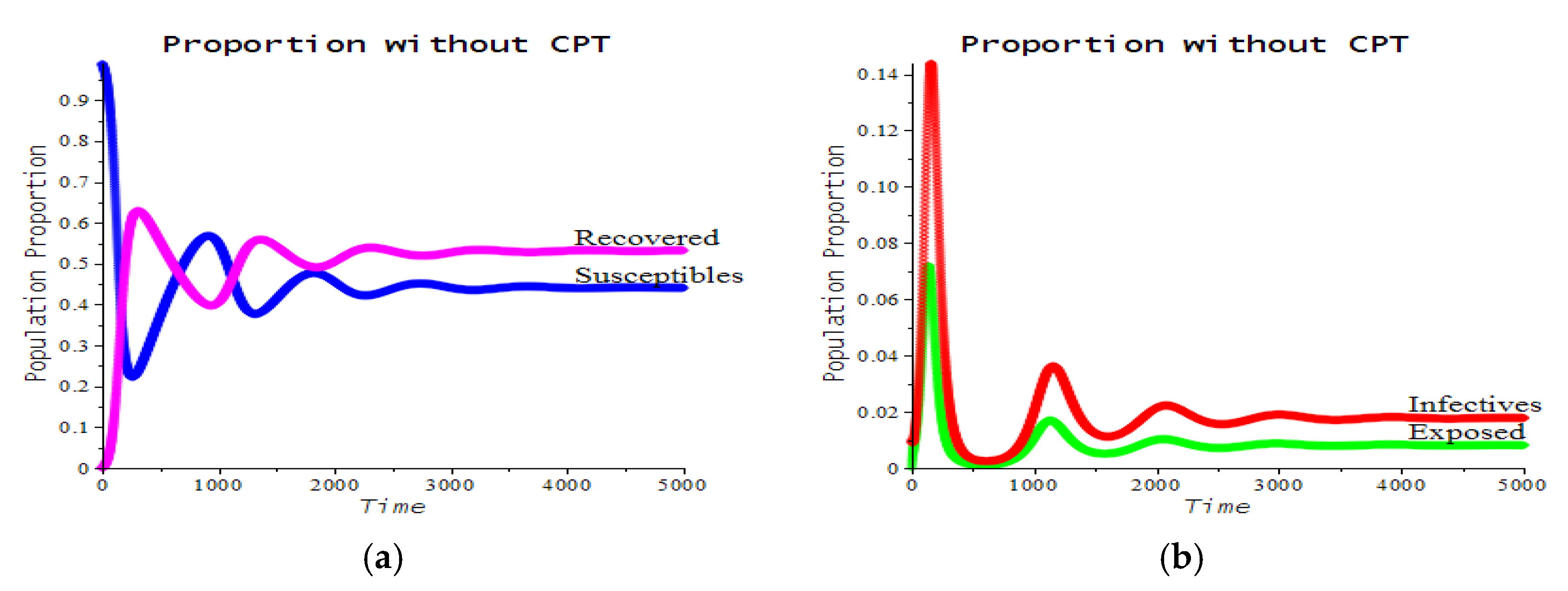
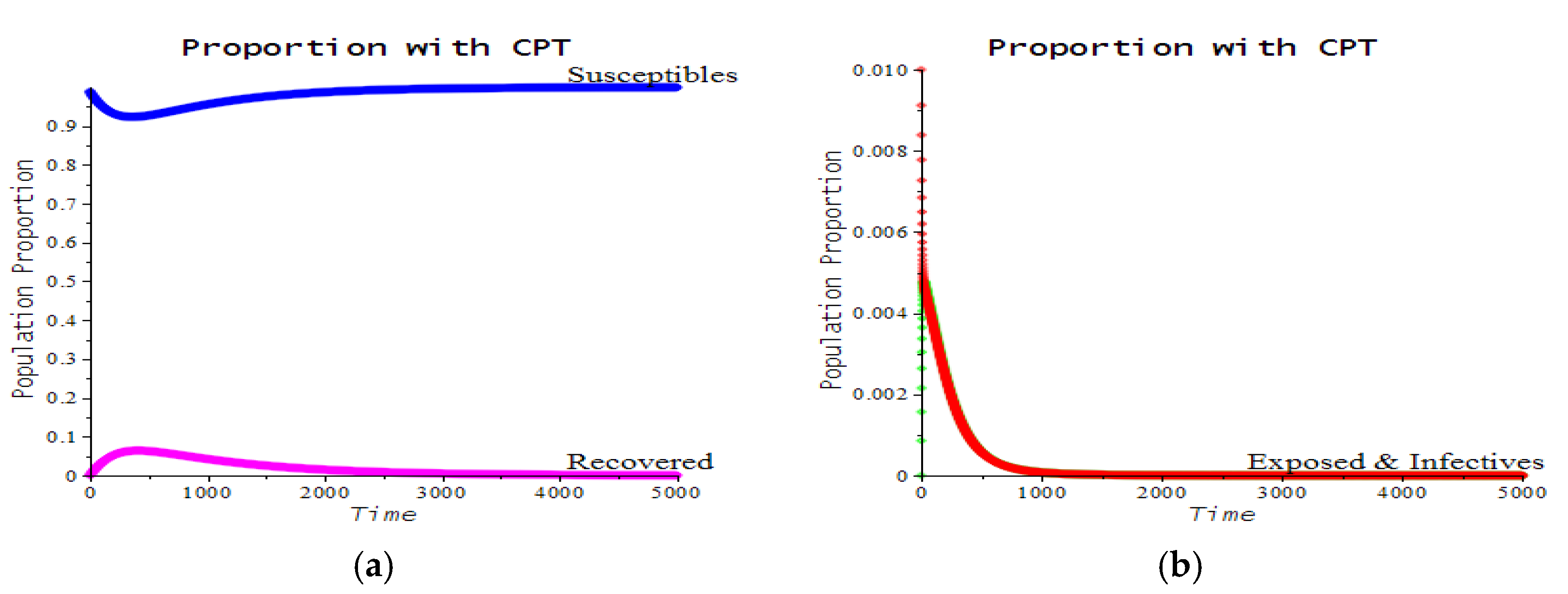
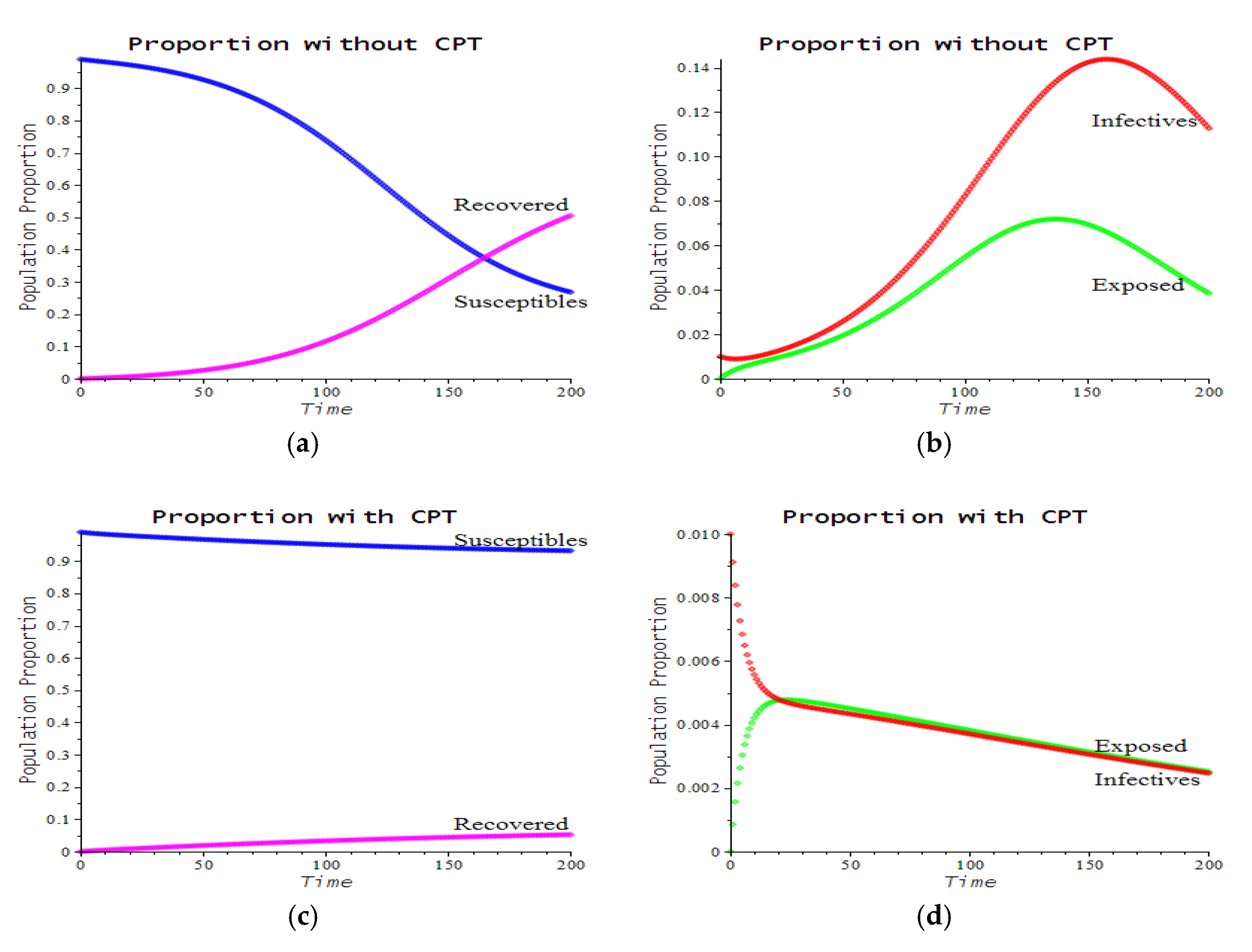
3.2. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- WHO. WHO Announces COVID-19 Outbreak a Pandemic. Available online: https://www.euro.who.int/en/health-topics/health-emergencies/coronavirus-covid-19/news/news/2020/3/who-announces-covid-19-outbreak-a-pandemic (accessed on 10 September 2021).
- Worldometer 2020. Available online: https://www.worldometers.info/coronavirus/ (accessed on 1 November 2021).
- FDA. FDA Issues Emergency Use Authorization for Convalescent Plasma as Potential Promising COVID–19 Treatment, Another Achievement in Administration’s Fight against Pandemic. Available online: https://www.fda.gov/news-events/press-announcements/fda-issues-emergency-use-authorization-convalescent-plasma-potential-promising-covid-19-treatment (accessed on 7 December 2020).
- Mayo Clinic. Patient Care & Health Information: Tests & Procedures: Convalescent Plasma Therapy. Available online: https://www.mayoclinic.org/tests-procedures/convalescent-plasma-therapy/about/pac-20486440 (accessed on 7 December 2020).
- Klassen, S.A.; Senefeld, J.W.; Johnson, P.W.; Carter, R.E.; Wiggins, C.C.; Shoham, S.; Grossman, B.J.; Henderson, J.P.; Musser, J.; Salazar, E.; et al. The Effect of Convalescent Plasma Therapy on Mortality among Patients With COVID-19: Systematic Review and Meta-Analysis. Mayo Clin. Proc. 2021, 96, 1262–1275. Available online: https://www.mayoclinicproceedings.org/article/S0025-6196(21)00140-3/fulltext (accessed on 18 October 2021). [CrossRef] [PubMed]
- CNN Indonesia. 4 RS di RI Yang Mulai Terapi Plasma Darah Obati Pasien Corona (in Bahasa Indonesia). Available online: https://www.cnnindonesia.com/teknologi/20200908163921-199-544140/4-rs-di-ri-yang-mulai-terapi-plasma-darah-obati-pasien-corona (accessed on 7 December 2020).
- Lewin, E. Australian COVID-19 Trials Add Convalescent Plasma as a Treatment. NewGP 30 July 2020. Available online: https://www1.racgp.org.au/newsgp/clinical/australian-covid-19-trials-add-convalescent-plasma (accessed on 1 November 2021).
- Agarwal, A.; Mukherjee, A.; Kumar, G.; Chatterjee, P.; Bhatnagar, T.; Malhotra, P.; on behalf of the PLACID Trial Collaborators. Convalescent plasma in the management of moderate COVID-19 in adults in India: Open label phase II multicentre randomised controlled trial (PLACID Trial). BMJ 2020, 371, 371. [Google Scholar] [CrossRef] [PubMed]
- Garroud, O.; Heshmati, F.; Pozzetto, B.; Lefrere, F.; Girot, R.; Saillol, A. Plasma therapy against infectious pathogens, as of yesterday, today and tomorrow. Transfus. Clin. Biol. 2016, 23, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Marson, P.; Cozza, A.; De Silvestro, G. The true historical origin of convalescent plasma therapy. Transfus. Apheresis Sci. 2020, 59, 102847. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Shi, Y. Convalescent plasma: Possible therapy for novel coronavirus disease 2019. Transfusion 2020, 60, 1078–1083. [Google Scholar] [CrossRef] [PubMed]
- Salazar, E.; Perez, K.K.; Ashraf, M.; Chen, J.; Castillo, B.; Christensen, P.A.; Eubank, T.; Bernard, D.W.; Eagar, T.N.; Long, S.W.; et al. Treatment of Coronavirus Disease 2019 (COVID-19) patients with convalescent plasma. Amer. J. Pathol. 2020, 190, 1680–1690. [Google Scholar] [CrossRef] [PubMed]
- Salazar, E.; Christensen, P.A.; Graviss, E.A.; Nguyen, D.T.; Castillo, B.; Chen, J.; Lopez, B.V.; Eagar, T.N.; Yi, X.; Zhao, P.; et al. Significantly decreased mortality in a large cohort of Coronavirus Disease 2019 (COVID-19) patients transfused early with convalescent plasma containing high-titer Anti-Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) spike protein IgG. Am. J. Pathol. 2020, 191, 90–107. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.T.; Rhind, S.G.; Beckett, A. Convalescent plasma for the prevention and treatment of COVID-19: A systematic review and quantitative analysis. JMIR Public Health Surveill. 2021, 7, e25500. [Google Scholar] [CrossRef] [PubMed]
- Huo, X.; Sun, X.; Bragazzi, N.L.; Wu, J. Effectiveness and feasibility of convalescent blood transfusion to reduce COVID-19 fatality ratio. Roy. Soc. Open Sci. 2020, 8, 202248. [Google Scholar] [CrossRef] [PubMed]
- Supriatna, A.K.; Husniah, H. Can convalescent plasma transfusion reduce the COVID-19 transmission? In Proceedings of the 2nd African International Conference on Industrial Engineering and Operations Management, IEOM, Harare, Zimbabwe, 7–10 December 2020; pp. 3116–3124. [Google Scholar]
- Nykamp, D.Q.; Morrissey, D.P. A Discrete SIR Infectious Disease Model. From Math Insight. Available online: http://mathinsight.org/discrete_sir_infectious_disease_model (accessed on 30 September 2021).
- Switkes, J. A Modified Discrete SIR Model. Coll. Math. J. 2003, 3, 399–402. [Google Scholar] [CrossRef][Green Version]
- Diekmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation, 1st ed.; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Anderson, R.M.; May, R.M.; Anderson, B. Infectious Diseases of Humans: Dynamics and Control, Revised ed.; Oxford University Press: London, UK, 1992. [Google Scholar]
- Brauer, F.; van den Driessche, P.; Wu, J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A.J. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Zhao, X.Q. The Theory of Basic Reproduction Ratios. In Dynamical Systems in Population Biology; Springer Nature Switzerland AG: Cham, Switzerland, 2003. [Google Scholar] [CrossRef]
- Klassen, S.A.; Senefeld, J.W.; Senese, K.A.; Johnson, P.W.; Wiggins, C.C.; Baker, S.E.; van Helmond, N.; Bruno, K.A.; Pirofski, L.; Shoham, S.; et al. Convalescent Plasma Therapy for COVID-19: A Graphical Mosaic of the Worldwide Evidence. Front. Med. 2021, 8, 684151. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.T.H.; Lin, H.M.; Baine, I.; Wajnberg, A.; Gumprecht, J.P.; Rahman, F.; Rodriguez, D.; Tandon, P.; Bassily-Marcus, A.; Bander, J.; et al. Convalescent plasma treatment of severe COVID-19: A propensity score–matched control study. Nat. Med. 2020, 26, 1708–1713. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wu, W.X.; Teng, Z.D. Complete dynamics in a nonlocal dispersal two-strain SIV epidemic model with vaccinations and latent delays. Appl. Comput. Math. 2020, 19, 360–391. [Google Scholar]
- Khalsaraei, M.M.; Shokri, A.; Ramos, H.; Heydari, S. A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease. Math. Comput. Simul. 2021, 182, 397–410. [Google Scholar] [CrossRef]
- Shokri, A.; Khalsaraei, M.M.; Molayi, M. Dynamically consistent NSFD methods for predator prey system. J. Appl. Comput. Mech. 2021, 7, 1565–1574. [Google Scholar] [CrossRef]
- Biswas, M.H.A.; Paiva, L.T.; de Pinho, M. A SEIR model for control of infectious diseases with constraints. Math. Biosci. Eng. 2014, 11, 761–784. [Google Scholar] [CrossRef]


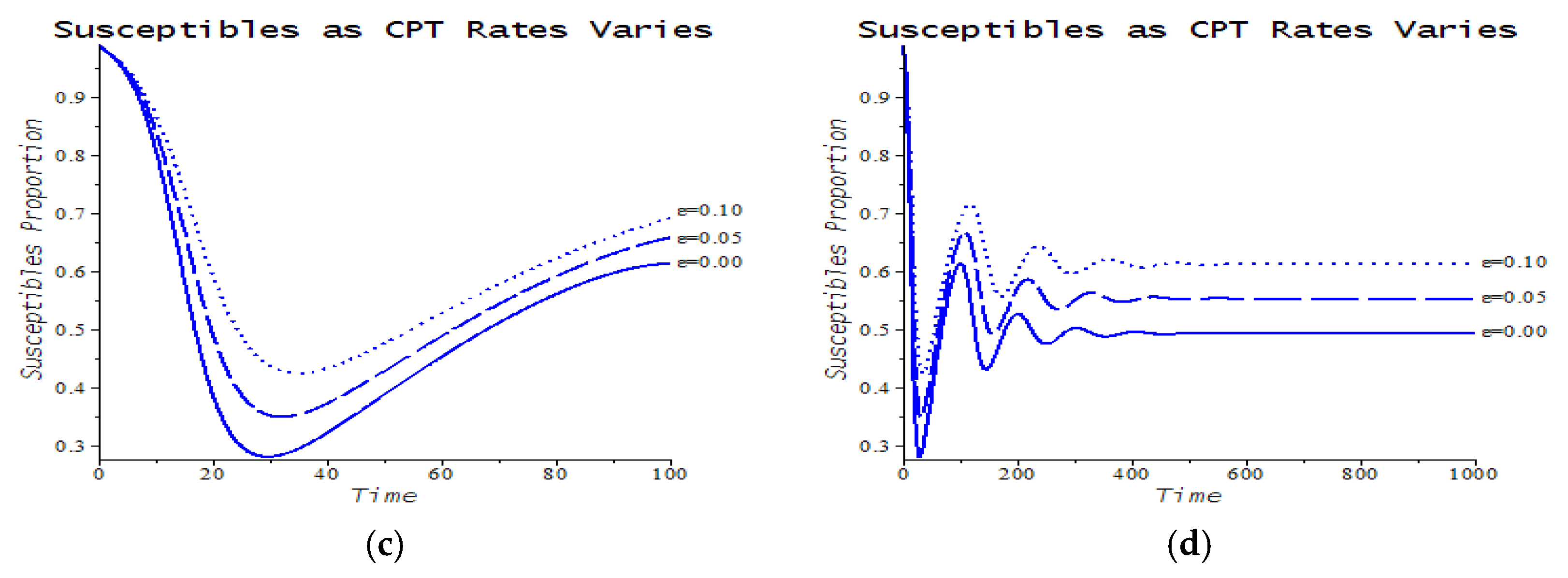
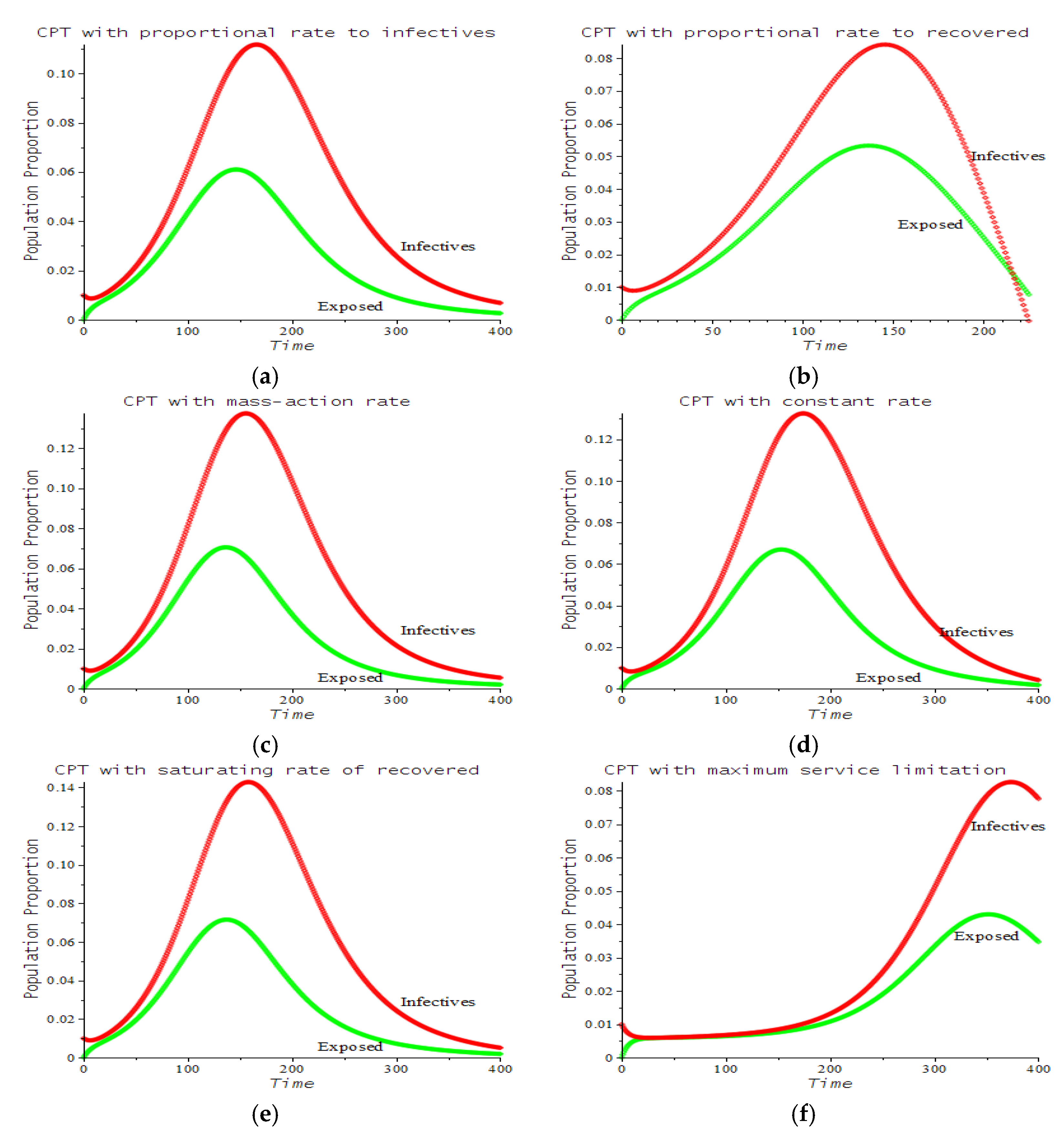
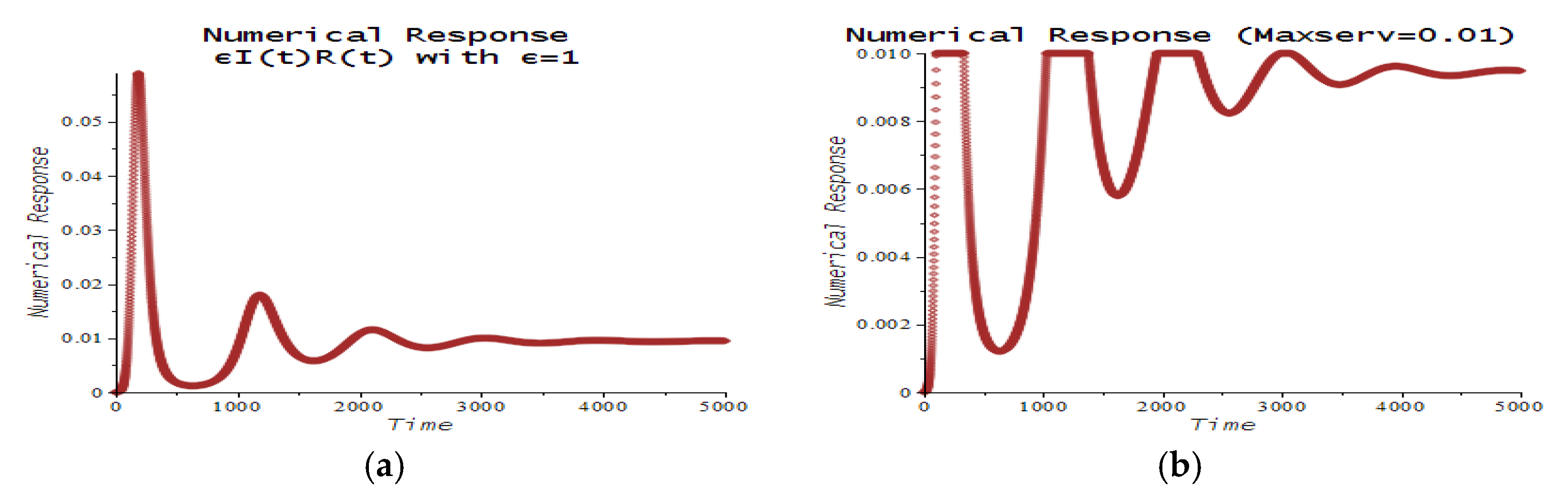
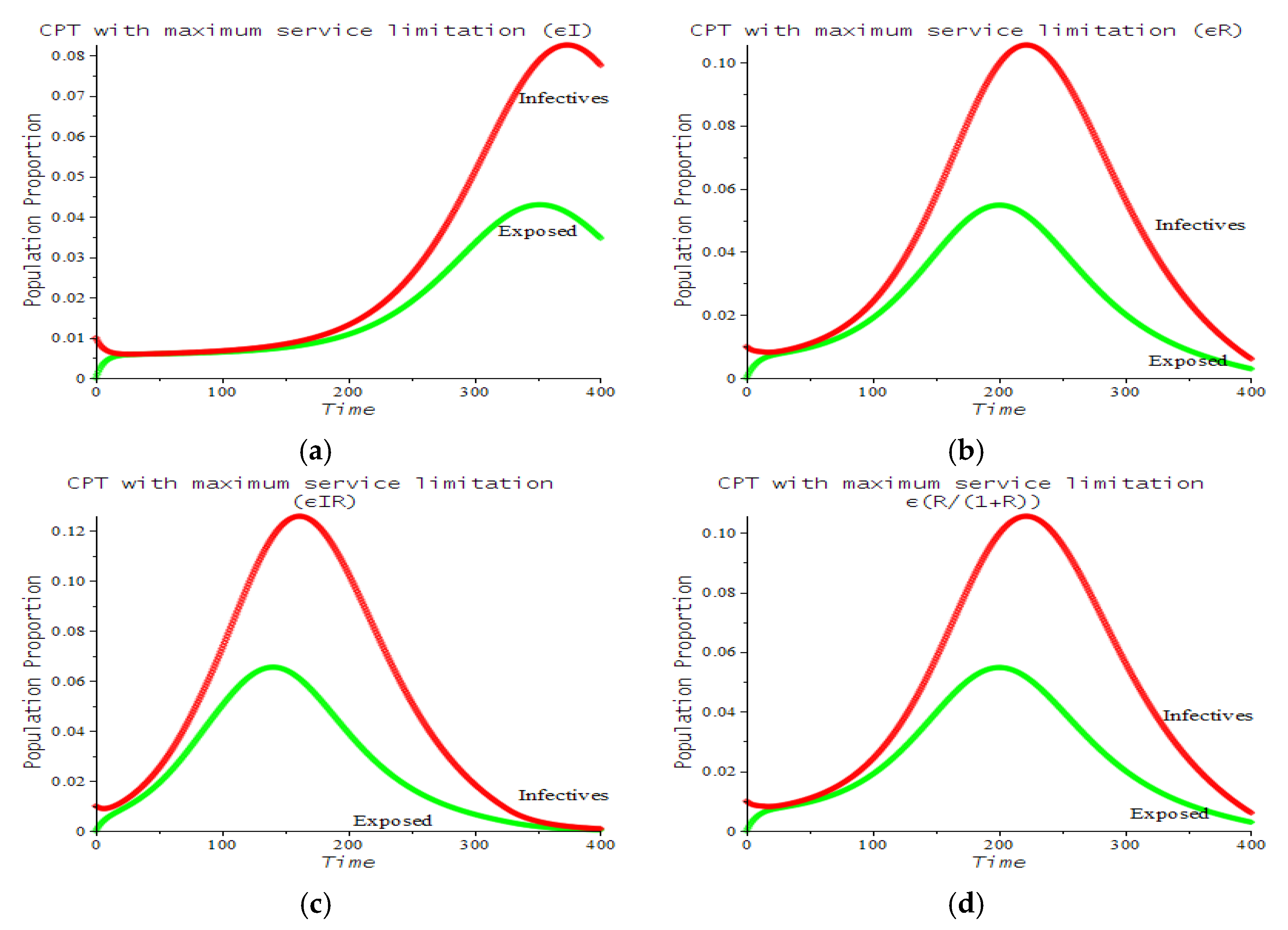
| Number | CPT Scenario | Numerical Response |
|---|---|---|
| 1 | Proportional rate to infectives | |
| 2 | Proportional rate to recovered | |
| 3 | Mass action rate (Lotka–Volterra) | |
| 4 | Constant rate | |
| 5 | Saturating rate (Michaelis–Menten) | |
| 6 | Maximum service limitation | |
| 7 | Maximum service limitation | |
| 8 | Maximum service limitation | |
| 9 | Maximum service limitation |
| Number | CPT Scenario | Numerical Response | Used in the Figures | Parameter Values in the Figures |
|---|---|---|---|---|
| 1 | Proportional rate to infectives | 7.a | ||
| 2 | Proportional rate to recovered | 7.b | ||
| 3 | Mass action rate (Lotka–Volterra) | 7.c | ||
| 4 | Constant rate | 7.d | ||
| 5 | Saturating rate (Michaelis–Menten) | 7.e | ||
| 6 | Maximum service limitation | 7.f, 9.a | , Maxserv = 0.0028 | |
| 7 | Maximum service limitation | 9.b | , Maxserv = 0.0028 | |
| 8 | Maximum service limitation | 9.c | , Maxserv = 0.0028 | |
| 9 | Maximum service limitation | 9.d | , Maxserv = 0.0028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Husniah, H.; Ruhanda, R.; Supriatna, A.K.; Biswas, M.H.A. SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission. Mathematics 2021, 9, 2857. https://doi.org/10.3390/math9222857
Husniah H, Ruhanda R, Supriatna AK, Biswas MHA. SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission. Mathematics. 2021; 9(22):2857. https://doi.org/10.3390/math9222857
Chicago/Turabian StyleHusniah, Hennie, Ruhanda Ruhanda, Asep K. Supriatna, and Md. H. A. Biswas. 2021. "SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission" Mathematics 9, no. 22: 2857. https://doi.org/10.3390/math9222857
APA StyleHusniah, H., Ruhanda, R., Supriatna, A. K., & Biswas, M. H. A. (2021). SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission. Mathematics, 9(22), 2857. https://doi.org/10.3390/math9222857







