Reachability and Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives
Abstract
:1. Introduction
2. Generalized Fractional Integrals, Derivatives and -Laplace Transform
3. Positive Linear Electrical Circuits Described by Generalized Fractional Derivatives
4. Reachability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives
5. Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives
6. Illustrative Examples
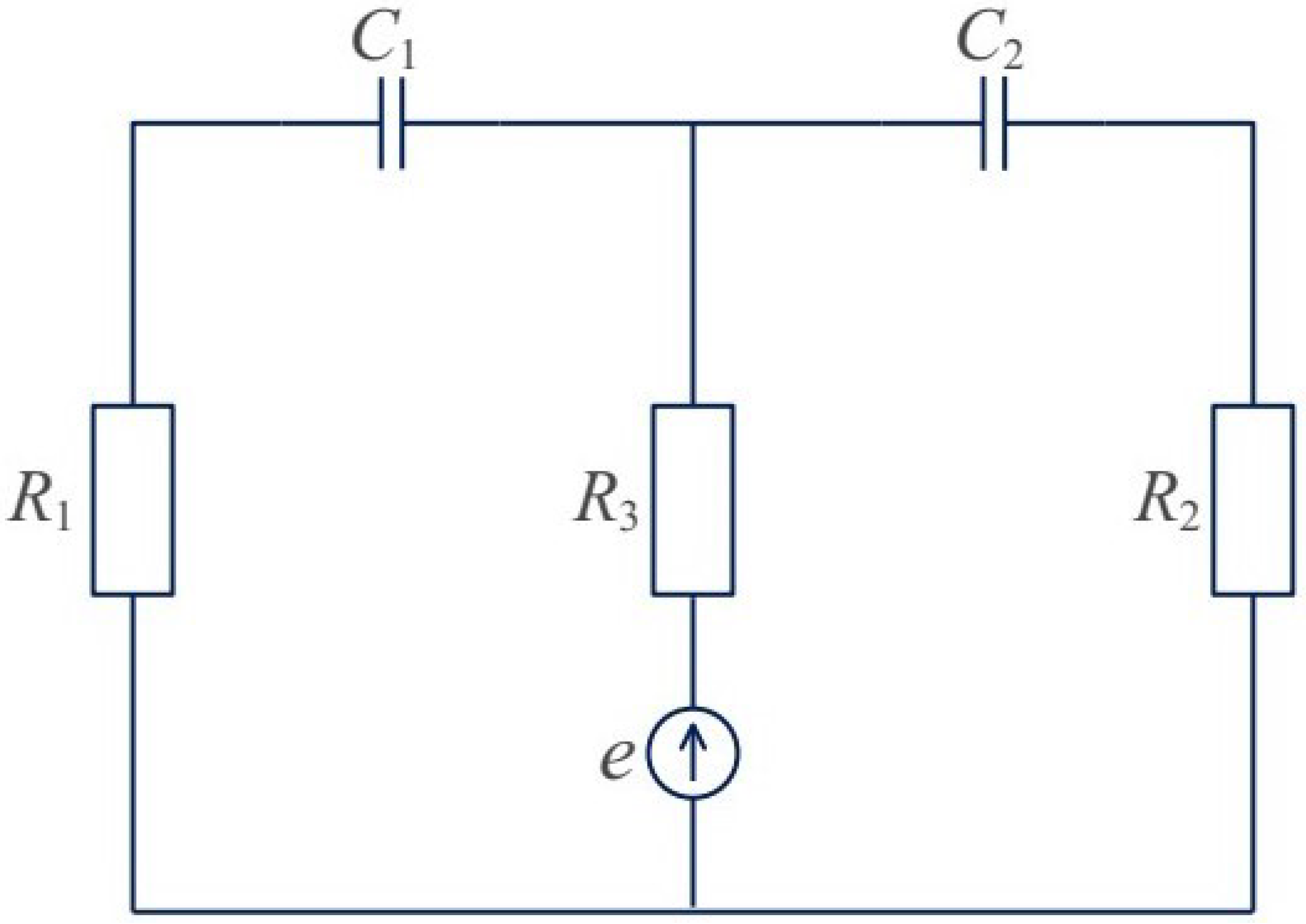
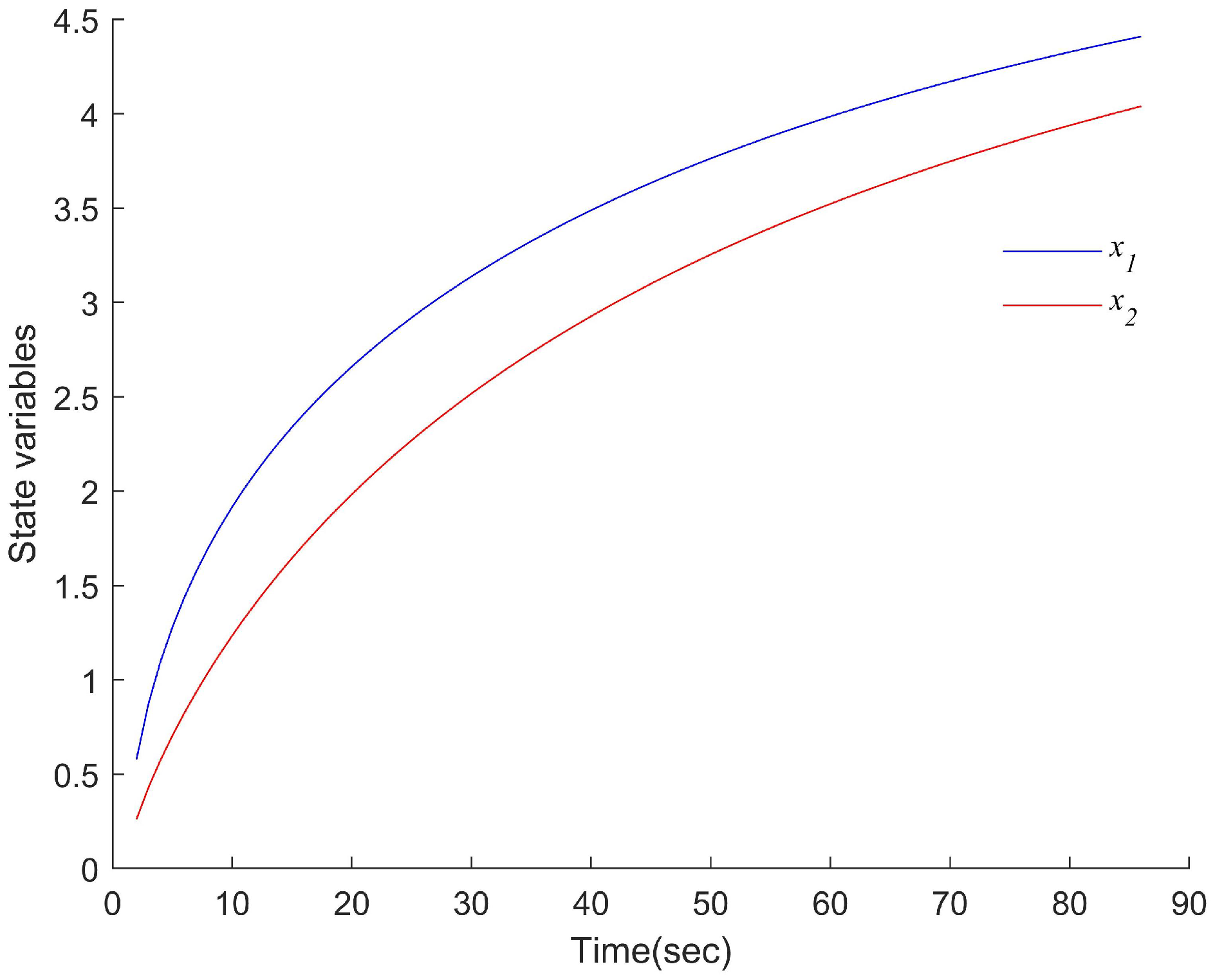
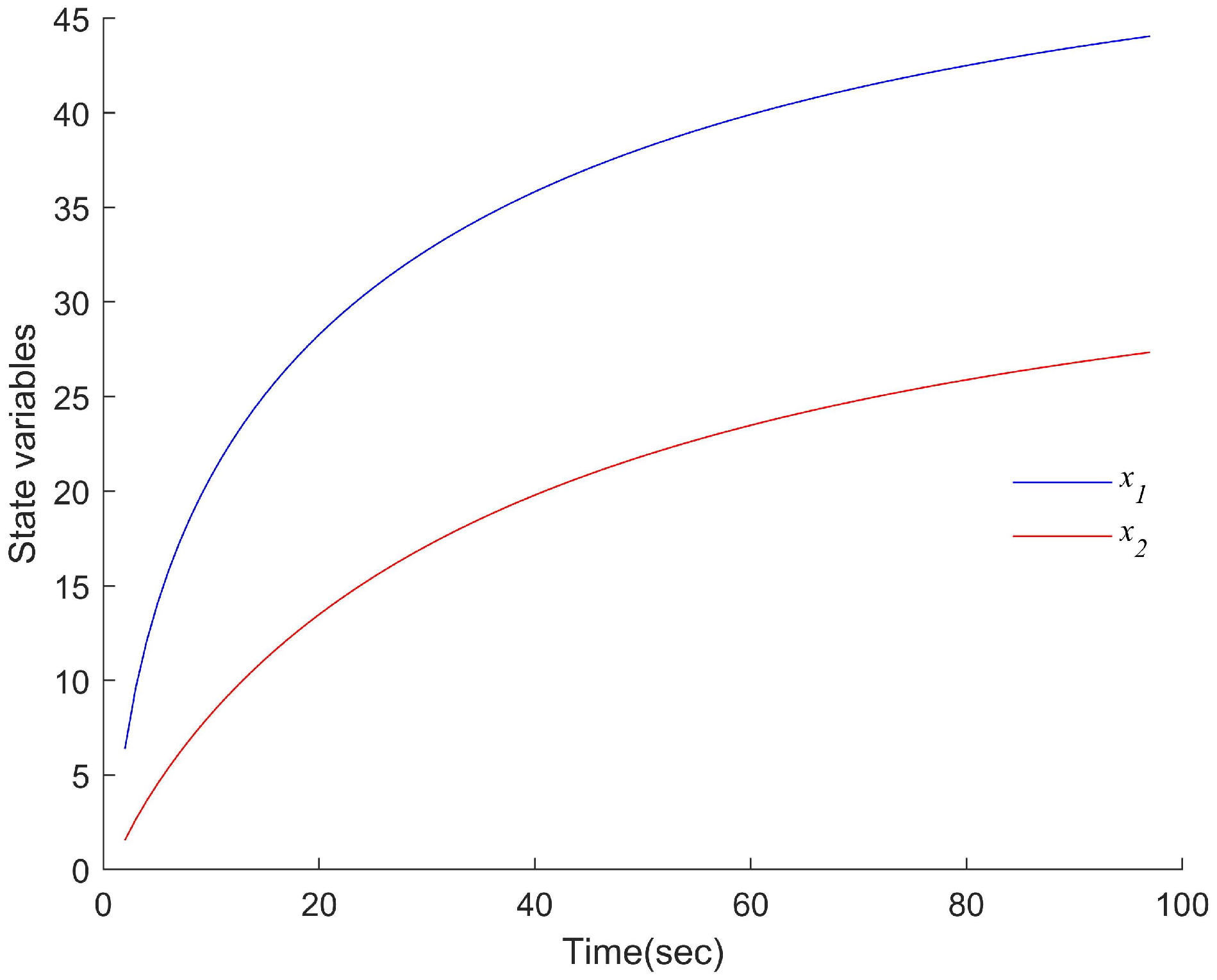
6.1. RC Circuit Systems
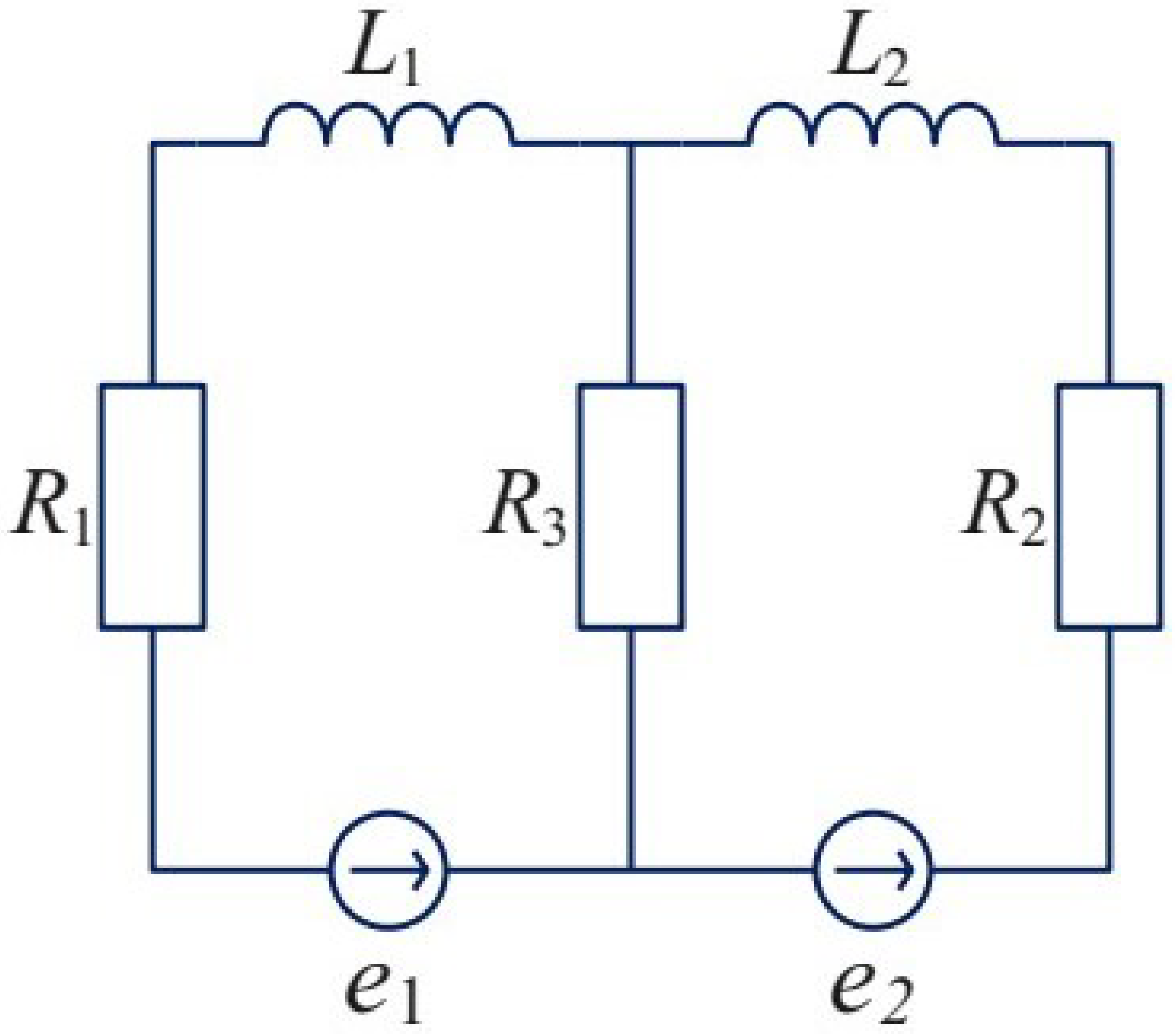
6.2. RL Circuit Systems
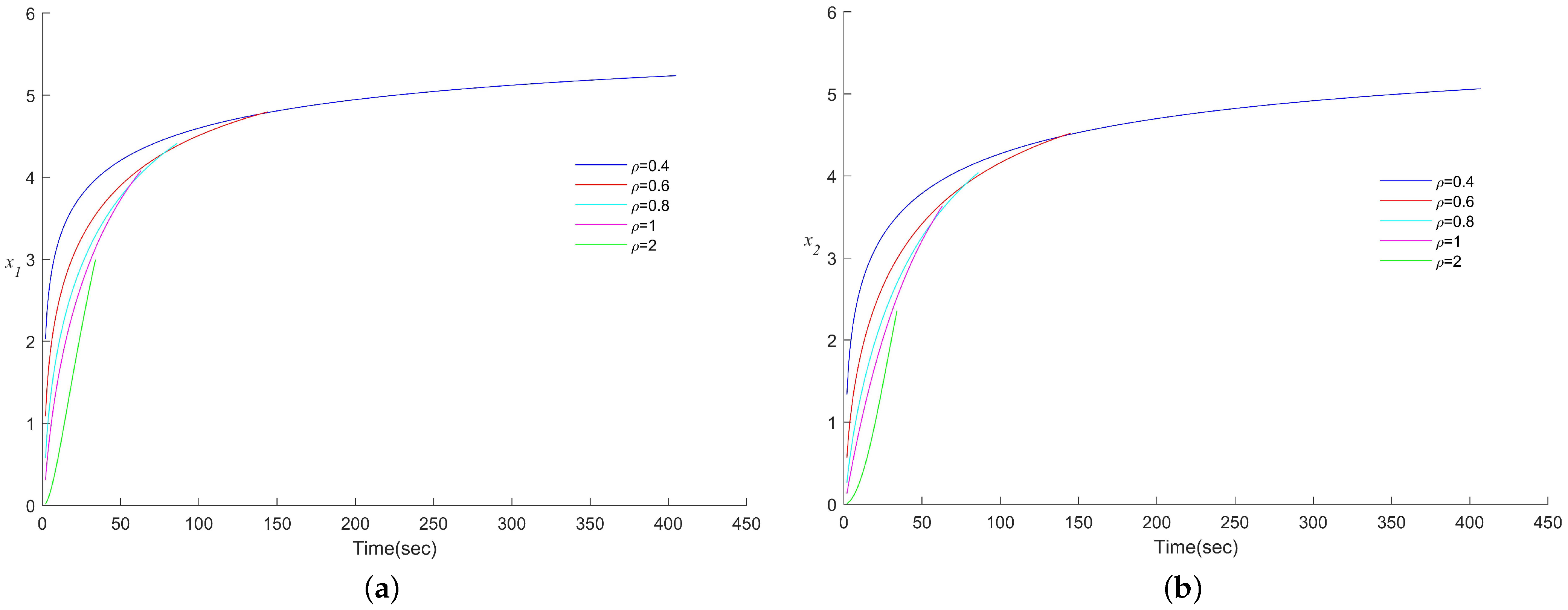
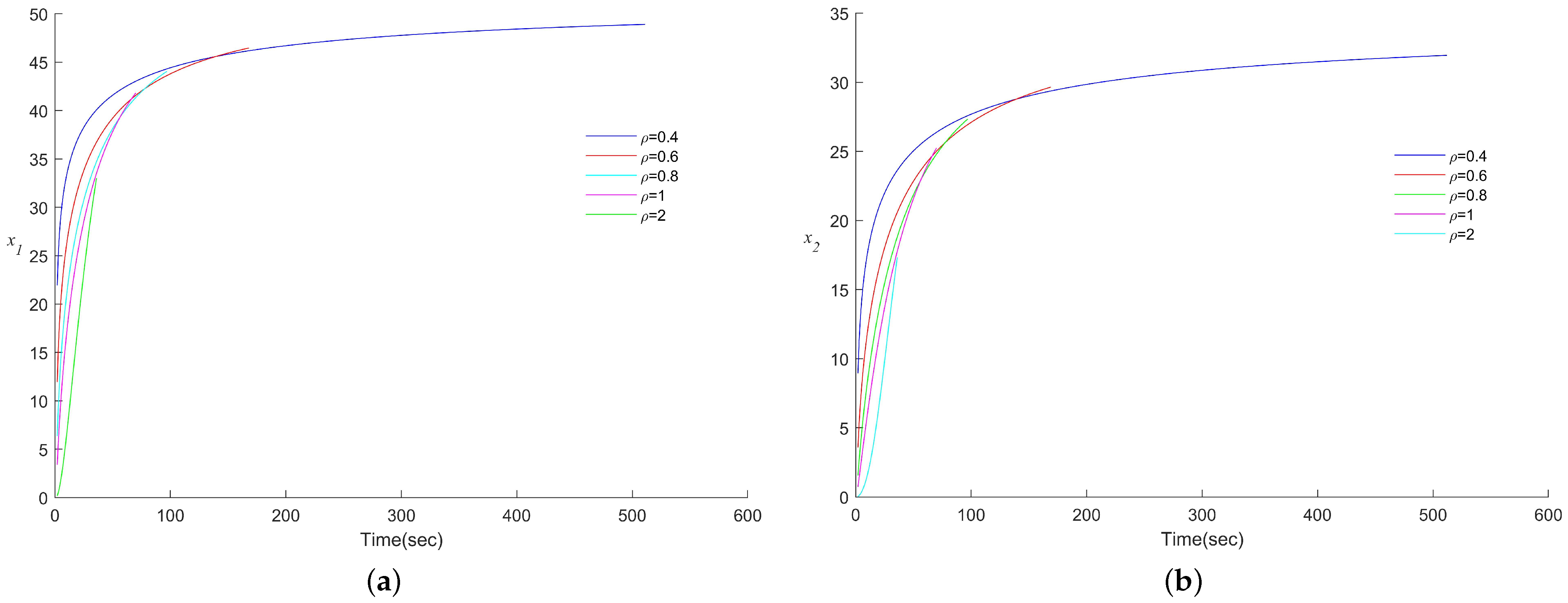
6.3. RC, RL Circuit Systems with Different Parameters
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Sene, N.; Fall, A. Homotopy perturbation ρ-Laplace transform method and its application to the fractional diffusion equation and the fractional diffusion-reaction equation. Fractal Fract. 2019, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, M.; Gomez, I. A fractional Fokker-Planck equation for non-singular kernel operators. J. Stat. Mech. Theory Exp. 2018, 2018, 123205. [Google Scholar] [CrossRef] [Green Version]
- Dos Santos, M. Fractional Prabhakar derivative in diffusion equation with non-static stochastic resetting. Physics 2019, 1, 40–58. [Google Scholar] [CrossRef] [Green Version]
- Sene, N.; Abdelmalek, K. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos Soli. Fract. 2019, 127, 158–164. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Katugampola, U. A new approach to generalized fractional derivatives. Bul. Math. Anal.Appl. 2014, 6, 1–15. [Google Scholar]
- Fahd, J.; Abdeljawad, T. A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 2018, 1, 88–98. [Google Scholar]
- Hristov, J. On the Atangana-Baleanu derivative and its relation to the fading memory concept: The diffusion equation formulation. In Trends in Theory and Applications of Fractional Derivatives with Mittag-Leffler Kernel; Gomez, J., Torres, L., Escobar, R., Eds.; Springer: Cham, Switzerland, 2019; pp. 175–193. [Google Scholar]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2013, 279, 57–66. [Google Scholar] [CrossRef]
- Khan, H.; Jarad, F.; Abdeljawad, T.; Khan, A. A singular ABC-fractional differential equation with ρ-Laplacian operator. Chaos Solitons Fractals 2019, 129, 56–61. [Google Scholar] [CrossRef]
- Sene, N. Fractional input stability for electrical circuits described by the Riemann-Liouville and the Caputo fractional derivatives. AIMS Math. 2019, 4, 147–165. [Google Scholar] [CrossRef]
- Kaczorek, T. Selected Problems of Fractional Systems Theory; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Application of Fractional Differential Equations, Volume 13; North-Holland Mathematics Studies; Elsevier Science: Amsterdam, The Netherlands, 2006; Volume 204, 523p. [Google Scholar]
- Kaczorek, T.; Rogowski, K. Fractional Linear Systems and Electrical Circuits; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Aguilar, J. Behavior characteristics of a cap-resistor, memcapacitor, and a memristor from the response obtained of RC and RL electrical circuits described by fractional differential equations. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1421–1433. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Aguilar, J.; Atangana, A. New insight in fractional differentiation: Power, exponential decay and Mittag-Leffler laws and applications. Eur. Phys. J. Plus 2017, 132, 13. [Google Scholar] [CrossRef]
- Aguilar, J.; Baleanu, D. Baleanu, Fractional Transmission Line with Losses. Z. Naturforschung A 2014, 69, 539–546. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Aguilar, J.; Escobar-Jimenez, R.; OlivaresPeregrino, V.; Taneco-Hernandez, M.; Guerrero-Ramirez, G. Electrical circuits RC and RL involving fractional operators with bi-order. Adv. Mech. Eng. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Morales-Delgado, V.; Gomez-Aguilar, J.; TanecoHernandez, M.; Escobar-Jimenez, R. Fractional operator without singular kernel: Applications to linear electrical circuits. Int. J. Circuit Theory Appl. 2018, 46, 2394–2419. [Google Scholar] [CrossRef]
- Morales-Delgado, V.; Gomez-Aguilar, J.; TanecoHernandez, M. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU-Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.; Morales-Delgado, V. Electrical circuits RC, LC, and RL described by AtanganaBaleanu fractional derivatives. Int. J. Circuit Theory Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Radwan, A.; Salama, K. Fractional-order RC and RL circuits. Circuits Syst. Signal Process. 2012, 31, 1901–1915. [Google Scholar] [CrossRef]
- Sene, N.; Gomez-Aguilar, J. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 260. [Google Scholar] [CrossRef]
- Si, X.; Yang, H. A new method for judgment and computation of stability and stabilization of fractional order positive systems with constraints. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2021, 40, 12–20. [Google Scholar]
- Si, X.; Yang, H. Optimization approach to the constrained regulation problem for linear continuous-time fractional-order systems. Int. J. Nonlinear Sci. Numer. Simul. 2021, 22, 1–16. [Google Scholar] [CrossRef]
- Ji, S.; Li, G. Existence of solution to nonlocal fractional differential inclusions via resolvent operators. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2021, 40, 103–108. [Google Scholar]
- Kaczorek, T. Stability of positive continuous-time linear systems with delays. Bull. Pol. Acad. Sci. Tech. Sci. 2009, 57, 395–398. [Google Scholar]
- Kaczorek, T. Stability Tests of Positive Fractional Continuous-time Linear Systems with Delays. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2013, 7, 211–215. [Google Scholar] [CrossRef]
- Sene, N. Stability analysis of the generalized fractional differential equations with and without exogenous inputs. J. Nonlinear Sci. Appl. 2019, 12, 562–572. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, Y.; Dai, X. Stability and Stabilization of the Fractional-order Power System with Time Delay. IEEE Trans. Circuits Syst. 2021, 68, 3446–3450. [Google Scholar] [CrossRef]
- Chao, C.; Chen, D.; Chiou, J. Stability Analysis and Robust Stabilization of Uncertain Fuzzy Time-Delay Systems. Mathematics 2021, 9, 2441. [Google Scholar] [CrossRef]
- Sene, N. Stability analysis of electrical RLC circuit described by the Caputo-Liouville generalized fractional derivative. Alex. Eng. J. 2020, 59, 2083–2090. [Google Scholar] [CrossRef]
- Erdelyi, A.; Kober, H. Some remarks on hankel transforms. Q. J. Math. 1940, 11, 212–221. [Google Scholar] [CrossRef]
- Herrmann, R. Towards a geometric interpretation of generalized fractional integrals—Erdelyi-Kober type integrals on RN as an example. Fract. Calc. Appl. Anal. 2014, 17, 361–370. [Google Scholar] [CrossRef] [Green Version]
- Jerzy, K. Controllability of Fractional Linear Systems with Delays. In Proceedings of the 25th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 23–26 August 2021; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2021. [Google Scholar]
- Gu, P.; Chen, Y.; Tian, S. Learnability of Linear Fractional-Order ILC Systems. IEEE Trans. Circuits Syst. 2021, 68, 963–967. [Google Scholar] [CrossRef]
- Kaczorek, T. Reachability and controllability to zero of positive fractional discrete-time systems. In Proceedings of the European Control Conference (ECC), Kos, Greece, 2–5 July 2007; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2007. [Google Scholar]
- Kaczorek, T. Invariant properties of positive linear electrical circuit. Arch. Elektrotech. 2019, 68, 875–890. [Google Scholar]
- Yuan, T.; Yang, H. Invariance of reachability and observability for fractional positive linear electrical circuit with delays. Arch. Elektrotech. 2021, 70, 513–530. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, T.; Yang, H.; Ivanov, I.G. Reachability and Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives. Mathematics 2021, 9, 2856. https://doi.org/10.3390/math9222856
Yuan T, Yang H, Ivanov IG. Reachability and Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives. Mathematics. 2021; 9(22):2856. https://doi.org/10.3390/math9222856
Chicago/Turabian StyleYuan, Tong, Hongli Yang, and Ivan Ganchev Ivanov. 2021. "Reachability and Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives" Mathematics 9, no. 22: 2856. https://doi.org/10.3390/math9222856
APA StyleYuan, T., Yang, H., & Ivanov, I. G. (2021). Reachability and Observability of Positive Linear Electrical Circuits Systems Described by Generalized Fractional Derivatives. Mathematics, 9(22), 2856. https://doi.org/10.3390/math9222856







