In Search of Complex Disease Risk through Genome Wide Association Studies

Abstract

The identification and characterisation of genomic changes (variants) that can lead to human diseases is one of the central aims of biomedical research. The generation of catalogues of genetic variants that have an impact on specific diseases is the basis of Personalised Medicine, where diagnoses and treatment protocols are selected according to each patient’s profile. In this context, the study of complex diseases, such as Type 2 diabetes or cardiovascular alterations, is fundamental. However, these diseases result from the combination of multiple genetic and environmental factors, which makes the discovery of causal variants particularly challenging at a statistical and computational level. Genome-Wide Association Studies (GWAS), which are based on the statistical analysis of genetic variant frequencies across non-diseased and diseased individuals, have been successful in finding genetic variants that are associated to specific diseases or phenotypic traits. But GWAS methodology is limited when considering important genetic aspects of the disease and has not yet resulted in meaningful translation to clinical practice. This review presents an outlook on the study of the link between genetics and complex phenotypes. We first present an overview of the past and current statistical methods used in the field. Next, we discuss current practices and their main limitations. Finally, we describe the open challenges that remain and that might benefit greatly from further mathematical developments.

1. Introduction

Complex traits, such as height, blood pressure, or some types of diseases, arise from the combination of multiple environmental and genetic factors (see Box 1 for definitions of fundamental concepts). In these, each of the involved genetic variants is expected to only make a marginal contribution to the whole phenotype, each explaining <1% and often <0.5%, of phenotypic variability [1,2,3]. Consequently, hundreds or even thousands of loci are likely to be involved for each trait [4,5,6]. Complex diseases, such as diabetes [7], asthma [8], cardiovascular diseases [9], or Alzheimer’s disease [10], tend to appear late in life and strongly affect the quality of life of millions of individuals around the world, exerting a large economic and social pressure on developed global healthcare systems. For instance, diabetes incurred in an estimated cost of USD 327 billion in 2017 in the United States alone, a value that increased 26% with respect to 2012 [11]. To help alleviate this burden, a long-standing goal of biomedicine has been to gain a better understanding of the molecular mechanisms and the genetic architecture behind these diseases, enabling better prognosis, prevention, and treatment protocols.

In addition to the multifactorial architecture of complex traits, covariate effects, population substructure, or disease heterogeneity [12] make the identification of the underlying causal genomic variants a statistical, mathematical, and computational challenge. The recent increase in sample sizes and the improvement of statistical frames have helped increase sensibility but have also imposed computational and methodological burdens that are becoming the bottleneck of these types of analyses. This increasing complexity has forced many studies to reduce their overall scope, which they may accomplish by excluding the analysis of the X chromosome or by restricting the analysis of the additive model, disregarding all other inheritance models that should be considered. This substantially limits the chances of identifying novel genetic markers that are associated with disease, as we recently demonstrated [13,14].

Despite these challenges, Genome-Wide Association Studies (GWAS) represent one of the most successful approaches for identifying genetic variants that are associated with the risk of developing particular complex diseases. In this review, we will provide an overview of the statistical models and approaches that are currently applied to the identification of association between genetic variants and complex diseases in biomedical research.

Box 1. Fundamental concepts.

• Complex trait or disease: A multifactorial phenotype resulting from the combination of numerous environmental and genetic factors.
• Genome-Wide Association Study (GWAS): A statistical method to discover the genomic variability that is associated with a complex trait or disease.
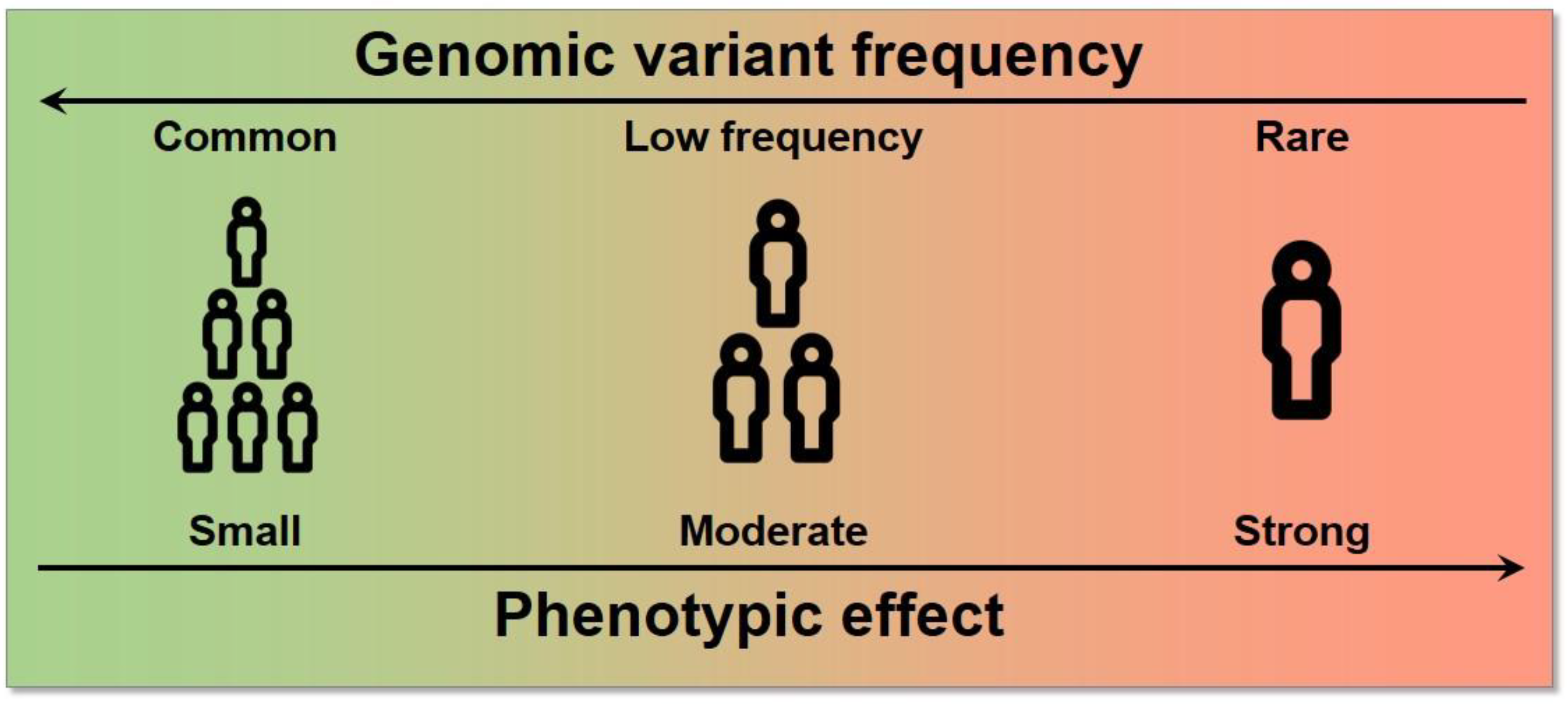
• Genomic or genetic variant: A genomic location known to present variability within a population.
• Personalised medicine: The application of preventive and treatment protocols adjusted to the patient’s genomic profile.
• Phenotype: A measurable characteristic in the individuals of a population, such as height, eye colour, blood pressure, or disease state.

2. Preliminary Genome Biology Concepts

The human genome is considerably variable. Two human beings differ in 4.1–5 million genomic sites on average, for a total of around 20 million bases (~0.6% of the total genome) [15]. This genetic variability determines not only the differences in physical appearance, such as height or eye colour, but also the predisposition of an idividual to develop diseases.

Distinguishing the genetic variants that are responsible of normal human variability from those affecting disease risk is thus fundamental to predict, diagnose, and possibly treat diseases, contributing to personalised medicine efforts. In this scenario, GWAS represents a resourceful strategy that can be used to identify variants that are associated with complex diseases. Despite substantial advancements, this remains a challenging task: in complex diseases, the contribution of each of the genetic variants to the final phenotype has been proven to be low and to come later in life, which is in contrast to rare diseases, where variants usually have a much stronger effect in the individual and may already be present during early developmental stages [1,14].

In general terms, each individual inherits this variability through parental germ cells. For example, when the genomic variation consists of a change at a single nucleotide position, it is called a Single Nucleotide Variant (SNV), but larger, structural variants (e.g., duplications, deletions) that have the potential of affecting up to millions of nucleotides also exist (see Box 2 for definitions of genomic concepts). As a result of the meiosis process, any genomic position (loci) is thus present in two copies (alleles). The set of alleles in a single homologous chromosome is defined as a haplotype, and the combination of all alleles identifies the individual’s genotype. The study of these genotypes in regard to their relationship with diseases is one of the central aims of biomedicine. It allows us to generate comprehensive genetic maps for each disease and to use them to easily screen, for example, newborns and to be able to predict the disease risk for that newborn and to plan preventive protocols.

Most genomic variants are biallelic, meaning that only two different alleles (generally named A and B) exist in the population. In this scenario and considering that all individuals have two copies of the genome, at any given variable locus (position), an individual displays one of three possible genotypes: AA, AB, or BB. When compared to the human reference genome [16], the allele matching the reference (e.g., A) is termed the reference allele, while the other (e.g., B) is termed the alternate allele. Consequently, the three possible genotypes are labelled as the homozygous reference (hom. ref. or AA), the homozygous alternate (hom. alt. or BB), or heterozygous (het. or AB).

Each of these genetic variants, which likely arose from single different individuals, are spread and fixed within the population over long periods of time and follow evolutionary rules based on the harm or benefit that each variation provides to the individual. As a consequence of this process, variants have different frequencies within each population, as they are carried by different proportions of individuals. Variants with frequencies $>5\%$ are defined as common, while variants with frequencies $1-5\%$ or $<1\%$ are defined as low-frequency and rare, respectively. SNVs with a frequency of >1% in the population are typically called Single Nucleotide Polymorphisms (SNPs). Since complex diseases are common, originally, only common variants were considered to be implicated (common disease-common variant hypothesis); the possibility of extending GWAS even to low-frequency and rare variants has shown, however, that variants across the entire frequency spectrum are likely to be involved [3]. The effect size, which is the contribution of these variants to the phenotype, is generally measured by an odds ratio (the odds of having the disease with the variant divided by the odds of having the disease without it) for a binary trait. Typically, an inverse relationship exists between the frequency of a variant and its effect on diseases: high-impact variants are normally found at lower frequencies because of a stronger negative selection pressure (Figure 1) [17].

Finally, it is worth noting that even though ~50% of the genome is inherited from each parent, the nucleotides in a chromosome are not inherited independently. Instead, the genomic material is exchanged in large, linked fragments, that are delimited by recombination hotspots, which are genomic regions that are more prone to recombination. As a result, these large genomic fragments contain multiple alleles that are inherited as a whole from the same parent; these alleles are said to be in linkage disequilibrium (LD).

Given this biological framework, we can now better appreciate the challenges of studying the genomic causes of complex traits and diseases. The main aim is to identify the genomic variability that leads to a higher risk of disease. However, it is likely that there are thousands of genomic loci with different levels of implications and with different frequencies in different populations. Therefore, the identification of unique causal variants is typically obscured by multiple variants in linkage disequilibrium, and the biological consequences of these variants are not immediately apparent. Thus, the study of complex traits and diseases remains an open prospect.

Box 2. Genomic concepts.

• Allele: One of the possible genomic sequences that exist in a population for a given locus.
• Allelic Frequency: The frequency in which a certain allele is found within a population.
• Genomic locus: A region of the genome.
• Genomic marker: A specific variant that is used as a proxy for nearby variants in high linkage disequilibrium.
• Genotype: The specific combination of alleles of an individual. When compared to a reference genome, the genotype of a variant may be reference homozygous, heterozygous, or alternate homozygous.
• Haplotype: The list of alleles that are present in the same homologous chromosome.
• Inheritance model: A quantitative model for how the genotype of a variant might contribute to the phenotype. The most frequently used is the additive model, but the dominant, recessive, and heterodominant models are also utilized.
• Linkage Disequilibrium (LD): When alleles are inherited together in an individual more often than expected by chance. This is a consequence of the inheritance of these alleles in haplotype blocks instead of them being independent of each other.
• Single nucleotide variant/polymorphism (SNV/SNP): The most frequent type of genomic variant, in which the alleles differ in a single nucleotide position. SNPs are SNVs with a frequency of >1%.

3. Genome Wide Association Studies (GWAS)

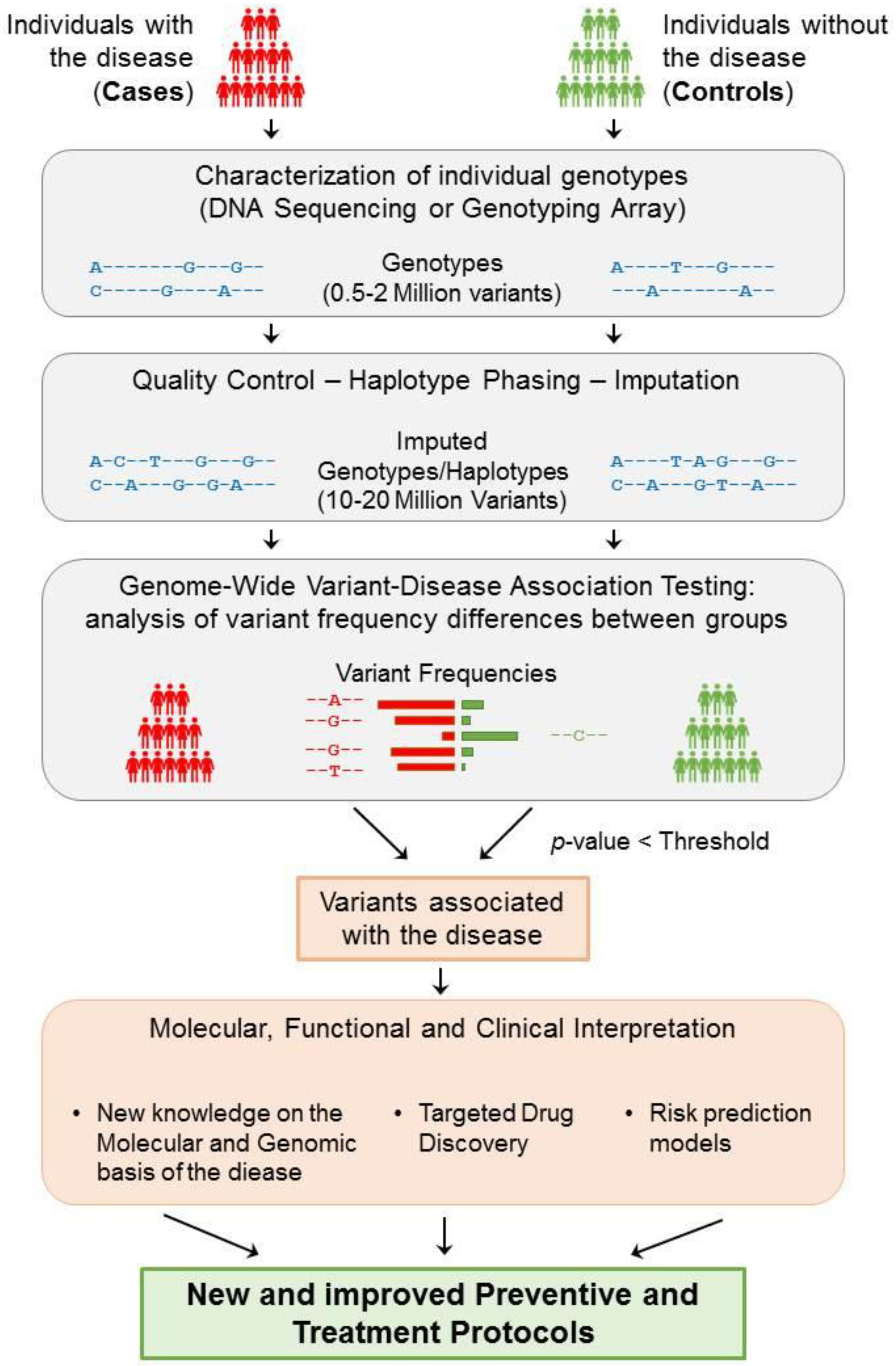
3.1. Definition

In order to take on this challenging task, GWAS was proposed as a statistical method that could be used to identify the genomic variants that are associated with complex traits or diseases. Specifically, GWAS are statistical analyses that aim to find the associations between genomic variability and a particular trait or disease [17]. Previous studies have required each functional hypothesis to be specifically tested in the context of a disease. In contrast, GWAS allow for the exploration of the genetic architecture of diseases at the genome-wide level, without the need of prior hypotheses beyond the existence of a genetic component behind the disease.

These studies collect genotypes and phenotypes of a large number of participants, generally in the order of tens of thousands, or even millions. To study a complex disease (binary trait), participants are separated into cases (affected) and controls (non-affected) (Figure 2). Then, a prior characterisation of the variation landscape is needed for each of the participating individuals, i.e., the genotypes and haplotypes, which are inferred from the lists of variants that have been identified within each participant. Whereas whole-genome sequencing currently provides the most complete map of genomic variation for an individual, it is still a very expensive and time-consuming assay, especially when considering the large number of participants within these types of studies. Instead, GWAS typically use DNA hybridisation microarray technologies, a more affordable alternative (see Box 3 for definitions of technical concepts). DNA microarrays, however, are designed to interrogate only a limited set of pre-selected genomic variants (generally between 500 k and 2 M) [18]. These variants are chosen to be common across the population, so that many of the individuals can carry them, and are also chosen considering LD blocks, so that only a single variant in each block is typically probed. In this manner, these subsets of variants are greatly informative and can be used to infer almost the full genotype variability landscape of each individual, as we will discuss in detail later (Section 4.2).

Then, each genomic variant is independently tested for significant differences in the genotype frequency between the two groups. Thus, if a variant is found to be present significantly more frequently in cases than they are in controls (or vice versa), then that variant is said to be associated with the disease (Figure 2). If the study is sufficiently powered, then a few genomic loci (containing a small number of variants, typically in high LD) will be identified as being significantly associated with the phenotype. For quantitative traits, the individual phenotypes are usually expressed as a continuous variable, and the association is evaluated based on the correlation between the trait and each variant genotype.

Finally, the genomic variants that are significantly associated with a trait or disease (termed “GWAS variants”) provide a list of candidates for further functional analyses to determine in which way they affect the function of the cell and, in the case of disease, ultimately help provide better prevention and treatment protocols.

3.2. Analytical Frameworks for GWAS

With the increasing interest in the study of complex traits, several statistical frameworks and tools have been developed in recent years in order to perform GWAS analyses [19]. In the following subsections, we will explain how these statistical models test for associations between genomic variability and phenotypes. We will mainly discuss methods to perform GWAS on binary traits (i.e., diseases). However, the analysis of quantitative traits is also presented. Moreover, given that the additive model is the most common in GWAS, the methodology will be formulated under this model. However, in Section 3.2.1, we will showcase how to work with the non-additive inheritance models. Hence, we will start with a simple model for binary traits by first detailing the use of contingency tables (Section 3.2.1) and will move towards more complete models, such as logistic regression (Section 3.2.2), regression model extensions (Section 3.2.3), and Bayesian regression analyses (Section 3.2.4).

In all of these analyses, to statistically model a GWAS, it is first necessary to define:

• The number of individuals included in the sample of the study $N$. In binary traits, these individuals are divided according to their phenotype, i.e., into $N_a$ cases (diseased) and $N_o$ controls (non-diseased), where $N=N_a+N_o$.
• A set of genomic variants $\left\{V_1,\dots ,V_m\right\},m\in \left\{1,\dots ,M|M<\infty \right\}$ that are analysed for each individual present in the population.
• The genotype $G_i$ for each variant, which can take a genotype value from $\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$. This genotype can be encoded differently depending on the hypothesised inheritance model by defining a function $f:G_{ij}\to \left\{0,1,2\right\}$, where $\left\{0,1,2\right\}$ encodes for additive $\left(f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=2\right)$, $\left\{0,1,1\right\}$ for dominant $\left(f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=1\right)$, $\left\{0,0,1\right\}$ for recessive $\left(f\left(AA\right)=0,f\left(AB\right)=0,f\left(BB\right)=1\right)$, or $\left\{0,1,0\right\}$ for heterodominant $\left(f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=0\right)$. For the purpose of statistical testing, one of the alleles, typically the alternate, is defined as the effect allele.
• Based on the space defined by the genotype, each genomic variant $V_i$ can be considered as a simple random variable $V_i:\mathsf{\Omega }\to G_i,$ so that $\forall g\in G_i\exists \omega \in \mathsf{\Omega }$ for which $V_i\left(\omega \right)=g$, with $\mathsf{\Omega }$ as the space of events.
• The phenotype $P_j$ for each individual in the population is given a trait of study, which, in the case of binary traits, is assigned as $\left\{0,1\right\}=\left\{control,case\right\}=\left\{diseased,non-diseased\right\}$. The phenotype can be modelled by a Bernoulli distribution $P_j~B\left(p_j\right)$, where $p_j$ is the unknown probability of an individual having the disease.

Then, for each tested genomic variant, two outputs are expected:

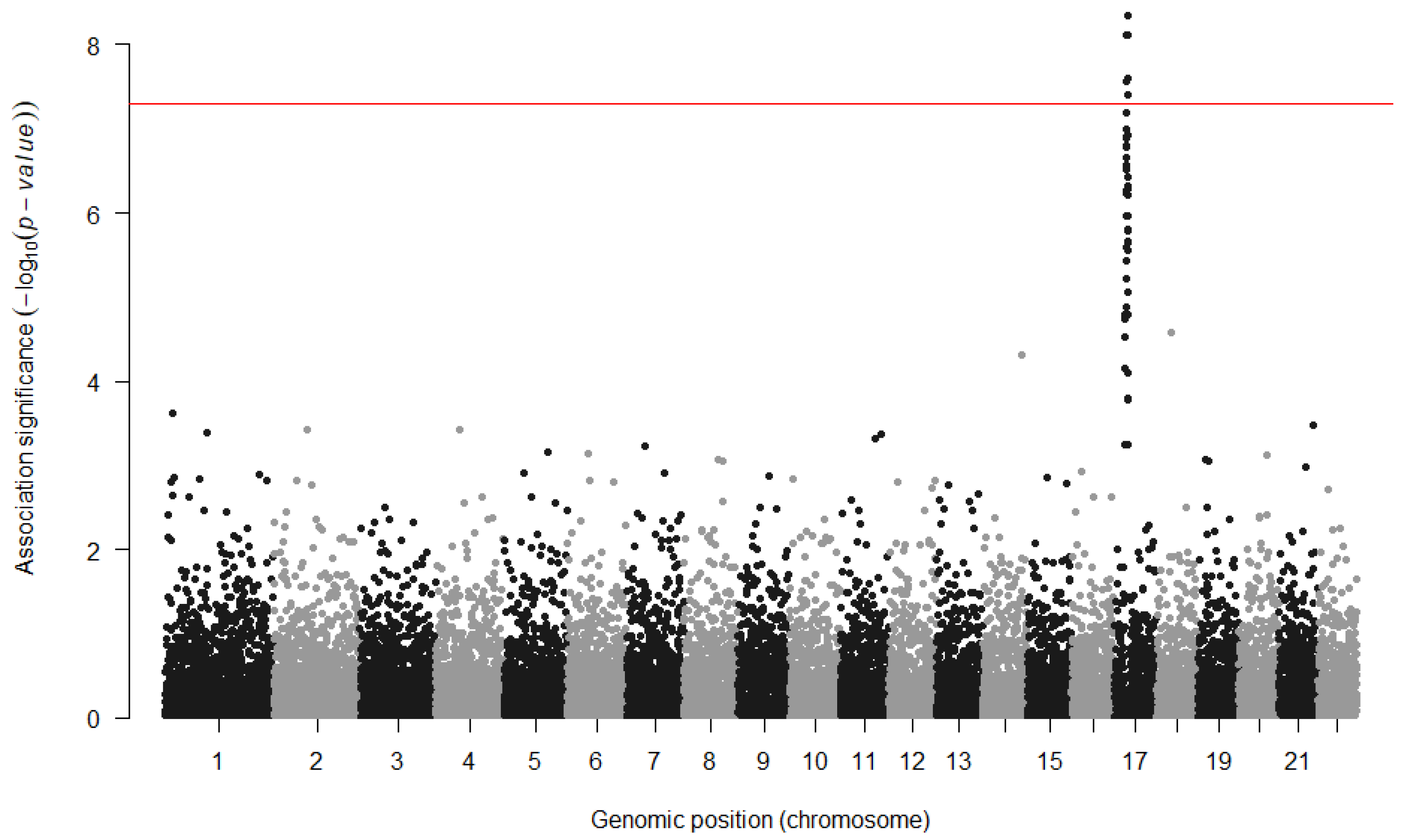
• A measure of the statistical confidence on the association with the phenotype in the form of a p-value.
• A measure of the effect size of having one of the alleles, which is typically expressed by beta ($\beta$) for quantitative traits and an odds ratio ($OR$) for binary traits.

3.2.1. Contingency Tables

The classical approach for finding associations between genotypes and a binary phenotype consists of constructing a 2 × 2 contingency table of the allelic counts in each group. Once the contingency table is prepared, the allele frequencies can be measured and tested to find any possible relation with the disease [20].

First, given a specific variant $V_i$ in a population with $N$ individuals, where $N_a$ are cases (diseased) and $N_o$ are controls (non-diseased) and where $N=N_a+N_o$, for each individual $j$ from the population of study, the space of the genotypes of each variant $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$ can be defined. Thus, the contingency table of the observed genotype counts in the population of study (

Table 1. Contingency table of observed genotypes.

	AA	AB	BB	Total
Cases	$n_{hom.ref.a}$	$n_{het.a}$	$n_{hom.alt.a}$	$N_a$
Controls	$n_{hom.ref.o}$	$n_{het.o}$	$n_{hom.alt.o}$	$N_o$
Total	$n_{hom.ref}$	$n_{het}$	$n_{hom.alt}$	$N$

) is constructed as:

Moreover, given that the genotype is defined by two alleles, a function $f$ can be defined relating the space of genotypes $G_i$ to the space of alleles $A_i=\left\{A,B\right\}$ as $f:G_i\to A_i$. In this case, the contingency table of the observed allelic counts in the population of study is obtained (

Table 2. Contingency table of observed allelic counts.

	A	B	Total
Cases	$2n_{hom.ref.a}+n_{het.a}$	$n_{het.a}+2n_{hom.alt.a}$	$2N_a$
Controls	$2n_{hom.ref.o}+n_{het.o}$	$n_{het.o}+2n_{hom.alt.o}$	$2N_o$
Total	$2n_{hom.ref}+n_{het}$	$n_{het}+2n_{hom.alt}$	$2N$

):

Particularly, each variant $V_i$ from the population can be defined as a simple random variable $V_i:\mathsf{\Omega }\to A_i,$ so that $\forall a\in A_i\exists \omega \in \mathsf{\Omega }$, which means that $V_i\left(\omega \right)=a$, with $\mathsf{\Omega }$ as the space of events. Therefore, a probability function can be defined by $p_i:\left\{a_i\in A_i\right\}\to \left[0,1\right]$, where $p_i=P\left(V_i=a_i\right)$. Thus, the expected allele counts $E\left(V_i=a_i\right)={{\displaystyle \sum }}^{}{a}_i{p}_i$ are expressed as (

Table 3. Contingency table of expected allelic counts.

	A	B
Cases	$\frac{2N_a\left(2n_{hom.ref}+n_{het}\right)}{2N}$	$\frac{2N_a\left(n_{het}+2n_{hom.alt}\right)}{2N}$
Controls	$\frac{2N_o\left(2n_{hom.ref}+n_{het}\right)}{2N}$	$\frac{2N_o\left(n_{het}+2n_{hom.alt}\right)}{2N}$

):

Under the assumption of independence of observing allele A or allele B in the study population, a Fisher’s exact test can be applied to these contingency tables to test for differences between the allelic frequencies in each group.

Moreover, if the sample size is large enough $\left(N>20\right)$ and under the assumption of independence, a chi-squared test can be performed instead to check for differences between the observed frequencies $\left(Observed=\frac{N.observations}{N.total}\right)$ and expected frequencies (which derived from Table 3, $Expected=\frac{N.expectedcounts}{N.total}$):

$${\displaystyle \sum }\frac{{\left(Observed-Expected\right)}^2}{Expected}~{\chi }_1^2.$$

To calculate the odds ratio $OR$, Table 3 can be simplified and annotated as (

Table 4. Simplified contingency table of expected allelic counts.

	A	B
Cases	$n_{Aa}$	$n_{Ba}$
Controls	$n_{Ao}$	$n_{Bo}$

):

As a result, from Table 4, the odds ratio can be expressed as $OR=\frac{\raisebox{1ex}{$n_{Ba}$}\!\left/ \!\raisebox{-1ex}{$n_{Bo}$}\right.}{\raisebox{1ex}{$n_{Aa}$}\!\left/ \!\raisebox{-1ex}{$n_{Ao}$}\right.}=\frac{n_{Ba}{n}_{Ao}}{n_{Aa}{n}_{Bo}}$.

Given that the additive model is the most common in GWAS, the methodology described above, which is based on the contingency tables, has been formulated under this model. For each individual $j$ in the population, the space for the genotypes of each variant $V_{ij}$ was defined as $G_{ij}=\left\{AA,AB,BB\right\}$. For the additive model, this space is encoded by defining a function $f:G_{ij}\to \left\{0,1,2\right\}$, where $f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=2$. Nonetheless, depending on the encoding of the different inheritance models, this function $f$ takes different values: $\left\{0,1,1\right\}$ for the dominant $\left(f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=1\right)$, $\left\{0,0,1\right\}$ for recessive $\left(f\left(AA\right)=0,f\left(AB\right)=0,f\left(BB\right)=1\right)$, or $\left\{0,1,0\right\}$ for heterodominant $\left(f\left(AA\right)=0,f\left(AB\right)=1,f\left(BB\right)=0\right)$. As a result, Table 1 can be reconstructed for the non-additive models, as shown in

Table 5. Contingency table of observed genotypes for the different genetic models.

	Dominant Model {0,1,1}		Recessive Model {1,0,0}		Heterodominant Model {0,1,0}
	AA	AB + BB	AA + AB	BB	AA + BB	AB	Total
Cases	$n_{hom.ref.a}$	$n_{het.a}+n_{hom.alt.a}$	$n_{hom.ref.a}+n_{het.a}$	$n_{hom.alt.a}$	$n_{hom.ref.a}+n_{hom.alt.a}$	$n_{het.a}$	$N_a$
Controls	$n_{hom.ref.o}$	$n_{het.o}+n_{hom.alt.o}$	$n_{hom.ref.o}+n_{het.o}$	$n_{hom.alt.o}$	$n_{hom.ref.o}+n_{hom.alt.o}$	$n_{het.o}$	$N_o$
Total	$n_{hom.ref}$	$n_{het}+n_{hom.alt}$	$n_{hom.ref}+n_{het}$	$n_{hom.alt}$	$n_{hom.ref}+n_{hom.alt}$	$n_{het}$	$N$

:

Moreover, this encoding can be applied to further study the different genetic models in each of the approaches that will be detailed in the following subsections.

Contingency tables were particularly successful in the first GWAS, leading to the identification of novel associations to complex disease [21,22]. Therefore, some common bioinformatic tools still include options to perform the chi-squared test for association [23]. However, one important issue that is not covered by the contingency table analyses is the fact that the thousands or millions of individuals in a GWAS can share some potentially confounding qualities, apart from the trait of interest, such as age or sex. The effects of these known covariates need to be corrected in order to avoid the concealment of the genomic associations to disease risk or the emergence of spurious associations.

3.2.2. Logistic Regression

Logistic regression models are broadly used for the study of GWAS to analyse the explainability of the phenotype in terms of the genotype. Particularly, the study of association under this model facilitates the simultaneous analysis of multiple variables, thus allowing the study of covariates in addition to genomic variants.

Therefore, a logistic regression model can be formulated based on the analysis of a population with $N$ individuals, where $N_a$ are cases (diseased) and $N_o$ are controls (non-diseased) and where $N=N_a+N_o$. For each individual $j$ in the population of study, the phenotype takes the values $P_j\in \left\{0,1\right\}=\left\{control,case\right\}=\left\{diseased,non-diseased\right\}$. Thus, the study of an individual $j$ being diseased can be modelled by a Bernoulli distribution $P_j~B\left(p_j\right)$, where $p_j$ is the unknown probability of an individual having the disease. As a result, the phenotype of the $N$ individuals of the population can be modelled by a binomial distribution $P~Bin\left(p_j,n_j\right)$. Particularly, based on the observation of $m\in \left\{1,\dots ,M|M<\infty \right\}$ genomic variants $V_i,i=1,\dots ,m$, where their genotype can take a value from the space $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$, the probability of an individual being diseased can be explained by the genotype as $p_j=E\left(\frac{P}{n_j}|G_{ij}\right)$. Consequently, the ratio of the probability of individual j having the disease or not, given a particular genotype, is expressed as $\frac{p_j}{1-p_j}$.

Therefore, a logit function transformation can be applied to this ratio

$$logit\left(p_j\right)=ln\left(\frac{p_j}{1-p_j}\right),$$

(1)

thus fitting the logistic regression model for each variant

$$logit\left(p_j\right)\sim {\beta }_0+{\beta }_1{G}_{ij}.$$

(2)

From this logistic regression model, beta coefficients ${\beta }_i,i=\left\{0,1\right\}$ are estimated, for example, by applying the maximum likelihood or least squares approaches.

The genotype effect on disease risk is then measured by the odds ratio, which can be calculated as

$$OR=exp\left({\beta }_1\right).$$

(3)

Finally, the association of the genotype with the disease is determined by testing the hypothesis of ${\beta }_1\ne 0$.

One of the advantages of the logistic regression model in GWAS analysis is the possibility of including covariate effects. To this end, the model can be extended so that the expected phenotype for individual $j$ with genotype $G_{ij}$ can be conditioned on t additional covariates $X_{kj}$ with $k=1,\dots ,t,t<\infty$, so that:

$$p_j=E(\frac{P}{n_j}|G_{ij},X_{1j},X_{2j},\dots ,X_{tj}).$$

Correspondingly, the logistic regression model

$$logit\left(p_j\right)\sim {\beta }_0+{\beta }_1{G}_{ij}+{\beta }_2{X}_{1j}+\dots +{\beta }_{t+1}{X}_{tj}$$

can be used to estimate the betas, which can then be tested for associations individually (${\beta }_1,{\beta }_2,\dots ,{\beta }_m\ne 0,m=1,\dots ,t+1$). In this case, the significant ${\beta }_k$ coefficients can be considered as measures of the genotype and covariate effects, and the $OR$ for each of them can be calculated as previously detailed in Equation (3). By including possible confounding effects as covariates in the logistic regression model, a more precise estimate of the genotype effect on disease and thus a more robust association result can be obtained.

Due to their power and flexibility, logistic regression models have been the most used approach in GWAS for complex diseases, leading to the discovery of novel loci and broadening the genetic and biological understanding of a variety of diseases [24,25]. In line with this success, many bioinformatic tools for logistic regression modelling and association have been developed [23,26,27,28].

3.2.3. Further Extensions and Developments of Regression Models in GWAS

All of the strategies presented in the previous sections were designed to work with binary phenotypes such as diseases. However, regression models can also be easily applied to the study of quantitative traits [29]. In this case, in a study of a population with $N$ individuals, for each individual $j$, the phenotype takes the values $P_j\in \sigma (ℝ)$ with $\sigma (ℝ)$ the Borel set. Thus, the study of the individual’s phenotype $P_j$ can be performed using a linear regression model based on the genotype of $m\in \left\{1,\dots ,M|M<\infty \right\}$ genomic variants $V_i,i=1,\dots ,m$, where each variant genotype can take a value from the space $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$. Therefore, the linear regression model is expressed as

$$P_j\sim {\beta }_0+{\beta }_1{G}_{ij}$$

(4)

and the betas ${\beta }_i$ are the parameters of the model. Particularly, the genotype effect on the risk of disease is measured by the beta $\beta ={\beta }_1$. Then, a hypothesis test for association is used to check whether the genotype is associated with the trait ${\beta }_1\ne 0$.

Overall, the regression methods for GWAS can be extended with a generalized linear model (GLM) [30]. If the trait is quantitative and if the assumptions of genotype independence, homoscedasticity, and normality of residuals hold, then a simple linear model can be fitted. If the trait is binary, under the same assumptions, a logit transformation can be applied, and a logistic regression model can then be fitted. When the assumptions are violated, different types of models can be derived, such as Poisson regression or ANOVA methods.

As a further extension of regression methods, mixed models have recently started to be applied in GWAS. Mixed models take their name from the regression of both fixed and random effects on the outcome variable. In GWAS, genotypes and non-genetic covariates are fitted as fixed effects, together with a genetic relationship matrix (GRM), which are fitted as a random effect. The GRM carries information on the genetic relatedness between the individuals of the study; mixed models therefore correct for genetic correlations between individuals, which are a major source of confounding in association. This way, the need for excluding related individuals from a GWAS is overcome, thus increasing the discovery power [31]. Similar to GLMs, mixed models can also be applied to quantitative or binary phenotypes, and tools for linear or logistic mixed models have been developed accordingly [32,33,34]. Mixed models have proven to be particularly suitable for GWAS in large biobanks [31,34,35,36].

In conclusion, regression models showed a considerable ability to accommodate different hypotheses in terms of covariates and genetic models, producing powerful and robust results. For these reasons, regression approaches are currently the method of choice in GWAS.

3.2.4. Bayesian Statistics

GWAS Bayesian approaches were developed in parallel to GWAS regression models as an attempt to refine and improve their results, increasing their discovery power.

Thus, based on the study of a population with $N$ individuals, where $N_a$ are cases (diseased) and $N_o$ are controls (non-diseased) and where $N=N_a+N_o$, for each individual $j$ in the population of study, the phenotype takes values $P_j\in \left\{0,1\right\}=\left\{control,case\right\}=\left\{diseased,non-diseased\right\}$ for binary traits, or $P_j\in \sigma (ℝ)$, with $\sigma (ℝ)$ the Borel set, for qualitative traits.

Under these scenarios, the logistic and linear regression models can be constructed as they are in Equations (2) and (4), respectively. Then, Bayesian results are provided in the form of the posterior probabilities of regression estimates:

$$P({\beta }_{1j}|G_{ij})\propto P(G_{ij}|{\beta }_{1j})P\left({\beta }_{1j}\right)$$

(5)

where $P(G_{ij}|{\beta }_{1j})$ is obtained from the regression model (e.g., the likelihood of observing a particular phenotype $L\left(Y_j|{\beta }_0,{\beta }_1\right)$) and where the prior $P\left({\beta }_{1j}\right)$ can be estimated based on ${\beta }_{1j}$ inference approaches, such as the Jacobian transformation, normal approximation or uniform distributions. These calculated posterior probabilities can be used as priors to fit a regression model again. Therefore, the ${\beta }_{ij}$ coefficients (thus the genotype effect on disease) will be better estimated, reducing the proportion of false-positive results [37,38].

Moreover, Bayesian methods can also be applied to reduce the dimensionality of a GWAS. Dimensionality reductions are based on the assumption that the number of variants with a non-zero effect p tends to be far smaller than the total number of analysed variants k ($k\gg p$). With Bayesian approaches, the initial set of variants $\left(V_1,\dots ,V_m\right),m\in \left\{1,\dots ,M|M<\infty \right\}$ is reduced to those with a higher probability of escaping the zero effect, relying on the posterior probability (5). A vector $\gamma$ is constructed by applying the indicator of the non-zero effect to each variant:

$$\gamma =\left(V_1,\dots ,V_m\right)1_{P\left({\beta }_{1j}|G_{ij}\right)\ne 0}\hspace{1em}\mathrm{where}\hspace{1em}{1}_{P\left({\beta }_{1j}|G_{ij}\right)\ne 0}=\{\begin{array}{cc}1,& P\left({\beta }_{1j}|G_{ij}\right)\ne 0\\ 0,& P\left({\beta }_{1j}|G_{ij}\right)=0\end{array}.$$

Therefore, under the binary trait scenario, which corresponds to the logistic regression model, the probability of an individual being diseased can be explained by the genotype as $p_j=E\left(\frac{P}{n_j}|G_{ij}\left(\gamma \right)\right)$. Thus, the ratio between the probability of individual j having the disease or not given a particular genotype will be expressed under the model $logit\left(p_j\right)\sim {\beta }_0+{\beta }_1{G}_{ij}\left(\gamma \right)$. Similarly, under the quantitative trait scenario, which corresponds to the linear regression model, the explanation of the individual phenotype based on its genotype is expressed by the model $P_j~{\beta }_0+{\beta }_1{G}_{ij}\left(\gamma \right)$. Last, a regression model is fitted to obtain the betas, which are tested to check whether the genotype is associated with the disease [39,40,41,42]. As a result of reducing the number of simultaneously performed tests, the multiple-testing correction burden is also reduced, thus increasing the detection power (Section 3.3).

Bayesian statistical methods have proven the relevance of reducing the number of tests to improve the results that can be obtained from GWAS [43,44]. Therefore, many bioinformatic tools have been developed and have been updated to facilitate the association analysis based on Bayesian models [28,32].

3.3. Statistical Interpretation of GWAS Results

As it is common in statistical analyses, a significance threshold is required to decide on the significance of the obtained results. This level of significance is measured with a p-value threshold, typically 0.05 or 0.01 for a 5% and 1% probability of rejecting the null hypothesis when it is true (false positive), respectively. However, in a GWAS, huge numbers of tests are performed (one for each genomic variant, usually in the order of millions). Therefore, multiple testing correction with an adjusted p-value threshold is needed to determine statistical significance.

For this purpose, the use of standard Bonferroni’s multiple-testing correction, which consists in dividing the p-value threshold by the total number of tests, could be suggested. However, this would assume full statistical independence between all of the performed tests. Given that genomic variants are not independent of each other, due to linkage disequilibrium (LD) as previously described, the resulting threshold would then be exceedingly stringent. Instead, GWAS typically assume that there are a million truly independent genomic loci, as was estimated in the European population [45]. With this assumption, the Bonferroni correction results in a p-value threshold [46] of

$$p=\frac{0.05}{\mathrm{1,000,000}}=5\times {10}^{-8}$$

which is the most commonly used threshold to accept or reject a GWAS association. This threshold is referred to as the genome-wide significance threshold.

The unconditional (absolute) validity of this estimation has however been questioned, and thus, the search for an adequate p-value threshold to use in GWAS has grown into a parallel subject of study. For instance, multiple additional statistical procedures have been proposed, such as the Sidak correction, False Discovery Rate (FDR), permutation test, Bayesian approaches, and dimensionality reduction-based methods.

The representation of the GWAS results presents a different challenge. In order to represent the millions of statistical results in a visual manner, the association p-values are typically displayed in a Manhattan plot (Figure 3). In this type of scatter plot, each genomic variant that has been tested for association is represented as a point, the X axis comprises all of the genomic positions, and the Y axis measures the obtained p-values, which are typically scaled in −log₁₀. The significance threshold (e.g., $5\times {10}^{-8})$ is marked with a horizontal line so that the results that are significant after multiple testing correction can be easily spotted. The name of these plots derives from the expectation that the results would look similar to the skyline of Manhattan, with significant loci rising as skyscrapers from the ground. In the reality of GWAS, however, these rich skylines are seldom obtained, as it is more common to observe only a handful of loci that reach such levels of significance.

In addition to identifying significant associations between genomic variants and phenotypes, GWAS also estimate the odds ratio ($OR$) for each genomic locus, an effect size estimate of the increased odds of having the disease per risk allele count [47]. An $OR=1$ thus implies no association with the disease, an $OR>1$ implies that the effect allele is a risk allele, increasing the risk of developing the disease, and an $OR<1$ implies a protective allele, decreasing the risk of disease. In the case of quantitative traits, which require no logarithm transformation, the magnitude of the effect can be directly measured using the $\beta$ coefficient of the regression. Thus, $\beta =0$ implies no association with the trait, but $\beta >0$ and $\beta <0$ imply a positive or negative association with the allele, respectively.

Unfortunately, effect sizes tend to be overestimated, which is mainly due to the bias caused by an effect named the winner’s curse. The quantification, correction, and bias-reduction on the effect size estimator has been a GWAS-parallel subject of study [48] given its relevance to the heritability contribution.

Box 3. Technical concepts.

• Beta: An estimation of the effect size of a variant for a quantitative phenotype: the coefficients obtained from fitting a regression of the genotypes to the phenotype.
• Cohort: A group of individuals.
• DNA hybridisation array: A technology to identify the genotypes of a specific subset of variants of an individual.
• Effect size: A measure of the contribution of a genomic variant to a specific phenotype.
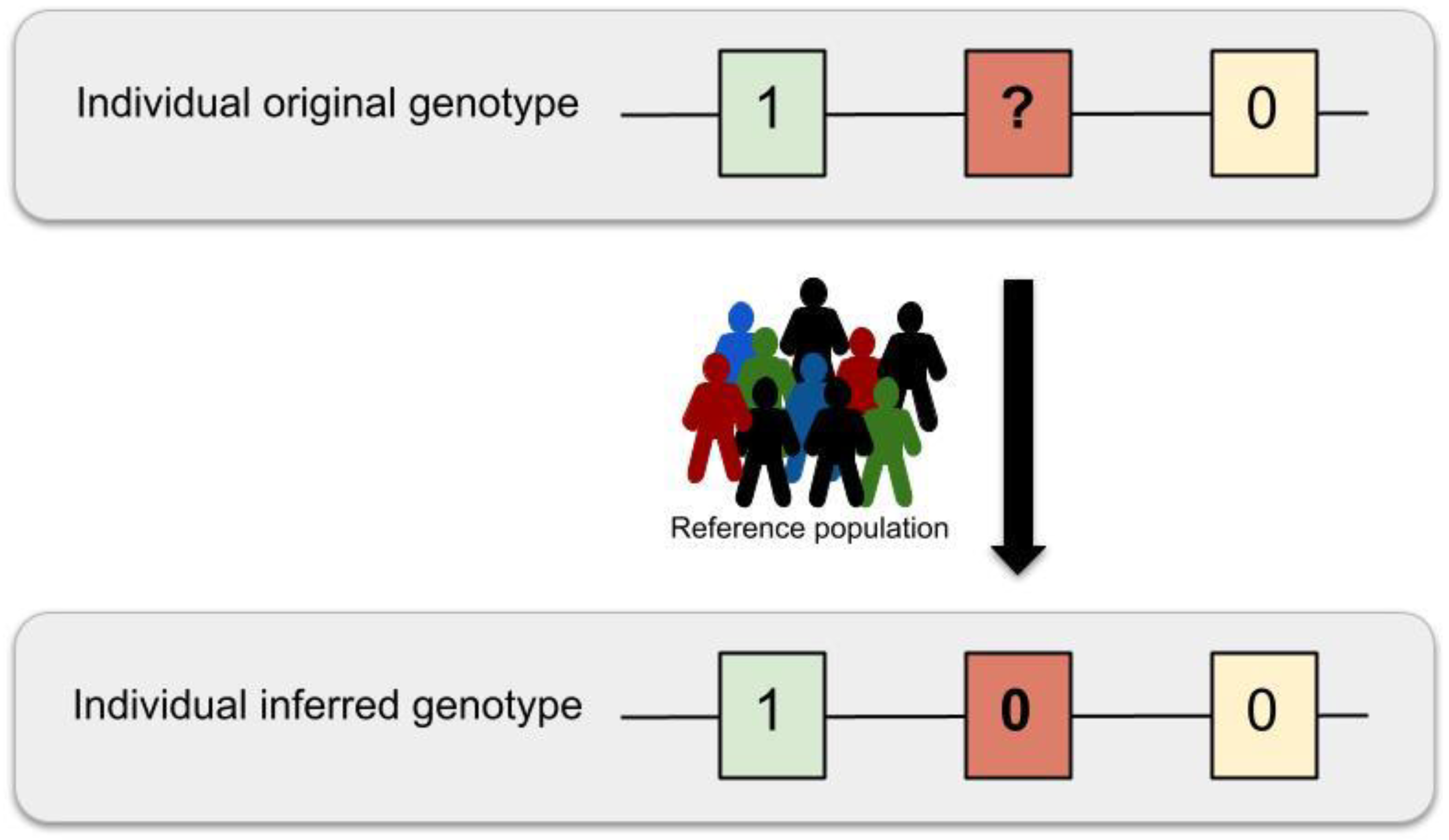
• Imputation: A statistical method to infer missing genotypes given a reduced set of known genotypes and a reference panel.
• Odds Ratio: An estimation of the effect size of a variant for a binary phenotype: the odds of having the disease with a variant divided by the odds of having the disease without it.
• Phasing: A statistical method to infer the haplotypes of an individual to determine which alleles belong to the same chromosomal sequence.
• Reference panel: A set of well characterised haplotypes of a group of individuals, used as a reference to infer non-genotyped variants in other individuals.
• Whole genome sequencing: A technology that provides the complete nucleotide sequence of an individual genome.

4. Current Practice and GWAS Limitations

GWAS have had a history of success in the study of complex traits, enabling the identification of the genomic loci involved in these phenotypes for the first time. Indeed, GWAS have so far discovered more than 276 thousand genomic associations for more than 4 thousand traits and diseases [49,50,51]. However, almost 20 years of analyses have also highlighted their limitations, which preclude more genomic associations from being identified [21,22]. Here, we discuss the main critical points of GWAS in detail, and we explain how the methodology can be extended to mitigate some of these. Next, we describe the most common complementary approaches and the existing alternatives that are attempting to solve these limitations.

4.1. Power and Sample Size

One of the main concerns in a GWAS is whether the study is powered enough to detect any association with a trait. The statistical power of association for a given variant strongly depends on the magnitude of its effect size and on its frequency in the population. Strong effect sizes are easier to capture, and common variants generally provide higher power. However, due to evolutionary selective pressures, effect sizes and frequencies are generally inversely correlated, with rarer alleles showing stronger $ORs$. In practical terms, current GWAS have mostly revealed associations for common variants with $ORs$ of around 1.05–1.3 [52].

A natural way to increase power in GWAS is to increase the size of the sample under study (N). Increasing sample size would allow the identification of smaller effects for common variants as well as open the possibility to study rare variants. Motivated by this need, large-scale initiatives have been established in the form of international consortia to pool multiple resources and thus generate larger cohorts for subsequent analyses. These efforts have pushed the discovery of new loci and our understanding of complex disease genetics [53,54,55,56]. Further, biobanks have been established to make these large collections of genotypic and phenotypic data available for future studies [57,58,59]. However, given the sensible nature of these genomic and medical data, accessibility restrictions have been put in place, which often hinder or discourage their reutilisation by further scientific efforts.

Another commonly used strategy to increase sample size in GWAS is meta-analysis based on the statistical combination of previous GWAS results from different studies on the same phenotype. Requiring only GWAS summary statistics (e.g., sample size, effect sizes and p-values), meta-analyses are far more cost-effective than the generation of new genotype–phenotype datasets and thus have been used extensively [13,60,61].

Meta-analysis approaches are based on a weighted sum of the effects obtained in each of the studies, thus providing an estimate of the association of each genetic marker over all of them. For example, in a meta-analysis for M studies where each variant $V_i$ has been assigned an effect ${\beta }_{ij}$ for the j-th study, a Stouffer’s Z-score can be calculated by assigning a weight for the estimated allelic effect on each study $w_{ij}$ so that the allelic effect across all the studies will be

$$Z_i=\frac{{{\displaystyle \sum }}_{j=1}^M{\beta }_{ij}{w}_{ij}}{\sqrt{{{\displaystyle \sum }}_{j=1}^M{w}_{ij}^2}}~{\chi }_1^2$$

which estimates the association to disease over all tests.

In addition, the genetic heterogeneity between the different studies is measured, which is based on Cochran’s Q-test, by the statistic

$$Q_i={\displaystyle \sum }_{j=1}^M{w}_{ij}{\left(Z_i-{\beta }_{ij}\right)}^2~{\chi }_{M_i-1}^2$$

for each SNV i. This measure helps to detect associations that are not consistent across the studies, which might then be filtered out if necessary.

Despite the proven value in increasing power, large sample sizes in GWAS present many challenges, nonetheless. The recruitment and genotyping of individuals might be extremely expensive in terms of time and resources. Despite having received more attention in recent years, data sharing is still limited and difficult, even in the form of summary statistics. Further, recent studies have estimated that unprecedented sample sizes, in the order of millions, might be needed to capture the entire spectrum of the variants associated with a trait [62]. Different strategies other than simply increasing the number of analysed samples might be thus more feasible to increase discovery power and will be briefly discussed in the following sections.

4.2. Increasing the Number of Genomic Variants

Another important factor in determining the discovery power is the correlation (LD) existing between the interrogated variants and the real, underlying causal variant [47]. Higher discovery power can be achieved by increasing the number of tested variants, thus obtaining a higher density coverage of the genome and increasing the probability of directly testing variants that are strongly correlated with the causal ones. However, as described in Section 2, GWAS typically use DNA microarray technologies, which only provide the genotypes for a limited subset (0.5 to 2 M) of all of the SNVs in a genome [63].

A technique that is commonly used to increase the number of variants that can be tested in a GWAS is genomic imputation. Starting from genotyping array data, genotypes of over 10 million variants can be inferred for an entire group of individuals (also named cohort) [64], with a reduced number of missing values [65,66].

Imputation is usually preceded by a phasing step, in which haplotypes for each individual are inferred starting from genotypes, typically from array data. Then, the studied haplotypes are statistically compared with those in reference panels, which are panels of thousands of individuals with a deeply characterised haplotype [15,67,68,69,70,71]. Through this comparison, the genotype probabilities for variants in the reference panels are imputed into the cohort haplotypes [72]. Several methods and tools have been developed to phase and impute [65,73,74,75,76]. Most of them are essentially based on Markov Chains (MC), Hidden Markov Models (HMM), Markov Chain Monte Carlo (MCMC), and the expectation-maximisation algorithm [28,77]. Other tools have also been developed to combine the imputation results from different panels [14].

As a result, given a population with $N$ individuals, where, $m\in \left\{1,\dots ,M|M<\infty \right\}$ variants $V_i,i=1,\dots m$, are inspected for each individual $j$, each variant genotype can take a value from the space of genotypes $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$. Based on the space defined by the genotype, each genomic variant $V_i$ can be considered as a simple random variable $V_i:\mathsf{\Omega }\to G_{ij},$ so that $\forall g\in G_{ij}\exists \omega \in \mathsf{\Omega }$ for which $V_i\left(\omega \right)=g$, with $\mathsf{\Omega }$ as the space of events. Under this scenario, the imputation model can be formalized by first stating that each variant genotype $G_{ij}$ for the individual $j$ has a corresponding haplotype $H_{ij}=\left\{\left(0,0\right),\left(0,1\right),\left(1,0\right),\left(1,1\right)\right\}$, which is defined by a function $f:G_{ij}\to H_{ij}$, where $f\left(AA\right)=\left(0,0\right),f\left(AB\right)=\left\{\left(0,1\right),\left(1,0\right)\right\},f\left(BB\right)=\left(1,1\right)$. Thus, the haplotype space $H_{ij}$ is a partition of the genotype space $G_{ij}$. For simplicity, each haplotype $H$ can be written as a pair set $H=\left(H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)}\right),H_{ij}^{\left(k\right)}\in \left\{0,1\right\},k\in \left\{1,2\right\}$. The aim of imputation is to infer the missing genotypes based on the posterior probability $P\left(G_{ij}|H\right)$ for each individual in a LD region by comparing the individual haplotypes in that region with the N haplotypes $H=\left\{H_1,H_2,\dots ,H_N\right\}$ present in a reference panel (Figure 4).

For example, in Hidden Markov Model (HMM) approaches, the posterior probability of each genotype, given the haplotype, can be calculated as

$$P\left(G_{ij}|H\right)={\displaystyle \sum }_{H_{ij}^{\left(1\right)}{H}_{ij}^{\left(2\right)}}P\left(G_{ij}|H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)},H\right)P\left(H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)}|H\right)$$

(6)

where the term $P(H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)}|H)$ is the prior probability for each hidden state change along the sequence, and $P(G_{ij}|H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)},H)$ models the probability that the genotype will be similar to the haplotypes that are copied from the reference. By estimating the genomic recombination rate across the region $\rho$ based on the effective population size and the mutation rate $\theta$, Equation (6) can be simplified to

$$P\left(G_{ij}|H,\theta ,\rho \right)=P\left(G_{ij}|H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)},\theta \right)P\left(H_{ij}^{\left(1\right)},H_{ij}^{\left(2\right)}|H,\rho \right)[64].$$

Given that both $\theta$ and $\rho$ can be estimated from the population of study and that the haplotypes can be inferred from the HMM, this model can be used to infer missing genotypes in the study population.

The accuracy of the different imputation methods can be assessed by masking known genotypes and imputing them using surrounding variants. The correlation between the estimations and the true values can be used to measure the imputation accuracy. Based on this method, current error rates range between 5.10 to 6.33% [28].

Genotype imputation offered the possibility of comprehensively investigating variants throughout the genome, including rare variants, at a large scale for the first time. However, the imputation of rare variants still presents difficulties. Although rare variants are present in reference panels, those are usually in low LD with the common variants from the genotyping array; therefore, they are imputed with less accuracy. Further, rare variants tend to be more private, and only a fraction of these can be possibly present in reference panels; thus, only a few can be imputed. In the future, when whole genome sequencing is affordable for large studies, the imputation process will cease to be necessary since all of the genomic variants will be obtained from the DNA of the participants. However, until then, genotype imputation provides the most valid alternative for comprehensive GWAS.

4.3. Genetic and Population Heterogeneity

Genetic heterogeneity between individuals of shared ancestry or between those of different ancestries is a factor that further complicates the study of polygenic traits. The same apparent phenotype (especially diseases) might be the result of different combinations of genomic variants in different individuals. Genetic heterogeneity is typically overlooked in GWAS, as individuals with the same broad disease are considered as a homogeneous group of cases. In this scenario, GWAS can only capture the most shared signals, and less prevalent genomic associations might be masked.

An attempt to reduce this issue has been made by classifying cases into sub-groups by using multiple clinical variables or by defining sub- or endo-phenotypes. For example, a disease such as Type 2 diabetes is broadly defined by a high content of glucose in the blood, but different clinical sub-types have recently been identified using measures such as age of disease onset or body-mass index [78]. The rationale is that these phenotypic sub-groups might reflect more genetically homogenous groups and may thus help us to identify the underlying genomic loci that differentiate them. Even though this strategy entails a decrease in the dimensional reduction of the sample size due to fragmentation, the power to discover the underlying genomic factors could be increased due to a reduction in the dilution of the relevant signals as a consequence of the homogeneity and less variability in the data [79].

Genetic heterogeneity is also significant between individuals of different ancestral backgrounds due to differences in variant frequencies (e.g., a rare variant in one ancestry might be common in another) and LD patterns. Early GWAS were performed with individuals of predominantly European or Caucasian ancestry, which raised the question of their relevance for individuals of other ancestries. Moreover, the possibility remained that common variants were only associated with complex diseases because they were in LD with rare, high-impact variants that were specific to the studied ancestry and thus that these associations would not replicate in other ancestries.

Since then, trans-ancestry (also named trans-ethnic) studies, which analyse samples of multiple ancestries together, have shown that the variants that were associated with the complex traits and diseases that were identified in these studies were predominantly consistent with those identified in ancestry-specific studies [80,81,82]. These findings suggest that these phenotypes are indeed driven by common variants and that their genetic architecture is mostly shared across different ancestries.

Albeit burdened with further increased sample collection and analytical complexities, these large studies have succeeded in the development of population genomics and have increased the genetic understanding of complex traits [82,83].

4.4. Complex Interactions

GWAS are typically applied to capture the effect of single independent variants on a phenotype. However, complex traits are understood to be caused by multiple genomic variants that interact with environmental variables [84,85]. Therefore, other analytical frameworks are needed to interrogate more complex interactions, such as gene-gene interactions (GxG) or gene–environment interactions (GxE) [86]. Given the computational and data acquisition challenges of these studies, these have only recently become feasible, thus providing a novel avenue to reveal new understanding of the aetiology of complex traits and diseases.

4.4.1. Gene–Gene Interactions (GxG) and Genomic Variant Epistasis

Complex phenotypes arise due to the combined effects of multiple genes. For example, 16 different genes have so far been linked to the determination of the eye colour phenotype [87]. In some cases, the effects on the phenotype of one of the genes might be enhanced, diminished, or changed by variability in a different but interacting gene. These effects are known as gene–gene (GxG) interactions. Particularly, the term epistasis can be used to describe the result of the interaction of multiple genomic variants in different loci when it is not just a linear combination of the individual gene effects.

Variant interaction models present a framework to analyse the combined effect of multiple genomic loci on complex traits. These focus on finding groups of interacting variants and compute the relative contribution of these subsets of variants to the total phenotypic variability [88,89,90]. However, the combinatorial nature of the problem leads to very computationally expensive analyses, given the large number of genomic variants in a genome. For example, hundreds of billions of tests will need to be performed just to inspect the association for pairwise combinations of 500,000 SNVs [84]. Further, additional measures need to be applied to solve issues such as the power needed to detect epistasis [84] or to scale the problem to a higher order interaction of genetic factors [88].

GxG interaction analysis can be extended from the methods proposed in Section 3.2. For example, in the case of a logistic regression model, in a population with $N$ individuals, for each individual $j$, the phenotype takes the values $P_j\in \left\{0,1\right\}=\left\{control,case\right\}=\left\{diseased,non-diseased\right\}$ and follows a Bernoulli distribution $P_j~B\left(p_j\right)$, where $p_j$ is the unknown probability of an individual being diseased. Thus, the phenotype of the individuals of the population follows a binomial distribution $P~Bin\left(p_j,n_j\right)$. Based on the observation of the $m\in \left\{1,\dots ,M|M<\infty \right\}$ genomic variants $V_i,i=1,\dots ,m$, where the variants genotype can take a value from the space $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$, the probability of an individual being diseased given their genotype can be expressed as $p_j=E\left(\frac{P}{n_j}|G_{ij}\right)$. Thus, for a pair of variants $G_{ij,1},G_{ij,2}$, this probability becomes $p_j=E(\frac{P}{n_j}|G_{ij,1},G_{ij,2})$. Under this scenario, the logit function can be applied to the ratio between the probability of the individual $j$ having the disease or not given a pair of genotypes (1). As such, the logistic regression model for the main effects can be expressed as

$$logit\left(Y_j\right)\sim {\beta }_0+{\beta }_1{G}_{ij,1}+{\beta }_2{G}_{ij,2}$$

to test whether the genotype is associated with the disease. As a result of that, the logistic regression model with main effects and pairwise interactions can be formulated [91] as

$$logit\left(Y_j\right)\sim {\beta }_0+{\beta }_1{G}_{ij,1}+{\beta }_2{G}_{ij,2}+{\beta }_3{G}_{ij,1}{G}_{ij,2}.$$

More recently, this problem has also been approached using machine learning methods, where the relationship between multiple variants and disease risk can be evaluated at once [88,92]. Several machine learning algorithms are commonly applied for solving classification, regression, or ranking problems, such as support vector machines, stochastic gradient descent, nearest neighbours, naive Bayes, Gaussian processes, neural networks, or decision trees. These methods can be applied within a supervised learning framework to find a list of variants with an effect on the disease and their combined effects. However, while these approaches have opened a new avenue for GxG analysis, they also suffer from problematic computational costs.

To work around this limitation, most studies have been forced to reduce the dimension of their input set, which is generally accomplished using multifactor-dimensionality reduction [93,94,95] or Bayesian inference [96,97]. Therefore, to facilitate the integration of multi-dimensionality reduction in GxG analysis, some bioinformatic tools have integrated this methodology in their software [23,98]. In addition, most studies also resort to restricting the genomic variants to test a selected subset of candidates based on prior biological knowledge, with the hypothesis that these are more likely to provide relevant biological insights. As a result, GxG and epistatic studies are generally limited in size and scope. This field remains open, and it is likely to provide further insights on the genomics of complex traits.

4.4.2. Gene-Environment Interactions (GxE)

The effect on complex phenotypes resulting from the environment (defined as all the non-genomic components) is often overlooked, but it plays a significant role in determining both the strength and the variability of a trait or disease. For example, even if type 2 diabetes is understood to have genomic causes, one of the best clinical predictors for risk is simply age, which is independent from the genomic components of the disease. However, the effects of environmental variables on an individual also can depend on their particular genomic background, e.g., the same food consumed by two individuals might have a different impact on their weight. This effect called named gene–environment (GxE) interaction.

Specifically, GxE interaction analyses focus on studying the environmental factors, such as diet, lifestyle, psychosocial stress, or airborne agents, and their relation with different genotype groups in terms of disease associations [99,100]. In an extension of the GWAS concept, Environment-Wide Association Studies (EWAS) analyse multiple environmental factors and compare them between different genotype subgroups of a complex disease in large-scale GxE multi-studies [101]. The most common approaches to study these GxE interactions are regression-based methods (Section 3.2), which are usually preceded by a filtering step [102,103,104].

Thanks to these studies, the genotype group information can be used to build better prognostic models and to identify possible high-penetrance or high-exposure subgroups to build better treatments [99,105]. However, much larger sample sizes are needed for the detection of interactions compared to marginal effect sample sizes. In addition, the complexity of measuring the environmental exposure, the difficulty of incorporating environmental measures to the models, the heterogeneity of the environmental exposures, and the lack of publicly available data represent important hurdles that limit the advancement of this field of study [99,100,105,106,107].

4.5. Biological Interpretation and Clinical Implications

GWAS have been successful in identifying multiple loci that are associated with complex traits. However, the biological interpretation and clinical application of these findings has proven to be very challenging.

First, because of linkage disequilibrium, GWAS can only provide associated genomic loci, encompassing multiple correlated variants. In addition, GWAS identify statistical associations, but it is well established that association does not imply causation. To attempt to overcome these limitations, further computational and experimental studies need to be pursued. Computational approaches include gene expression studies and enrichment analyses of gene, pathway, epigenomic, and regulatory elements or Mendelian randomisation analyses, which are used to gain further biological insights [108,109]. Simultaneously, wet-lab experiments with cell lines, model organisms, or further human studies also need to be used to answer the biological hypotheses that are inferred from these analyses.

As an attempt to produce some clinical insight directly from GWAS results, Polygenic Risk Scores (PRS) have recently been developed. PRS are based on the premise of evaluating the total risk of disease of a genome by considering all of its genomic variants with known disease associations [110].

Particularly, PRS compute the relative risk of an individual from the population of study to develop a disease. Therefore, in a study of a population with $N$ individuals, for each individual $j$ in the population of study, given $m\in \left\{1,\dots ,M|M<\infty \right\}$ genomic variants $V_i,i=1,\dots ,m$, where the variants genotype can take a value from the genotypes space $G_{ij}=\left\{AA,AB,BB\right\}=\left\{hom.ref,het,hom.alt\right\}$, GWAS models can be applied to estimate the effects ${\beta }_i$ for each genotype (Section 3.2). Then, a PRS can be calculated based on the sum of the individual genotypes $G_{ij}$ weighted by the estimated effects for that genotype ${\beta }_j$, resulting from the GWAS analysis [111]. Thus, each individual score $S_i$ is calculated using the equation $S_j={\displaystyle \sum }_{i=1}^M{G}_{ij}{\beta }_i$. As each individual $j$ will have an associated score $S_j$, the score can be observed as an independent variable explaining the phenotype $P$ of the individual. Consequently, under a similar scenario to the one explained in Section 3.2.2 for binary traits, $P\in \left\{0,1\right\}=\left\{control,case\right\}$, with $P~Bin\left(p_j,n_j\right)$ and $p_j$ being the probability of an individual being diseased. For example, the probability of an individual being diseased can be explained by the score as $p_j=E\left(\frac{P}{n_j}|S_j\right)$. Therefore, the logit can be applied to the ratio between the probability of the individual having the disease or not, given a particular score, to fit the logistic regression model $logit\left(p_j\right)\sim {\beta }_0+{\beta }_1{S}_j$. For quantitative traits, where the individual phenotype takes values $P_j\in \sigma (ℝ)$, with $\sigma (ℝ)$ the Borel set, a linear regression model could then be fitted to explain the phenotype based on the individuals score as $P_j\sim {\beta }_0+{\beta }_1{S}_j$.

The distribution of the scores across the population of study follows a normal distribution, in which the left tail contains the individuals with the lowest risk of developing the disease, and the right those with the highest risk (Figure 5). However, although the use of PRS has shown potential, statistically significant differences in disease risk are typically only found when comparing the individuals at the tails of the distributions (e.g., the individuals with the highest 5% of scores have a 3x higher risk of disease than those with the lowest 5% scores), thus only providing limited insights for the majority of the population.

Overall, the combination of cell biology studies [112,113] with GWAS results have produced a greater understanding of the biology behind complex diseases [56]. However, the study of the specific biological mechanisms that mediate the association between genotype and disease remains one of the main open fields of study in biomedicine, and the advancement of personalised medicine depends on its success.

4.6. Comprehensive GWAS Strategies for New Discoveries: An Example

As detailed in the previous sections, different strategies can be put in place to achieve good power and to produce discoveries in GWAS. Here, we describe an example of how an improved, comprehensive methodology for GWAS can reveal novel association loci in a previously analysed, publicly available cohort. In this study [14], 22 age-related diseases were analysed in 62,281 subjects from the GERA cohort. Ninety-four significant loci were identified, of which twenty-six had never been reported before, despite the fact that the data had already been previously analysed.

A first essential feature in driving novel discovery was an extended imputation step. Imputation was performed using four reference panels yielding 16,059,686 variants to test for association. The variants encompassed a broad spectrum of frequencies and types, including 2.6 M low-frequency and 5.5 M rare variants as well as 1.6 M small insertion/deletions (indels), which are normally absent from DNA microarrays and were thus excluded from analysis. Indeed, 3 of the 26 new loci corresponded to low-frequency variants, and 7 corresponded to rare variants. Further, only a fraction of the 26 new loci would have been genome-wide significant if the imputation had been performed with only one of the individual haplotype panels.

A second feature ensuring an increased discovery power was the use of multiple inheritance models in association testing. Typical GWAS only consider the additive model, according to which disease risk is proportional to the number of risk alleles in a genotype. However, dominant, recessive, or even more complex allelic interactions are known to exist. Indeed, 20 of the 94 loci only showed genome-wide significance when non-additive tests were applied. When focusing on the novel findings, 13 out 26 (50%) would have been missed if considering the additive model only, indicating again the strength of this approach in pushing discovery. Three of the thirteen non-additive signals corresponded to rare variants with large recessive effects (OR 4.3–19.0).

This study highlighted the value of open access and data sharing since the re-analysis using more refined and extensive methodologies led to the discovery of novel loci and disease insights. The entire GWAS strategy for this comprehensive methodology was integrated into a publicly available framework named GUIDANCE in order to facilitate further studies.

5. Conclusions

In the recent years, the increasing availability of DNA and phenotypic information and the ease of access to computational power and tools, combined with the statistical methods that we have discussed here, have greatly advanced our understanding of the genomic basis of complex traits and diseases. In this review we have presented an overview of Genome-Wide Association Studies, a broadly successful method that can be used to find associations between genomic variation and complex traits. Specially, the application of these methodologies has led to the discovery of more than 276 thousand genomic associations, for more than 4 thousand traits and diseases [49,50,51].

However, a significant proportion of the underlying genetic causes is still known to be missing, an effect termed missing heritability [114]. Here, we presented the main known GWAS limitations and discussed their consequences, which might partially explain this effect. The need for statistical power is forcing studies to increase the size of their samples, which comes at the expense of increasing computational and statistical challenges, which impose important limitations to these approaches [13,14,90]. However, future gene–gene, epistasis, and gene–environment interaction studies might also be able to recapitulate some of this missing heritability and provide new insights for a better understanding of the genetic basis of complex traits and diseases.

Despite providing knowledge and relevant candidate markers for diseases, an important limitation of this type of analysis is still the low applicability of the results that are obtained into clinical practice. In the case of rare diseases, variants are identified on patients with the disease to obtain an accurate diagnosis. In contrast, in the case of complex diseases, the aim is to generate maps of genetic predictors for disease risk and to apply them before the disease phenotype appears, ideally as we are born, allowing the design of preventive clinical protocols. But unfortunately, the multifactorial nature of complex diseases makes the prediction of their risk highly challenging. Current efforts include the generation of polygenic risk scores to predict risk and disease by combining multiple genetic signals identified through GWAS. It is therefore necessary to improve the methodological and statistical frames around association studies to align with the increase of samples and with the growing computational limitations.

Similarly, the functional interpretation of associated variants to contribute to this applicability into the clinics is also challenging and has not been well resolved. Currently, the vast majority of variants that are significantly associated with a specific disease or trait through GWAS do not directly disrupt gene sequences. Rather, these are found between genes, regulating the expression of these genes [56,115,116] and not their specific function, as is often the case in rare diseases. This makes the functional interpretation of associated variants a tedious task that also requires experimental validation.

Finally, it is important to be aware that around 79% of GWAS participants are of European ancestry, despite Europeans representing only 16% of the global population [117]. As a consequence, GWAS-derived results are predictably biased; for example PRS show lower predictive accuracies in non-Europeans [82,118]. Thus, extending GWAS to under-represented ancestries, including minority groups and isolated or indigenous populations might help improve our understanding of complex diseases. Indeed, some studies have shown how African/American and Hispanic/Latino populations contribute disproportionately to GWAS discovery, providing more signals than European samples with similar sample sizes [117]. This is likely due to their genetic specificities, in terms of allele frequencies or LD patterns, which would also favour the functional interpretation and the discovery of causal variants in known loci. Several recent initiatives in this direction include the H3Africa consortium [119] or the human pangenome project [120].

Altogether, GWAS have proven to be an efficient strategy to identify the genetic factors behind complex diseases. But despite the efforts, we believe we have uncovered only the tip of the iceberg, considering the amount of different factors, including genetic variants, that are involved in the risk, offset, and progression of these complex diseases. Coordinated work across disciplines, including deep mathematical and statistical expertise, are thus required to advance and to start building clinically relevant models for disease prediction based on solid genetic architectures.