Control Method for Flexible Joints in Manipulator Based on BP Neural Network Tuning PI Controller
Abstract
:1. Introduction
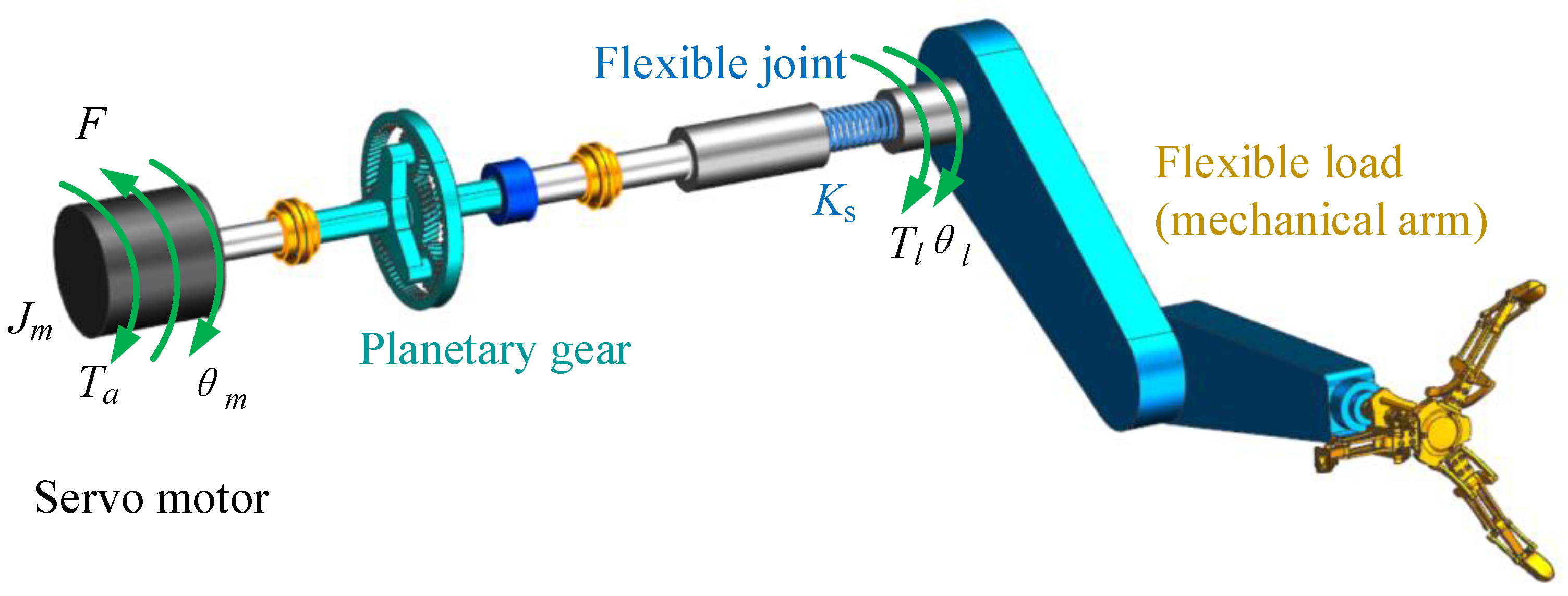
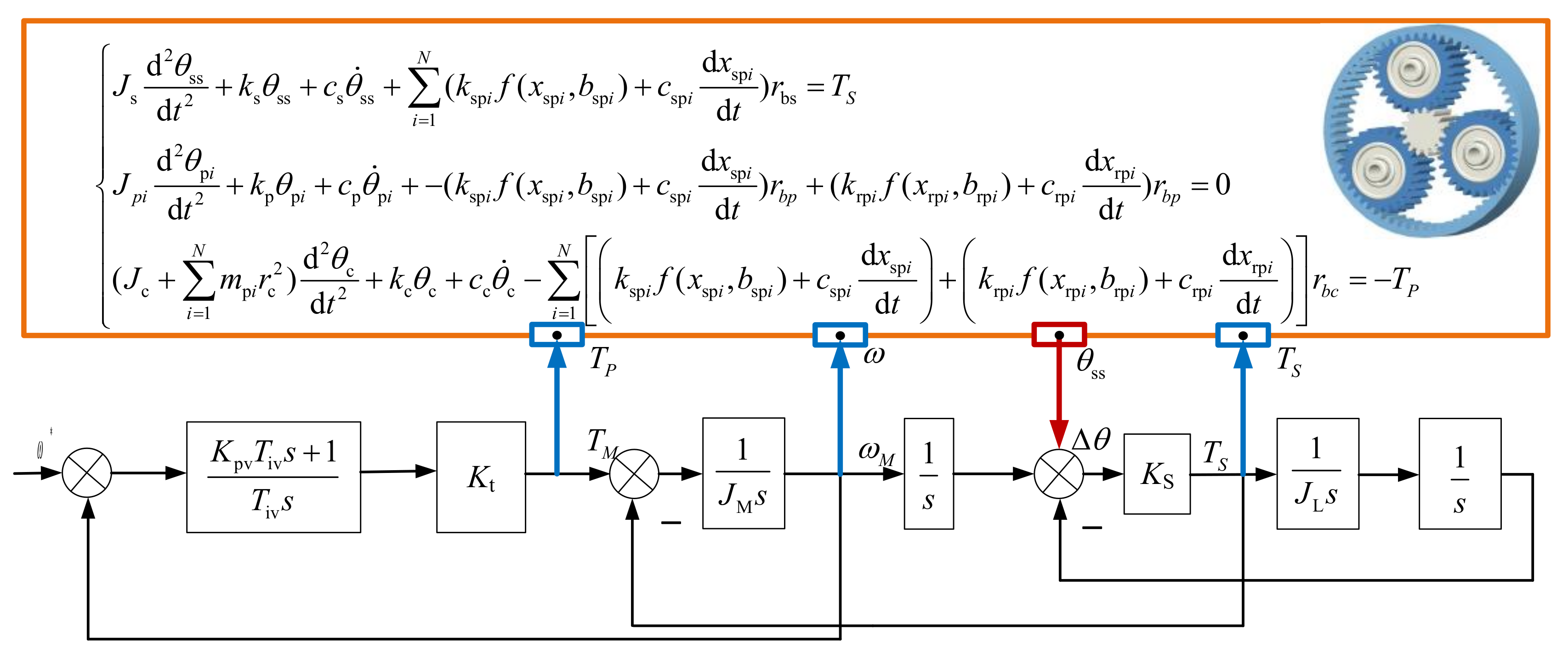
2. Dynamic Modeling of Flexible Joint Considering Gear Angle Error and Friction Torque
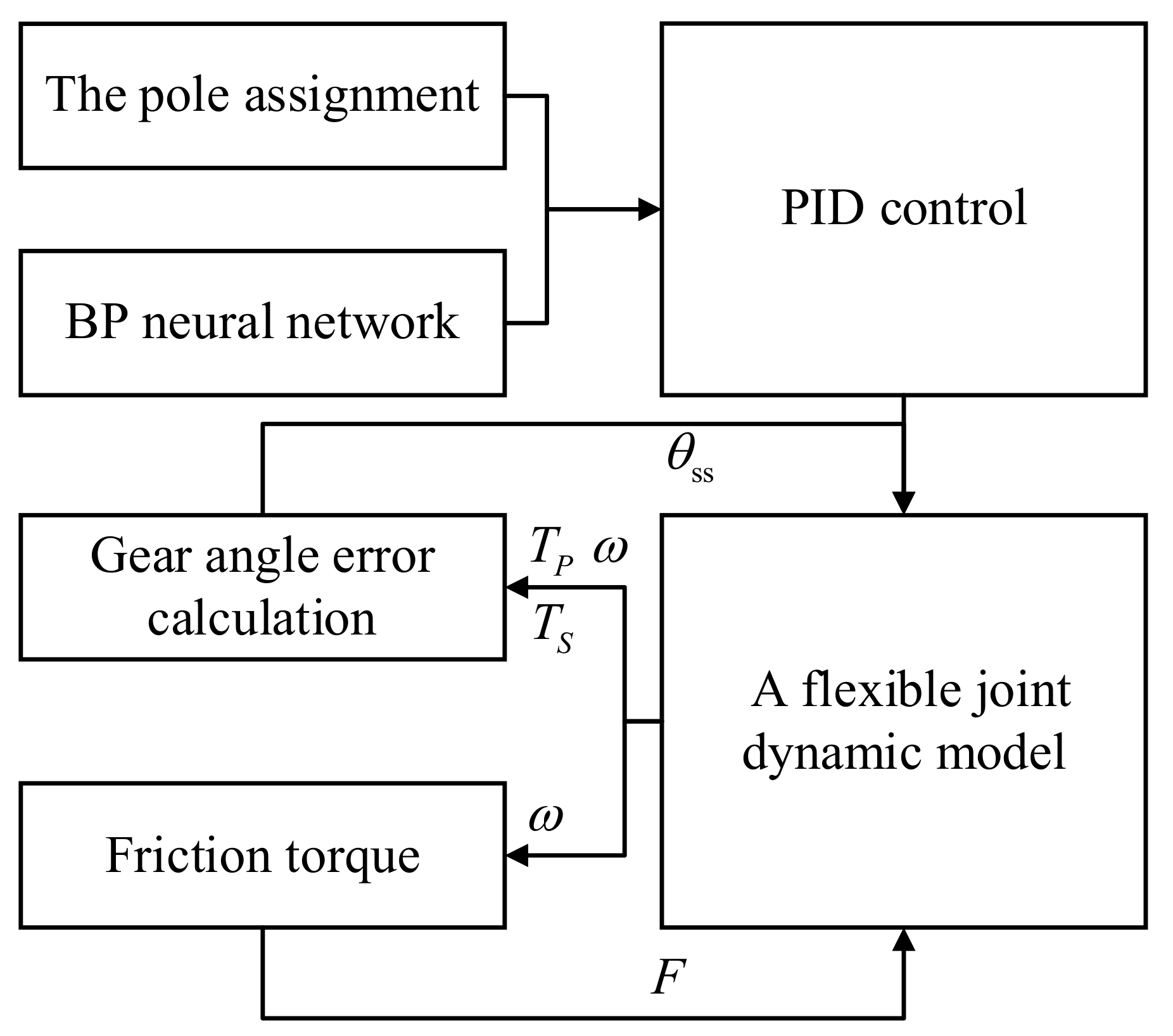
3. Joint Control Strategy Based on BP Neural Network and Pole Placement Method
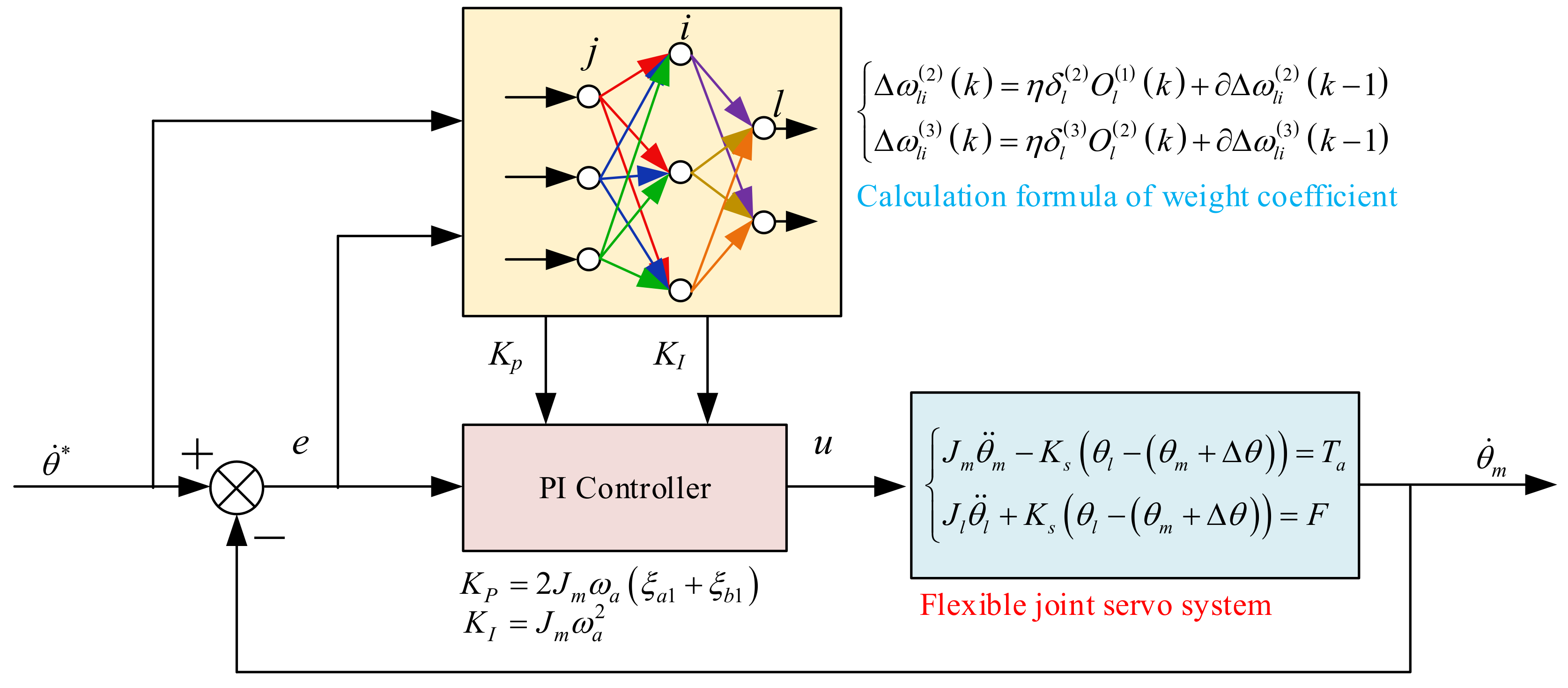
3.1. Controller Parameters Tuning Based on Pole Assignment
3.2. Controller Parameters Tuning Based on BP Neural Network
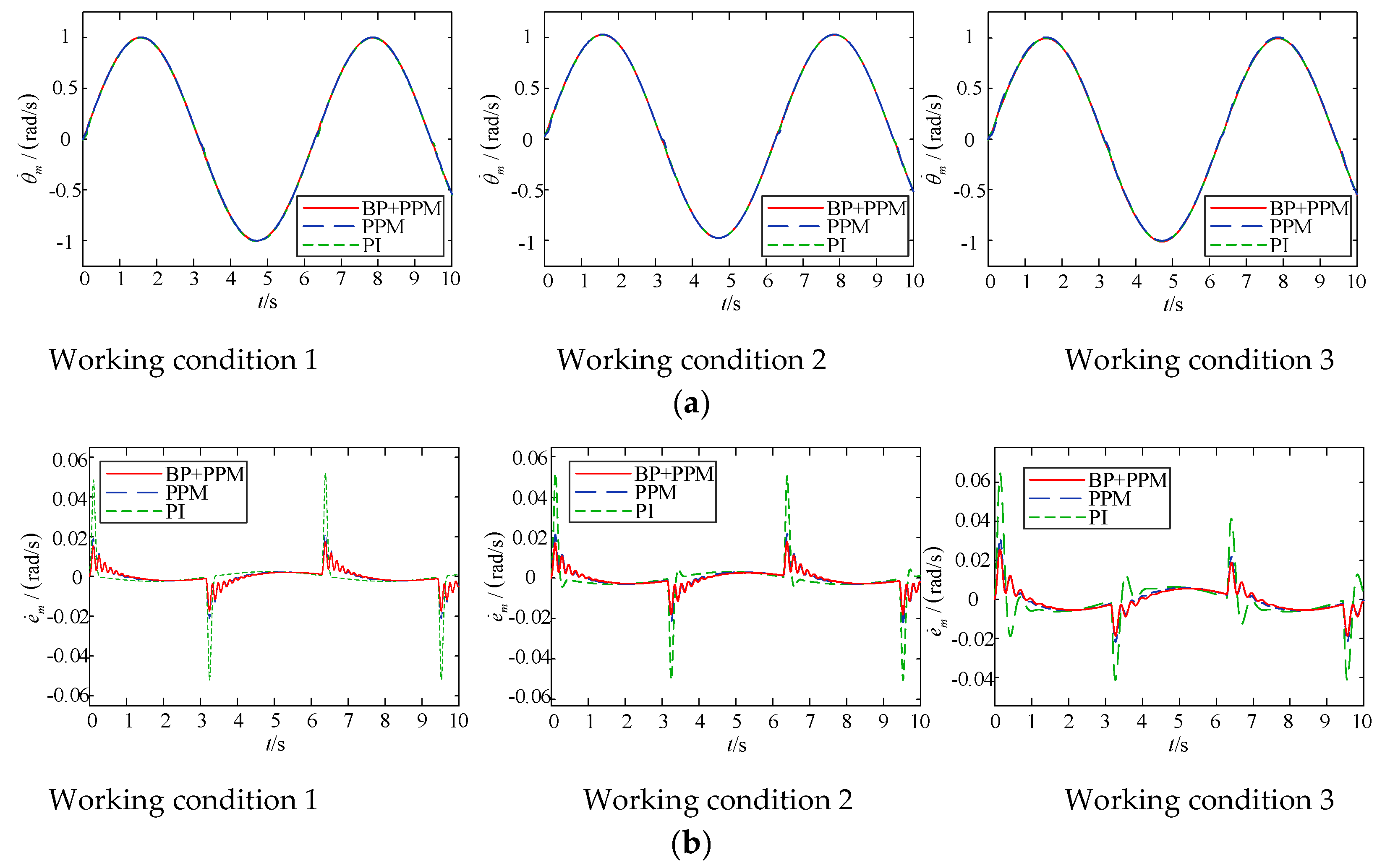
4. Numerical Simulation Analysis
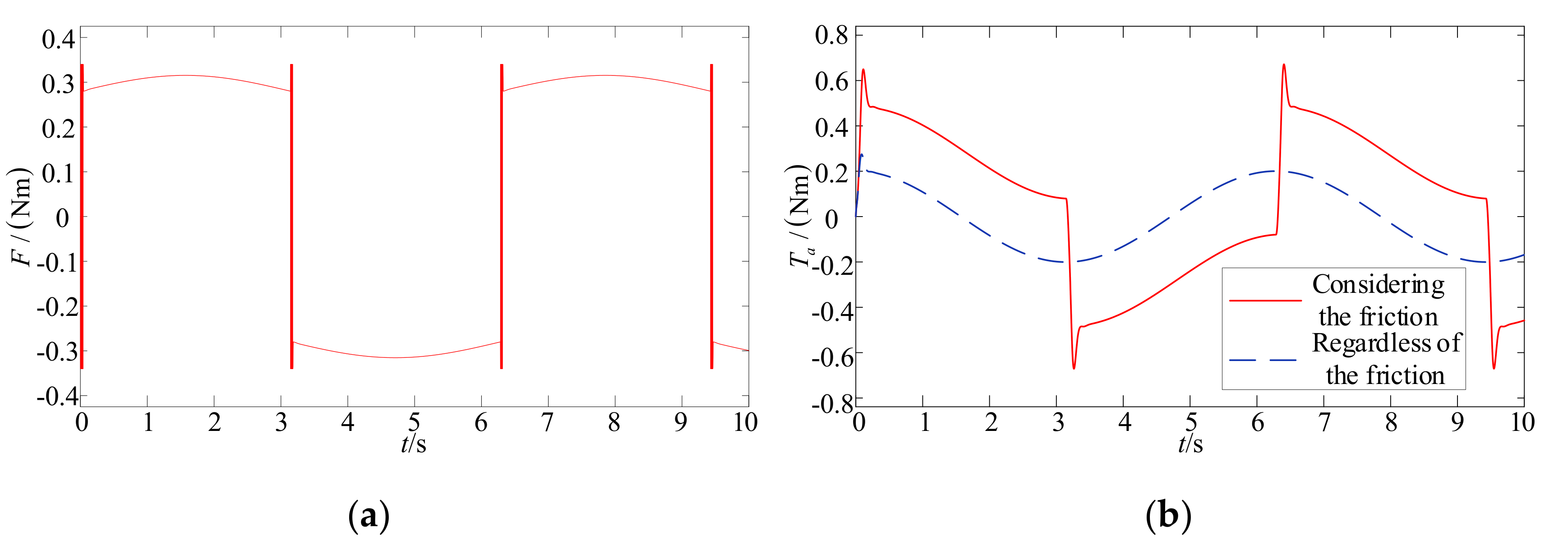
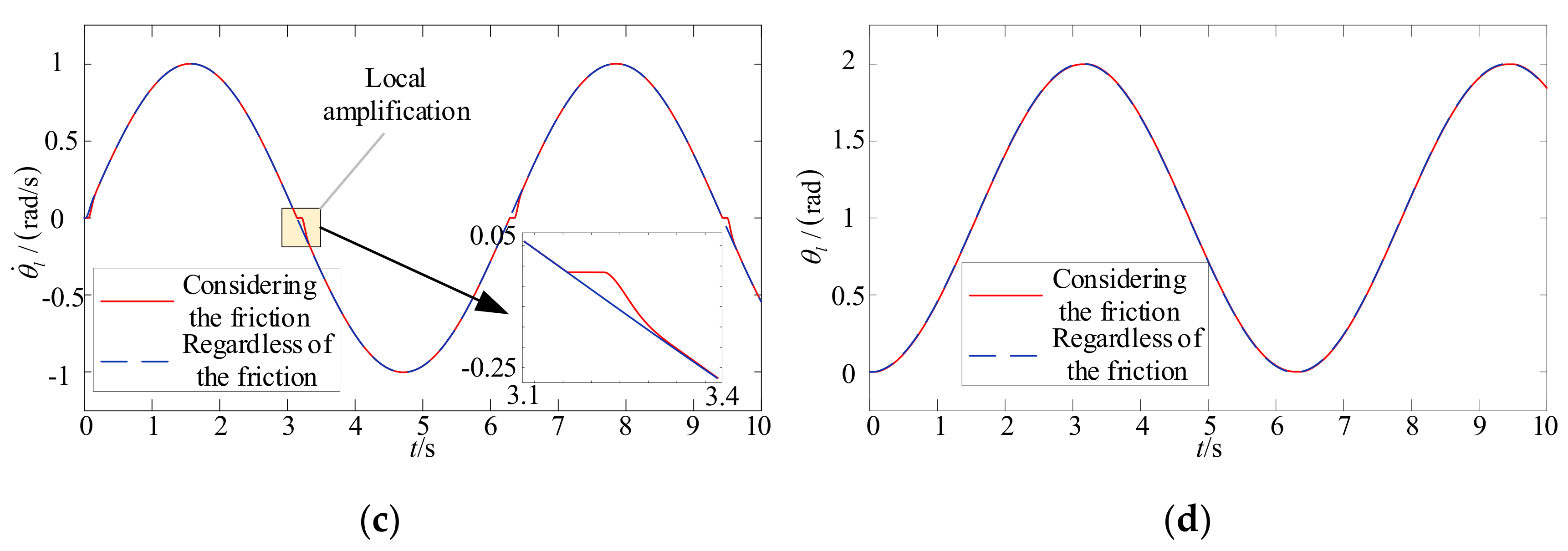
4.1. The Effect of Friction on the System
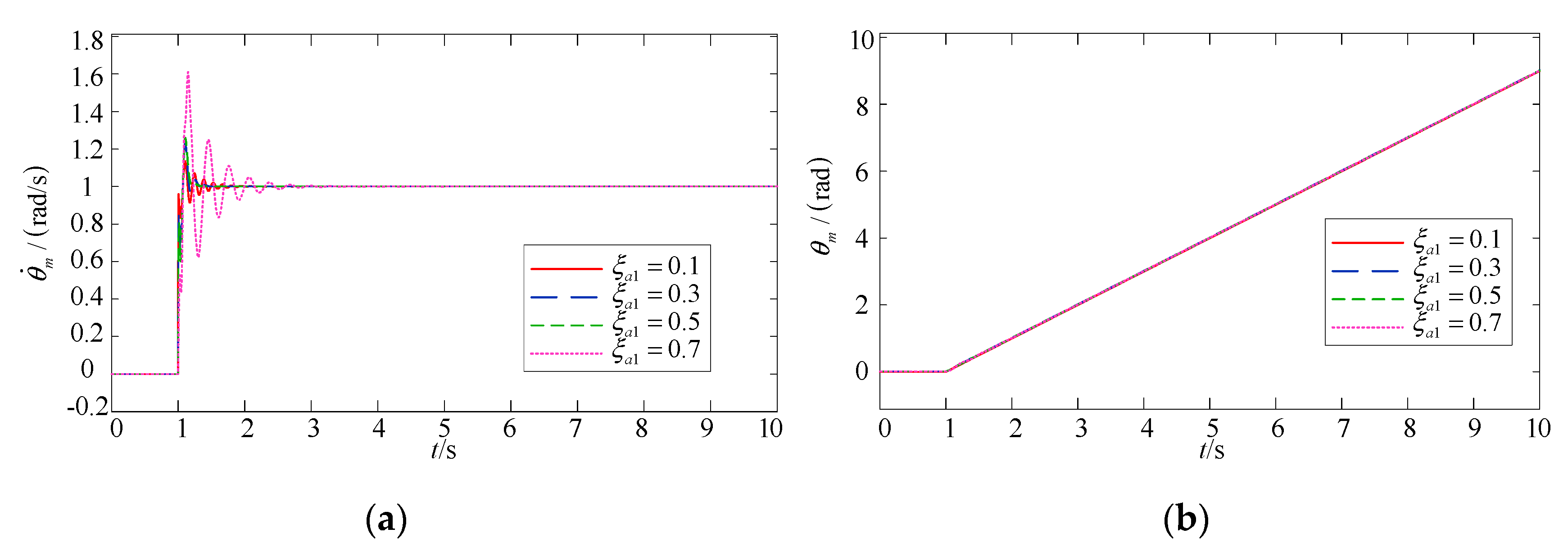
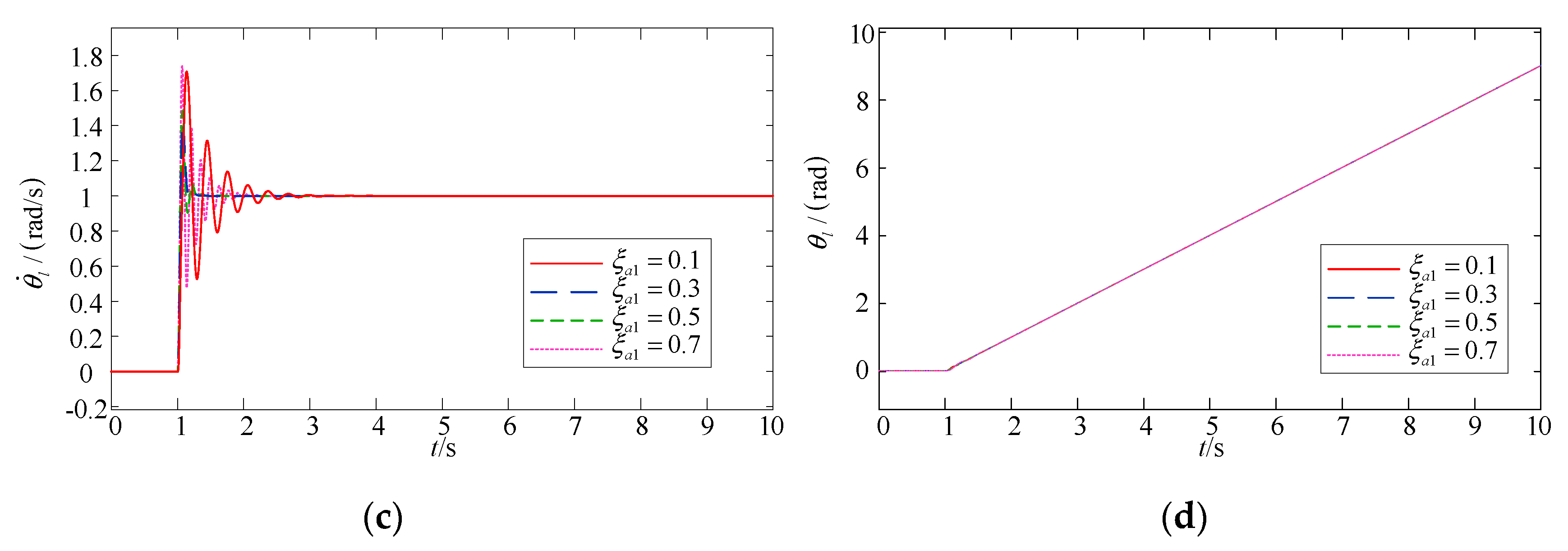
4.2. The Influence of Pole Damping Coefficient on System Output
4.3. Joint Control Strategy of BP Neural Network and Pole Assignment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, F.; Li, X.; Guo, Y.; Shang, D. Analysis of Contact Mechanical Characteristics of Flexible Parts in Harmonic Gear Reducer. Shock Vib. 2021, 2021, 5521320. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control. Ind. Robot. 2006, 17, 709–737. [Google Scholar] [CrossRef]
- Ma, C.; Cao, J.; Qiao, Y. Polynomial-Method-Based Design of Low-Order Controllers for Two-Mass Systems. IEEE Trans. Ind. Electron. 2013, 60, 969–978. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Zare, K.; Catalao, J. Network-constrained joint energy and flexible ramping reserve market clearing of power- and heat-based energy systems: A two-stage hybrid igdt–stochastic framework. IEEE Syst. J. 2020, 99, 1–10. [Google Scholar] [CrossRef]
- O’Sullivan, T.M.; Bingham, C.M.; Schofield, N. High-Performance Control of Dual-Inertia Servo-Drive Systems Using Low-Cost Integrated SAW Torque Transducers. IEEE Trans. Ind. Electron. 2006, 53, 1226–1237. [Google Scholar] [CrossRef] [Green Version]
- Bang, J.S.; Shim, H.; Park, S.K.; Seo, J.H. Robust Tracking and Vibration Suppression for a Two-Inertia System by Combining Backstepping Approach With Disturbance Observer. IEEE Trans. Ind. Electron. 2010, 57, 3197–3206. [Google Scholar] [CrossRef]
- Yan, Z.; Lai, X.Z.; Meng, Q.X.; Zhang, P.; Wu, M. Tracking control of single-link flexible-joint manipulator with unmodeled dynamics and dead zone. Int. J. Robust Nonlinear Control 2020, 31, 1270–1287. [Google Scholar] [CrossRef]
- Zuo, Y.F.; Mei, J.; Zhang, X.A.; Lee, C.H.T. Simultaneous Identification of Multiple Mechanical Parameters in a Servo Drive System Using Only One Speed. IEEE Trans. Power Electron. 2021, 36, 716–726. [Google Scholar] [CrossRef]
- Sehoon, O.; Kyoungchul, K. High-Precision Robust Force Control of a Series Elastic Actuator. IEEE-ASME Trans. Mechatron. 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Li, T.; Zhu, R.; Bao, H.; Xiang, C.; Liu, H. Nonlinear Torsional Vibration Modeling and Bifurcation Characteristic Study of a Planetary Gear Train. J. Mech. Eng. 2011, 47, 76–83. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Xu, J.; Yang, Z.; Chen, R. Dynamic characteristics analysis of planetary gear system with internal and external excitation under turbulent wind load. Sci. Prog. 2021, 104, 1–21. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Yang, Z.; Chen, R.; Yang, H. The influence of tooth surface wear on dynamic characteristics of gear-bearing system based on fractal theory. J. Comput. Nonlinear Dyn. 2020, 15, 041004. [Google Scholar] [CrossRef]
- Shao, M.; Huang, Y.; Silberschmidt, V.V. Intelligent Manipulator with Flexible Link and Joint: Modeling and Vibration Control. Shock. Vib. 2020, 2020, 4671358. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.P.; Wang, D.; Wu, J. Dynamic performance analysis of parallel manipulators based on two-inertia-system. Mech. Mach. Theory 2019, 137, 237–253. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J. Speed control of two-inertia system by PI/PID control. IEEE Trans. Ind. Electron. 2000, 47, 603–609. [Google Scholar] [CrossRef]
- Fu, X.; Ai, H.; Li, C. Repetitive Learning Sliding Mode Stabilization Control for a Flexible-Base, Flexible-Link and Flexible-Joint Space Robot Capturing a Satellite. Appl. Sci. 2021, 11, 8077. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Su, J.; Kim, Y.I.; Kim, Y.C. Robust Disturbance Observer for Two-Inertia System. IEEE Trans. Ind. Electron. 2013, 60, 2700–2710. [Google Scholar] [CrossRef]
- Cong, W.; Zheng, M.; Wang, Z.; Tomizuka, M. Robust Two-Degree-of-Freedom Iterative Learning Control for Flexibility Compensation of Industrial Robot Manipulators. In Proceedings of the International Conference on Robotics and Automation (ICRA) 2016 IEEE, Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Chang, W.; Li, Y.; Tong, S. Adaptive Fuzzy Backstepping Tracking Control for Flexible Robotic Manipulator. IEEE/CAA J. Autom. Sin. 2021, 8, 1923–1930. [Google Scholar] [CrossRef] [Green Version]
- Yin, M.; Xu, Z.; Zhao, Z.; Wu, H. Mechanism and Position Tracking Control of a Robotic Manipulator Actuated by the Tendon-Sheath. J. Intell. Robot. Syst. 2020, 100, 849–862. [Google Scholar] [CrossRef]
- Shang, D.; Li, X.; Yin, M.; Li, F. Control Method of Flexible Manipulator Servo System Based on a Combination of RBF Neural Network and Pole Placement Strategy. Mathematics 2021, 9, 896. [Google Scholar] [CrossRef]
- Kawai, Y.; Yokokura, Y.; Ohishi, K.; Miyazaki, T. High-robust force control for environmental stiffness variation based on duality of two-inertia system. IEEE Trans. Ind. Electron. 2020, 68, 850–860. [Google Scholar] [CrossRef]
- Li, X.; Shang, D.; Li, H.; Li, F. Resonant Suppression Method Based on PI control for Serial Manipulator Servo Drive System. Sci. Prog. 2020, 103. [Google Scholar] [CrossRef] [PubMed]
- Matthew, B. The Mechanics of Jointed Structures. Overv. Const. Models 2018, 14, 207–221. [Google Scholar] [CrossRef]
- Shuai, M.; Tza, B.; Gg Ja, B.; Xlc, D.; Hjg, E. Analytical investigation on load sharing characteristics of herringbone planetary gear train with flexible support and floating sun gear-sciencedirect. Mech. Mach. Theory. 2020, 144, 103670. [Google Scholar] [CrossRef]
- Li, L.; Luo, Z.; He, F.; Sun, K.; Yan, X. An improved partial similitude method for dynamic characteristic of rotor systems based on Levenberg–Marquardt method. Mech. Syst. Signal Proc. 2022, 165, 108405. [Google Scholar] [CrossRef]
- Kahraman, A.; Singh, R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system. J. Sound Vib. 1991, 146, 135–156. [Google Scholar] [CrossRef]







| Parameters | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| Flexible load inertia Jl/kgm2 | 0.186 | 0.256 | 0.573 |
| Motor inertia Jm/kgm2 | 0.062 | 0.062 | 0.062 |
| Torsional stiffness Ks/Nm/rad | 305 | 305 | 305 |
| Anti-resonant frequency ωa | 40.4943 | 34.5168 | 23.0713 |
| Resonant frequency ωn | 80.9885 | 78.1714 | 73.8352 |
| Inertia ratio | 3 | 4.1290 | 9.2419 |
| Pole damping coefficient | 0.3 | 0.3 | 0.3 |
| Controller parameters for pole assignment | 14/101 | 16/73 | 22/33 |
| Common PI controller parameters | 20/80 | 20/80 | 20/80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Li, X.; Xu, J.; Shang, D.; Qu, X. Control Method for Flexible Joints in Manipulator Based on BP Neural Network Tuning PI Controller. Mathematics 2021, 9, 3146. https://doi.org/10.3390/math9233146
Yang H, Li X, Xu J, Shang D, Qu X. Control Method for Flexible Joints in Manipulator Based on BP Neural Network Tuning PI Controller. Mathematics. 2021; 9(23):3146. https://doi.org/10.3390/math9233146
Chicago/Turabian StyleYang, Hexu, Xiaopeng Li, Jinchi Xu, Dongyang Shang, and Xingchao Qu. 2021. "Control Method for Flexible Joints in Manipulator Based on BP Neural Network Tuning PI Controller" Mathematics 9, no. 23: 3146. https://doi.org/10.3390/math9233146
APA StyleYang, H., Li, X., Xu, J., Shang, D., & Qu, X. (2021). Control Method for Flexible Joints in Manipulator Based on BP Neural Network Tuning PI Controller. Mathematics, 9(23), 3146. https://doi.org/10.3390/math9233146






