1. Introduction
Most physical and chemical systems in nature are open classical or quantum systems. The corresponding dynamics are usually well described by considering an environment with an infinite number of degrees of freedom [
1,
2]. The dynamics of open quantum systems [
3] is a central issue in different areas of physics, such as materials science, atomic, molecular and statistical physics of complex systems. The interaction between a system and its environment often leads to dissipation, quantum fluctuations and the irreversible evolution of the system. These processes affect surface dynamics, surface tunneling, non-adiabatic effects, and so on. Many disciplines, from physics to biology, have developed increasingly powerful methods for modeling open quantum systems [
4,
5].
The adsorption of rare gases has been of interest from the pioneering work by Langmuir [
6]. The diffusion of atoms/molecules on metal surfaces is usually considered in the quantum regime due to internal and/or external vibrations of adsorbates, as well as energy fluctuations at microscopic scale [
7,
8]. These studies provide valuable information on adsorbate–substrate and adsorbate–adsorbate interactions. Thus, it seems to be essential to study these phenomena using the theoretical formalism of open quantum systems in order to better understand the main microscopic and elementary processes occurring at surfaces. Moreover, these processes can be seen many times as a preliminary step in the study of more complicated phenomena as, for example, in heterogeneous catalysis [
9], crystal growth, chemical vapor deposition [
7], desorption [
10], adhesion [
11], photon–electron- induced surface reactions [
12], etc.
Depending on the surface temperature, surface coverage and the adsorbate–substrate interaction, diffusion times can vary by orders of magnitude [
13,
14]. The experimental techniques used for the characterization of surface diffusion can be classified according to the diffusion time that they are capable of measuring, such as fast or slow diffusion. Scanning tunneling microscopy (STM) [
15] and field ion microscopy (FIM) [
16] are especially useful for slow diffusion, where the time between jumps is of the order of seconds. These measurements provide a direct observation of the diffusion process. Among the different experimental techniques used to study these processes and also extract information indirectly about interaction potentials, the so-called quasielastic He atom scattering (QHAS) [
17,
18,
19,
20] is considered as the surface science analogue of quasielastic neutron scattering, which is widely and successfully applied to analyze fast diffusion (time between jumps of the order of microseconds). In order to interpret QHAS results, a more elaborate theory is needed to have reliable adsorbate–adsorbate and adsorbate–substrate interactions. A more recent experimental and powerful technique is also available, the so-called He spin echo (HeSE), which is similar to the neutron spin echo with ultra-high energy resolution [
21]. In the QHAS technique, the so-called
dynamic structure factor or
scattering law is directly measured, which provides us with line shapes for three elementary processes: the adsorbate diffusion process, low frequency adsorbate internal motions, and surface phonon excitations. The inverse Fourier transform in the frequency domain of the dynamic structure factor is the so-called
intermediate scattering function which is an observable in the HeSE technique. This function provides us with the same information as the dynamic structure factor but in the time domain.
During the past few decades, many efforts have also been carried out to devise various phenomenological models [
22] and more recently to derive via first-principles the dissipation functional from microscopic Hamiltonian [
23]. Pertinent to surface dynamics, the effect of surface degrees of freedom into atom/molecule-surface dynamics within the density matrix approach is included [
24,
25,
26]. In this formalism, microscopic events, such as quantum jumps, which exist in open individual systems, disappear by ensemble average. An alternative and less explored method consists of using a set of stochastic wave functions. The master equation for this method is a particular case of stochastic differential equations (SDE) known as the It
equation [
4]. This method reduces the dimensional problem from
to
N. In this sense, the SDE provides, aside from its statistical equivalent to the master equation, a more convenient description of individual systems. This is important for the study of quantum noise in mesoscopic [
27] systems and individual atoms/molecules [
28]. As far as we know, this is the first time that this theoretical analysis has been carried out in the surface diffusion context.
In particular, in this work, we have analyzed the QHAS experimental results by Ellis et al. [
20] where, for the first time, experimental evidence for a two-dimensional (2D) ideal gas of Xe atoms on Pt(111) at low coverage (
), low incident helium atom energy (
meV) and surface temperature
K is observed. This observation implies that Xe atoms behave as independent particles on the Pt(111) surface during a certain time, the well-known ballistic regime in diffusion processes. This regime is established for times
, where
is the friction coefficient. This study is carried out for a flat and corrugated surface and the corresponding results are compared with experimental and previous Langevin numerical results within the ballistic regime [
14,
20,
29].
The paper is organized as follows. In
Section 2, we briefly present the Linblad formalism, as well as the equivalent stochastic differential equation for open quantum systems. In
Section 3, numerical results are presented and discussed in the ballistic regime for flat and corrugated surfaces. Finally,
Section 4 summarizes the conclusions that can be drawn from this work.
3. Results and Discussion
As discussed above, the ISF is a key observable in the surface diffusion context. If the surface coverage
is low, the adsorbates can be considered as independent particles, that is, the adsorbate–adsorbate interaction can be safely neglected. Thus, the ISF now reads as
For our problem, is the wave vector transfer parallel to the surface, and are the position operators of the adatom/adsorbate in the unidimensional space and the initial position operator, respectively. The x-dimension can also be considered as one of the symmetry directions of the surface, where the projection on the wave vector transfer is carried out.
The stochastic wave functions
are obtained by numerically solving (
35) and using the splitting operator method together with the Fast Fourier transform (FFT). The terms with only
or
operators are propagated in the coordinate or momentum space, respectively. All the initial conditions for the position are chosen to be the same,
, and the propagation of the wave function moves towards negative values of
x since the initial velocity of the adsorbate is assumed negative,
. Based on previous works [
8,
18,
29], the initial momentum
satisfies the Boltzmann relation:
, where
T is the surface temperature and
m is the adsorbate mass (Xe). The initial wave function
is a Gaussian function given by
where
is the corresponding width.
The one dimensional discrete stochastic wave function is evaluated at
N equally spaced points belonging to the interval
, with
N being a power of 2 in order to use the FFT method. The discrete wave function is given at each time
t by
The normalization of the numerical wave function is calculated as
where
is the length between two consecutive points of the grid. The normalized stochastic wave function is thus calculated as
The mean value of any operator
can be expressed as
From the definition of scalar product, the ISF (
36) is now written as
where the mean value of the operator
and
can be obtained from (
40). Thus, the ISF
is then calculated according to
where
is the ISF for each stochastic realization. These values are calculated independently and summed up to have the average value
. The stochastic differential Equation (
35) is solved
times. For a number of realizations of
, the numerical stability for the mean value
is achieved. In particular, the unidimensional space
x is chosen to be in the interval
, where
and
. The number of points chosen is
. The increment
can be calculated from
. For these parameters, the value obtained for this increment is
. For simplicity, from now on,
is replaced by
3.1. Flat Surface
It is important to first analyze the diffusion on a flat surface,
. This example is representative of low corrugated surfaces where the role of the activation barrier is negligible since the adsorbate thermal energy is much greater than the barrier. The adsorbate-surface interaction is through the friction coefficient
. In the limiting case of small friction and flat potential, the results of the simulations have been compared with the case of a two-dimensional (2D) ideal gas. The ISF (
36) for the 2D ideal gas is a Gaussian function
where
is the initial thermal adsorbate velocity.
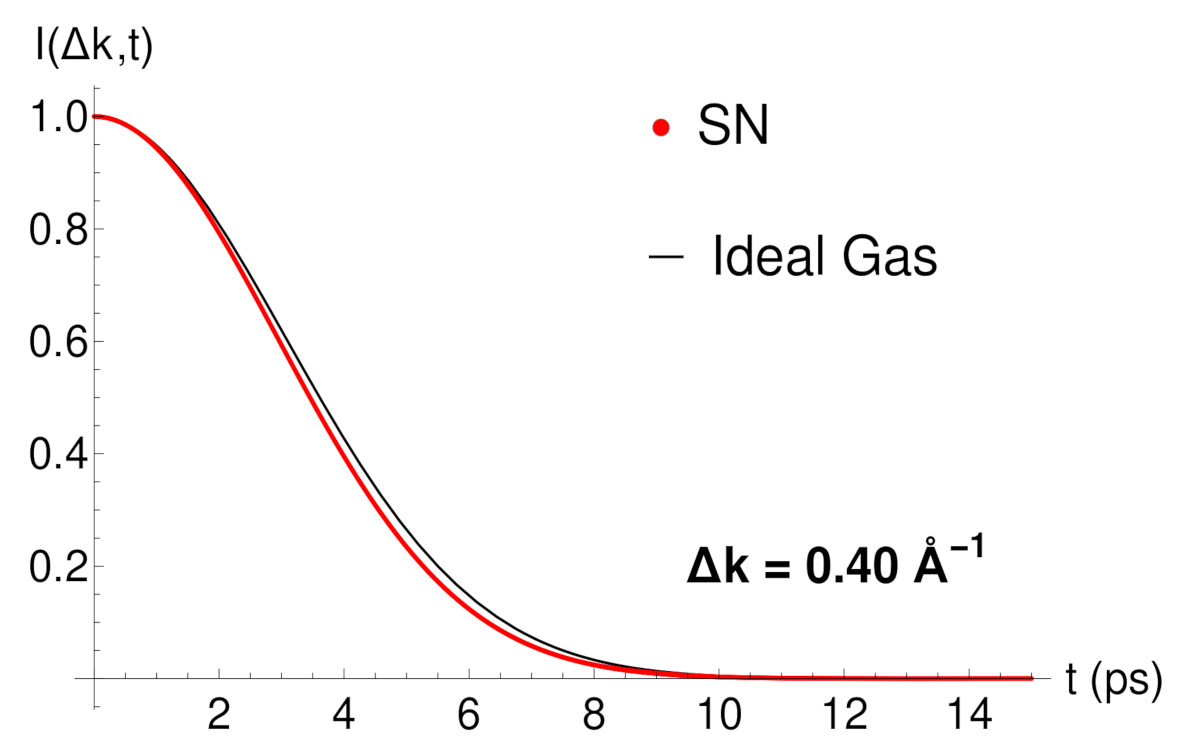
In
Figure 1, and in order to first check our propagation method,
is plotted versus the propagation time for the surface parallel wave vector transfer
, friction coefficient
, flat potential
, surface temperature
K and initial adsorbate velocity
m/s with negative direction. The propagation time
t of the stochastic wave function
and the time step
are chosen to be equal to
ps and
ps, respectively. These values correspond to a number of time steps of
. In
Figure 1, our numerical simulation (SN) in red is also plotted showing a very good agreement with the analytic function (
43), valid for a 2D ideal gas. This result indicates that the Xe-Pt(111) system under these conditions behave as a true 2D ideal gas where the diffusion of the adsorbate Xe is completely free on the Pt(111) surface. This behavior observed in
Figure 1 is also reproduced for different
values in the interval
analyzed. This free particle motion is kept at very long times.
The next step is now to study the behavior of this system in the ballistic regime at different friction coefficients for a flat surface and compare with experimental results and previous standard Langevin simulations [
20]. As mentioned above, this regime is only valid at times
. For such a goal, our purpose is to see how good the Gaussian function, which describes the ballistic regime, is. The Fourier transform in time of the Gaussian ISF is again a Gaussian function which corresponds to the DSF. The full width at half maximum (FWHM) of the SDF,
, is extracted and plotted at different frictions for different momentum transfer values
. The friction coefficients
used in these simulations are equal to the values used in a previous work [
20]. By fitting the ISF to a Gaussian function with width
,
, the values of
can be obtained from
through
The width in time space
of the ISF for a 2D ideal gas (
43) is
. Using (
44), the dependence of
with the parallel wave vector transfer
is given by
Figure 2 shows a comparison between the numerical results of
as a function of the parallel wave vector transfer
at
K for two different values of the friction coefficient,
ps
, and by assuming the corrugation of the Pt(111) surface to be negligible. Black lines correspond to Equation (
45). Left top panel (a) displays our numerical simulations. Langevin molecular dynamics simulations are displayed on the right top panel (b) [
20] for the same conditions. In panel (c), the fitting to a Gaussian function of the ISF at very short times and small friction is also plotted. The numerical results are in good agreement with those obtained in Ref. [
20]. The slope of
decreases as the friction coefficient increases. For a fixed value of
, the value of
is higher for
ps
, so the width in the time domain is smaller and the function
decays faster. Thus, at higher values of
, the fitting has to be carried out at smaller times. In panel (c), the ballistic regime (
ps) seems to be well described around 0.8 ps. For
ps
, the friction is high enough to drastically reduce the ballistic regime at very, very short times. In this case, the interaction with the substrate is very important and the diffusive regime is reached at times
. This regime is not studied here.
3.2. Corrugated Potential
The potential energy surface (PES) is simulated using the pairwise additive potential approximation between the Xe and a square network of Pt atoms with a distance equal to the unit cell length . To ensure that the metal surface is large enough so that the boundary effects do not influence the interaction potential, the number of cells of the surface in the plane is increased until the variation in the potential is as small as a given threshold, say meV.
A cosine corrugation function is proposed to represent the potential energy surface of the Xe-Pt(111) system given by
, where
meV and
meV. These values are obtained by fitting the cosine function to the PES numerical result. Both numerical and analytic PSE are very similar because the amplitude of the interaction potential takes an approximated value equal to
meV and the periodicity match with the unit cell length of the Pt for both cases. The unidimensional corrugated potential is then used in the simulations with the form
. The amplitude
is taken so that the energy barrier for this potential (
) coincides with the Langevin molecular simulations [
20]. In
Figure 3, the directions (010) and (100) of the metallic surface of Pt are plotted for the corrugated potential
and
, respectively, in the interval
. The shape of the potential cutoff along the (010) direction is analogous to the (100). Thus, the diffusion of the Xe adsorbate on the metal surface of Pt is studied using the (100) direction for the interaction potential.
In
Figure 4, the influence of surface corrugation on the Xe-Pt(111) system for a simulation with small friction coefficient
ps
and surface temperature
K is analyzed.
Figure 4 shows the quasielastic broadening
as a function of
. The slope of
decreases as
increases. The adsorbate thermal energy can be obtained from
. For a temperature of
K, the thermal energy is
meV. If the energy barrier is less than
meV, the adsorbate can diffuse more or less freely over the metal surface of Pt. For energy barriers belonging to this range, the system is in a ballistic regime at very short times. If
meV, the difference between both energies is small and the system is at the limit where some Xe gas particles can be trapped, but others can diffuse over the surface. However, if
meV the thermal energy is not enough to overcome the barrier and almost all the adsorbate particles are trapped in the potential valley and there is no diffusion. In panel (c), the propagation time is much smaller than 1 ps in order to be in the ballisitc regime,
. In this case, the chosen energy barrier is
meV and the fitting to a Gaussian function is worse. The system under these conditions behaves as a free 2D gas within a unit cell for very short times, particles are trapped inside the potential valley. If a lower barrier energy is chosen, the corresponding fitting is better and the propagation time in this regime is longer. Our numerical results are in good agreement with those obtained by Langevin molecular simulations [
20] and experimental data marked by triangles and squares at low
values.
4. Conclusions
The stochastic wave function formalism has been briefly reviewed and applied to the diffusion of a Xe gas on a Pt(111) surface. The Lindblad master equation, when it is solved by means of stochastic wave functions, provides a good physical description of the ballistic regime in this diffusion process. It provides an efficient numerical scheme to study the quantum dynamics of open systems. As far as we know, this is the first time this theoretical formalism has been applied to the surface diffusion context, since most of works use the Langevin formalism (in its generalized or standard version). This is particularly encouraging since recent experiments with better spatial and time resolutions (HeSE technique) tend to reveal the underlying properties of individual systems and their jump events directly in the time domain. New results for low and moderate values of the surface coverage for the Xe/Pt(111) system have been recently obtained. Thus, thanks to this type of study with quite satisfactory results, the next step will be to extend this theoretical formalism to deal with the diffusion regime, . This would allow us to consider more physical systems where recent experimental results are waiting for a better interpretation. Adsorbates, such as , , , etc., on metallic surfaces have been studied by using the HeSE technique. For light adsorbates, quantum methods are more convenient than classical ones. In the surface diffusion context, this extension, which would be carried out for the first time, is again very promising.
Perspectives
The dependence with the surface temperature and coverage can be studied for a better understanding of microscopic processes. It is suggested to also extend and improve this numerical method for times greater than 20 ps with periodic two-dimensional interaction potential in order to reach the Brownian regime. This method turns out to be a valuable alternative for dealing with more diffusive systems studied via QHAS or HeSE such as, for example, Na-Cu(001), Ar-MgO(100), etc., which have been previously considered within the Langevin formalism [
14,
18,
40].