Multidimensional Fairness Equilibrium Evaluation of Urban Housing Expropriation Compensation Based on VIKOR
Abstract
:1. Introduction
2. Literature Review
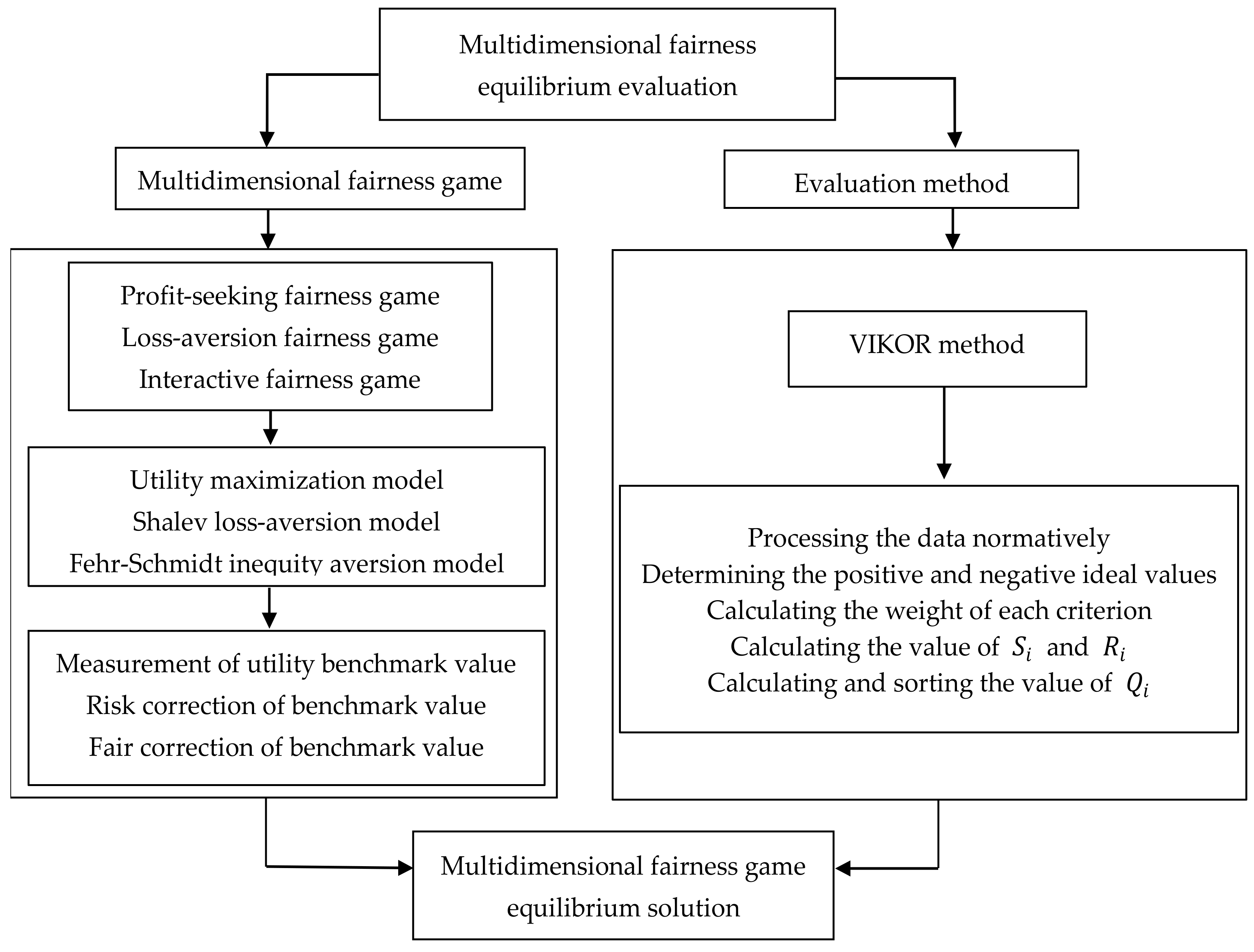
3. Analysis Framework
3.1. Profit-Seeking Fairness of Urban Housing Expropriation Compensation
3.2. Loss Aversion Fairness of Urban Housing Expropriation Compensation
3.3. Interactive Fairness of Urban Housing Expropriation Compensation
4. Modelling
4.1. Profit-Seeking Fairness Game Model of Urban Housing Expropriation Compensation
4.2. Loss Aversion Fairness Game Model of Urban Housing Expropriation Compensation
4.3. Interactive Fairness Game Model of Urban Housing Expropriation Compensation
5. Multidimensional Fairness Equilibrium Evaluation Based on VIKOR
6. Case Analysis
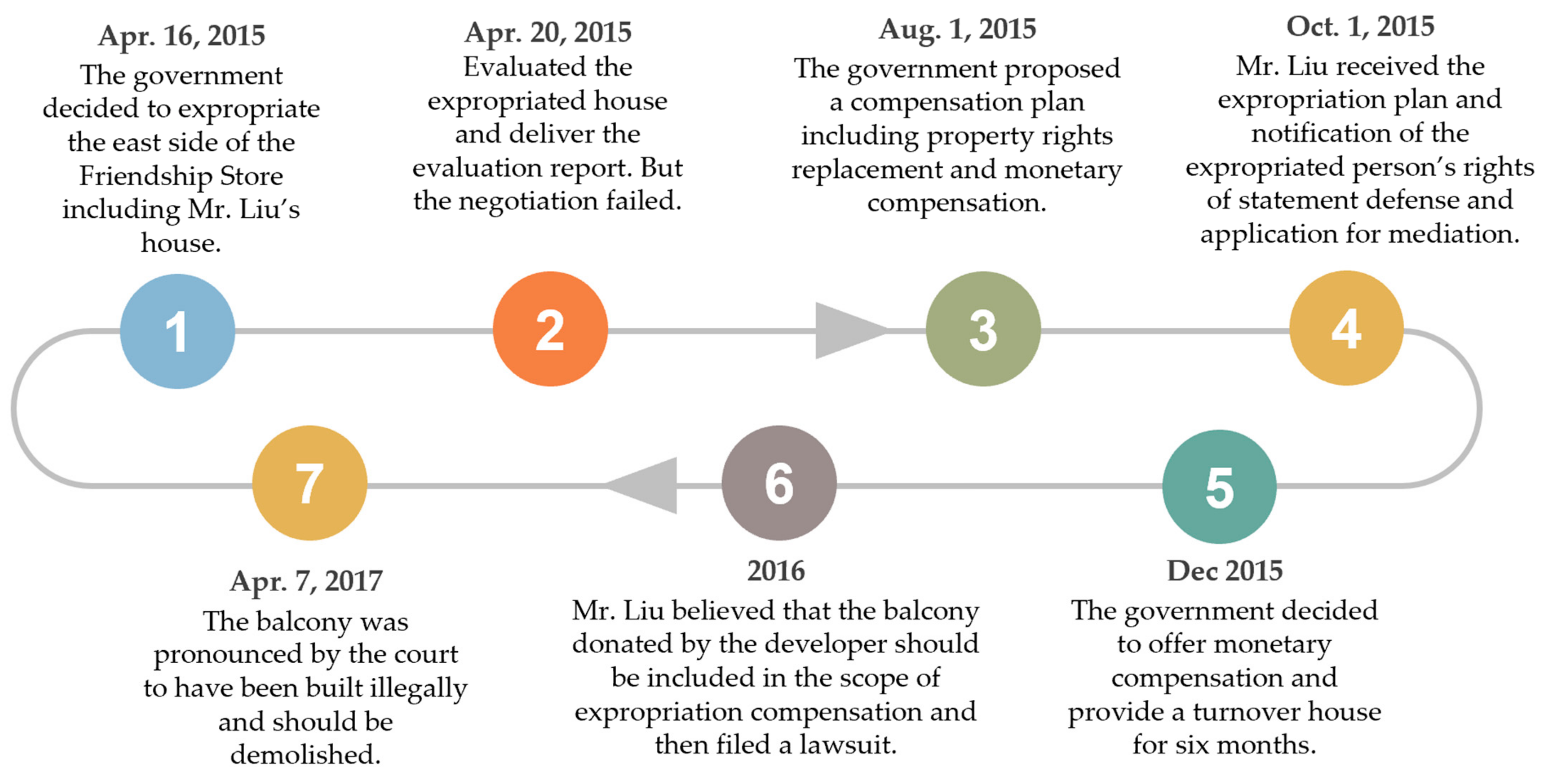
6.1. Case Overview
6.2. Case Data Analysis
6.3. Ranking Selection of Expropriation Compensation Scheme Based on VIKOR
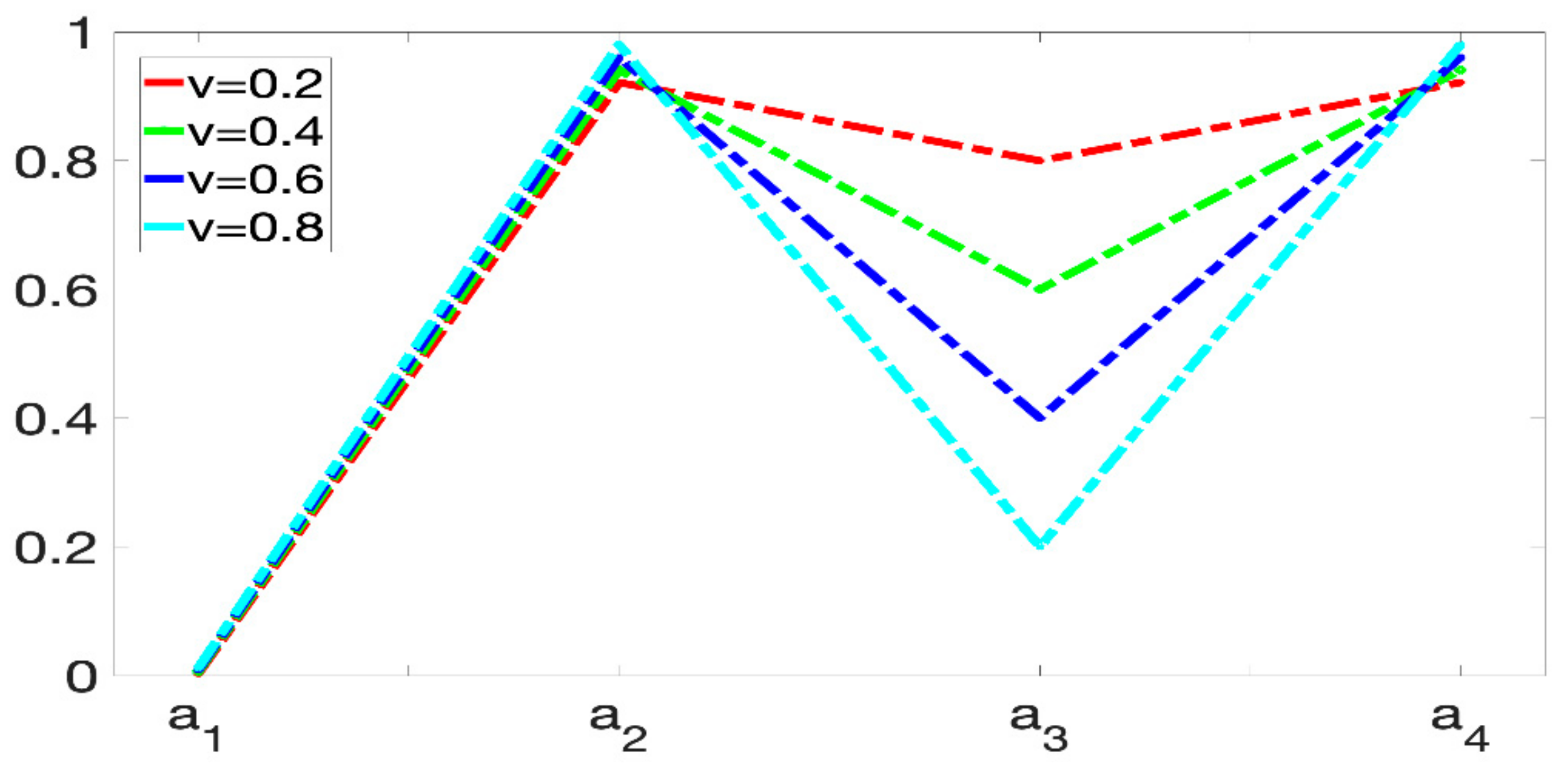
6.4. Sensitivity Analysis
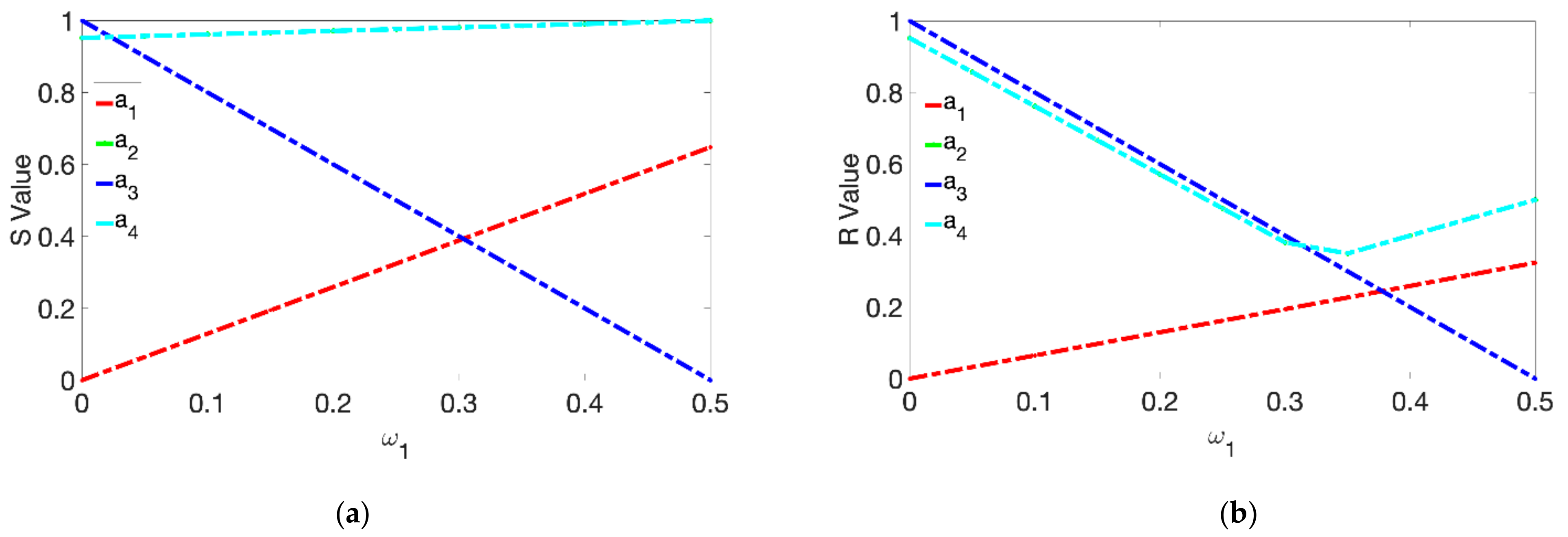
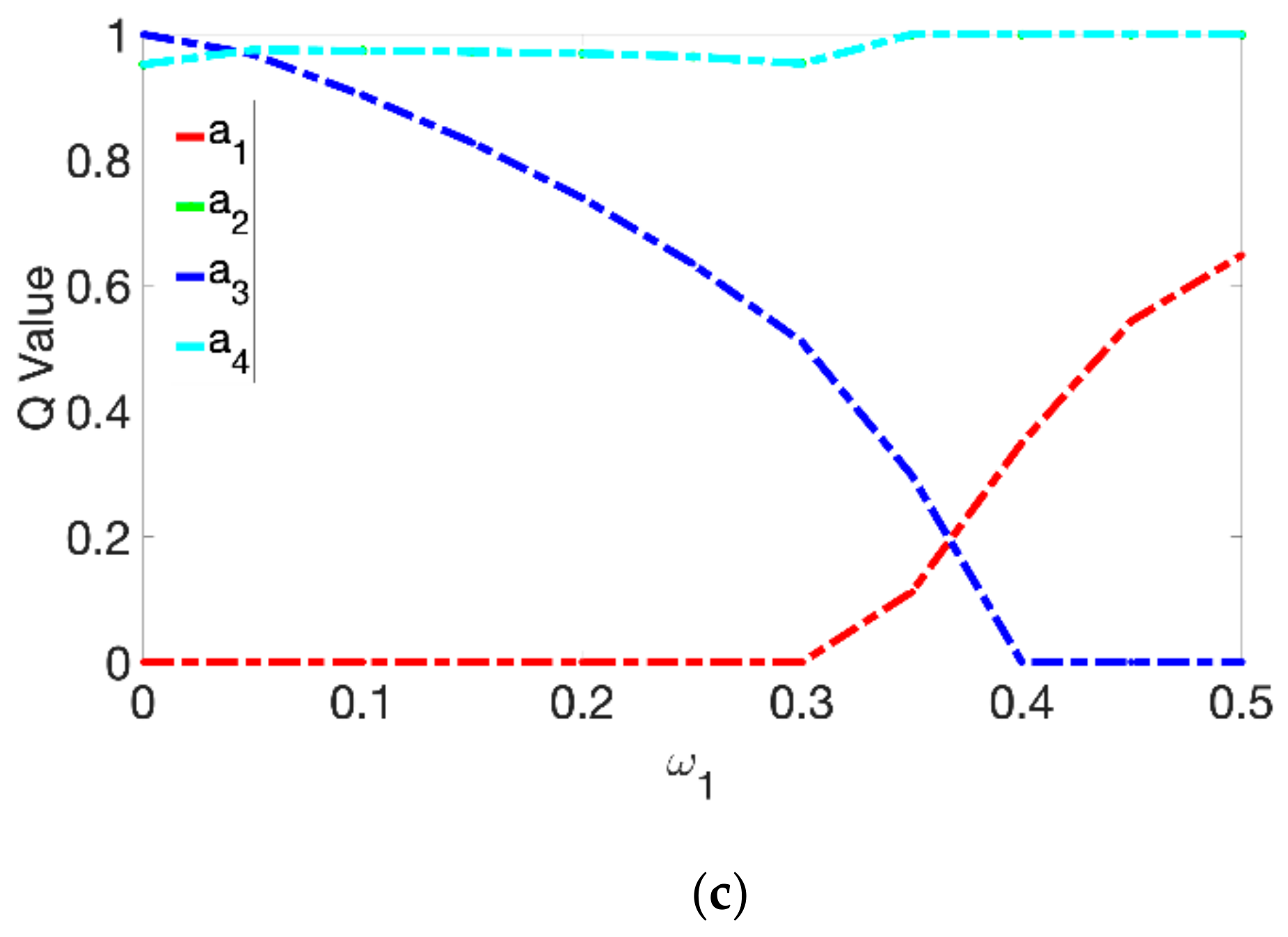
6.4.1. Sensitivity Analysis of the Criteria Weights
6.4.2. Sensitivity Analysis of Decision-Making Mechanism Coefficient
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marans, R.W. Quality of urban life and environmental sustainability studies: Future linkage opportunities. Habitat Int. 2015, 45, 47–52. [Google Scholar] [CrossRef]
- Wang, W.; Peng, H. A fuzzy multi-criteria evaluation framework for urban sustainable development. Mathematics 2020, 8, 330. [Google Scholar] [CrossRef] [Green Version]
- Geng, B. Ten specific problems of house expropriation and compensation on state-owned land—Starting from three communique cases. Appl. Law 2017, 9, 89–98. [Google Scholar]
- Moslem, S.; Gul, M.; Farooq, D.; Celik, E.; Ghorbanzadeh, O.; Blaschke, T. An integrated approach of Best-Worst Method (BMW) and triangular fuzzy sets for evaluating driver behavior factors related to road safety. Mathematics 2020, 8, 414. [Google Scholar] [CrossRef] [Green Version]
- Riaz, M.; Sałabun, W.; Farid, H.M.A.; Ali, N.; Watróbski, J. A robust q-rung orthopair fuzzy information aggregation using einstein operations with application to sustainable energy planning decision management. Energies 2020, 13, 2155. [Google Scholar] [CrossRef]
- Thong, N.T.; Lan, L.H.; Chou, S.; Son, L.H. An extended TOPSIS method with unknown weight information in dynamic neutrosophic environment. Mathematics 2020, 8, 401. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Watróbski, J.; Shekhovtsov, A. Are MCDA methods benchmarkable? A comparative study of TOPSIS, VIKOR, COPRAS, and PROMETHEE II methods. Symmetry 2020, 12, 1549. [Google Scholar] [CrossRef]
- An, L.; Chen, Z. Multi-criteria decision analysis based on rough sets. Control Decis. 2013, 28, 1–12. [Google Scholar]
- Palczewski, K.; Sałabun, W. The fuzzy TOPSIS applications in the last decade. Proc. Comput. Sci. 2019, 159, 2294–2303. [Google Scholar] [CrossRef]
- Sałabun, W. The mean error estimation of TOPSIS method using a fuzzy reference models. J. Theor. Appl. Comput. Sci. 2013, 7, 40–50. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Peldschus, F.; Turskis, Z. Multi-attribute assessment of road design solutions by using the COPRAS method. Balt. J. Road Bridge Eng. 2007, 2, 195–203. [Google Scholar]
- Brans, J.P.; Vincke, P.; Mareschal, B. How to select and how to rank projects: The PROMETHEE method. Eur. J. Oper. Res. 1986, 24, 228–238. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Z.; Liao, H.; Xu, Z. ELECTRE II method to deal with probabilistic linguistic term sets and its application to edge computing. Nonliner Dyn. 2019, 3, 2125–2143. [Google Scholar] [CrossRef]
- Xu, D.; Wei, X.; Ding, H.; Bin, H. A new method based on PROMETHEE and TODIM for multi-attribute decision-making with single-valued neutrosophic sets. Mathematics 2020, 8, 1816. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Op. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef] [Green Version]
- Tversky, A. Loss aversion in riskless choice: A reference-dependent model. Q. J. Econ. 1991, 106, 1039–1061. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Advances in prospect theory cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar]
- Shalev, J. Loss Aversion in Repeated Games. CORE Discussion Papers 1998014. Available online: https://econpapers.repec.org/paper/corlouvco/1998014.htm (accessed on 1 February 1998).
- Shalev, J. Loss aversion equilibrium. Int. J. Game Theory 2000, 29, 269–287. [Google Scholar] [CrossRef]
- Cornes, R.; Hartley, R. Loss aversion and the tullock paradox. Keele Econ. Res. Pap. 2003, 4390, 1129–1130. [Google Scholar]
- Bateman, I.; Kahneman, D.; Munro, A.; Starmer, C.; Sugden, R. Testing competing models of loss aversion: An adversarial collaboration. J. Public Econ. 2005, 89, 1561–1580. [Google Scholar] [CrossRef]
- Gimpel, H. Loss aversion and reference-dependent preferences in multi-attribute negotiations. Group Decis. Negotiat. 2007, 16, 303–319. [Google Scholar] [CrossRef]
- Loehman, E. Rank dependent expected utility: Stochastic dominance, risk preference, and certainty equivalence. J. Math. Psychol. 1994, 38, 159–197. [Google Scholar] [CrossRef]
- Hyndman, K. Repeated bargaining with reference-dependent preferences. Int. J. Game Theory 2011, 40, 527–549. [Google Scholar] [CrossRef]
- Dittrich, D.A.S.; Güth, W.; Kocher, M.G.; Christou, P.P. Loss aversion and learning to bid. Economica 2012, 79, 226–257. [Google Scholar] [CrossRef]
- Driesen, B.; Perea, A.; Peters, H. Alternating offers bargaining with loss aversion. Math. Soc. Sci. 2012, 64, 103–118. [Google Scholar] [CrossRef] [Green Version]
- Herweg, F.; Schmidt, K.M. Loss aversion and inefficient renegotiation. Rev. Econ. Stud. 2015, 82, 297–332. [Google Scholar] [CrossRef] [Green Version]
- Kameda, H.; Altman, E.; Touati, C.; Legrand, A. Nash equilibrium based fairness. Math. Methods Op. Res. 2012, 76, 43–65. [Google Scholar] [CrossRef] [Green Version]
- Masatlioglu, Y.; Raymond, C. A behavioral analysis of stochastic reference dependence. Am. Econ. Rev. 2016, 106, 2760–2782. [Google Scholar] [CrossRef] [Green Version]
- Kőszegi, B.; Rabin, M. Reference-dependent risk attitudes. Am. Econ. Rev. 2007, 97, 1047–1073. [Google Scholar] [CrossRef] [Green Version]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Falk, A.; Fischbacher, U. A theory of reciprocity. Games Econ. Behav. 2006, 54, 293–315. [Google Scholar] [CrossRef]
- Dufwenberg, M.; Kirchsteiger, G. A theory of sequential reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef] [Green Version]
- Kohler, S. Altruism and fairness in experimental decisions. J. Econ. Behav. Org. 2011, 80, 101–109. [Google Scholar] [CrossRef]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Kagel, J.H.; Wolfe, K.W. Tests of fairness models based on equity considerations in a three-person ultimatum Game. Exp. Econ. 2001, 4, 203–219. [Google Scholar] [CrossRef]
- Charness, G.; Haruvy, E. Altruism, equity and reciprocity in a gift-exchange experiment: An encompassing approach. Games Econ. Behav. 2002, 40, 203–231. [Google Scholar] [CrossRef] [Green Version]
- Kritikos, A.S. The impact of compulsory arbitration on bargaining behavior: An experimental study. Econ. Gov. 2006, 7, 293–315. [Google Scholar] [CrossRef]
- Fehr, E.; Kremhelmer, S.; Schmidt, K.M. Fairness and the optimal allocation of ownership rights. Econ. J. 2008, 118, 1263–1284. [Google Scholar] [CrossRef]
- Brikaa, M.G.; Zheng, Z.; Ammar, E. Resolving indeterminacy approach to solve multi-criteria zero-sum matrix games with intuitionistic fuzzy goals. Mathematics 2020, 8, 305. [Google Scholar] [CrossRef] [Green Version]
- Bao, H.; Ye, Q.; Xu, S. Conflict and governance of rural collective-owned land expropriation: An interdisciplinary literature comment. China Land Sci. 2014, 28, 82–88. [Google Scholar]
- Pu, Y. Considerations on China’s social disputes resolution mechanism based on behavioral game theory. China Soft Sci. 2012, 1, 183–192. [Google Scholar]
- Ye, J.; Feng, L.; Lang, Y.; Prosterman, R. A survey study on rural land use rights In China in 2016—Survey results in 17 provinces and policy recommendations. Manag. World 2018, 34, 98–108. [Google Scholar]
- Wei, G. A Survey of game experiments and theoretical models on fairness preference. J. Quant. Tech. Econ. 2006, 8, 152–161. [Google Scholar]
- Wu, X. Non-accident governance logic: How the local government softens the nail households: Based on surveys on three communities in city A, Jiangsu province. J. Nanjing Agric. Univ. 2018, 18, 42–51, 158. [Google Scholar]
- Guo, L.; Wang, L. The pricing dilemma and conflicts in house expropriation. Chin. Public Adm. 2015, 1, 21–26. [Google Scholar]
- Wu, Z. The interest appeal and expression mechanism of demolition vulnerable groups in urban renewal. Truth Seek. 2013, 5, 63–67. [Google Scholar]
- Shi, J.; Zhu, J. Behavior choice of people whose house will be dismantled from the point of view of game theory. Urban Probl. 2013, 04, 72–77. [Google Scholar]
- Shalev, J. Loss aversion in a multi-period model. Math. Soc. Sci. 1997, 33, 203–226. [Google Scholar] [CrossRef]
- Bao, H. Farmer’s reaction and equilibrium of distributing the incremental land value arising from land expropriation in urban-rural fringe. China Land Sci. 2009, 23, 32–36. [Google Scholar]
- Bao, H.; Zhao, J.; Yang, Y. Complexity of land requisition conflicts and the stimulus-response model of the agents. China Land Sci. 2012, 26, 61–66, 74. [Google Scholar]
- Kizielewicz, B.; Watróbski, J.; Sałabun, W. Identification of relevant criteria set in the MCDA process—Wind farm location case study. Energies 2020, 13, 6548. [Google Scholar] [CrossRef]
- Li, G.; Li, J.; Sun, X.; Wu, D. Research on a combined method of subjective-objective weighting based on the ordered information and intensity information. Chin. J. Manag. Sci. 2017, 25, 179–187. [Google Scholar]
- Tian, J.; Zhang, P.; Wang, K.; Wang, Y. The integrating model of expert’s opinion based on Delphi method. Syst. Eng. Theory Pract. 2004, 1, 57–62. [Google Scholar]
- Saaty, T.L. The modern science of multicriteria decision making and its practical applications: The AHP/ANP approach. Op. Res. 2013, 61, 1101–1118. [Google Scholar] [CrossRef]
- Zhu, X.; Wei, G. Discussion on the fine standard of dimensionless method in entropy method. Stat. Decis. 2015, 2, 12–15. [Google Scholar]
- Chen, Y.; Wei, W. Empirical analysis of national air pollution based on triple weighting and systematic cluster analysis. Stat. Decis. 2015, 11, 100–103. [Google Scholar]
- Wang, H. The limit conditions for forming of a system evaluating index by the PCA method. Syst. Eng. Theory Pract. 1996, 9, 24–29. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Multicriteria planning of post-earthquake sustainable reconstruction. Comput. Aided Civ. Infrastruct. Eng. 2002, 17, 211–220. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, X. VIKOR method for uncertain risky multi-attribute decision making based on regret theory. Stat. Decis. 2019, 1, 47–51. [Google Scholar]
- Jiang, W. Risky fuzzy multi-criteria decision method based on prospect theory and VIKOR. Control Decis. 2014, 29, 2287–2291. [Google Scholar]
- China Judgment Online, Document No. 263, Hunan Provincial Higher People’s Court Administrative Judgment (2017) Xiang (the Abbreviation of Hunan Province), Xing (the Abbreviation of the Administrative Case), Final (the Abbreviation of the Final Judgment). Available online: http://wenshu.court.gov.cn/content/content?DocID=e0e2aaf7-cb76-40df-aa5f-a85e00f394d4&KeyWord=%E6%88%BF%E5%B1%8B%E5%BE%81%E6%94%B6 (accessed on 4 January 2018).
- Hong, Y.; Xu, D.; Xiang, K.; Qiao, H.; Cui, X. Multi-attribute decision-making based on preference perspective with interval neutrosophic sets in venture capital. Mathematics 2019, 7, 257. [Google Scholar] [CrossRef] [Green Version]
- Stanković, M.; Stević, Ž.; Kumar Das, D.; Subotić, M.; Pamučar, D. A new fuzzy MARCOS method for road traffic risk analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef] [Green Version]
- Sałabun, W.; Urbaniak, K. A new coefficient of rankings similarity in decision-making problems. In Computational Science—ICCS 2020; ICCS 2020. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; pp. 632–645. [Google Scholar]
- Ramsey, D.M. A game theoretic model of choosing a valuable good via a short list heuristic. Mathematics 2020, 8, 199. [Google Scholar] [CrossRef] [Green Version]
- Rong, Y.; Liu, Y.; Pei, Z. Novel multiple attribute group decision-making methods based on linguistic intuitionistic fuzzy information. Mathematics 2020, 8, 322. [Google Scholar] [CrossRef] [Green Version]

| The Expropriator | The Expropriated Person | |
|---|---|---|
| Acceptance | Boycott | |
| Fair Expropriation | , | , |
| Unfair Expropriation | , | , |
| The Expropriator | The Expropriated Person | |
|---|---|---|
| Acceptance | Boycott | |
| Fair Expropriation | , | , |
| Unfair Expropriation | , | , |
| The Expropriator | The Expropriated Person |
|---|---|
| Acceptance | |
| Fair Expropriation | , |
| Unfair Expropriation | , |
| The Expropriator | The expropriated person |
| Boycott | |
| Fair Expropriation | , |
| Unfair Expropriation | , |
| Utility Value of the Expropriator and the Expropriated Person | |
|---|---|
| Profit-Seeking Fairness | |
| Loss Aversion Fairness | |
| Interactive Fairness | , |
| Utility Value of the Expropriator and the Expropriated Person | |
|---|---|
| Profit-Seeking Fairness | |
| Loss Aversion Fairness | |
| Interactive Fairness | , |
| Utility Value of the Expropriator and the Expropriated Person | |
|---|---|
| Profit-Seeking Fairness | |
| Loss Aversion Fairness | |
| Interactive Fairness | , |
| Utility Value of the Expropriator and the Expropriated Person | |
|---|---|
| Profit-Seeking Fairness | |
| Loss Aversion Fairness | |
| Interactive Fairness | , |
| The Expropriator | The Expropriated Person | |
|---|---|---|
| Acceptance | Boycott | |
| Fair Expropriation | 1,912,800 − 805,677 = 1,107,123, 805,677 | 1,912,800 − 805,677 − 70,000 = 1,037,123, 805,677 − 40,000 = 765,677 |
| Unfair Expropriation | 1,912,800 − 676,949 = 1,235,851, 676,949 | 1,912,800 − 805,677 − 70,000 = 1,037,123, 805,677 − 40,000 = 765,677 |
| The expropriator | The Expropriated Person | |
|---|---|---|
| Acceptance | Boycott | |
| Fair Expropriation | 1,107,123 − (1,235,851 − 1,107,123) = 978,395, 805,677 − (1,290,492 − 805,677) = 320,862 | 1,037,123 − (1,235,851 − 1,037,123) = 838,395, 765,677 − (1,290,492 − 765,677) = 240,862 |
| Unfair Expropriation | 1,912,800 − 676,949 = 1,235,851, 676,949 − (1,290,492 − 676,949) = 63,406 | 1,037,123 − (1,235,851 − 1,037,123) = 838,395, 765,677 − (1,290,492 − 765,677) = 24,086 |
| The Expropriator | The Expropriated Person | |
|---|---|---|
| Acceptance | Boycott | |
| Fair Expropriation | 1,107,123 − 0.7 × (1,107,123 − 805,677) = 896,111, 805,677 − 0.9 × (1,107,123 − 805,677) = 534,376 | 1,037,123 − 0.7 × (1,037,123 − 765,677) = 847,111, 765,677 − 0.9 × (1,037,123 − 765,677) = 521,376 |
| Unfair Expropriation | 1,235,851 − 0.7 × (1,235,851 − 676,949) = 844,620, 676,949 − 0.9 × (1,235,851 − 676,949) = 173,937 | 1,037,123 − 0.7 × (1,037,123 − 765,677) = 847,111, 765,677 − 0.9 × (1,037,123 − 765,677) = 521,376 |
| Plans | The Expropriator and the Expropriated Person | ||
|---|---|---|---|
| Profit-Seeking Fairness Value | Loss Aversion Fairness Value | Interactive Fairness Value | |
| 1,107,123, 805,677 | 978,395, 320,862 | 896,111, 534,376 | |
| 1,037,123, 765,677 | 838,395, 240,862 | 847,111, 521,376 | |
| 1,235,851, 676,949 | 1,235,851, 63,406 | 844,620, 173,837 | |
| 1,037,123, 765,677 | 838,395, 240,862 | 847,111, 521,376 | |
| Plans | Profit-Seeking Fairness | Loss Aversion Fairness | Interactive Fairness |
|---|---|---|---|
| 0.352, 1 | 0.352, 1 | 1, 1 | |
| 0, 0.689 | 0, 0.689 | 0.048, 0.964 | |
| 1, 0 | 1, 0 | 0, 0 | |
| 0, 0.689 | 0, 0.689 | 0.048, 0.964 |
| Criterion | Profit-Seeking Fairness | Loss Aversion Fairness | Interactive Fairness |
|---|---|---|---|
| Weight | 0.3059, 0.3346 | 0.3059, 0.3346 | 0.3882, 0.3309 |
| Plans | |||
|---|---|---|---|
| 0.3964, 0 | 0.1982, 0 | 0.0069, 0 | |
| 0.9814, 0.2200 | 0.3696, 0.1041 | 0.9510, 0.2655 | |
| 0.3882, 1.0000 | 0.3882, 0.3346 | 0.5000, 1.0000 | |
| 0.9814, 0.3110 | 0.3696, 0.1041 | 0.9510, 0.3110 |
| Plans | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5832 | 0.2916 | 0.5436 | 0.1296 | 0.0648 | 0 | 0.4277 | 0.2138 | 0.0681 | |
| 0.9952 | 0.4500 | 1.0000 | 0.9616 | 0.7616 | 0.9739 | 0.9837 | 0.3300 | 0.9604 | |
| 0.1000 | 0.1000 | 0 | 0.8000 | 0.8000 | 0.9029 | 0.3400 | 0.3400 | 0.5000 | |
| 0.9952 | 0.4500 | 1.0000 | 0.9616 | 0.7616 | 0.9739 | 0.9837 | 0.3300 | 0.9604 | |
| Plans | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0.2835 | 0.1400 | 0.2973 | 0.0910 | 0.0311 | 0.0649 | 0.2175 | 0.1026 | 0.2597 | |
| 1.0000 | 0.4500 | 1.0000 | 1.0000 | 0.8000 | 1.0000 | 1.0000 | 0.3400 | 1.0000 | |
| 0.3110 | 0.1400 | 0.3110 | 0.3110 | 0.2488 | 0.3110 | 0.3110 | 0.1057 | 0.3110 | |
| Plans | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3964 | 0.1982 | 0.0014 | 0.0028 | 0.0042 | 0.0056 | 0.0070 | 0.0083 | 0.0097 | 0.0111 | 0.0125 | |
| 0.9814 | 0.3696 | 0.9117 | 0.9215 | 0.9313 | 0.9411 | 0.9510 | 0.9608 | 0.9706 | 0.9804 | 0.9902 | |
| 0.3882 | 0.3882 | 0.9000 | 0.8000 | 0.7000 | 0.6000 | 0.5000 | 0.4000 | 0.3000 | 0.2000 | 0.1000 | |
| 0.9814 | 0.3696 | 0.9117 | 0.9215 | 0.9313 | 0.9411 | 0.9510 | 0.9608 | 0.9706 | 0.9804 | 0.9902 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Zou, Y.; Zhao, X.; Hong, K.; Zhang, Y. Multidimensional Fairness Equilibrium Evaluation of Urban Housing Expropriation Compensation Based on VIKOR. Mathematics 2021, 9, 430. https://doi.org/10.3390/math9040430
Cao Z, Zou Y, Zhao X, Hong K, Zhang Y. Multidimensional Fairness Equilibrium Evaluation of Urban Housing Expropriation Compensation Based on VIKOR. Mathematics. 2021; 9(4):430. https://doi.org/10.3390/math9040430
Chicago/Turabian StyleCao, Zhaoyu, Yucheng Zou, Xu Zhao, Kairong Hong, and Yanwei Zhang. 2021. "Multidimensional Fairness Equilibrium Evaluation of Urban Housing Expropriation Compensation Based on VIKOR" Mathematics 9, no. 4: 430. https://doi.org/10.3390/math9040430
APA StyleCao, Z., Zou, Y., Zhao, X., Hong, K., & Zhang, Y. (2021). Multidimensional Fairness Equilibrium Evaluation of Urban Housing Expropriation Compensation Based on VIKOR. Mathematics, 9(4), 430. https://doi.org/10.3390/math9040430







