Driven Qubit by Train of Gaussian-Pulses

Abstract

The simplest non-dissipative 2-level atom system, a qubit, excited by a train of resonant n-Gaussian laser pulses is investigated. This concerns examination of the averaged atomic variables, the intensity-intensity correlation function, and the transient fluorescent radiation. Analytical formulas for the above expressions are obtained. Computational results show that the transient spectra with the initial ground and coherent atomic states exhibit asymmetric Mollow structure with dip structure, dense oscillation, and narrowing, and depends on the pulse number $\left(n\right)$, the repetition time $\left({\tau }_R\right)$, and the observed time.

1. Introduction

Controlling the state dynamics of a 2-level atom (qubit) is achieved by investigating its interaction with short laser pulses; thus, control its desired final state [1,2,3]. Of equal interest, is the investigation of the spectral lines and intensity correlation function of the fluorescent light due to such interaction. The simplest model of a dissipative 2-level atom excited by a strong idealized CW laser was discussed by Mollow [4], where the fluorescent spectrum has a triple Lorentzian shape which observed experimentally by various researchers [5,6,7]. Study of the spectral lines of the fluorescent radiation provides information about the fidelity of the atomic system with respect to the excitation frequency and its response to a specific selected frequency. For non-dissipative pulsed-driven qubits, transient fluorescent spectrum have been investigated for various pulse shapes (see References [8,9,10,11] and refs. therein). In general, investigation of pulsed-driven qubits are essential for topics, like quantum computation and quantum information sciences (see References [12,13] and refs. therein). The produced radiation of such interaction can be used in optical information processing and as a carrier of signal information, as well [14]. Furthermore, investigating the non-classical effect of photon anti-bunching, i.e., the process of emitting single photon at a time, has been investigated theoretically [15,16,17,18] and experimentally [19,20,21] for dissipative single atom resonance fluorescence model [4]. Practically, single photon light sources are essential in quantum computation and quantum key distribution processes [22,23,24].

The purpose of the present paper was to investigate both the transient fluorescent spectrum and the photon anti-bunching effect for a non-dissipative qubit driven by a train of resonant Gaussian laser pulses. The paper is presented as follows. In Section 2, we introduce the model Bloch equations and its exact analytical solutions, together with the n-Gaussian pulse shape. In Section 3, we present the computational results for the averaged atomic variables (polarization and inversion) and the second- order intensity correlation function. Section 4 is devoted to the derivation of the transient spectrum analytically, followed by the computational results for the spectrum in Section 5. Finally, a conclusion is given in Section 6.

2. Model Equations and Pulse Shape

2.1. Bloch Equations

For a single 2-level atom of excited and ground states, $|e\rangle$ and $|g\rangle$, respectively, and of transition frequency ${\omega }_o$ interacting with a resonant laser pulse of circular (envelope) frequency ${\omega }_o$ and of arbitrary shape $f\left(t\right)$, the total Hamiltonian operator has the form (in units of $\hslash =1$, where ℏ is the reduced Planck’s constant) (cf. Reference [11]),

$$\widehat{H}={\omega }_o{\widehat{S}}_z\left(t\right)+\frac{\mathrm{\Omega }\left(t\right)}{2}(e^{-i{\omega }_{o}t}{\widehat{S}}_{+}\left(t\right)+e^{i{\omega }_{o}t}{\widehat{S}}_{-}\left(t\right)).$$

(1)

The notations are: The Pauli spin-$\frac{1}{2}$ atomic operators ${\widehat{S}}_{\pm ,z}$ obey the commutation relations: $[{\widehat{S}}_{\pm },{\widehat{S}}_z]=\mp {\widehat{S}}_{\pm },[{\widehat{S}}_{+},{\widehat{S}}_{-}]=2{\widehat{S}}_z$ and the real parameter $\mathrm{\Omega }\left(t\right)={\mathrm{\Omega }}_{o}f\left(t\right)$, with ${\mathrm{\Omega }}_o$ is the associated laser Rabi frequency. Note, the Hamiltonian (1) is taken within the rotating wave approximation (RWA) where fast oscillatory terms in $e^{\pm 2i{\omega }_{o}t}$ are discarded. Heisenberg equations of motion for the rotated operators ${\widehat{\sigma }}_{\pm }\left(t\right)={\widehat{S}}_{\pm }\left(t\right)e^{\pm i{\omega }_{o}t},{\widehat{\sigma }}_z\left(t\right)\equiv {\widehat{S}}_z\left(t\right)$ according to the Hamiltonian (1) are of the form (cf. Reference [11]).

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{+}^{·}& =-i{\mathrm{\Omega }}_{o}f\left(t\right){\widehat{\sigma }}_z\hfill \\ \hfill & ={\left({\widehat{\sigma }}_{-}^{·}\right)}^{†},\hfill \\ \hfill {\widehat{\sigma }}_z^{·}& =-\frac{i{\mathrm{\Omega }}_{o}f\left(t\right)}{2}\left({\widehat{\sigma }}_{+}-{\widehat{\sigma }}_{-}\right).\hfill \end{array}$$

(2)

The exact operator solutions with initial time $t_o$ are given by Reference [10].

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{+}\left(t\right)& =C_{+}\left(t\right){\widehat{\sigma }}_{+}\left(t_o\right)+C_{-}\left(t\right){\widehat{\sigma }}_{-}\left(t_o\right)+C_z\left(t\right){\widehat{\sigma }}_z\left(t_o\right)\hfill \\ \hfill & ={\left({\widehat{\sigma }}_{-}\left(t\right)\right)}^{†}\hfill \\ \hfill {\widehat{\sigma }}_z\left(t\right)& ={\widehat{\sigma }}_z\left(t_o\right)cos\left(\omega \left(t\right)\right)-\frac{i}{2}\left({\widehat{\sigma }}_{+}\left(t_o\right)-{\widehat{\sigma }}_{-}\left(t_o\right)\right)sin\left(\omega \left(t\right)\right),\hfill \end{array}$$

(3)

where the c-number functions $C_{\pm ,z}\left(t\right)$ are given by:

$$\begin{array}{c}\hfill C_{\pm }\left(t\right)=\frac{1}{2}(1\pm cos\left(\omega \left(t\right)\right)),\\ \hfill C_z\left(t\right)=-isin\left(\omega \left(t\right)\right),\end{array}$$

(4)

and the pulse shape-dependent parameter $\omega \left(t\right)$ is given by,

$$\omega \left(t\right)=\underset{t_o}{\overset{t}{\int }}f\left(t^{\prime }\right)d{t}^{\prime }.$$

(5)

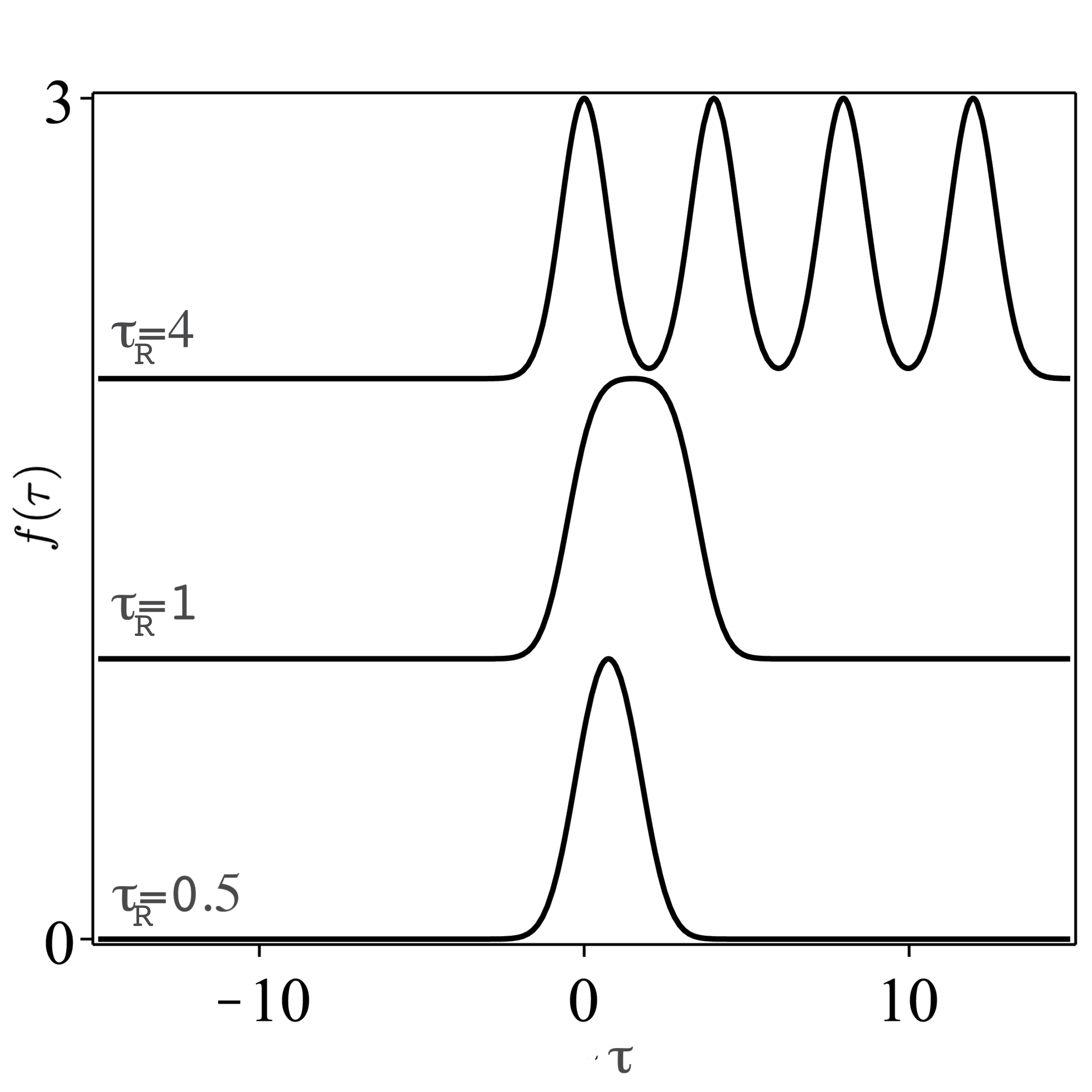
2.2. Pulse Shape

For a train of n-Gaussian pulses, the envelope shape has the form:

$$f\left(\tau \right)=\sum _{k=1}^n{e}^{-{(\tau -(k-1){\tau }_R)}^2},$$

(6)

with the normalized $\tau =t/{\tau }_o$, where ${\tau }_o$ is the full width of a single pulse at half-maximum, and ${\tau }_R=t_R/{\tau }_o$ is the normalized repetition time. Figure 1 shows the case of $n=4$ pulse (as an example), with ${\tau }_R>1({\tau }_R<1),$ where the overlapping takes place as a single pulse for ${\tau }_R<1$, while, for ${\tau }_R=1$, the same feature persists but with a broader peak. For ${\tau }_R>1$, the four pulses are distinct.

Substituting Equation (6) into Equation (5), we have [25]:

$$\begin{array}{cc}\hfill \omega \left(\tau \right)& ={\mathrm{\Omega }}_o\underset{t_o\to -\infty }{\overset{\tau }{\int }}f\left(t^{\prime }\right)d{t}^{\prime }\hfill \\ \hfill & ={\mathrm{\Omega }}_o\sum _{k=1}^n\underset{t_o\to -\infty }{\overset{\tau }{\int }}{e}^{-{(t^{\prime }-(k-1){\tau }_R)}^2}d{t}^{\prime }\hfill \\ \hfill & ={\mathrm{\Omega }}_1\sum _{k=1}^n\left[1+erf(\tau +b_k)\right],\hfill \end{array}$$

(7)

where ${\mathrm{\Omega }}_1={\mathrm{\Omega }}_o{\displaystyle \frac{{\tau }_o\sqrt{\pi }}{2}},$$b_k=-(k-1){\tau }_R$, $erf\left(z\right)=\frac{2}{\sqrt{\pi }}{\int }_o^z{e}^{-z^{\prime 2}}d{z}^{\prime }$ is the error function [26], and have taken $t_o\to -\infty$, since Gaussian pulses are of infinite extent (not smooth switching).

3. Atomic Behavior and Intensity Correlation

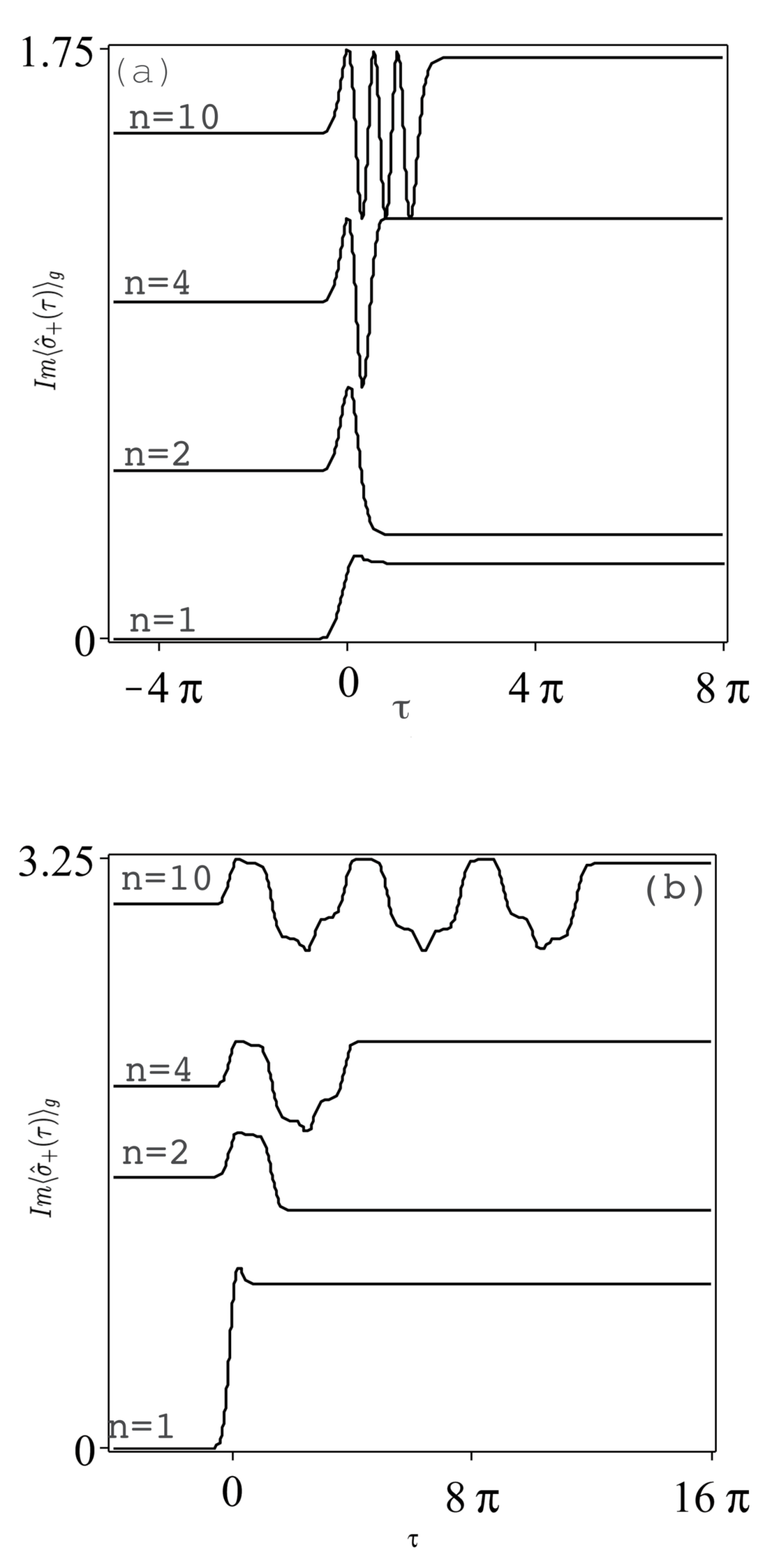
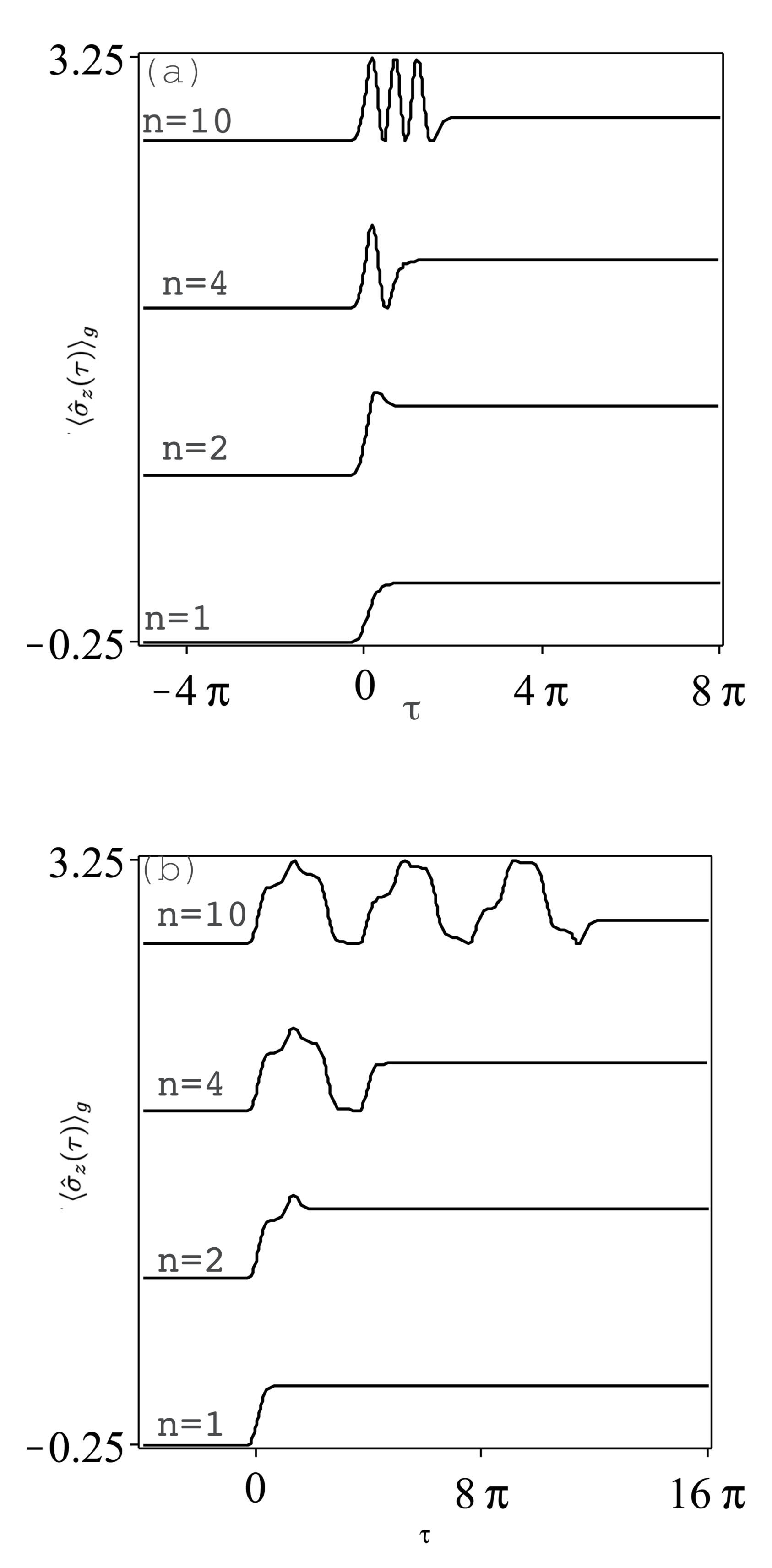
3.1. Mean Polarization and Inversion

For an atom initially in the atomic coherent state, $|\theta ,\varphi \rangle =cos\left(\frac{\theta }{2}\right)|g\rangle +sin\left(\frac{\theta }{2}\right)e^{-i\varphi }|e\rangle$, where $\theta \in [0,\pi ],\varphi \in [0,2\pi ]$ are the atomic excitation and phase parameters, respectively, we have the initial atomic average values, ${\langle {\widehat{\sigma }}_{\pm }\left(t_o\right)\rangle }_{\theta ,\varphi }=\frac{1}{2}sin\left(\theta \right)e^{\pm i\varphi },{\langle {\widehat{\sigma }}_z\left(t_o\right)\rangle }_{\theta ,\varphi }=-\frac{1}{2}cos\left(\theta \right)$ [27,28]. Hence, the time-dependent atomic averages from Equation (3) have the forms:

$$\begin{array}{cc}\hfill {\langle {\widehat{\sigma }}_{+}\left(\tau \right)\rangle }_{\theta ,\varphi }& =\frac{1}{2}sin\theta cos\varphi +\frac{i}{2}\left(cos\theta sin\left(\omega \right(\tau \left)\right)+sin\theta sin\varphi cos\left(\omega \right(\tau \left)\right)\right)\hfill \\ \hfill & ={\langle {\widehat{\sigma }}_{-}\left(\tau \right)\rangle }_{\theta ,\varphi }^{*}\hfill \\ \hfill {\langle {\widehat{\sigma }}_z\left(\tau \right)\rangle }_{\theta ,\varphi }& =-\frac{1}{2}cos\theta cos\left(\omega \left(\tau \right)\right)+\frac{1}{2}sin\theta sin\varphi sin\left(\omega \left(\tau \right)\right).\hfill \end{array}$$

(8)

The dispersive component of the atomic polarization, $Re{\langle {\widehat{\sigma }}_{+}\left(\tau \right)\rangle }_{\theta ,\varphi }$, is constant and non-zero for $\theta \ne 0,\pi$ and $\varphi \ne \frac{\pi }{2},\frac{3\pi }{2}$. For the initial ground state $|g\rangle$, the absorptive polarization component, $Im{\langle {\widehat{\sigma }}_{+}\left(\tau \right)\rangle }_g$, is essentially zero for $\tau <0$ and for ${\tau }_R<1$, as in Figure 2a, where it reaches its constant value almost monotonical for $n=1$ pulse. For increasing number of pulses and for larger $\tau$, the reach to the larger constant value is of oscillatory behavior. For ${\tau }_R>1$, as in Figure 2b, the same behavior occurs but with peaks of oscillations spread over larger interval of $\tau >0$. The average atomic inversion ${\langle {\widehat{\sigma }}_z\left(\tau \right)\rangle }_g$—Figure 3a,b—show the same trend as in Figure 2 but with less constant value for increasing $\tau$. For initial atomic coherent state, e.g., $|\theta =\frac{\pi }{3},\varphi =0\rangle$, we have the same qualitative behavior but with less absolute values of the minima and maxima values of the oscillating peaks.

It is worth nothing that n-Gaussian pulses can act as $\pi -$pulse or $2\pi$-pulse if the pulse area from Equation (6), $\omega (\infty )=\pi$ or $2\pi ,$ respectively. This corresponds to associated Rabi frequency ${\mathrm{\Omega }}_o^{\prime }\equiv {\mathrm{\Omega }}_o{\tau }_o=\sqrt{\pi }/n$ or $2\sqrt{\pi }/n$, respectively.

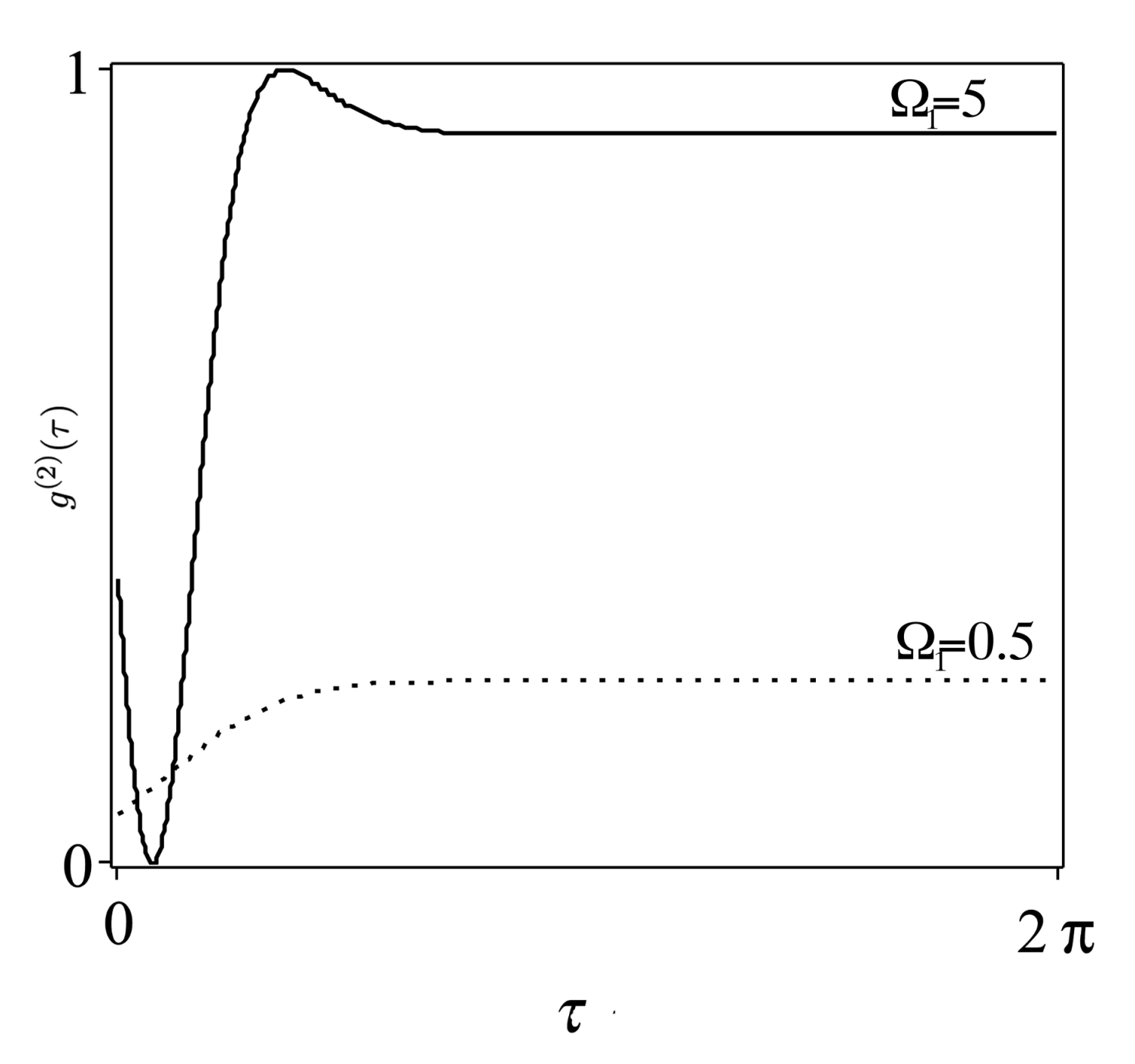
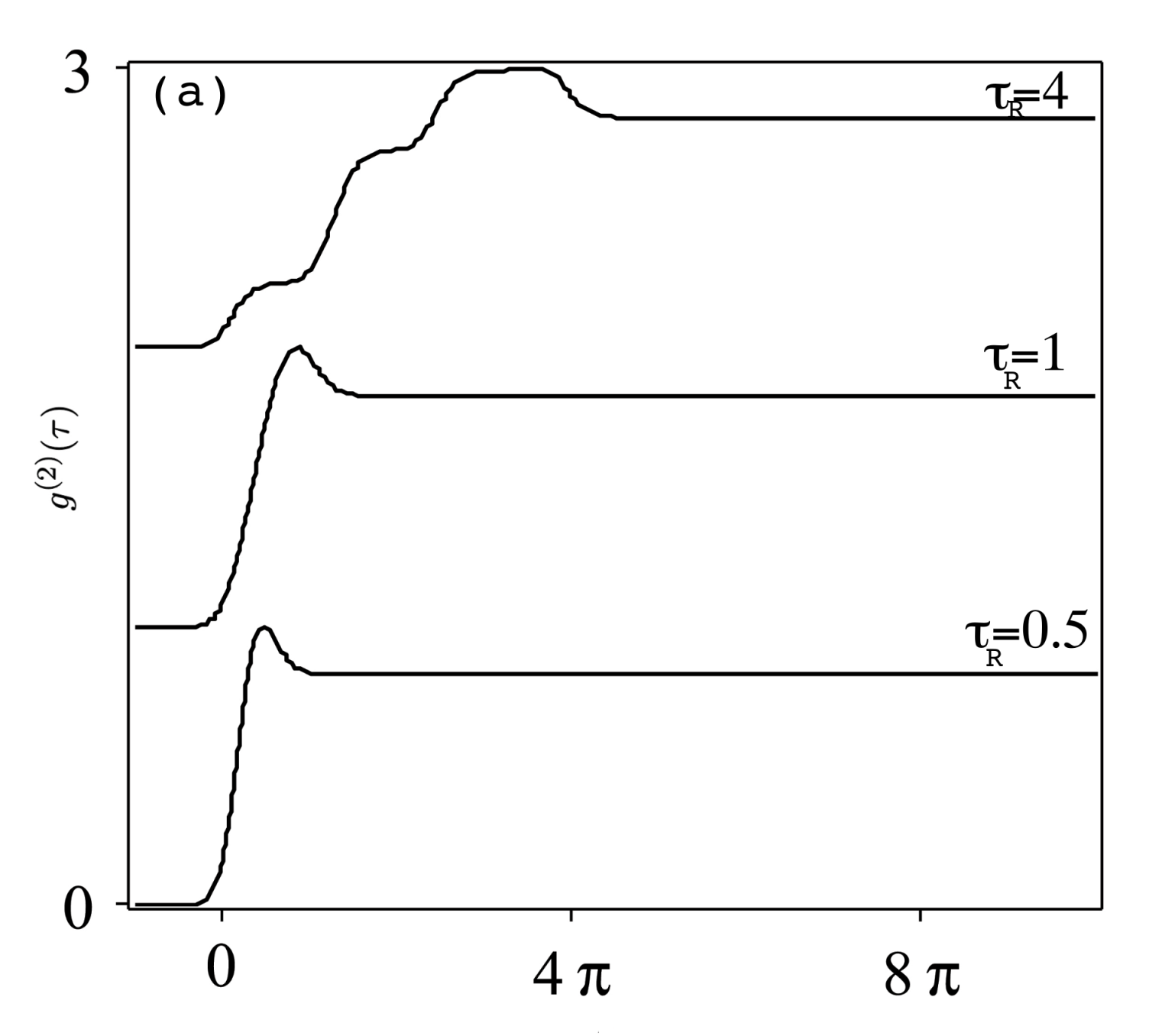
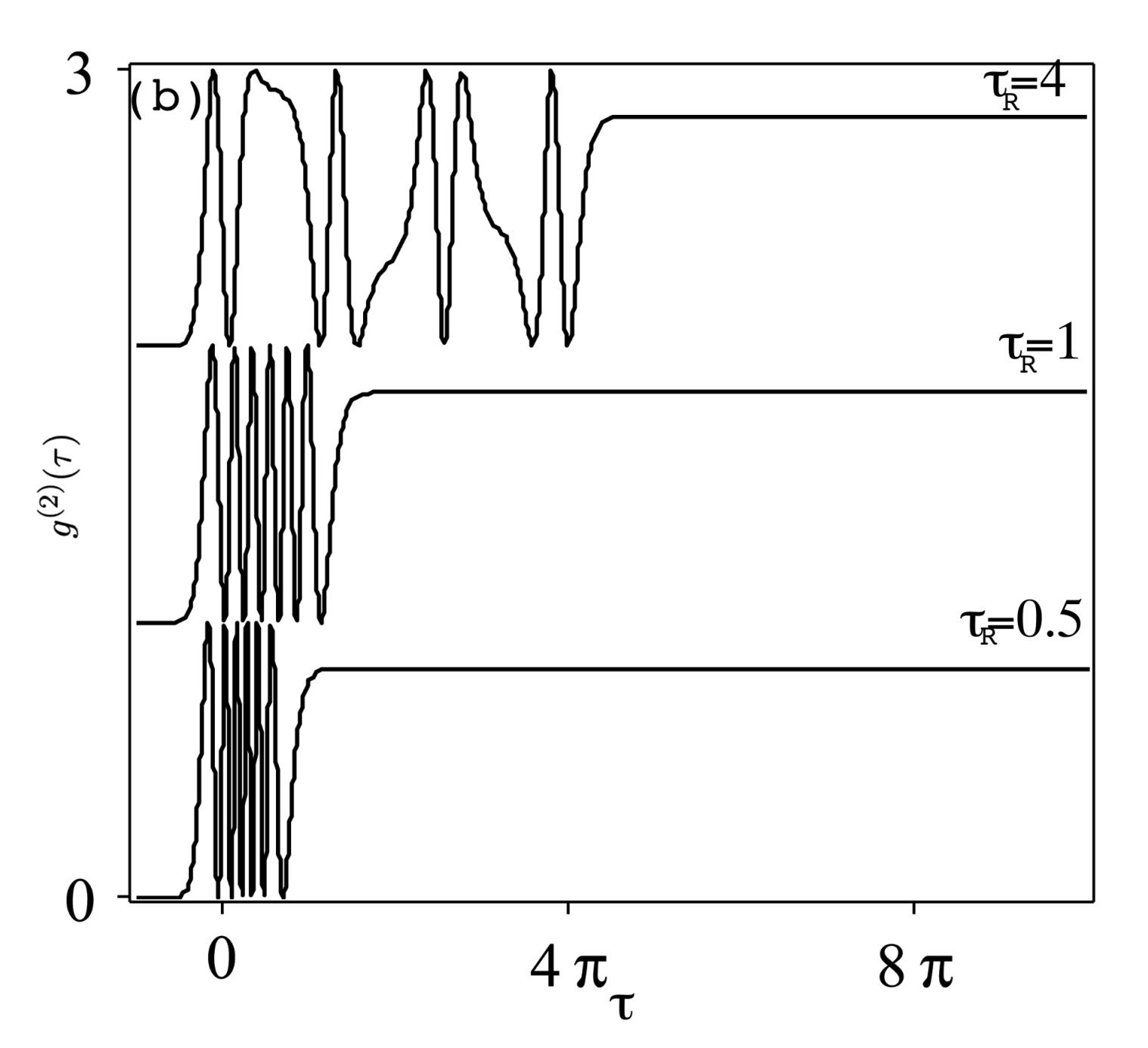
3.2. Intensity Correlation

The normalized intensity-intensity (second order) correlation function for a single qubit is given by Reference [20],

$$g^{\left(2\right)}(t,\tau )={\langle \frac{1}{2}+{\sigma }_z\left(\tau \right)\rangle }_g/\langle \frac{1}{2}+{\sigma }_z\left(t\right)\rangle ,$$

(9)

where the suffix ${\langle \cdots \cdots \rangle }_g$ means the average is calculated with initial ground state condition. For initially excited atom at $t=t_o$, $\langle \frac{1}{2}+{\sigma }_z\left(t\right)\rangle =1,$ then for $g^{\left(2\right)}\left(\tau \right)\equiv g^{\left(2\right)}(t=t_o,\tau )=1$, it corresponds to coherent light (Poissonian statistics), while, for $g^{\left(2\right)}\left(\tau \right)>1(g^{\left(2\right)}\left(\tau \right)<1)$, it corresponds to bunching (anti-bunching) effect, i.e., super-Poissonian (sub-Piossonian) statistics. For one pulse case $(n=1)$, as in Figure 4, and for weak pulse strength, ${\mathrm{\Omega }}_1=0.5,$$g^{\left(2\right)}\left(\tau \right)$ has a constant value $<1$ (anti-bunching) for $\tau >1$, while, for strong pulse strength, ${\mathrm{\Omega }}_1=5,g^{\left(2\right)}\left(\tau \right)$, shows oscillations of short duration around $\tau =0$, with constant value $g^{\left(2\right)}\left(\tau \right)\simeq 0.9$ for $\tau >0$. Effects of larger pulse number $n>1$ and the repetition time ${\tau }_R$ are shown in Figure 5. In Figure 5a, with $n=4$ and ${\mathrm{\Omega }}_1=0.5$, $g^{\left(2\right)}\left(\tau \right)\le 1$ for ${\tau }_R\le 1$ with non-monotonic behavior near $\tau =0$ and of constant value $\simeq 0.9$. For ${\tau }_R>1$, the reach to the constant value $g^{\left(2\right)}\left(\tau \right)\simeq 0.2$ takes place as a step-like structure. Increasing the pulse strength to ${\mathrm{\Omega }}_1=5$, as in Figure 5b, has the effect of inducing n-dense peaks around $\tau =0$ for ${\tau }_R<1$, which tend to spread over large period of $\tau >0$ with ${\tau }_R>1$.

4. Fluorescent Spectrum

The transient fluorescent spectrum is given by Reference [29].

$$\begin{array}{cc}\hfill S(t,D,\mathrm{\Gamma })& =2\mathrm{\Gamma }\underset{-\infty }{\overset{t}{\int }}d{t}_1\underset{-\infty }{\overset{t}{\int }}d{t}_2{e}^{(-\mathrm{\Gamma }+i{\omega }_f)(t-t_1)}\hfill \\ \hfill & \times e^{(-\mathrm{\Gamma }-i{\omega }_f)(t-t_2)}\langle {\widehat{S}}_{+}\left(t_1\right){\widehat{S}}_{-}\left(t_2\right)\rangle .\hfill \end{array}$$

(10)

Here, ${\omega }_f$ and $\mathrm{\Gamma }$ are the frequency and width of the detector’s filter, respectively. The auto-correlation function ${\langle {\widehat{S}}_{+}\left(t_1\right){\widehat{S}}_{-}\left(t_2\right)\rangle }_{\theta ,\varphi }$ with ${\widehat{S}}_{\pm }\left(t\right)={\widehat{\sigma }}_{\pm }\left(t\right)e^{\mp i{\omega }_{o}t}$ for initial atomic coherent state $|\theta ,\varphi \rangle$ are calculated using (3) and (8). Hence, the spectrum has the form [10].

$$\begin{array}{cc}\hfill S{(t,D,\mathrm{\Gamma })}_{\theta ,\varphi }& =2\mathrm{\Gamma }{e}^{-2\mathrm{\Gamma }t}{[\mid I_1\left(t\right)|}^{2}co{s}^2\left(\frac{\theta }{2}\right)+\mid I_2\left(t\right){{|}^2+\mid I_3\left(t\right)|}^{2}si{n}^2\left(\frac{\theta }{2}\right)\hfill \\ \hfill & -\frac{1}{2}Re(I_3\left(t\right)I_4\left(t\right)sin\left(\theta \right)e^{i\varphi })+\frac{1}{2}Re(I_1\left(t\right)I_4\left(t\right)sin\left(\theta \right)e^{-i\varphi })].\hfill \end{array}$$

(11)

The quantities $I_i\left(t\right);i=1..4$ are given by.

$$\begin{array}{cc}\hfill I_1\left({\tau }_1\right)& ={\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}{C}_{-}\left(t^{\prime }\right)d{t}^{\prime },\hfill \\ \hfill I_2\left({\tau }_1\right)& ={\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}{C}_z\left(t^{\prime }\right)d{t}^{\prime },\hfill \\ \hfill I_3\left({\tau }_1\right)& ={\int }_{-\infty }^{{\tau }_{!}}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}{C}_{+}\left(t^{\prime }\right)d{t}^{\prime },\hfill \\ \hfill I_4\left({\tau }_1\right)& ={\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}{C}_z^{*}\left(t^{\prime }\right)d{t}^{\prime },\hfill \end{array}$$

(12)

where $D={\omega }_f-{\omega }_o$ is the detector’s detuning parameter, and ${\tau }_1=\mathrm{\Gamma }t$.

Using (4) for $C_{\pm ,z}$ we get,

$$\begin{array}{cc}\hfill I_{1,3}\left({\tau }_1\right)& ={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}\left(1\mp cos\left(\omega \left(t^{\prime }\right)\right)\right)d{t}^{\prime }\hfill \\ \hfill I_{2,4}\left({\tau }_1\right)& =\mp i{\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}sin\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }.\hfill \end{array}$$

(13)

To minimize the calculations of $I_i(i=1..4)$, we notice that, for real x [26],

$$erf\left(x\right)\approx \left\{\begin{array}{c}1,ifx\gtrsim 4\hfill \\ -1,ifx\lesssim -4.\hfill \end{array}\right.$$

(14)

Hence, from (13), we have,

$$I_{1,3}\left({\tau }_1\right)={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{e^{(\mathrm{\Gamma }+iD){\tau }_1}}{(\mathrm{\Gamma }+iD)}}\mp R\left({\tau }_1\right)\right],$$

(15)

where

$$\begin{array}{cc}\hfill R\left({\tau }_1\right)& ={\int }_{-\infty }^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}cos\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }\hfill \\ \hfill & ={\int }_{-\infty }^{-4}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}cos\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }+{\int }_{-4}^4{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}cos\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }+{\int }_4^{{\tau }_1}{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}cos\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }.\hfill \end{array}$$

(16)

From (7), using (14), we have, for $|{\tau }_1+b_k|>4$,

$$\omega \left({\tau }_1\right)={\mathrm{\Omega }}_1\sum _{k=1}^n\left[1+erf({\tau }_1+b_k)\right]$$

$$\approx {\mathrm{\Omega }}_1\sum _{k=1}^n\left\{\begin{array}{cc}(1-1),\hfill & {\tau }_1+b_k<-4\hfill \\ (1+1);\hfill & {\tau }_1+b_k>4\hfill \end{array}\right.$$

$$={\mathrm{\Omega }}_1\left\{\begin{array}{cc}0;\hfill & {\tau }_1+b_k<-4\hfill \\ \left(2n\right);\hfill & {\tau }_1+b_k>4.\hfill \end{array}\right.$$

(17)

Using (17) in (16) and by turn into (15) we have,

$$\begin{array}{cc}\hfill I_{1,3}\left({\tau }_1\right)& ={\displaystyle \frac{1}{2(\mathrm{\Gamma }+iD)}}\left[(1\mp cos\left(2n{\mathrm{\Omega }}_1\right))e^{(\mathrm{\Gamma }+iD){\tau }_1}\mp \left(1-cos\left(2n{\mathrm{\Omega }}_1\right)\right)e^{4(\mathrm{\Gamma }+iD)}\right]\mp {\displaystyle \frac{1}{2}}{A}_1,\hfill \end{array}$$

(18)

where

$$A_1={\int }_{-4}^4{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}cos\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }.$$

(19)

Similarly, from (13), we have,

$$\begin{array}{cc}\hfill I_{2,4}\left({\tau }_1\right)& =\mp i\left[A_2+{\displaystyle \frac{sin\left(2n{\mathrm{\Omega }}_1\right)}{\mathrm{\Gamma }+iD}}(e^{(\mathrm{\Gamma }+iD){\tau }_1}-e^{4(\mathrm{\Gamma }+iD)})\right],\hfill \end{array}$$

(20)

where

$$A_2={\int }_{-4}^4{e}^{(\mathrm{\Gamma }+iD)t^{\prime }}sin\left(\omega \left(t^{\prime }\right)\right)d{t}^{\prime }.$$

(21)

The two integrals $A_{1,2}$ given by (19), (21) are treated numerically. In the following section, we present the computational plot of the normalized spectrum $S_i\left(D^{\prime }\right)=S_i(\tau ,D^{\prime })/max\left(S_i(\tau ,D^{\prime })\right)$ against the normalized detuning $D^{\prime }=D/\mathrm{\Gamma }$ for fixed values of ${\tau }_1=\mathrm{\Gamma }t$, ${\mathrm{\Omega }}_1$ in the two cases of initial ground and coherent atomic states $(i=g,c)$ for $n\ge 1$ pulse number.

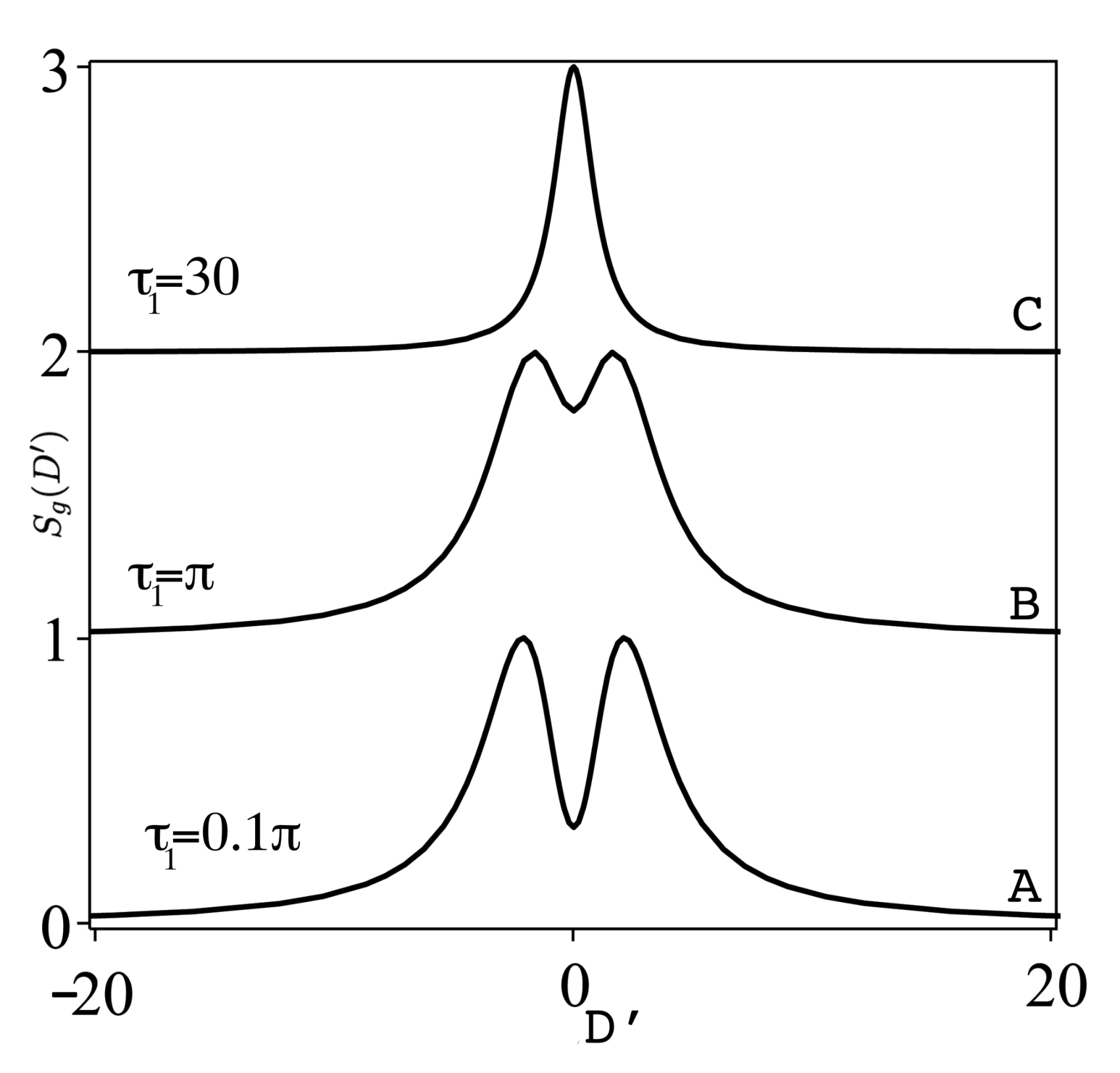
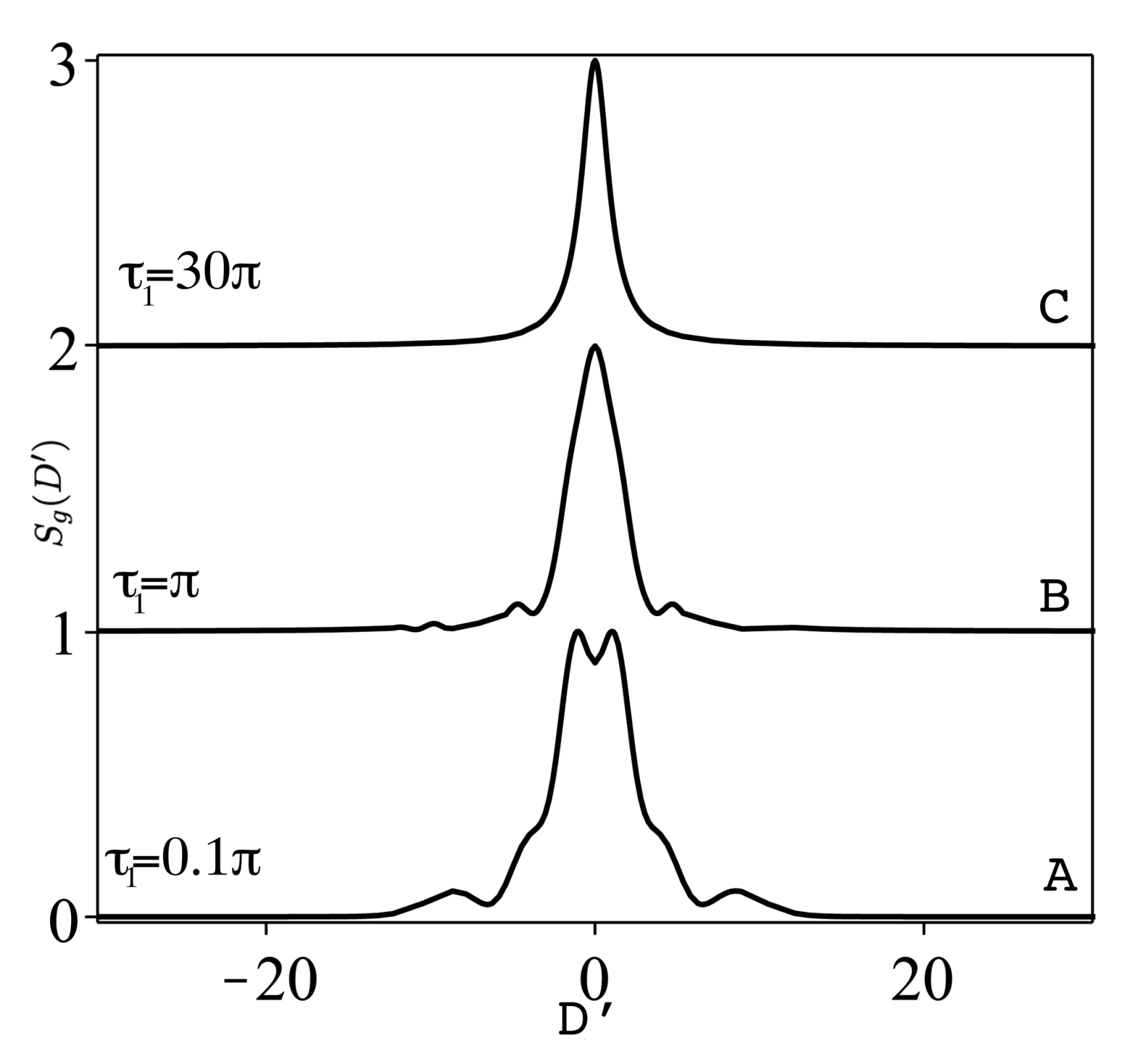
5. Computational Results for the Spectrum

5.1. Initial Ground State

In this case, the spectrum in (11) is reduced to the form:

$$S_g({\tau }_1,D,\mathrm{\Gamma })=2\mathrm{\Gamma }{e}^{-2{\tau }_1}\left(\mid I_1\left({\tau }_1\right){{|}^2+\mid I_2\left({\tau }_1\right)|}^2\right).$$

(22)

For weak field (${\mathrm{\Omega }}_1=0.5$) and for early observation ${\tau }_1=0.1\pi$ (curve A—Figure 6), the spectrum $S_g\left(D^{\prime }\right)$ is a single Lorentzian with a hole burning shape at $D^{\prime }=0.$ For increasing ${\tau }_1=\pi$, the dip at the top decreases (curve B—Figure 6), and the spectrum turns to a single narrowed Lorentzian with larger ${\tau }_1=30\pi$ (curve C—Figure 6). For larger number of pulses, e.g., $n\ge 10$, the spectrum is essentially a single Lorentzian for ${\tau }_R\le 1.$

For strong field (${\mathrm{\Omega }}_1=10$) and $n=1$ pulse and for early observation ${\tau }_1=0.1\pi ,$ the spectrum $S_g\left(D^{\prime }\right)$ is composed of a Lorentzian of small dip at its top with two small side bands (curve A in Figure 7). Increasing ${\tau }_1\ge \pi$ tends to wash the dip structure and the side band, and the spectrum turns to a single Lorentzain (curve B,C, Figure 7). For larger number of pulses $(n=10)$, as in Figure 8, and, for early time ${\tau }_1=0.1\pi$, the spectrum is a Mollow triplet with side bands are farther (nearer) from the central peak for ${\tau }_R>1({\tau }_R<1).$ For increasing time ${\tau }_1=\pi$, we have the same feature but with relatively higher weight of the side bands and occurrence of small ringing between the central peak and the side peaks. With further increase of time ${\tau }_1=30\pi$, the spectrum becomes a single central peak irrelevant of ${\tau }_R>1({\tau }_R<1)$.

5.2. Initial Coherent State

With initial atomic coherent state, e.g., $|\theta =\pi /2,\varphi =\pi \rangle ,{\tau }_1=0.1\pi$, and for one pulse $(n=1)$ and weak field strength $({\mathrm{\Omega }}_1=0.5)$—curve A in Figure 9—, the spectrum has a symmetric Lorentzian shape. For stronger field strength $({\mathrm{\Omega }}_1=20)$, the would be Mollow triplet with initial ground state is now becoming asymmetric with small oscillatory behavior for increasing $\left|D^{\prime }\right|$—curve B in Figure 9. These asymmetry and oscillations are attributed to both the strong Rabi oscillations and the interference terms due to the initial atomic coherent dispersion $(\theta \ne 0,\pi )$. In the case of $n=10$ pulse, as in Figure 10, the spectrum has three peaks structure with asymmetrical side peaks of dense ringing in between with ${\tau }_R<1$. With increased ${\tau }_R\ge 1$, the two asymmetrical side peaks are less apart.

6. Conclusions

The model of a non-dissipative qubit coupled to a train of resonant Gaussian pulses is theoretically investigated. This concerns the averaged atomic behavior (polarization and inversion), intensity-intensity correlation function, and transient fluorescent spectrum. Exact analytical results are derived in terms of the error function. The main results are:

(i)

The absorptive component of the atomic polarization and the atomic inversion for the initial ground and coherent atomic states reach constant values in an oscillatory form: the number of oscillations and its time speed increase with larger number of pulses and for relatively larger repetition time of pulses. The constant values of the atomic absorptive polarization and inversion are due to the nature of the infinite extent of the Gaussian pulses.

(ii)

The anti-bunching effect in the emitted radiation is shown for both weak and strong pulse strength. For larger number of pulses $(n\ge 1$) and strong strength of the field, the photon statistics of the emitted radiation becomes coherent (i.e., $g^{\left(2\right)}\left(\tau \right)=1$) at certain times before the reach to its constant sub-Poissonian value, $g^{\left(2\right)}\left(\tau \right)<1$, for repetition time ${\tau }_R>1({\tau }_R<1)$.

(iii)

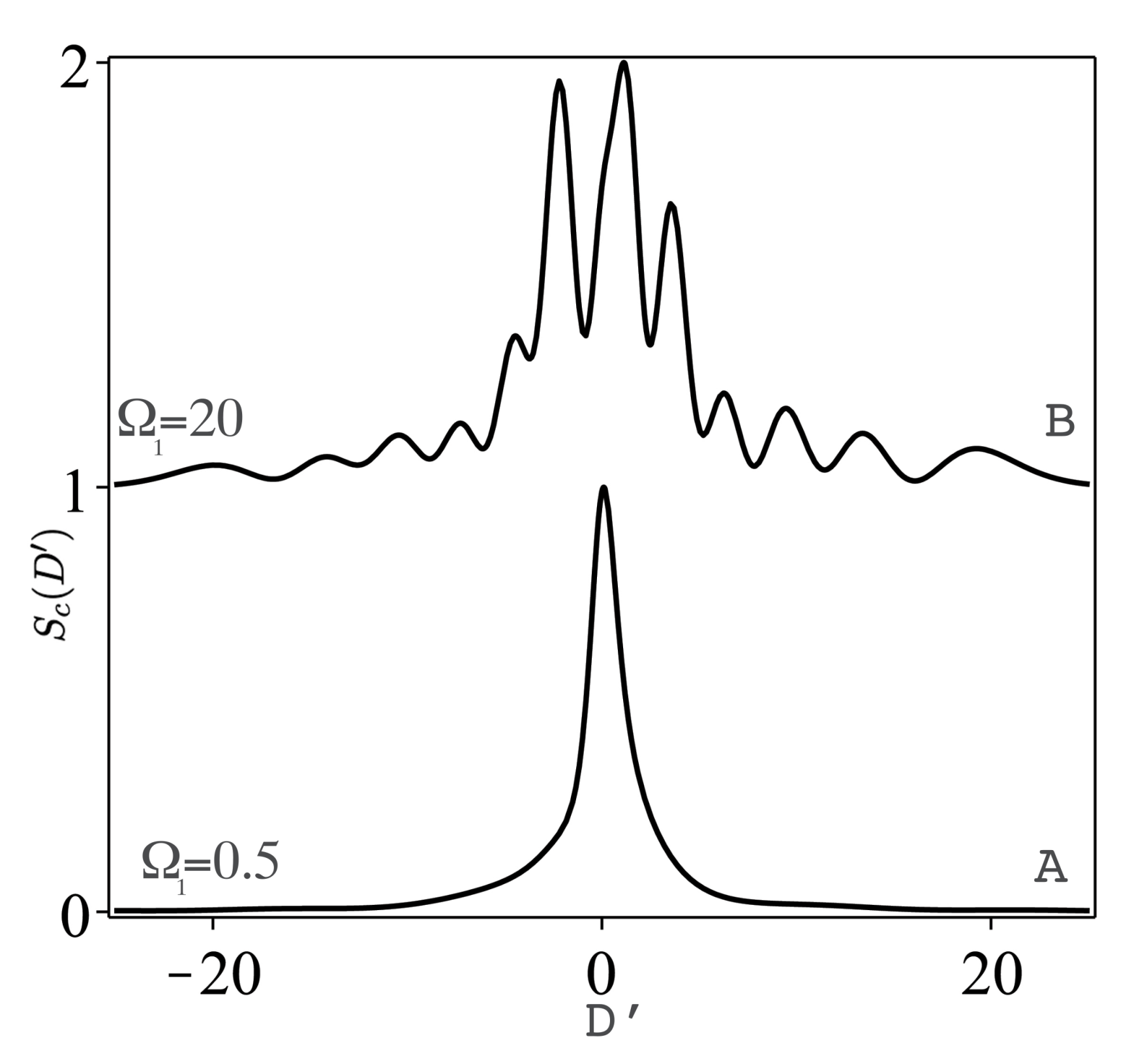
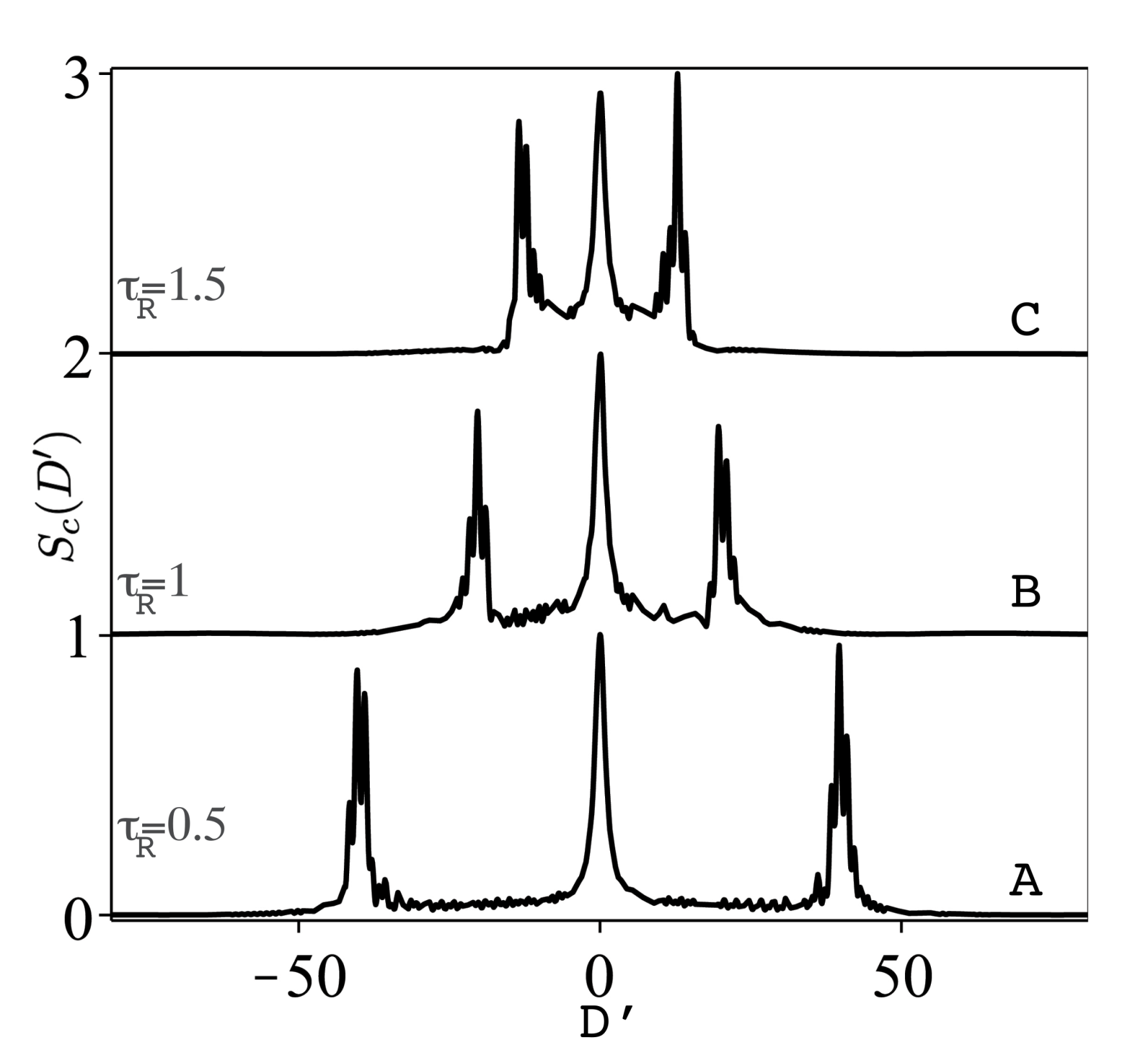
The transient fluorescent spectrum in the one pulse case $(n=1)$ and for weak pulse excitation with initial ground state shows a symmetric single Lorentzian with dip-structure at earlier time of observation, which vanishes with increasing time. For strong pulse excitation with initial ground state, earlier observation of the spectrum exhibits a single Lorentzian with both dip structure and side bands which vanish with larger time. For larger number of pulses, $n\ge 10,$, the spectrum is of Mollow triplet Lorentzian type, where the side bands get nearer (farther) to the central peak with ${\tau }_R>1({\tau }_R<1)$. The initial atomic coherent state in the case of $n=1$ pulse introduces asymmetry in the strong field case due to the Rabi oscillations and interference occurred with initial coherent dispersion processes. For many pulses, $n\ge 10$, and, for repetition time, ${\tau }_R>1({\tau }_R<1)$, the asymmetrical side bands in the spectrum are farther (nearer) apart.

The case of chirped Gaussian pulses will be treated in a future work, as the model Bloch equations have no exact analytical solutions, and this requires approximate analytical treatment.