Age-Specific Mathematical Model for Tuberculosis Transmission Dynamics in South Korea
Abstract
1. Introduction
2. Mathematical Models
2.1. Data and Sources
2.2. Mathematical Model for TB Transmission Dynamics
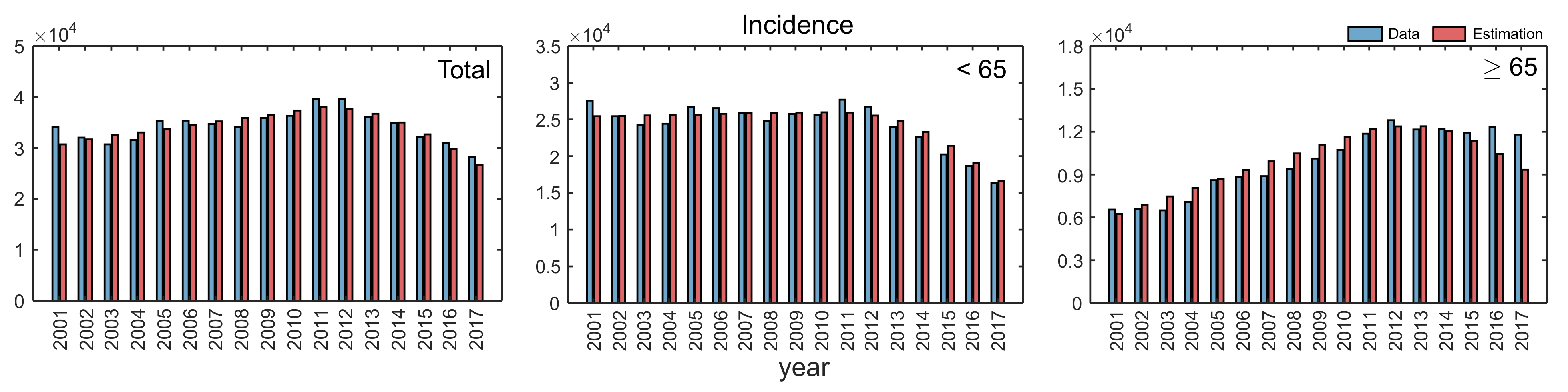
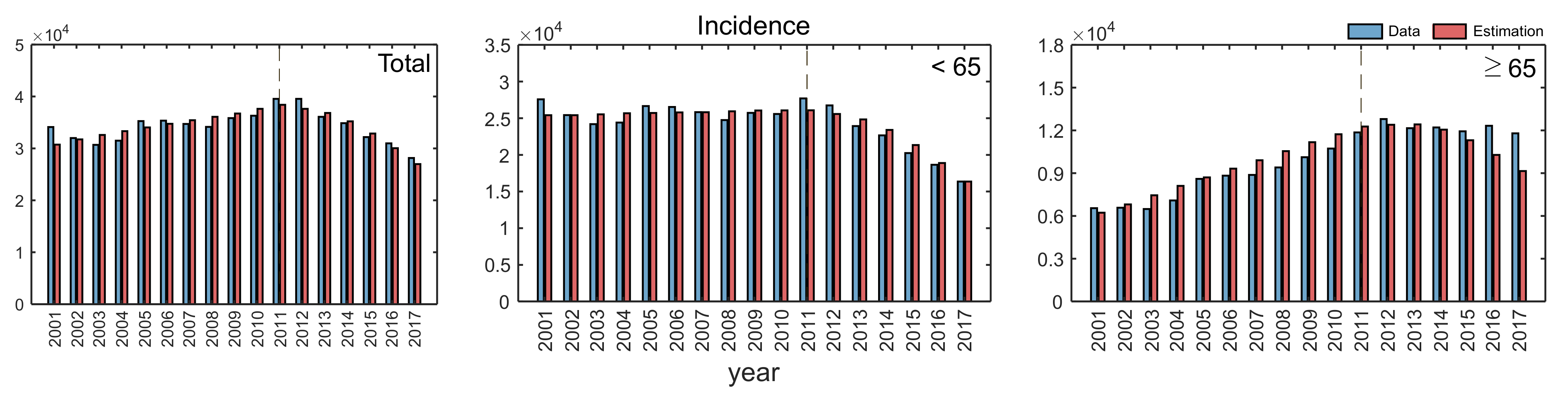
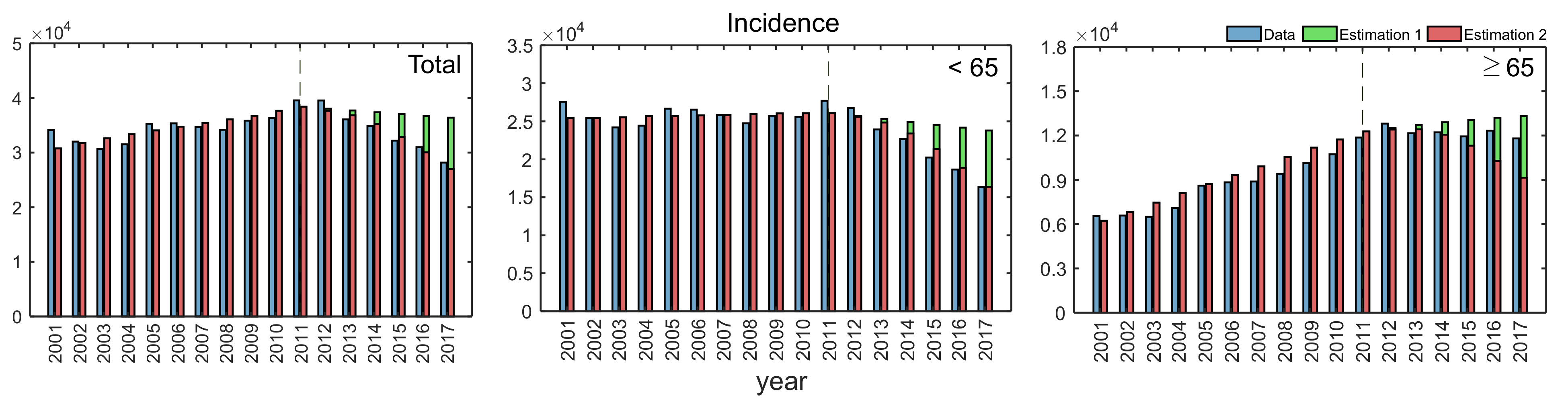
3. Numerical Results
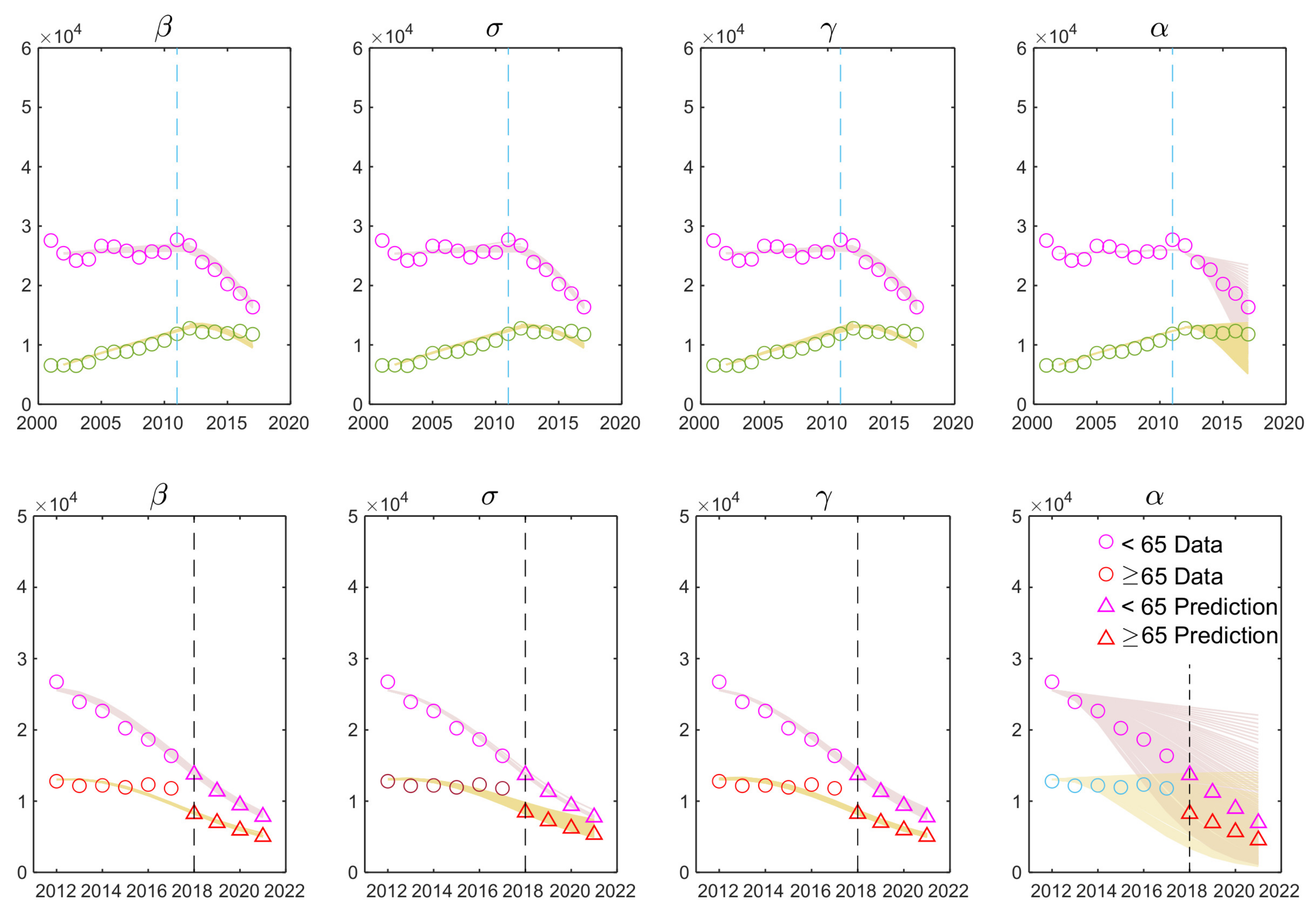
3.1. Estimated Parameters
3.2. Sensitivity Analysis
3.3. Impacts of Key Parameters on Incidence
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
The Basic Reproduction Number 0
References
- World Health Organization. Global Tuberculosis Report; WHO: Geneva, Switzerland, 2019; Available online: https://www.who.int/tb/publications/global_report/en/ (accessed on 1 July 2020).
- DOTS Expansion Working Group, World Health Organization & Stop TB Partnership. DOTS Expansion Working Group Strategic Plan, 2006–2015. Available online: https://apps.who.int/iris/handle/10665/69360 (accessed on 1 July 2020).
- World Health Organization. THE END TB Strategy; Global Strategy and Targets for Tuberculosis Prevention, Care and Control after 2015. Available online: https://www.who.int/tb/en/ (accessed on 1 July 2020).
- Min, J.; Kim, H.W.; Ko, Y.; Oh, J.Y.; Kang, J.Y.; Lee, J.; Park, Y.J.; Lee, S.; Park, J.S.; Kim, J.S. Tuberculosis Surveillance and Monitoring under the National Public-Private Mix Tuberculosis Control Project in South Korea 2016–2017. Tuberc. Respir. Dis. 2020, 83, 218–227. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control. Epidemiol. Infect. 1992, 757. [Google Scholar] [CrossRef]
- Feng, Z.; Castillo-Chavez, C.; Capurro, A.F. A Model for Tuburculosis with Exogeneous Reinfection. Theor. Popul. Biol. 2000, 57, 235–347. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, J.P.; Castillo-Chavez, C. Mathematical Modeling of tuberculosis epidemics. Math. Biosci. Eng. 2009, 6, 209–237. [Google Scholar] [PubMed]
- Blaser, N.; Zahnd, C.; Hermans, S.; Salazar-Vizcaya, L.; Estill, J.; Morrow, C.; Egger, M.; Keiser, O.; Wood, R. Tuberculosis in Cape Town: An age-structured transmission model. Epidemics 2016, 14, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Li, M.; Yuan, S. Analysis of Transmission and Control of Tuberculosis in Mainland China, 2005–2016, Based on the Age-Structure Mathematical Model. Int. J. Environ. Res. Public Health 2017, 14, 1192. [Google Scholar] [CrossRef]
- Cao, H.; Gao, X.; Yan, D.; Zhang, S. The dynamics of an age-structured TB transmission model with relapse. Math. Methods Appl. Sci. 2020, 43, 3807–3826. [Google Scholar] [CrossRef]
- Cao, H.; Zhou, Y. The discrete age-structured SEIT model with application to tuberculosis transmission in China. Math. Comput. Model. 2012, 55, 385–395. [Google Scholar] [CrossRef]
- Fatmawati; Dyah Purwati, U.; Riyudha, F.; Tasman, H. Optimal control of a discrete age-structured model for tuberculosis transmission. Heliyon 2020, 6, e03030. [Google Scholar] [CrossRef]
- Renardy, M.; Kirschner, D.E. A Framework for Network-Based Epidemiological Modeling of Tuberculosis Dynamics Using Synthetic Datasets. Bull. Math. Biol. 2020, 82, 78. [Google Scholar] [CrossRef]
- Kim, S.; Choe, S.; Kim, J.; Nam, S.; Shin, Y.; Lee, S. What Does a Mathematical Model Tell About the Impact of Reinfection in Korean Tuberculosis Infection? Osong Public Health Res. Perspect. 2014, 5. [Google Scholar] [CrossRef]
- Whang, S.; Choi, S.; Jung, E. A dynamic model for tuberculosis transmission and optimal treatment strategies in South Korea. J. Theor. Biol. 2011, 279, 120–131. [Google Scholar] [CrossRef] [PubMed]
- Piergallini, T.J.; Turner, J. Tuberculosis in the elderly: Why inflammation matters. Exp. Gerontol. 2018, 105, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Moliva, J.I.; Duncan, M.A.; Olmo-Fontánez, A.; Akhter, A.; Arnett, E.; Scordo, J.M.; Ault, R.; Sasindran, S.J.; Azad, A.K.; Montoya, M.J.; et al. The Lung Mucosa Environment in the Elderly Increases Host Susceptibility to Mycobacterium tuberculosis Infection. J. Infect. Dis. 2019, 220, 514–523. [Google Scholar] [CrossRef] [PubMed]
- Korea Centers for Disease Control and Prevention. Annual Report on the Notified Tuberculosis in Korea in 2018. Available online: http://tbzero.cdc.go.kr/tbzero/index.html (accessed on 1 June 2020).
- Korea Centers for Disease Control and Prevention. The 2nd Tuberculosis Management Master Plan. 2018. Available online: http://tbzero.cdc.go.kr/tbzero/contents.do (accessed on 1 June 2020).
- Korean Statistical Information Service. Available online: http://kosis.kr/statHtml/statHtml.do?orgId=101&tblId=DT_1B040M5&conn_path=I3 (accessed on 4 February 2020).
- van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Prem, K.; Cook, A.R.; Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017, 13, e1005697. [Google Scholar] [CrossRef]
- Korea Centers for Disease Control and Prevention. Analysis of Korean National LTBI Mass Screening Program and Establishment of LTBI Cohort. 2018. Available online: https://cris.nih.go.kr/cris/search/search_result_&st01.jsp?seq=13749 (accessed on 1 July 2020).
- Han, S.S.; Lee, S.J.; Yim, J.J.; Song, J.H.; Lee, E.H.; Kang, Y.A. Evaluation and treatment of latent tuberculosis infection among healthcare workers in Korea: A multicentre cohort analysis. PLoS ONE 2019, 14, e0222810. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Borgdorff, M.W.; Nagelkerke, N.J.; de Haas, P.E.; van Soolingen, D. Transmission of Mycobacterium tuberculosis depending on the age and sex of source cases. Am. J. Epidemiol. 2001, 154, 934–943. [Google Scholar] [CrossRef]
- Blower, S.M.; Mclean, A.R.; Porco, T.C.; Small, P.M.; Hopewell, P.C.; Sanchez, M.A.; Moss, A.R. The intrinsic transmission dynamics of tuberculosis epidemics. Nat. Med. 1995, 1, 815–821. [Google Scholar] [CrossRef]
- Tufariello, J.M.; Chan, J.; Flynn, J.L. Latent tuberculosis: Mechanisms of host and bacillus that contribute to persistent infection. Lancet Infect. Dis. 2003, 3, 578–590. [Google Scholar] [CrossRef]
- Cho, K.S. Tuberculosis control in the Republic of Korea. Epidemiol. Health 2018, 40, e2018036. [Google Scholar] [CrossRef]
- Chang, K.C.; Leung, C.C.; Yew, W.W.; Ho, S.C.; Tam, C.M. A Nested Case–Control Study on Treatment-related Risk Factors for Early Relapse of Tuberculosis. Am. J. Respir. Crit. Care Med. 2004, 170, 1124–1130. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Lim, H.; Cho, Y.; Park, Y.S.; Lee, S.; Yang, S.; Yoo, C.; Kim, Y.W.; Han, S.K.; Yim, J. Recurrence after successful treatment among patients with multidrug-resistant tuberculosis. Int. J. Tuberc. Lung Dis. 2011, 15, 1331–1333. [Google Scholar] [CrossRef] [PubMed]
- Mirsaeidi, M.; Sadikot, R. Patients at high risk of tuberculosis recurrence. Int. J. Mycobacteriol. 2018, 7, 1–6. [Google Scholar] [PubMed]
- Jeon, D.S. Latent tuberculosis infection: Recent progress and challenges in South Korea. Korean J. Intern. Med. 2020, 35, 269–275. [Google Scholar] [CrossRef]
- Getahun, H.; Matteelli, A.; Chaisson, R.E.; Raviglione, M. Latent Mycobacterium tuberculosis infection. N. Engl. J. Med. 2015, 372, 2127–2135. [Google Scholar] [CrossRef] [PubMed]
- Basera, T.J.; Ncayiyana, J.; Engel, M.E. Prevalence and risk factors of latent tuberculosis infection in Africa: A systematic review and meta-analysis protocol. BMJ Open 2017, 7, e012636. [Google Scholar] [CrossRef]



| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | |
|---|---|---|---|---|---|---|---|---|---|
| Total | 47,877,049 | 48,125,745 | 48,308,386 | 48,485,314 | 48,683,040 | 48,887,027 | 49,130,354 | 49,404,648 | 49,656,757 |
| Group 1 (<65) | 43,715,475 | 43,741,042 | 43,688,138 | 43,614,886 | 43,558,518 | 43,495,760 | 43,406,999 | 43,345,725 | 43,311,428 |
| Group 2 (≥65) | 4,161,574 | 4,384,703 | 4,620,248 | 4,870,428 | 5,124,522 | 5,391,267 | 5,723,355 | 6,058,923 | 6,345,329 |
| 559,934 | 496,911 | 495,036 | 476,958 | 438,707 | 451,759 | 496,822 | 465,892 | 444,849 | |
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
| Total | 49,879,812 | 50,111,476 | 50,345,325 | 50,558,952 | 50,763,158 | 50,951,720 | 51,112,972 | 51,230,705 | 51,301,009 |
| Group 1 (<65) | 43,270,507 | 43,240,464 | 43,144,834 | 42,975,199 | 42,782,445 | 42,569,268 | 42,352,819 | 42,029,211 | 41,612,986 |
| Group 2 (≥65) | 6,609,305 | 6,871,012 | 7,200,491 | 7,583,753 | 7,980,713 | 8,382,452 | 8,760,153 | 9,201,494 | 9,688,023 |
| 470,171 | 471,265 | 484,550 | 436,455 | 435,435 | 438,420 | 406,243 | 357,771 | 326,822 |
| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | |
|---|---|---|---|---|---|---|---|---|---|
| Total | 34,123 | 32,010 | 30,687 | 31,503 | 35,269 | 35,361 | 34,710 | 34,157 | 35,845 |
| Group 1 (<65) | 27,576 | 25,432 | 24,197 | 24,414 | 26,664 | 26,530 | 25,827 | 24,750 | 25,725 |
| Group 2 (≥65) | 6547 | 6578 | 6490 | 7089 | 8605 | 8831 | 8883 | 9407 | 10,120 |
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
| Total | 36,305 | 39,557 | 39,545 | 36,089 | 34,869 | 32,181 | 30,982 | 28,161 | 26,433 |
| Group 1 (<65) | 25,573 | 27,698 | 26,747 | 23,932 | 22,658 | 20,243 | 18,654 | 16,363 | 14,404 |
| Group 2 (≥65) | 10,732 | 11,859 | 12,798 | 12,157 | 12,211 | 11,938 | 12,328 | 11,798 | 12,029 |
| Variable | Description | Initial Value |
|---|---|---|
| Total population size | 43,715,475, 4,161,574 | |
| Susceptible class | 26,602,668, 2,013,417 | |
| Exposed class | 17,038,672, 2,141,610 | |
| Infected class | 34,135, 6547 | |
| Treated class | 40,000, 4000 |
| Parameter | Description | Value | Source |
|---|---|---|---|
| Recruitment of Group 1 | See Table 1 | [20] | |
| Recruitment rate from Group 1 to Group 2 | 1/65 | [20] | |
| Per-capita natural death rate | 0.0005, 0.05 | [20] | |
| Progression rate from E to I | 0.0015–0.0018, 0.00280–0.0038 | [18] | |
| Early detection and treatment rate for latent TB | 0–0.18 for 2012–2018 | Assumed | |
| Contact rate | 0.9208, 0.0792, 0.3515, 0.6485 | [22] | |
| , | Transmission rate | Estimated | - |
| , | Relapse rate | Estimated | - |
| , | Recovery rate | Estimated | - |
| : Transmission Rate | : Relapse Rate | : Recovery Rate | ||
|---|---|---|---|---|
| One-age group | 2001–2018 | 1.4014 | 0.0003438 | 1.1338 |
| Age years | 2001–2018 | 1.6100 | 0.0001150 | 1.3434 |
| Age years | 2001–2018 | 1.2642 | 0.0003529 | 0.8585 |
| : Transmission Rate | : Relapse Rate | : Recovery Rate | ||
|---|---|---|---|---|
| One-age group | –2011 | 1.4524 | 0.0014410 | 1.1302 |
| 2012– | 1.2192 | 0.0004803 | 1.2754 | |
| Age <65 years | –2011 | 1.7249 | 0.0003150 | 1.1791 |
| 2012– | 1.2588 | 0.0000313 | 1.5050 | |
| Age ≥65 years | –2011 | 1.3312 | 0.0010760 | 0.6625 |
| 2012– | 1.1986 | 0.0001055 | 0.7812 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Park, H.-Y.; Ryu, H.; Kwon, J.-W. Age-Specific Mathematical Model for Tuberculosis Transmission Dynamics in South Korea. Mathematics 2021, 9, 804. https://doi.org/10.3390/math9080804
Lee S, Park H-Y, Ryu H, Kwon J-W. Age-Specific Mathematical Model for Tuberculosis Transmission Dynamics in South Korea. Mathematics. 2021; 9(8):804. https://doi.org/10.3390/math9080804
Chicago/Turabian StyleLee, Sunmi, Hae-Young Park, Hohyung Ryu, and Jin-Won Kwon. 2021. "Age-Specific Mathematical Model for Tuberculosis Transmission Dynamics in South Korea" Mathematics 9, no. 8: 804. https://doi.org/10.3390/math9080804
APA StyleLee, S., Park, H.-Y., Ryu, H., & Kwon, J.-W. (2021). Age-Specific Mathematical Model for Tuberculosis Transmission Dynamics in South Korea. Mathematics, 9(8), 804. https://doi.org/10.3390/math9080804









