Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives
Abstract
:1. Introduction
2. Preliminaries
- i.
- the trivial solution of (1) is called stable if for any there exists such that, for every satisfying , we have for any ;
- ii.
- the trivial solution of (1) is called asymptotically stable if it is stable and there exists such that for ;
- iii.
- the trivial solution of (1) is called -asymptotically stable if it is stable and there exists such that, for any , we have:
3. Mittag–Leffler Functions, Derivatives and Asymptotic Behavior
3.1. The Prabhakar Function and Its Asymptotic Properties
3.2. Asymptotic Behavior of Derivatives of the ML Function
3.3. Behavior of Derivatives of the ML Function When
4. Stability of Linear Systems of Single-Order FDEs
- i.
- -asymptotically stable if and only if
- ii.
- stable if and only if and the eigenvalues of A which satisfy have index 1.
- converges to 0 as , if and only if ; moreover, in this case, as ;
- if , the function is unbounded;
- if , the function is bounded if and only if .
- has two eigenvalueslaying on the border of the stability sector and both having index 2; according to Theorem 1, the system produces unbounded solutions as clearly shown in the left plot of Figure 3;
- has the same two eigenvaluesof, laying on the border of the stability sector , but their index is now 1; the expected bounded solutions are shown in the right plot of Figure 3;
- has two eigenvalueswith index 2, as , but now they lay inside the stability sector ; the asymptotically stable solutions are illustrated in the left plot of Figure 4;
- has two eigenvalueswith index 1, as , but lying outside the stability sector ; the resulting unbounded solutions are illustrated in the right plot of Figure 4.
5. Stability of Linear Multi-Order Systems of FDEs
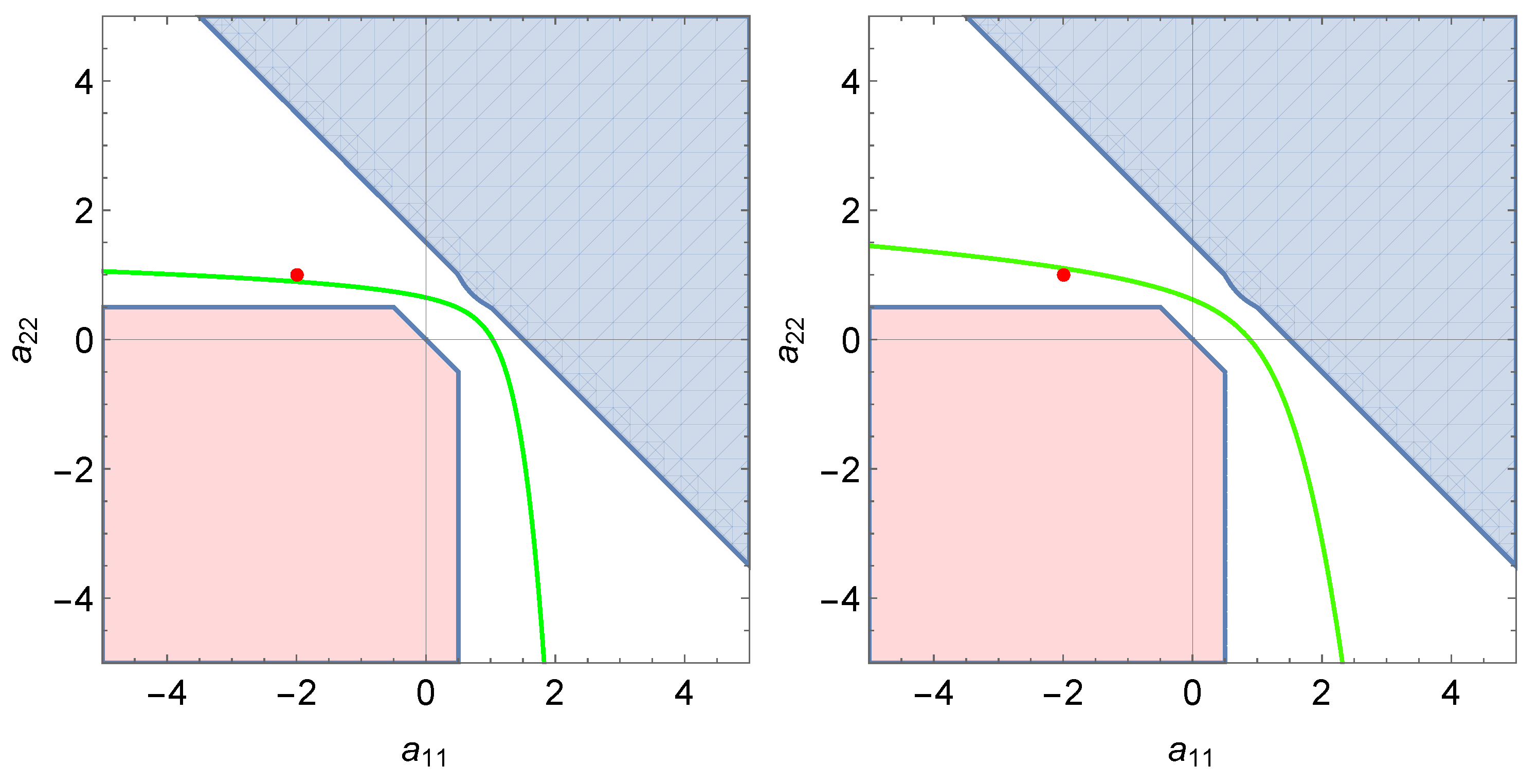
5.1. Stability of Two-Dimensional Systems of FDEs with Different Fractional Orders
- i.
- The curve is the graph of a smooth, decreasing, concave bijective function in the -plane.
- ii.
- The curve lies outside the third quadrant of the -plane.
- 1.
- if , then the system is unstable, for any choice of the fractional orders , based on Theorem 4;
- 2.
- if , then the system is unstable, for any choice of the fractional orders , based on Theorem 4;
- 3.
- if , then the system is asymptotically stable, for any choice of the fractional orders , based on Theorem 5;
- 4.
- if , then the stability properties of the system depend on choice of the fractional orders and Theorem 3 should be applied.
5.2. Stability of Higher Dimensional Systems of FDEs with Specific Structures
- system (12) is asymptotically stable if and only if
- -
- for any and
- -
- , for any , where and are the main diagonal elements of matrix , and is defined in Lemma 1.
- system (12) is unstable if at least one of the following holds:
- -
- there exists such that the matrix has at least one eigenvalue such that or
- -
- there exists such that , where and are the main diagonal elements of matrix , and is defined in Lemma 1.
5.3. Stability of Higher Dimensional Systems of FDEs with Special Fractional Orders
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDE | Fractional differential equation |
| ML | Mittag–Leffler |
| LT | Laplace transform |
References
- Li, C.; Zhang, F. A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 2011, 193, 27–47. [Google Scholar] [CrossRef]
- Rivero, M.; Rogosin, S.V.; Tenreiro Machado, J.A.; Trujillo, J.J. Stability of fractional order systems. Math. Probl. Eng. 2013, 2013, 356215. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, D.; Zhang, H. Stability analysis on a class of nonlinear fractional-order systems. Nonlinear Dyn. 2016, 86, 1023–1033. [Google Scholar] [CrossRef]
- Tuan, H.T.; Trinh, H. Global attractivity and asymptotic stability of mixed-order fractional systems. IET Control Theory Appl. 2020, 14, 1240–1245. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Sabatier, J.; Farges, C. On stability of commensurate fractional order systems. Int. J. Bifurc. Chaos 2012, 22, 1250084. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Lu, J. Stability analysis of linear fractional differential system with multiple time delays. Nonlinear Dyn. 2007, 48, 409–416. [Google Scholar] [CrossRef]
- Deng, W.; Li, C.; Guo, Q. Analysis of fractional differential equations with multi-orders. Fractals 2007, 15, 173–182. [Google Scholar] [CrossRef]
- Petras, I. Stability of fractional-order systems with rational orders. Fract. Calc. Appl. Anal. 2009, 12, 269–298. [Google Scholar]
- Diethelm, K. Multi-term fractional differential equations, multi-order fractional differential systems and their numerical solution. J. Eur. Syst. Autom. 2008, 42, 665–676. [Google Scholar] [CrossRef]
- Bonnet, C.; Partington, J.R. Coprime factorizations and stability of fractional differential systems. Syst. Control Lett. 2000, 41, 167–174. [Google Scholar] [CrossRef]
- Trächtler, A. On BIBO stability of systems with irrational transfer function. arXiv 2016, arXiv:1603.01059. [Google Scholar]
- Diethelm, K.; Siegmund, S.; Tuan, H. Asymptotic behavior of solutions of linear multi-order fractional differential systems. Fract. Calc. Appl. Anal. 2017, 20, 1165–1195. [Google Scholar] [CrossRef] [Green Version]
- Brandibur, O.; Kaslik, E. Stability properties of a two-dimensional system involving one Caputo derivative and applications to the investigation of a fractional-order Morris-Lecar neuronal model. Nonlinear Dyn. 2017, 90, 2371–2386. [Google Scholar] [CrossRef] [Green Version]
- Brandibur, O.; Kaslik, E. Stability of two-component incommensurate fractional-order systems and applications to the investigation of a FitzHugh-Nagumo neuronal model. Math. Methods Appl. Sci. 2018, 41, 7182–7194. [Google Scholar] [CrossRef] [Green Version]
- Brandibur, O.; Kaslik, E. Exact stability and instability regions for two-dimensional linear autonomous multi-order systems of fractional-order differential equations. Fract. Calc. Appl. Anal. 2021, 24, 225–253. [Google Scholar] [CrossRef]
- Atanackovic, T.; Dolicanin, D.; Pilipovic, S.; Stankovic, B. Cauchy problems for some classes of linear fractional differential equations. Fract. Calc. Appl. Anal. 2014, 17, 1039–1059. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; Chen, Y.Q. Stability of fractional-order linear time-invariant systems with multiple noncommensurate orders. Comput. Math. Appl. 2012, 64, 3053–3058. [Google Scholar] [CrossRef] [Green Version]
- Čermák, J.; Kisela, T. Asymptotic stability of dynamic equations with two fractional terms: Continuous versus discrete case. Fract. Calc. Appl. Anal. 2015, 18, 437. [Google Scholar] [CrossRef]
- Čermák, J.; Kisela, T. Stability properties of two-term fractional differential equations. Nonlinear Dyn. 2015, 80, 1673–1684. [Google Scholar] [CrossRef]
- Brandibur, O.; Kaslik, E. Stability analysis of multi-term fractional-differential equations with three fractional derivatives. J. Math. Anal. Appl. 2021, 495, 124751. [Google Scholar] [CrossRef]
- Haubold, H.; Mathai, A.; Saxena, R. Mittag–Leffler Functions and Their Applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef] [Green Version]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag–Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Paris, R.B. Exponentially small expansions in the asymptotics of the Wright function. J. Comput. Appl. Math. 2010, 234, 488–504. [Google Scholar] [CrossRef] [Green Version]
- Paris, R.B. Asymptotics of the Special Functions of Fractional Calculus. In Handbook of Fractional Calculus with Applications; De Gruyter: Berlin, Germany, 2019; Volume 1, pp. 297–325. [Google Scholar]
- Giusti, A.; Colombaro, I.; Garra, R.; Garrappa, R.; Polito, F.; Popolizio, M.; Mainardi, F. A practical guide to Prabhakar fractional calculus. Fract. Calc. Appl. Anal. 2020, 23, 9–54. [Google Scholar] [CrossRef] [Green Version]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag-Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef] [Green Version]
- Giusti, A. General fractional calculus and Prabhakar’s theory. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105114. [Google Scholar] [CrossRef] [Green Version]
- Kochubei, A.N. General fractional calculus, evolution equations, and renewal processes. Integral Equ. Oper. Theory 2011, 71, 583–600. [Google Scholar] [CrossRef] [Green Version]
- Brunner, H. Volterra Integral Equations: An Introduction to Theory and Applications; Cambridge University Press: Cambridge, UK, 2017; Volume 30. [Google Scholar]
- Gripenberg, G.; Londen, S.O.; Staffans, O. Volterra Integral and fUnctional Equations; Cambridge University Press: Cambridge, UK, 1990; Volume 34. [Google Scholar]
- Lubich, C. A stability analysis of convolution quadratures for Abel-Volterra integral equations. IMA J. Numer. Anal. 1986, 6, 87–101. [Google Scholar] [CrossRef]
- Tsalyuk, Z. Volterra integral equations. J. Sov. Math. 1979, 12, 715–758. [Google Scholar] [CrossRef]
- Doetsch, G. Introduction to the Theory and Application of the Laplace Transformation; Springer: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013; p. xviii+643. [Google Scholar]
- Garrappa, R.; Popolizio, M. Computing the matrix Mittag-Leffler function with applications to fractional calculus. J. Sci. Comput. 2018, 77, 129–153. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandibur, O.; Garrappa, R.; Kaslik, E. Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives. Mathematics 2021, 9, 914. https://doi.org/10.3390/math9080914
Brandibur O, Garrappa R, Kaslik E. Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives. Mathematics. 2021; 9(8):914. https://doi.org/10.3390/math9080914
Chicago/Turabian StyleBrandibur, Oana, Roberto Garrappa, and Eva Kaslik. 2021. "Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives" Mathematics 9, no. 8: 914. https://doi.org/10.3390/math9080914
APA StyleBrandibur, O., Garrappa, R., & Kaslik, E. (2021). Stability of Systems of Fractional-Order Differential Equations with Caputo Derivatives. Mathematics, 9(8), 914. https://doi.org/10.3390/math9080914






