Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Statistical Analysis
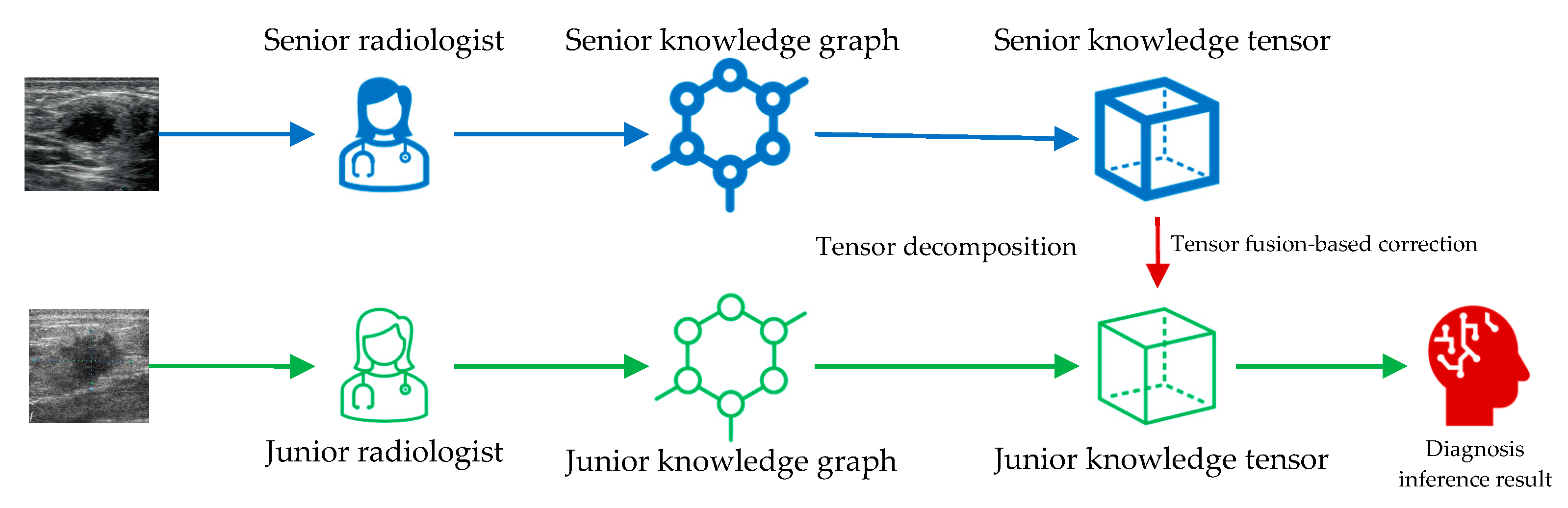
2.3. Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework
2.4. Construction of the Knowledge Graph
2.5. Inference Based on TuckER
2.6. Tensor Fusion-Based Correction
2.7. Data Augmentation
2.8. Evaluation Metrics
3. Results
3.1. Data Description
3.2. Knowledge Tensor-Aided Diagnosis Performance
3.3. Comparison with Traditional Machine Learning Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Croswell, J.M.; Ransohoff, D.F.; Kramer, B.S. Principles of Cancer Screening: Lessons from History and Study Design Issues. Semin. Oncol. 2010, 37, 202–215. [Google Scholar] [CrossRef] [Green Version]
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer Statistics, 2022. CA A Cancer J. Clin. 2022, 72, 7–33. [Google Scholar] [CrossRef]
- Azhari, H. Ultrasound: Medical Imaging and Beyond (An Invited Review). CPB 2012, 13, 2104–2116. [Google Scholar] [CrossRef]
- Pathan, R.K.; Alam, F.I.; Yasmin, S.; Hamd, Z.Y.; Aljuaid, H.; Khandaker, M.U.; Lau, S.L. Breast Cancer Classification by Using Multi-Headed Convolutional Neural Network Modeling. Healthcare 2022, 10, 2367. [Google Scholar] [CrossRef]
- Li, G.; An, C.; Yu, J.; Huang, Q. Radiomics Analysis of Ultrasonic Image Predicts Sensitive Effects of Microwave Ablation in Treatment of Patient with Benign Breast Tumors. Biomed. Signal Process. Control. 2022, 76, 103722. [Google Scholar] [CrossRef]
- Huang, Q.; Miao, Z.; Zhou, S.; Chang, C.; Li, X. Dense Prediction and Local Fusion of Superpixels: A Framework for Breast Anatomy Segmentation in Ultrasound Image with Scarce Data. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Mendelson, E.B.; Böhm-Vélez, M.; Berg, W.A.; Whitman, G.J.; Feldman, M.I.; Madjar, H. ACR BI-RADS® Ultrasound. In ACR BI-RADS® Atlas, Breast Imaging Reporting and Data System; American College of Radiology: Reston, VA, USA, 2013. [Google Scholar]
- Wiacek, A.; Oluyemi, E.; Myers, K.; Mullen, L.; Bell, M.A.L. Coherence-Based Beamforming Increases the Diagnostic Certainty of Distinguishing Fluid from Solid Masses in Breast Ultrasound Exams. Ultrasound Med. Biol. 2020, 46, 1380–1394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wiacek, A.; Oluyemi, E.; Myers, K.; Ambinder, E.; Bell, M.A.L. Coherence Metrics for Reader-Independent Differentiation of Cystic from Solid Breast Masses in Ultrasound Images. Ultrasound Med. Biol. 2023, 49, 256–268. [Google Scholar] [CrossRef]
- Agu, N.N.; Wu, J.T.; Chao, H.; Lourentzou, I.; Sharma, A.; Moradi, M.; Yan, P.; Hendler, J. AnaXNet: Anatomy Aware Multi-Label Finding Classification in Chest X-ray. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2021, Virtual, 27 September–1 October 2021; de Bruijne, M., Cattin, P.C., Cotin, S., Padoy, N., Speidel, S., Zheng, Y., Essert, C., Eds.; Springer International Publishing: Cham, Germany, 2021; pp. 804–813. [Google Scholar]
- Chabi, M.-L.; Borget, I.; Ardiles, R.; Aboud, G.; Boussouar, S.; Vilar, V.; Dromain, C.; Balleyguier, C. Evaluation of the Accuracy of a Computer-Aided Diagnosis (CAD) System in Breast Ultrasound According to the Radiologist’s Experience. Acad. Radiol. 2012, 19, 311–319. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of Deep Learning: Concepts, CNN Architectures, Challenges, Applications, Future Directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef]
- Feng, X.; Huang, Q.; Li, X. Ultrasound Image De-Speckling by a Hybrid Deep Network with Transferred Filtering and Structural Prior. Neurocomputing 2020, 414, 346–355. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.; Sun, J.; Zheng, J.; Wang, S.; Wang, G.; Ding, Y.; Zhao, J.; Zhang, J. Intelligent Diagnosis Algorithm for Thyroid Nodules Based on Deep Learning and Statistical Features. Biomed. Signal Process. Control. 2022, 78, 103924. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, Q.; Liu, L. Classification of Tumor in One Single Ultrasound Image via a Novel Multi-View Learning Strategy. Pattern Recognit. 2023, 143, 109776. [Google Scholar] [CrossRef]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. Nat Mach Intell 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Ye, L. Multi-Task/Single-Task Joint Learning of Ultrasound BI-RADS Features. IEEE Trans Ultrason Ferroelectr Freq Control 2021, 69, 691–701. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, D.; Lu, Z.; Zhou, S.; Li, J.; Liu, L.; Chang, C. A Novel Image-to-Knowledge Inference Approach for Automatically Diagnosing Tumors. Expert Syst. Appl. 2023, 229, 120450. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, Z.; Liu, L.; Huang, Q. Deep Fusion of Human-Machine Knowledge with Attention Mechanism for Breast Cancer Diagnosis. Biomed. Signal Process. Control. 2023, 84, 104784. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, Q.; Li, X. Segmentation Information with Attention Integration for Classification of Breast Tumor in Ultrasound Image. Pattern Recognit. 2021, 124, 108427. [Google Scholar] [CrossRef]
- Xi, J.; Miao, Z.; Liu, L.; Yang, X.; Zhang, W.; Huang, Q.; Li, X. Knowledge Tensor Embedding Framework with Association Enhancement for Breast Ultrasound Diagnosis of Limited Labeled Samples. Neurocomputing 2022, 468, 60–70. [Google Scholar] [CrossRef]
- Xi, J.; Sun, D.; Chang, C.; Zhou, S.; Huang, Q. An Omics-to-Omics Joint Knowledge Association Subtensor Model for Radiogenomics Cross-Modal Modules from Genomics and Ultrasonic Images of Breast Cancers. Comput. Biol. Med. 2023, 155, 106672. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties. Int. Stat. Rev./Rev. Int. De Stat. 1989, 57, 238. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach Learn 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Hogan, A.; Blomqvist, E.; Cochez, M.; D’amato, C.; Melo, G.D.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S.; et al. Knowledge Graphs. ACM Comput. Surv. 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-Relational Data. In Proceedings of the 26th International Conference on Neural Information Processing Systems—Volume 2, Lake Tahoe, NV, USA, 5–10 December 2013; Curran Associates Inc.: Red Hook, NY, USA, 2013; pp. 2787–2795. [Google Scholar]
- Balazevic, I.; Allen, C.; Hospedales, T. TuckER: Tensor Factorization for Knowledge Graph Completion. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, 3–7 November 2019; Association for Computational Linguistics: Hong Kong, China, 2019; pp. 5185–5194. [Google Scholar]
- Statistical Product and Service Solutions 2020. Available online: https://www.ibm.com/products/spss-statistics (accessed on 28 April 2023).
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics 1988, 44, 837. [Google Scholar] [CrossRef] [PubMed]
- Tucker, L.R. Some Mathematical Notes on Three-Mode Factor Analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef]
- Buja, A.; Stuetzle, W.; Shen, Y. Loss Functions for Binary Class Probability Estimation and Classification: Structure and Applications. Work. Draft Novemb. 2005, 3, 13. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API Design for Machine Learning Software: Experiences from the Scikit-Learn Project. arXiv 2013, arXiv:arXiv:1309.0238. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27:1–27:27. [Google Scholar] [CrossRef]
- Hong, A.S.; Rosen, E.L.; Soo, M.S.; Baker, J.A. BI-RADS for Sonography: Positive and Negative Predictive Values of Sonographic Features. Am. J. Roentgenol. 2005, 184, 1260–1265. [Google Scholar] [CrossRef]



| Statistic Item | Statistic Value |
|---|---|
| Number of cases | 1219 |
| With age recorded | 1190 (97.62%) |
| Average ages with recording | 48.08 (13–87) |
| Number of images | 3413 |
| Benign | 746 (21.86%) |
| Malignant | 2667 (78.14%) |
| Knowledge | Accuracy | Precision | Sensitivity | Specificity | F1 Score | AUC (95% CI) | p Value |
|---|---|---|---|---|---|---|---|
| Junior radiologist | 0.791 | 0.893 | 0.768 | 0.832 | 0.826 | 0.849 (0.823–0.876) | <0.001 |
| Senior radiologist | 0.944 | 0.967 | 0.946 | 0.942 | 0.957 | 0.983 (0.975–0.992) | <0.001 |
| Tensor-fused | 0.809 | 0.909 | 0.783 | 0.856 | 0.841 | 0.887 (0.864–0.909) | - |
| Methods | Accuracy | Precision | Sensitivity | Specificity | F1 Score | AUC (95% CI) | p Value |
|---|---|---|---|---|---|---|---|
| KNN | 0.874 | 0.972 | 0.830 | 0.955 | 0.895 | 0.950 (0.934–0.965) | <0.001 |
| SVM | 0.946 | 0.957 | 0.959 | 0.921 | 0.958 | 0.980 (0.972–0.989) | 0.428 |
| Knowledge tensor | 0.944 | 0.967 | 0.946 | 0.942 | 0.957 | 0.983 (0.975–0.992) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Xiao, L.; Wang, G.; Liu, Y.; Liu, L.; Huang, Q. Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework. Healthcare 2023, 11, 2014. https://doi.org/10.3390/healthcare11142014
Li G, Xiao L, Wang G, Liu Y, Liu L, Huang Q. Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework. Healthcare. 2023; 11(14):2014. https://doi.org/10.3390/healthcare11142014
Chicago/Turabian StyleLi, Guanghui, Lingli Xiao, Guanying Wang, Ying Liu, Longzhong Liu, and Qinghua Huang. 2023. "Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework" Healthcare 11, no. 14: 2014. https://doi.org/10.3390/healthcare11142014
APA StyleLi, G., Xiao, L., Wang, G., Liu, Y., Liu, L., & Huang, Q. (2023). Knowledge Tensor-Aided Breast Ultrasound Image Assistant Inference Framework. Healthcare, 11(14), 2014. https://doi.org/10.3390/healthcare11142014






