Team Size and Composition in Home Healthcare: Quantitative Insights and Six Model-Based Principles
Abstract
1. Introduction
1.1. Background: Existing Literature
1.2. Background: Practice
1.3. Contribution
2. Methods
3. Results
3.1. Data Analysis
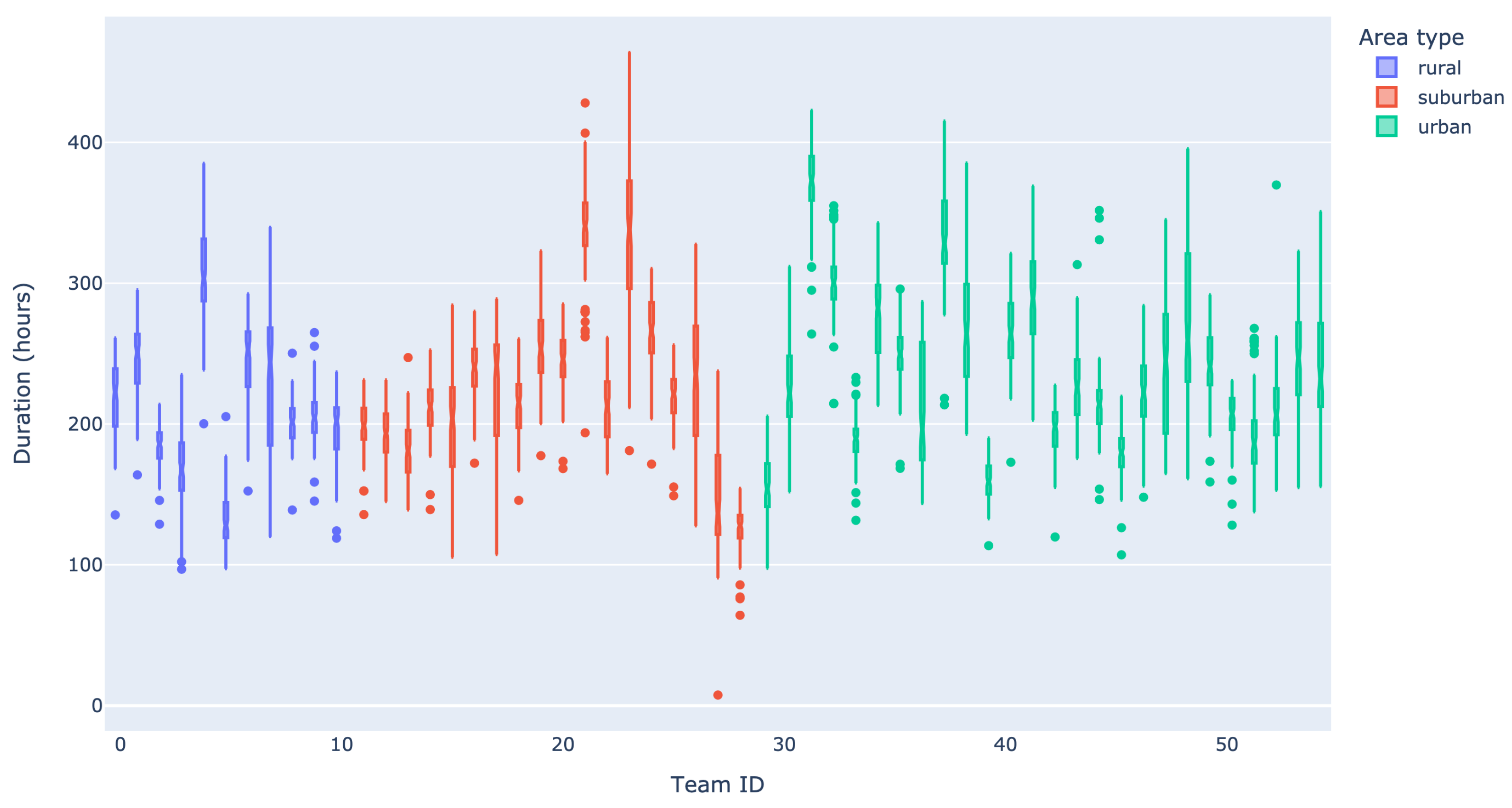
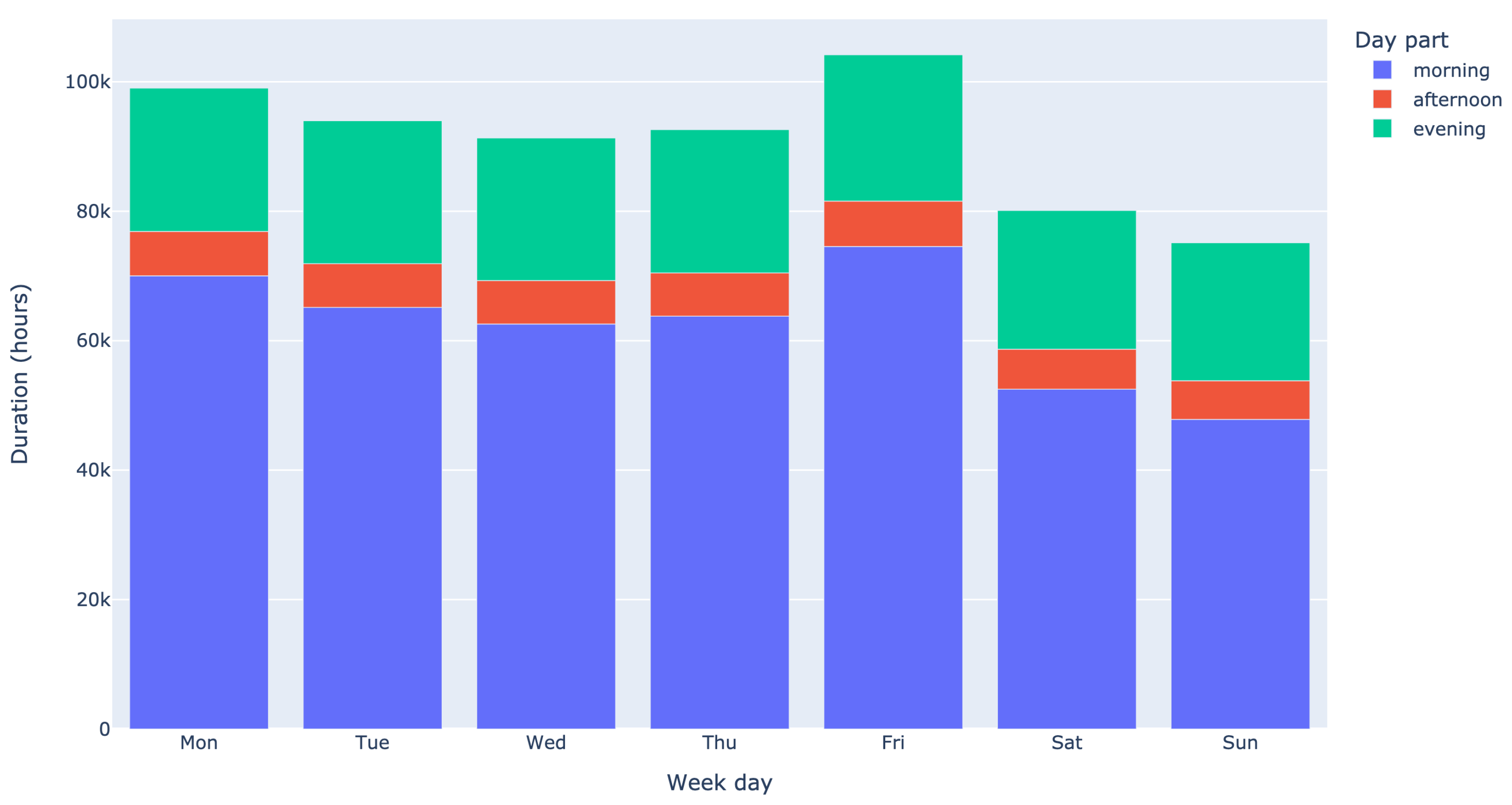
3.1.1. Volume of Care
3.1.2. Case Demand
3.1.3. Arrival Rate
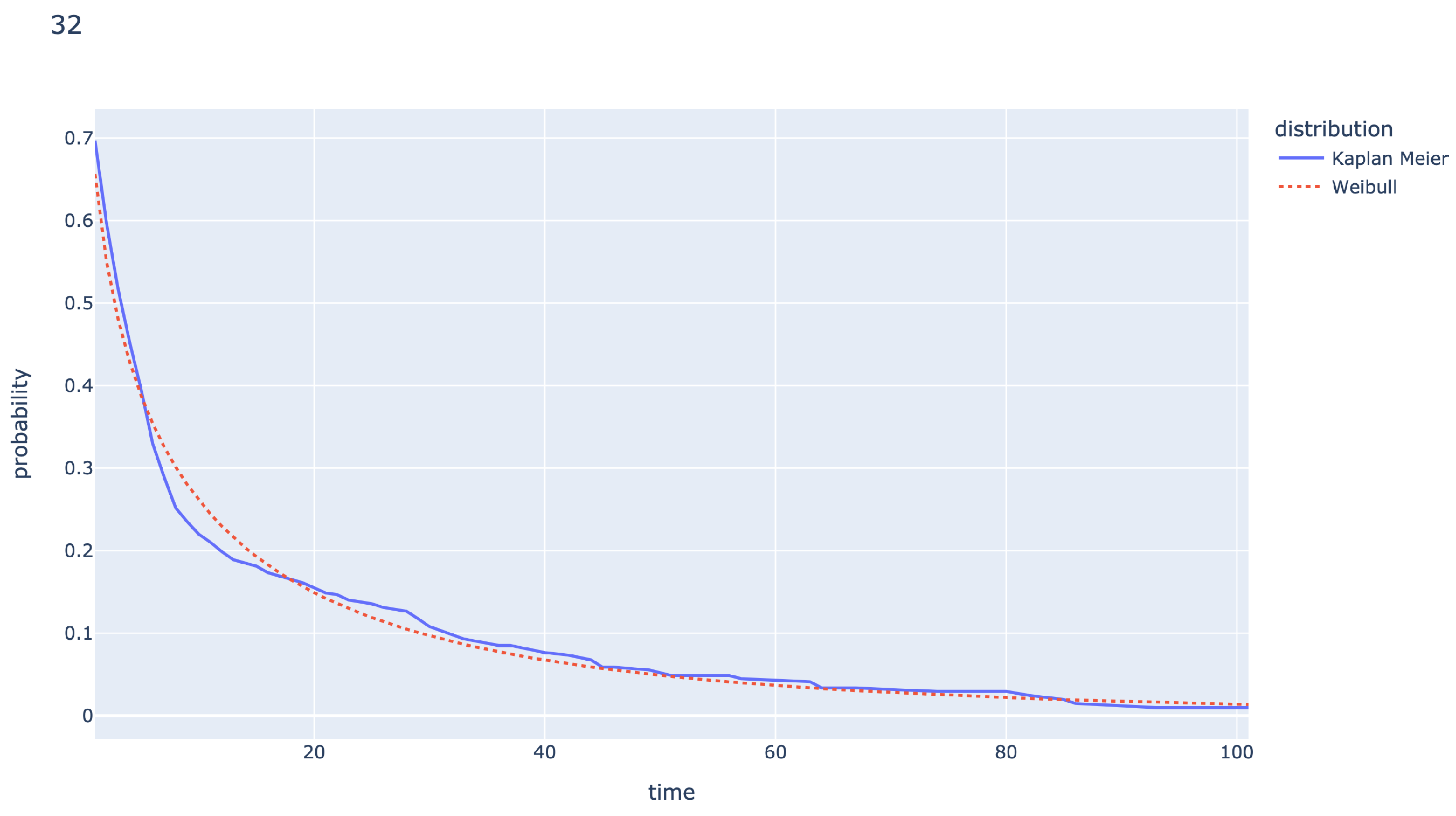
3.1.4. Length of Stay
3.2. Model-Based Principles
3.2.1. Modeling Care Demand and Required Capacity
Model
Application
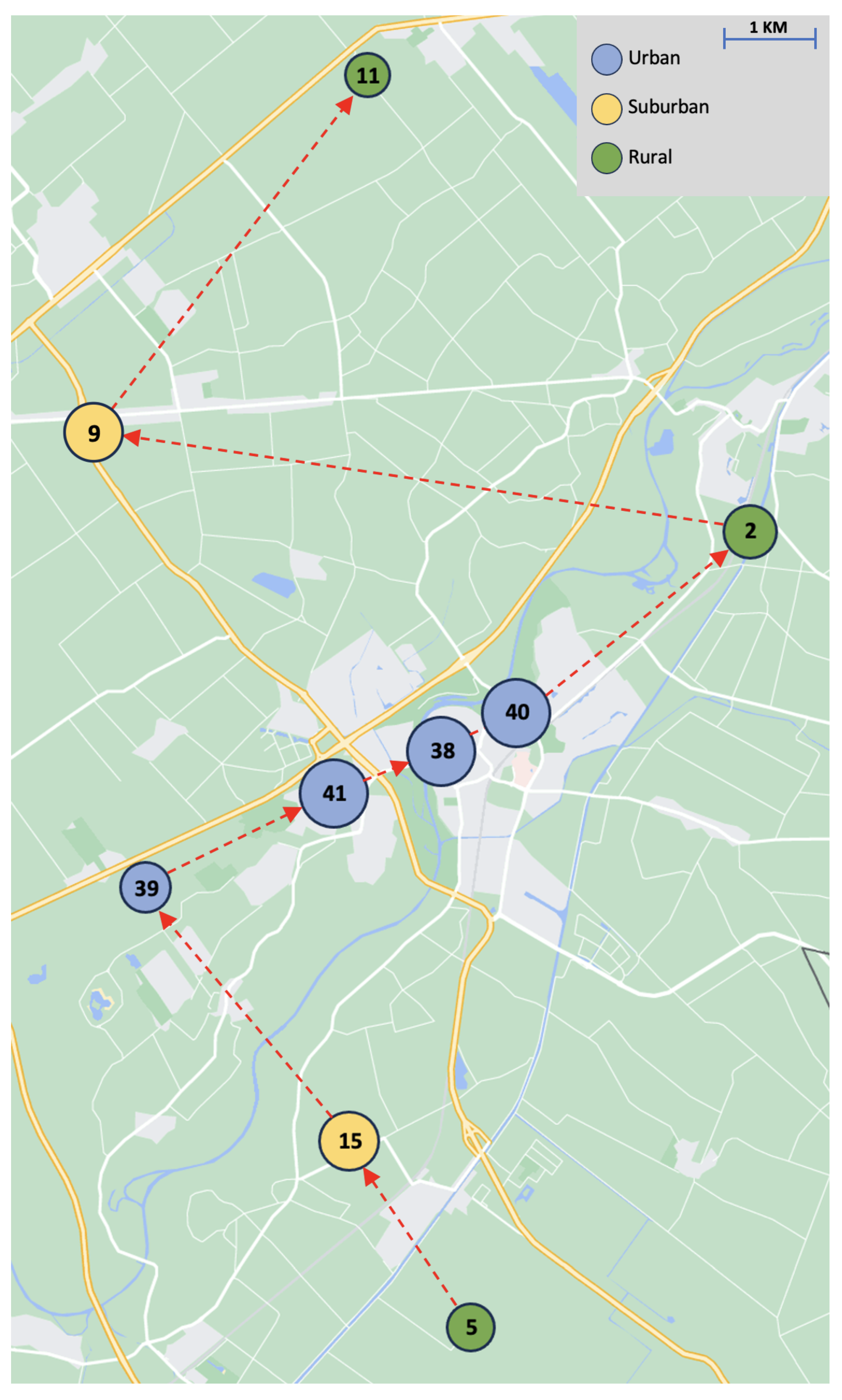
3.2.2. Modeling Travel Time
Model
Application
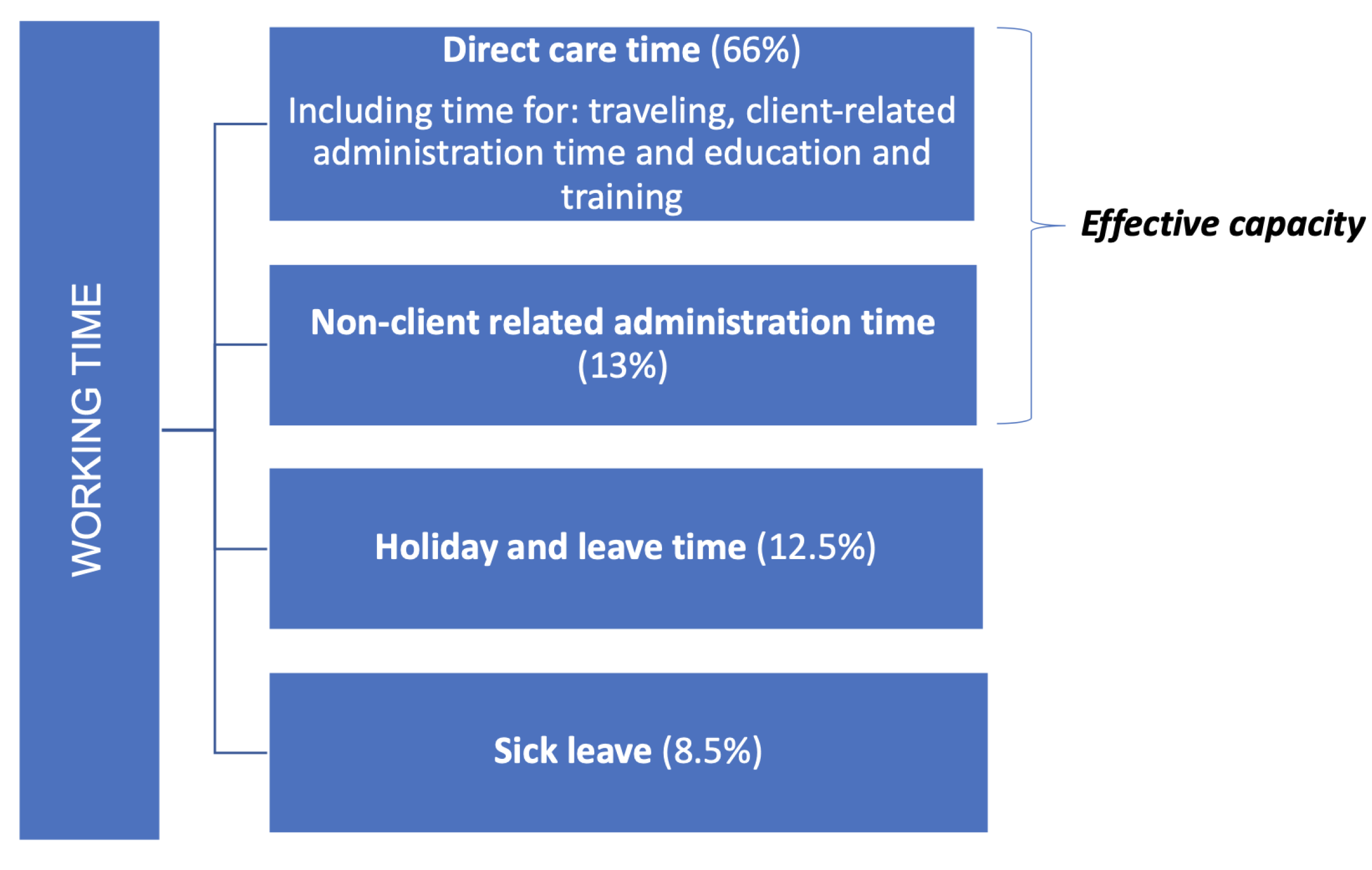
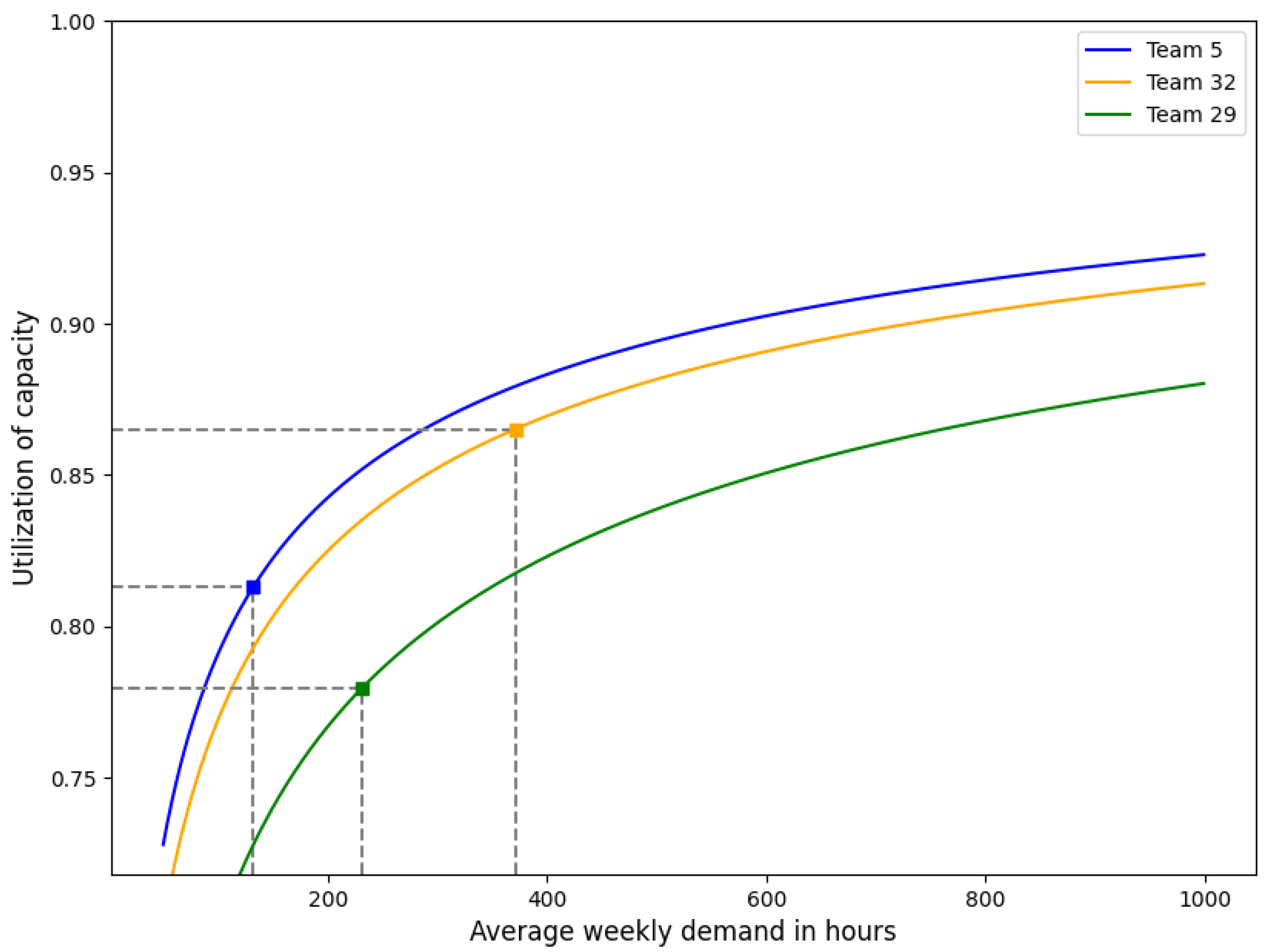
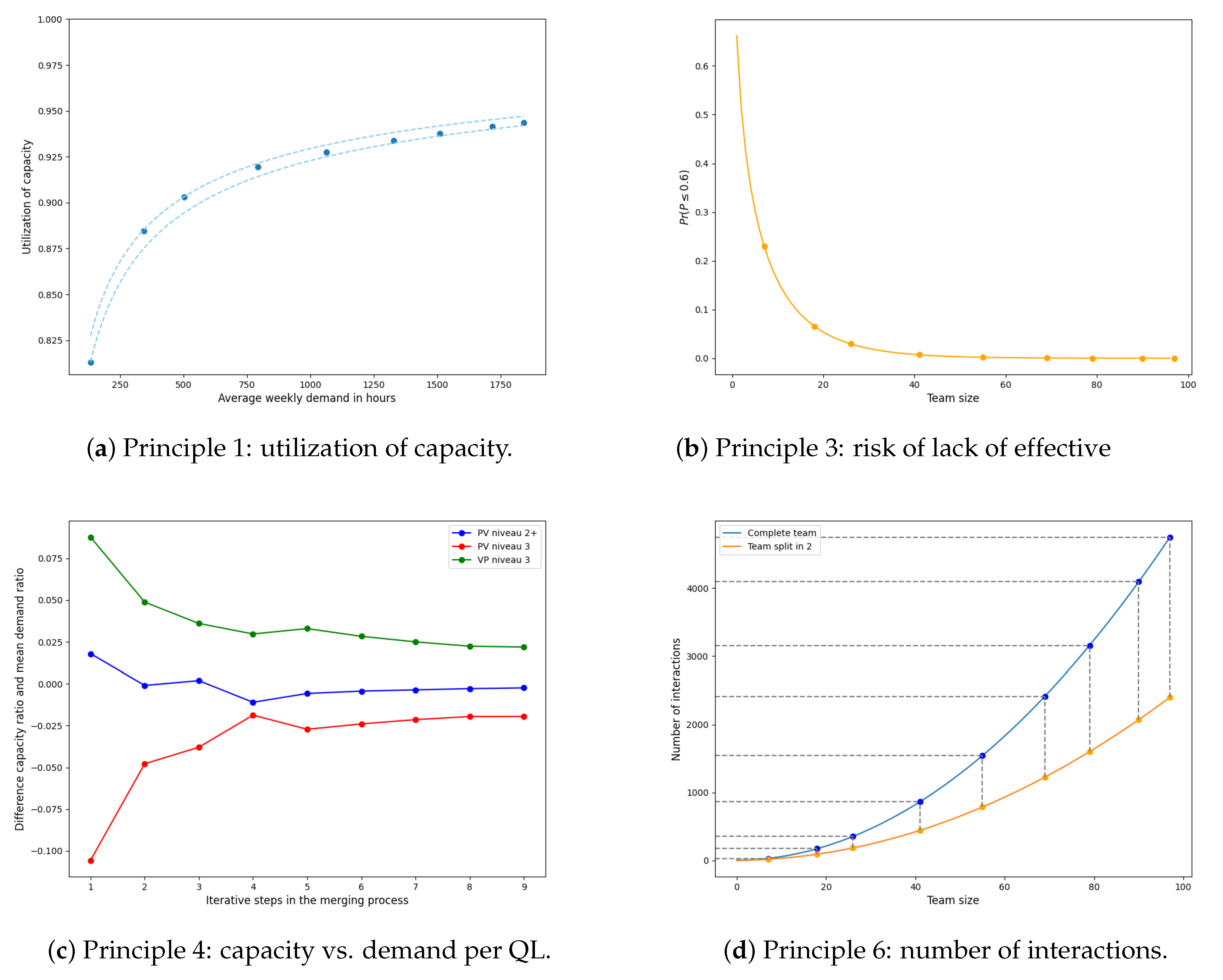
3.2.3. Modeling Effective Capacity
Model
Application
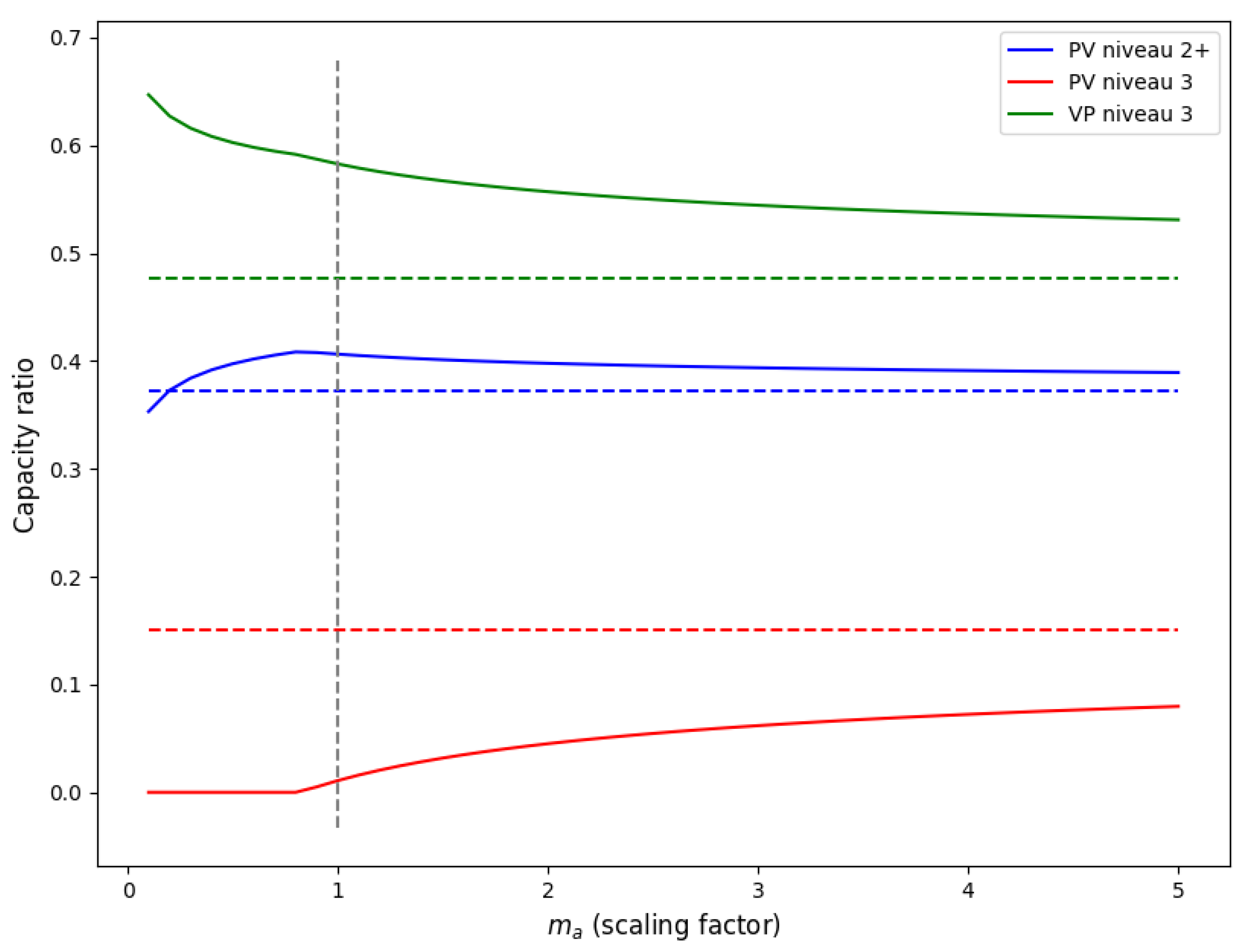
3.2.4. Modeling Required Capacity per Qualification Level
Model
Application
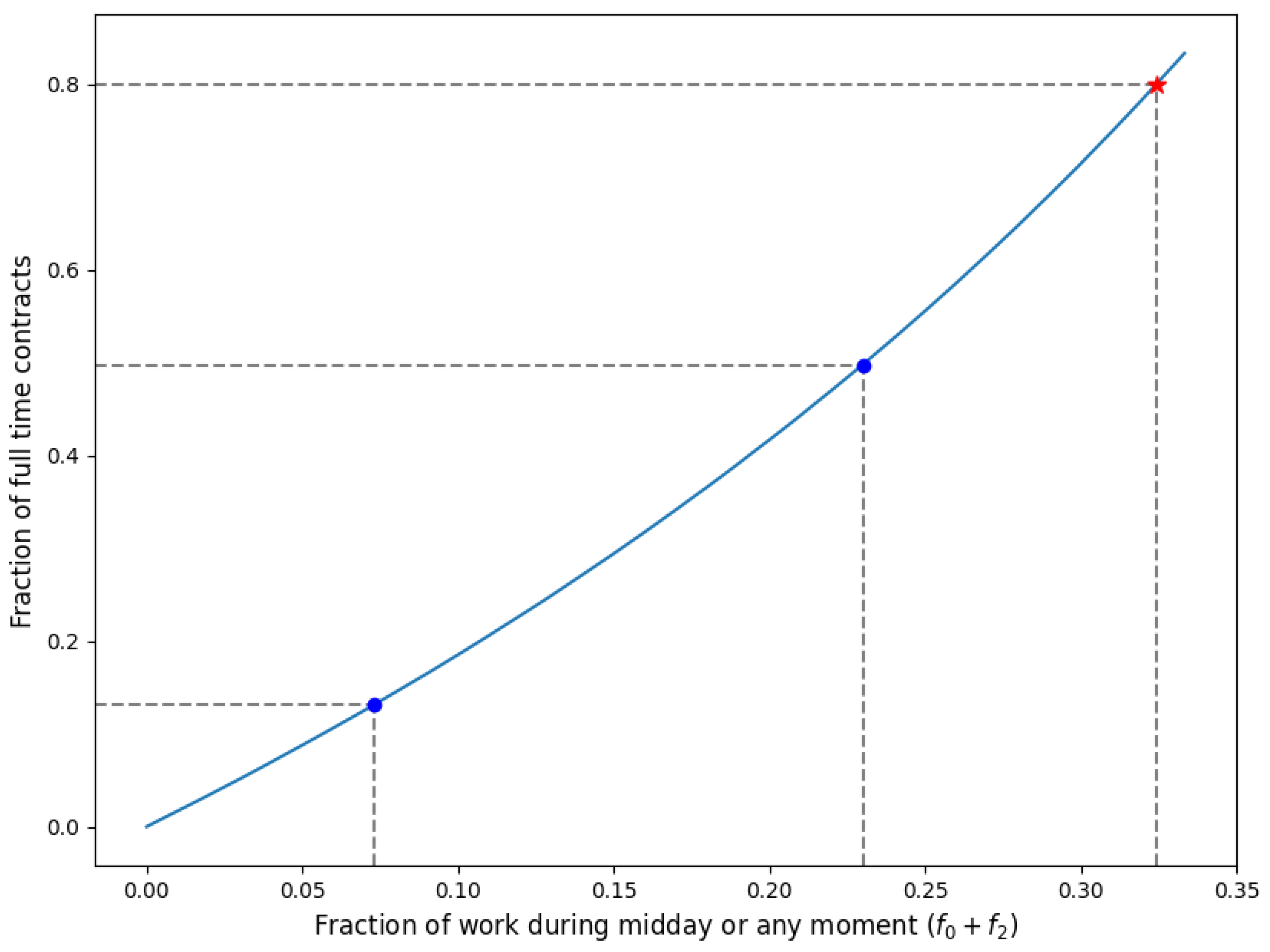
3.2.5. Modeling Required Contract Type
Model
Application
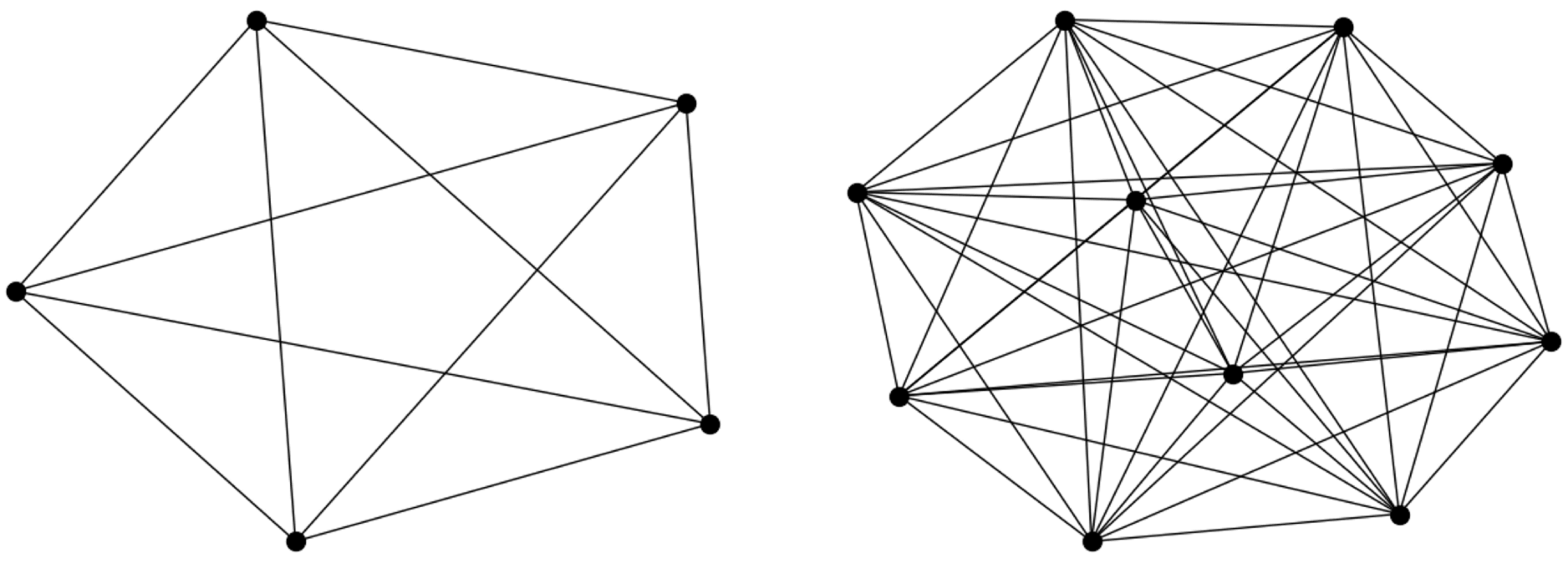
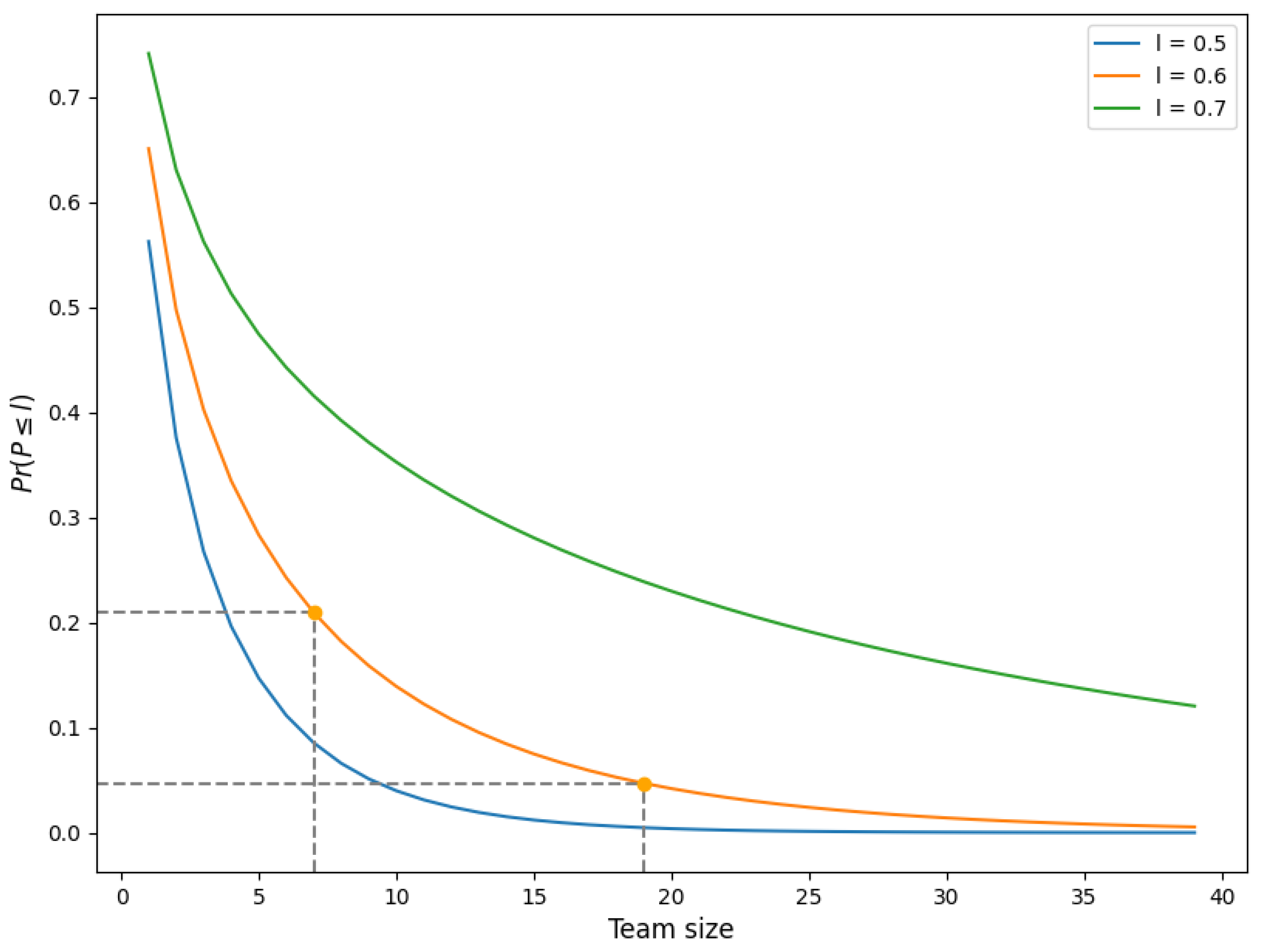
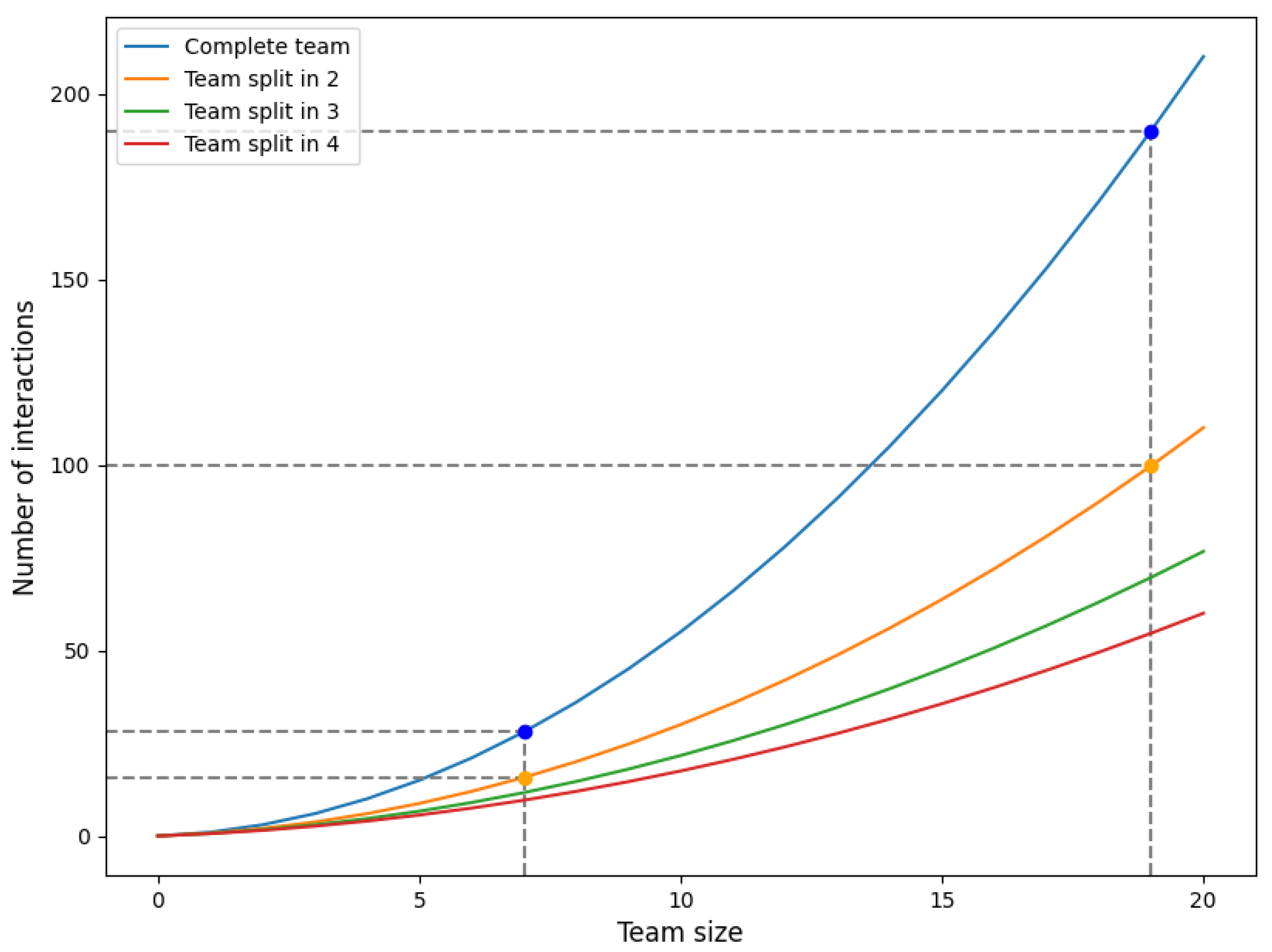
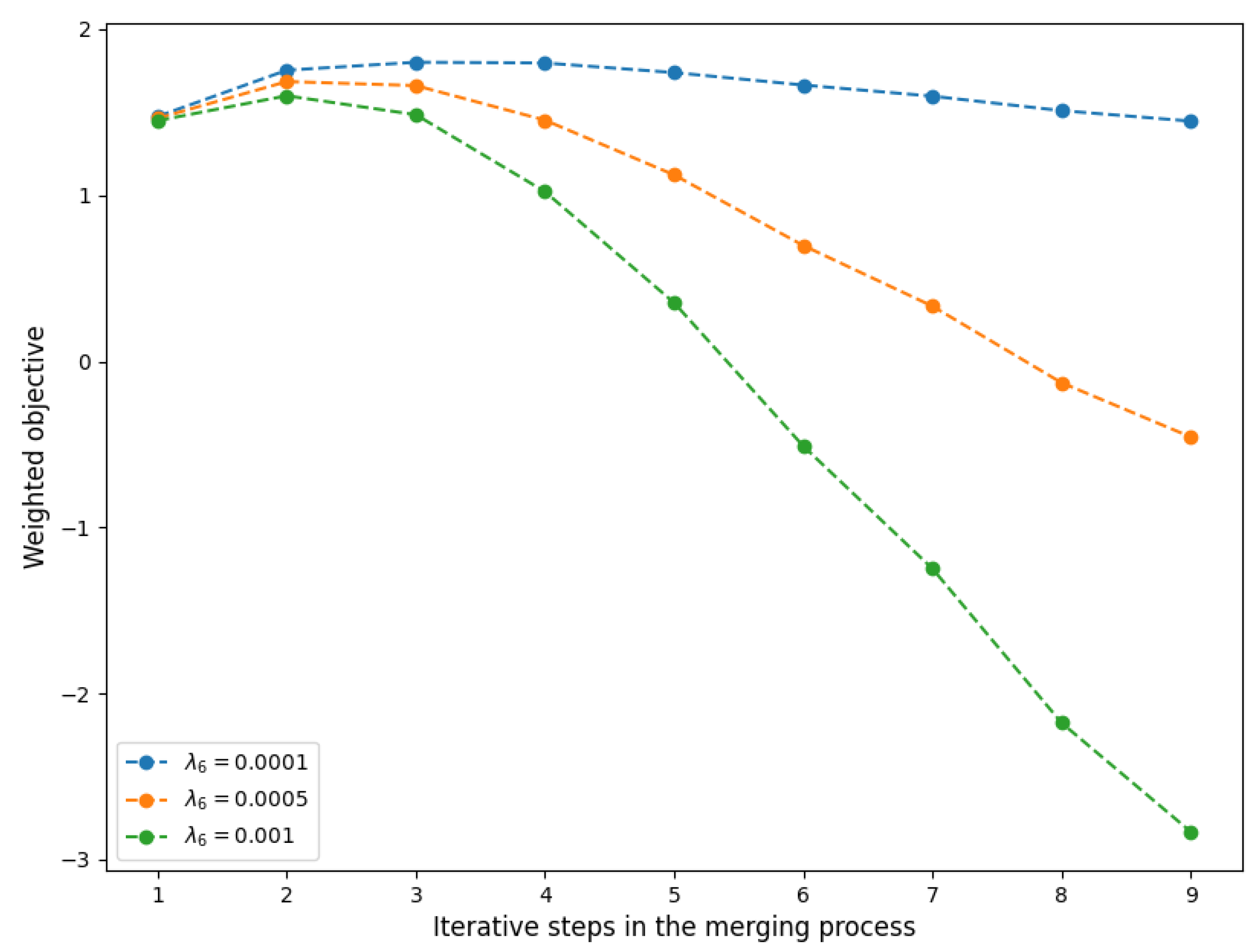
3.2.6. Modeling Complexity of Team Size
Model
Application
4. Practice Based Scenarios
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Knight, S.; Tjassing, H. Health care moves to the home. World Health 1994, 4, 413–444. [Google Scholar]
- CBS. 2021. Available online: https://www.cbs.nl/nl-nl/nieuws/2021/50/prognose-bevolkingsgroei-trekt-weer-aan (accessed on 3 September 2023).
- Meerding, W.J.; Bonneux, L.; Polder, J.J.; Koopmanschap, M.A.; van der Maas, P.J. Demographic and epidemiological determinants of healthcare costs in Netherlands: Cost of illness study. BMJ 1998, 317, 111–115. [Google Scholar] [CrossRef] [PubMed]
- VWS. 2023. Available online: https://www.prognosemodelzw.nl/binaries/prognosemodelzw/documenten/brieven/2023/03/21/nieuwe-arbeidsmarktprognose-zorg-en-welzijn/Nieuwe+arbeidsmarktprognose+zorg+en+welzijn.pdf (accessed on 2 September 2023).
- Vernet. 2023. Available online: https://zorgkrant.nl/arbeid-cao/16737-ziekte-verzuim-zorgsector-gestegen-naar-recordhoogte (accessed on 10 September 2023).
- Hulshof, P.J.; Kortbeek, N.; Boucherie, R.J.; Hans, E.W.; Bakker, P.J. Taxonomic classification of planning decisions in health care: A structured review of the state of the art in OR/MS. Health Syst. 2012, 1, 129–175. [Google Scholar] [CrossRef]
- Matta, A.; Chahed, S.; Sahin, E.; Dallery, Y. Modelling home care organisations from an operations management perspective. Flex. Serv. Manuf. J. 2014, 26, 295–319. [Google Scholar] [CrossRef]
- Grieco, L.; Utley, M.; Crowe, S. Operational research applied to decisions in home health care: A systematic literature review. J. Oper. Res. Soc. 2021, 72, 1960–1991. [Google Scholar] [CrossRef]
- Cissé, M.; Yalçındağ, S.; Kergosien, Y.; Şahin, E.; Lenté, C.; Matta, A. OR problems related to Home Health Care: A review of relevant routing and scheduling problems. Oper. Res. Health Care 2017, 13, 1–22. [Google Scholar] [CrossRef]
- Di Mascolo, M.; Martinez, C.; Espinouse, M.L. Routing and scheduling in home health care: A literature survey and bibliometric analysis. Comput. Ind. Eng. 2021, 158, 107255. [Google Scholar] [CrossRef]
- Fikar, C.; Hirsch, P. Home health care routing and scheduling: A review. Comput. Oper. Res. 2017, 77, 86–95. [Google Scholar] [CrossRef]
- Christensen, E.W. Scale and scope economies in nursing homes: A quantile regression approach. Health Econ. 2004, 13, 363–377. [Google Scholar] [CrossRef]
- Moeke, D.; van de Geer, R.; Koole, G.; Bekker, R. On the performance of small-scale living facilities in nursing homes: A simulation approach. Oper. Res. Health Care 2016, 11, 20–34. [Google Scholar] [CrossRef][Green Version]
- Ni Luasa, S.; Dineen, D.; Zieba, M. Technical and scale efficiency in public and private Irish nursing homes—A bootstrap DEA approach. Health Care Manag. Sci. 2018, 21, 326–347. [Google Scholar] [CrossRef] [PubMed]
- Benzarti, E.; Sahin, E.; Dallery, Y. Operations management applied to home care services: Analysis of the districting problem. Decis. Support Syst. 2013, 55, 587–598. [Google Scholar] [CrossRef]
- Ozturk, O.; Begen, M.A.; Zaric, G.S. Home Health Care Services Management: Districting Problem Revisited. In Proceedings of the Industrial Engineering in the Internet-of-Things World: Selected Papers from the Virtual Global Joint Conference on Industrial Engineering and Its Application Areas, GJCIE 2020, Online, 14–15 August 2020; Springer: Berlin/Heidelberg, Germany, 2022; pp. 407–421. [Google Scholar] [CrossRef]
- Moeke, D.; Koole, G.; Verkooijen, L. Scale and skill-mix efficiencies in nursing home staffing: Inside the black box. Health Syst. 2014, 3, 18–28. [Google Scholar] [CrossRef]
- van Eeden, K.; Moeke, D.; Bekker, R. Care on demand in nursing homes: A queueing theoretic approach. Health Care Manag. Sci. 2016, 19, 227–240. [Google Scholar] [CrossRef]
- Nikzad, E.; Bashiri, M.; Abbasi, B. A matheuristic algorithm for stochastic home health care planning. Eur. J. Oper. Res. 2021, 288, 753–774. [Google Scholar] [CrossRef]
- Restrepo, M.I.; Rousseau, L.M.; Vallée, J. Home healthcare integrated staffing and scheduling. Omega 2020, 95, 102057. [Google Scholar] [CrossRef]
- Rodriguez, C.; Garaix, T.; Xie, X.; Augusto, V. Staff dimensioning in homecare services with uncertain demands. Int. J. Prod. Res. 2015, 53, 7396–7410. [Google Scholar] [CrossRef]
- Koopmans, L.; Damen, N.; Wagner, C. Does diverse staff and skill mix of teams impact quality of care in long-term elderly health care? An exploratory case study. BMC Health Serv. Res. 2018, 18, 1–12. [Google Scholar] [CrossRef]
- Buchan, J.; Calman, L. Skill-Mix and Policy Change in the Health Workforce: Nurses in Advanced Roles; OECD Publishing: Paris, France, 2005. [Google Scholar] [CrossRef]
- Green, L.V. How many hospital beds? Inq. J. Health Care Organ. Provis. Financ. 2002, 39, 400–412. [Google Scholar] [CrossRef] [PubMed]
- Cattani, K.; Schmidt, G.M. The pooling principle. Informs Trans. Educ. 2005, 5, 17–24. [Google Scholar] [CrossRef]
- Joustra, P.; Van der Sluis, E.; Van Dijk, N.M. To pool or not to pool in hospitals: A theoretical and practical comparison for a radiotherapy outpatient department. Ann. Oper. Res. 2010, 178, 77–89. [Google Scholar] [CrossRef]
- van Dijk, N.M.; van der Sluis, E. To pool or not to pool in call centers. Prod. Oper. Manag. 2008, 17, 296–305. [Google Scholar] [CrossRef]
- Moeke, D.; Bekker, R. Capacity planning in healthcare: Finding solutions for healthy planning in nursing home care. In Integrating the Organization of Health Services, Worker Wellbeing and Quality of Care; Springer: Berlin/Heidelberg, Germany, 2020; pp. 171–195. [Google Scholar] [CrossRef]
- van Leeuwaarden, J.; Mathijsen, B.; Zwart, A. Economies-of-Scale in many-server queueing systems: Tutorial and partial review of the QED halfin–whitt heavy-traffic regime. SIAM Rev. 2019, 61, 403–440. [Google Scholar] [CrossRef]
- Whitt, W. Understanding the efficiency of multi-server service systems. Manag. Sci. 1992, 38, 708–723. [Google Scholar] [CrossRef]
- NZA. Available online: https://www.nza.nl/zorgsectoren/wijkverpleging/kerncijfers-wijkverpleging (accessed on 10 January 2023).
- Vektis. Available online: https://www.vektis.nl/intelligence/publicaties/factsheet-wijkverpleging-2022 (accessed on 10 January 2023).
- De Veer, A.; Groot, K.d.; Brinkman, M.; Francke, A. Administratieve Druk: Méér dan Kwestie van Tijd; NIVEL: The Netherlands, 2017; Available online: https://www.nivel.nl/sites/default/files/bestanden/factsheet_administratie_druk.pdf (accessed on 1 August 2023).
- FBZ. Available online: https://www.fbz.nl/caos/verpleeg-verzorgingshuizen-en-thuiszorg/ (accessed on 10 May 2023).
- Kasanen, E.; Lukka, K.; Siitonen, A. The constructive approach in management accounting research. J. Manag. Account. Res. 1993, 5. [Google Scholar]
- Bekker, R.; Koeleman, P. Scheduling admissions and reducing variability in bed demand. Health Care Manag. Sci. 2011, 14, 237–249. [Google Scholar] [CrossRef] [PubMed]
- Dorfman, R. A formula for the Gini coefficient. Rev. Econ. Stat. 1979, 146–149. [Google Scholar] [CrossRef]
- Tijms, H. A First Course in Stochastic Models; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Pang, G.; Whitt, W. Infinite-server queues with batch arrivals and dependent service times. Probab. Eng. Informational Sci. 2012, 26, 197–220. [Google Scholar] [CrossRef]
- Daw, A.; Pender, J. On the distributions of infinite server queues with batch arrivals. Queueing Syst. 2019, 91, 367–401. [Google Scholar] [CrossRef]
- Borovkov, A. On limit laws for service processes in multi-channel systems. Sib. Math. J. 1967, 8, 746–763. [Google Scholar] [CrossRef]
- Whitt, W. Heavy-Traffic Approximations for Service Systems With Blocking. AT&T Bell Lab. Tech. J. 1984, 63, 689–708. [Google Scholar] [CrossRef]
- Akkerman, F.; Mes, M. Distance approximation to support customer selection in vehicle routing problems. Ann. Oper. Res. 2022, 1–29. [Google Scholar] [CrossRef]
- Figliozzi, M. Planning approximations to the average length of vehicle routing problems with time window constraints. Transp. Res. Part Methodol. 2009, 43, 438–447. [Google Scholar] [CrossRef]
- Beardwood, J.; Halton, J.; Hammersley, J. The shortest path through many points. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1959; Volume 55, pp. 299–327. [Google Scholar] [CrossRef]
- Mei, X.; Curtin, K.; Turner, D.; Waters, N.; Rice, M. Approximating the Length of Vehicle Routing Problem Solutions Using Complementary Spatial Information. Geogr. Anal. 2022, 55, 125–154. [Google Scholar] [CrossRef]
- Hoegl, M. Smaller teams–better teamwork: How to keep project teams small. Bus. Horizons 2005, 48, 209–214. [Google Scholar] [CrossRef]
- Gallivan, S. Challenging the role of calibration, validation and sensitivity analysis in relation to models of health care processes. Health Care Manag. Sci. 2008, 11, 208–213. [Google Scholar] [CrossRef]
- Arabzadeh, B. Reconfiguration of Inpatient Services to Reduce Bed Pressure in Hospitals. Ph.D. Thesis, University of London, London, UK, 2022. [Google Scholar]
- Bekker, R.; Koole, G.; Roubos, D. Flexible bed allocations for hospital wards. Health Care Manag. Sci. 2017, 20, 453–466. [Google Scholar] [CrossRef]
- Best, T.J.; Sandıkçı, B.; Eisenstein, D.D.; Meltzer, D.O. Managing hospital inpatient bed capacity through partitioning care into focused wings. Manuf. Serv. Oper. Manag. 2015, 17, 157–176. [Google Scholar] [CrossRef]
- Izady, N.; Mohamed, I. A clustered overflow configuration of inpatient beds in hospitals. Manuf. Serv. Oper. Manag. 2021, 23, 139–154. [Google Scholar] [CrossRef]
- Koeleman, P.M.; Bhulai, S.; van Meersbergen, M. Optimal patient and personnel scheduling policies for care-at-home service facilities. Eur. J. Oper. Res. 2012, 219, 557–563. [Google Scholar] [CrossRef]
| Area Type | Teams | Planned Care (h/wk) | Clients | Clients/ |
|---|---|---|---|---|
| Urban | 26 | 238 (51) | 221 (51.4) | 71 (31.4) |
| Suburban | 18 | 224 (54) | 238 (61.3) | 11 (5.4) |
| Rural | 11 | 213 (46) | 176 (53.6) | 3 (1.1) |
| Qualification Level | Description | Type of Tasks | Proportion of Total Planned Care |
|---|---|---|---|
| 1 | PV niveau 2+ | Personal Care | 67% |
| 2 | PV niveau 3 | Personal Care | 9% |
| 3 | VP niveau 3 | Nursing | 24% |
| Area Type | Active Clients per Day | Total Distance (km) per Day | Travel per Client |
|---|---|---|---|
| Urban | 83 (18.6) | 10.0 (9.1) | 0.12 |
| Suburban | 76 (24.7) | 14.0 (7.2) | 0.18 |
| Rural | 69 (16.4) | 26.5 (6.0) | 0.39 |
| Team ID | Mean Demand | (Implied) | |||||
|---|---|---|---|---|---|---|---|
| 2 | 183.46 | 1.99 | 1.10 | 3.61 | 3.18 | 0.79 | 25.50 |
| 5 | 132.30 | 1.58 | 1.30 | 3.00 | 3.72 | 0.74 | 27.93 |
| 9 | 206.06 | 3.69 | 1.12 | 3.24 | 3.13 | 0.78 | 17.25 |
| 11 | 125.41 | 2.43 | 1.64 | 3.06 | 1.97 | 0.79 | 16.85 |
| 15 | 211.13 | 3.06 | 1.28 | 2.78 | 2.15 | 0.77 | 24.81 |
| 38 | 268.71 | 3.64 | 1.78 | 3.82 | 3.23 | 0.81 | 19.32 |
| 39 | 159.07 | 3.49 | 1.68 | 2.68 | 2.51 | 0.78 | 17.03 |
| 40 | 265.53 | 3.04 | 1.19 | 3.60 | 3.50 | 0.75 | 24.29 |
| 41 | 290.75 | 5.33 | 0.90 | 3.31 | 3.44 | 0.82 | 16.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clapper, Y.; ten Hove, W.; Bekker, R.; Moeke, D. Team Size and Composition in Home Healthcare: Quantitative Insights and Six Model-Based Principles. Healthcare 2023, 11, 2935. https://doi.org/10.3390/healthcare11222935
Clapper Y, ten Hove W, Bekker R, Moeke D. Team Size and Composition in Home Healthcare: Quantitative Insights and Six Model-Based Principles. Healthcare. 2023; 11(22):2935. https://doi.org/10.3390/healthcare11222935
Chicago/Turabian StyleClapper, Yoram, Witek ten Hove, René Bekker, and Dennis Moeke. 2023. "Team Size and Composition in Home Healthcare: Quantitative Insights and Six Model-Based Principles" Healthcare 11, no. 22: 2935. https://doi.org/10.3390/healthcare11222935
APA StyleClapper, Y., ten Hove, W., Bekker, R., & Moeke, D. (2023). Team Size and Composition in Home Healthcare: Quantitative Insights and Six Model-Based Principles. Healthcare, 11(22), 2935. https://doi.org/10.3390/healthcare11222935






