Upholding or Breaking the Law of Superposition in Pharmacokinetics
Abstract
1. Introduction
Law of Superposition
2. Modeling a Hypothetical Drug “Canadamycin”
2.1. Pharmacokinetics after a Single Intravenous Dose
2.2. Pharmacokinetics after Multiple Intravenous Dosing
2.3. Pharmacokinetics after Multiple Oral Dosing
3. Breaking the Law of Superposition
- The dosing is in a range where the pharmacokinetics are linear and dose proportional;
- The rate and extent of absorption and average clearance are the same for each dosing interval;
- Each dose acts independently from one another, and the sum of all these dosing events provides the total concentration of the drug in circulation.
3.1. Less than Proportional Increase in AUC (AUCSS < AUCSingle Dose)
3.2. More than Proportional Increase in AUC (AUCSS > AUCSingle Dose)
3.3. Other Factors Affecting Adherence to the Law of Superposition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garza, I.; Swanson, J.W. Prophylaxis of migraine. Neuropsychiatr. Dis. Treat. 2006, 2, 281–291. [Google Scholar] [CrossRef] [PubMed]
- Ong, J.J.Y.; De Felice, M. Migraine Treatment: Current Acute Medications and Their Potential Mechanisms of Action. Neurotherapeutics 2018, 15, 274–290. [Google Scholar] [CrossRef] [PubMed]
- Diener, H.-C.; Holle-Lee, D.; Nägel, S.; Dresler, T.; Gaul, C.; Göbel, H.; Heinze-Kuhn, K.; Jürgens, T.; Kropp, P.; Meyer, B.; et al. Treatment of migraine attacks and prevention of migraine: Guidelines by the German Migraine and Headache Society and the German Society of Neurology. Clin. Transl. Neurosci. 2019, 3, 3. [Google Scholar] [CrossRef]
- Do, T.P.; Guo, S.; Ashina, M. Therapeutic novelties in migraine: New drugs, new hope? J. Headache Pain 2019, 20, 37. [Google Scholar] [CrossRef] [PubMed]
- Borbély, A.A.; Mattmann, P.; Loepfe, M.; Fellmann, I.; Gerne, M.; Strauch, I.; Lehmann, D. A single dose of benzodiazepine hypnotics alters the sleep EEG in the subsequent drug-free night. Eur. J. Pharmacol. 1983, 89, 157–161. [Google Scholar] [CrossRef]
- Johnson, L.C.; Chernik, D.A. Sedative-hypnotics and human performance. Psychopharmacology 1982, 76, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Malpas, A.; Rowan, A.J.; Boyce, C.R.; Scott, D.F. Persistent behavioural and electroencephalographic changes after single doses of nitrazepam and amylobarbitone sodium. Br. Med. J. 1970, 2, 762–764. [Google Scholar] [CrossRef][Green Version]
- Kornetsky, C.; Vates, T.S.; Kessler, E.K. A comparison of hypnotic and residual psychological effects of single doses of chlorpromazine and secobarbital in man. J. Pharmacol. Exp. Ther. 1959, 127, 51–54. [Google Scholar] [CrossRef]
- Eckburg, P.B.; Jain, A.; Walpole, S.; Moore, G.; Utley, L.; Manyak, E.; Dane, A.; Melnick, D. Safety, Pharmacokinetics, and Food Effect of Tebipenem Pivoxil Hydrobromide after Single and Multiple Ascending Oral Doses in Healthy Adult Subjects. Antimicrob. Agents Chemother. 2019, 63, e00618-19. [Google Scholar] [CrossRef]
- Chua, H.C.; Tse, A.; Smith, N.M.; Mergenhagen, K.A.; Cha, R.; Tsuji, B.T. Combatting the Rising Tide of Antimicrobial Resistance: Pharmacokinetic/Pharmacodynamic Dosing Strategies for Maximal Precision. Int. J. Antimicrob. Agents 2021, 57, 106269. [Google Scholar] [CrossRef]
- Xie, J.; Roberts, J.A.; Lipman, J.; Cai, Y.; Wang, H.; Zhao, N.; Xu, X.; Yang, S.; Li, Y.; Zhang, K. Pharmacokinetic/pharmacodynamic adequacy of polymyxin B against extensively drug-resistant Gram-negative bacteria in critically ill, general ward and cystic fibrosis patient populations. Int. J. Antimicrob. Agents 2020, 55, 105943. [Google Scholar] [CrossRef] [PubMed]
- Bunke, C.M.; Aronoff, G.R.; Luft, F.C. Pharmacokinetics of common antibiotics used in continuous ambulatory peritoneal dialysis. Am. J. Kidney Dis. 1983, 3, 114–117. [Google Scholar] [CrossRef] [PubMed]
- Kang, W.Y.; Lee, H.W.; Gwon, M.R.; Cho, S.; Shim, W.S.; Lee, K.T.; Yang, D.H.; Seong, S.J.; Yoon, Y.R. A Pharmacokinetic Drug Interaction Between Fimasartan and Linagliptin in Healthy Volunteers. Drug Des. Dev. Ther. 2020, 14, 2101–2111. [Google Scholar] [CrossRef] [PubMed]
- Moon, S.J.; Yu, K.S.; Kim, M.G. An Assessment of Pharmacokinetic Interaction Between Lobeglitazone and Sitagliptin After Multiple Oral Administrations in Healthy Men. Clin. Ther. 2020, 42, 1047–1057. [Google Scholar] [CrossRef] [PubMed]
- Ghim, J.L.; Phuong, N.T.T.; Kim, M.J.; Kim, E.J.; Song, G.S.; Ahn, S.; Shin, J.G.; Kim, E.Y. Pharmacokinetics of fixed-dose combination of atorvastatin and metformin compared with individual tablets. Drug Des. Dev. Ther. 2019, 13, 1623–1632. [Google Scholar] [CrossRef] [PubMed]
- Sheng, L.; Cao, W.; Lin, P.; Chen, W.; Xu, H.; Zhong, C.; Yuan, F.; Chen, H.; Li, H.; Liu, C.; et al. Safety, Tolerability and Pharmacokinetics of Single and Multiple Ascending Doses of Benfotiamine in Healthy Subjects. Drug Des. Dev. Ther. 2021, 15, 1101–1110. [Google Scholar] [CrossRef]
- Kim, J.R.; Kim, S.; Huh, W.; Ko, J.W. No pharmacokinetic interactions between candesartan and amlodipine following multiple oral administrations in healthy subjects. Drug Des. Dev. Ther. 2018, 12, 2475–2483. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Jarugula, V.; Dieterich, H.A.; Howard, D.; Dole, W.P. Clinical pharmacokinetics and pharmacodynamics of aliskiren. Clin. Pharmacokinet. 2008, 47, 515–531. [Google Scholar] [CrossRef]
- Wang, W.; Husan, F.; Chow, S.C. The impact of patient compliance on drug concentration profile in multiple doses. Stat. Med. 1996, 15, 659–669. [Google Scholar] [CrossRef]
- Wang, W. Patient Compliance and its Impact on Steady State Pharmacokinetics. In Applied Statistics in the Pharmaceutical Industry: with Case Studies Using S-Plus, 1st ed.; Millard, S.P., Krause, A., Eds.; Springer: New York, NY, USA, 2001; pp. 217–236. [Google Scholar] [CrossRef]
- van Rossum, J.M. Pharmacokinetics of accumulation. J. Pharm. Sci. 1968, 57, 2162–2165. [Google Scholar] [CrossRef]
- Wang, W.; Ouyang, S.P. The formulation of the principle of superposition in the presence of non-compliance and its applications in multiple dose pharmacokinetics. J. Pharmacokinet. Biopharm. 1998, 26, 457–469. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.H. Dose-dependent pharmacokinetics: Experimental observations and theoretical considerations. Biopharm. Drug Dispos. 1994, 15, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Cutler, D.J. Numerical deconvolution by least squares: Use of prescribed input functions. J. Pharmacokinet. Biopharm. 1978, 6, 227–241. [Google Scholar] [CrossRef] [PubMed]
- Cutler, D.J. Numerical deconvolution by least squares: Use of polynomials to represent the input function. J. Pharmacokinet. Biopharm. 1978, 6, 243–263. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Campos, F.; Ferrero, C.; Colom, H.; Jiménez-Castellanos, M.R. In vivo absorption behaviour of theophylline from starch-methyl methacrylate matrix tablets in beagle dogs. Int. J. Pharm. 2015, 478, 684–692. [Google Scholar] [CrossRef] [PubMed]
- Chiou, W.L. Rapid compartment- and model-independent estimation of times required to attain various fractions of steady-state plasma level during multiple dosing of drugs obeying superposition principle and having various absorption or infusion kinetics. J. Pharm. Sci. 1979, 68, 1546–1547. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Hutmacher, M.M.; Frame, B.; Miller, R. An alternative method for population pharmacokinetic data analysis under noncompliance. J. Pharmacokinet. Pharmacodyn. 2008, 35, 219–233. [Google Scholar] [CrossRef] [PubMed]
- Ma, L. Analysis of Nonlinear Pharmacokinetic Systems and the Nonlinear Disposition of Phenylbutazone in Equine (Horses). Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 13 June 2013. [Google Scholar]
- McCoy, A.T.; Bartels, M.J.; Rick, D.L.; Saghir, S.A. TK Modeler version 1.0, a Microsoft® Excel®-based modeling software for the prediction of diurnal blood/plasma concentration for toxicokinetic use. Regul. Toxicol. Pharmacol. 2012, 63, 333–343. [Google Scholar] [CrossRef]
- Mengozzi, G.; Intorre, L.; Bertini, S.; Giorgi, M.; Soldani, G. Comparative bioavailability of two sustained-release theophylline formulations in the dog. Pharmacol. Res. 1998, 38, 481–485. [Google Scholar] [CrossRef]
- Thron, C.D. Linearity and superposition in pharmacokinetics. Pharmacol. Rev. 1974, 26, 3–31. [Google Scholar]
- Tuntland, T.; Ethell, B.; Kosaka, T.; Blasco, F.; Zang, R.X.; Jain, M.; Gould, T.; Hoffmaster, K. Implementation of pharmacokinetic and pharmacodynamic strategies in early research phases of drug discovery and development at Novartis Institute of Biomedical Research. Front. Pharmacol. 2014, 5, 174. [Google Scholar] [CrossRef]
- van Rossum, J.M.; de Bie, J.E. Systems dynamics in clinical pharmacokinetics. An introduction. Clin. Pharmacokinet. 1989, 17, 27–44. [Google Scholar] [CrossRef]
- Peletier, L.A.; de Winter, W. Impact of saturable distribution in compartmental PK models: Dynamics and practical use. J. Pharmacokinet. Pharmacodyn. 2017, 44, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Gabrielsson, J.; Meibohm, B.; Weiner, D. Pattern Recognition in Pharmacokinetic Data Analysis. AAPS J. 2016, 18, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Mehrotra, N.; Gupta, M.; Kovar, A.; Meibohm, B. The role of pharmacokinetics and pharmacodynamics in phosphodiesterase-5 inhibitor therapy. Int. J. Impot. Res. 2007, 19, 253–264. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Boeckmann, A.; Vick, A. Implementation of dose superimposition to introduce multiple doses for a mathematical absorption model (transit compartment model). J. Pharmacokinet. Pharmacodyn. 2012, 39, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Siwale, R.C.; Sani, S.N. Multiple-Dosage Regimens. In Applied Biopharmaceutics & Pharmacokinetics, 8th ed.; Ducharme, M.P., Shargel, L., Eds.; McGraw Hill Education: New York, NY, USA, 2022. [Google Scholar]
- Mehvar, R. Dependence of time to reach steady-state on the length of dosage interval. Ann. Pharmacother. 2008, 42, 1518–1519. [Google Scholar] [CrossRef]
- Hieb, B.R.; Shrewsbury, B. Consecutive intravenous infusions: Simulation of two compartment pharmacokinetic drugs. Comput. Programs Biomed. 1980, 12, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Brocks, D.R.; Mehvar, R. Rate and extent of drug accumulation after multiple dosing revisited. Clin. Pharmacokinet. 2010, 49, 421–438. [Google Scholar] [CrossRef]
- van Rossum, J.M.; van Lingen, G.; Burgers, J.P.T. Dose-dependent pharmacokinetics. Pharmacol. Ther. 1983, 21, 77–99. [Google Scholar] [CrossRef]
- Nation, R.L.; Evans, A.M.; Milne, R.W. Pharmacokinetic drug interactions with phenytoin (Part I). Clin. Pharmacokinet. 1990, 18, 37–60. [Google Scholar] [CrossRef]
- Yáñez, J.A.; Remsberg, C.M.; Sayre, C.L.; Forrest, M.L.; Davies, N.M. Flip-flop pharmacokinetics–delivering a reversal of disposition: Challenges and opportunities during drug development. Ther. Deliv. 2011, 2, 643–672. [Google Scholar] [CrossRef]
- Stewart, B.H.; Kugler, A.R.; Thompson, P.R.; Bockbrader, H.N. A saturable transport mechanism in the intestinal absorption of gabapentin is the underlying cause of the lack of proportionality between increasing dose and drug levels in plasma. Pharm. Res. 1993, 10, 276–281. [Google Scholar] [CrossRef]
- Proctor, W.R.; Bourdet, D.L.; Thakker, D.R. Mechanisms underlying saturable intestinal absorption of metformin. Drug Metab. Dispos. 2008, 36, 1650–1658. [Google Scholar] [CrossRef]
- Hanada, K.; Ikemi, Y.; Kukita, K.; Mihara, K.; Ogata, H. Stereoselective first-pass metabolism of verapamil in the small intestine and liver in rats. Drug Metab. Dispos. 2008, 36, 2037–2042. [Google Scholar] [CrossRef]
- Kalam, M.N.; Rasool, M.F.; Rehman, A.U.; Ahmed, N. Clinical pharmacokinetics of propranolol hydrochloride: A review. Curr. Drug Metab. 2020, 21, 89–105. [Google Scholar] [CrossRef]
- Karlsson, M.O.; Molnar, V.; Freijs, A.; Nygren, P.; Bergh, J.; Larsson, R. Pharmacokinetic models for the saturable distribution of paclitaxel. Drug Metab. Dispos. 1999, 27, 1220–1223. [Google Scholar]
- Eling, T.E.; Pickett, R.D.; Orton, T.C.; Anderson, M.W. A study of the dynamics of imipramine accumulation in the isolated perfused rabbit lung. Drug Metab. Dispos. 1975, 3, 389–399. [Google Scholar]
- Ha, H.R.; Chen, J.; Freiburghaus, A.U.; Follath, F. Metabolism of theophylline by cDNA-expressed human cytochromes P-450. Br. J. Clin. Pharmacol. 1995, 39, 321–326. [Google Scholar] [CrossRef]
- Bernus, I.; Dickinson, R.G.; Hooper, W.D.; Eadie, M.J. Dose-dependent metabolism of carbamazepine in humans. Epilepsy Res. 1996, 24, 163–172. [Google Scholar] [CrossRef]
- Patel, B.A.; Chu, C.K.; Boudinot, F.D. Pharmacokinetics and saturable renal tubular secretion of zidovudine in rats. J. Pharm. Sci. 1989, 78, 530–534. [Google Scholar] [CrossRef] [PubMed]
- Hendel, J.; Nyfors, A. Nonlinear renal elimination kinetics of methotrexate due to saturation of renal tubular reabsorption. Eur. J. Clin. Pharmacol. 1984, 26, 121–124. [Google Scholar] [CrossRef] [PubMed]
- Babu, E.; Takeda, M.; Narikawa, S.; Kobayashi, Y.; Yamamoto, T.; Cha, S.H.; Sekine, T.; Sakthisekaran, D.; Endou, H. Human organic anion transporters mediate the transport of tetracycline. Jpn. J. Pharmacol. 2002, 88, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Hornecker, M.; Blanchet, B.; Billemont, B.; Sassi, H.; Ropert, S.; Taieb, F.; Mir, O.; Abbas, H.; Harcouet, L.; Coriat, R.; et al. Saturable absorption of sorafenib in patients with solid tumors: A population model. Investig. New Drug. 2012, 30, 1991–2000. [Google Scholar] [CrossRef] [PubMed]
- Graham, R.A.; Hop, C.E.C.A.; Borin, M.T.; Lum, B.L.; Colburn, D.; Chang, I.; Shin, Y.G.; Malhi, V.; Low, J.A.; Dresser, M.J. Single and multiple dose intravenous and oral pharmacokinetics of the hedgehog pathway inhibitor vismodegib in healthy female subjects. Br. J. Clin. Pharmacol. 2012, 74, 788–796. [Google Scholar] [CrossRef]
- Yoon, Y.-R.; Shin, J.-G.; Cha, I.-J.; Kim, K.-A.; Shim, J.-C.; Kim, Y.-H.; Shin, J.-B. Pharmacokinetic analysis on autoinduction of carbamazepine metabolism. J. Korean Soc. Clin. Pharmacol. Ther. 1996, 4, 139–147. [Google Scholar] [CrossRef]
- Chetty, M.; Miller, R.; Seymour, M.A. Phenytoin auto-induction. Ther. Drug Monit. 1998, 20, 60–62. [Google Scholar] [CrossRef]
- Shand, D.G.; Hammill, S.C.; Aanonsen, L.; Pritchett, E.L.C. Reduced verapamil clearance during long-term oral administration. Clin. Pharmacol. Ther. 1981, 30, 701–703. [Google Scholar] [CrossRef]
- Abernethy, D.R.; Wainer, I.W.; Anacleto, A.I. Verapamil metabolite exposure in older and younger men during steady-state oral verapamil administration. Drug Met. Dispos. 2000, 28, 760–765. [Google Scholar]
- Lalonde, R.L.; Pieper, J.A.; Straka, R.J.; Bottorff, M.B.; Mirvis, D.M. Propranolol pharmacokinetics and pharmacodynamics after single doses and at steady-state. Eur. J. Clin. Pharmacol. 1987, 33, 315–318. [Google Scholar] [CrossRef]
- Barone, J.A.; Koh, J.G.; Bierman, R.H.; Colaizzi, J.L.; Swanson, K.A.; Gaffar, M.C.; Moskovitz, B.L.; Mechlinski, W.; Van de Velde, V. Food interaction and steady-state pharmacokinetics of itraconazole capsules in healthy male volunteers. Antimicrob. Agents Chemother. 1993, 37, 778–784. [Google Scholar] [CrossRef]
- Vrijens, B.; Goetghebeur, E. The impact of compliance in pharmacokinetic studies. Stat. Methods Med. Res. 1999, 8, 247–262. [Google Scholar] [CrossRef]
- Martinez, M.N.; Amidon, G.L. A mechanistic approach to understanding the factors affecting drug absorption: A review of fundamentals. J. Clin. Pharmacol. 2002, 42, 620–643. [Google Scholar] [CrossRef]
- Singh, B.N. Effects of food on clinical pharmacokinetics. Clin. Pharmacokinet. 1999, 37, 213–255. [Google Scholar] [CrossRef]
- Gershkovich, P.; Hoffman, A. Effect of a high-fat meal on absorption and disposition of lipophilic compounds: The importance of degree of association with triglyceride-rich lipoproteins. Eur. J. Pharm. Sci. 2007, 32, 24–32. [Google Scholar] [CrossRef]
- Yousef, M.; Silva, D.; Bou-Chacra, N.; Davies, N.M.; Löbenberg, R. The lymphatic system: A sometimes forgotten compartment in pharmaceutical sciences. J. Pharm. Pharm. Sci. 2021, 24, 533–547. [Google Scholar] [CrossRef]
- König, J.; Müller, F.; Fromm, M.F. Transporters and drug-drug interactions: Important determinants of drug disposition and effects. Pharmacol. Rev. 2013, 65, 944–966. [Google Scholar] [CrossRef]
- Tornio, A.; Filppula, A.M.; Niemi, M.; Backman, J.T. Clinical studies on drug–drug interactions involving metabolism and transport: Methodology, pitfalls, and interpretation. Clin. Pharmacol. Ther. 2019, 105, 1345–1361. [Google Scholar] [CrossRef]
- Hall, S.D.; Thummel, K.E.; Watkins, P.B.; Lown, K.S.; Benet, L.Z.; Paine, M.F.; Mayo, R.R.; Turgeon, D.K.; Bailey, D.G.; Fontana, R.J.; et al. Molecular and physical mechanisms of first-pass extraction. Drug Met. Dispos. 1999, 27, 161–166. [Google Scholar]
- Bachmann, K. Drug–drug interactions with an emphasis on drug metabolism and transport. In Pharmacology Principles and Practice, Hacker, M., Messer, W., Bachmann, K., Eds.; Academic Press: Cambridge, MA, USA, 2009; pp. 303–325. [Google Scholar] [CrossRef]
- DeVane, C.L. Clinical significance of drug binding, protein binding, and binding displacement drug interactions. Psychopharmacol. Bull. 2002, 36, 5–21. [Google Scholar]
- Heuberger, J.; Schmidt, S.; Derendorf, H. When is protein binding important? J. Pharm. Sci. 2013, 102, 458–3467. [Google Scholar] [CrossRef] [PubMed]



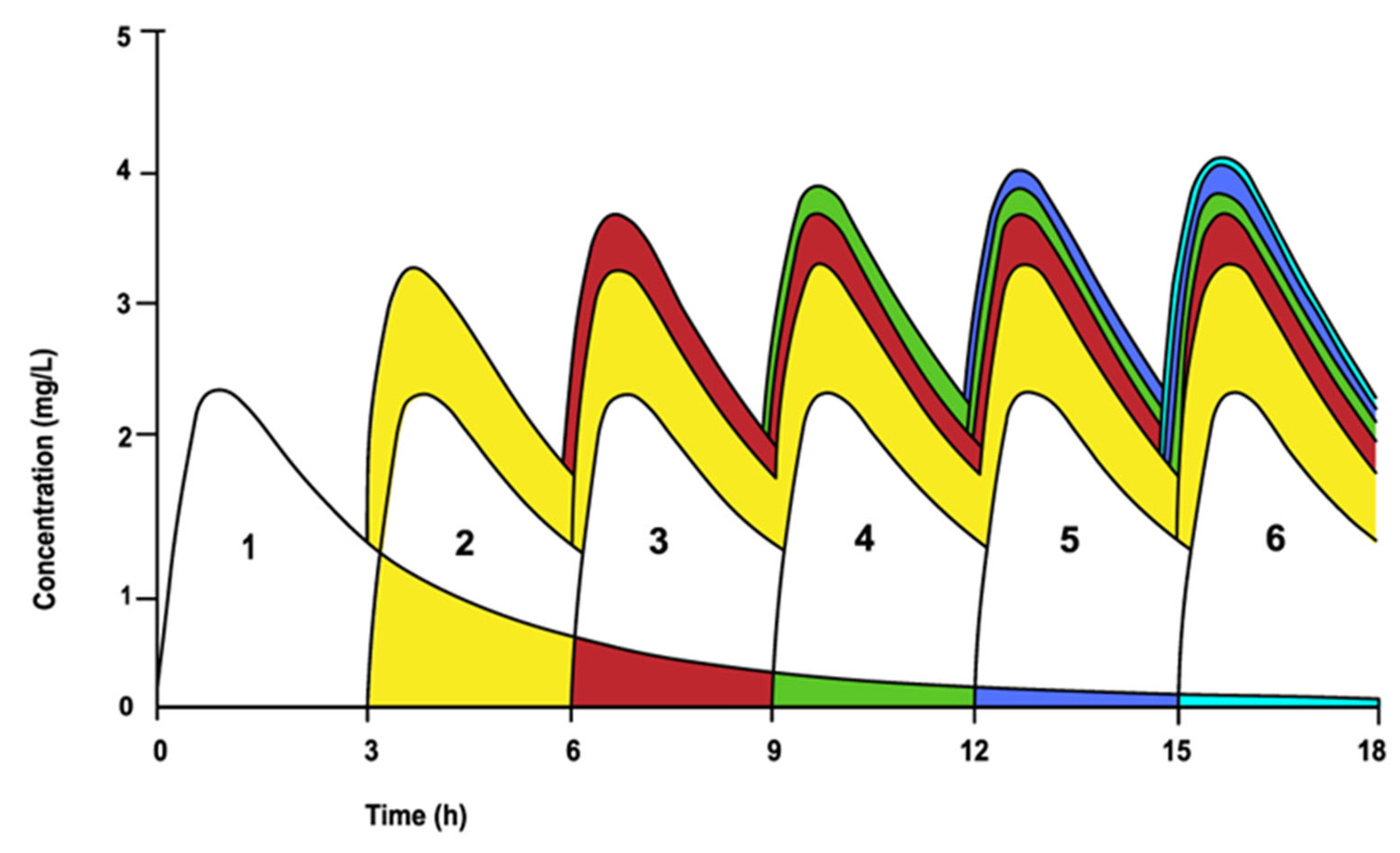

| Dose | Canadamycin (mg/L) | Start Multiple | Trough End (r) | Time (h) | Concentration Lost during Dosage Interval |
|---|---|---|---|---|---|
| 1 | 20.00 | 20.00 | 5.0 | 8 | 15.00 |
| 2 | 5.00 | 25.00 | 6.25 | 16 | 18.75 |
| 3 | 1.25 | 26.25 | 6.56 | 24 | 19.69 |
| 4 | 0.3125 | 26.56 | 6.64 | 32 | 19.92 |
| 5 | 0.078125 | 26.64 | 6.66 | 40 | 19.98 |
| 6 | 0.01953125 | 26.66 | 6.67 | 48 | 19.99 |
| 7 | 0.004882812 | 26.67 | 6.67 | 54 | 20.00 |
| ADME Process | Main Related Causes of Non-Linearity | Examples | ||
|---|---|---|---|---|
| Absorption | Carrier-mediated transport | Gabapentin [46], Metformin [47] | ||
| Saturable pre-systemic loss | Gut metabolism | Verapamil [48] | ||
| First-pass metabolism | Propranolol [49] | |||
| Distribution | Saturable plasma protein binding | Paclitaxel [50] | ||
| Saturable tissue binding | Imipramine [51] | |||
| Elimination | Metabolism | Saturable metabolism | Theophylline [52] | |
| Enzyme induction | Carbamazepine [53] | |||
| Excretion | Saturable renal excretion | Saturable active secretion | Zidovudine [54] | |
| Saturable reabsorption | Methotrexate [55] | |||
| Saturable biliary excretion | Tetracycline [56] | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousef, M.; Yáñez, J.A.; Löbenberg, R.; Davies, N.M. Upholding or Breaking the Law of Superposition in Pharmacokinetics. Biomedicines 2024, 12, 1843. https://doi.org/10.3390/biomedicines12081843
Yousef M, Yáñez JA, Löbenberg R, Davies NM. Upholding or Breaking the Law of Superposition in Pharmacokinetics. Biomedicines. 2024; 12(8):1843. https://doi.org/10.3390/biomedicines12081843
Chicago/Turabian StyleYousef, Malaz, Jaime A. Yáñez, Raimar Löbenberg, and Neal M. Davies. 2024. "Upholding or Breaking the Law of Superposition in Pharmacokinetics" Biomedicines 12, no. 8: 1843. https://doi.org/10.3390/biomedicines12081843
APA StyleYousef, M., Yáñez, J. A., Löbenberg, R., & Davies, N. M. (2024). Upholding or Breaking the Law of Superposition in Pharmacokinetics. Biomedicines, 12(8), 1843. https://doi.org/10.3390/biomedicines12081843









