A New Class of Counting Distributions Embedded in the Lee–Carter Model for Mortality Projections: A Bayesian Approach

Abstract

The Lee–Carter model, the dominant mortality projection modeling in the literature, was criticized for its homoscedastic error assumption. This was corrected in extensions to the model based on the assumption that the number of deaths follows Poisson or negative binomial distributions. We propose a new class of families of counting distributions, namely, the ABM class, which belongs to a wider class of natural exponential families. This class is characterized by its variance functions and contains the Poisson and the negative binomial distributions as special cases, offering an infinite class of additional counting distributions to be considered. We are guided by the principle that the choice of distribution should be made from a pool of distributions as large as possible. To this end, and following a data mining approach, a training set of historical mortality data of the population could be modeled using the ABM’s rich choice of distributions, and the chosen distribution should be the one that proved to offer superior projection results on a test set of mortality data. As an alternative to parameter estimation via the singular value decomposition used in the classical Lee–Carter model, we adopted Bayesian estimation, harnessing the Markov Chain Monte Carlo methodology. A numerical study demonstrates that when fitting mortality data using this new class of distributions, while traditional distributions may provide desirable projections for some populations, for others, alternative distributions within the ABM class can potentially produce superior results for the entire population or particular age groups, such as the oldest-old.

1. Introduction

The seminal paper by Lee and Carter (1992) (LC) introduced a model which is one of the most well-known and widely applied models for forecasting mortality rates. Within this model, the time series of the log mortality rates, $ln{m}_{xt},$ of each age is described by an age-specific intercept ${\alpha }_x$ plus a common trend $k_t$ for all age groups multiplied by an age-specific coefficient ${\beta }_x,$

$$ln{m}_{xt}={\alpha }_x+{\beta }_x{k}_t+{\epsilon }_{xt}.$$

The error term ${\epsilon }_{xt}$ is assumed to be distributed with a mean 0 and variance ${\sigma }_{\epsilon }^2$, reflecting influences missed by the model. The age and time-specific mortality rate $m_{xt}$ is calculated as $(D_{xt}/E_{xt})$, where $D_{xt}$ denotes the number of deaths in a population at age $x,$$x=1,2,\cdots ,P,$ and at time $t,t=1,2,\cdots ,T$, and $E_{xt}$ is the exposure to the risk of death. To ensure the identifiably of model parameters, constraints are imposed such that the sum of ${\beta }_x$ over age is 1 and the sum of $k_t$ over time is 0. To forecast mortality rates into the future, a simple random walk with drift is proposed for $k_t$:

$$k_t=k_{t-1}+\theta +w_t.$$

The homoscedastic error assumption of the Lee–Carter model was criticized for its limiting impact on predictions (Brouhns et al. 2002; Danesi et al. 2015; Idrizi 2018). This led to the introduction of the Poisson log-bilinear LC-type model (Brouhns et al. 2002), which, in contrast, is intrinsically heteroscedastic, namely:

$$D_{xt}\sim Poisson\left({\mu }_{xt}\right),{\mu }_{xt}=E_{xt}{m}_{xt}.$$

Here, the number of dead is directly modelled by a Poisson distribution, whose parameter is estimated by maximum likelihood estimation (MLE). This alternative approach gained momentum and alternative discrete distributions were proposed. In particular, a binomial distribution was proposed by Wang and Lu (2005) and a negative binomial distribution was suggested by Delwarde et al. (2007) and Renshaw and Haberman (2008). See Azman and Pathmanathan (2022) for further discussion of these distributions within the GLM framework.

The Lee–Carter model has been widely used for many purposes (Shair et al. 2018), such as forecasting mortality reduction factors, assessing the adequacy of retirement income, population projections and the projection of mortality trends for the oldest-old (older than 80, and in some sources 85). This age group is of considerable interest for policymakers as it is destined to grow as a proportion of the entire population and can outstrip existing infrastructures’ capacity (Buettner 2002). This is a fairly recent phenomenon. In Canada, for instance (Legare et al. 2015), the 21st century brought about the most significant gain in life expectancy at age 85 (7.79% for women and 9.93% for men). Clearly, policies need to be devised that can meet people’s special needs in what is called the fourth age Baltes and Smith (2003), and accurate mortality projection for this age group is a must. We shall, therefore, focus on the adequacy of potential underlying discrete distribution functions to produce accurate mortality projections using the Lee–Carter model for this age group. This will be discussed in Section 4.

In essence, while the above-cited papers relied on popular and commonly used discrete distributions, one cannot say that one particular distribution is universally superior. Indeed, it is entirely plausible to assume that there is a winning distribution for any given population or even for a specific population at a certain age range. Ideally, one should consider a rich class of family of counting distributions, much richer than the two already suggested, and use the data to pick the most suitable distribution for the population under study. This paper proposes an infinitely countable set of families of counting distributions, where the Poisson, negative binomial and Abel families of distributions are special cases. Our aim is to study this family, incorporate it into the framework of the LC model and use real data to seek the most suitable distribution for mortality projection. While there is little doubt that the distributions discussed above could prove adequate for specific populations or age groups, other distributions within the suggested family could have the upper hand.

The paper is organized as follows. Section 2 presents the new class of counting distributions. Section 3 is devoted to the new class and its Bayesian framework. Section 4 (divided into Section 4.1: Methods and Section 4.2: Results) reports a numerical study in which superior members of this class are chosen for mortality projections of the oldest-old in three populations. Finally, Section 5 offers a discussion.

2. A New Class of Counting Distributions on the Set of Nonnegative Integers ${\mathbb{N}}_{\mathbf{0}}$

The new class of families of counting distributions on the non-negative integers belongs to a wider class of natural exponential families (NEFs), characterized by their variance functions (VFs). In order to comprehend this class we decompose this section into subsections. We first present some preliminaries on NEFs and their associated VFs. We then introduce a class of NEFs having polynomial structure and then suggest the new class of families of counting distributions, named ABM, first introduced by Awad et al. (2016), where the class was defined and its usefulness for mortality projections was preliminary sketched. Furthermore, such a class has been investigated by Bar-Lev and Ridder (2021a, 2021b) from a classical frequency approach and has shown superiority with respect to various metrics or goodness-of-fit tests for different count datasets (for further details see item 6 in Section 2.3).

2.1. NEFs—Some Preliminaries

The following preliminaries are mainly taken from Letac and Mora (1990) and are briefly presented here for completeness.

Let $\nu$ be a non-Dirac positive Radon measure on $\mathbb{R}$, and $L\left(\theta \right)=\int e^{\theta x}\nu \left(dx\right)$ its Laplace transform. Assuming that $\Theta =\mathtt{int}\{\theta \in \mathbb{R}:L(\theta )<\infty \}\ne \varphi$, then the NEF generated by $\nu$ is defined by the probability distributions

$$\mathcal{F}=\left\{F_{\theta }:F_{\theta }\left(\nu \left(dx\right)\right)=e^{\theta x-\kappa \left(\theta \right)}\nu \left(dx\right),\theta \in \Theta \right\},$$

(1)

where $\kappa \left(\theta \right)=logL\left(\theta \right)$, the cumulant transform of $\nu$, is strictly convex and real analytic on $\Theta$. If $X_{\theta }$ represents a r.v. having distribution $F_{\theta }$ of the form given in (1) then the expectation and variance of $X_{\theta }$ are given, respectively, by $E\left(X_{\theta }\right)\doteq m={\kappa }^{\prime }\left(\theta \right)$ and $V\left(X_{\theta }\right)={\kappa }^{″}\left(\theta \right)$ where $m={\kappa }^{\prime }\left(\theta \right)$ is strictly monotone and thus its inverse, say, $\theta =\psi \left(m\right),m\in M={\kappa }^{\prime }(\Theta )$ is well defined. The set M of all means of (1) is called the mean parameter space of $\mathcal{F}$. The variance of $F_{\theta }$ can be expressed in terms of m by $V\left(m\right)={\kappa }^{″}\left(\theta \right)={\kappa }^{″}\left(\psi \left(m\right)\right)$. The pair $(V,M)$ is called the VF of $\mathcal{F}$ and it uniquely determines $\mathcal{F}$ within the class of NEFs. For example, $(m,{\mathbb{R}}^{+})$ and $(m^2,{\mathbb{R}}^{+})$ are, respectively, the VFs of the Poisson and exponential NEFs and are uniquely determined by them.

2.2. The Mean Value Parametrization of NEFs

As indicated above, the VF of an NEF $\mathcal{F}$ uniquely determines F within the class of NEFs. Let $(V,M)$ be a given VF of an NEF $\mathcal{F}$ generated by $\nu$. Then, simple calculations show both $\theta =\psi \left(m\right)$ and the cumulant transform $\kappa \left(\theta \right)=\kappa \left(\psi \right(m\left)\right)$ of $\nu$ can be expressed in terms of m as:

$$\theta =\psi \left(m\right)=\int \frac{dm}{V\left(m\right)}+c_1,k\left(\theta \right)=k\left(\psi \left(m\right)\right)=\int \frac{m}{V\left(m\right)}dm+c_2,$$

(2)

where one needs to determine the constants $c_1$ and $c_2$ so that $F_{\theta },$ $\theta \in \Theta$, constitutes a probability distribution (not an easy task). Accordingly, a mean value parametrization of an NEF $\mathcal{F}$ generated by a measure $\nu$ is given by:

$$\mathcal{F}=\left\{exp\left\{\psi \left(m\right)x-k\left(\psi \right(m\left)\right)\right\}\nu \left(dx\right),m\in M\right\}.$$

(3)

Such a representation of $\mathcal{F}$ is more natural as it is expressed in terms of the mean m rather than a somewhat artificial parameter $\theta$. A comprehensive description of NEFs in terms of their mean value representation is reviewed in Bar-Lev and Kokonendji (2017).

Remark 1. 

The task of computing the constants $c_1$ and $c_2$ is not simple and might be rather cumbersome. However, from a Bayesian perspective, when (3) is used as a prior distribution on m, then in the calculation of the respective posterior distribution, such constants are cancelled out (as the likelihood function is the only relevant component). As this paper is concerned with a Bayesian framework, one can assume without any loss of generality that $c_1=c_2=0$. Henceforth, we indeed assume so.

2.3. Polynomial VFs of Counting NEFs Supported on the Set of Nonnegative Integers ${\mathbb{N}}_0$

The innovative and breakthrough Proposition 4.4 of Letac and Mora (1990, p. 13) provided conditions under which a given VF $(V,M)$ is associated with a counting NEF F supported on the set of non-negative integers ${\mathbb{N}}_0$, i.e., where all members of F are composed of counting distributions on ${\mathbb{N}}_0$. They provided general examples of two classes of VFs which fulfill the premises of their Proposition 4.4 and thus their associated NEFs’ distributions are supported on the non-negative integers. One of these two classes has the form:

$$V\left(m\right)=m\prod _{i=1}^k\left(1+\frac{m}{p_i}\right),p_i>0,i=1,\cdots ,k,k\in {\mathbb{N}}_0,M={\mathbb{R}}^{+},\mathrm{where}\prod _{i=1}^0\doteq 1.$$

(4)

They proved that such VFs constitute counting NEFs supported on ${\mathbb{N}}_0,$ namely, counting distributions with non-negative integer support. Moreover, their Proposition 4.4 enables to compute (at least theoretically and numerically) the corresponding measure $\nu$ (we skip details as they are irrelevant for our Bayesian framework analysis). Note that the two special cases of (4) with $k=0$ and $k=1$ correspond, respectively, to the Poisson and negative binomial NEFs. However, the general setting (4) for $k\ge 3$ does not allow an explicit calculation of $\theta =\psi \left(m\right)$ and $k\left(\theta \right)=k\left(\psi \right(m\left)\right)$ in (2), implying that the mean value parametrization of the corresponding NEFs in the form (3) is not explicitly expressible in terms of m and thus becomes useless for any practical consideration.

2.4. A New Class of Polynomial VFs—The ABM NEFs

As we already noted, the fact that a given pair $(V,M)$ is known to be a VF of some NEF does not necessarily enable the construction of the corresponding mean value parameterization (3), as in most cases the integrals for $\psi \left(m\right)$ and $k\left(\psi \right(m\left)\right)$ in (2) are not explicitly expressible analytically in closed forms, and indeed, this is the situation for the class (4) in its general form. Consequently, one needs to search for subclasses of (4) for which the integrals in (2) can be computed explicitly. One such special subclass takes the above point into consideration. Indeed, by taking in (4) the special case where

$$p_1=p_2=\cdots =p_k,$$

and denoting

$$p_2\doteq k\in {\mathbb{N}}_0,$$

we obtain a subclass of (4) with VFs with the form:

$$(V,M)=m{\left(1+\frac{m}{p_1}\right)}^{p_2},{\mathbb{R}}^{+}),p_1>0,p_2\in {\mathbb{N}}_0.$$

(5)

As (5) is a subclass of (4) and (4) satisfies the premises of Proposition 4.4 of Letac and Mora (1990) it follows that the subclass (5) are VFs associated with counting NEFs supported on the non-negative integers.

The subclass of VFs in (5) (hereafter called the ABM class) was first introduced by Awad et al. (2016) who showed that the corresponding $\psi \left(m\right)$ and $k\left(\psi \right(m\left)\right)$ (calculated from (2)) have, as opposed to the general form in (4), the following closed forms (the exact proof details appear in Bar-Lev and Kokonendji 2017):

$$\theta =\psi \left(m\right)=ln\frac{m}{p_1+m}+\sum _{i=1}^{p_2-1}\frac{1}{i}\frac{p_1^i}{{(p_1+m)}^i}+c_1,\mathrm{where}\sum _{i=1}^0=0,$$

and

$$\kappa \left(\psi \left(m\right)\right)=-\frac{p_1^{p_2}}{(p_2-1){(m+p_1)}^{p_2-1}}+c_2.$$

Thus, its mean value parametrization is given by the probability distribution:

$$\begin{array}{cc}\hfill F(m,\nu \left(dx\right))& =exp\left\{x\left[ln\frac{m}{p_1+m}+\sum _{i=1}^{p_2-1}\frac{1}{i}\frac{p_1^i}{{(p_1+m)}^i}+c_1\right]\right.\hfill \\ \\ & \left.+\frac{p_1^{p_2}}{(p_2-1){(m+p_1)}^{p_2-1}}+c_2\right\},m\in {\mathbb{R}}^{+},p_1>0,p_2\in \mathbb{N}\hfill \end{array},$$

(6)

where hereafter we denote this probability distribution by $ABM(p_1,p_2),$ where $p_1$ is a positive real number and $p_2$ is a non-negative integer. (For a classical frequency approach, the constants $c_1$ and $c_2$ have been computed by Bar-Lev and Ridder 2021b). However, as noted above, for a Bayesian framework they are cancelled out when computing the posterior distribution and thus can be taken to be $c_1=c_2=0$ without any loss of generality).

Note that the ABM class of VFs ${\left\{m{\left(1+\frac{m}{p_1}\right)}^{p_2},p_1>0\right\}}_{{}^{p_2\in {\mathbb{N}}_0}}$, or alternatively, the corresponding class ${\left\{ABM(p_1,p_2)\right\}}_{p_2\in {\mathbb{N}}_0}$ of NEFs is composed of an infinitely countable set of families of counting NEFs supported on the non-negative integers. As special cases, this class contains the Poisson NEF ($p_2=0$), the negative binomial NEF ($p_2=1)$ and the Abel NEF ($p_2=2$), (c.f., Letac and Mora 1990, p. 31; Bar-Lev and Ridder 2019, for applications to car accident claims of a Swedish insurance company dataset).

Summarizing, this ABM NEF has the following features:

• It is a class of counting distributions supported on the non-negative integers;
• It is overdispersed as $V\left(m\right)/m>1$;
• It allows a mean value parameterization in a closed form;
• It is infinitely divisible, which allows the construction of an exponential dispersion model (EDM) with dispersion parameter space equal to ${\mathbb{R}}^{+}$. EDMs are used to describe the error distribution in generalized linear models (see Jorgensen 1987, 1997);
• $p_1$ is an unknown parameter to be estimated (see next section). $p_2\in {\mathbb{N}}_0$ is a parameter governing the particular model within the ABM class and is considered to be a decision variable (note that different values of $p_2$ determine different ABM NEFs). Accordingly, for given national datasets (i.e., those of US, Ireland and Ukraine), the goal will be to locate that value of $p_2$, which minimizes a respective RMSE (see in the sequel). However, due to the rather cumbersome and intractable structure of the ABM probabilities (or likelihood) in (6) and the fact that the larger the $p_2$, the larger the number of elements in the summands appearing in (6), no analytic solution for an optimal $p_2$ is feasible at all for achieving such a goal. Consequently, only numerical search algorithms are plausible. The search starts with $p_2=0$ (the Poisson NEF), $p_2=1$ (the negative binomial NEF), $p_2=2$ (the Abel NEF) and so on;
• As already noted, the ABM class ${\left\{ABM(p_1,p_2)\right\}}_{{}^{p_2}\in {\mathbb{N}}_0}$ is composed of infinitely countable set of families of counting NEFs supported on the non-negative integers and thus can also be used to model real datasets by employing the classical frequency approach (and not only Bayesian). Indeed, the ABM class has been compared in Bar-Lev and Ridder (2021a, 2021b) with other common counting probability models (such as Poisson-inverse Gaussian distribution, new logarithmic distribution, an exponentiated discrete Lindley distribution) for various real count datasets stemming from automobile insurance claims, marketing, biometry, health, and social sciences (none of which is related to mortality projections). Members of the ABM counting class have shown superiority with respect to various metrics for goodness-of-fit tests (chi-squared test, Akaike information criterion (AIC), root-mean-square error (RMSE) and Kullback–Leibler divergence (KL)), and provided a much better fit for each of the datasets considered (more details can be found in Bar-Lev and Ridder 2021b).

3. ABM Based LC Model and its Bayesian Framework

As an alternative to parameter estimation via the singular value decomposition used in the classical LC model or the MLE in the cases discussed above, we adopt the Bayesian approach which offers advantages succinctly expressed in Antonio et al. (2015): a. The calibration and forecast steps are combined, which leads to more consistent estimates of the period effects; b. The Bayesian approach provides a natural framework for incorporating parameter uncertainty in mortality forecasts, which is relevant—for example—in the new insurance regulatory framework of Solvency II. The Bayesian approach allows adequate handling of small populations and missing data. Like Czado et al. (2005) and Pedroza (2006), we harness the power of the Markov Chain Monte Carlo (MCMC) methodology to estimate the model parameters and execute mortality projection. We note that the interest in Bayesian solutions in the context of mortality projections has recently gained momentum (Ellison et al. 2020; Graziani 2020; Hilton et al. 2019; Hunt and Blake 2020; Kogure et al. 2019; Liu et al. 2020; Njenga and Sherris 2020; Wong et al. 2018).

Suppose the number of deaths $D_{xt}$ in a population at age x and time t is distributed as follow:

$$D_{xt}\sim ABM(p_1,p_2)\left({\mu }_{xt}\right),{\mu }_{xt}=E_{xt}{m}_{xt},m_{xt}=exp({\alpha }_x+{\beta }_x{k}_t),$$

where

$$\alpha ={({\alpha }_{x_{min}},\cdots ,{\alpha }_{x_{max}})}^{\prime },\beta ={({\beta }_{x_{min}},\cdots ,{\beta }_{x_{max}})}^{\prime },k=(k_{t_{min}},\cdots ,k_{t_{max}}).$$

Bayesian estimation of the unknown parameters $\alpha ,\beta ,k$ and $p_1$ are based on the joint posterior distribution function of $\alpha ,\beta ,k$ and $p_1$ given $(E_{xt},D_{xt})$, when $x=x_{min},x_{min}+1,\cdots ,x_{max},$ $t=t_{min},t_{min}+1,\cdots ,t_{max}$. The first step in the Bayesian estimation is to determine the prior probability functions for these parameters.

The prior distribution for ${\mathit{k}}_{\mathit{t}}$ and $\mathit{\theta }$

Let $k_t=k_{t-1}+\theta +w_t,$ and let $w_t\sim N(0,{\sigma }_w^2)$ and hence $k_t\sim N(\theta ,t{\sigma }_w^2)$. we assume ${\sigma }_w^{-2}\sim gamma(a_k,b_k)$ and $\theta \sim$$N({\theta }_0,{\sigma }_{\theta }^2)$. The hyper-parameters ${\theta }_0,a_k,b_k$ and ${\sigma }_{\theta }^2$ are arbitrary initial values.

The prior distribution for ${\mathit{\beta }}_{\mathit{x}}$

We assume ${\beta }_x\sim N(0,{\sigma }_{\beta }^2)$ ∀ x, where ${\sigma }_{\beta }^{-2}\sim gamma(a_{\beta },b_{\beta })$. The hyper-parameters $a_{\beta },b_{\beta }$ are arbitrary initial values.

The prior distribution for ${\mathit{\alpha }}_{\mathit{x}}$

We suppose that the prior distribution of ${\alpha }_x\sim N({\alpha }_{0x},{\sigma }_{\alpha }^2)$ ∀ x, where ${\sigma }_{\alpha }^{-2}\sim gamma(a_{\alpha },b_{\alpha })$. The hyper-parameters ${\alpha }_{0x},a_{\alpha }$ and $b_{\alpha }$ are arbitrary initial values.

The prior distribution for ${\mathit{p}}_{\mathbf{1}}$

We let $p_1\sim gamma(a_{p_1},b_{p_1})$. The hyper-parameters $a_{p_1},b_{p_1}$ are arbitrary initial values.

MH (Metropolis–Hastings) Algorithm for Estimating the Parameters $\alpha ,\beta ,k$ and $p_1$

Suppose the $D_{xt}^{}{}^{\prime }s$ are independent random variables, which are distributed as (6) and $g(\Xi )$ is the joint prior distribution of the unknown parameters $\Xi ={(\alpha ,\beta ,k,p_1)}^{\prime }$. Then, the posterior distribution of $\Xi ,$ given all available data $D=\left\{d_{xt}\right\}$ and $p_2,$ can be represented as follows:

$$\begin{array}{c}f(\Xi \mid D,p_2)\propto \hfill \\ \hspace{1em}\prod _x\prod _{t}exp\left[d_{xt}\left(ln\frac{E_{xr}{m}_{xt}}{p_1+E_{xt}{m}_{xt}}+\sum _{i=1}^{p_2-1}\frac{1}{i}\frac{p_1^i}{\left(p_1+E_{xt}{m}_{xt}\right)}\right)+\frac{p_1^{p_2}}{\left(p_2-1\right){\left(p_1+E_{xt}{m}_{xt}\right)}^{p_2-1}}\right]\times g(\Xi ).\hfill \end{array}$$

See Appendix A for the marginal posterior distributions of $\alpha ,\beta ,k$ and $p_1$. We now describe the estimation of $\alpha ,\beta ,k$ and $p_1$ using the MH, conditioned on the data and all other parameters at their respective iterations. The superscript denotes the iteration number of the parameter of interest.

Estimation of ${\mathit{k}}_{\mathit{t}}$ using the MH algorithm

Let the marginal posterior distribution of $k_t$ be $f(k_t\mid D,\alpha ,\beta ,k_{-t},\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)$. The estimation of $k_t,$ is achieved by the following steps, where.

• Draw $k_t^{*}$ from the proposal density function $N(k_t^{\left(i\right)},{\sigma }_t^2)$, such that ${\sigma }_t^2$ is assumed known;
• Calculate the following probability:

  $$\Psi \left(k_t^{\left(i\right)},k_t^{*}\right)=min\left(1,\frac{f(k_t^{*}\mid D,\alpha ,\beta ,k_{-t}^{\left(i\right)},\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}{f(k_t^{\left(i\right)}\mid D,\alpha ,\beta ,k_{-t}^{\left(i\right)},\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}\right),$$

  where $k_{-t}={(k_{tmin},\dots ,k_{t-1},k_{t+1},\dots .k_{tmax})}^{\prime };$
• Draw a value u from uniform probability function in range $U(0,1)$ and decide in accordance with the following formula:

  $$\left\{\begin{array}{c}ifu\le \Psi \left(k_t^{\left(i\right)},k_t^{*}\right)\mathrm{then}{k}_t^{(i+1)}=k_t^{*}\hfill \\ ifu>\Psi \left(k_t^{\left(i\right)},k_t^{*}\right)\mathrm{then}{k}_t^{(i+1)}=k_t^{\left(i\right)};\hfill \end{array}\right\}.$$
• Going over all values of t, we have:

  $$k^{(i+1)}={\left(k_{t_{min}}^{(i+1)},\cdots ,k_t^{(i+1)},k_{t+1}^{\left(i\right)},\cdots ,k_{t_{max}}^{\left(i\right)}\right)}^{\prime };$$
• Transforming $k^{(i+1)}$ and ${\alpha }^{\left(i\right)}$ to assure identifiably:

  $$k^{(i+1)}-\overline{k}\to k^{(i+1)},{\alpha }^{\left(i\right)}+{\beta }^{\left(i\right)}\overline{k}\to {\alpha }^{\left(i\right)},$$

  where

  $$\overline{k}=\frac{1}{T}\left(\sum _{j\le t}{k}_j^{(i+1)}+\sum _{j>t}{k}_j^{\left(i\right)}\right);$$
• Repeat steps 1 to 5.

Estimation of ${\mathit{\beta }}_{\mathit{x}}$ using MH algorithm

Let the marginal posterior distribution of ${\beta }_x$ be $f({\beta }_x\mid D,\alpha ,{\beta }_{-x},k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1).$ The estimation of ${\beta }_x$ is achieved by the following steps.

• Draw ${\beta }_x^{*}$ from the proposal density function $N({\beta }_x^{\left(i\right)},{\sigma }_{\beta }^2)$, such that ${\sigma }_{\beta }^2$ is assumed to be known;
• Calculate the following probability:

  $$\Psi \left({\beta }_x^{\left(i\right)},{\beta }_x^{*}\right)=min\left(1,\frac{f({\beta }_x^{*}\mid D,\alpha ,{\beta }_{-x}^{\left(i\right)},k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}{f({\beta }_x^{\left(i\right)}\mid D,\alpha ,{\beta }_{-x}^{\left(i\right)},k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}\right),$$

  where

  $${\beta }_{-x}={({\beta }_{xmin},\cdots ,{\beta }_{x-1},{\beta }_{x+1},\cdots .{\beta }_{xmax})}^{\prime }.$$
• Draw a value u from uniform probability function in range $U(0,1)$ and decide in accordance with the following formula:

  $$\left\{\begin{array}{c}ifu\le \Psi \left({\beta }_x^{\left(i\right)},{\beta }_x^{*}\right)then{\beta }_x^{(i+1)}={\beta }_x^{*}\hfill \\ ifu>\Psi \left({\beta }_x^{\left(i\right)},{\beta }_x^{*}\right)then{\beta }_x^{(i+1)}={\beta }_x^{\left(i\right)};\hfill \end{array}\right\}.$$
• Going over all values of x, we have:

  $${\beta }^{(i+1)}=\left({\beta }_{x_{min}}^{(i+1)},\cdots ,{\beta }_x^{(i+1)},{\beta }_{x+1}^{\left(i\right)},\cdots ,{\beta }_{x_{max}}^{\left(i\right)}\right){;}^{\prime }.$$
• Transforming $k^{(i+1)}$ and ${\beta }^{(i+1)}$ to assure identifiably:

  $$\frac{{\beta }^{(i+1)}}{{\beta }_{sum}}\to {\beta }^{(i+1)},k^{(i+1)}\times {\beta }_{sum}\to k^{(i+1)},$$

  where

  $${\beta }_{sum}=\left(\sum _{j\le x}{\beta }_j^{(i+1)}+\sum _{j>x}{\beta }_j^{\left(i\right)}\right);$$
• Repeat steps 1 to 5.

Estimation of ${\mathit{\alpha }}_{\mathit{x}}$ using MH algorithm

Let the marginal posterior distribution of ${\alpha }_x$ be $f({\alpha }_x\mid D,{\alpha }_{-x},\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1).$ The estimation of ${\alpha }_x,$ is achieved by the following steps;

• Draw ${\alpha }_x^{*}$ from the proposal density function $N({\alpha }_x^{\left(i\right)},{\sigma }_{\alpha }^2)$, such that ${\sigma }_{\alpha }^2$ is assumed known;
• Calculate the following probability:

  $$\Psi \left({\alpha }_x^{\left(i\right)},{\alpha }_x^{*}\right)=min\left(1,\frac{f({\alpha }_x^{*}\mid D,{\alpha }_{-x}^{\left(i\right)},\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}{f({\alpha }_x^{\left(i\right)}\mid D,{\alpha }_{-x}^{\left(i\right)},\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)}\right),$$

  where

  $${\alpha }_{-t}={({\alpha }_{xmin},\dots ,{\alpha }_{x-1},{\alpha }_{x+1},\dots .{\alpha }_{xmax})}^{\prime };$$
• Draw a value u from uniform probability function in range $U(0,1)$ and decide in accordance with the following formula:

  $$\left\{\begin{array}{c}ifu\le \Psi \left({\alpha }_x^{\left(i\right)},{\alpha }_x^{*}\right)then{\alpha }_x^{(i+1)}={\alpha }_x^{*}\hfill \\ ifu>\Psi \left({\alpha }_x^{\left(i\right)},{\alpha }_x^{*}\right)then{\alpha }_x^{(i+1)}={\alpha }_x^{\left(i\right)};\hfill \end{array}\right\}.$$
• Receiving ${\alpha }^{(i+1)}$ in $(i+1)$th iteration as follows:

  $${\alpha }_x^{(i+1)}=\left({\alpha }_{x_{min}}^{(i+1)},\dots ,{\alpha }_x^{(i+1)},{\alpha }_{x+1}^{\left(i\right)},\dots ,{\alpha }_{x_{max}}^{\left(i\right)}\right);$$
• Repeat steps 1 to 4.

Estimation of ${\mathit{p}}_{\mathbf{1}}$ using MH algorithm

Let the marginal posterior distribution of $p_1$ be $f(p_1\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2)$, proportional to the product of the likelihood (6) and the gamma prior distribution of $p_1$. The estimation of $p_1$ is achieved by the following steps;

• Draw $p_1^{*}$ from the probability function $gamma({\alpha }_{p_1},b_{p_1})$, such that ${\alpha }_{p_1}$ and $b_{p_1}$ are hyperparameters and are assumed known;
• Calculate the following probability:

  $$\Psi \left(p_1^{\left(i\right)},p_1^{*}\right)=min\left(1,\frac{f(p_1^{*}\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2)}{f(p_1^{\left(i\right)}\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2)}\right);$$
• Draw a value u from uniform probability function in range $U(0,1)$ and decide in accordance with the following formula:

  $$\left\{\begin{array}{c}ifu\le \Psi \left(p_1^{\left(i\right)},p_1^{*}\right)then{p}_1^{(i+1)}=p_1^{*}\hfill \\ ifu>\Psi \left(p_1^{\left(i\right)},p_1^{*}\right)then{p}_1^{(i+1)}=p_1^{\left(i\right)};\hfill \end{array}\right\}.$$
• Then receiving $p^{(i+1)}$ in $(i+1)$th iteration;
• Repeat steps 1 to 4.

Estimation of $\mathit{\theta }\mathbf{,}{\mathit{\sigma }}_{\mathit{\alpha }}^{\mathbf{2}}\mathbf{,}{\mathit{\sigma }}_{\mathit{\beta }}^{\mathbf{2}}$ and ${\mathit{\sigma }}_{\mathit{w}}^{\mathbf{2}}$ using the Gibbs sampler

The Gibbs sampler can be used for estimating $\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2$ and ${\sigma }_w^2$ since the marginal posterior distribution of these parameters can be written explicitly (See: (Czado et al. 2005)). The following are the marginal posterior sampling distributions of each of these parameters, conditioned on the data and all other parameters at their respective iterations.

1. Sampling $\theta$:

The posterior probability function of the parameter $\theta$, is presented as follows:

$$f(\theta \mid D,\alpha ,\beta ,k,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)=f(\theta \mid k,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)\propto f(k\mid \theta ,{\sigma }_w^2)f\left(\theta \right).$$

The prior probability function of the parameter $\theta$ is $N({\theta }_0,{\sigma }_{\theta }^2)$, and the hyper-parameters ${\theta }_0$ and ${\sigma }_{\theta }^2$ are set by the user, hence the posterior probability function of the parameter is:

$$(\theta \mid k,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,{\sigma }_w^2)\sim N\left(\frac{{\theta }_0{\sigma }_w^2}{T{\sigma }_{\theta }^2+{\sigma }_w^2},{\left(T{\sigma }_{\theta }^2+{\sigma }_w^2\right)}^{-1}\right).$$

2. Sampling ${\sigma }_{\alpha }^2$:

The posterior probability function of the parameter ${\sigma }_{\alpha }^2$ is presented as follows:

$$f({\sigma }_{\alpha }^2\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)\propto f(\alpha \mid {\sigma }_{\alpha }^2)f\left({\sigma }_{\alpha }^2\right).$$

The prior probability function of the parameter ${\sigma }_{\alpha }^2$ such that ${\sigma }_{\alpha }^{-2}\sim gamma(a_{\alpha },b_{\alpha })$, and the hyper-parameters $a_{\alpha }$ and $b_{\alpha }$ are set by the user, so the posterior probability function of the parameter is:

$$({\sigma }_{\alpha }^{-2}\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\beta }^2,{\sigma }_w^2,p_1)\sim gamma\left(a_{\alpha }+\frac{x_{max}}{2},b_{\alpha }+\frac{1}{2}\sum _{x=x_{min}}^{x_{max}}{\left({\alpha }_x-\overline{\alpha }\right)}^2\right),$$

where

$$\overline{\alpha }=\frac{1}{x_{max}}\sum _{x=x_{min}}^{x_{max}}{\alpha }_x.$$

3. Sampling ${\sigma }_{\beta }^2$:

The posterior probability function of the parameter ${\sigma }_{\beta }^2$ is presented as follows:

$$f({\sigma }_{\beta }^2\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_w^2,p_1)\propto f(\beta \mid {\sigma }_{\beta }^2)f\left({\sigma }_{\beta }^2\right).$$

The prior probability function of the parameter ${\sigma }_{\beta }^2$ such that ${\sigma }_{\beta }^{-2}\sim gamma(a_{\beta },b_{\beta })$, and the hyper-parameters $a_{\beta }$ and $b_{\beta }$ are set by the user, so the posterior probability function of the parameter is:

$$({\sigma }_{\beta }^{-2}\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_w^2,p_1)\sim gamma\left(a_{\beta }+\frac{x_{max}}{2},b_{\beta }+\frac{1}{2}\sum _{x=x_{min}}^{x_{max}}{\left({\beta }_x\right)}^2\right).$$

4. Sampling ${\sigma }_w^2$:

The posterior probability function of the parameter ${\sigma }_w^2$, is presented as follows:

$$f({\sigma }_w^2\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,p_1)\propto f(k\mid {\sigma }_w^2)f\left({\sigma }_w^2\right).$$

The prior probability function of the parameter ${\sigma }_w^2$ such that ${\sigma }_w^{-2}\sim gamma(a_k,b_k)$, and the hyper-parameters $a_k$ and $b_k$ are set by the user, so the posterior probability function of the parameter is:

$$({\sigma }_w^{-2}\mid D,\alpha ,\beta ,k,\theta ,{\sigma }_{\alpha }^2,{\sigma }_{\beta }^2,p_1)\sim gamma\left(a_k+\frac{T}{2},b_k+\frac{1}{2}\sum _{t=t_{min}}^{t_{max}}{\left(k_t-k_{t-1}-\theta \right)}^2\right).$$

4. Numerical Experiment

4.1. Methods

To test the adequacy of the ABM class, we analyzed mortality data of men in Ireland, Ukraine and the USA, downloaded from the database of Human Mortality Database (https://www.mortality.org accessed on 8 March 2013). The data contain the number of dead and the size of the population exposed to risk by age and year; Ireland’s and the USA’s data are for 1950–2007, and Ukraine’s data are for 1959–2009. This analysis aims to examine sixteen models within the ABM class, $p_2=0,\dots ,15$, with a particular emphasis on forecasting the mortality of the oldest-old (see below an argumentation for the restriction of the values of $p_2$ to $\{0,\dots ,15\}$). These models also include the Poisson and negative binomial models which feature widely in the literature, for which $p_1=0$ and $p_2=1$, respectively. Adopting a data mining approach, the models were fitted using training sets and were examined using test sets. The training sets contained data up to 2000 and the test sets, aimed at monitoring the quality of predictions, contained data from 2001 to 2007 for Ireland and the USA, and from 2001 to 2009 for Ukraine. Predictions are carried out with the estimated parameters, $ln\left[m_{x,t+s}\right]={\stackrel{\wedge }{\alpha }}_x+\stackrel{\wedge }{\beta }*{\stackrel{\wedge }{k}}_{t+s},s=1,2,\dots ,$ where model performance (using the test sets) was checked using the root of the mean squared errors (RMSE), which was calculated in two ways:

• Predicting mortality rates $\left(\mu \right)$ by age. In other words, after model parameters were estimated, mortality rates were predicted for a given age across years. For instance, predicting mortality rates for those age 70 was carried out over the years beyond 2000;
• Predicting mortality rates $\left(\mu \right)$ by cohort. In other words, after model parameters were estimated, mortality rates were predicted for a cohort that was at a particular age at the beginning of the test period. For example, predicted mortality rates in 2001–2007 for a cohort aged 70 in 2001.

For every member of the ABM class (controlled by $p_2$), the Markov chains used to obtain posterior distributions/parameter estimates comprised 4000 iterations with the first 1000 considered a burn-in period. Convergence was established using graphical means and a sensitivity analysis ascertained that the choice of arbitrary initial hyper-parameters did not affect the final outcomes. We report the outcomes for the Poisson distribution ($p_2=0)$ and the negative binomial distribution ($p_2=1)$. In addition, we examined the ABM members for which $p_2\in \{2,\cdots ,15\}.$ We limited our reporting to $p_2\in \{2,\cdots ,15\}$ since, for the data under study, increasing $p_2$ beyond 15 (our study explored all models up to $p_2=50)$ did not alter our findings of the optimal $p_2$ for varying ages and resulted in much larger RMSE than those found up to $p_2$ = 15. In practice, we analyzed all 16 models within the $p_2$ range and, for each, we estimated $p_1$ as well as all other unknown parameters. Finally, we reported graphically the RMSE for the Poisson, negative binomial and for the ABM member which produced the minimal RMSE for various ages.

4.2. Results

Figure 1a,b shows Ireland’s mortality projections by age and cohort, respectively. A superior model for an age range is the one which produced the smallest RMSE. It is evident that the Poisson performs best for most ages above 70, with the negative binomial lagging behind. However, at a very old age, the Poisson diverges and the best ABM member to be chosen instead is $ABM(·,p_2=3).$ A similar result is shown for the USA (Figure 2a,b), except that the best ABM for the very old is $ABM(·,p_2=4)$. A different picture emerges when we focus on Ukraine’s mortality projections by age and cohort (Figure 3a,b, respectively). While the Poisson and negative binomial perform well (with Poisson being better), for ages above 96 (by cohort) or 104 (by age), the negative binomial drifts away, leaving $ABM(·,p_2=10)$ to be the winner of the ABM class. Clearly, the recommended projection policy for Ukraine is to use the Poisson for most ages but to rely on $ABM(·,p_2=10)$ for very old ages. 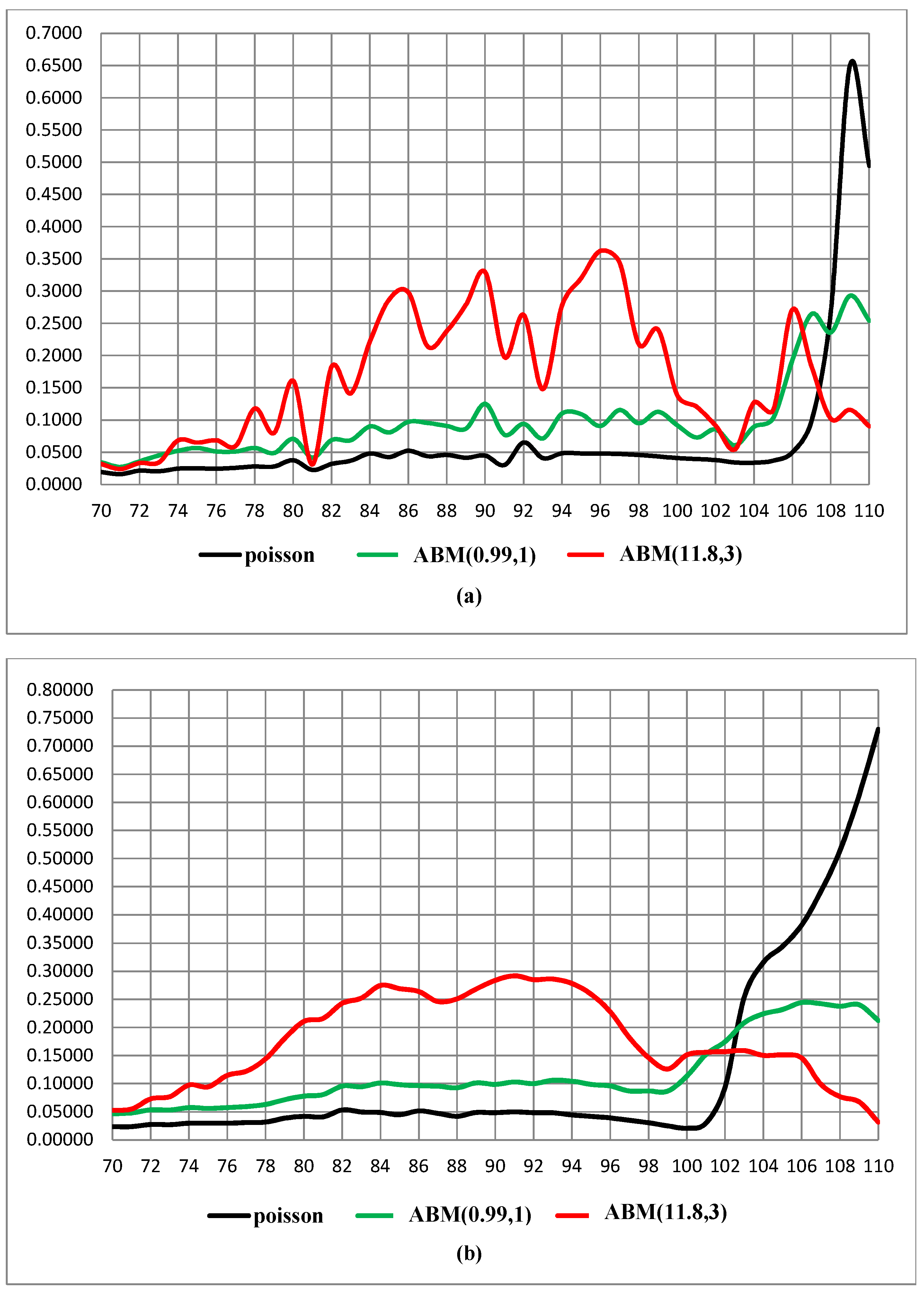Naturally, other countries with their specific national datasets may yield different ABM models (i.e., different $p_2$’s) for mortality projections.

5. Discussion

Several extensions to the LC model assume that the number of deaths is distributed Poisson or negative binomial. These distributions have offered adequate mortality projections in several populations reported in the literature. It is not implausible that cases where these two failed were not reported. Rather than deciding a priori to choose a particular distribution, we aimed to enrich the LC model by allowing a richer pool of candidate distributions. The chosen distribution would be the one providing the best projection for the population and age range under study. To achieve this goal, we proposed a new class of counting distributions on the non-negative integers, the ABM class, which belongs to a wider class of natural exponential families characterized by their variance functions. This class includes the Poisson and negative binomial distributions which are included in an infinitely countable set of additional members. A data mining approach was adopted whereby the model is fitted using a training set and tested using a test set with the RMSE used to pick the winning model. As an alternative to parameter estimation via the singular value decomposition (SVD) used in the classical LC model, we adopted Bayesian estimation, harnessing the Markov Chain Monte Carlo (MCMC) methodology. While we do not suggest that MCMC is superior to SVD (for a comparison of the two, see Ichikawa et al. 2021), we still promote the former since the Bayesian framework frees us from the burden of calculating the normalizing constant of the ABM. This is indeed a great plus, even though running the MCMC requires more computer time for the mid-size databases of the kind used for national mortality projections. We note, however, that the use of MCMC is rather costly and might fail if the dataset is huge. So, perhaps other Bayesian techniques such as Variational Bayes can be more helpful. However, employing such a suggestion is beyond the scope of this paper. We examined ABM models for three countries and established that, for the countries examined, the commonly adopted Poisson distribution is justified except for a very old age for which an alternative member of the ABM class offers better projection. We do not claim that to suggest a superior model. When deciding on an underlying model, one can adopt as an example the Poisson model or the negative binomial model. Rather than adopting a model, we suggest adopting a class of models (the ABM) comprising the Poisson, negative binomial, and numerous other counting distributions. The superiority of this approach lies in the ability to choose a model amongst candidate models. Since no one single model necessarily fits every population and every age group well, the ABM class could allow picking, as an example, the Poisson for members of the population aged under 50, the negative binomial for those aged 50 to 80, and another member of the class to the oldest-old. The suggested criteria for preferring one member of the class over another is the mean squared projection errors (RMSE). This advantage is gained at the cost of additional complexity, which is justified given the financial benefits associated with more accurate modeling. We conclude that it is no longer appropriate to assume a single distribution for the whole process of mortality projection. Instead, for every country and every relevant range of ages, a desirable approach is to pick a member of the ABM class that provides the best mortality projection. In the numerical study reported here, neither the Poisson nor the negative binomial distributions adequately serve the very oldest-old and superior alternatives are within reach in the suggested novel ABM class of distributions.