Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters
Abstract
:1. Introduction
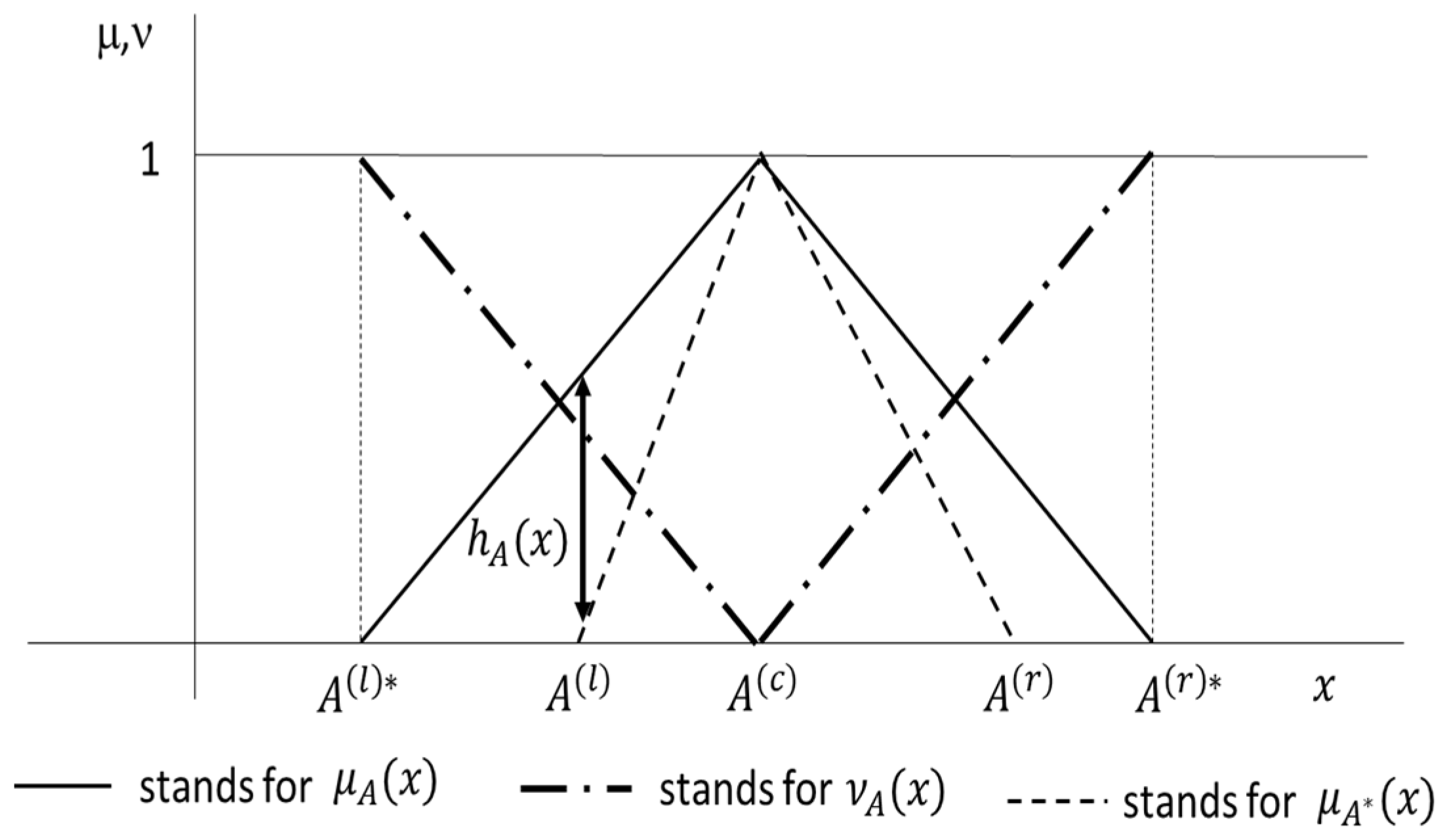
2. Intuitionistic Fuzzy Numbers
2.1. Fuzzy Numbers and Intuitionistic Fuzzy Numbers
- i.
- is normal, i.e.,
- ii.
- is convex, i.e.,
- i.
- ,
- ii.
- i.
- It is normal, i.e.,
- ii.
- is convex,
- iii.
- and is concave:
2.2. Intuitionistic Fuzzy Number Arithmetic
- The local optima at the internal points where . Thus, is negative semidefinite if is obtained at and positive semidefinite if .
- If there are no local optima in , the argument that optimizes is found at the vertex of the domain .
3. An Intuitionistic Fuzzy Framework for Evaluating Life Contingencies for Heterogeneous Life Expectancies
3.1. Modelling One-Year Death Probabilities with Intuitionistic Fuzzy Numbers
- A widely used method for determining is the numerical rating system (Kita 2000), which is particularly prevalent in the life-settlement market (Xu 2020). With this method, , where represents a percentage increase in the death probability associated with the jth factor; that is, it is a so-called debit. Conversely, implies a decrease in the probability of death as the factor increases LE; that is, it is credit. The debits and credits can be precisely estimated (Werth 1995) or expressed imprecisely using fluctuation bands instead of clear values; in this last case, IFNs could be suitable for modelling them. According to Xu and Hoesch (2018), medical underwriting for life settlements is inherently imprecise due to several factors. Base mortality tables inherited from the life insurance market introduce inaccuracies in mortality rates for elderly populations because data for these age groups are scarce (Braun and Xu 2020). Other factors also contribute to biased and imprecise information fitting for debits and credit. These include the false application of information, lack of critical information, and incorporation of irrelevant and false information. These factors emphasize the need to assess life-settlement prices by introducing variability bands in mortality multipliers when calculating LS prices (Xu and Hoesch 2018).
- Lim and Shyamalkumar (2022) indicated that to fit the mortality multiplier, unreported deaths must be considered, whose knowledge is inherently vague because data on this issue in practice are incomplete. They outline that a commonly agreed estimate is “approximately 5%” with seniors ranging from “5–7%,”. Note that these statements are vague and imprecise and are, therefore, susceptible to being modelled with a TIFN whose base TFN may be 5%, 5.5%, or 7%.
- Goodwin et al. (2006) recommend that, in tariffing involving older people with impairments, seeking the judgement of a professional gerontologist is advisable. Fuzzy-set instruments can naturally model subjective information from experts (Shapiro 2004).
- Evaluating not only central values but also extreme mortality scenarios is common practice in insurance markets. Richards (2008) provided an example in the context of life annuities, and Xu and Hoesch (2018) expressed extreme scenarios in the 5th and 95th percentiles. In Andrés-Sánchez and González-Vila (2023), the use of a fuzzy triangular number is justified for shaping a mortality multiplier that can be considered “most reliable” and for two extreme scenarios below and above this central value. The use of TIFNs generalizes the use of TFNs involving a central scenario and two pairs of extreme scenarios, below and above this central value. In these pairs, while one scenario might be factually extreme (e.g., percentiles 10 and 90), the other could be potentially extreme (e.g., comparable to percentiles 0.5 and 99.5).
- In the life-settlement market, reliable values of life expectancy and, consequently, the mortality multiplier are typically expressed not by a crisp parameter but with a set of crisp estimates. This is because the LE of the insured is often reported by at least two independent medical underwriters (Xu 2020). Therefore, for a given policy, if the set of multipliers by LE providers is , it seems reliable to give a fuzzy quantification to the mortality multiplier, as “it must be approximately and “it may fluctuate in margins depending on ” (Andrés-Sánchez and González-Vila 2023).
- The derivation of the sensitivity of death probability to risk factors through regression methods, as developed by Meyricke and Sherris (2013), assumes that the estimation of death probabilities and coefficients involves probabilistic confidence intervals. The results of Couso et al. (2001), Dubois et al. (2004), and Sfiris and Papadopoulos (2014) facilitate the inference of fuzzy numbers using probabilistic confidence intervals. These findings were employed in a regression framework by Adjenughwure and Papadopoulos (2020) and Al-Kandari et al. (2020), where the variables of interest were predicted by fuzzy numbers induced from probabilistic confidence interval estimates derived from statistical regression. Remark 6 shows that TIFN can be induced from the estimated TFN.
- Of course, fuzzy one-year standard mortality probabilities may consider an impairment common to a wide proportion of the population, for which the evaluator has developed mortality tables ad hoc (Drinkwater et al. 2006). An example of this is the mortality tables for smokers. If a person has no other cause of impairment, .
3.2. Modelling the Probabilities of Survival and the Curated Life Expectancy with Intuitionistic Fuzzy Numbers
3.3. Pricing Immediate Whole-Life Annuities and Immediate Whole-Life Insurance with Intuitionistic Fuzzy Parameters
4. Pricing Special-Rate Annuities and Life Settlements with Intuitionistic Fuzzy Parameters
4.1. Obtaining the Periodical Payment of a Substandard Annuity with Intuitionistic Fuzzy Number Parameters
4.2. Pricing Life Settlements with Intuitionistic Fuzzy Number Parameters
5. Conclusions and Further Research
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Pseudocodes for Table 2 |
| . |
| . |
| and to obtain -cuts. |
| by the adjusted death probability |
| by evaluating , . |
| Step 6: Calculate . |
| and ? |
| If the response to step 7 is negative, then stop. |
| If the response to step 7 is positive, then go to step 8. |
| by considering and . |
| by considering and . |
| Step 10: Do you want to know the errors by the triangular approximates? |
| If the response is negative, then stop. |
| If the response is positive, then go to step 11. |
| by . |
| by . |
| Pseudocodes for Table 3 |
| . |
| and. |
| and to obtain-cuts and . |
| by for the adjusted death probability |
| by evaluating , . |
| by and as the present value . |
| -cuts of and the present value |
| and ? |
| If the response to step 8 is negative, then stop. |
| If the response to step 8 is positive, then go to step 9. |
| by considering and . |
| by considering and . |
| Step 11: Do you want to know the errors by the triangular approximates? |
| If the response is negative, then stop. |
| If the response is positive, then go to step 12. |
| by . |
| by . |
| Pseudocodes for Table 4 |
| and state the premium . |
| and . |
| and to obtain -cuts and . |
| the adjusted death probability |
| evaluate in . |
| Step 6: Obtain by and as the present value . |
| , . |
| ? |
| If the response is negative, then stop. |
| If the response is positive, then go to step 9. |
| by considering and . |
| Step 10: Do you want to know the errors by the triangular approximation? |
| If the response is negative, then stop. |
| If the response is positive, then go to step 11. |
| by . |
| Pseudocodes for Table 6 |
| the death benefit and periodical premiums . |
| and. |
| and to obtain -cuts and . |
| the adjusted death probability |
| by evaluating in |
| Step 6: Obtain and as follows: |
| ? |
| If the response to step 7 is negative, then stop. |
| If the response to step 7 is positive, then go to step 8. |
| by considering and . |
| Step 9: Do you want to know the errors by the triangular approximation? |
| If the response is negative, then stop. |
| If the response is positive, then go to step 10. |
| by . |
References
- Aalaei, Mahboubeh. 2022. Pricing life settlements in the secondary market using fuzzy internal rate of return. Journal of Mathematics and Modelling in Finance 2: 53–62. [Google Scholar] [CrossRef]
- AA-Partners Ltd. 2017. AAP Life Settlement Valuation. Retrieved on 10th of September 2022. Available online: https://www.aa-partners.ch/fileadmin/files/Valuation/AAP_Life_Settlement_Valuation_-_Manual_V6.0.pdf (accessed on 30 October 2023).
- Adjenughwure, Kingsley, and Basil Papadopoulos. 2020. Fuzzy-statistical prediction intervals from crisp regression models. Evolving Systems 11: 201–13. [Google Scholar] [CrossRef]
- Al-Kandari, Maryam, Kingsley Adjenughwure, and Kyriakos Papadopoulos. 2020. A Fuzzy-Statistical Tolerance Interval from Residuals of Crisp Linear Regression Models. Mathematics 8: 1422. [Google Scholar] [CrossRef]
- Anderton, W. Nicholas, and Geoffrey H. Robb. 1998. Impaired Lives Annuities. In Medical Selection of Life Risks. London: Palgrave Macmillan UK, pp. 169–71. [Google Scholar]
- Andrés-Sánchez, Jorge de. 2012. Claim reserving with fuzzy regression and the two ways of ANOVA. Applied Soft Computing 12: 2435–41. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de. 2014. Fuzzy claim reserving in nonlife insurance. Computer Science and Information Systems 11: 825–38. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de. 2023. Fuzzy Random Option Pricing in Continuous Time: A Systematic Review and an Extension of Vasicek’s Equilibrium Model of the Term Structure. Mathematics 11: 2455. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Laura González-Vila. 2012. Using fuzzy random variables in life annuities pricing. Fuzzy Sets and Systems 188: 27–44. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Laura González-Vila. 2017a. Some computational results for the fuzzy random value of life actuarial liabilities. Iranian Journal of Fuzzy Systems 14: 1–25. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Laura M. González-Vila. 2017b. The valuation of life contingencies: A symmetrical triangular fuzzy approximation. Insurance: Mathematics and Economics 72: 83–94. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Laura M. González-Vila. 2019. A fuzzy-random extension of the Lee-Carter mortality prediction model. International Journal of Computational Intelligence Systems 12: 775–94. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Antonio Terceño. 2003. Applications of fuzzy regression in actuarial analysis. Journal of Risk and Insurance 70: 665–99. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, and Laura González-Vila. 2023. Life settlement pricing with fuzzy parameters. Applied Soft Computing 148: 110924. [Google Scholar] [CrossRef]
- Andrés-Sánchez, Jorge de, Laura González-Vila, and Aihua Zhang. 2020. Incorporating fuzzy information in pricing substandard annuities. Computers and Industrial Engineering 145: 106475. [Google Scholar] [CrossRef]
- Anzilli, Luca, and Gisella Facchinetti. 2017. New definitions of mean value and variance of fuzzy numbers: An application to the pricing of life insurance policies and real options. International Journal of Approximate Reasoning 91: 96–113. [Google Scholar] [CrossRef]
- Anzilli, Luca, Gisella Facchinetti, and Tommaso Pirotti. 2018. Pricing of minimum guarantees in life insurance contracts with fuzzy volatility. Information Sciences 460: 578–93. [Google Scholar] [CrossRef]
- Apaydin, Aysen, and Furkan Baser. 2010. Hybrid fuzzy least-squares regression analysis in claims reserving with geometric separation method. Insurance: Mathematics and Economics 47: 113–22. [Google Scholar] [CrossRef]
- Atanassov, Krassimir. 1986. Intuitionistic fuzzy sets. Fuzzy Sets and Systems 20: 87–96. [Google Scholar] [CrossRef]
- Atanassov, Krassimir. 1989. More on intuitionistic fuzzy sets. Fuzzy Sets and Systems 33: 37–45. [Google Scholar] [CrossRef]
- Bauer, Daniel, Jochen Russ, and Nan Zhu. 2020. Asymmetric information in secondary insurance markets: Evidence from the life settlements market. Quantitative Economics 11: 1143–75. [Google Scholar] [CrossRef]
- Bayeg, Selami, and Rasiye Mert. 2021. On intuitionistic fuzzy version of Zadeh’s extension principle. Notes on Intuitionistic Fuzzy Sets 27: 9–17. [Google Scholar] [CrossRef]
- Betzuen, Amancio, Mariano Jiménez, and Juan A. Rivas. 1997. Actuarial mathematics with fuzzy parameters: An application to collective pension plans. Fuzzy Economic Review 2: 47–66. [Google Scholar] [CrossRef]
- Bhaumik, Ankar, Sankar K. Roy, and Deng-Feng Li. 2017. Analysis of triangular intuitionistic fuzzy matrix games using robust ranking. Journal of Intelligent and Fuzzy Systems 33: 327–36. [Google Scholar] [CrossRef]
- Boltürk, Eda, and Cengiz Kahraman. 2022. Interval-valued and circular intuitionistic fuzzy present worth analyses. Informatica 33: 693–711. [Google Scholar] [CrossRef]
- Braun, Alexander, and Jiahua Xu. 2020. Fair value measurement in the life settlement market. The Journal of Fixed Income 29: 100–23. [Google Scholar] [CrossRef]
- Brockett, Patrick L., Shuo-li Chuang, Yinglu Deng, and Richard D. MacMinn. 2013. Incorporating longevity risk and medical information into life settlement pricing. Journal of Risk and Insurance 80: 799–826. [Google Scholar] [CrossRef]
- Buckley, James J. 1987. The fuzzy mathematics of finance. Fuzzy Sets and Systems 21: 257–73. [Google Scholar] [CrossRef]
- Buckley, James J. 1992. Solving fuzzy equations in economics and finance. Fuzzy Sets and Systems 48: 289–96. [Google Scholar] [CrossRef]
- Buckley, James J., and Yunxia Qu. 1990. On using α-cuts to evaluate fuzzy equations. Fuzzy Sets and Systems 38: 309–12. [Google Scholar] [CrossRef]
- Bundock, Gary. 2006. Application Processing. In Brackenridge’s Medical Selection of Life Risks. Edited by R. D. C. Brackenridge and W. John Elder. London: Palgrave Macmillan. [Google Scholar]
- Burillo, Pedro, and Humberto Bustince. 1996. Construction theorems for intuitionistic fuzzy sets. Fuzzy Sets and Systems 84: 271–81. [Google Scholar] [CrossRef]
- Cassú, Carles, Pere Planas, Joan Carles Ferrer, and Joan Bonet. 1996. Accumulated capital for the retirement plans in fuzzy finance mathematics. Fuzzy Economic Review 1: 83–92. [Google Scholar] [CrossRef]
- Couso, Inés, Susana Montes, and Pedro Gil. 2001. The necessity of the strong α-cuts of a fuzzy set. International Journal of Uncertain Fuzziness Knowledge-Based Systems 2: 249–62. [Google Scholar] [CrossRef]
- Cummins, David J., and Richard A. Derrig. 1997. Fuzzy financial pricing of property-liability insurance. North American Actuarial Journal 1: 21–40. [Google Scholar] [CrossRef]
- Derrig, Richard A., and Kristoff M. Ostaszewski. 1997. Managing the tax liability of a property-liability insurance company. Journal of Risk and Insurance 64: 695–711. [Google Scholar] [CrossRef]
- Derrig, Richard A., and Kristoff M. Ostaszewski. 2006. Fuzzy Set Theory. In Encyclopedia of Actuarial Science. Edited by Josef L. Teugels, Bjorn Sundt and Soren Asmussen. Chichester: John Willey and Sons Ltd. [Google Scholar] [CrossRef]
- Devolder, Pierre. 1988. Le taux d’actualization en assurance. Geneva Papers on Risk and Insurance 13: 265–72. [Google Scholar] [CrossRef]
- Dębicka, Joanna, Stanislaw Heilpern, and Agnieszka Marciniuk. 2022. Modelling Marital Reverse Annuity Contract in a Stochastic Economic Environment. Statistika: Statistics and Economy Journal 102: 261–81. [Google Scholar] [CrossRef]
- Dong, Ming-Gao, and Shou-Yi Li. 2016. Project investment decision making with fuzzy information: A literature review of methodologies based on taxonomy. Journal of Intelligent and Fuzzy Systems 30: 3239–52. [Google Scholar] [CrossRef]
- Dong, Weimin, and Haresh C. Shah. 1987. Vertex method for computing functions of fuzzy variables. Fuzzy Sets and Systems 24: 65–78. [Google Scholar] [CrossRef]
- Drinkwater, Matthew, Joseph E. Montminy, Eric T. Sondergeld, Christopher G. Raham, and Chad R. Runchey. 2006. Substandard annuities. Technical Report. LIMRA International Inc. and the Society of Actuaries, in Collaboration with Ernst & Young LLP. Available online: https://www.soa.org/Files/Research/007289-Substandard-annuities-full-rpt-REV-8-21.pdf (accessed on 10 October 2023).
- Dubois, Didier, and Henry Prade. 1993. Fuzzy numbers: An overview. Readings in Fuzzy Sets for Intelligent Systems, 112–48. [Google Scholar] [CrossRef]
- Dubois, Didier, and Henry Prade. 2012. Gradualness, uncertainty and bipolarity: Making sense of fuzzy sets. Fuzzy Sets and Systems 192: 3–24. [Google Scholar] [CrossRef]
- Dubois, Didier, Laurent Folloy, Gilles Mauris, and Henry Prade. 2004. Probability–possibility transformations, triangular fuzzy sets, and probabilistic inequalities. Reliable Computing 10: 273–97. [Google Scholar] [CrossRef]
- Eling, Martin, and Stefan Holder. 2013. Maximum technical interest rates in life insurance in Europe and the United States: An overview and comparison. The Geneva Papers on Risk and Insurance-Issues and Practice 38: 354–75. [Google Scholar] [CrossRef]
- Ersen, Huseyin Y., Oktay Tas, and Cengit Kahraman. 2018. Intuitionistic fuzzy real-options theory and its application to solar energy investment projects. Engineering Economics 29: 140–50. [Google Scholar] [CrossRef]
- Ersen, Huseyin Y., Oktay Tas, and Umut Ugurlu. 2023. Solar Energy Investment Valuation With Intuitionistic Fuzzy Trinomial Lattice Real Option Model. IEEE Transactions on Engineering Management 70: 2584–93. [Google Scholar] [CrossRef]
- Gatzert, Nadine. 2010. The secondary market for life insurance in the UnitedKingdom, Germany, and the United States: Comparison and overview. Risk Management and Insurance Review 13: 279–301. [Google Scholar] [CrossRef]
- Gatzert, Nadine, and Udo Klotzki. 2016. Enhanced annuities: Drivers of and barriers to supply and demand. The Geneva Papers on Risk and Insurance-Issues and Practice 41: 53–77. [Google Scholar] [CrossRef]
- Goodwin, Linda S., Paul E. Hankwitz, and Martin L. Engman. 2006. Underwriting older ages. In Brackenridge’s Medical Selection of Life Risks. Edited by R. D. C. Brackenridge and W. John Elder. London: Palgrave Macmillan. [Google Scholar]
- Haktanır, Elif, and Cengit Kahraman. 2023. Intuitionistic fuzzy risk adjusted discount rate and certainty equivalent methods for risky projects. International Journal of Production Economics 257: 108757. [Google Scholar] [CrossRef]
- Heberle, Jochen, and Anne Thomas. 2014. Combining chain-ladder claims reserving with fuzzy numbers. Insurance: Mathematics and Economics 55: 96–104. [Google Scholar] [CrossRef]
- Heberle, Jochen, and Anne Thomas. 2016. The fuzzy Bornhuetter–Ferguson method: An approach with fuzzy numbers. Annals of Actuarial Science 10: 303–21. [Google Scholar] [CrossRef]
- Jiménez, Mariano, and Juan A Rivas. 1998. Fuzzy number approximation. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 6: 69–78. [Google Scholar] [CrossRef]
- Kahraman, Cengit, Da Ruan, and Ethem Tolga. 2002. Capital budgeting techniques using discounted fuzzy versus probabilistic cash flows. Information Sciences 142: 57–76. [Google Scholar] [CrossRef]
- Kahraman, Cengit, S. Çevik Onar, and Basar Öztayşi. 2015. Engineering economic analyses using intuitionistic and hesitant fuzzy sets. Journal of Intelligent and Fuzzy Systems 29: 1151–68. [Google Scholar] [CrossRef]
- Kaufmann, Arnold. 1986. Fuzzy subsets applications in OR and management. In Fuzzy Sets Theory and Applications. Edited by André Jones, Arnold Kaufmann and Hans Jürgen Zimmermann. Dordrecht: Springer, pp. 257–300. [Google Scholar]
- Kita, Michael W. 2000. The rating of substandard lives. In Medical Selection of Life Risks. London: Palgrave Macmillan UK, pp. 61–88. [Google Scholar]
- Koissi, Marie-Claire, and Arnold F. Shapiro. 2006. Fuzzy formulation of the Lee–Carter model for mortality forecasting. Insurance: Mathematics and Economics 39: 287–309. [Google Scholar] [CrossRef]
- Kreinovich, Vladik, Olga Kosheleva, and Shahnaz N. Shahbazova. 2020. Why Triangular and Trapezoid Membership Functions: A Simple Explanation. In Recent Developments in Fuzzy Logic and Fuzzy Sets. Studies in Fuzziness and Soft Computing. Edited by Shahnaz N. Shahbazova, Michio Sugeno and Janusz Kacprzyk. Cham: Springer, vol. 391. [Google Scholar] [CrossRef]
- Kumar, Gaurav, and Rakesh K. Bajaj. 2014. Implementation of intuitionistic fuzzy approach in maximizing net present value. International Journal of Mathematical and Computational Sciences 8: 1069–73. [Google Scholar] [CrossRef]
- Kumar, P. Senthil, and R. Jahir Hussain. 2015. A method for solving unbalanced intuitionistic fuzzy transportation problems. Notes on Intuitionistic Fuzzy Sets 21: 54–65. [Google Scholar] [CrossRef]
- Kung, Ko-Lun, Mi-Hun Hsieh, Jing-Lung Peng, Chenghsien J. Tsai, and Jennifer L. Wang. 2021. Explaining the risk premiums of life settlements. Pacific-Basin Finance Journal 68: 101574. [Google Scholar] [CrossRef]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modelling and forecasting US mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Lemaire, Jean. 1990. Fuzzy insurance. ASTIN Bulletin: The Journal of the IAA 20: 33–55. [Google Scholar] [CrossRef]
- Lim, Hong-Beng, and Nariankadu D. Shyamalkumar. 2022. Evaluating Medical Underwriters in Life Settlements: Problem of Unreported Deaths. North American Actuarial Journal 26: 298–322. [Google Scholar] [CrossRef]
- Lubovich, Jandra, Jon Sabes, and Paul Siegert. 2008. Introduction to Methodologies Used to Price Life Insurance Policies in Life Settlement Transactions. SSRN. [Google Scholar] [CrossRef]
- Mahapatra, G. S., and Tapan K. Roy. 2013. Intuitionistic fuzzy number and its arithmetic operation with application on system failure. Journal of Uncertain Systems 7: 92–107. [Google Scholar]
- Meyricke, Ramona, and Michael Sherris. 2013. The determinants of mortality heterogeneity and implications for pricing annuities. Insurance: Mathematics and Economics 53: 379–87. [Google Scholar] [CrossRef]
- Mircea, Iulian, and Michaela Covrig. 2015. A discrete time insurance model with reinvested surplus and a fuzzy number interest rate. Procedia Economics and Finance 32: 1005–11. [Google Scholar] [CrossRef]
- Mitchell, Harvey B. 2004. Ranking-intuitionistic fuzzy numbers. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 12: 377–86. [Google Scholar] [CrossRef]
- Muzzioli, Silvia, and Bernard De Baets. 2016. Fuzzy approaches to option price modelling. IEEE Transactions on Fuzzy Systems 25: 392–401. [Google Scholar] [CrossRef]
- Nguyen, Hung T. 1978. A note on the extension principle for fuzzy sets. Journal of Mathematical Analysis and Aplications 64: 369–80. [Google Scholar] [CrossRef]
- Nowak, Piotr, and Maciej Romaniuk. 2017. Catastrophe bond pricing for the two-factor Vasicek interest rate model with automatized fuzzy decision making. Soft Computing 21: 2575–97. [Google Scholar] [CrossRef]
- Olivieri, Annamaria. 2006. Heterogeneity in survival models. Applications to pensions and life annuities. Belgian Actuarial Bulletin 6: 23–39. [Google Scholar] [CrossRef]
- Olivieri, Annamaria, and Ermanno Pitacco. 2016. Frailty and risk classification for life annuity portfolios. Risks 4: 39. [Google Scholar] [CrossRef]
- Ostaszewski, K. 1993. An Investigation into Possible Applications of Fuzzy Sets Methods in Actuarial Science. Schaumburg: Society of Actuaries. [Google Scholar]
- Pitacco, Ermanno. 2017. Life Annuities. Products, Guarantees, Basic Actuarial Models. Available online: https://ssrn.com/abstract=2887359 (accessed on 30 October 2023).
- Pitacco, Ermanno. 2019. Heterogeneity in mortality: A survey with an actuarial focus. European Actuarial Journal 9: 3–30. [Google Scholar] [CrossRef]
- Pitacco, Ermanno, and Daniela Y. Tabakova. 2022. Special-rate life annuities: Analysis of portfolio risk profiles. Risks 10: 65. [Google Scholar] [CrossRef]
- Promislow, S. David. 2014. Fundamentals of Actuarial Mathematics. New York: John Wiley and Sons. [Google Scholar]
- Rasheed, Farah, Sagida Kousar, Javid Shabbir, Nasreen Kausar, Dragan Pamucar, and Yaé Ulrich Gaba. 2021. Use of intuitionistic fuzzy numbers in survey sampling analysis with application in electronic data interchange. Complexity 2021: 9989477. [Google Scholar] [CrossRef]
- Richards, Stephen J. 2008. Applying survival models to pensioner mortality data. British Actuarial Journal 14: 257–303. [Google Scholar] [CrossRef]
- Sfiris, Dimitris S., and Basil K. Papadopoulos. 2014. Nonasymptotic fuzzy estimators based on confidence intervals. Information Sciences 279: 446–59. [Google Scholar] [CrossRef]
- Shapiro, Arnold F. 2004. Fuzzy logic in insurance. Insurance: Mathematics and Economics 35: 399–424. [Google Scholar] [CrossRef]
- Shapiro, Arnold F. 2013. Modelling future lifetime as a fuzzy random variable. Insurance: Mathematics and Economics 53: 864–70. [Google Scholar] [CrossRef]
- Shen, Yonghong, and Wei Chen. 2012. Multivariate extension principle and algebraic operations of intuitionistic fuzzy sets. Journal of Applied Mathematics 845090. [Google Scholar] [CrossRef]
- Sosa, Ivan, and Oscar Montes. 2022. Understanding the InsurTech dynamics in the transformation of the insurance sector. Risk Management Insurance Review 25: 35–68. [Google Scholar] [CrossRef]
- Szymański, Andrzej, and Agnieszka Rossa. 2021. The modified fuzzy mortality model based on the algebra of ordered fuzzy numbers. Biometrical Journal 63: 671–89. [Google Scholar] [CrossRef]
- Terceño, Antonio, Jorge de Andrés-Sánchez, M. Gloria Barberà, and Tomás Lorenzana. 2003. Using fuzzy set theory to analyse investments and select portfolios of tangible investments in uncertain environments. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 11: 263–81. [Google Scholar] [CrossRef]
- Ungureanu, Daniela, and Raluca Vernic. 2015. On a fuzzy cash flow model with insurance applications. Decisions in Economics and Finance 38: 39–54. [Google Scholar] [CrossRef]
- Villacorta, Pablo J., Laura M. González-Vila, and Jorge de Andrés-Sánchez. 2021. Fuzzy Markovian Bonus-Malus Systems in Nonlife Insurance. Mathematics 9: 347. [Google Scholar] [CrossRef]
- Werth, Martin. 1995. Preferred Lives––A More Complete Method of Risk Assessment. Staple Inn Actuarial Society. Available online: https://www.actuaries.org.uk/system/files/documents/pdf/preferred.pdf (accessed on 30 October 2023).
- World Cancer Research Fund International. 2023. Cancer Survirval Statistics. Available online: https://www.wcrf.org/cancer-trends/worldwide-cancer-data/ (accessed on 12 January 2024).
- Woundjiagué, Apollinaire, Martin Le Roux Bidima, and Mwangi Ronald Waweru. 2019. A fuzzy least-squares estimation of a hybrid log-poisson regression and its goodness of fit for optimal loss reserves in insurance. International Journal of Fuzzy Systems 21: 930–44. [Google Scholar] [CrossRef]
- Wu, Liang, Jie-fang Liu, Jun-tao Wang, and Ya-ming Zhuang. 2016. Pricing for a basket of LCDS under fuzzy environments. SpringerPlus 5: 1–12. [Google Scholar] [CrossRef]
- Xu, Jiahua. 2020. Dating death: An empirical comparison of medical underwriters in the US life settlement market. North American Actuarial Journal 24: 36–56. [Google Scholar] [CrossRef]
- Xu, Jiahua, and Adrian Hoesch. 2018. Predicting longevity: An analysis of potential alternatives to life expectancy reports. Journal of Investing 27: 65–79. [Google Scholar] [CrossRef]
- Xu, Weidong, Chongfeng Wu, Weijun Xu, and Hongyi Li. 2009. A jump-diffusion model for option pricing under fuzzy environments. Insurance: Mathematics and Economics 44: 337–44. [Google Scholar] [CrossRef]
- Yuan, Xuehai, Hongxing Li, and Cheng Zhang. 2014. The theory of intuitionistic fuzzy sets based on the intuitionistic fuzzy special sets. Information Sciences 277: 284–98. [Google Scholar] [CrossRef]
- Zadeh, Lotfi A. 1965. Fuzzy Sets. Information and Control 8: 338–53. [Google Scholar] [CrossRef]
| Issue | Papers |
|---|---|
| Life insurance pricing (cash-flow discounting) | Lemaire (1990), Ostaszewski (1993), Andrés-Sánchez and Terceño (2003), Shapiro (2004), Andrés Sánchez and González-Vila (2012, 2017a, 2017b, 2023), Andrés-Sánchez et al. (2020), Aalaei (2022), Dębicka et al. (2022). |
| Life insurance pricing (final value) | Cassú et al. (1996), Betzuen et al. (1997), |
| Insurance pricing (option pricing) | Xu et al. (2009), Anzilli and Facchinetti (2017), Nowak and Romaniuk (2017), Anzilli et al. (2018). |
| Nonlife insurance (cash-flow discounting) | Derrig and Ostaszewski (1997), Cummins and Derrig (1997), Andrés-Sánchez and Terceño (2003), Andrés-Sánchez (2014), |
| Nonlife insurance (terminal value) | Mircea and Covrig (2015), Ungureanu and Vernic (2015), |
| Claim reserving | Andrés-Sánchez and Terceño (2003), Apaydin and Baser (2010), Andrés-Sánchez (2012), Heberle and Thomas (2014), Heberle and Thomas (2016), Woundjiagué et al. (2019). |
| 10-Year Life Probability for x = 65 | Life Expectancy for x = 65 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| α | β | ||||||||
| 1 | 0 | 0.4592 | 0.4592 | 0.4592 | 0.4592 | 9.10 | 9.10 | 9.10 | 9.10 |
| 0.75 | 0.25 | 0.4439 | 0.4749 | 0.4364 | 0.4830 | 8.87 | 9.34 | 8.77 | 9.47 |
| 0.5 | 0.5 | 0.4290 | 0.4912 | 0.4146 | 0.5079 | 8.66 | 9.59 | 8.45 | 9.86 |
| 0.25 | 0.75 | 0.4146 | 0.5079 | 0.3938 | 0.5340 | 8.45 | 9.86 | 8.16 | 10.29 |
| 0 | 1 | 0.4007 | 0.5252 | 0.3740 | 0.5612 | 8.26 | 10.15 | 7.89 | 10.77 |
| α | β | ||||||||
| 1 | 0 | 0.4592 | 0.4592 | 0.4592 | 0.4592 | 9.10 | 9.10 | 9.10 | 9.10 |
| 0.75 | 0.25 | 0.4445 | 0.4757 | 0.4379 | 0.4847 | 8.89 | 9.36 | 8.80 | 9.52 |
| 0.5 | 0.5 | 0.4299 | 0.4922 | 0.4166 | 0.5102 | 8.68 | 9.62 | 8.50 | 9.94 |
| 0.25 | 0.75 | 0.4153 | 0.5087 | 0.3953 | 0.5357 | 8.47 | 9.88 | 8.19 | 10.35 |
| 0 | 1 | 0.4007 | 0.5252 | 0.3740 | 0.5612 | 8.26 | 10.15 | 7.89 | 10.77 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.0015 | 0.0015 | 0.0034 | 0.0035 | 0.002 | 0.002 | 0.004 | 0.006 |
| 0.5 | 0.5 | 0.0021 | 0.0020 | 0.0047 | 0.0045 | 0.002 | 0.003 | 0.005 | 0.008 |
| 0.25 | 0.75 | 0.0016 | 0.0015 | 0.0037 | 0.0033 | 0.002 | 0.002 | 0.004 | 0.006 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.0017 = 0.0017 0.0017 | 0.0039 = 0.0038 0.0038 | 0.0020 = 0.0026 = 0.0023 | 0.0043 0.0062 0.0053 | ||||||
| Whole Life Annuity | Whole Life Insurance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| α | β | ||||||||
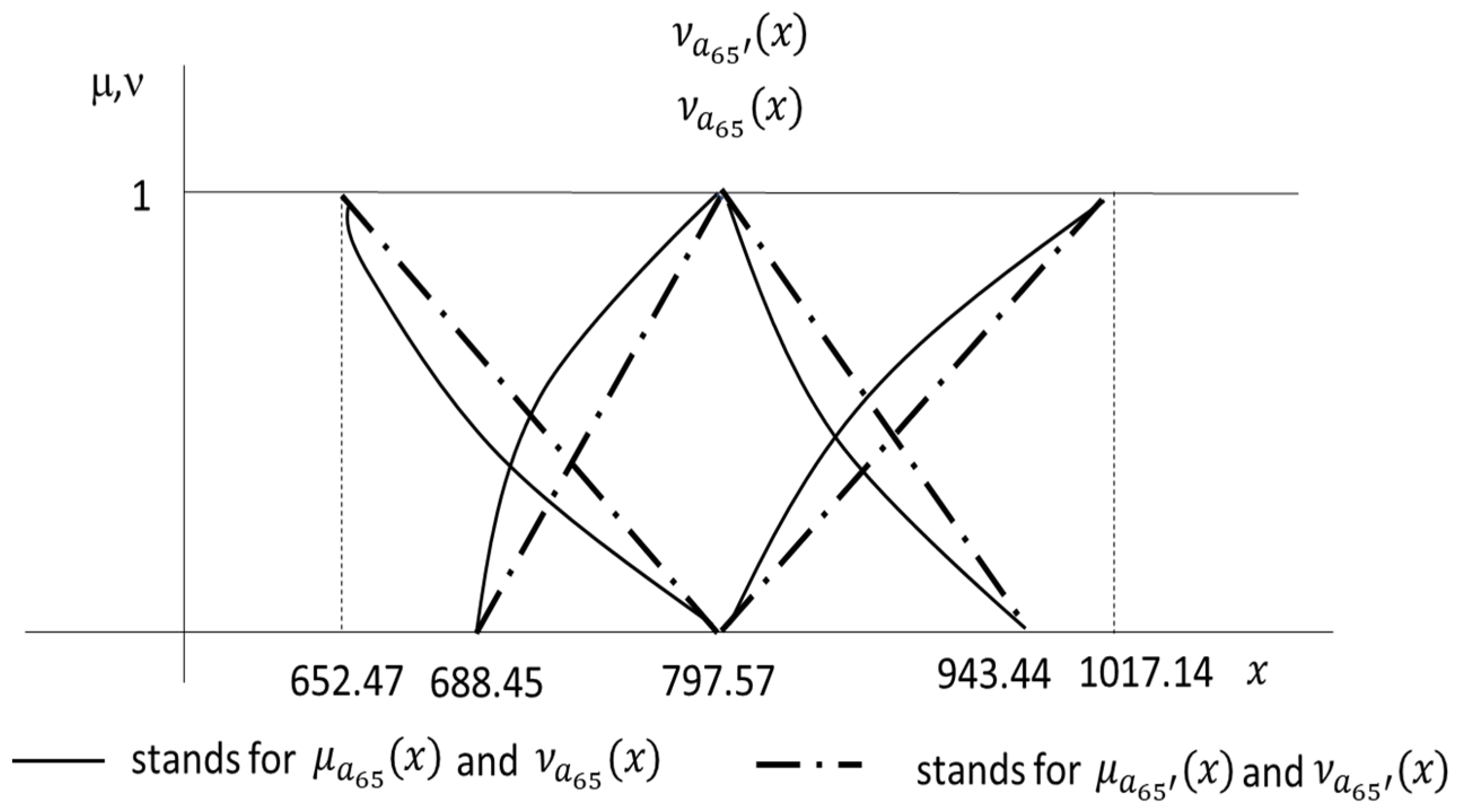
| 1 | 0 | 797.57 | 797.57 | 797.57 | 797.57 | 82.40 | 82.40 | 82.40 | 82.40 |
| 0.75 | 0.25 | 767.44 | 829.95 | 756.02 | 843.58 | 80.12 | 84.66 | 79.43 | 85.30 |
| 0.5 | 0.5 | 739.34 | 864.85 | 718.32 | 894.83 | 77.81 | 86.91 | 76.39 | 88.14 |
| 0.25 | 0.75 | 713.06 | 902.56 | 683.94 | 952.27 | 75.47 | 89.13 | 73.26 | 90.92 |
| 0 | 1 | 688.45 | 943.44 | 652.47 | 1017.14 | 73.11 | 91.33 | 70.04 | 93.65 |
| α | β | ||||||||
| 1 | 0 | 797.57 | 797.57 | 797.57 | 797.57 | 82.40 | 82.40 | 82.40 | 82.40 |
| 0.75 | 0.25 | 770.29 | 834.04 | 761.30 | 852.46 | 80.08 | 84.63 | 79.31 | 85.21 |
| 0.5 | 0.5 | 743.01 | 870.51 | 725.02 | 907.35 | 77.75 | 86.87 | 76.22 | 88.02 |
| 0.25 | 0.75 | 715.73 | 906.97 | 688.74 | 962.25 | 75.43 | 89.10 | 73.13 | 90.83 |
| 0 | 1 | 688.45 | 943.44 | 652.47 | 1017.14 | 73.11 | 91.33 | 70.04 | 93.65 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.0037 | 0.0049 | 0.0070 | 0.0105 | 0.0005 | 0.0003 | 0.0015 | 0.0010 |
| 0.5 | 0.5 | 0.0050 | 0.0065 | 0.0093 | 0.0140 | 0.0007 | 0.0004 | 0.0022 | 0.0013 |
| 0.25 | 0.75 | 0.0037 | 0.0049 | 0.0070 | 0.0105 | 0.0005 | 0.0003 | 0.0018 | 0.0009 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| = 0.00248 = 0.00327 = 0.00288 | = 0.00466 = 0.00700 0.00583 | = 0.00082 = 0.00056 = 0.00069 | = 0.00271 = 0.00166 = 0.00218 | ||||||
| α | β | ||||||||
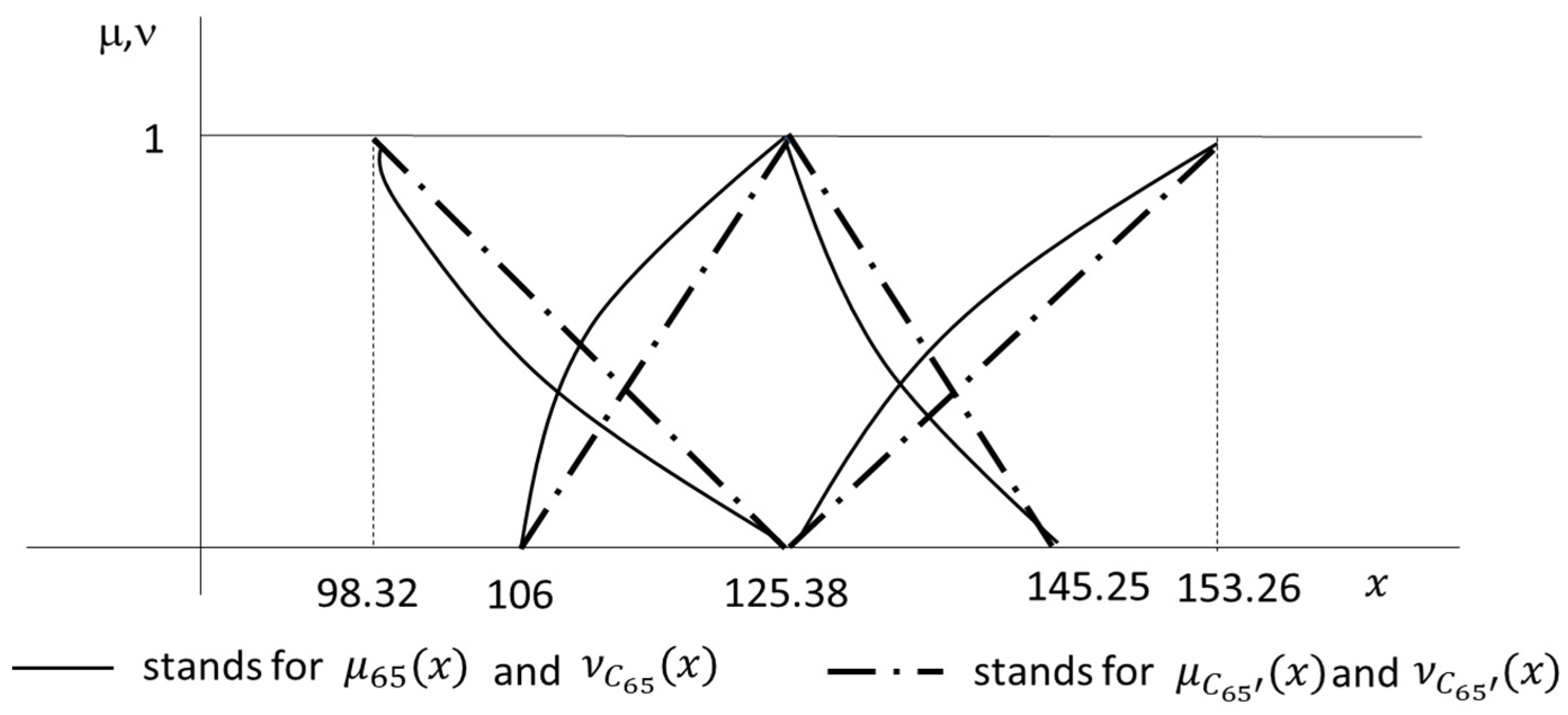
| 1 | 0 | 125.38 | 125.38 | 125.38 | 125.38 | 167.87 | 167.87 | 167.87 | 167.87 |
| 0.75 | 0.25 | 120.49 | 130.30 | 118.54 | 132.27 | 161.33 | 174.46 | 158.59 | 177.24 |
| 0.5 | 0.5 | 115.63 | 135.26 | 111.75 | 139.21 | 154.83 | 181.09 | 149.39 | 186.69 |
| 0.25 | 0,75 | 110.80 | 140.24 | 105.01 | 146.21 | 148.38 | 187.78 | 140.26 | 196.24 |
| 0 | 1 | 106.00 | 145.25 | 98.32 | 153.26 | 141.97 | 194.51 | 131.20 | 205.89 |
| α | β | ||||||||
| 1 | 0 | 125.38 | 125.38 | 125.38 | 125.38 | 167.87 | 167.87 | 167.87 | 167.87 |
| 0.75 | 0.25 | 120.53 | 130.35 | 118.61 | 132.35 | 161.39 | 174.53 | 158.70 | 177.37 |
| 0.5 | 0.5 | 115.69 | 135.32 | 111.85 | 139.32 | 154.92 | 181.19 | 149.54 | 186.88 |
| 0.25 | 0.75 | 110.84 | 140.29 | 105.08 | 146.29 | 148.44 | 187.85 | 140.37 | 196.38 |
| 0 | 1 | 106.00 | 145.25 | 98.32 | 153.26 | 141.97 | 194.51 | 131.20 | 205.89 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.00038 | 0.00035 | 0.00061 | 0.00061 | 0.00041 | 0.00041 | 0.00073 | 0.00077 |
| 0.5 | 0.5 | 0.00052 | 0.00045 | 0.00085 | 0.00078 | 0.00057 | 0.00052 | 0.00101 | 0.00099 |
| 0.25 | 0.75 | 0.00041 | 0.00033 | 0.00066 | 0.00056 | 0.00044 | 0.00038 | 0.00078 | 0.00071 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| = 0.00026 = 0.00023 = 0.00024 | = 0.00042 = 0.00040 0.00041 | = 0.00028 = 0.00027 = 0.00027 | = 0.00050 = 0.00050 0.00050 | ||||||
| Values (x) | Membership | Nonmembership | Indeterminacy | |||||
|---|---|---|---|---|---|---|---|---|
| LE | UE | |||||||
| Median | 125.45 | 125.45 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 50%CI | 120.87 | 129.93 | 0.77 | 0.77 | 0.17 | 0.16 | 0.06 | 0.07 |
| 90%CI | 114.36 | 136.46 | 0.43 | 0.44 | 0.41 | 0.40 | 0.16 | 0.16 |
| 95%CI | 112.20 | 138.70 | 0.32 | 0.33 | 0.49 | 0.48 | 0.19 | 0.19 |
| 99%CI | 108.09 | 143.41 | 0.11 | 0.09 | 0.64 | 0.65 | 0.25 | 0.26 |
| 99.99%CI | 102.33 | 151.42 | 0.00 | 0.00 | 0.85 | 0.93 | 0.15 | 0.07 |
| α | β | ||||||||
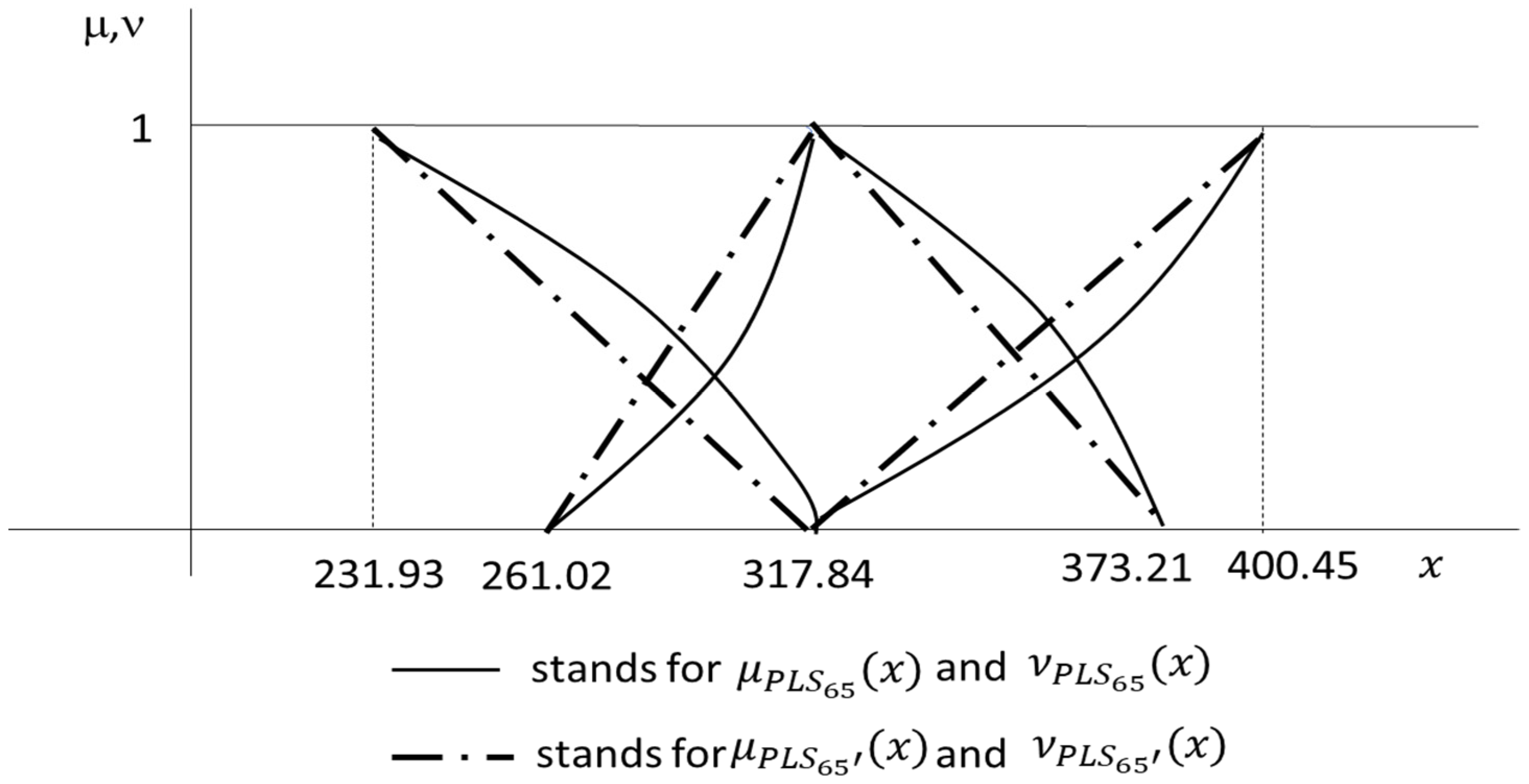
| 1 | 0 | 317.84 | 317.84 | 317.84 | 317.84 | 597.07 | 597.07 | 597.07 | 597.07 |
| 0.75 | 0.25 | 303.78 | 331.80 | 296.72 | 338.75 | 585.46 | 608.44 | 579.56 | 614.05 |
| 0.5 | 0.5 | 289.63 | 345.68 | 275.38 | 359.48 | 573.60 | 619.59 | 561.48 | 630.52 |
| 0.25 | 0.75 | 275.38 | 359.48 | 253.79 | 380.04 | 561.48 | 630.52 | 542.79 | 646.53 |
| 0 | 1 | 261.02 | 373.21 | 231.93 | 400.45 | 549.09 | 641.25 | 523.44 | 662.09 |
| α | β | ||||||||
| 1 | 0 | 317.84 | 317.84 | 317.84 | 317.84 | 597.07 | 597.07 | 597.07 | 597.07 |
| 0.75 | 0.25 | 303.63 | 331.68 | 296.36 | 338.49 | 585.07 | 608.11 | 578.66 | 613.33 |
| 0.5 | 0.5 | 289.43 | 345.52 | 274.89 | 359.14 | 573.08 | 619.16 | 560.26 | 629.58 |
| 0.25 | 0.75 | 275.22 | 359.37 | 253.41 | 379.80 | 561.08 | 630.20 | 541.85 | 645.84 |
| 0 | 1 | 261.02 | 373.21 | 231.93 | 400.45 | 549.09 | 641.25 | 523.44 | 662.09 |
| α | β | ||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.75 | 0.25 | 0.0005 | 0.0004 | 0.00121 | 0.00078 | 0.0007 | 0.0005 | 0.0015 | 0.0012 |
| 0.5 | 0.5 | 0.0007 | 0.0005 | 0.00180 | 0.00095 | 0.0009 | 0.0007 | 0.0022 | 0.0015 |
| 0.25 | 0.75 | 0.0006 | 0.0003 | 0.00151 | 0.00065 | 0.0007 | 0.0005 | 0.0017 | 0.0011 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| = 0.00036 = 0.00023 = 0.00030 | = 0.00093 = 0.00046 0.00070 | = 0.00046 = 0.00034 = 0.00040 | = 0.00106 = 0.00077 = 0.00092 | ||||||
| Values (x) | Membership | Nonmembership | Indeterminacy | |||||
|---|---|---|---|---|---|---|---|---|
| LE | UE | |||||||
| Median | 318.09 | 318.09 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 50%CI | 304.16 | 331.77 | 0.76 | 0.75 | 0.16 | 0.17 | 0.08 | 0.08 |
| 90%CI | 283.01 | 283.01 | 0.39 | 0.39 | 0.41 | 0.41 | 0.21 | 0.21 |
| 95%CI | 275.84 | 357.49 | 0.26 | 0.28 | 0.49 | 0.48 | 0.25 | 0.24 |
| 99%CI | 263.09 | 368.84 | 0.04 | 0.08 | 0.64 | 0.62 | 0.33 | 0.30 |
| 99.99%CI | 235.89 | 394.97 | 0.00 | 0.00 | 0.95 | 0.93 | 0.05 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés-Sánchez, J.d. Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters. Risks 2024, 12, 29. https://doi.org/10.3390/risks12020029
Andrés-Sánchez Jd. Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters. Risks. 2024; 12(2):29. https://doi.org/10.3390/risks12020029
Chicago/Turabian StyleAndrés-Sánchez, Jorge de. 2024. "Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters" Risks 12, no. 2: 29. https://doi.org/10.3390/risks12020029
APA StyleAndrés-Sánchez, J. d. (2024). Pricing Life Contingencies Linked to Impaired Life Expectancies Using Intuitionistic Fuzzy Parameters. Risks, 12(2), 29. https://doi.org/10.3390/risks12020029







