Using Futures Prices and Analysts’ Forecasts to Estimate Agricultural Commodity Risk Premiums
Abstract
:1. Introduction
2. Agricultural Commodities
3. The Risk Premium Model
The Proposed 5-Factor Model
4. Data
4.1. Futures
4.2. Analysts’ Forecasts
5. Results
5.1. Comparing Models with and Without a Crop-Year Factor
5.2. The 5F Model, Using Futures and Analysts’ Forecasts
Model Fit
5.3. Risk Premiums
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
A General N-Factor Model
| 1 | Initially, the Keynes–Hicks theory focused on producers as hedgers shorting futures to manage crop price risks, with speculators taking long positions for a risk premium. This theory was later expanded to allow hedgers and speculators to assume long or short positions in futures markets. |
| 2 | There may also be risk premium transfers between hedgers to hedgers, speculators to speculators, and speculators to hedgers, but the theory of net hedging pressure focuses on the market’s net positions. |
| 3 | However, the proposed model benefits from having more factors and parameters. |
| 4 | Similar results are obtained for soybeans and SRW wheat. |
References
- Aït-Youcef, Camille. 2019. How index investment impacts commodities: A story about the financialization of agricultural commodities. Economic Modelling 80: 23–33. [Google Scholar] [CrossRef]
- Aglasan, Serkan, Roderick M. Rejesus, Stephen Hagen, and William Salas. 2023. Cover Crops, Crop Insurance Losses, and Resilience to Extreme Weather Events. American Journal of Agricultural Economics 106: 1–25. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Xiaohui Gao, and Alberto G. Rossi. 2019. Understanding the Sources of Risk Underlying the Cross Section of Commodity Returns. Management Science 65: 619–41. [Google Scholar] [CrossRef]
- Basu, Devraj, and Joëlle Miffre. 2013. Capturing the risk premium of commodity futures: The role of hedging pressure. Journal of Banking & Finance 37: 2652–64. [Google Scholar]
- Beck, Stacie E. 1993. A Rational Expectations Model of Time Varying Risk Premia in Commodities Futures Markets: Theory and Evidence. International Economic Review 34: 149–68. [Google Scholar] [CrossRef]
- Beck, Stacie E. 1994. Cointegration and Market Efficiency in Commodities Futures Markets. Applied Economics 26: 249–57. [Google Scholar] [CrossRef]
- Beckmann, Joscha, and Robert Czudaj. 2014. Non-linearities in the relationship of agricultural futures prices. European Review of Agricultural Economics 41: 1–23. [Google Scholar] [CrossRef]
- Boyd, Naomi E., Jeffrey H. Harris, and Bingxin Li. 2018. An update on speculation and financialization in commodity markets. Journal of Commodity Markets 10: 91–104. [Google Scholar] [CrossRef]
- Brignoli, Paolo Libenzio, Alessandro Varacca, Cornelis Gardebroek, and Paolo Sckokai. 2024. Machine learning to predict grains futures prices. Agricultural Economics 55: 479–97. [Google Scholar] [CrossRef]
- Cifuentes, Sebastián, Gonzalo Cortazar, Hector Ortega, and Eduardo S. Schwartz. 2020. Expected prices, futures prices and time-varying risk premiums: The case of copper. Resources Policy 69: 101825. [Google Scholar] [CrossRef]
- CME Group. 2024. Comparing New Crop and Old Crop Risk. Available online: https://www.cmegroup.com/articles/2023/new-crop-vs-old-crop-risk-of-the-past-year.html (accessed on 8 November 2024).
- Cortazar, Gonzalo, and Lorenzo Naranjo. 2006. An N-Factor Gaussian Model Of Oil Futures Prices. The Journal of Futures Markets 26: 243–68. [Google Scholar] [CrossRef]
- Cortazar, Gonzalo, Cristobal Millard, Hector Ortega, and Eduardo S. Schwartz. 2019. Commodity Price Forecasts, Futures Prices, and Pricing Models. Management Science 65: 4141–55. [Google Scholar] [CrossRef]
- Cortazar, Gonzalo, Hector Ortega, Maximiliano Rojas, and Eduardo S. Schwartz. 2021. Commodity index risk premium. Journal of Commodity Markets 22: 100156. [Google Scholar] [CrossRef]
- Cortazar, Gonzalo, Philip Liedtke, Hector Ortega, and Eduardo S. Schwartzd. 2022. Time-Varying Term Structure of Oil Risk Premia. The Energy Journal 43: 571–91. [Google Scholar] [CrossRef]
- Dutt, Hans R., and John Fenton. 1997. Crop Year Influences and Variability of the Agricultural Futures Spreads. The Journal of Futures Markets 17: 341–67. [Google Scholar] [CrossRef]
- Fainé, Francisco Ignacio Fainé. 2010. Modelación Estocástica Multifactorial de los Precios Futuros de Commodities Agrícolas y su Estimación Mediante el Filtro de Kalman. Master’s thesis, Pontificia Universidad Católica de Chile, Santiago, Chile. Available online: https://repositorio.uc.cl/xmlui/handle/11534/1868 (accessed on 8 November 2024).
- Fama, Eugene F., and Kenneth R. French. 1987. Commodity Futures Prices: Some Evidence on Forecast Power, Premiums, and the Theory of Storage. The Journal of Business 60: 55–73. [Google Scholar] [CrossRef]
- Frank, Julieta, and Philip Garcia. 2009. Time-varying risk premium: Further evidence in agricultural futures markets. Applied Economics 41: 715–25. [Google Scholar] [CrossRef]
- French, Kenneth R. 1986. Detecting Spot Price Forecasts In Futures Prices. The Journal of Business 59: S39–S54. [Google Scholar] [CrossRef]
- Gorton, Gary B., Fumio Hayashi, and K. Geert Rouwenhorst. 2012. The Fundamentals of Commodity Futures Returns. Review of Finance 17: 35–105. [Google Scholar] [CrossRef]
- Hevia, Constantino, Ivan Petrella, and Martin Sola. 2018. Risk premia and seasonality in commodity futures. Journal of Applied Econometrics 33: 853–73. [Google Scholar] [CrossRef]
- Hicks, John Richard. 1939. Value and Capital: An Inquiry into Some Fundamental Principles of Economic Theory. Oxford: Clarendon Press. [Google Scholar]
- Hirshleifer, David. 1990. Hedging pressure and futures price movements in a general equilibrium model. Econometrica: Journal of the Econometric Society 58: 411–28. [Google Scholar] [CrossRef]
- Huang, Joshua, Teresa Serra, and Philip Garcia. 2020. Are futures prices good price forecasts? Underestimation of price reversion in the soybean complex, European Review of Agricultural Economics 47: 178–99. [Google Scholar] [CrossRef]
- Irwin, Scott H., and Dwight R. Sanders. 2012. Financialization and Structural Change in Commodity Futures Markets. Journal of Agricultural and Applied Economics 44: 371–96. [Google Scholar] [CrossRef]
- Kaldor, Nicholas. 1939. Speculation and Economic Stability. The Review of Economic Studies 7: 1–27. [Google Scholar] [CrossRef]
- Kalman, Rudolph Emil. 1960. A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME–Journal of Basic Engineering 82: 35–45. [Google Scholar] [CrossRef]
- Karali, Berna, Scott H. Irwin, and Olga Isengildina-Massa. 2020. Supply Fundamentals and Grain Futures Price Movements. American Journal of Agricultural Economics 102: 548–68. [Google Scholar] [CrossRef]
- Keynes, John Maynard. 1930. A Treatise on Money. The Applied Theory of Money. London: Macmillan and Co., vol. 2. [Google Scholar]
- Koekebakker, Steen, and Gudbrand Lien. 2004. Volatility and Price Jumps in Agricultural Futures Prices-Evidence from Wheat Options. American Journal of Agricultural Economics 86: 1018–31. [Google Scholar] [CrossRef]
- Kolb, Robert W. 1992. Is normal backwardation normal? Journal of Futures Markets 12: 75–91. [Google Scholar] [CrossRef]
- Li, Jian, and Jean-Paul Chavas. 2023. A dynamic analysis of the distribution of commodity futures and spot prices. American Journal of Agricultural Economics 105: 122–43. [Google Scholar] [CrossRef]
- Mitra, Sophie, and Jean-Marc Boussard. 2012. A simple model of endogenous agricultural commodity price fluctuations with storage. Agricultural Economics 43: 1–15. [Google Scholar] [CrossRef]
- Ordu, Beyza Mina, Adil Oran, and Ugur Soytas. 2018. Is food financialized? Yes, but only when liquidity is abundant. Journal of Banking and Finance 95: 82–96. [Google Scholar] [CrossRef]
- Pérez Zañartu, José Antonio. 2023. Risk Premium Structure of Agricultural Commodities. Master’s thesis, Pontificia Universidad Católica de Chile, Santiago, Chile. [Google Scholar]
- Prager, Daniel, Christopher Burns, Sarah Tulman, and James MacDonald. 2020. Farm Use of Futures, Options, and Marketing Contracts; EIB-219. Washington, DC: U.S. Department of Agriculture, Economic Research Service, pp. 1–33. [CrossRef]
- Sanders, Dwight R., and Scott H. Irwin. 2010. A speculative bubble in commodity futures prices? Cross-sectional evidence. Agricultural Economics 41: 25–32. [Google Scholar] [CrossRef]
- Scheinkman, Jose A., and Jack Schechtman. 1983. A Simple Competitive Model with Production and Storage. The Review of Economic Studies 50: 427–41. [Google Scholar] [CrossRef]
- Sørensen, Carsten. 2002. Modeling seasonality in agricultural commodity futures. The Journal of Futures Markets 22: 393–426. [Google Scholar] [CrossRef]
- Telser, Lester G. 1958. Futures Trading and the Storage of Cotton and Wheat. Journal of Political Economy 66: 233–55. [Google Scholar] [CrossRef]
- Tokgoz, Simla, Wei Zhang, Siwa Msangi, and Prapti Bhandary. 2012. Biofuels and the future of food: Competition and complementarities. Agriculture 2: 414–35. [Google Scholar] [CrossRef]
- USDA. 2022a. Data Products, Wheat Data; September 8, Retrieved from Documentation. Available online: https://www.ers.usda.gov/data-products/wheat-data/documentation/ (accessed on 8 November 2024).
- USDA. 2022b. Farm Practices & Management, Risk Management; June 16, Retrieved from Risk in Agriculture. Available online: https://www.ers.usda.gov/topics/farm-practices-management/risk-management (accessed on 8 November 2024).
- Vollmer, Teresa, Helmut Herwartz, and Stephan von Cramon-Taubadel. 2020. Measuring price discovery in the European wheat market using the partial cointegration approach. European Review of Agricultural Economics 47: 1173–200. [Google Scholar] [CrossRef]
- Working, Holbrook. 1948. Theory of the Inverse Carrying Charge in Futures Markets. Journal of Farm Economics 30: 1–28. [Google Scholar] [CrossRef]
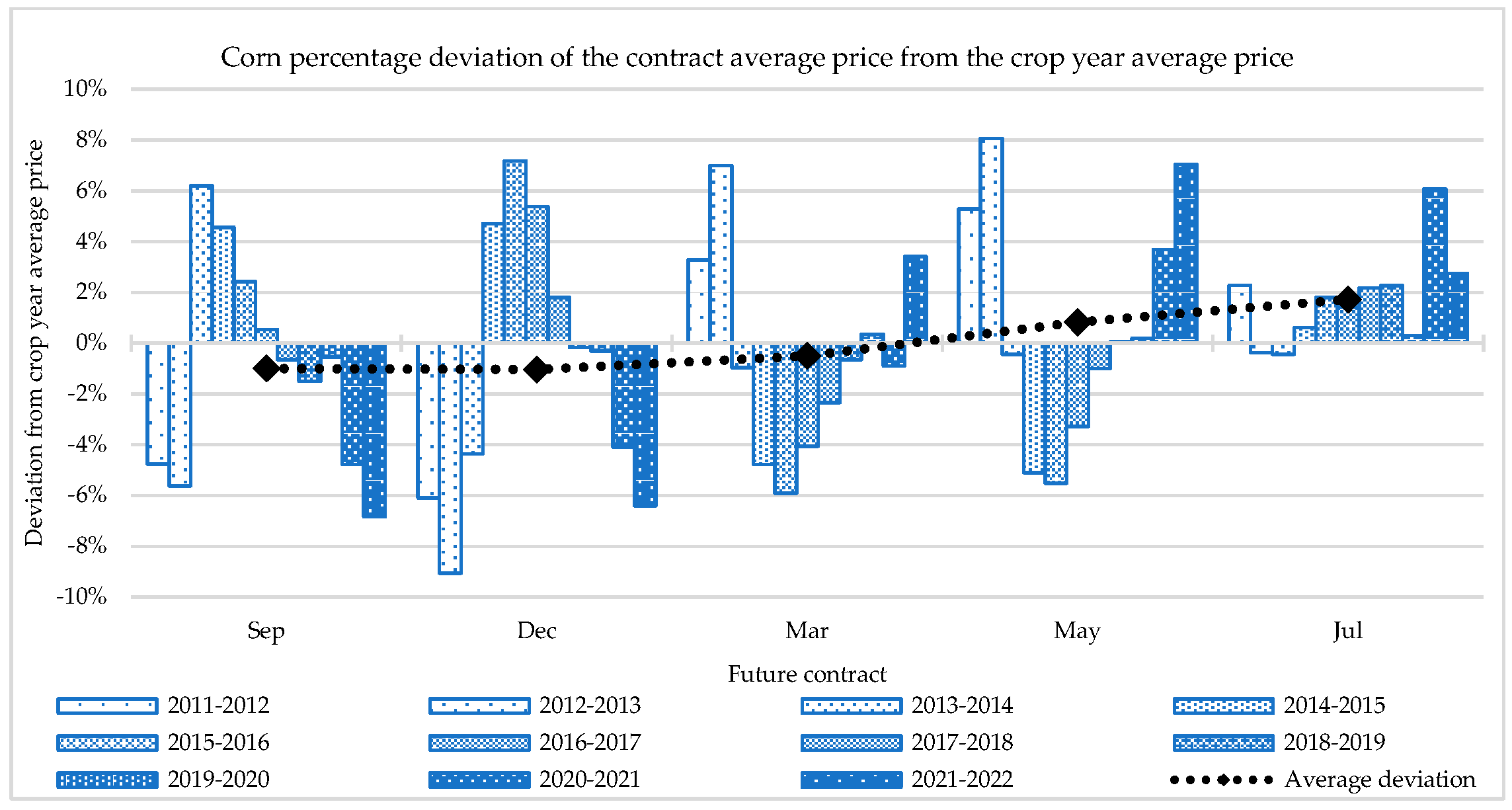


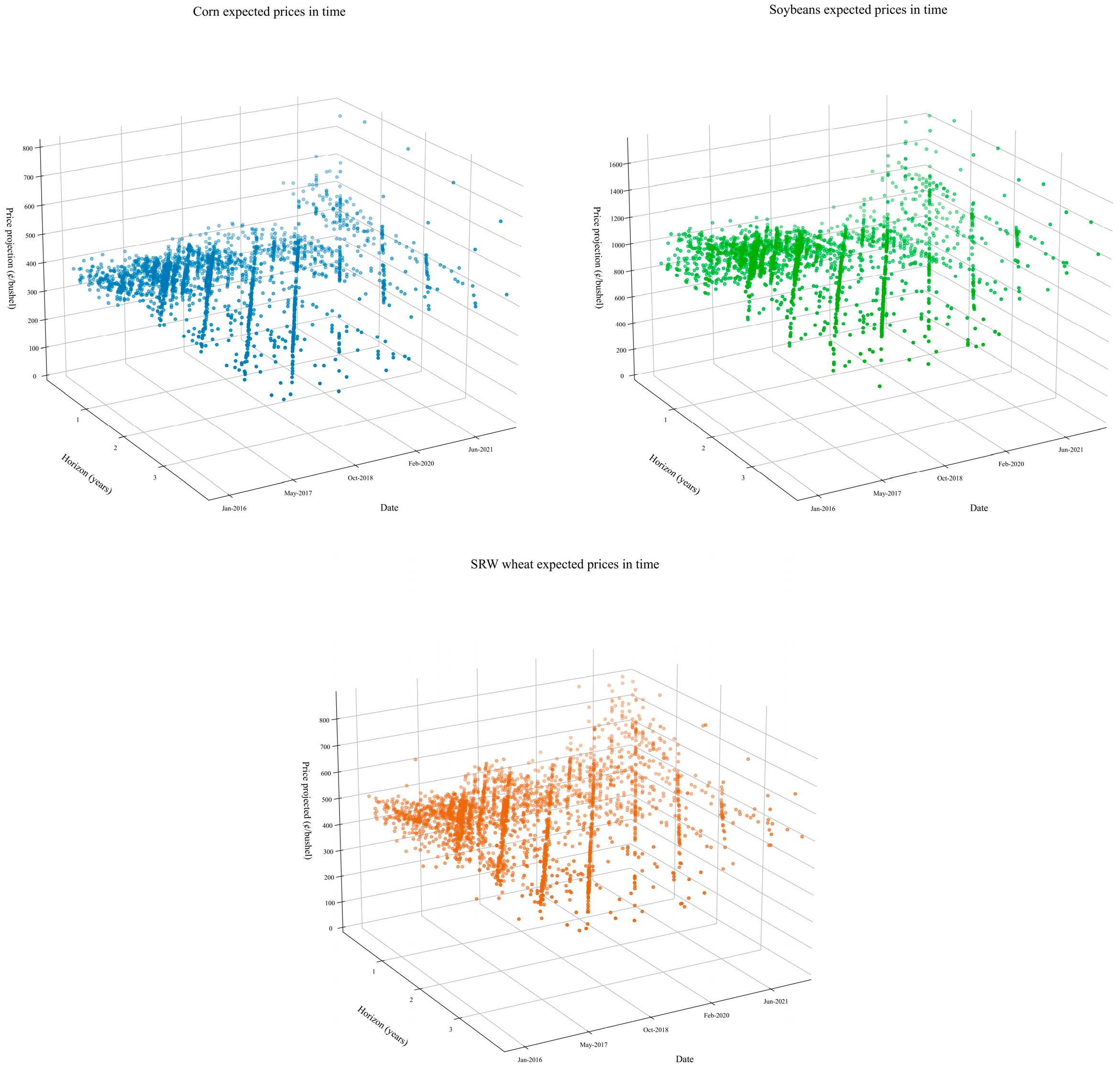

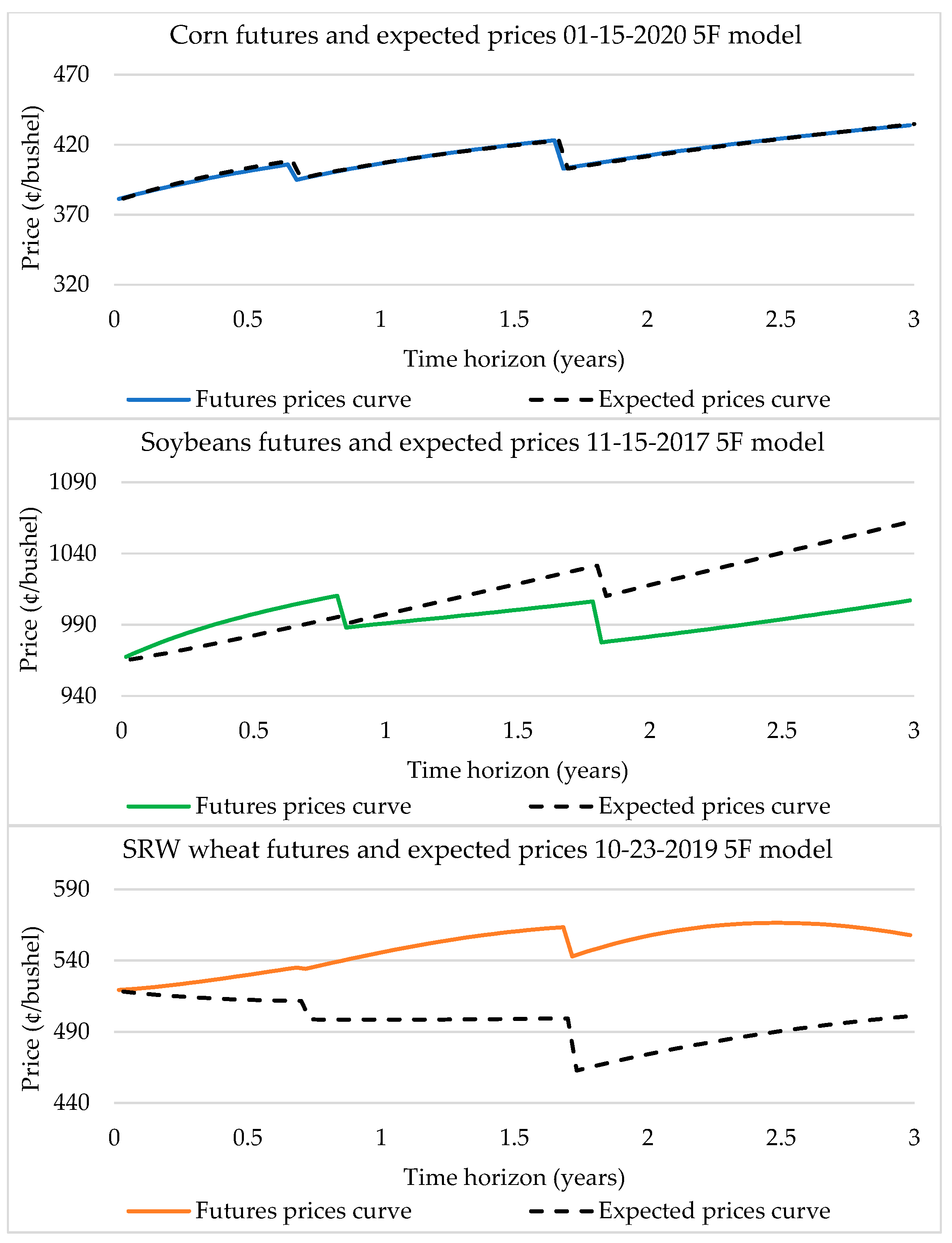

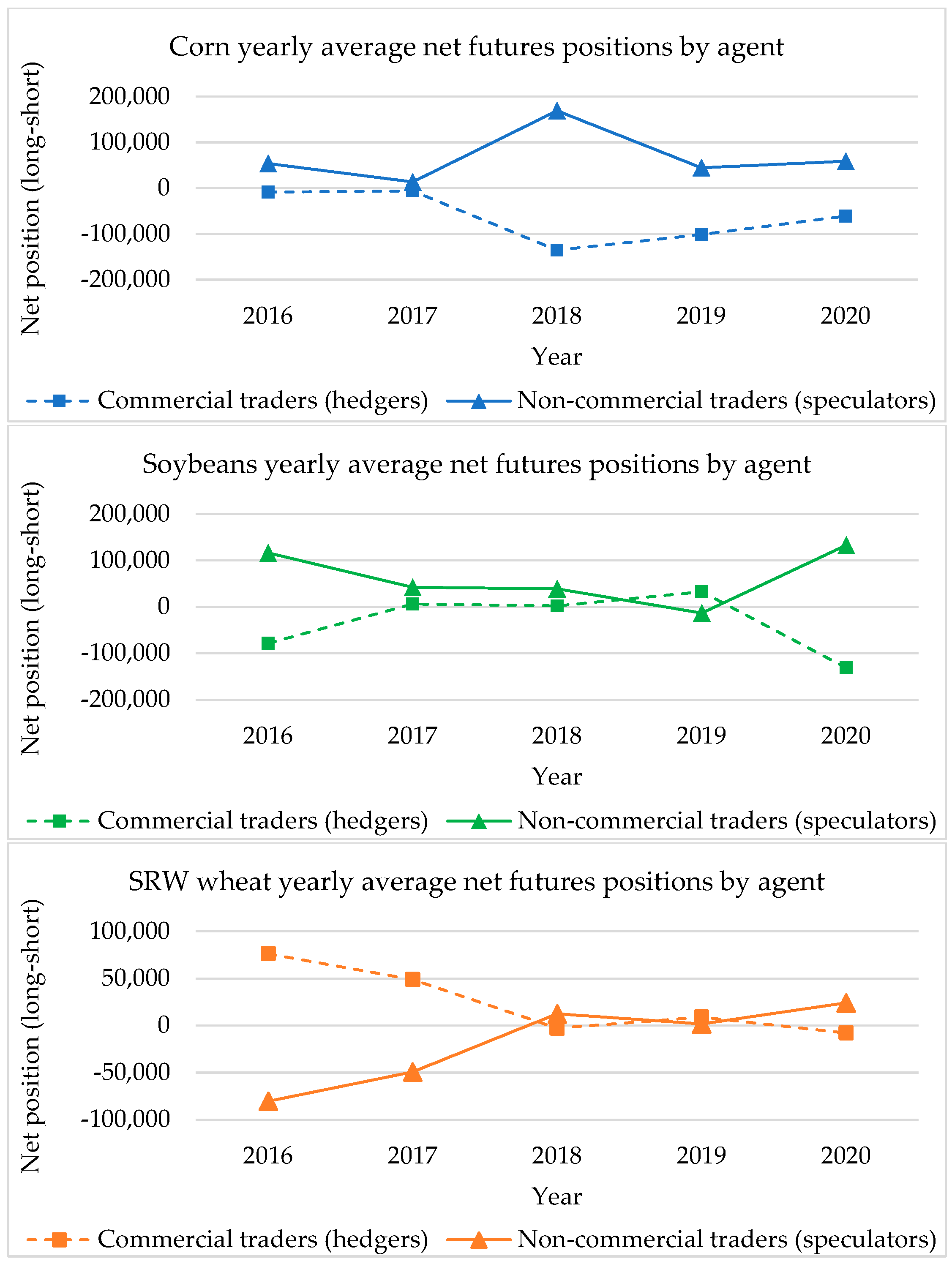
| Commodity | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corn | P | P | H | H | H | |||||||
| Soybeans | P | P | H | H | ||||||||
| SRW wheat | H | H | P | P | ||||||||
| P | Plant | Mid-season | H | Harvest | ||||||||
| Corn | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 377.23 | 24.24 | 474.50 | 304.50 | 0.3175 | 582 |
| 2 | 397.22 | 24.48 | 461.75 | 315.50 | 1.0555 | 1044 |
| 3 | 409.45 | 15.91 | 440.00 | 359.50 | 1.9980 | 913 |
| Soybeans | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 969.54 | 83.50 | 1303.75 | 814.25 | 0.3426 | 884 |
| 2 | 961.54 | 55.70 | 1150.25 | 827.75 | 1.0635 | 1566 |
| 3 | 952.82 | 40.28 | 1032.00 | 831.75 | 2.0094 | 1398 |
| SR Wheat | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 493.71 | 57.21 | 640.75 | 361.00 | 0.3169 | 542 |
| 2 | 529.53 | 41.46 | 641.50 | 428.50 | 1.0161 | 1044 |
| 3 | 557.59 | 28.54 | 632.75 | 487.25 | 2.0163 | 1044 |
| Corn | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 380.89 | 25.38 | 510.00 | 325.00 | 0.4545 | 257 |
| 2 | 394.17 | 25.31 | 500.00 | 325.00 | 0.9949 | 643 |
| 3 | 414.25 | 28.75 | 500.00 | 363.00 | 1.9635 | 246 |
| Soybeans | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 969.63 | 67.45 | 1440.00 | 825.00 | 0.4522 | 266 |
| 2 | 969.09 | 63.02 | 1600.00 | 820.00 | 0.9879 | 668 |
| 3 | 997.66 | 63.34 | 1200.00 | 875.00 | 1.9653 | 248 |
| SR Wheat | ||||||
| Marketing crop | Mean price | Price SD | Max price | Min price | Mean maturity | Number of |
| year (i) | (¢/bushel) | (¢/bushel) | (¢/bushel) | (years) | observations | |
| 1 | 481.17 | 42.09 | 650.00 | 351.00 | 0.4851 | 313 |
| 2 | 480.82 | 45.17 | 680.00 | 265.26 | 1.0302 | 711 |
| 3 | 486.05 | 56.91 | 711.00 | 260.59 | 1.9643 | 306 |
| Model | Commodity | MAPE | MAPE | Nº of Parameters | Log-Likelihood |
|---|---|---|---|---|---|
| In-Sample | Out-of-Sample | ||||
| 5F | Corn | 0.1282 | 0.3547 | 26 | 12,273 |
| Soybeans | 0.2135 | 0.4092 | 26 | 18,543 | |
| SRW wheat | 0.2120 | 0.2498 | 26 | 11,731 | |
| 3F | Corn | 0.6654 | 2.1468 | 13 | 9809 |
| Soybeans | 0.5314 | 1.0644 | 13 | 15,974 | |
| SRW wheat | 0.4642 | 0.7986 | 13 | 10,777 | |
| 3F with seasonality | Corn | 0.3929 | 1.6503 | 17 | 10,761 |
| Soybeans | 0.3709 | 0.7562 | 17 | 17,100 | |
| SRW wheat | 0.3813 | 0.6251 | 17 | 11,181 |
| Corn | ||||
|---|---|---|---|---|
| Parameter | Estimate | Deviation | t-Statistic | p-Value |
| 1.2879 *** | 0.0326 | 39.448 | 0 | |
| 1.2428 *** | 0.0297 | 41.804 | 0 | |
| 1.0033 *** | 0.0796 | 12.610 | 0 | |
| 0.6799 *** | 0.0500 | 13.599 | 0 | |
| 0.0085 | 0.0117 | 0.7285 | 0.3054 | |
| 1.2032 | 1.1130 | 1.0811 | 0.2220 | |
| −1.1849 | 1.1141 | −1.0636 | 0.2262 | |
| −0.0079 * | 0.0044 | −1.7754 | 0.0827 | |
| −0.0060 | 0.0042 | −1.4213 | 0.1452 | |
| −0.6151 *** | 0.1060 | −5.8042 | 0 | |
| 0.6215 *** | 0.1049 | 5.9229 | 0 | |
| 0.0073 | 0.1234 | 0.0590 | 0.3979 | |
| −0.0340 | 0.1037 | −0.3279 | 0.3776 | |
| −0.9998 *** | 0.0001 | −10854 | 0 | |
| 0.3110 *** | 0.1046 | 2.9730 | 0.0051 | |
| 0.5136 *** | 0.1192 | 4.3079 | 0 | |
| −0.3140 *** | 0.1036 | −3.0305 | 0.0043 | |
| −0.5106 *** | 0.1186 | −4.3033 | 0.0001 | |
| 0.3147 *** | 0.1139 | 2.7632 | 0.0091 | |
| 0.0671 *** | 0.0046 | 14.701 | 0 | |
| 4.9349 *** | 1.4887 | 3.3149 | 0.0018 | |
| 5.0632 *** | 1.4867 | 3.4056 | 0.0013 | |
| 0.0767 *** | 0.0078 | 9.8950 | 0 | |
| 0.2065 *** | 0.0188 | 10.986 | 0 | |
| 0.0249 ** | 0.0118 | 2.1102 | 0.0435 | |
| 0.0024 *** | 0.0000 | 139.77 | 0 | |
| 0.0680 *** | 0.0006 | 107.57 | 0 | |
| Log-likelihood | 14,772 | |||
| Data | Commodity | MAPE | MAPE |
|---|---|---|---|
| In-Sample | Out-of-Sample | ||
| Corn | 0.1317 | 0.3847 | |
| Futures prices | Soybeans | 0.2147 | 0.4046 |
| SRW wheat | 0.2142 | 0.2275 | |
| Corn | 5.1329 | 10.2856 | |
| Expected prices | Soybeans | 4.2061 | 14.4784 |
| SRW wheat | 7.7592 | 11.7089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortazar, G.; Ortega, H.; Pérez, J.A. Using Futures Prices and Analysts’ Forecasts to Estimate Agricultural Commodity Risk Premiums. Risks 2025, 13, 9. https://doi.org/10.3390/risks13010009
Cortazar G, Ortega H, Pérez JA. Using Futures Prices and Analysts’ Forecasts to Estimate Agricultural Commodity Risk Premiums. Risks. 2025; 13(1):9. https://doi.org/10.3390/risks13010009
Chicago/Turabian StyleCortazar, Gonzalo, Hector Ortega, and José Antonio Pérez. 2025. "Using Futures Prices and Analysts’ Forecasts to Estimate Agricultural Commodity Risk Premiums" Risks 13, no. 1: 9. https://doi.org/10.3390/risks13010009
APA StyleCortazar, G., Ortega, H., & Pérez, J. A. (2025). Using Futures Prices and Analysts’ Forecasts to Estimate Agricultural Commodity Risk Premiums. Risks, 13(1), 9. https://doi.org/10.3390/risks13010009







