An Empirical Study on Stochastic Mortality Modelling under the Age-Period-Cohort Framework: The Case of Greece with Applications to Insurance Pricing
Abstract
:1. Introduction
2. Mortality Modelling
2.1. The Age-Period-Cohort Framework
2.2. Data and Assumptions
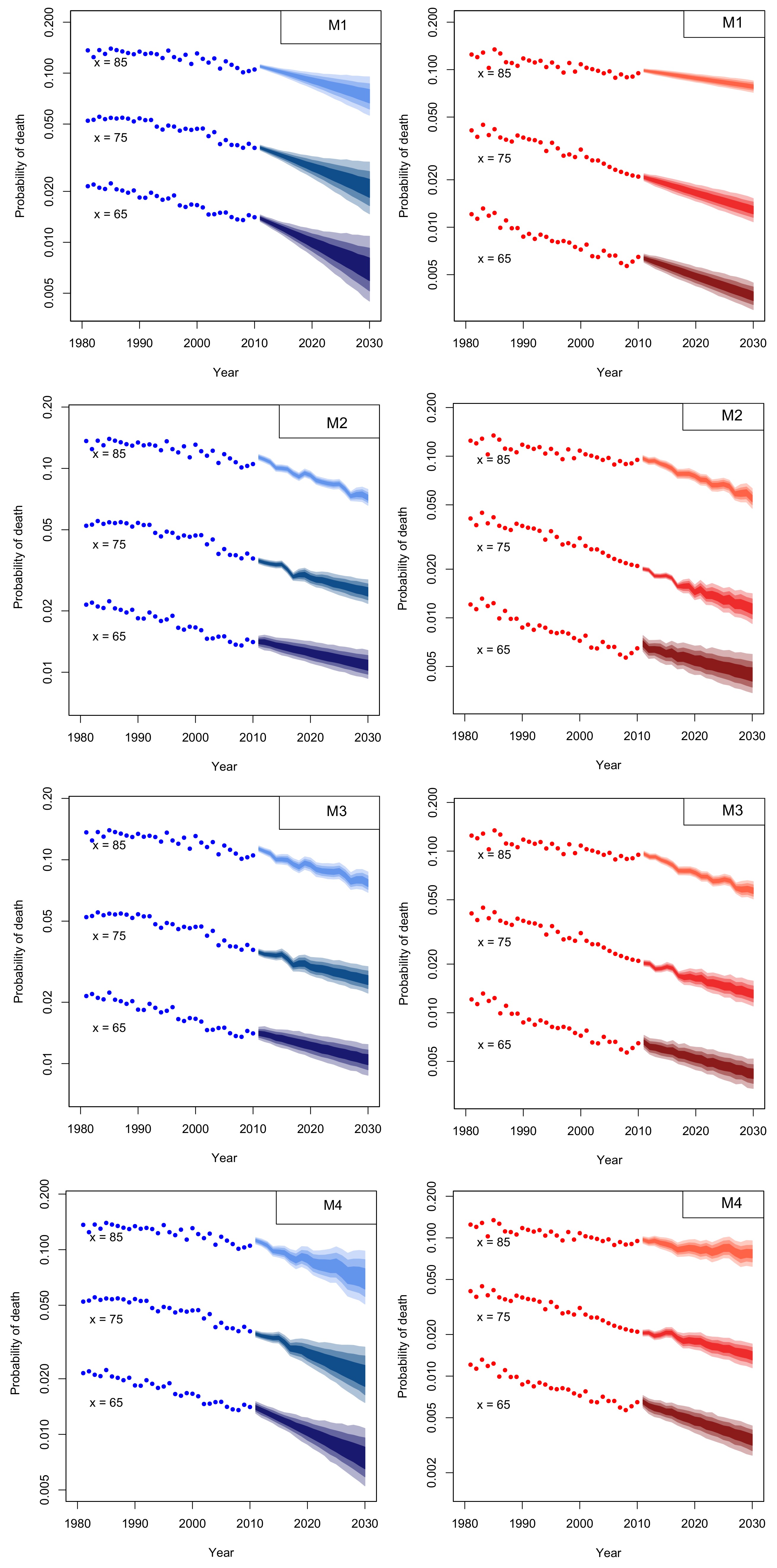
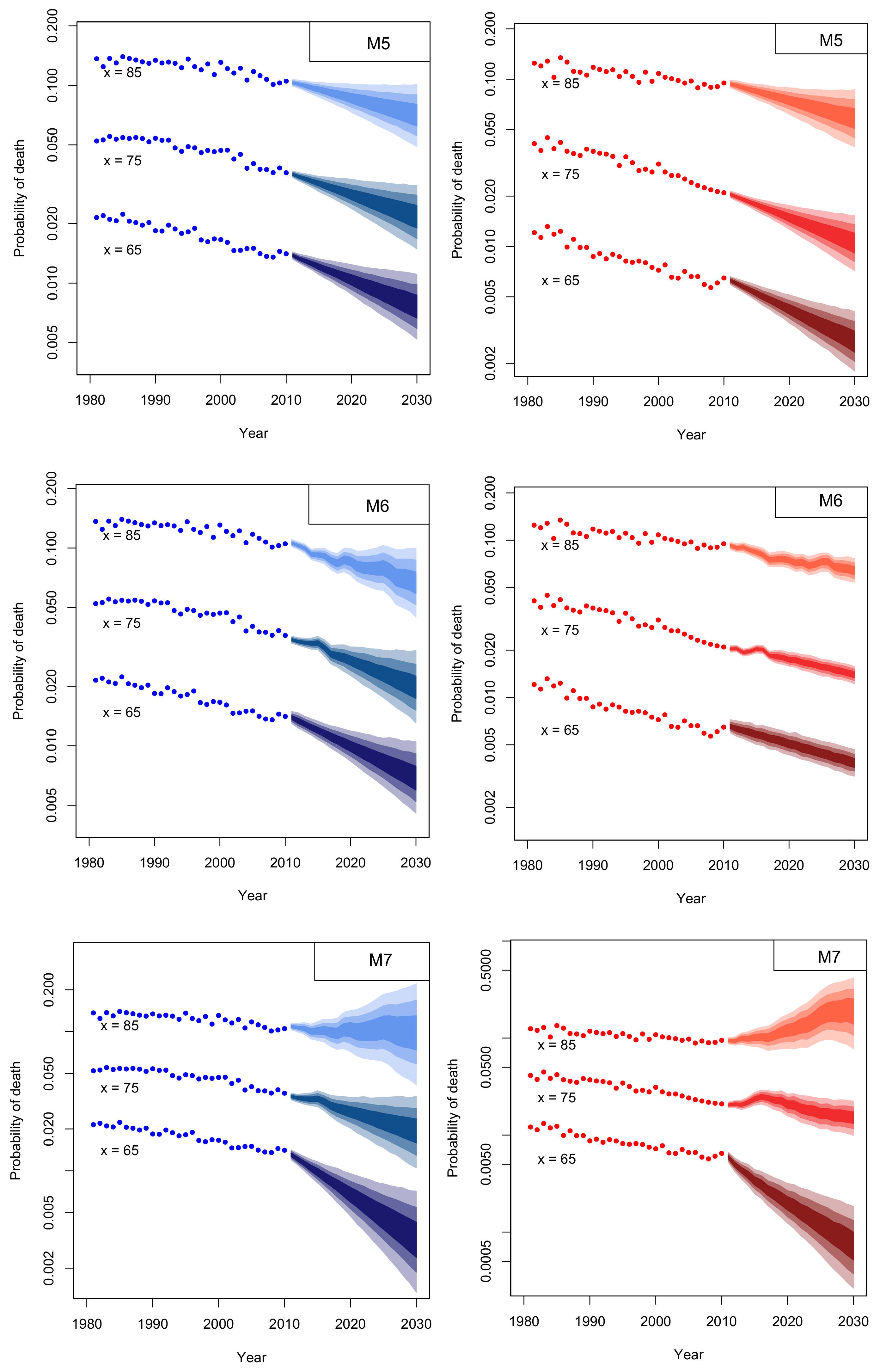
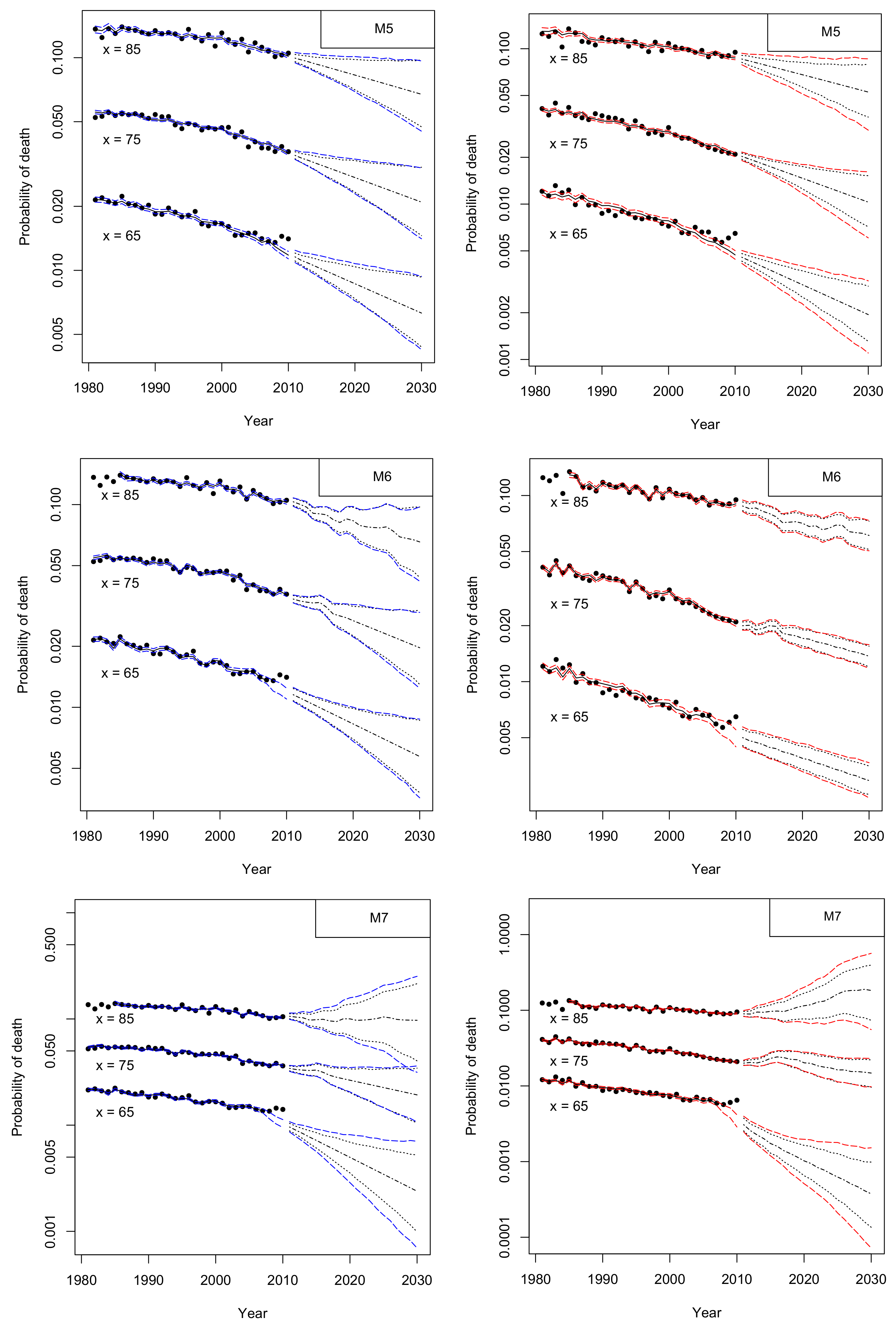
2.3. Reviewing Mortality Models
3. Model Fit
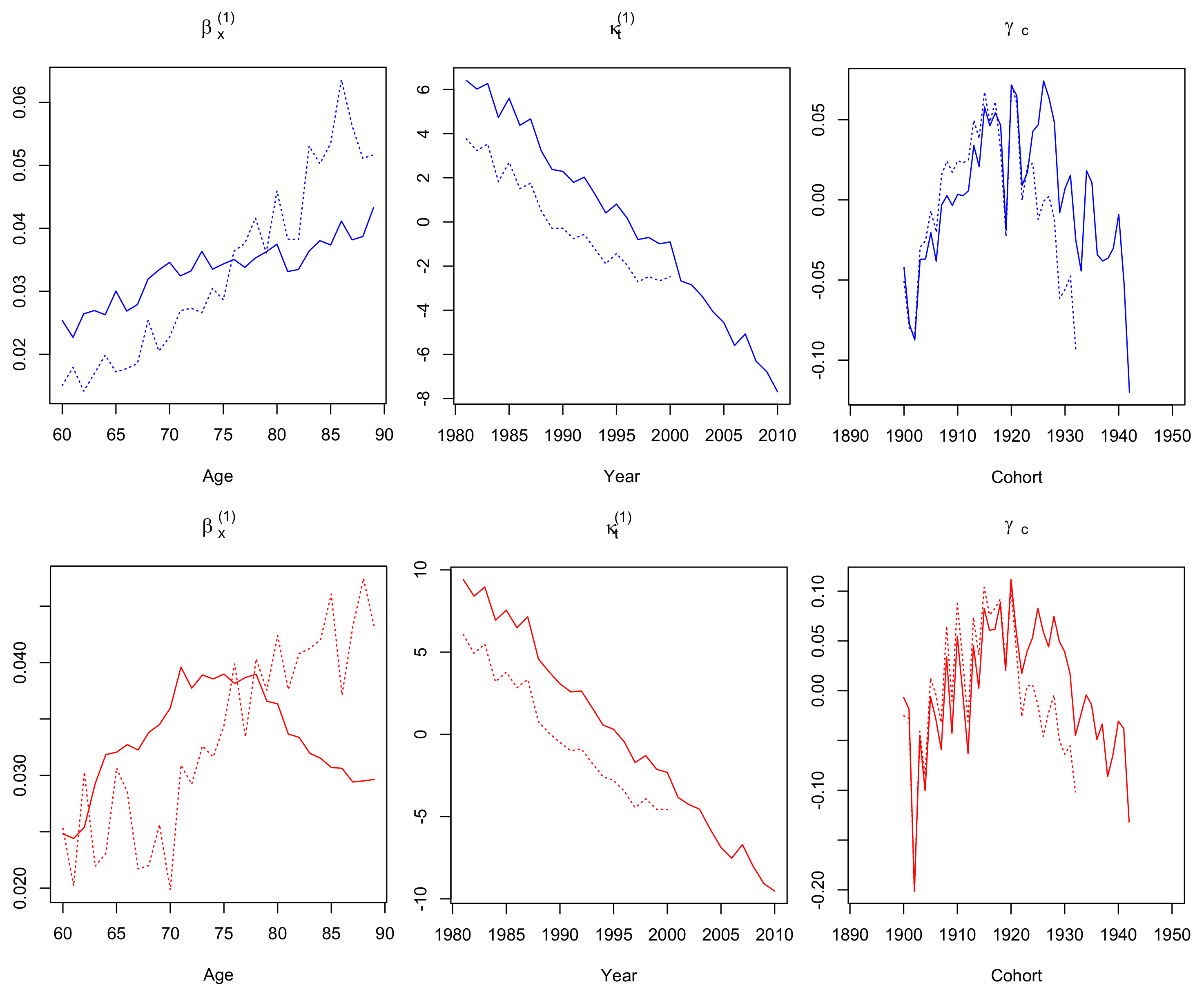
3.1. Parameter Estimates
Robustness
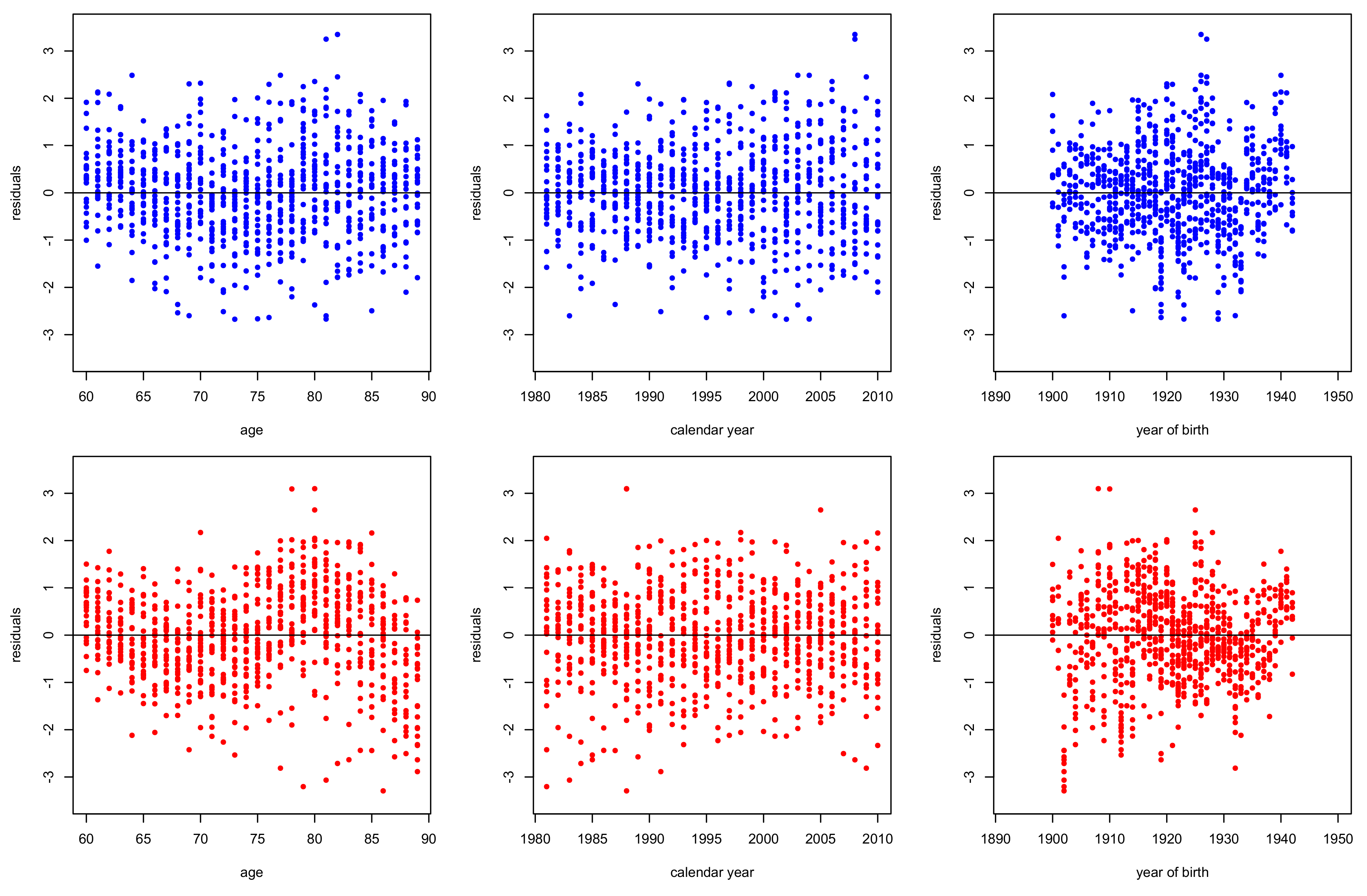
3.2. Goodness of Fit Diagnostics
3.2.1. Information Criteria
3.2.2. Likelihood-Ratio Test
4. Mortality Projection
4.1. Assessing Parameter Risk
4.2. Application in Insurance-Related Products
5. Results
Comparison with Original Papers
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Animated Plots



References
- Akaike, Hirotugu. 1974. A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control 19: 716–23. [Google Scholar] [CrossRef]
- Aro, Helena, and Teemu Pennanen. 2011. A user-friendly approach to stochastic mortality modelling. European Actuarial Journal 1: 151–67. [Google Scholar] [CrossRef]
- Booth, Heather, Rob J. Hyndman, Leonie Tickle, and Piet De Jong. 2006. Lee-Carter mortality forecasting: A multi-country comparison of variants and extensions. Demographic Research 15: 289–310. [Google Scholar] [CrossRef]
- Booth, Heather, John Maindonald, and Len Smith. 2002. Applying Lee-Carter under conditions of variable mortality decline. Population Studies 56: 325–36. [Google Scholar] [CrossRef] [PubMed]
- Booth, Heather, and Leonie Tickle. 2008. Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3: 3–43. [Google Scholar] [CrossRef]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef]
- Butt, Zoltan, Steve Haberman, and Han Lin Shang. 2014. The ilc Package in R: Generalised Lee-Carter Models Using Iterative Fitting Algorithms. R Package Version 1.0. Available online: http://cran.r-project.org/package=ilc (accessed on 15 December 2016).
- Cairns, Andrew J. G., David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, and Marwa Khalaf-Allah. 2011. Mortality density forecasts: An analysis of six stochastic mortality models. Insurance: Mathematics and Economics 48: 355–67. [Google Scholar] [CrossRef]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Carter, Lawrence R., and Ronald D. Lee. 1992. Modeling and forecasting US sex differentials in mortality. International Journal of Forecasting 8: 393–411. [Google Scholar] [CrossRef]
- Currie, Iain D. 2006. Smoothing and Forecasting Mortality Rates with P-Splines. London: Institute and Faculty of Actuaries, Available online: https://www.actuaries.org.uk/documents/smoothing-and-forecasting-mortality-rates-p-splines-handouts (accessed on 20 November 2016).
- Currie, Iain D. 2016. On fitting generalized linear and non-linear models of mortality. Scandinavian Actuarial Journal 2016: 356–83. [Google Scholar] [CrossRef]
- De Jong, Piet, and Leonie Tickle. 2006. Extending Lee–Carter Mortality Forecasting. Mathematical Population Studies 13: 1–18. [Google Scholar] [CrossRef]
- Debón, Ana, Francisco Martínez-Ruiz, and Francisco Montes. 2010. A geostatistical approach for dynamic life tables: The effect of mortality on remaining lifetime and annuities. Insurance: Mathematics and Economics 47: 327–36. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Gaille, Séverine. 2012. Forecasting mortality: When academia meets practice. European Actuarial Journal 2: 49–76. [Google Scholar] [CrossRef]
- Haberman, Steven, and Arthur Renshaw. 2011. A comparative study of parametric mortality projection models. Insurance: Mathematics and Economics 48: 35–55. [Google Scholar] [CrossRef]
- Hatzopoulos, Petros, and Steven Haberman. 2009. A parameterized approach to modeling and forecasting mortality. Insurance: Mathematics and Economics 44: 103–23. [Google Scholar] [CrossRef]
- Hobcraft, John, Jane Menken, and Samuel Preston. 1982. Age, period, and cohort effects in demography: A review. Population Index 48: 4–43. [Google Scholar] [CrossRef] [PubMed]
- Human Mortality Database. 2017. University of California, Berkeley (USA), and Max Planck Institute for Demographic Research (Germany). Available online: www.mortality.org (accessed on 10 October 2017).
- Hunt, Andrew, and David Blake. 2015. On the Structure and Classification of Mortality Models. Pension Institute Working Paper. Available online: http://www.pensions-institute.org/workingpapers/wp1506.pdf (accessed on 9 February 2016).
- Hunt, Andrew, and Andrés M. Villegas. 2015. Robustness and convergence in the Lee-Carter model with cohort effects. Insurance: Mathematics and Economics 64: 186–202. [Google Scholar] [CrossRef]
- Hurvich, Clifford M., and Chih-Ling Tsai. 1989. Regression and time series model selection in small samples. Biometrika 76: 297–307. [Google Scholar] [CrossRef]
- Hyndman, Rob J., Heather Booth, Leonie Tickle, and John Maindonald. 2017. Demography: Forecasting Mortality, Fertility, Migration and Population Data. R Package Version 1.20. Available online: https://CRAN.R-project.org/package=demography (accessed on 25 May 2017).
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics and Data Analysis 51: 4942–56. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the Performance of the Lee-Carter Method for Forecasting Mortality. Demography 38: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and Forecasting U.S. Mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Lovász, Enrico. 2011. Analysis of Finnish and Swedish mortality data with stochastic mortality models. European Actuarial Journal 2011: 259–89. [Google Scholar] [CrossRef]
- Maccheroni, Carlo, and Samuel Nocito. 2017. Backtesting the Lee–Carter and the Cairns–Blake–Dowd Stochastic Mortality Models on Italian Death Rates. Risks 5: 34. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Pitacco, Ermanno, Michel Denuit, Steven Haberman, and Annamaria Olivieri. 2009. Modelling Longevity Dynamic for Pensions and Annuity Business. Oxford: Oxford University Press. [Google Scholar]
- Plat, Richard. 2009. On stochastic mortality modeling. Insurance: Mathematics and Economics 45: 393–404. [Google Scholar]
- Renshaw, Arthur E., and Steven Haberman. 2003. Lee-Carter mortality forecasting with age-specific enhancement. Insurance: Mathematics and Economics 33: 255–72. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee-Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
- Renshaw, Arthur E., and Steve Haberman. 2008. On simulation-based approaches to risk measurement in mortality with specific reference to Poisson Lee-Carter modelling. Insurance: Mathematics and Economics 42: 797–816. [Google Scholar] [CrossRef]
- Schwarz, Gideon. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar] [CrossRef]
- Shang, Han Lin, Heather Booth, and Rob J. Hyndman. 2011. Point and interval forecasts of mortality rates and life expectancy: A comparison of ten principal component methods. Demographic Research 25: 173–214. [Google Scholar] [CrossRef]
- Stoeldraijer, Lenny, Coen van Duin, Leo van Wissen, and Fanny Janssen. 2013. Impact of different mortality forecasting methods and explicit assumptions on projected future life expectancy: The case of the Netherlands. Demographic Research 29: 323–54. [Google Scholar] [CrossRef]
- Tsai, Cary Chi-Liang, and Tzuling Lin. 2016. Incorporating the Bühlmann credibility into mortality models to improve forecasting performances. Scandinavian Actuarial Journal 2015: 419–40. [Google Scholar] [CrossRef]
- Turner, Heather, and David Firth. 2015. Generalized Nonlinear Models in R: An Overview of the Gnm Package. Available online: http://cran.r-project.org/package=gnm (accessed on 7 February 2016).
- Van Berkum, Frank, Katrien Antonio, and Michel Vellekoop. 2016. The impact of multiple structural changes on mortality predictions. Scandinavian Actuarial Journal 2016: 581–603. [Google Scholar] [CrossRef]
- Villegas, Andres, Pietro Millossovich, and Vladimir Kaishev. 2017. StMoMo: An R Package for Stochastic Mortality Modelling. R Package Version 0.4.0. Available online: https://CRAN.R-project.org/package=StMoMo (accessed on 15 April 2018).
- Xie, Yihui. 2013. animation: An R Package for Creating Animations and Demonstrating Statistical Methods. Journal of Statistical Software 53: 1–27. [Google Scholar] [CrossRef]
| 1 | According to Cairns et al. (2009), the force of mortality can be viewed as the instantaneous death rate at exact time for a person aged exactly at time . |
| 2 | For instance, Hyndman and Shahid Ullah (2007) used functional data analysis and penalized regression splines in their modelling framework. |
| 3 | Due to the limited availability of Greek data in HMD, years 2011–2013 correspond to a percentage of 10% of the whole fitting year span. |
| 4 | As Hunt and Blake (2015) point out, in practice, has proved the most popular extension of the original Cairns et al. (2006) model, since it gives a better fit to their data than and the age function for the cohort parameters in may be more complicated to fit data due to the estimation of the additional constant parameter . |
| 5 | The sum of the estimated parameters minus those that reflect each model’s constraints. |
| 6 | The probabilities of death in the last year of the fitting period. |
| 7 | Inconsistency in male ranking results is expected, since BIC criterion penalizes stronger models with more parameters. |















| Model | Structure | Original Papers |
|---|---|---|
| Lee and Carter (1992) | ||
| Renshaw and Haberman (2006) | ||
| Currie (2006) | ||
| Plat (2009) | ||
| Cairns et al. (2006) | ||
| Cairns et al. (2009) | ||
| Cairns et al. (2009) |
| Males | |||||
| Model | Maximum Log Likelihood | Effective Parameters | AIC | AIC(c) | BIC |
| 4487.643 | 88 | 9151.287(7) | 9172.483(7) | 9566.560(7) | |
| 4191.779 | 129 | 8641.558(4) | 8689.610(4) | 9250.311(4) | |
| 4218.961 | 100 | 8637.922(3) | 8665.708(3) | 9109.823(2) | |
| 4202.953 | 128 | 8661.907(5) | 8709.151(5) | 9265.940(5) | |
| 4501.146 | 60 | 9122.291(6) | 9131.835(6) | 9405.432(6) | |
| 4209.024 | 101 | 8620.048(2) | 8648.429(2) | 9096.669(1) | |
| 4160.547 | 130 | 8581.094(1) | 8629.960(1) | 9194.565(3) | |
| Females | |||||
| 4980.632 | 88 | 10,137.265(6) | 10,158.461(6) | 10,552.538(6) | |
| 4254.321 | 129 | 8766.643(3) | 8814.694(3) | 9375.395(3) | |
| 4367.542 | 100 | 8935.085(4) | 8962.870(4) | 9406.986(4) | |
| 4235.015 | 128 | 8726.030(2) | 8773.275(2) | 9330.064(2) | |
| 5279.019 | 60 | 10,678.038(7) | 10,687.581(7) | 10,961.178(7) | |
| 4474.985 | 101 | 9151.969(5) | 9180.349(5) | 9628.590(5) | |
| 4209.487 | 130 | 8678.975(1) | 8727.841(1) | 9292.447(1) | |
| Males | ||||
| : Nested Model | : General Model | Likelihood Ratio Test Statistic | Degrees of Freedom | -Value |
| 591.730 | 41 | 0.0001 | ||
| 54.364 | 29 | 0.0001 | ||
| 32.015 | 28 | 0.0001 | ||
| 584.240 | 41 | 0.0001 | ||
| 681.200 | 70 | 0.0001 | ||
| 96.955 | 29 | 0.0001 | ||
| Females | ||||
| 1452.600 | 41 | 0.0001 | ||
| 226.440 | 29 | 0.0001 | ||
| 265.050 | 28 | 0.0001 | ||
| 1608.100 | 41 | 0.0001 | ||
| 2139.100 | 70 | 0.0001 | ||
| 530.990 | 29 | 0.0001 | ||
| Males | |||
| Model | |||
| ARIMA(0,2,2) | —– | —– | |
| ARIMA(0,1,1) with drift | —– | —– | |
| ARIMA(1,1,0) with drift | —– | —– | |
| ARIMA(0,2,2) | ARIMA(2,1,0) with drift | —– | |
| ARIMA(1,2,1) | ARIMA(2,1,0) with drift | —– | |
| ARIMA(0,2,2) with drift | ARIMA(0,1,1) with drift | —– | |
| ARIMA(1,2,1) | ARIMA(2,2,0) | ARIMA(0,1,1) with drift | |
| Females | |||
| Model | |||
| ARIMA(1,1,0) with drift | —– | —– | |
| ARIMA(3,1,0) with drift | —– | —– | |
| ARIMA(3,1,0) with drift | —– | —– | |
| ARIMA(1,1,0) with drift | ARIMA(1,1,0) with drift | —– | |
| ARIMA(0,2,2) | ARIMA(0,1,0) with drift | —– | |
| ARIMA(0,1,1) with drift | ARIMA(0,1,1) with drift | —– | |
| ARIMA(2,1,0) with drift | ARIMA(2,2,0) | ARIMA(0,1,1) with drift | |
| Model | for Males | for Females |
|---|---|---|
| ARIMA(2,1,0) | ARIMA(2,1,1) with drift | |
| ARIMA(0,0,1) | ARIMA(4,1,1) | |
| ARIMA(0,0,2) | ARIMA(4,1,1) | |
| ARIMA(0,1,3) | ARIMA(3,0,2) | |
| ARIMA(0,0,1) | ARIMA(4,0,1) |
| Fitted Jump-off Rates | |||||||
| Males | |||||||
| Error | |||||||
| 0.332(6) | 0.251(1) | 0.253(2) | 0.287(3) | 0.327(5) | 0.295(4) | 0.346(7) | |
| 10.194(4) | 6.496(1) | 6.583(2) | 9.385(3) | 10.935(6) | 10.559(5) | 15.697(7) | |
| Females | |||||||
| 0.207(4) | 0.147(1) | 0.165(2) | 0.219(5) | 0.234(6) | 0.198(3) | 0.281(7) | |
| 10.363(3) | 6.052(1) | 7.981(2) | 12.239(5) | 13.396(6) | 11.216(4) | 22.340(7) | |
| Actual Jump-off Rates | |||||||
| Males | |||||||
| Error | |||||||
| 0.273(6) | 0.213(3) | 0.208(2) | 0.192(1) | 0.289(7) | 0.237(4) | 0.247(5) | |
| 6.780(5) | 5.222(2) | 5.086(1) | 5.371(3) | 6.916(6) | 6.020(4) | 8.545(7) | |
| Females | |||||||
| 0.213(6) | 0.180(3) | 0.168(2) | 0.196(4) | 0.200(5) | 0.165(1) | 0.250(7) | |
| 7.073(5) | 5.570(2) | 5.336(1) | 6.225(4) | 7.283(6) | 5.866(3) | 11.818(7) | |
| Life Insurance | |||||||
| Males | |||||||
| Error | |||||||
| 2.222(6) | 1.242(1) | 2.284(7) | 2.199(5) | 2.020(4) | 1.456(2) | 1.799(3) | |
| 7.651(6) | 5.536(1) | 8.895(7) | 7.626(5) | 7.412(4) | 5.557(2) | 6.490(3) | |
| Females | |||||||
| 1.605(6) | 0.870(1) | 0.885(2) | 1.494(5) | 0.914(3) | 1.016(4) | 2.150(7) | |
| 9.264(5) | 6.404(1) | 6.901(3) | 9.268(6) | 6.426(2) | 6.930(4) | 11.883(7) | |
| Pure Endowment | |||||||
| Males | |||||||
| Error | |||||||
| 1.605(6) | 0.927(1) | 1.666(7) | 1.590(5) | 1.451(4) | 1.039(2) | 1.293(3) | |
| 4.114(7) | 2.190(1) | 4.094(6) | 4.064(5) | 3.619(4) | 2.531(2) | 3.212(3) | |
| Females | |||||||
| 1.198(6) | 0.623(1) | 0.651(2) | 1.091(5) | 0.690(3) | 0.738(4) | 1.556(7) | |
| 2.615(6) | 1.282(2) | 1.242(1) | 2.250(5) | 1.408(3) | 1.565(4) | 3.240(7) | |
| Life Annuity | |||||||
| Males | |||||||
| Error | |||||||
| 7.711(6) | 5.506(2) | 8.132(7) | 7.637(5) | 6.781(4) | 5.225(1) | 5.924(3) | |
| 1.127(6) | 0.785(2) | 1.168(7) | 1.112(5) | 0.980(4) | 0.748(1) | 0.856(3) | |
| Females | |||||||
| 5.484(6) | 2.465(1) | 2.944(2) | 4.995(5) | 3.254(4) | 3.091(3) | 6.466(7) | |
| 0.754(6) | 0.325(1) | 0.386(2) | 0.673(5) | 0.439(4) | 0.416(3) | 0.873(7) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozikas, A.; Pitselis, G. An Empirical Study on Stochastic Mortality Modelling under the Age-Period-Cohort Framework: The Case of Greece with Applications to Insurance Pricing. Risks 2018, 6, 44. https://doi.org/10.3390/risks6020044
Bozikas A, Pitselis G. An Empirical Study on Stochastic Mortality Modelling under the Age-Period-Cohort Framework: The Case of Greece with Applications to Insurance Pricing. Risks. 2018; 6(2):44. https://doi.org/10.3390/risks6020044
Chicago/Turabian StyleBozikas, Apostolos, and Georgios Pitselis. 2018. "An Empirical Study on Stochastic Mortality Modelling under the Age-Period-Cohort Framework: The Case of Greece with Applications to Insurance Pricing" Risks 6, no. 2: 44. https://doi.org/10.3390/risks6020044
APA StyleBozikas, A., & Pitselis, G. (2018). An Empirical Study on Stochastic Mortality Modelling under the Age-Period-Cohort Framework: The Case of Greece with Applications to Insurance Pricing. Risks, 6(2), 44. https://doi.org/10.3390/risks6020044






