Bayesian Predictive Analysis of Natural Disaster Losses
Abstract
1. Introduction
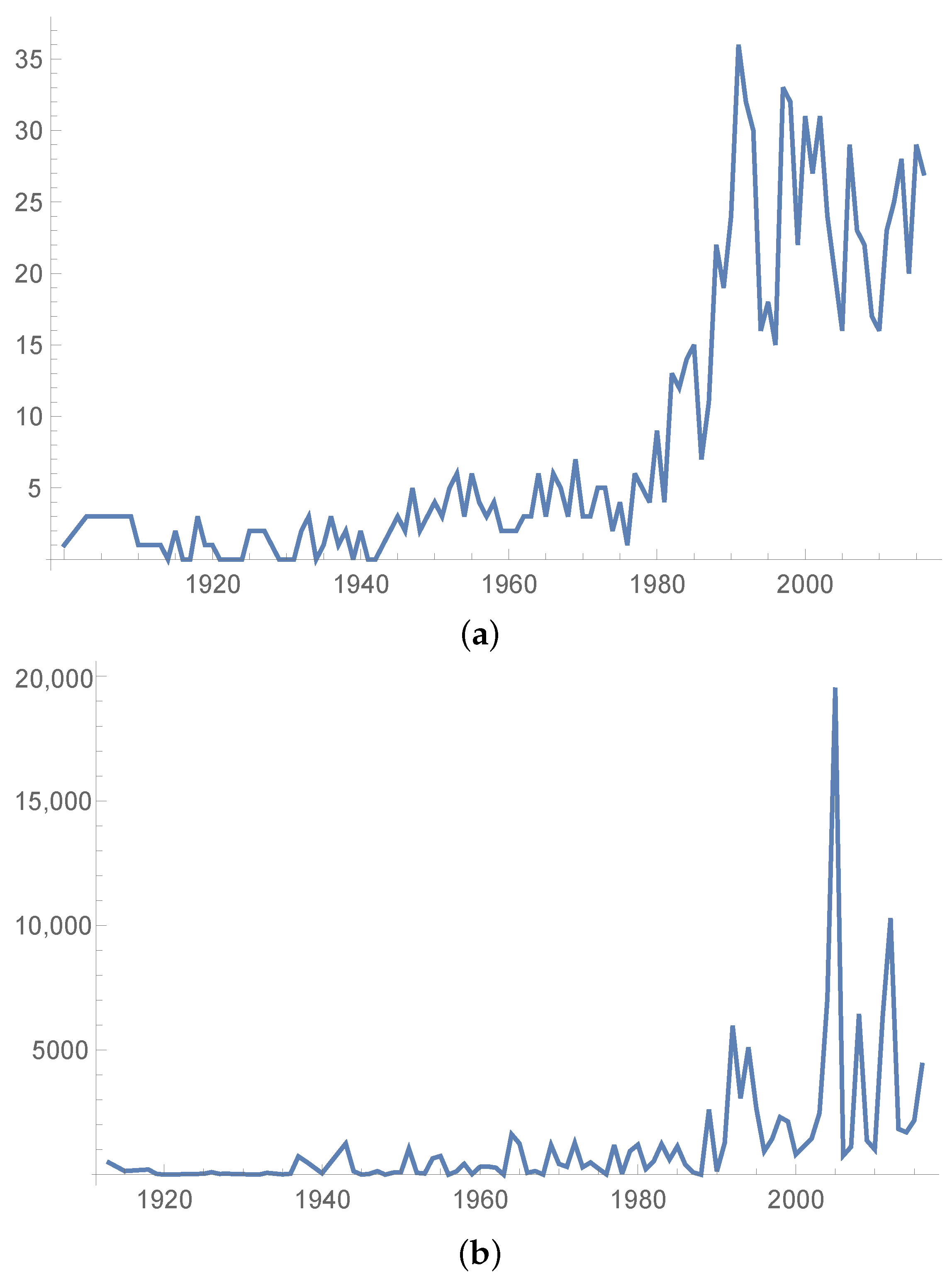
2. Natural Losses in the US
2.1. The Data
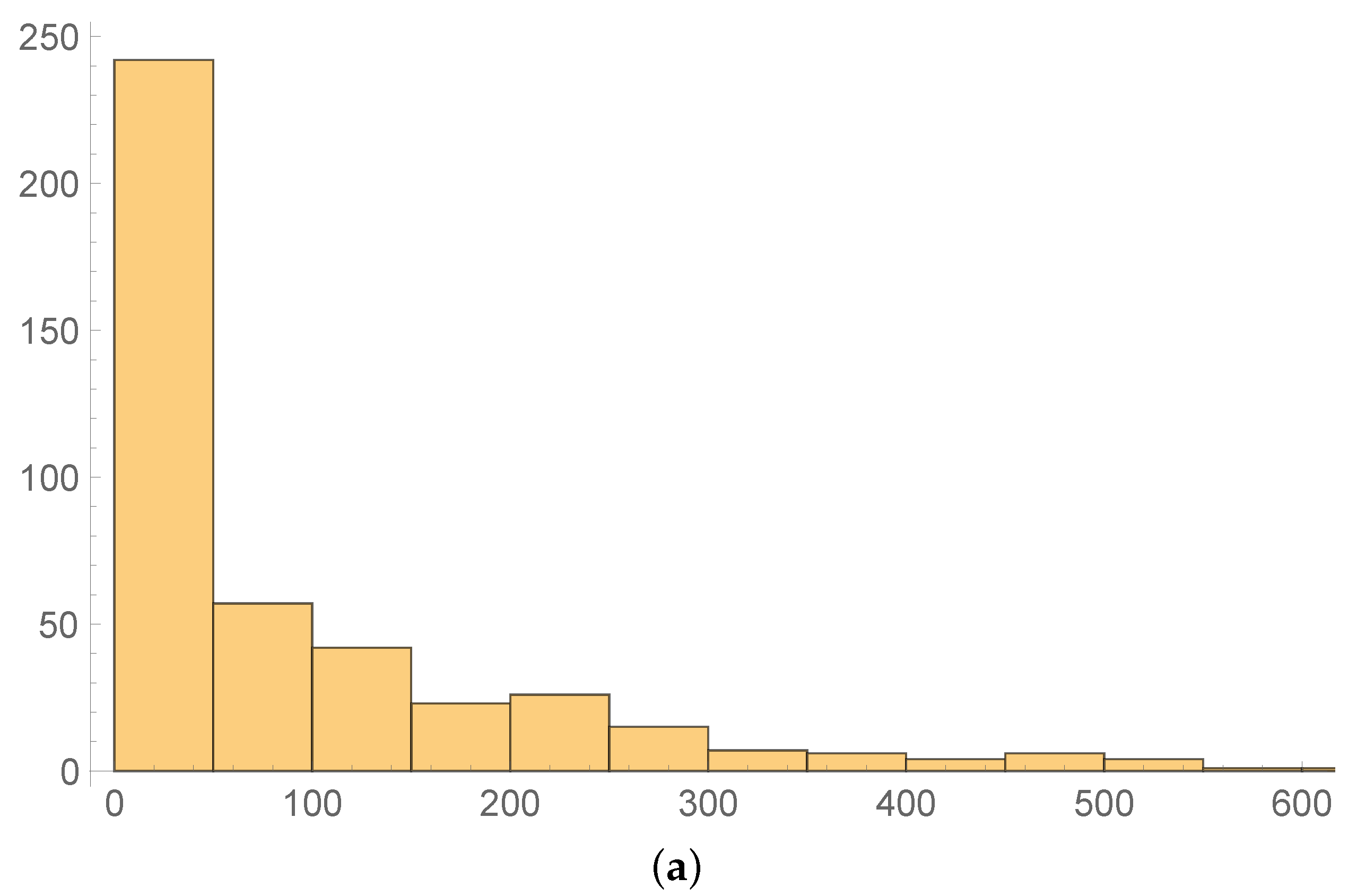
2.2. The i.i.d. Assumption for Loss Severity
2.3. Non-Parametric Distribution of Loss Severity
3. Composite Models
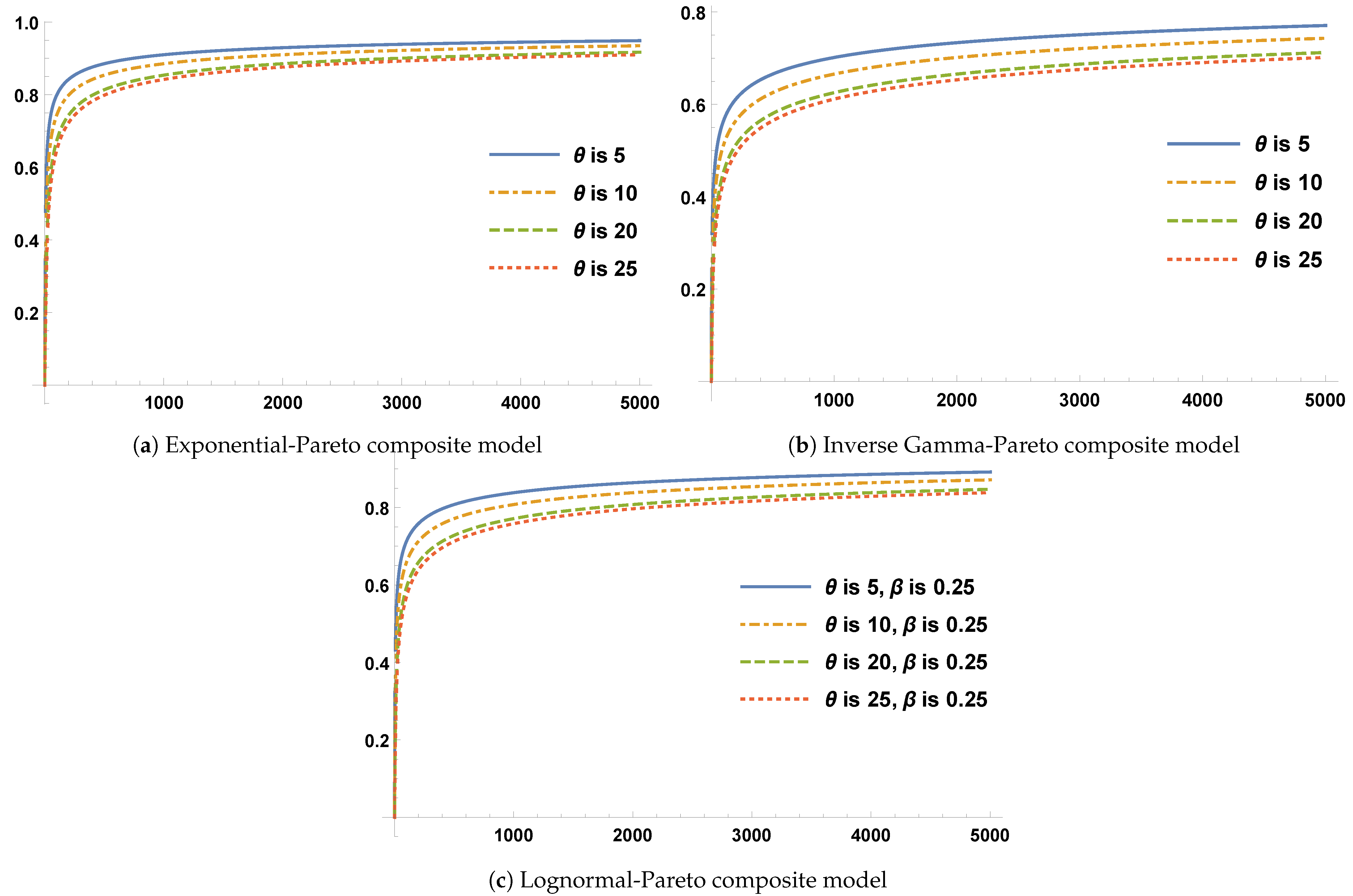
3.1. Three Composite Distributions
3.2. Model Selection for Loss Severity
- 1.
- Sort the sample of the natural disaster damage losses in an increasing order, i.e., , where n is the sample size. Let be the size of the partial sample of the first losses . Start from .
- 2.
- Compute the maximum likelihood estimates and as in Table 3 for the given . If is in between , we found ; otherwise, increase by 1.
- 3.
- Repeat Step 2 for till . The ML estimates of the parameters are found based on the correct .
4. The Bayesian Estimate
4.1. Bayesian Estimator of LN-Pareto
- Sort the sample of size n in increasing order, i.e., and let be the size of the partial sample of the first losses . Start from .
- Compute the Bayes estimate via (8) for the given .
- Compute the conditional Bayes estimate of via (7), given from Step 2. If , then we found . otherwise, increase by 1.
- Repeat Step 2 and 3 for till , and we found the correct .
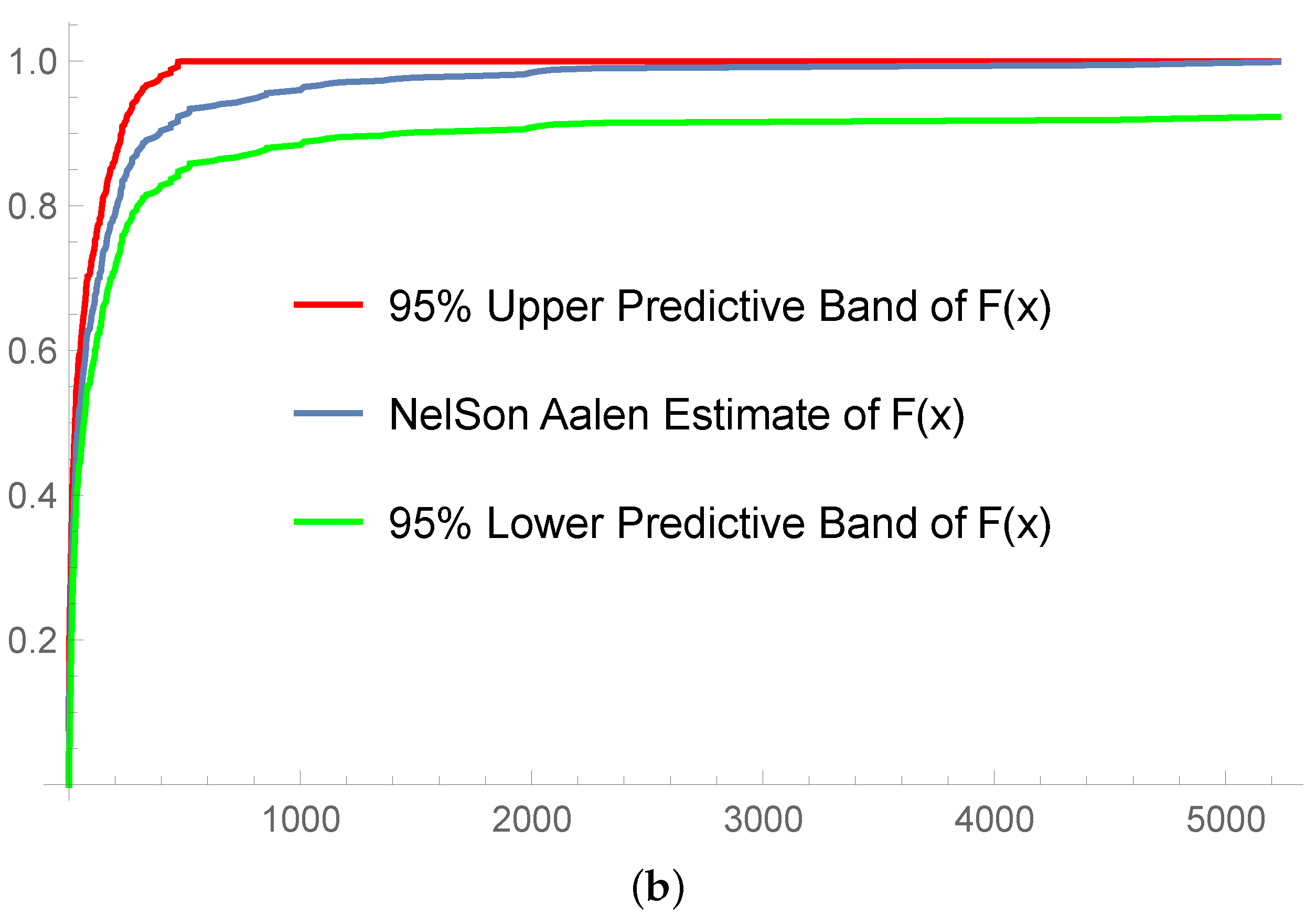
4.2. Validation by Simulation
4.3. Bayesian Estimates of Three Composite Models
5. Risk Measures
Value at Risk and Tailed Value at Risk
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
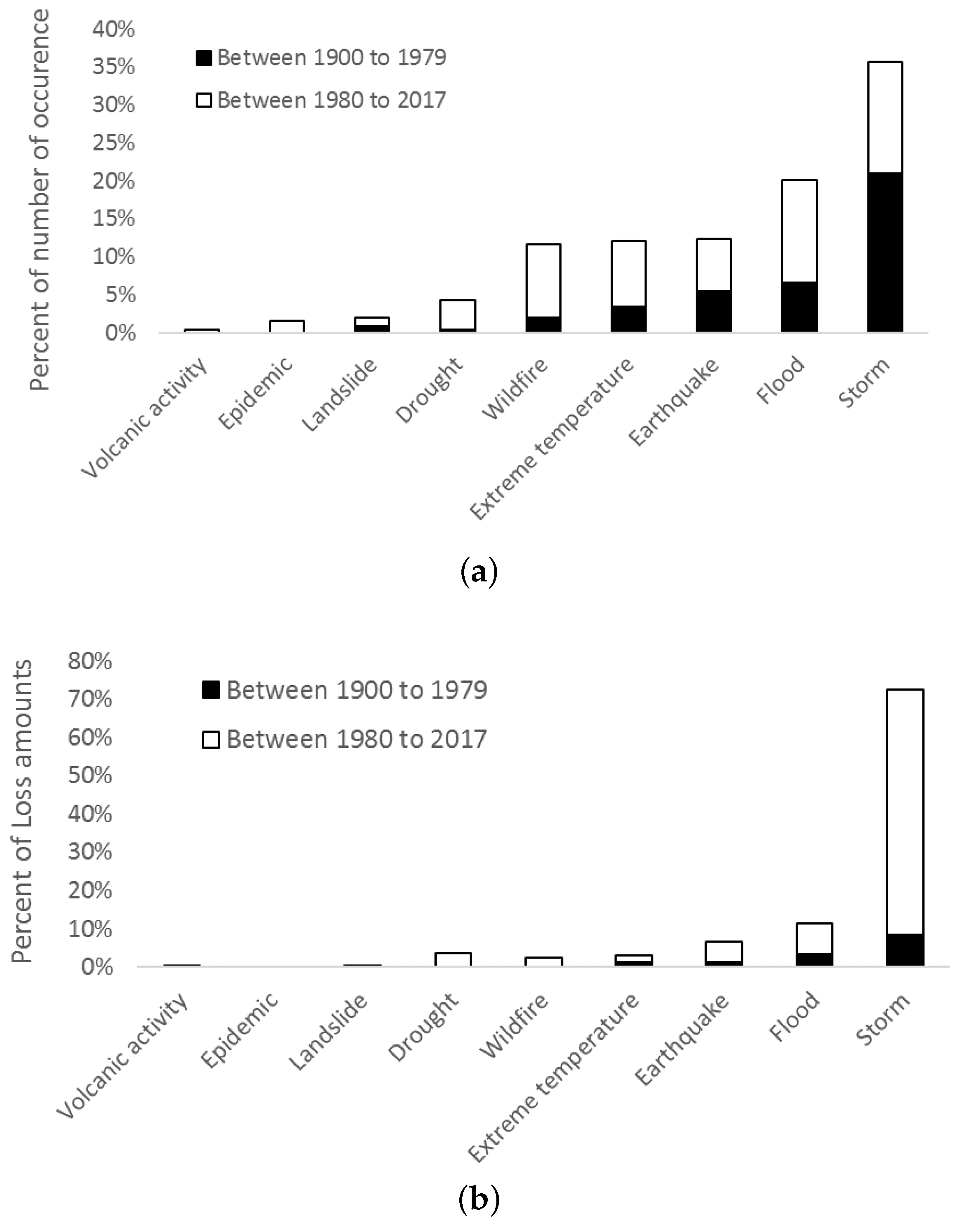
Appendix A. Number and Loss Amounts of Natural Events from 1900 to 2016
| 1900 to 1980 | 1980 to 2016 | 1900 to 2016 | % of All Events | |
|---|---|---|---|---|
| Drought | 11 | 4.26% | ||
| Earthquake | 32 | 12.40% | ||
| Epidemic | 4 | 1.55% | ||
| Extreme temperature | 31 | 12.02% | ||
| Flood | 52 | 20.16% | ||
| Landslide | 5 | 1.94% | ||
| Storm | 92 | 35.66% | ||
| Volcanic activity | 1 | 0.39% | ||
| Wildfire | 30 | 11.63% | ||
| Total | 258 | 100.00% |
| 1900 to 1979 | 1980 to 2016 | 1900 to 2016 | % of All Damages | |
|---|---|---|---|---|
| Drought | 4371.623471 | 3.62% | ||
| Earthquake | 7975.435381 | 6.60% | ||
| Epidemic | 0 | 0.00% | ||
| Extreme temperature | 3776.856375 | 3.13% | ||
| Flood | 13,772.64483 | 11.40% | ||
| Landslide | 2.027634158 | 0.00% | ||
| Storm | 87,642.85441 | 72.54% | ||
| Volcanic activity | 250.4927427 | 0.21% | ||
| Wildfire | 3035.724612 | 2.51% | ||
| Total | 120,827.6595 | 100.00% |
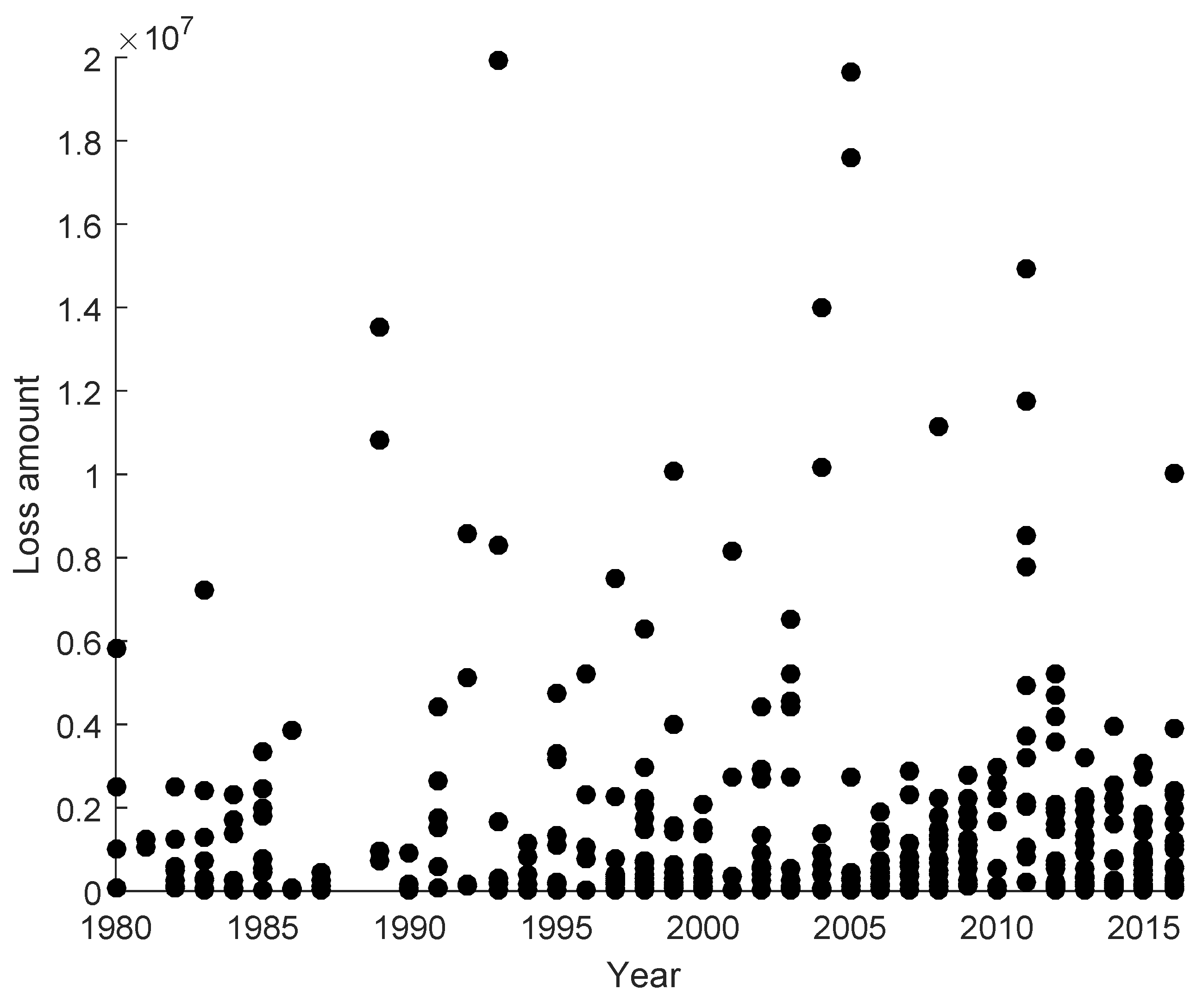
Appendix B. Damage Losses from Natural Events from 1980 to 2016
| Year | # of Losses | Loss | Loss | Loss | Loss | Loss | … | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1980 | 6 | 1019.45 | 87.38 | 58.25 | 2504.93 | 5825.41 | 2504.93 | ||||
| 1981 | 2 | 1056.14 | 1217.20 | ||||||||
| 1982 | 8 | 572.04 | 2487.12 | 84.31 | 99.48 | 248.71 | 104.46 | 497.42 | 1243.56 | ||
| 1983 | 9 | 7229.13 | 2409.71 | 74.70 | 15.06 | 1265.10 | 722.91 | 240.97 | 313.26 | 36.15 | |
| 1984 | 10 | 1683.05 | 80.85 | 2309.98 | 69.30 | 46.20 | 39.27 | 80.85 | 265.65 | 69.30 | 1385.99 |
| 1985 | 10 | 2453.60 | 2007.49 | 3345.82 | 26.99 | 758.39 | 1784.44 | 446.11 | 22.31 | 516.59 | 0.89 |
| 1986 | 5 | 1.58 | 3832.23 | 87.59 | 65.70 | 54.75 | |||||
| 1987 | 7 | 450.01 | 8.45 | 242.96 | 33.80 | 122.54 | 21.13 | 10.56 | |||
| 1988 | 0 | ||||||||||
| 1989 | 4 | 13,548.78 | 10,839.03 | 735.51 | 967.77 | ||||||
| 1990 | 6 | 23.32 | 73.45 | 183.63 | 918.16 | 64.27 | 82.63 | ||||
| 1991 | 9 | 59.03 | 2643.25 | 52.86 | 4405.41 | 52.86 | 1762.17 | 1497.84 | 1762.17 | 590.33 | |
| 1992 | 8 | 128.30 | 171.07 | 145.41 | 8553.35 | 5132.01 | 153.96 | 171.07 | 45,332.75 | ||
| 1993 | 7 | 315.58 | 207.62 | 166.09 | 8304.74 | 19,931.38 | 1660.95 | 12.46 | |||
| 1994 | 7 | 161.95 | 3.24 | 404.87 | 48,584.41 | 1133.64 | 809.74 | 3.40 | |||
| 1995 | 12 | 196.86 | 3307.18 | 4724.55 | 1330.75 | 1102.39 | 3149.70 | 4724.55 | 157.48 | 15.75 | 15.75 |
| 3149.70 | 4724.55 | ||||||||||
| 1996 | 6 | 1070.78 | 5200.92 | 13.00 | 2294.52 | 764.84 | 30.59 | ||||
| 1997 | 17 | 269.17 | 3.74 | 2.99 | 366.37 | 74.77 | 373.84 | 224.31 | 299.07 | 747.69 | 149.54 |
| 224.31 | 299.07 | 89.72 | 747.69 | 747.69 | 2243.06 | 7476.85 | |||||
| 1998 | 25 | 2061.41 | 2945.61 | 1472.44 | 406.39 | 690.57 | 6294.66 | 220.87 | 147.24 | 88.35 | 6.63 |
| 73.62 | 0.88 | 92.03 | 1472.44 | 2.94 | 1774.21 | 544.80 | 663.33 | 92.03 | 295.22 | ||
| 2208.65 | 736.22 | 397.56 | 92.03 | 295.22 | |||||||
| 1999 | 18 | 648.28 | 144.06 | 3976.11 | 288.84 | 1440.62 | 216.09 | 132.54 | 100.84 | 10,084.33 | 288.84 |
| 144.06 | 1440.62 | 10.08 | 90.04 | 288.12 | 0.43 | 1584.68 | 432.19 | ||||
| 2000 | 16 | 627.20 | 292.69 | 2090.65 | 139.38 | 39.72 | 11.29 | 1393.77 | 231.37 | 69.69 | 125.44 |
| 305.24 | 13.94 | 27.88 | 487.82 | 1533.15 | 696.88 | ||||||
| 2001 | 12 | 338.80 | 31.17 | 2.44 | 8131.24 | 17.62 | 27.10 | 13.55 | 40.66 | 5.42 | 9.49 |
| 4.07 | 2710.41 | ||||||||||
| 2002 | 16 | 533.65 | 267.49 | 6.67 | 17.34 | 5.34 | 2935.05 | 26.68 | 267.49 | 1334.11 | 26.68 |
| 400.23 | 933.88 | 2668.23 | 601.02 | 8.81 | 4402.57 | ||||||
| 2003 | 13 | 6521.93 | 32.61 | 5217.54 | 138.26 | 4395.78 | 260.88 | 521.75 | 22.17 | 65.22 | 4565.35 |
| 4.43 | 2739.21 | 260.88 | |||||||||
| 2004 | 14 | 381.17 | 5.72 | 1397.61 | 889.39 | 76.23 | 0.22 | 20,328.81 | 79.41 | 13,976.06 | 22,869.91 |
| 10,164.40 | 2.67 | 1.27 | 635.28 | ||||||||
| 2005 | 11 | 307.23 | 245.78 | 36.87 | 430.12 | 6.55 | 430.12 | 2740.48 | 19,662.63 | 17,573.48 | 301.08 |
| 122.89 | |||||||||||
| 2006 | 20 | 1428.61 | 714.31 | 1904.82 | 308.34 | 14.29 | 535.73 | 101.19 | 1190.51 | 8.33 | 19.05 |
| 119.05 | 18.45 | 39.12 | 29.76 | 113.10 | 357.15 | 29.76 | 178.58 | 107.15 | 428.58 | ||
| 2007 | 15 | 32.41 | 578.77 | 810.28 | 150.48 | 2893.85 | 364.63 | 1157.54 | 578.77 | 162.06 | 405.14 |
| 2315.08 | 347.26 | 347.26 | 694.52 | 347.26 | |||||||
| 2008 | 16 | 501.63 | 2.23 | 780.32 | 1783.58 | 113.70 | 1337.69 | 200.65 | 33,442.22 | 1449.16 | 2229.48 |
| 668.84 | 1114.74 | 1226.21 | 11,147.41 | 122.62 | 401.31 | ||||||
| 2009 | 12 | 185.71 | 1901.83 | 111.87 | 268.49 | 2796.80 | 559.36 | 1230.59 | 671.23 | 2237.44 | 1118.72 |
| 950.91 | 1678.08 | ||||||||||
| 2010 | 7 | 2586.57 | 2971.80 | 13.76 | 2201.33 | 110.07 | 1651.00 | 550.33 | |||
| 2011 | 14 | 2133.97 | 195.26 | 11,736.86 | 14,937.82 | 2027.28 | 7789.01 | 1066.99 | 3200.96 | 800.24 | 3734.45 |
| 4908.14 | 213.40 | 2133.97 | 8535.90 | ||||||||
| 2012 | 22 | 182.94 | 1620.30 | 1881.64 | 219.52 | 181.89 | 627.21 | 2090.71 | 52,267.70 | 2.09 | 52.27 |
| 4181.42 | 209.07 | 522.68 | 5226.77 | 4704.09 | 104.54 | 3554.20 | 1463.50 | 1986.17 | 731.75 | ||
| 219.52 | 20,907.08 | ||||||||||
| 2013 | 26 | 1648.42 | 1133.29 | 309.08 | 3193.82 | 309.08 | 2163.55 | 22.05 | 515.13 | 927.24 | 2.06 |
| 25.76 | 25.76 | 2.06 | 334.84 | 180.30 | 309.08 | 1957.50 | 10.30 | 1339.34 | 2.06 | ||
| 206.05 | 103.03 | 2266.58 | 103.03 | 103.03 | 1133.29 | ||||||
| 2014 | 19 | 2.03 | 2027.63 | 101.38 | 3953.89 | 273.73 | 66.91 | 1622.11 | 709.67 | 172.35 | 101.38 |
| 253.45 | 91.24 | 212.90 | 253.45 | 1622.11 | 760.36 | 2534.54 | 2230.40 | 20.28 | |||
| 2015 | 28 | 172.14 | 506.31 | 1417.66 | 961.98 | 1012.62 | 162.02 | 1417.66 | 2734.06 | 658.20 | 101.26 |
| 81.01 | 2.03 | 708.83 | 101.26 | 961.98 | 151.89 | 1417.66 | 2.03 | 1721.45 | 101.26 | ||
| 273.41 | 141.77 | 911.35 | 607.57 | 405.05 | 151.89 | 3037.85 | 1822.71 | ||||
| 2016 | 25 | 550.00 | 125.00 | 3900.00 | 2000.00 | 2400.00 | 1000.00 | 1100.00 | 300.00 | 1000.00 | 150.00 |
| 50.00 | 10,000.00 | 100.00 | 600.00 | 550.00 | 10,000.00 | 1200.00 | 275.00 | 20.00 | 1200.00 | ||
| 100.00 | 2300.00 | 1600.00 | 1200.00 | 2300.00 |
References
- Akaike, Hirotogu. 1973. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, USSR, Armenia, 2–8 September 1971. Edited by B. N. Petrov and F. Csaki. Budapest: Akademia Kiado, pp. 267–81. [Google Scholar]
- Aminzadeh, Mostafa S., and Min Deng. 2018. Bayesian Predictive Modeling for Exponential-Pareto Composite Distribution. Variance 12: 59–68. [Google Scholar]
- Aminzadeh, Mostafa S., and Min Deng. 2019. Bayesian Predictive Modeling for Inverse Gamma-Pareto Composite Distribution. Communications in Statistics-Theory and Methods 48: 1938–54. [Google Scholar] [CrossRef]
- Bakar, S.A. Abu, Nor A. Hamzah, Mastoureh Maghsoudi, and Saralees Nadarajah. 2015. Modeling loss data using composite models. Insurance: Mathematics and Economics 61: 146–54. [Google Scholar]
- Burnham, Kenneth P., and David R. Anderson. 2002. Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach, 2nd ed. New York: Springer. [Google Scholar]
- Cooray, Kahadawala, and Chin-I Cheng. 2015. Bayesian estimators of the lognormal-Pareto composite distribution. Scandinavian Actuarial Journal 6: 500–15. [Google Scholar] [CrossRef]
- Cooray, Kahadawala, and Malwane M.A. Ananda. 2005. Modeling actuarial data with a composite lognormal-Pareto model. Scandinavian Actuarial Journal 5: 321–34. [Google Scholar] [CrossRef]
- Gibbons, Jean Dickinson, and Subhabrata Chakraborti. 2003. Nonparametric Statistical Inference, 4th ed., Revised and Expanded. Statistics Textbooks and Monographs. Boca Raton: CRC Press, vol. 168. [Google Scholar]
- Kass, Robert E., and Adrian E. Raftery. 1995. Bayes Factors. Journal of the American Statistical Association 90: 773–95. [Google Scholar] [CrossRef]
- Levi, Charles, and Christian Partrat. 1991. Statistical Analysis of Natural Events in the United States. ASTIN Bulletin: The Journal of the IAA 21: 253–76. [Google Scholar] [CrossRef][Green Version]
- Schwarz, Gideon. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar]
- Teodorescu, Sandra, and Raluca Vernic. 2006. A composite Exponential-Pareto distribution. The Annals of the Ovidius, University of Constanta, Mathematics Series 1: 99–108. [Google Scholar]
| 1 | |
| 2 | |
| 3 | The CPI data was download from Bureau of Labor Statistics https://data.bls.gov/pdq/SurveyOutputServlet. |
| Pairs | Kendall Tau Statistics (p-Value) | Spearman Statistics (p-Value) |
|---|---|---|
| The Composite pdf | |||
|---|---|---|---|
| Exp-Pareto | , | ||
| IG-Pareto | , | where , , | |
| LN-Pareto | where |
| Composite Model | ML Estimates of Parameters |
|---|---|
| Exp-Pareto | , where . |
| IG-Pareto | , where , , . |
| LN-Pareto | If , , , where ; otherwise, , , where , . |
| Model | ML Estimates of Parameters | |||
|---|---|---|---|---|
| Exp-Pareto | 2698.02 | 5398.05 | 5402.19 | |
| IG-Pareto | 2719.35 | 5440.7 | 5444.83 | |
| LN-Pareto | 2327.74 | 4659.49 | 4667.76 | |
| Exponential Exp() | ||||
| Inverse Gamma | 2813.29 | 5630.58 | 5638.85 | |
| IG( ) | ||||
| Lognormal | 3058.66 | 6121.31 | 6129.58 | |
| LN( ) |
| () | |||||||||
| n | |||||||||
| 20 | 7.8604 | 4.0640 | 0.4747 | 0.1611 | 5.6933 | 2.0959 | 0.4641 | 0.0402 | |
| 50 | 7.8942 | 3.8006 | 0.4435 | 0.1121 | 5.7941 | 1.2265 | 0.4338 | 0.0688 | |
| 100 | 7.6421 | 3.6415 | 0.4333 | 0.1056 | 5.8745 | 1.1874 | 0.4058 | 0.0960 | |
| () | |||||||||
| n | |||||||||
| 20 | 21.8966 | 12.2540 | 0.5878 | 0.2626 | 20.5062 | 5.5390 | 0.5341 | 0.0345 | |
| 50 | 19.9977 | 4.9775 | 0.5738 | 0.2431 | 20.5262 | 3.3892 | 0.5025 | 0.0065 | |
| 100 | 19.5730 | 3.6691 | 0.5467 | 0.1830 | 21.2182 | 3.0585 | 0.4629 | 0.0379 | |
| () | |||||||||
| n | |||||||||
| 20 | 5.342 | 1.2443 | 1.510 | 0.3811 | 5.076 | 0.3877 | 1.480 | 0.02047 | |
| 50 | 5.041 | 0.5606 | 1.528 | 0.2181 | 5.038 | 0.2526 | 1.451 | 0.0492 | |
| 100 | 5.035 | 0.2344 | 1.516 | 0.1389 | 5.111 | 0.2196 | 1.406 | 0.0941 | |
| ( ) | |||||||||
| n | |||||||||
| 20 | 20.698 | 3.3162 | 1.560 | 0.4157 | 20.556 | 1.8798 | 1.460 | 0.04030 | |
| 50 | 20.763 | 3.0164 | 1.468 | 0.2479 | 20.460 | 1.0797 | 1.404 | 0.09601 | |
| 100 | 20.218 | 2.6237 | 1.466 | 0.2839 | 20.637 | 0.9563 | 1.324 | 0.1762 | |
| Model | Prior Distributions | Bayesian Estimates | |||
|---|---|---|---|---|---|
| Exp-Pareto | Inverse-Gamma(10, 5) | 2697.57 | 5397.13 | 5401.27 | |
| IG-Pareto | Gamma(50, 1) | 2699.17 | 5400.34 | 5404.48 | |
| LN-Pareto | LN(1.61352, 2.857) Gamma(20,500, 1.1 × 10) | 2327.63 | 4659.27 | 4667.54 |
| Models | |||
|---|---|---|---|
| Bayesian Estimation | Exp-Pareto | 1073 | 30,723 |
| IG-Pareto | 58,212 | 98,041 | |
| LN-Pareto | 11,070 | 75,860 | |
| ML Estimation | Exp-Pareto | 1185 | 31,770 |
| IG-Pareto | 38,029 | 94,619 | |
| LN-Pareto | 11,963 | 76,946 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, M.; Aminzadeh, M.; Ji, M. Bayesian Predictive Analysis of Natural Disaster Losses. Risks 2021, 9, 12. https://doi.org/10.3390/risks9010012
Deng M, Aminzadeh M, Ji M. Bayesian Predictive Analysis of Natural Disaster Losses. Risks. 2021; 9(1):12. https://doi.org/10.3390/risks9010012
Chicago/Turabian StyleDeng, Min, Mostafa Aminzadeh, and Min Ji. 2021. "Bayesian Predictive Analysis of Natural Disaster Losses" Risks 9, no. 1: 12. https://doi.org/10.3390/risks9010012
APA StyleDeng, M., Aminzadeh, M., & Ji, M. (2021). Bayesian Predictive Analysis of Natural Disaster Losses. Risks, 9(1), 12. https://doi.org/10.3390/risks9010012





