A Comprehensive CFD Assessment of Wheat Flow in Wheat Conveying Cyclone Validation and Performance Analysis by Experimental Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cyclone Geometry and Experimental Setup
2.2. Separation Efficiency
2.3. Numerical Procedure and Simulation Setup
2.4. Boundary Condition
2.5. Discrete Phase Model
2.6. Cyclone Meshing and Grid Independence Test
3. Results and Discussion
3.1. Validation
3.2. Comparison of Various Inlet Velocities and Mass Flow Rates
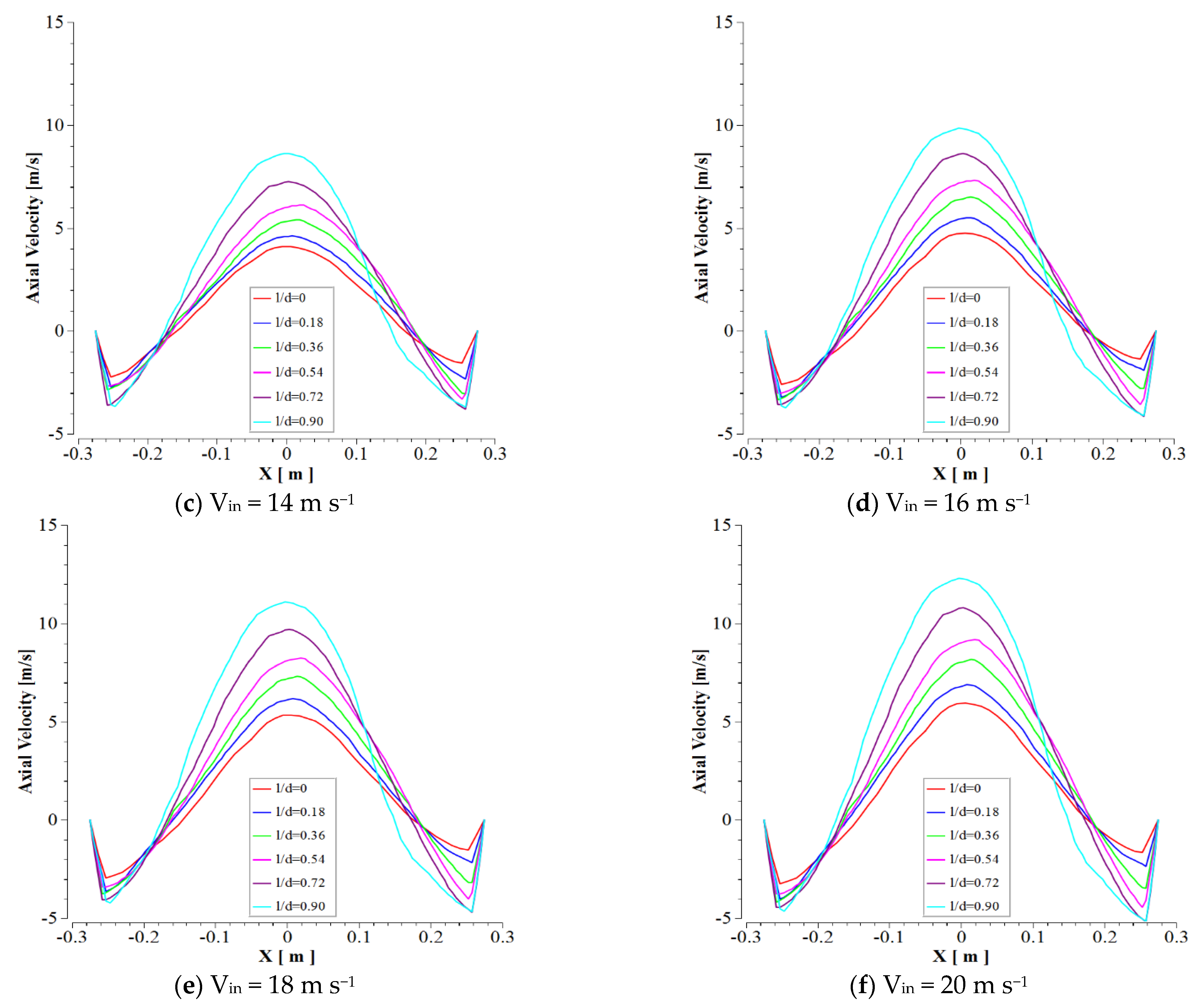
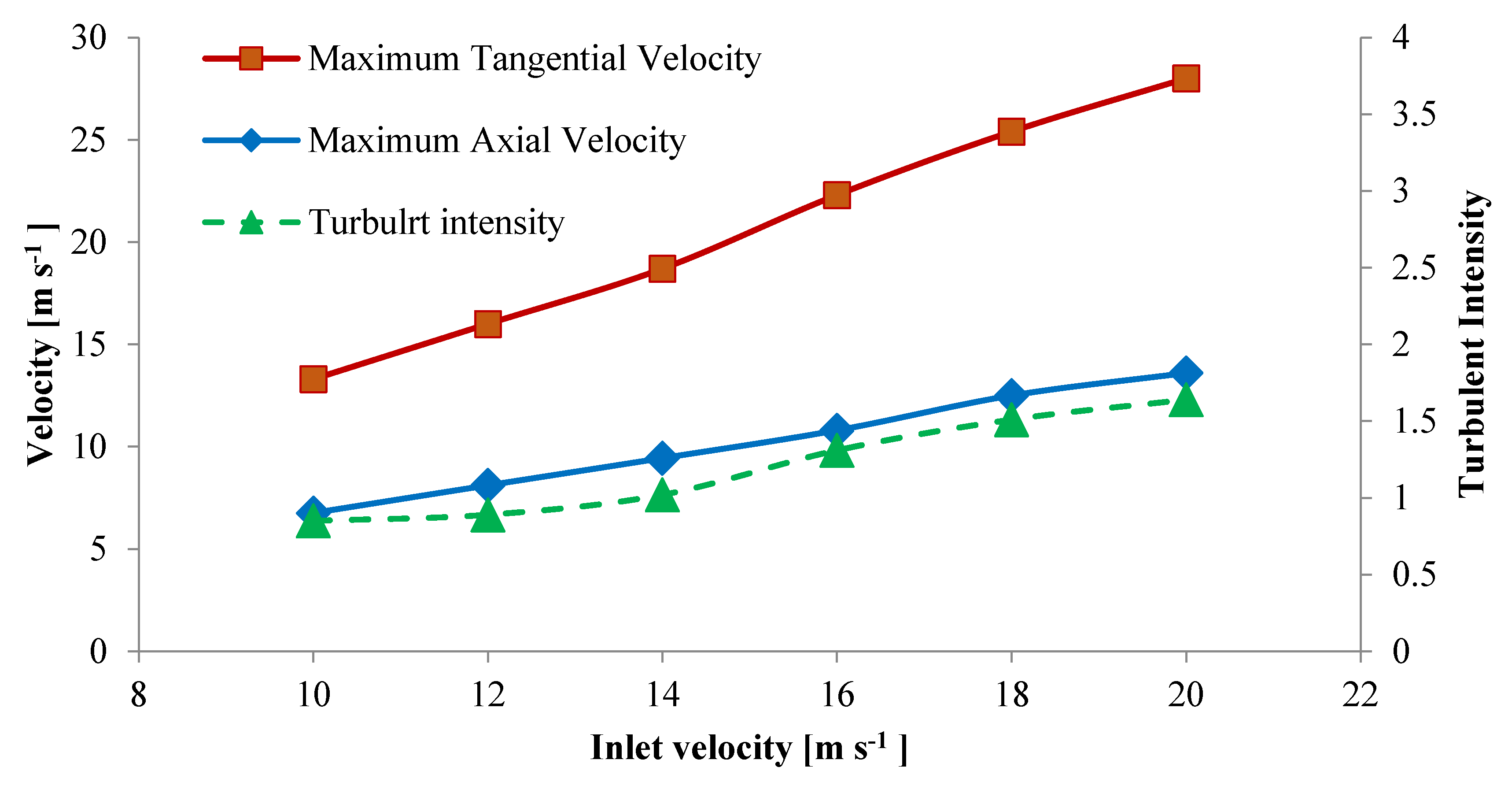
3.3. Axial Velocity
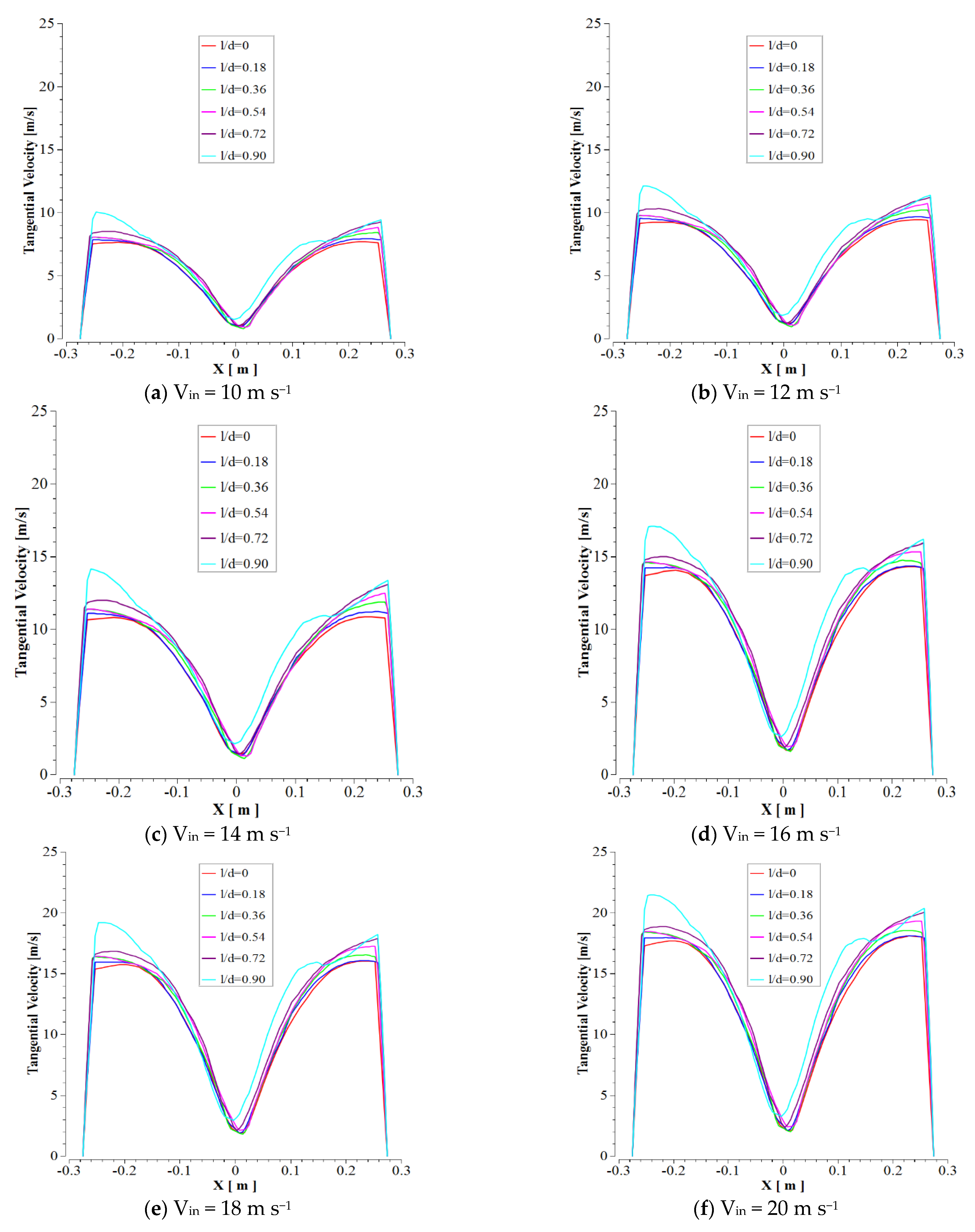
3.4. Tangential Velocity
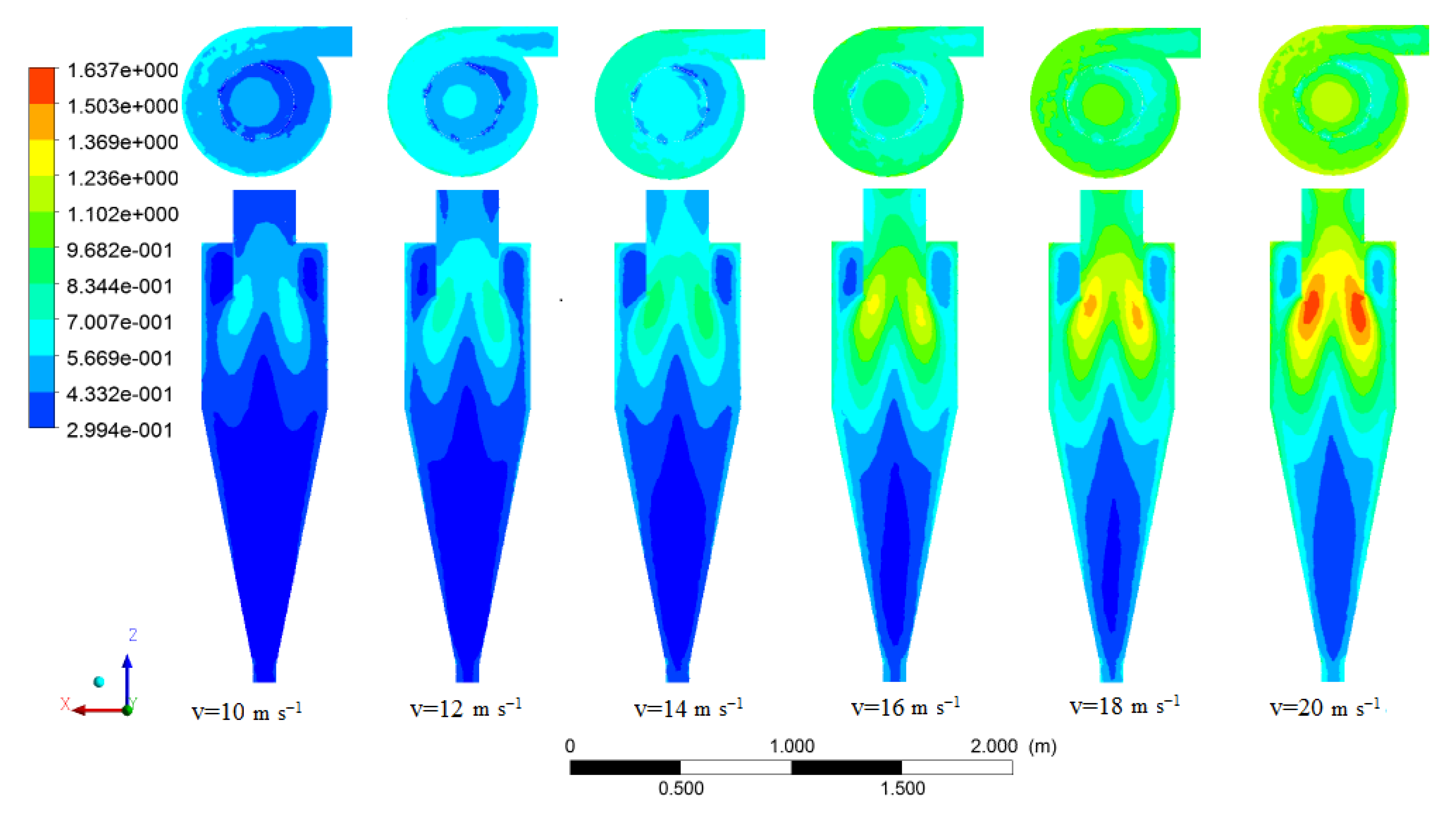
3.5. Turbulent Intensity
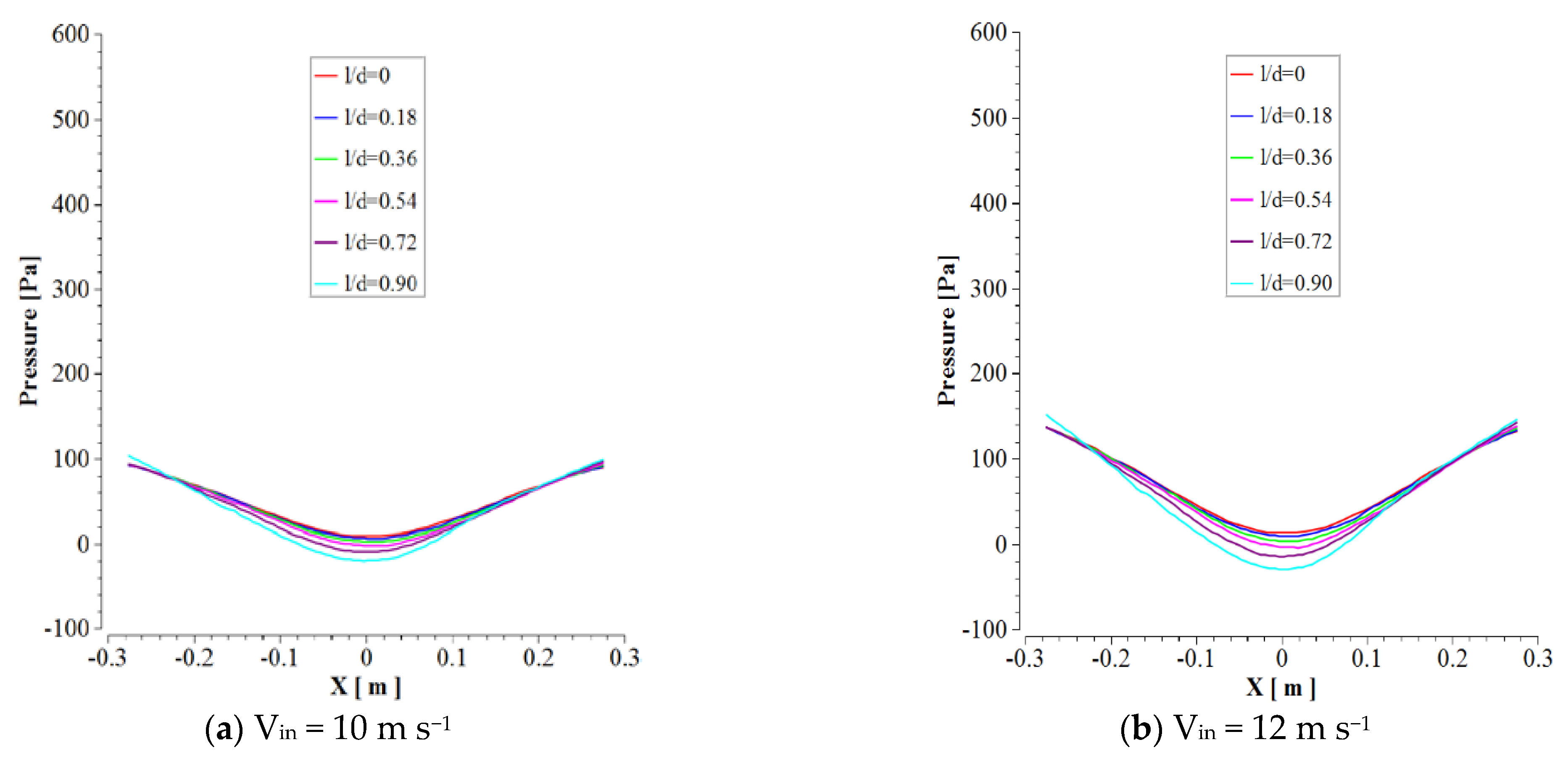
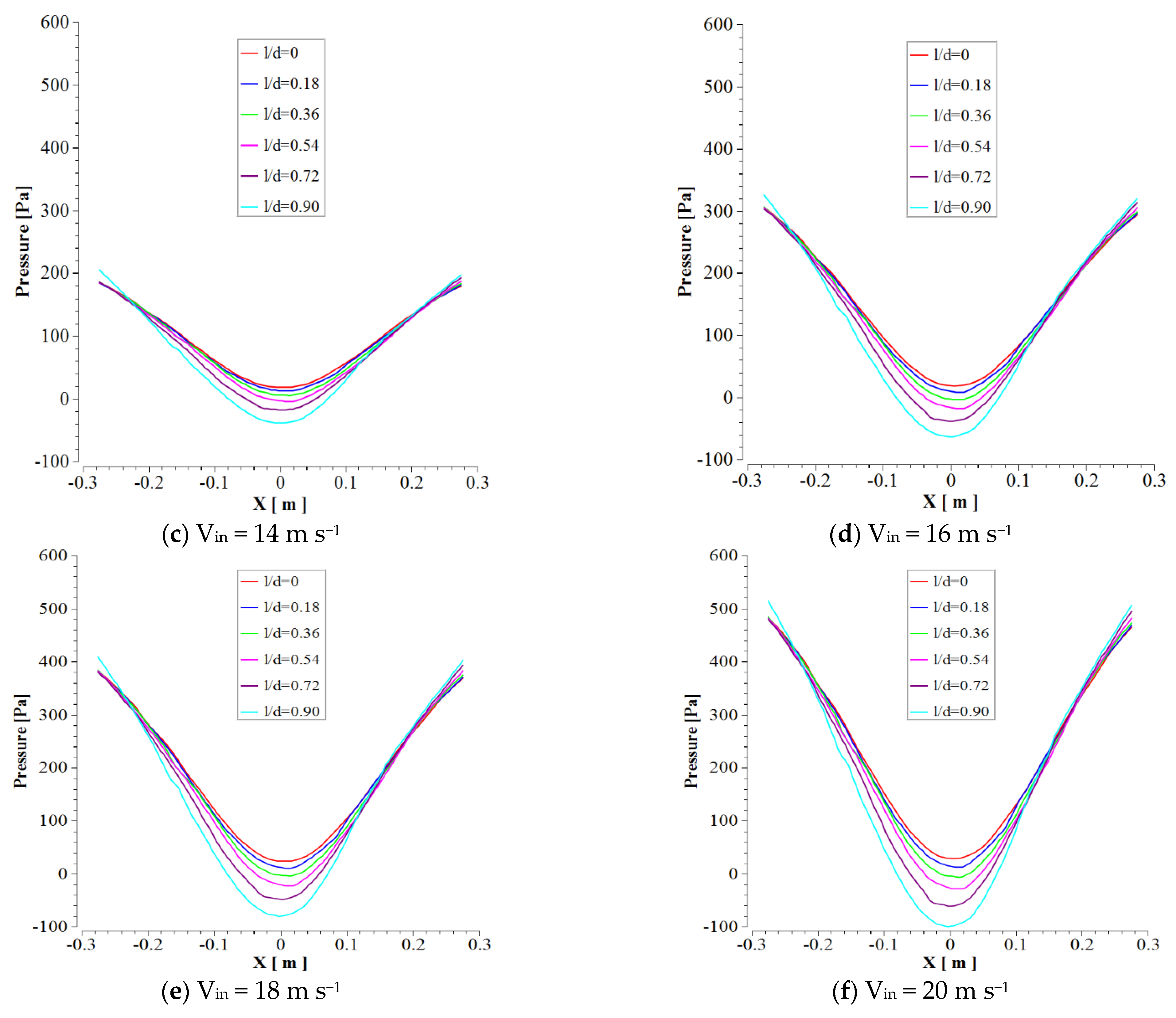
3.6. Static Pressure
3.7. Separation Efficiency
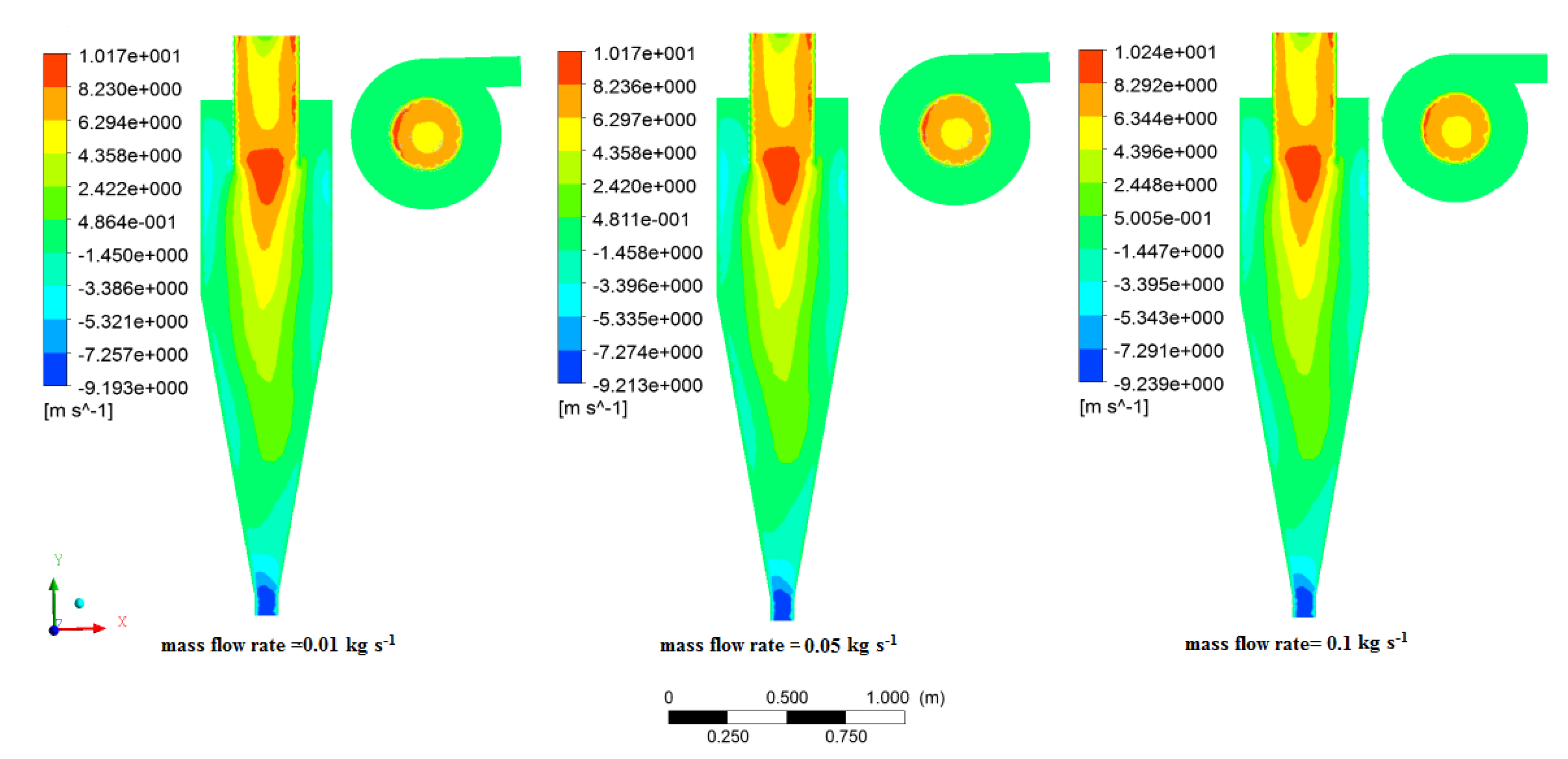
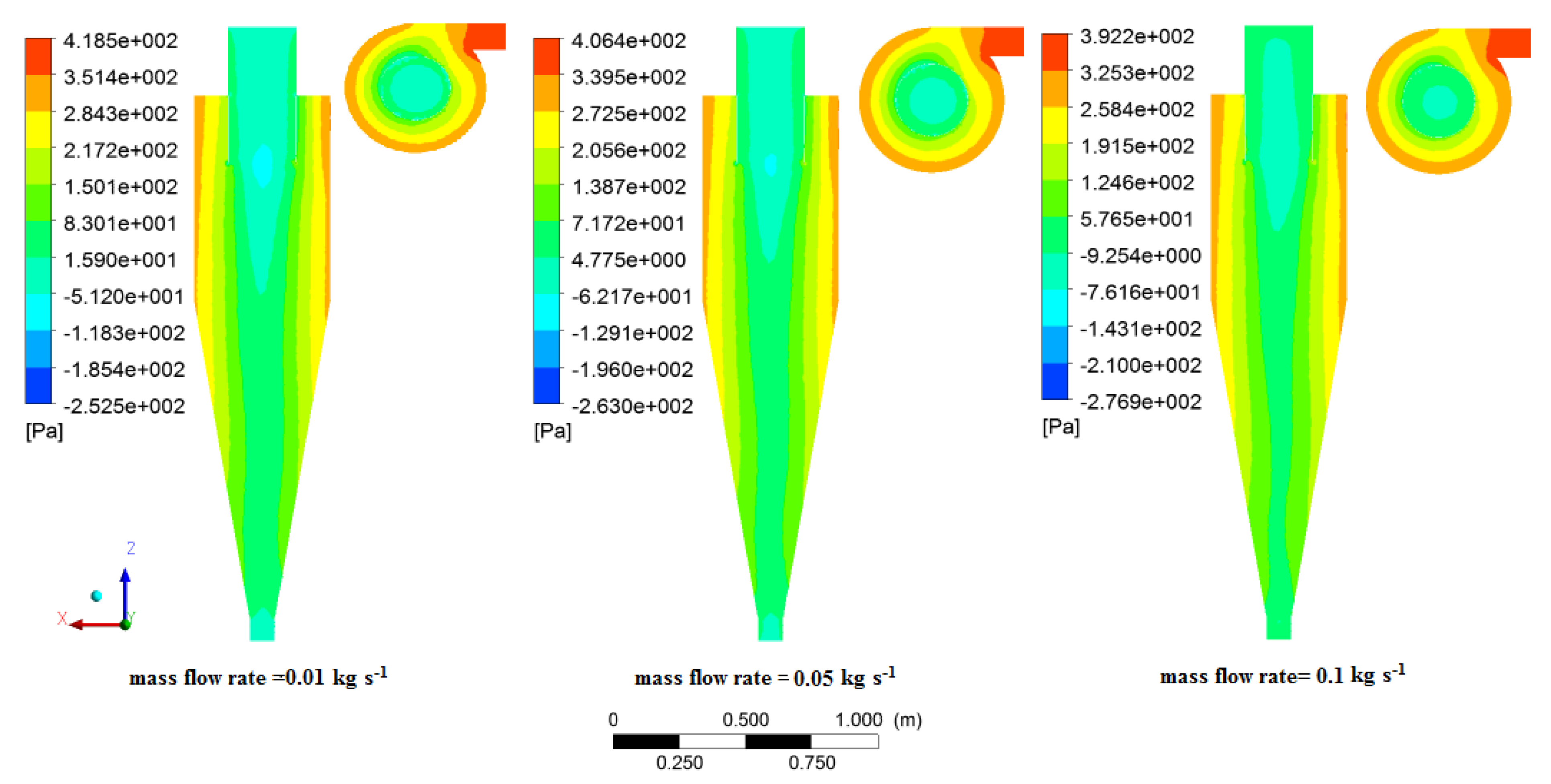
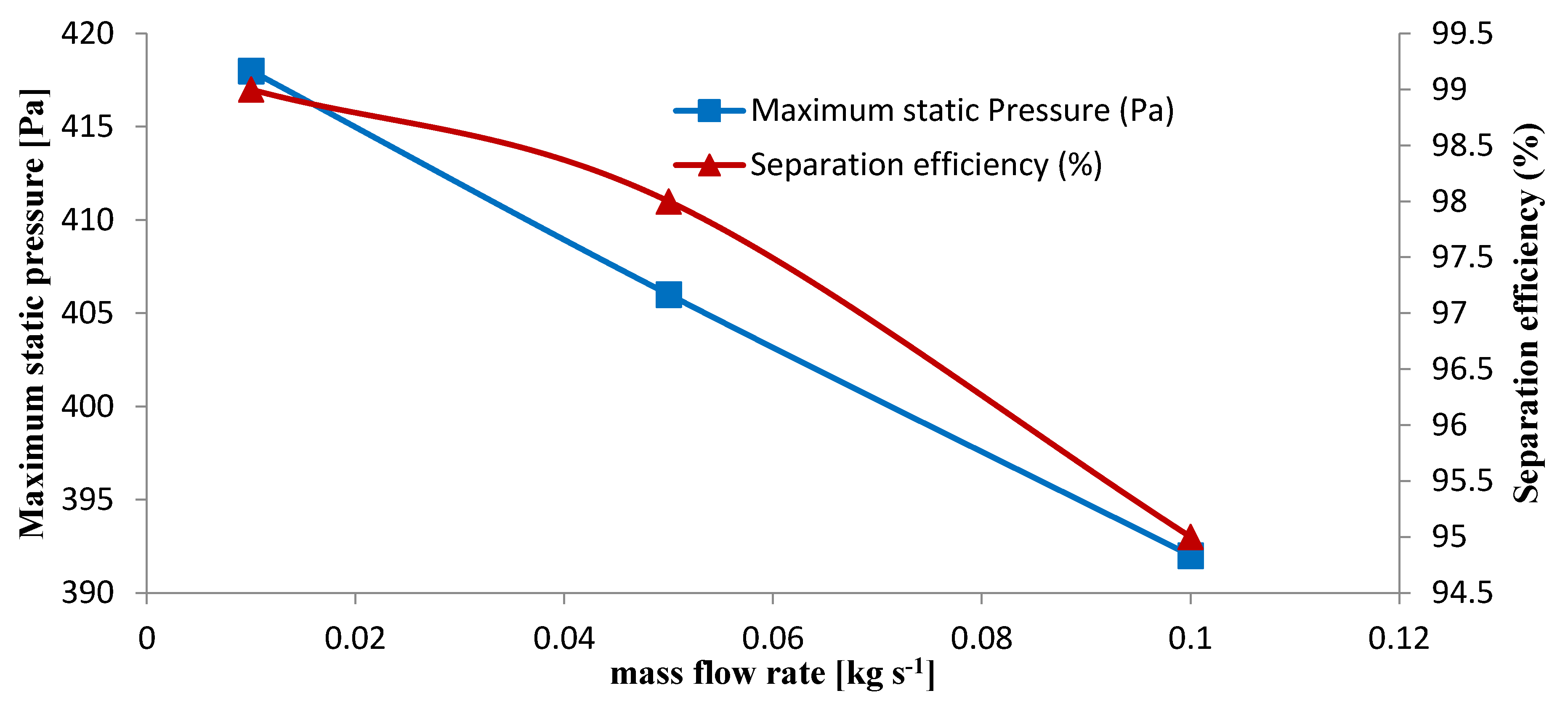
3.8. Static Pressure and Separation Efficiency in Various Mass Flow Rate
4. Conclusions
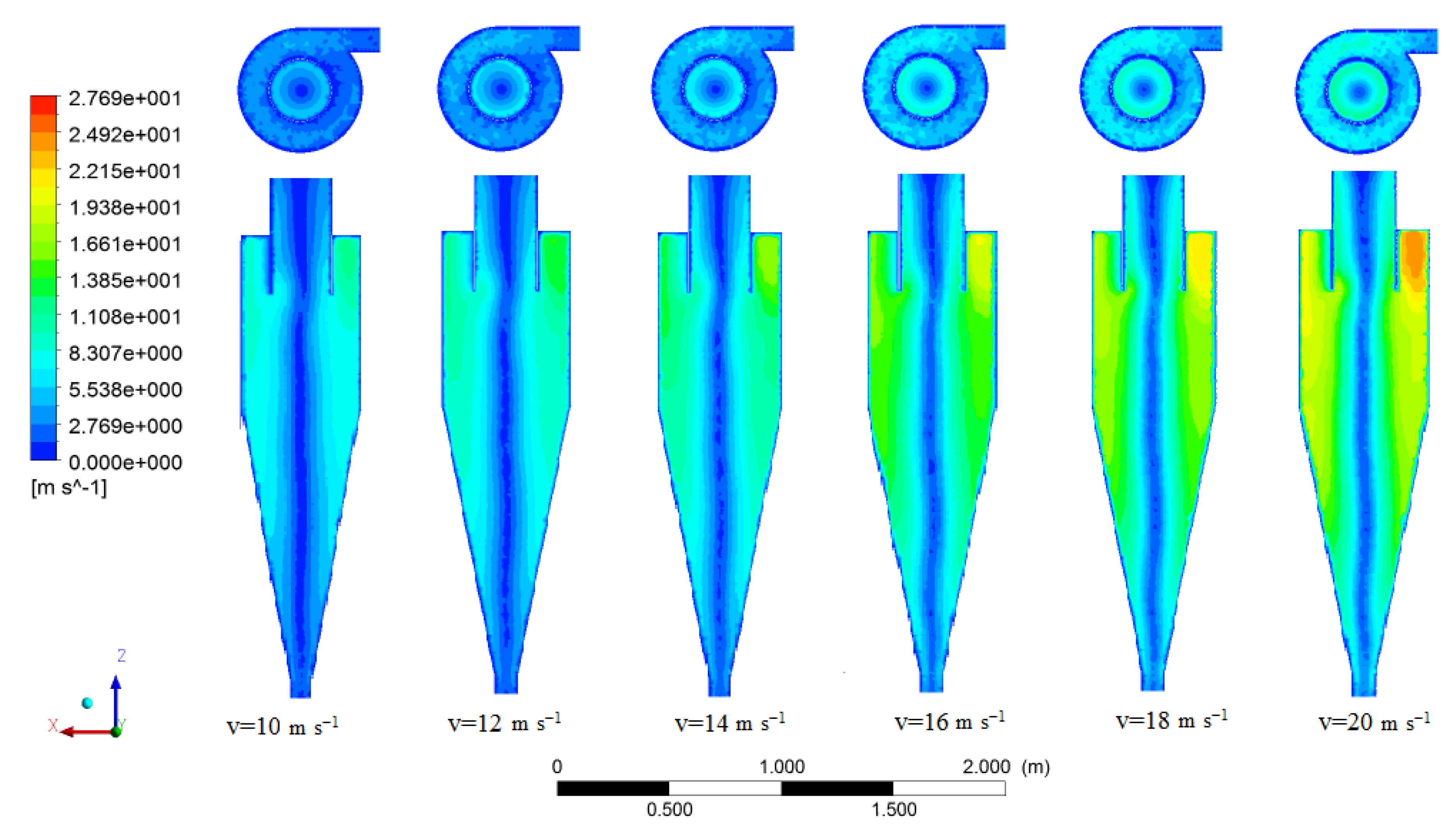
- The pressure drop increased with increasing inlet velocity, while the separation efficiency increased to 16 m s−1, and subsequently indicated a decreasing trend for 18 and 20 m s−1 inlet velocities. Minimum pressure drop was obtained along the vortex finder axis, and the maximum pressure drop was obtained in the top section of the cyclone wall, demonstrating a uniform trend in all inlet velocities. In terms of compromise between the pressure drop and separation efficiency in wheat conveying within a cyclone, the velocity of 16 m s−1 was determined as the best inlet velocity between all inlet velocities.
- The turbulent intensity as an effective factor in separation efficiency increased with increasing inlet velocity. One of the factors to reduce separation efficiency is the increase in the turbulent intensity and effectiveness.
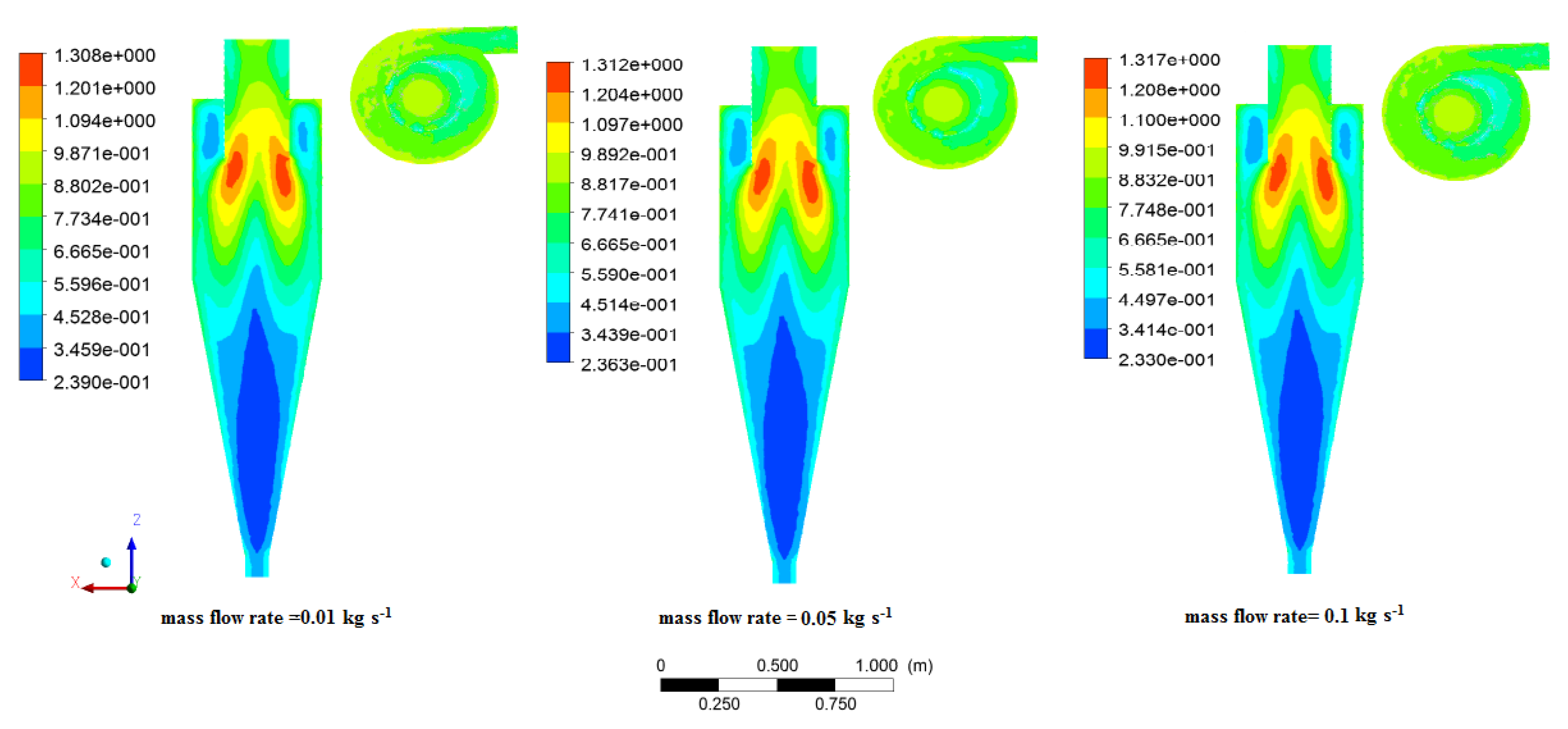
- In the second case, increasing the mass flow rate resulted in a decrement in pressure drop and separation efficiency. Additionally, the distribution of axial velocity in the mass flow rate of 0.01 to 0.05 remained almost constant and increasing to 0.1 observed a minor increase. It can be conducted that increasing the mass flow rate in the desired range has a negligible effect on the axial velocity distribution. The tangential velocity decreased with increasing mass flow rate. Additionally, increasing the mass flow rate was insignificant in the turbulent intensity within the cyclone.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Misiulia, D.; Elsayed, K.; Andersson, A.G. Geometry optimization of a deswirler for cyclone separator in terms of pressure drop using CFD and artificial neural network. Sep. Purif. Technol. 2017, 185, 10–23. [Google Scholar] [CrossRef]
- Miller, B.G. Clean Coal Engineering Technology; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Gimbun, J.; Chuah, T.; Fakhru’L-Razi, A.; Choong, T.S. The influence of temperature and inlet velocity on cyclone pressure drop: A CFD study. Chem. Eng. Process. Process. Intensif. 2005, 44, 7–12. [Google Scholar] [CrossRef]
- Gimbun, J.; Chuah, T.G.; Choong, T.S.Y.; Engineering, N.R. Evaluation on Empirical Models for the prediction of cyclone efficiency. J. Inst. Eng. 2006, 67, 54–58. [Google Scholar]
- Gimbun, J. CFD Simulation of Aerocyclone Hydrodynamics and Performance at Extreme Temperature. Eng. Appl. Comput. Fluid Mech. 2008, 2, 22–29. [Google Scholar] [CrossRef] [Green Version]
- Wasilewski, M.; Brar, L.S. Effect of the inlet duct angle on the performance of cyclone separators. Sep. Purif. Technol. 2019, 213, 19–33. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.; Elsayed, K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 2015, 286, 668–677. [Google Scholar] [CrossRef]
- Zhao, B. Prediction of gas-particle separation efficiency for cyclones: A time-of-flight model. Sep. Purif. Technol. 2012, 85, 171–177. [Google Scholar] [CrossRef]
- Wan, G.; Sun, G.; Xue, X.; Shi, M. Solids concentration simulation of different size particles in a cyclone separator. Powder Technol. 2008, 183, 94–104. [Google Scholar] [CrossRef]
- Sun, X.; Kim, S.; Yang, S.D.; Kim, H.S.; Yoon, J.Y. Multi-objective optimization of a Stairmand cyclone separator using response surface methodology and computational fluid dynamics. Powder Technol. 2017, 320, 51–65. [Google Scholar] [CrossRef]
- Sun, X.; Yoon, J.Y. Multi-objective optimization of a gas cyclone separator using genetic algorithm and computational fluid dynamics. Powder Technol. 2018, 325, 347–360. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and optimization of cyclone separators with eccentric vortex finders using large eddy simulation and artificial neural network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Farahani, S.M.N.; Tahmasbi, V.; Safikhani, H.; Abbassi, A. Effects of Using Ribs on Flow Pattern and Performance of Cyclone Separators. Eng. Appl. Comput. Fluid Mech. 2011, 5, 180–187. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.K.; Shukla, P.; Ghosh, P. Evaluation of Numerical Schemes for Dispersed Phase Modeling of Cyclone Separators. Eng. Appl. Comput. Fluid Mech. 2011, 5, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Le, D.K.; Yoon, J.Y. Numerical investigation on the performance and flow pattern of two novel innovative designs of four-inlet cyclone separator. Chem. Eng. Process. Process. Intensif. 2020, 150, 107867. [Google Scholar] [CrossRef]
- Lim, J.-H.; Park, S.-I.; Lee, H.-J.; Zahir, M.Z.; Yook, S.-J. Performance evaluation of a tangential cyclone separator with additional inlets on the cone section. Powder Technol. 2020, 359, 118–125. [Google Scholar] [CrossRef]
- Nassaj, O.R.; Toghraie, D.; Afrand, M. Effects of multi inlet guide channels on the performance of a cyclone separator. Powder Technol. 2019, 356, 353–372. [Google Scholar] [CrossRef]
- Qiang, L.; Qinggong, W.; Weiwei, X.; Zilin, Z.; Konghao, Z. Experimental and computational analysis of a cyclone separator with a novel vortex finder. Powder Technol. 2020, 360, 398–410. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, J.; Wang, J.; Mao, Y.; Wei, Y. Analysis of the effect of vortex on the flow field of a cylindrical cyclone separator. Sep. Purif. Technol. 2019, 211, 438–447. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Z.; Xiao, G.; Hu, X.; Chen, H.; Zhang, R.; Luo, X.; Wang, J.; Yang, Y. Monitoring the hydrodynamics and critical variation of separation efficiency of cyclone separator via acoustic emission technique with multiple analysis methods. Powder Technol. 2020, 373, 174–183. [Google Scholar] [CrossRef]
- Fanayi, A.R.; Nikbakht, A.M. A CFD Study of the Effects of Feed Diameter on the Pressure Drop in Acyclone Separator. Int. J. Food Eng. 2015, 11, 71–77. [Google Scholar] [CrossRef]
- Coffield, D.; Shepherd, D. Tutorial guide to Unix sockets for network communications. Comput. Commun. 1987, 10, 21–29. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters. Comput. Fluids 2011, 51, 48–59. [Google Scholar] [CrossRef]
- Xiang, R.; Lee, K. Numerical study of flow field in cyclones of different height. Chem. Eng. Process. Process. Intensif. 2005, 44, 877–883. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Optimization of the cyclone separator geometry for minimum pressure drop using mathematical models and CFD simulations. Chem. Eng. Sci. 2010, 65, 6048–6058. [Google Scholar] [CrossRef]
- Chuah, T.; Gimbun, J.; Choong, T.S. A CFD study of the effect of cone dimensions on sampling aerocyclones performance and hydrodynamics. Powder Technol. 2006, 162, 126–132. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Elsayed, K.; Ahmadi, G. Influence of the dipleg shape on the performance of gas cyclones. Sep. Purif. Technol. 2020, 233, 116000. [Google Scholar] [CrossRef]
- Zhou, F.; Sun, G.; Zhang, Y.; Ci, H.; Wei, Q. Experimental and CFD study on the effects of surface roughness on cyclone performance. Sep. Purif. Technol. 2018, 193, 175–183. [Google Scholar] [CrossRef]
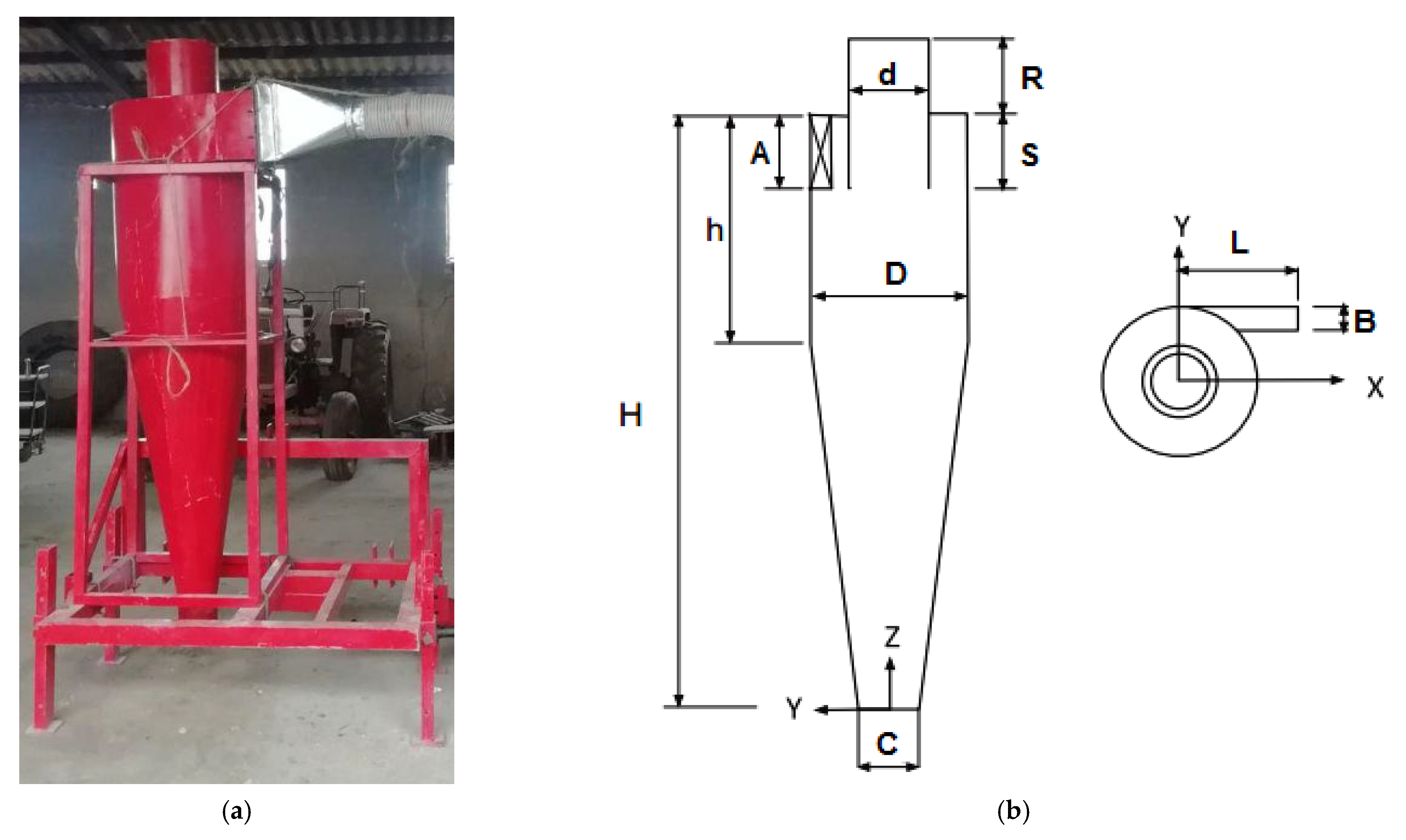









| Parameters | Values (cm) |
|---|---|
| Body diameter (D) | 55 |
| Gas outlet diameter (d) | 27.5 |
| Inlet height (A) | 27.5 |
| Inlet width (B) | 11 |
| Gas outlet duct length (R) | 27.5 |
| Total Height (H) | 220 |
| Cylindrical section Height (h) | 82.5 |
| Cone-tip diameter (C) | 19.25 |
| Vortex finder height (S) | 27.5 |
| Inlet length (L) | 35 |
| Boundary Condition Type | Value/Condition |
|---|---|
| velocity inlet | m s−1 |
| Pressure outlet | Atmospheric pressure |
| Wall | No-slip condition |
| Property | Value |
|---|---|
| Density | 790 kgm−3 |
| Minimum diameter | 0.2 cm |
| Maximum diameter | 0.8 cm |
| Mean Diameter | 0.5 cm |
| Numerical Setting | Scheme |
|---|---|
| Pressure distribution | PRESTO |
| Pressure-velocity coupling | SIMPLE |
| Momentum discretization | Second-Order Upwind |
| Turbulent Kinetic Energy | Second-Order Upwind |
| Turbulent Dissipation Rate | Second-Order Upwind |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dizajyekan, S.N.; Shahgholi, G.; Rezvanivand Fanaei, A.; Rostampour, V.; Sharabiani, V.R.; Szymanek, M.; Marczuk, A. A Comprehensive CFD Assessment of Wheat Flow in Wheat Conveying Cyclone Validation and Performance Analysis by Experimental Data. Processes 2022, 10, 1. https://doi.org/10.3390/pr10010001
Dizajyekan SN, Shahgholi G, Rezvanivand Fanaei A, Rostampour V, Sharabiani VR, Szymanek M, Marczuk A. A Comprehensive CFD Assessment of Wheat Flow in Wheat Conveying Cyclone Validation and Performance Analysis by Experimental Data. Processes. 2022; 10(1):1. https://doi.org/10.3390/pr10010001
Chicago/Turabian StyleDizajyekan, Sajed Naiemi, Gholamhossein Shahgholi, Adel Rezvanivand Fanaei, Vahid Rostampour, Vali Rasooli Sharabiani, Mariusz Szymanek, and Andrzej Marczuk. 2022. "A Comprehensive CFD Assessment of Wheat Flow in Wheat Conveying Cyclone Validation and Performance Analysis by Experimental Data" Processes 10, no. 1: 1. https://doi.org/10.3390/pr10010001
APA StyleDizajyekan, S. N., Shahgholi, G., Rezvanivand Fanaei, A., Rostampour, V., Sharabiani, V. R., Szymanek, M., & Marczuk, A. (2022). A Comprehensive CFD Assessment of Wheat Flow in Wheat Conveying Cyclone Validation and Performance Analysis by Experimental Data. Processes, 10(1), 1. https://doi.org/10.3390/pr10010001








