Experimental Research of a Regenerative Heat Exchanger
Abstract
:1. Introduction
- -
- Geometric: the nozzle overall dimensions, equivalent channel diameter, channel wall thickness;
- -
- Thermophysical: heat capacity and regenerative nozzle material density;
- -
- Operating: air capacity and velocity in the regenerator nozzle, and the regenerator cycle time.
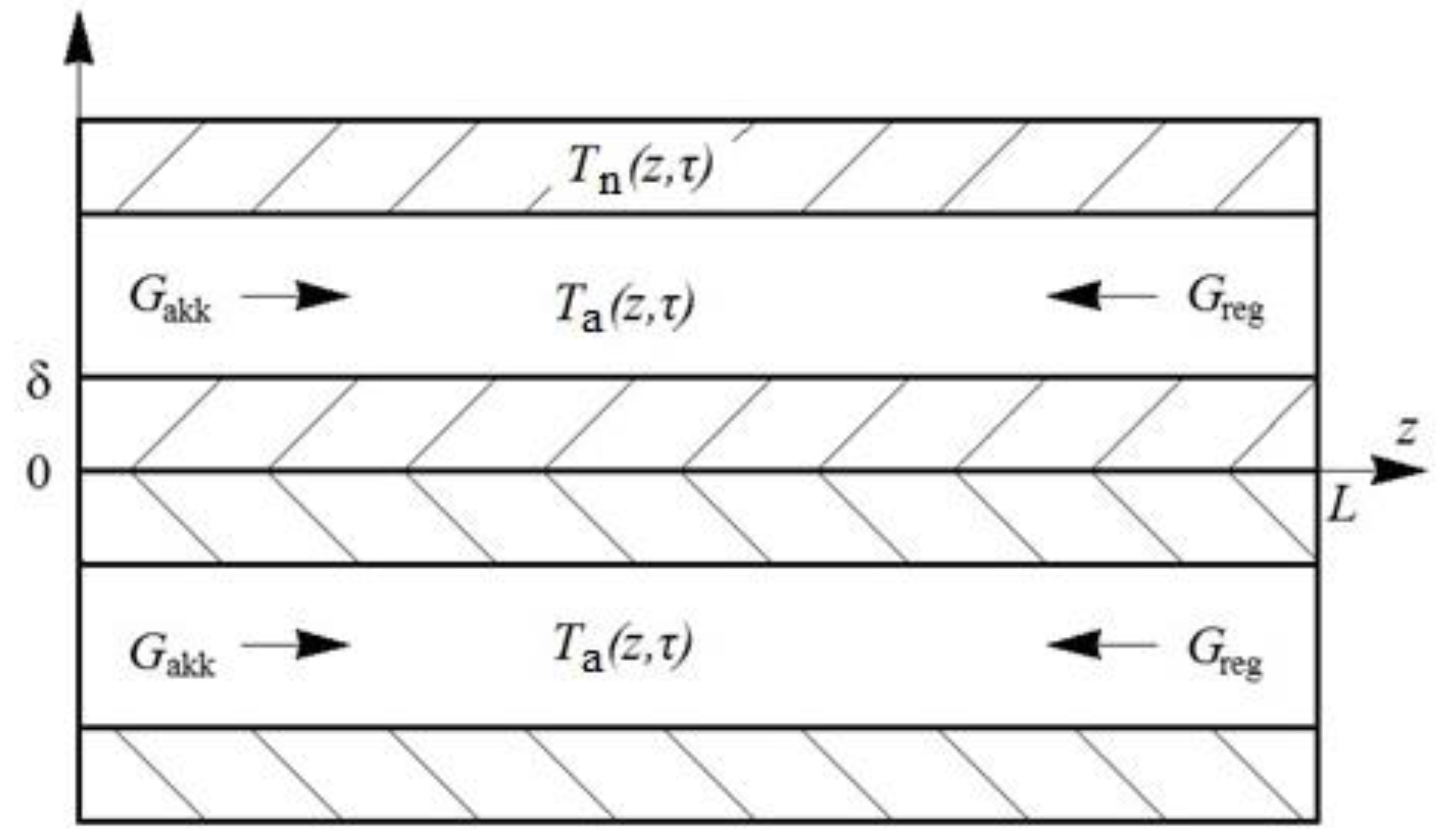
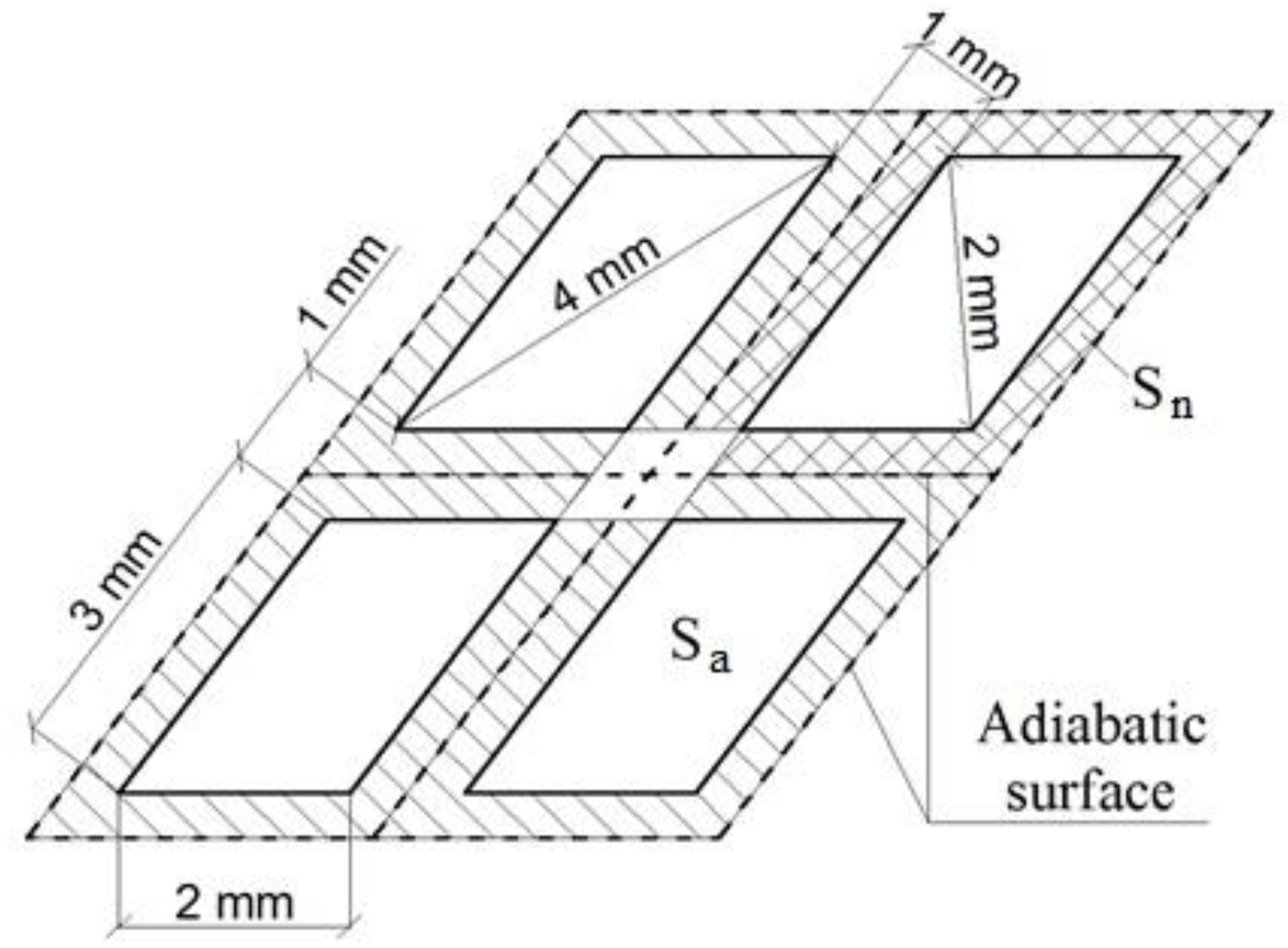
2. Materials and Methods
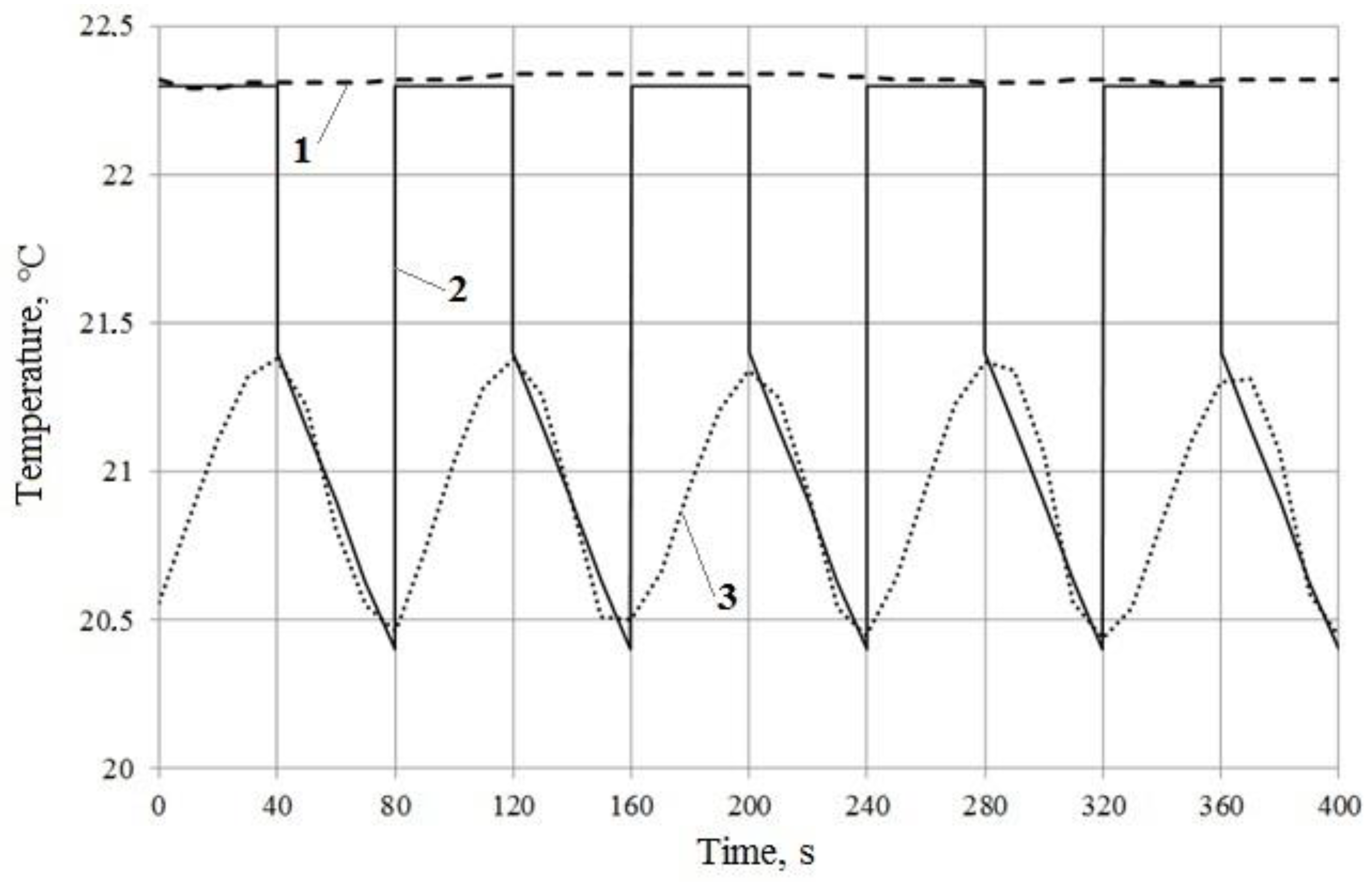
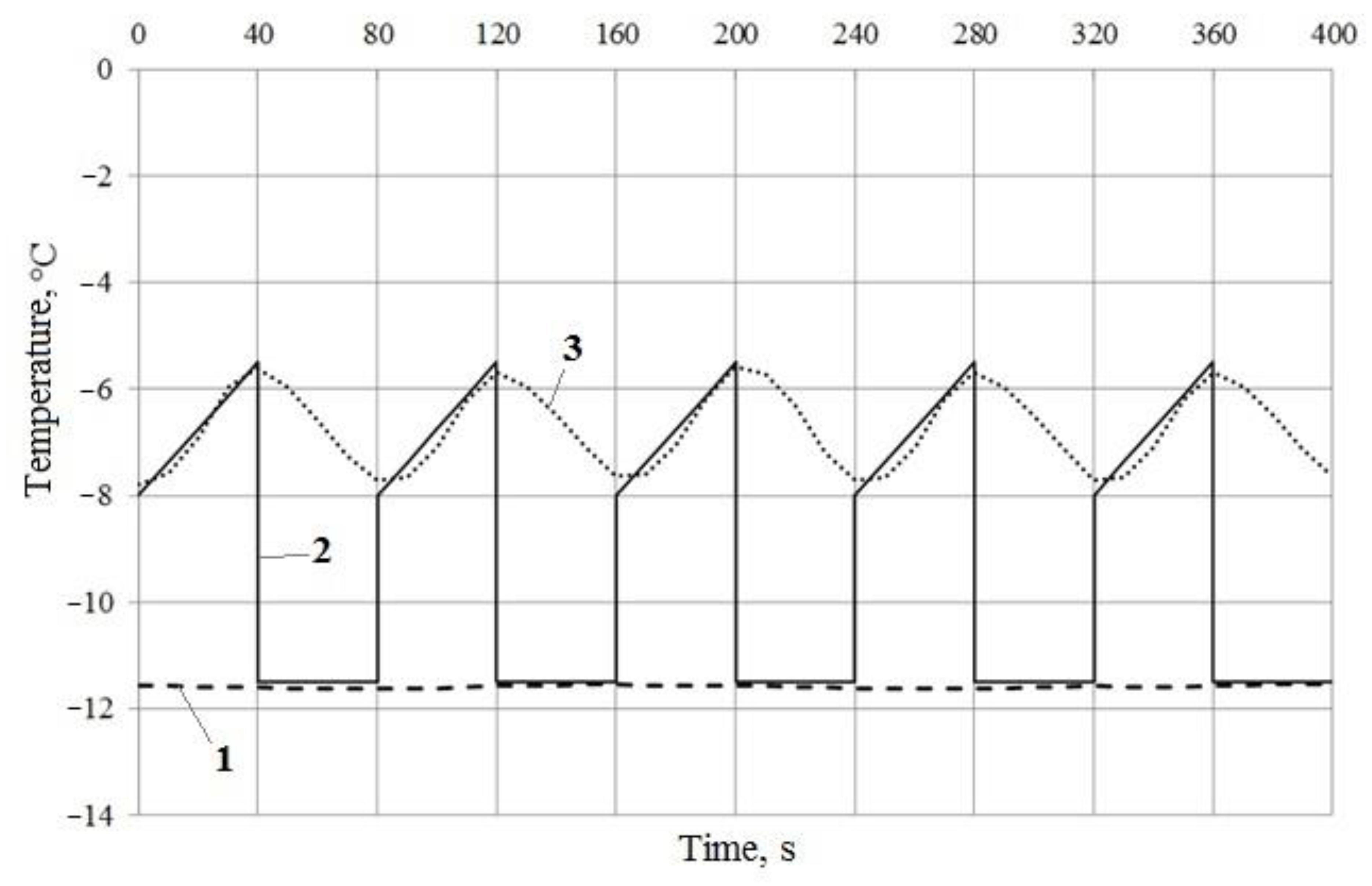
3. Results
- -
- Outdoor temperature Tout = −11.6 °C;
- -
- Indoor temperature Tin = 22.3 °C;
- -
- Total volumetric air flow L0 = 31 m3/h = 8.61·10−3 m3/s;
- -
- Total mass air flow G0 = 9.24·10−3 kg/s;
- -
- Air flow through a single channel G = 2.65·10−6 kg/s;
- -
- Thermal energy accumulation/regeneration stage time τakk = τreg = 40 s;
- -
- Channel length l = 0.15 m;
- -
- Equivalent diameter d = 0.0016 m;
- -
- Density of the nozzle material pn = 1400 kg/m3;
- -
- Specific mass heat capacity of the nozzle material cn = 2000 J/kg·K;
- -
- Specific mass heat capacity of air ca = 1005 J/kg·K;
- -
- Atmospheric pressure p = 9.81·104 Pa.
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roulet, C.-A.; Heidt, F.; Foradini, F.; Pibiri, M.-C. Real heat recovery with air handling units. Energy Build. 2001, 33, 495–502. [Google Scholar] [CrossRef]
- Haniff, M.F.; Selamat, H.; Yusof, R.; Buyamin, S.; Ismail, F.S. Review of HVAC scheduling techniques for buildings towards energy-efficient and cost-effective operations. Renew. Sustain. Energy Rev. 2013, 27, 94–103. [Google Scholar] [CrossRef]
- Fakhrabadi, F.; Kowsary, F. Optimal design of a regenerative heat and mass exchanger for indirect evaporative cooling. Appl. Therm. Eng. 2016, 102, 1384–1394. [Google Scholar] [CrossRef]
- Sinitsyn, A.A.; Monarkin, N.N.; Rogulina, T.V. Federal law of power saving and opportunity of developing new the switching heat recovery devices for heat supply needs. World Appl. Sci. J. 2013, 27, 361–365. [Google Scholar] [CrossRef]
- Penev, A.; Tsokov, L. Application of polymer thermal store material in fixed honeycomb regenerative heat exchanger. In Proceedings of the E3S Web of Conferences, Sozopol, Bulgaria, 19–21 September 2020; p. 01001. [Google Scholar] [CrossRef]
- Aktershev, S.P. The regenerative heat exchanger with periodic veering of the flow. In Proceedings of the XXXV Siberian Thermophysical Seminar, STS 2019, Novosibirsk, The Soviet Union, 27–29 August 2019; Institute of Physics Publishing: Novosibirsk, Russia, 2019; p. 012125. [Google Scholar]
- Monarkin, N.; Sinitsyn, A.; Pavlov, M.; Akhmetov, T. The influence of main parameters of regenerative heat exchanger on its energy efficiency. In Proceedings of the E3s Web of Conferences, Prague, Czech Republic, 14–15 May 2020; EDP Sciences: Prague, Czech Republic, 2020; p. 01024. [Google Scholar] [CrossRef]
- Monarkin, N.; Sinitsyn, A.; Karpov, D.; Akhmetov, T. Method for designing energy-efficient ventilation systems based on regenerative heat exchangers. In Proceedings of the E3s Web of Conferences, Prague, Czech Republic, 14–15 May 2020; EDP Sciences: Prague, Czech Republic, 2020; p. 01037. [Google Scholar] [CrossRef]
- Solovyev, S.A. A probabilistic approach to estimation of the ultimate load of end-bearing piles on settlement criterion. Mag. Civ. Eng. 2020, 96, 70–78. [Google Scholar] [CrossRef]
- Solovyeva, A.; Solovyev, S. Reliability analysis of rhs steel trusses joints based on the p-boxes approach. Int. J. Comput. Civ. Struct. Eng. 2021, 17, 87–97. [Google Scholar] [CrossRef]
- Nizovtsev, M.I.; Borodulin, V.Y.; Letushko, V.N. Regenerative heat exchanger with a periodic change in the airflow direction for room ventilation. Thermophys. Aeromechanics 2015, 22, 755–765. [Google Scholar] [CrossRef]
- Skrzycki, M.; Jedlikowski, A.; Anisimov, S. Efficiency of heat recovery of storage matrix regenerative heat exchanger. In Proceedings of the Indoor Air Quality and Environment, the XVII International Scientific Conference, Moscow, Russia, 11–18 September 2019; Gvozdkov, A.N., Ed.; Volgograd State Medical University: Moscow, Russia, 2019; pp. 159–165. [Google Scholar]
- Monarkin, N.N.; Lukin, S.V.; Kochkin, A.A. Mathematical model of heat transfer in a thin-walled regenerator. Privolzhskii Nauchnyi Zhurnal. 2018, 3, 57–62. [Google Scholar]
- Monarkin, N.; Lukin, S.; Anurov, Y.M.; A Tihomirov, B.; A Agasiants, G.; Galileev, S.M.; Akhmetov, T.R. Thermal and aerodynamic efficiency of a stationary switching regenerative heat exchanger. In IOP Conference Series: Earth and Environmental Science, Proceedings of the International Scientific Conference on Efficient Waste Treatment 2018, EWT 2018, St. Petersburg, Russia, 13–14 December 2018; Institute of Physics Publishing: Petersburg, Russia, 2019; p. 012067. [Google Scholar] [CrossRef]
- Karpov, D. The active method of control the thermal conductivity of building materials and products. Bull. Belgorod State Technol. Univ. Named V. G. Shukhov 2019, 4, 57–62. [Google Scholar] [CrossRef]
- Karpov, D.; Agafonov, V.; Pisarenko, V.; Berezin, P.; Derevianko, O.; Makoev, S.; Egororov, M. Determination of thermal diffusivity for rigid body at non-stationary thermal conditions. In IOP Conference Series: Earth and Environmental Science, Proceedings of the Collection of materials International Scientific and Practical Conference, Kazan, Russia, 29 October–2 November 2018; Institute of Physics and IOP Publishing Limited: Kazan, Russia, 2019; p. 012097. [Google Scholar] [CrossRef]

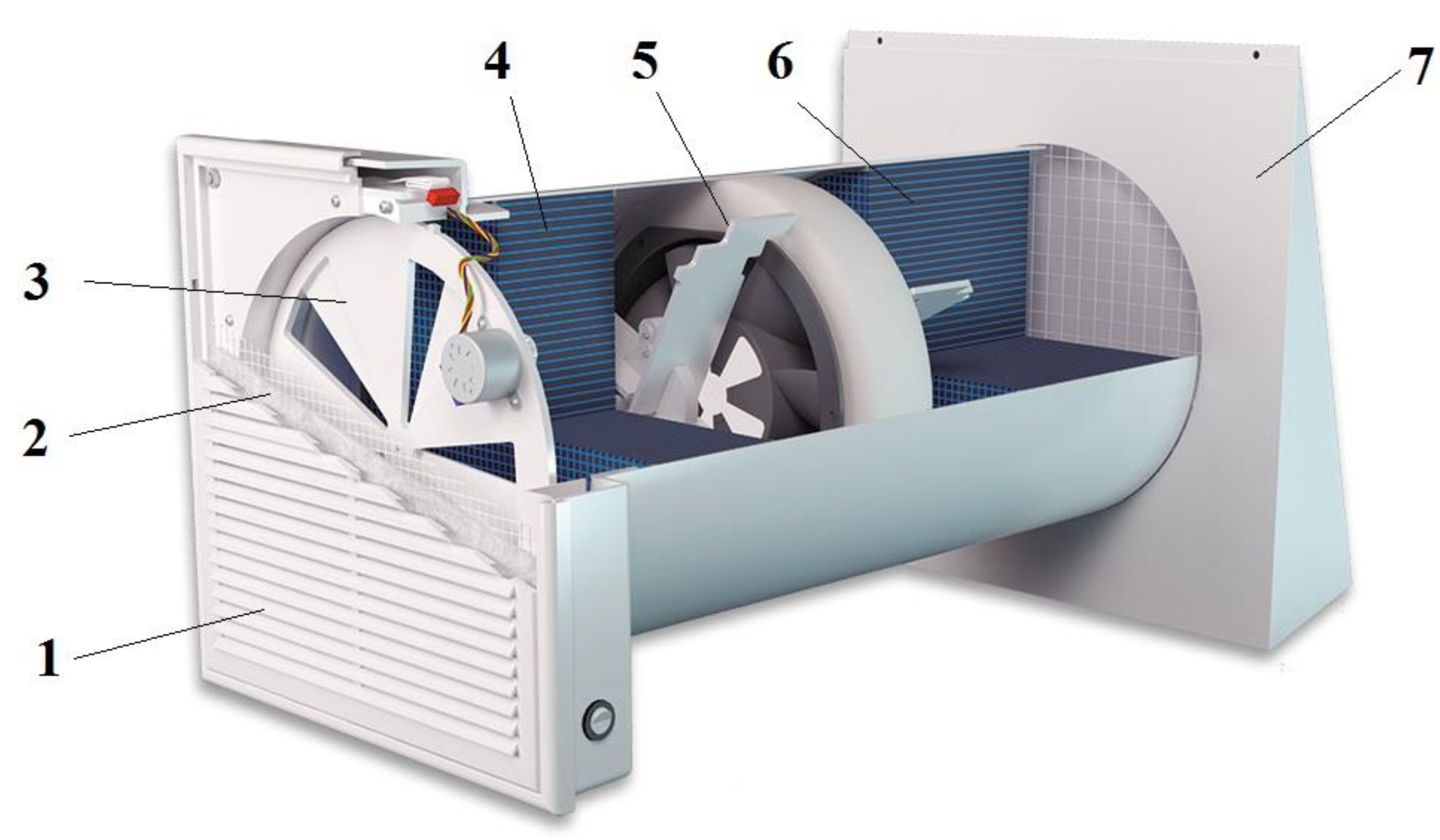




| Parameter | Measurement Unit | Value |
|---|---|---|
| Operating temperature range | °C | −40–+50 |
| Capacity | m3/h | 13–50 |
| Capacity control | - | stepless |
| Efficiency | % | 71–92 |
| Supply voltage | V/Hz | 220/50 |
| Energy consumption, max | W | 15 |
| Noise level, max | dBA | 40 |
| Wall thickness | mm | 450–600 |
| Channel diameter in the wall for installation | mm | 220 |
| No. | Measuring Instrument | Functionality | Main Technical Specifications |
|---|---|---|---|
| 1 |  Multi-channel temperature recorder TEREM 3.2 manufactured by NPP Interpribor, LLC | Temperature monitoring of various purpose objects | - Number of channels: 8–256; - Number of adapters: 1–32 pcs; - Number of sensors connected to the adapter: up to 16 pcs; - Intervals: 10 s/24 h; - Temperature measurement error limits: ±1 °C. - Communication line length with the adapters of: the sensors: up to 20 m; the electronic unit: up to 500 m; - Memory capacity: 1 MB; - Interface: USB; - Overall dimensions of the electronic unit: 150 by 76 by 27 mm; - Weight of the electronic unit: 0.15 kg. |
| 2 |  Digital module Terem 3.2 | Connection of sensors to the temperature recorder | - Number of channels for sensors: 8; - Connection: threaded; - Number of channels for recorders: 2; - Overall dimensions of the electronic unit: 150 by 70 by 25 mm; - Weight of the electronic unit: 0.12 kg. |
| 3 |  Thermohygrometric sensor DTG-2.0 | Measuring ambient air temperature and humidity | - Maximum measurement temperature: 125 °C; - Standard cable length: 3 m. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monarkin, N.; Monarkina, T. Experimental Research of a Regenerative Heat Exchanger. Processes 2022, 10, 100. https://doi.org/10.3390/pr10010100
Monarkin N, Monarkina T. Experimental Research of a Regenerative Heat Exchanger. Processes. 2022; 10(1):100. https://doi.org/10.3390/pr10010100
Chicago/Turabian StyleMonarkin, Nikolay, and Tat’yana Monarkina. 2022. "Experimental Research of a Regenerative Heat Exchanger" Processes 10, no. 1: 100. https://doi.org/10.3390/pr10010100
APA StyleMonarkin, N., & Monarkina, T. (2022). Experimental Research of a Regenerative Heat Exchanger. Processes, 10(1), 100. https://doi.org/10.3390/pr10010100





