The Low-Carbon Scheduling Optimization of Integrated Multispeed Flexible Manufacturing and Multi-AGV Transportation

Abstract

As low-carbon and sustainable manufacturing becomes the mainstream development direction of the current manufacturing industry, the traditional heavy industry manufacturing enterprises in China urgently need to transform. For the heavy cement equipment manufacturing enterprise investigated here, there is a large amount of energy waste during the manufacturing operation due to scheduling confusion. In particular, the multispeed, multi-function machining and the transportation of multiple automated guided vehicles (multi-AGV) are the main influencing factors. Therefore, this paper addresses a novel low-carbon scheduling optimization problem that integrated multispeed flexible manufacturing and multi-AGV transportation (LCSP-MSFM & MAGVT). First, a mixed-integer programming (MIP) model is established to minimize the comprehensive energy consumption and makespan in this problem. In the MIP model, a time-node model is built to describe the completion time per workpiece, and a comprehensive energy consumption model based on the operation process of the machine and the AGV is established. Then, a distribution algorithm with a low-carbon scheduling heuristic strategy (EDA-LSHS) is estimated to solve the proposed MIP model. In EDA-LSHS, the EDA with a novel probability model is used as the main algorithm, and the LSHS is presented to guide the search direction of the EDA. Finally, the optimization effect and actual performance of the proposed method are verified in a case study. The experimental results show that the application of the proposed method in actual production can save an average of 43.52% comprehensive energy consumption and 64.43% makespan, which effectively expands the low-carbon manufacturing capacity of the investigated enterprise.

1. Introduction

With the intensification of global environmental problems (e.g., greenhouse effect, extreme weather), the transformation towards low-carbon and sustainability of global manufacturing industry is imminent. Under the cooperation framework of the Paris Agreement, China has actively committed to achieving peak carbon emissions by 2030 and reducing carbon emissions per unit of gross domestic product (GDP) by 40–45% compared with 2005 levels [1]. In this context, a series of stringent carbon emission policies have been promulgated, which has greatly restricted the development of a large number of high-consumption and high-emission traditional heavy industry manufacturing enterprises in China [2]. As is well-known, energy consumption is a major contributor to carbon emissions, and therefore, improving energy efficiency can effectively reduce carbon emissions in manufacturing [3]. For traditional heavy industry manufacturing enterprises, integrating a new generation of intelligent manufacturing technologies and mining key operation elements in the manufacturing environment (e.g., machine operation and transportation process) to carry out energy efficiency optimization is a significant way to promote the development of low-carbon and sustainable manufacturing.

In response to the above problems, this paper takes a typical heavy cement equipment manufacturing enterprise as the object to develop energy conservation research, which has guiding significance for the low-carbon transformation of traditional heavy industry manufacturing. Through the investigation, the enterprise has made the following adjustments for the manufacturing environment in the face of more stringent carbon emission policies and upgrading of the industrial structure: (1) The adjustability of the function and speed level of the machines have increased, and (2) multiple automatic guided vehicles (multi-AGV) with high energy efficiency are introduced as transportation equipment. However, the complexity and flexibility of the manufacturing environment greatly increase with the addition of the above conditions. The correlation and interplay of multi-state machining planning and multi-AGV transportation planning make the overall scheduling of the manufacturing process extremely difficult. Since conventional scheduling methods are difficult to apply effectively, the production of the investigated enterprise is still controlled by traditional manual scheduling. Constrained by the limitations of human decision-making, this mode leads to massive energy waste, scheduling conflicts, and other disadvantages. Therefore, there is an urgent need to research an effective scheduling method for the investigated enterprise to improve its low-carbon manufacturing level.

According to the above analysis, this paper introduces a novel low-carbon scheduling problem integrated with multispeed flexible manufacturing and multi-AGV transportation (LCSP-MSFM & MAGVT). The focus of this paper is the relationship between the workpiece processing sequence, the machine processing state, and the AGV path to realize optimal low-carbon scheduling. The contributions of this paper are as follows:

(1)

A mixed-integer programming (MIP) model is formulated to describe the LCSP-MSFM & MAGVT. The objectives of the MIP model are to optimize the comprehensive energy consumption and makespan simultaneously during the manufacturing operation.

(2)

In the proposed MIP model, a time-node model is built to describe the completion time per workpiece, and a comprehensive energy consumption model based on the operation process of the machine and AGV is established.

(3)

An estimation of distribution algorithm with a low-carbon scheduling heuristic strategy (EDA-LSHS) is developed to solve the proposed MIP model. In EDA, a novel probabilistic model is established to generate scheduling solutions satisfying the constraints. In LSHS, energy consumption optimization strategies for the machine processing, the AGV load state, and the AGV no-load transportation are proposed to guide the search direction of EDA.

The remainder of this paper is organized as follows: a review of the literature on the scheduling optimization of low-carbon manufacturing and manufacturing scheduling considering transportation is presented in the next section. The proposed MIP model is established in detail in Section 3. In Section 4, the proposed EDA-LSHS is mainly introduced. Then, in Section 5, a case study based on the LCSP-MSFM & MAGVT is carried out to verify the actual performance and optimization effect of the proposed method. Finally, in Section 6, the conclusions and further research prospects for this problem are presented.

2. Literature Review

The introduced LCSP-MSFM & MAGVT mainly studies the following two fields: the scheduling optimization of low-carbon manufacturing and manufacturing scheduling considering transportation. To better discuss the problem, this section reviews the latest research in the two fields and summarizes the related research status.

2.1. Scheduling Optimization of Low-Carbon Manufacturing

As the academic circle pays more attention to environmental issues, scholars have carried out a series of studies on the scheduling optimization of low-carbon manufacturing under different workshop operation modes. The research focus mainly covers three aspects: problem modeling, algorithm design, and integrated applications.

In view of the actual production condition constraints, it is a key research point to use various discrete mathematical models to describe scheduling problems. To improve the energy efficiency of hybrid-flow shop scheduling, Han et al. [4] proposed a new realistic mixed-flow shop scheduling model considering the potential impacts of human factors. Experiments showed that a real-life problem of the foundry plant was solved by the model and the scheduling solutions completely met the delivery requirement. For the green scheduling problem of a distributed hybrid-flow shop, Dong and Ye [5] established a distributed two-stage reentrant hybrid-flow shop bi-level scheduling model considering the power supply allocation scheme of distributed energy resources, energy storage system, and main grid. Through a large number of experiments, it was proved that the model can effectively reduce carbon emissions and energy costs under the TOU electricity price. In a distributed heterogeneous welding-flow shop scheduling problem, Wang et al. [6] proposed an energy-efficient optimization model to minimize the total energy consumption and makespan simultaneously. The model formulated three sub-problems: job assignment among factories, job scheduling within each factory, and deciding the number of machines upon each job. Wang et al. [7] proposed a multi-objective mathematical model that considers the dynamic reconfiguration processes and devices’ adjustable processing modes simultaneously to minimize both the makespan and the whole device’s energy consumption for the hybrid-flow shop scheduling. The real-world cases verified that the model were successfully applied to a hot-rolling shop. For an energy-efficient flexible job-shop problem with variable machining speeds, Wei et al. [8] established an energy-aware estimation model considering five running conditions on machines and applied hybrid energy-efficient scheduling measures to achieve good workshop energy efficiency. To realize the multi-objective optimization scheduling of manufacturing processes with feedback, Quan et al. [9] proposed a virtual workflow modeling method for the parallel manufacturing of manifold jobs. The method achieved the static and dynamic multi-objective optimization scheduling of manufacturing processes with nonlinear feedback by the two mechanisms of virtual modeling and evolutionary optimization.

In order to improve the optimization effect of low-carbon scheduling, innovative algorithm design is an important research goal. For the green scheduling problem of a permutation-flow shop, Saber and Ranjbar [10] developed a multi-objective decomposition-based heuristic algorithm to minimize the total tardiness and the total carbon emissions. Extensive computational experiments showed that the algorithm has significant superiority to the other developed solution approaches. For the energy-efficient scheduling of a distributed permutation-flow shop problem with limited buffers, Lu et al. [11] proposed a Pareto-based collaborative multi-objective optimization algorithm to minimize makespan and total energy consumption. The experiments verified the effectiveness and performance of the algorithm compared with well-known algorithms on instances. Qin et al. [12] proposed a modified iterative greedy algorithm based on a swap strategy to optimize pollution emissions and energy consumption in an energy-efficient blocking hybrid-flow shop scheduling problem. The experimental results demonstrated that the algorithm outperformed the compared algorithms and could obtain a better solution. To address the energy-efficiency problem of unrelated parallel machines with sequence-dependent setup times, Jovanovic and Voß [13] proposed a novel fixed set search metaheuristic based on greedy randomized adaptive search. The experimental results showed that the fixed set search significantly outperformed other population-based metaheuristics. For the dual resource constrained flexible job-shop scheduling problem with loading and unloading time, Wu et al. [14] proposed an improved non-dominated sorting genetic algorithm II with similarity-based scheduling and demonstrated that the algorithm can effectively reduce the loading and unloading time of fixtures while ensuring a level of makespan. Xu et al. [15] developed a hybrid genetic algorithm and tabu search with three-layer encoding to solve the distributed and flexible job-shop scheduling problem considering energy efficiency. The comparison experiment verified the advantages of the hybrid algorithm over genetic algorithm and tabu search. Li et al. [16] designed an improved artificial bee colony algorithm to solve the multi-objective low-carbon flexible job-shop scheduling problem. The results demonstrated that the algorithm achieves a better performance compared with MOPSO, MODE and NSGA-II.

In the face of complex manufacturing scheduling environment, solutions can be effectively obtained through the integrated application of different methods. For the low carbon flexible job-shop problem under recessive disturbance, Zhou et al. [17] proposed an adaptive hybrid dynamic scheduling strategy integrated ensemble deep forest to reduce the impact of machine idling and production status deviation. The experiment results revealed the strategy delivers excellent performances both in decision accuracy and schedule repairing. For the flexible job-shop scheduling problem with uncertain processing time, Li et al. [18] integrated fuzzy mathematics and self-adaptive multi-objective evolutionary method to minimize the makespan and the total workload simultaneously. The results demonstrated that the integrated method outperforms the compared multi-objective optimization algorithms in solving the problem. Rakovitis et al. [19] developed a grouping-based decomposition approach integrated unit-specific event-based time representation to reduce energy consumption for the energy-efficient flexible job-shop scheduling problem. The experiment demonstrated that the proposed decomposition approach can achieve up to 43.1% less energy consumption in comparison to the existing gene-expression programming-based algorithm. For the robust scheduling problem of flexible machining job shop, Duan and Wang [20] proposed a new robust optimization method integrated a dynamic event response strategy that takes into account dynamic events, total energy consumption, manufacturing time and the comprehensive reusability. The results showed that the integrated method can effectively adjust the scheduling plan to respond to dynamic events to achieve stable scheduling in an uncertain environment. To tackle a green job-shop scheduling problem considering the energy consumption during machine idle time, Afsar et al. [21] applied fuzzy mathematical modeling to deal with the uncertainty of processing times and proposed an enhanced memetic algorithm integrated with a multi-objective evolutionary algorithm. Experimental results validate the proposed method with respect to hypervolume, indicator and empirical functions. For the many-objective distributed flexible job-shop collaborative green scheduling problem, Sang and Tan [22] proposed a dual-mode environment selection method integrated with the neighborhood structure based on collaborative adjustment of process and equipment. Experiment shows the method has important engineering application value for the intelligent factory.

The above literature systematically studied the scheduling optimization problem of low-carbon manufacturing from three perspectives of problem modeling, algorithm design, and integrated application. Its research objectives are mainly the optimization of low-carbon scheduling indicators (e.g., energy consumption and carbon emission) in a classic manufacturing environment, which provides realistic references and beneficial inspirations for the workshop machining aspects of this paper. However, these studies lack consideration of the transportation process. For heavy industry manufacturing enterprises, transportation causes huge energy waste due to the large self-weight of the workpieces. This is a non-negligible part of the operation process of heavy industry manufacturing. Therefore, the above studies are limited in terms of the integrated low-carbon scheduling optimization of machining and transportation processes.

2.2. Manufacturing Scheduling Considering Transportation

With the deepening of the research on manufacturing scheduling, scholars are gradually becoming concerned about the impacts of transportation on scheduling processes. A review of the relevant literature reveals that existing research mainly focuses on analyzing the impacts of the addition of transportation conditions on different workshop manufacturing environments.

For flow shop scheduling considering transportation, Yuan et al. [23] introduced a flow-shop group scheduling problem considering sequence-dependent setup time between groups and round-trip transportation time between machines and proposed a novel discrete differential evolution mechanism with a cooperative optimization strategy to synergistically evolve both the sequence of jobs in each group and the sequence of groups. Wang and Wang [24] considered the impact of transportation time on a distributed flow shop with flexible assembly scheduling and proposed a cooperative memetic algorithm with feedback to solve the problem. The results demonstrated the effectiveness of both the feedback mechanism and local intensification, and the comparisons showed that the algorithm outperformed the existing algorithms. For a flexible flow-shop scheduling problem with random and state-dependent batch transport, Zhang et al. [25] established an open queueing network with blocking and proposed a decomposition method of state space. The accuracy and efficiency of the proposed method were demonstrated by comparing the results with simulations from numerical experiments.

For job-shop scheduling considering transportation, Yan et al. [26] established a finite transportation conditions model and designed a genetic algorithm based on three-layer encoding with redundancy and decoding with correction to solve the flexible job-shop scheduling problem under finite transportation conditions. The results verified that the proposed finite transportation conditions have significant impacts on scheduling under different scales of scheduling problems and transportation times. To address the flexible job-shop scheduling problem integrated with multiple automated guided vehicles, He et al. [27] proposed a green scheduling model that considered machine processing, sequence-dependent setup, and automated guided vehicles transport, and they developed an effective multi-objective evolutionary algorithm. The experimental results demonstrated that the algorithm was significantly better at solving the problem than three other well-known algorithms. Sun et al. [28] proposed a hybrid many-objective evolutionary algorithm with tabu search to settle the many-objective flexible job-shop scheduling problem with transportation and setup times. Extensive numerical experiments on 28 benchmarks confirmed the effectiveness of the algorithm. To address the integrated green scheduling problem of flexible job-shop and crane transportation, Liu et al. [29] presented an integrated algorithm where a genetic algorithm is employed to perform the global search, a glowworm swarm optimization algorithm is applied to perform the local search, and a green transport heuristic strategy is proposed for guiding the search direction of the algorithm. Computational experiments showed that the algorithm has a significant superiority to the other approaches.

For other forms of workshop scheduling considering transportation, Sun et al. [30] proposed two scheduling models with a set of tight deadlock-avoidance constraints to address a robotic job-shop scheduling problem that considered the scheduling of job operations and the movement of the robot simultaneously. Numerical examples illustrated that the proposed models could completely avoid transportation conflicts by considering deadlock and robot movement. Tan et al. [31] introduced a low-carbon joint scheduling problem in a flexible open-shop environment with constrained automatic guided vehicle transportation and developed an enhanced multi-objective particle swarm optimization solving algorithm with problem-knowledge-based neighborhood search. A comprehensive case study verified the algorithm make significant promotion on the convergence and comprehensive quality. To solve the energy-efficient crane scheduling problem in workshops, Zhao et al. [32] proposed a digital twins-driven multi-crane scheduling and crane number selection approach. Under the digital twins framework, a multi-crane system based on simulation was built in a virtual space, which can generate a solution based on the crane scheduling rules, interference detection, and avoidance methods.

The above literature studied the manufacturing scheduling problem under various transportation conditions (AGV, crane, robot, etc.) and in different workshop forms (e.g., flow shop, job shop, open shop, robotic shop). Most of these studies incorporated transport time as a constraint into the scheduling model but lacked consideration of the impacts of the transportation processes on the machining processes. Since machining and transportation interplay with each other in the operation of the workshop, it is not complete to consider machining with the transport time constraint alone. Furthermore, a few scholars have considered the impact of the integrated scheduling of machining and transportation, e.g., He et al. [27] and Liu et al. [29]. However, these two methods only consider the constant state machining or single device transportation, which are not capable of solving the scheduling optimization of complex constrained manufacturing with multi-state machines and multiple transport devices. Therefore, existing related research has certain limitations in facing the novel problem raised in this paper.

2.3. Overview

According to the above literature review, for the scheduling optimization of low-carbon manufacturing, the latest research has largely centered on the energy optimization of the machining process and ignores the impact of transportation. For manufacturing scheduling considering transportation, most scholars add transportation time as a constraint to machine scheduling but do not consider the coordination of transportation and machining. In actual manufacturing environments, the machining process has a clear interaction with the transportation process, which synergistically affects the optimization results of the low-carbon scheduling. Therefore, comprehensively considering the machining and transportation is of significance for low-carbon scheduling optimization. To the best of our knowledge, no scholar has conducted corresponding research on the low-carbon scheduling optimization of integrated multispeed flexible manufacturing and multi-AGV transportation. Therefore, this paper focuses on exploring and addressing these shortcomings.

3. Formulation

In this section, the low-carbon scheduling problem of multispeed flexible manufacturing and multi-AGV transportation based on the investigated heavy cement equipment manufacturing enterprise is introduced in detail. Then, a MIP model considering comprehensive energy consumption and makespan is formulated. All the notes in this paper are in Nomenclature.

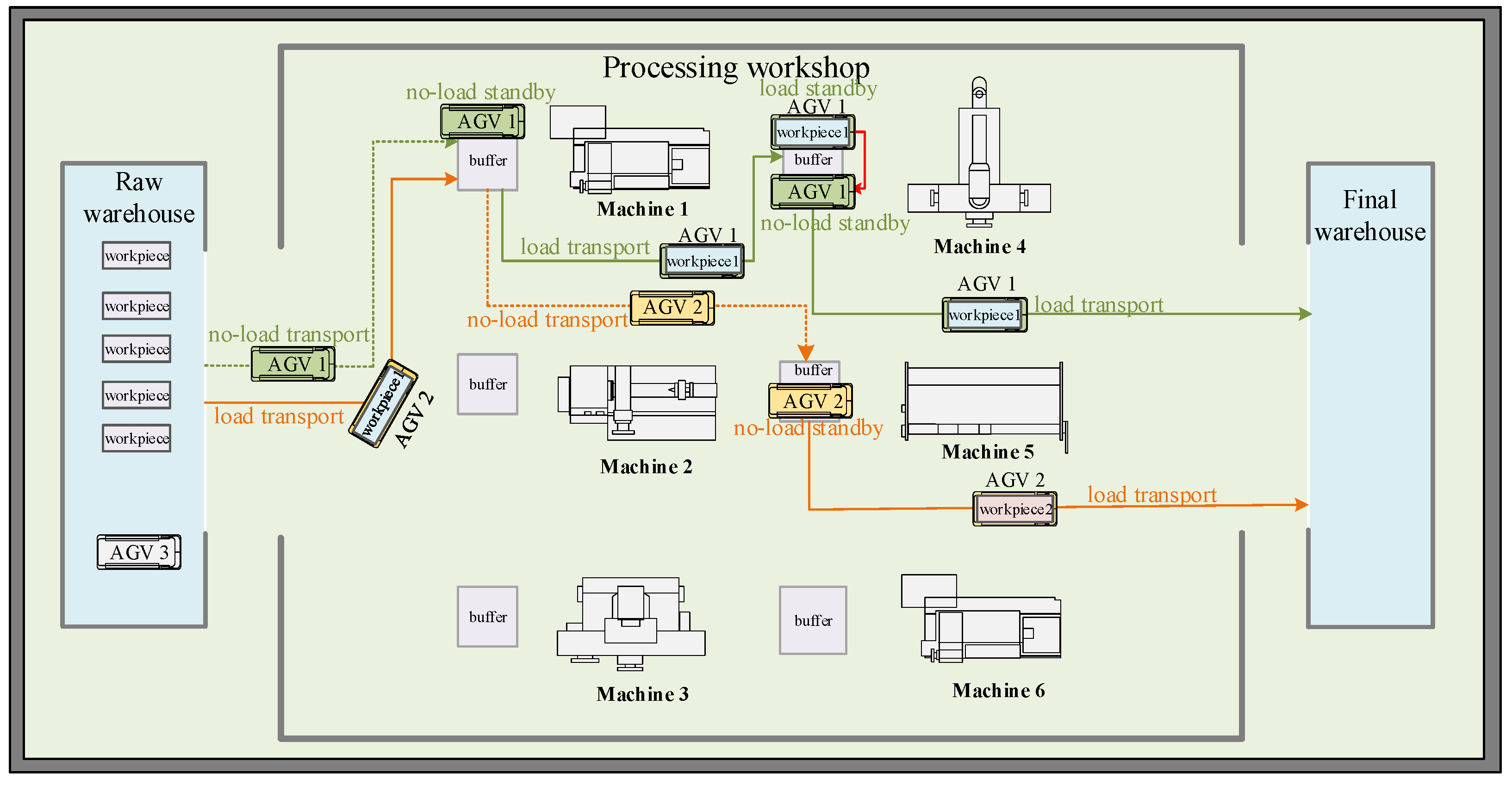
3.1. Problem Description

In the actual manufacturing workshop of the investigated enterprise, the machines work in a flexible status (the speed and function of the machines can be adjusted), and the transportation equipment is multiple AGVs. The multispeed flexible machines have two states: processing and standby. The operation process of the AGV is divided into transportation (no-load and load) and standby (no-load and load). The operation task in the above flexible manufacturing environment includes the following three links: (1) the AGV paths are planned to transport workpieces between machines; (2) the workpieces are arranged to be processed on suitable machines; (3) the processing power and time of the machines are controlled by adjusting the speed. In this paper, the dual objectives in LCSP-MSFM & MAGVT are as follows: (1) minimize the comprehensive energy consumption for the operation of the machines and AGVs and (2) minimize the makespan.

Figure 1 shows the working layout of the workshop in the investigated enterprise. The raw warehouse stores several workpieces to be processed and three AGVs. Then, the final warehouse stores the processed workpieces and the AGVs that complete the tasks. The processing workshop has six multi-speed machines, and each machine has a buffer to park the AGV. The buffer can realize the loading and unloading of the workpiece on the AGV. To further show the operation process of the workshop, this part of the process is described in detail as follows: (1) First, the AGV1 runs to the buffer area of machine 1 with no load and waits without load until workpiece 1 is entirely process. Afterward, AGV1 transports workpiece 1 to the buffer area of machine 4 and stays loaded until the workpiece being processed on machine 4 is finished. Then, AGV1 switches from load standby to no-load standby state and waits without load until workpiece 1 is processed completely. Finally, AGV 1 executes the additional processing of workpiece 1 (workpiece 1 is shipped to the final warehouse). (2) AGV2 first transports workpiece 1 to the buffer area of machine 1. Then, AGV2 runs to the buffer area of machine 5 with no load and waits without load until workpiece 2 is processed completely. Ultimately, AGV 2 executes the additional processing of workpiece 2. The above AGV operations are parallel in time.

3.2. Assumptions

• Each machine can only process one workpiece at a time, and each workpiece can only be processed by one machine at the same time.
• Each AGV can only transport one workpiece at a time, and each workpiece can only be transported by one AGV at the same time.
• If $O_{i(j-1)}$ and $O_{ij}$ are processed on the same machine, $O_{ij}$ does not need to be transported by the AGV.
• The machines that can be selected for each workpiece process are the machines available for it.
• All AGVs are fully charged and fault-free during the makespan.
• Assume that the raw warehouse is virtual machine $M_0$ and the final warehouse is virtual machine $M_{m+1}$; each workpiece has additional transportation to deliver the finished workpiece to the final warehouse.
• The starting point of all AGVs and workpieces is in the raw material warehouse, and the ending point is in the finished product warehouse.
• The machine only turns on when the first workpiece on it arrives and turns off only when the last workpiece on it completes.

3.3. Time-Node Model

In order to accurately describe the operating state of the machine and the AGV, a time-node model based on six time-node variables is established in this section. The time-node variables are as follows: the start and end times of the machine in the processing stage and the start and end times of the no-load and load states of the AGV.

3.3.1. The Start Time of No-Load State of AGV

The start time of the no-load state of transportation task $R_{ij}$ is divided into two cases as shown in Formula (1): First, when $R_{ij}$ is the first transportation task on the corresponding AGV, its no-load state start time is 0; second, the start time of the no-load state of $R_{ij}$ is calculated according to the formula in other cases:

$$VS{T}_{ijw}^{no}=\{\begin{array}{l}0,{\displaystyle \sum _{w=1}^u{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{\mathrm{s}}_{ijglw}=0}}}\\ {\displaystyle \sum _{w=1}^u{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}VC{T}_{glw}^{lo}\times s_{ijglw}},}}\mathrm{other}\end{array}$$

(1)

3.3.2. The End Time of No-Load State of AGV

The end time of the no-load state of $R_{ij}$ is expressed by Formula (2). There are two situations that make $R_{ij}$ does not have a no-load transportation state: (1) The previous adjacent process $O_{i(j-1)}$ and process $O_{ij}$ corresponding to $R_{ij}$ are processed on the same machine; and (2) $R_{ij}$ is both the first process of the corresponding workpiece and the first transportation task of the corresponding AGV. In other cases, the end time of the no-load state of $R_{ij}$ is greater of the AGV no-load arrival time and the processing completion time of the previous $O_{i(j-1)}$.

$$VC{T}_{ijw}^{no}=\{\begin{array}{l}VS{T}_{ijw}^{no},{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{y}_{ijglk}\times (i-g+1)\times (j-l)=1\mathrm{or}({\displaystyle \sum _{w=1}^u{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{s}_{ijglw}=0\mathrm{and}j=1)}}}}}}}\\ \max \{VS{T}_{ijw}^{no}+{\displaystyle \sum _{w=1}^u{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{k^{\prime }=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{x}_{i(j-1)kh}\times c_{glw{k}^{\prime }}\times s_{ijkh}\times z_{glw}\times z_{ijw}\times \frac{L_{k{k}^{\prime }}}{v_{no}}}}},}}}C{T}_{i(j-1)kh}\text{}},\mathrm{other}\end{array}$$

(2)

3.3.3. The Start Time of Load State of AGV

The start time of the load state of $R_{ij}$ is expressed by Formula (3). The AGV only has two states of no-load and load. When the no-load state ends, the AGV immediately enters the load state:

$$VS{T}_{ijw}^{lo}=VC{T}_{ijw}^{no}$$

(3)

3.3.4. The End Time of Load State of AGV

The end time of the load state of $R_{ij}$ is divided into two cases as shown in Formula (4): First, there is no load state for $R_{ij}$ when the previous adjacent process $O_{i(j-1)}$ and process $O_{ij}$ are processed on the same machine; second, the end time of load state of $R_{ij}$ is the greater of the AGV load arrival time and the processing completion time of process $O_{i^{\prime }{j}^{\prime }}$ in other cases. The processing completion time of $O_{i^{\prime }{j}^{\prime }}$ is calculated by Formula (5), where $O_{i^{\prime }{j}^{\prime }}$ is processed before $O_{ij}$ on the machine corresponding to $O_{ij}$.

$$VC{T}_{ijw}^{lo}=\{\begin{array}{l}VS{T}_{ijw}^{lo},({\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{y}_{ijglk}\times (i-g+1)\times (j-1)=1)}}}}\\ \max \{VS{T}_{ijw}^{lo}+{\displaystyle \sum _{w=1}^u{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{k^{\prime }=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{\displaystyle \sum _{h^{\prime }=1}^{H_{k^{\prime }}}{z}_{ijw}\times x_{i(j-1)kh}\times x_{ij{k}^{\prime }{h}^{\prime }}\times \frac{L_{k{k}^{\prime }}}{v_{lo}},C{T}_{i^{\prime }{j}^{\prime }{k}^{\prime }}\text{}},\mathrm{other}}}}}}\end{array}$$

(4)

$$C{T}_{i^{\prime }{j}^{\prime }{k}^{\prime }}={\displaystyle \sum _{k^{\prime }=0}^{m+1}{\displaystyle \sum _{h=1}^{H_{k^{\prime }}}{\displaystyle \sum _{t=1}^n{\displaystyle \sum _{p=1}^{N_t+1}{y}_{ijtp{k}^{\prime }}\times x_{tp{k}^{\prime }h}\times C{T}_{tp{k}^{\prime }h}}}}}$$

(5)

3.3.5. The Start Time of Processing State of Machine

The start time of $O_{ij}$ includes two cases as shown in Formula (6): When $O_{i(j-1)}$ and $O_{ij}$ are processed on the same machine, the start time of $O_{ij}$ is equal to the end time of process $O_{i^{\prime }{j}^{\prime }}$; In other cases, the start time of $O_{ij}$ is equal to the end time of load state of transportation task $R_{ij}$.

$$S{T}_{ijkh}=\{\begin{array}{l}C{T}_{i^{\prime }{j}^{\prime }k},({\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{y}_{ijglk}\times (i-g+1)\times (j-l)=1)}}}}\\ VC{T}_{ijw}^{lo},\mathrm{other}\end{array}$$

(6)

3.3.6. The End Time of Processing State of Machine

The end time of $O_{ij}$ is equal to the sum of the start time of $O_{ij}$ and its processing time on the corresponding machine, as shown in Formula (7):

$$C{T}_{ijkh}=S{T}_{ijkh}+{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{x}_{ijkh}\times T_{ijkh}}}$$

(7)

3.4. Comprehensive Energy Consumption Model

In this section, a comprehensive energy consumption model based on the above time-node model is established to represent the energy consumption including the machine (processing and standby states) and AGV (load transportation, no-load transportation, load standby, and no-load standby states).

3.4.1. The Energy Consumption of the Machine Operation Process

The energy consumption of the machine operation can be divided into two parts: standby and processing.

(1)

The energy consumption of the standby state of the machine

The machine standby energy consumption of $O_{ij}$ is shown in Formula (8). In particular, there is no machine standby energy consumption when the process is an additional process $O_{i(N_i+1)}$.

$$E_{ij}^{pnm}=\{\begin{array}{l}0,j=N_i+1\\ {\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{x}_{ijkh}\times x_{glkh}\times y_{ijglk}\times (S{T}_{ijkh}-C{T}_{glkh})}}}\times }{P}_{kh}^{no},\mathrm{other}\end{array}$$

(8)

(2)

The energy consumption of the processing state of the machine

The processing energy consumption of $O_{ij}$ is expressed by Formula (9):

$$E_{ij}^{plm}={\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{x}_{ijkh}\times T_{ijkh}}}\times P_{kh}^{lo}$$

(9)

(3)

The total energy consumption of the machine operation

Based on the two states of processing and standby, the total energy consumption of the machine operation is calculated with Formula (10):

$$E_m={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{N_i+1}(E_{ij}^{plm}+E_{ij}^{pnm})}}$$

(10)

3.4.2. The Energy Consumption of the AGV Operation

During the operation of the AGV, the AGV sometimes needs no-load transport to collect the workpiece. The no-load standby time occurs when the workpiece has not completed the previous machining process. When the workpiece is loaded, the AGV transports the workpiece to the target machine. If the target machine is processing another workpiece, the load standby time is generated. Therefore, the energy consumption corresponding to the above four states is generated during the operation of the AGV.

(1)

The energy consumption of the no-load transportation of the AGV

The no-load transportation energy consumption of the AGV is calculated by multiplying the no-load transportation time by the AGV’s no-load transportation power. In particular, the no-load transportation time of $R_{ij}$ is calculated with Formula (11). Then, the no-load transportation energy consumption of $R_{ij}$ is calculated with Formula (12):

$$V{T}_{ij}^{pnv}={\displaystyle \sum _{w=1}^u{\displaystyle \sum _{g=1}^n{\displaystyle \sum _{l=1}^{N_g+1}{\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{k^{\prime }=0}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{x}_{i(j-1)kh}\times c_{glw{k}^{\prime }}\times s_{ijglw}\times z_{glw}\times \frac{L_{k{k}^{\prime }}}{v_{no}}}}}}}}$$

(11)

$$E_{ij}^{pnv}=V{T}_{ij}^{pnv}\times V{P}_{no}^p$$

(12)

(2)

The energy consumption of the load transportation of the AGV

The load transportation energy consumption of the AGV is calculated by multiplying the load transportation time by the AGV’s load transportation power. Formula (13) shows the calculation of the load transportation time of $R_{ij}$. Then, the calculation of the load transportation energy consumption of $R_{ij}$ is shown as Formula (14):

$$V{T}_{ij}^{plv}={\displaystyle \sum _{k=0}^{m+1}{\displaystyle \sum _{k^{\prime }=1}^{m+1}{\displaystyle \sum _{h=1}^{H_k}{\displaystyle \sum _{h^{\prime }=1}^{H_{k^{\prime }}}{x}_{i(j-1)kh}\times x_{ij{k}^{\prime }{h}^{\prime }}\times \frac{L_{k{k}^{\prime }}}{v_{lo}}}}}}$$

(13)

$$E_{ij}^{plv}=V{T}_{ij}^{plv}\times V{P}_{lo}^p$$

(14)

(3)

The energy consumption of the no-load standby state of the AGV

The no-load standby energy consumption of the AGV is calculated by multiplying the no-load standby time by the AGV’s no-load standby power. In particular, the no-load standby time of $R_{ij}$ is calculated with Formula (15). Then, the no-load standby energy consumption of $R_{ij}$ is calculated with Formula (16):

$$V{T}_{ij}^{tnv}={\displaystyle \sum _{w=1}^u{z}_{ijw}\times (VC{T}_{ijw}^{no}-VS{T}_{ijw}^{no})-V{T}_{ij}^{pnv}}$$

(15)

$$E_{ij}^{tnv}=V{T}_{ij}^{tnv}\times V{P}_{no}^n$$

(16)

(4)

The energy consumption of the load standby state of the AGV

The load standby energy consumption of the AGV is calculated by multiplying the load standby time by the AGV’s load standby power. Formula (17) shows the calculation of the load standby time of $R_{ij}$ Therefore, the calculation of the load standby energy consumption of $R_{ij}$ is shown as Formula (18):

$$V{T}_{ij}^{tlv}={\displaystyle \sum _{w=1}^u{z}_{ijw}\times (VC{T}_{ijw}^{lo}-VS{T}_{ijw}^{lo})-V{T}_{ij}^{plv}}$$

(17)

$$E_{ij}^{tlv}=V{T}_{ij}^{tlv}\times V{P}_{lo}^p$$

(18)

(5)

The total energy consumption of the AGV operation process

The total energy consumption of all transportation tasks is calculated with Formula (19):

$$E_t={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{N_i+1}(E_{ij}^{pnv}+}}{E}_{ij}^{tnv}+E_{ij}^{plv}+E_{ij}^{tlv})$$

(19)

3.4.3. The Comprehensive Energy Consumption in the Workshop

The comprehensive energy consumption in the workshop including the operation processes of the machine and the AGV is calculated with Formula (20):

$$E=E_m+E_t$$

(20)

3.5. The Formulation of the Mixed-Integer Programming Model

In this paper, the mixed-integer programming model has two optimization objectives.

$$\mathrm{Objective}1:\min f_1=C{T}_{\max }$$

(21)

$$\mathrm{Objective}2\text{:}\min f_2=E$$

(22)

where objective 1 is to minimize the makespan and objective 2 is to minimize the total comprehensive energy consumption of the operation process of the machine and the AGV in the makespan. In particular, the scheduling optimization problem is transformed from dual-objective to single-objective by converting makespan and comprehensive energy consumption into costs. The cost function is as follows:

$$\mathrm{Cost}=(1-\mathsf{\lambda })\times \mathrm{CT}\times f_1+\mathsf{\lambda }\times \mathrm{CE}\times f_2$$

(23)

In Formula (23), $\mathsf{\lambda }$ is the weight coefficient of the total comprehensive energy consumption in the objective function. The decision maker adjusts $\mathsf{\lambda }$ through the actual demand to make the products meet the optimal situation and achieve the purpose of low-carbon scheduling. The CT denotes the average unit processing time price, and CE represents the unit energy consumption price.

The constraints of the MIP model are as follows:

$$C{T}_{ijkh}-T_{ijkh}\ge C{T}_{i(j-1)k^{\prime }{h}^{\prime }}$$

(24)

$$S{T}_{ijkh}+G(1-y_{ijglk})\ge C{T}_{glkh}$$

(25)

$$VS{T}_{glw}^{no}+G(1-s_{ijglw})\ge VC{T}_{ijw}^{lo}$$

(26)

$$VC{T}_{ijw}^{no}=\max \{VS{T}_{ijw}^{no}+\frac{L_{k{k}^{\prime }}}{v_{no}},C{T}_{i(j-1)k^{\prime }h}\}$$

(27)

$$VS{T}_{ijw}^{lo}=VC{T}_{ijw}^{no}$$

(28)

$$VC{T}_{ijw}^{lo}=\max \{VS{T}_{ijw}^{lo}+\frac{L_{k{k}^{\prime }}}{v_{lo}},C{T}_{i^{\prime }{j}^{\prime }k}\}$$

(29)

$$S{T}_{ijkh}=VC{T}_{ijw}^{lo}$$

(30)

$$C{T}_{ijkh}=S{T}_{ijkh}+T_{ijkh}$$

(31)

$${\displaystyle \sum _{w=1}^W{z}_{ijw}}=1$$

(32)

$${\displaystyle \sum _{k=1}^m{\displaystyle \sum _{h=1}^{H_k}{x}_{ijkh}=1}}$$

(33)

$${\displaystyle \sum _{w=1}^u{\displaystyle \sum _{k=1}^m{c}_{ijkw}}=1}$$

(34)

Formula (24) represents the workpiece processed through the process sequence. Formula (25) is a machine that can only process one workpiece at a time. Formula (26) is an AGV that can only take one transportation task at a time. Formula (27) is the end of the no-load state of the AGV that requires reaching the machine, and the workpiece on the machine is completed. Formula (28) represents the AGV immediately entering the load state when the no-load state ends. Formula (29) is the end of the AGV load state that requires reaching the machine, and the machine is idle. Formula (30) is that the workpiece can be processed after the AGV load state ends. Formula (31) is the processing state of a workpiece that cannot be interrupted. Formula (32) is that the per transportation task selects one AGV at most. Formula (33) is the per-workpiece process that selects one machine at most. Formula (34) is the per-workpiece process that selects one AGV to park next to one machine at most.

The constraints of the decision variables are as follows:

$$x_{ijkh}=\{\begin{array}{l}1,\mathrm{process}{O}_{ij}\mathrm{selects}h\mathrm{speed}\text{-}\mathrm{level}\mathrm{for}\mathrm{processing}\mathrm{on}\mathrm{machine}k\\ 0,\mathrm{other}\end{array}$$

(35)

$$y_{ijglk}=\{\begin{array}{l}1,\mathrm{process}{O}_{ij}\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}k\mathrm{after}\mathrm{process}{O}_{gl}\\ 0,\mathrm{other}\end{array}$$

(36)

$$s_{ijglw}=\{\begin{array}{l}1,\mathrm{task}{R}_{ij}\mathrm{is}\mathrm{transported}\mathrm{on}AG{V}_w\mathrm{after}\mathrm{task}{R}_{gl}\\ 0,\mathrm{other}\end{array}$$

(37)

$$c_{ijwk}=\{\begin{array}{l}1,\mathrm{task}{R}_{ij}\mathrm{selects}AG{V}_w\mathrm{to}\mathrm{park}\mathrm{next}\mathrm{to}\mathrm{machine}k\\ 0,\mathrm{other}\end{array}$$

(38)

$$z_{ijw}=\{\begin{array}{l}1,\mathrm{task}{R}_{ij}\mathrm{selects}AG{V}_w\mathrm{for}\mathrm{transportation}\\ 0,\mathrm{other}\end{array}$$

(39)

4. Methodology

In this section, the EDA-LSHS is developed to solve the proposed MIP model. The algorithm framework and the combined effect of EDA and LSHS are introduced in Section 4.1. Then, the representation of the solution, the method of encoding and decoding, LSHS, and EDA are described in detail in the remaining sections.

4.1. The EDA-LSHS

The EDA is a new probabilistic model-based swarm evolution algorithm. It guides the evolution of the population macroscopically through the probability matrix and has the advantages of strong global search ability and fast convergence speed. However, because it describes the macroscopic evolution of the population, its local search ability is weak, and it is difficult to jump out of the optimal local solution. Therefore, to enhance the local search strategy of the EDA, a LSHS with strong local search ability is proposed to guide the search for EDA. In the LSHS, strategy 1 (machine processing energy consumption optimization) is to adjust the machine speed levels to reduce the energy consumption of the processing state of the machine, strategy 2 (AGV load state energy consumption optimization) is to select idle candidate machines to reduce AGV load standby time and load transportation time, and strategy 3 (AGV no-load transportation energy consumption optimization) is to select the appropriate AGV to reduce the energy consumption of the AGV in no-load transportation.

Figure 2 shows the flowchart of the EDA-LSHS. The process of the proposed EDA-LSHS is as follows:

Step 1: Initialize the population, the EDA-related parameters, and the probability matrices.

Step 2: Select a dominant population updated probability matrix.

Step 3: Generate a new offspring population by sampling based on the updated probability matrix.

Step 4: The offspring population is updated with the LSHS. First, strategy 1 updates the offspring-encoding vectors by searching for the candidate speed for each workpiece process. Then, strategy 2 updates the offspring-encoding vectors by seeking the idle candidate machine for each workpiece process. Lastly, strategy 3 updates the offspring-encoding vectors by looking for the suitable AGV for each workpiece process.

Step 5: Update the population and judge whether the iteration is over. If yes, end the iteration and output the optimized scheduling solution; otherwise, return to step 2.

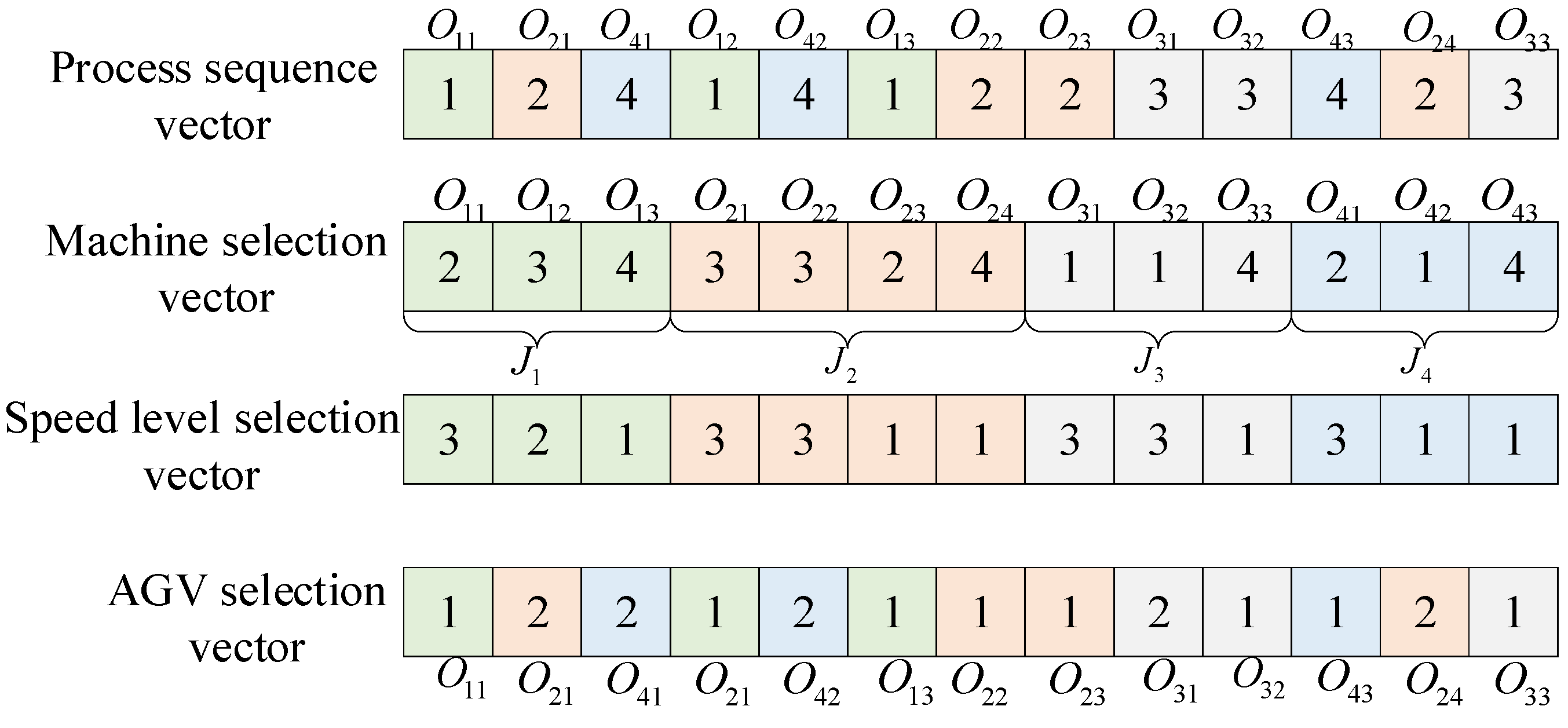
4.2. Representation of the Solution

In this paper, the scheduling scheme is in two states: the operation of the machine and AGV. The operation of the machine can be divided into process sequence vector, machine selection vector, and speed selection vector. The operation of the AGV can be described as an AGV selection vector. A feasible scheduling solution is represented by the above four vectors.

4.3. Encoding and Decoding

In this paper, a four-segment encoding method is adopted. Then, to better express the encoding method in detail, a practical instance is described as follows: Suppose that for the machining task, there are three multispeed machines and four workpieces, each machine has three speeds, and each speed has corresponding processing power. Workpiece 1 has two processes, workpiece 2 has three processes, workpiece 3 has two processes, and workpiece 4 has two processes. In particular, each process has an additional process that sends the finished workpiece to the final warehouse. Furthermore, each process has different processing times for different speed on the corresponding machine. Then, suppose for the AGV transportation task that there are 2 AGVs and that each AGV has different comprehensive powers in the four states of no-load transportation, no-load standby, load transportation, and load standby. All AGVs are the same model and transport at different speeds in no-load and load conditions. The resulting encoding form of a scheduling solution for the above actual instance is represented in Figure 3.

The decoding result corresponding to the above encoding vector is described in the form of the Gantt chart shown in Figure 4. More importantly, in the decoding process, we propose a corresponding decoding strategy for the special case when the adjacent processes of the workpiece take place on the same machine. The details of the above decoding strategy are as follows: Suppose process $O_{ij}$ and $O_{i(j-1)}$ are the adjacent processes of workpiece $i$; they all are processed on machine $k$. The transportation task $R_{ij}$ is transported by AGV $w$. $O_{gl}$ is processed on machine $k$ before $O_{ij}$. $R_{pq}$ is transported by AGV $k$ after $R_{ij}$. Therefore, the processing start time of $O_{ij}$ is the completion time of $O_{gl}$, and $O_{ij}$ has no transportation time. Then, AGV $w$ does not execute $R_{ij}$ but directly executes $R_{pq}$ during decoding.

4.4. Low-Carbon Scheduling Heuristic Strategy

The LSHS is introduced here to conduct the heuristic search for individuals from the EDA and guide the search direction of the EDA to obtain better solutions. The LSHS contains the following three heuristic strategies: machine processing energy consumption optimization, AGV load state energy consumption optimization, and AGV no-load transportation energy consumption optimization.

4.4.1. Strategy 1: Machine Processing Energy Consumption Optimization

During the manufacturing operation, the machine processing generates considerable energy consumption. In a multispeed flexible manufacturing environment, machines have different speeds to process the workpieces. If a workpiece is processed at a lower speed without affecting the makespan and the continuity of the workpiece, the above energy consumption can be significantly reduced. Therefore, the energy consumption of the machine processing is optimized by a minimization strategy. Its detailed steps are as follows:

Step 1: Suppose process $O_{ij}$ is processed at machine $k$ with at speed $h$. Speed $h_r$ belongs to $H_k$, and $h_r$ is not equal to $h$. $O_{i^{″}{j}^{″}}$ is processed on machine $k$ after $O_{ij}$.

Step 2: If the power of $h_r$ is less than $h$, $h_r$ is defined as the candidate speed $h_{rc}$. If there is a $h_{rc}$, go to step 3; otherwise, go to step 6.

Step 3: Calculate the evaluation value for per $h_{rc}$ with Formula (40).

Step 4: Compare the evaluation values $V_1(h,h_{rc},O_{ij})$ of all $h_{rc}$. If the maximum evaluation value is greater than 0, replace the original encoding speed $h$ with $h_{rc}$ with maximum evaluation value and update the encoding string; otherwise, keep $h$ unchanged.

Step 5: Perform steps 1–4 for each process in the order of process sequence

$$V_1(h,h_{rc},O_{ij})=(E_{ij}^{plm}(k,h)+E_{i^{″}{j}^{″}}^{tlv}(k,h))-(E_{ij}^{plm}(k,h_{rc})+E_{i^{″}{j}^{″}}^{tlv}(k,h_{rc}))$$

(40)

Machine processing energy consumption $E_{ij}^{plm}$ and AGV load standby energy consumption $E_{ij}^{tlv}$ are calculated with Formulas (9) and (18), respectively.

4.4.2. Strategy 2: AGV Load State Energy Consumption Optimization

The process of transporting heavy workpieces by AGVs between machines can cause enormous energy consumption. It is possible to effectively reduce the above energy consumption by selecting the processing machine with the shortest distance from the current machine in the available machine set. Furthermore, the excessive load standby time of AGV is harmful to the continuity of the processed workpiece and causes a delay in the makespan. The above load standby time can be eliminated by choosing an idle machine in the available machine set to process the workpiece. Therefore, the AGV load state energy consumption, including load transportation and load standby, needs to be further optimized through a minimization strategy. Its detailed steps are as follows:

Step 1: Suppose $O_{ij}$ is processed on machine $k$. Machine $k_r$ belongs to ${\psi }_{ij}$. Calculate the load transportation time per $k_r$ that belongs to ${\psi }_{ij}$ with Formula (13). If the load transportation time of $k_r$ is less than that of the original encoded machine $k$, $k_r$ is defined as the candidate machine $k_{rc}$. If there is no $k_{rc}$, go to step 6; otherwise, go to step 2.

Step 2: Determine whether there is a load standby time for $O_{ij}$ with Formula (17). If there is a load standby time for $O_{ij}$, go to step 3; otherwise, go to step 6.

Step 3: Determine if $k_{rc}$ for $O_{ij}$ is idle when the load transportation task $R_{ij}$ starts. If it is idle, $k_{rc}$ is defined as the idle candidate machine $k_{ric}$. If there is no $k_{ric}$, go to step 6; otherwise, go to step 4.

Step 4: Calculate the evaluation value per $k_{ric}$ with Formula (41).

Step 5: Compare the evaluation values $V_2(k,k_{ric},O_{ij})$ for all $k_{ric}$. If the maximum evaluation value is greater than 0, replace the original encoding machine $k$ with the $k_{ric}$ with the maximum evaluation value and update the encoding string; otherwise, keep $k$ unchanged.

Step 6: Perform steps 1–5 for each process in the order of process sequence

$$V_2(k,k_{ric},O_{ij})=(E_{ij}^{plv}(k)+E_{ij}^{plm}(k)+E_{ij}^{tlv}(k))-(E_{ij}^{plv}(k_{ric})+E_{ij}^{plm}(k_{ric}))$$

(41)

Machine processing energy consumption $E_{ij}^{plm}$, AGV load transportation energy consumption $E_{ij}^{plv}$, and AGV load standby energy consumption $E_{ij}^{tlv}$ are calculated with Formulas (9), (14), and (18), respectively.

4.4.3. Strategy 3: AGV No-Load Transportation Energy Consumption Optimization

Under the unreasonable arrangement and discontinuous operation of AGV transportation tasks, numerous no-load transportation energy consumption values for the AGVs are generated in the production of the investigated enterprise. Obviously, the AGVs that are reasonably reselected can significantly reduce the above energy consumption. Therefore, a minimization strategy can be adopted to optimize the AGV no-load transportation energy consumption. The detailed steps are as follows:

Step 1: Suppose that $O_{ij}$ is processed on machine $k$, $O_{i(j-1)}$ is processed on machine $k^{\prime }$ and $O_{gl}$ is processed on machine $k^{\prime }$ after $O_{i(j-1)}$. $AG{V}_a$ takes transportation task $R_{ij}$, and $AG{V}_b$ takes $R_{gl}$ in the original encoding vector.

Step 2: If $AG{V}_a$ and $AG{V}_b$ are the same AGV, go to step 7; otherwise, go to step 3.

Step 3: If the load arrival time of $R_{gl}$ is less than or equal to the complete processing time of $O_{i(j-1)}$, replace the $AG{V}_a$ in the original encoding vector with $AG{V}_b$ and update the encoding vector, then go to step 7; otherwise, go to step 4.

Step 4: If the no-load arrival time of $R_{ij}$ is less than or equal to the processing complete time of $O_{i(j-1)}$, go to step 5; otherwise, go to step 6.

Step 5: Calculate the evaluation value by the Formula (42). If the evaluation value is less than or equal to 0, go to step 7; otherwise, replace the $AG{V}_a$ in the original encoding vector with $AG{V}_b$ and update the encoding vector, then go to step 7.

Step 6: Calculate the evaluation value with Formula (43). If the evaluation value is less than or equal to 0, go to step 7; otherwise, replace the $AG{V}_a$ in the original encoding vector with $AG{V}_b$, and update the encoding vector.

Step 7: Perform steps 1–6 for each process in the order of process sequence

$$V_3(AG{V}_a,AG{V}_b,O_{ij})=(E_{ij}^{pnv}+E_{ij}^{tnv})-(VC{T}_{glb}^{lo}-C{T}_{i(j-1)k^{\prime }h})\times P_{k^{\prime }h}^{no}$$

(42)

$$V_4(AG{V}_a,AG{V}_b,O_{ij})=(E_{ij}^{pnv}+E_{ij}^{pnm})-(VC{T}_{glb}^{lo}-C{T}_{i(j-1)k^{\prime }h})\times P_{k^{\prime }h}^{no}$$

(43)

Machine standby energy consumption $E_{ij}^{pnm}$, AGV no-load transportation energy consumption $E_{ij}^{pnv}$, and AGV no-load standby energy consumption $E_{ij}^{tnv}$ are calculated with Formulas (8), (12), and (16), respectively. Then, the end time of load state of AGV $VC{T}_{glb}^{lo}$ and the end time of processing state of machine $C{T}_{i(j-1)k^{\prime }h}$ are calculated with Formulas (4) and (7), respectively.

To make the AGV no-load transportation energy optimization strategy easier to understand, an example is given to describe the above strategy in detail as follows: Suppose there are three workpieces, three machines, and two AGVs. As shown in Figure 5, $M_4^t$, $AG{V}_1^t$, and $AG{V}_2^t$ are the updated $M_4$, $AG{V}_1$, and $AG{V}_2$ after adopting strategy 3 to replace the AGV. In particular, process $O_{13}$ has a no-load transportation time and $O_{32}$ is processed on $M_2$ after $O_{12}$. Then, $O_{13}$ and $O_{32}$ are transported by $AG{V}_1$ and $AG{V}_2$, respectively. This example needs to be calculated with Formula (43): Suppose, $V_4(AG{V}_1,AG{V}_2,O_{13})>0$, then replace $AG{V}_1$ for $O_{13}$ with $AG{V}_2$. In Figure 5, the results after the optimization with strategy 3 are as follows: (1) the AGV no-load transportation time of $O_{13}$ is eliminated and (2) the makespan is significantly reduced due to the AGV running in parallel at the time level.

4.5. Estimation of Distribution Algorithm

The concept of the estimation of distribution algorithm (EDA) was first proposed in 1996 and developed rapidly [33]. As an emerging stochastic optimization algorithm based on statistical principles, the EDA generates excellent new individuals by predicting the optimal search area by sampling the search space and statistical learning. Moreover, the EDA has robust global search ability and fast convergence based on the macro-level evolution of the search space. The EDA generates new populations by sampling according to the probability matrix. Consequently, this section focuses on the probability model’s initialization and update mechanism.

4.5.1. Population Initialization and Fitness Value

The initial population is randomly generated to ensure the diversity of the initial population and allow the initial population to cover the solution space [34]. Then, the initial population is encoded by a four-segment coding method in Section 4.3.

Since the LCSP-MSFM & MAGVT is a minimum optimization problem, the objective function needs to be transformed into a fitness function form according to Formula (23) to represent the fit per individual in the population. The fitness function is as follows:

$$F=\frac{1}{\mathsf{\lambda }\times \mathrm{CT}\times f_1+(1-\mathsf{\lambda })\times \mathrm{CE}\times f_2}$$

(44)

4.5.2. Probability Model and Update Mechanism

In this paper, probability matrices A, B, C, and D are established for the process sequence vector, machine selection vector, speed level selection vector, and AGV selection vector, respectively.

Elements $a_{si}(t)$ in process sequence matrix $A(t)$ represents the probability that the solution of workpiece $i$ appears on or before the $s\text{-}\mathrm{th}$ position in the $t\text{-}\mathrm{th}$ iteration. The larger the value, the earlier $i$ is processed, which reflects the processing priority of the workpiece.

Element $b_{ijk}(t)$ in machine selection matrix $B(t)$ represents the probability that process $O_{ij}$ is processed on machine $k$ in the $t\text{-}\mathrm{th}$ iteration. The larger the value, the greater the probability that $O_{ij}$ is processed on the $k$, which reflects the degree to which $O_{ij}$ selects the machine.

Element $c_{ijkh}(t)$ in speed level selection matrix $C(t)$ represents the probability that process $O_{ij}$ selects speed $h$ for processing on machine $k$ in the $t\text{-}\mathrm{th}$ iteration. The larger the value, the greater the probability that $O_{ij}$ selects $h$ processing speed on $k$, which reflects the degree to which $O_{ij}$ selects the speed on the machine.

Elements $d_{ijw}(t)$ in AGV selection matrix $D(t)$ represents the probability that the transportation task $R_{ij}$ select $AG{V}_w$ to transport in the $t\text{-}\mathrm{th}$ iteration. The larger the value, the greater the probability that $R_{ij}$ selects $AG{V}_w$ to transport, which reflects the degree to that selects the AGV to transportation.

Initialize the probability matrix A, B, C, and D by Formulas (45)–(48).

$$a_{si}(0)=\frac{1}{n},i=1,2,\dots ,n.s=1,2,\dots ,N_{all}+n.$$

(45)

$$b_{ijk}(0)=\{\begin{array}{l}\frac{1}{\frac{{\displaystyle \sum _{h=1}^{H_k}{T}_{ijkh}}}{H_k}}\mathrm{process}{O}_{ij}\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}k\\ 0\mathrm{other}\end{array}$$

(46)

$$\begin{gathered} AG{V}_w\left(46\right) \\ {c}_{ijkh}(0)=\{\begin{array}{l}\frac{1}{H_k},\mathrm{process}{O}_{ij}\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}k\\ 0,\mathrm{other}\end{array} \end{gathered}$$

(47)

$$d_{ijw}(0)=\frac{1}{u},w=1,2,\dots ,u$$

(48)

To select the top $\eta$% individuals with fitness from the population of the current generation to form the dominant population, probability matrixes A, B, C, and D are updated according to the following formulas:

$$a_{si}(t+1)=(1-{\alpha }_1)\times a_{si}(t)+\frac{{\alpha }_1}{s\times N_{\eta }}\times {\displaystyle \sum _{e=1}^{N_{\eta }}{\delta }_{si}^e(t)}$$

(49)

$$b_{ijk}(t+1)=(1-{\alpha }_2)\times b_{ijk}(t)+\frac{{\alpha }_2}{N_{\eta }}\times {\displaystyle \sum _{e=1}^{N_{\eta }}{\varphi }_{ijk}^e(t)}$$

(50)

$$c_{ijkh}(t+1)=(1-{\alpha }_3)\times c_{ijkh}(t)+\frac{{\alpha }_3}{N_{\eta }}\times {\displaystyle \sum _{e=1}^{N_{\eta }}{\xi }_{ijkh}^e(t)}$$

(51)

$$d_{ijw}(t+1)=(1-{\alpha }_4)\times d_{ijw}(t)+\frac{{\alpha }_4}{N_{\eta }}\times {\displaystyle \sum _{e=1}^{N_{\eta }}{\chi }_{ijw}^e(t)}$$

(52)

where ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, and ${\alpha }_4$$\in (0,1)$ are the learning rates of probability matrices A, B, C, and D. $N_{\eta }$ is the number of the individuals in the dominant populations. ${\delta }_{si}^e$, ${\varphi }_{ijk}^e$, ${\xi }_{ijkh}^e$, and ${\chi }_{ijw}^e$ are the following indicator functions of the $e\text{-}\mathrm{th}$ individuals in the dominant population; they satisfy the following constraints:

$${\delta }_{si}^e=\{\begin{array}{l}1,\mathrm{workpiece}i\mathrm{appears}\mathrm{before}\mathrm{or}\mathrm{in}\mathrm{position}s\\ 0,\mathrm{other}\end{array}$$

(53)

$${\varphi }_{ijk}^e=\{\begin{array}{l}1,\mathrm{process}{O}_{ij}\mathrm{is}\mathrm{processed}\mathrm{on}\mathrm{machine}k\\ 0,\mathrm{other}\end{array}$$

(54)

$${\xi }_{ijkh}^e=\{\begin{array}{l}1,\mathrm{process}{O}_{ij}\mathrm{selects}\mathrm{speed}\mathrm{level}h\mathrm{to}\mathrm{process}\mathrm{on}\mathrm{machine}k\\ 0,\mathrm{other}\end{array}$$

(55)

$${\chi }_{ijw}^e=\{\begin{array}{l}1,\mathrm{transportation}\mathrm{task}{R}_{ij}\mathrm{is}\mathrm{transported}\mathrm{by}AG{V}_w\\ 0,\mathrm{other}\end{array}$$

(56)

4.5.3. Generate New Population

New dominant individuals are generated by sampling according to probability matrices A, B, C, and D. Note that the process sequence vector should be generated first to ensure that a newly available solution is generated. Workpiece $i$ is selected with the probability $a_{si}$ per position $s$. If $i$ has already appeared $N_i+1$ times in the process sequence vector, it means all processes of $i$ are arranged. Then, the whole column $a_{1i},a_{2i},\dots ,a_{(N_{all}+n)i}$ of matrix A will be set as 0. Next, sampling to generate the machine selection vector through matrix B, $k$ is selected with probability $b_{ijk}$ per process $O_{ij}$. Similarly, the speed selection vector and AGV selection vector are generated according to matrices C and D, respectively. An individual is generated with the above method.

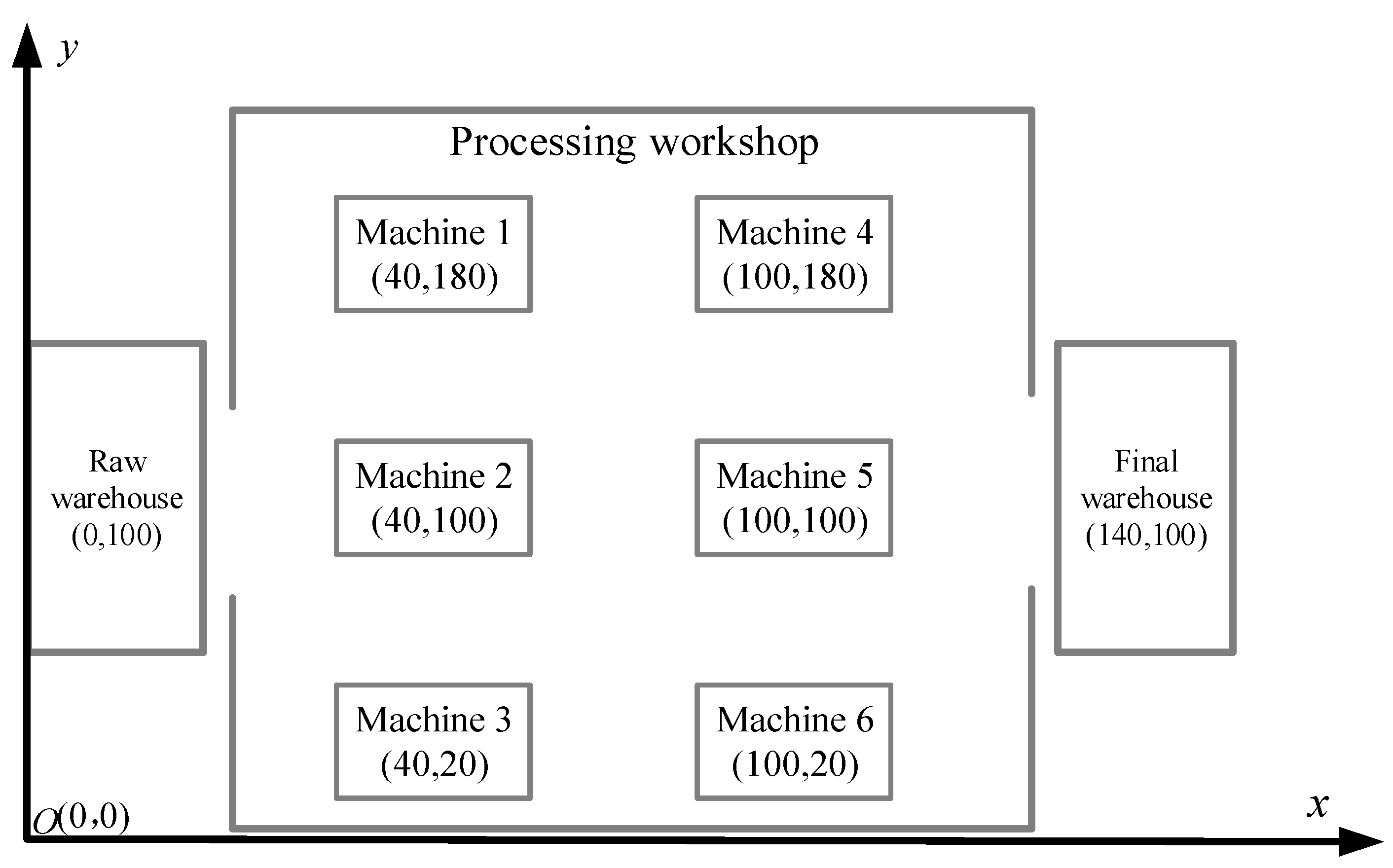
5. Case Study

In this section, the performance and optimization effects of the proposed EDA-LSHS are shown with a case study. The experiment is compiled and run in an Intel Core i7-8750H, 2.2 GHz CPU, 8.00 G RAM, Win 10 64-bit operating system with MATLAB 2019 as a programming environment. The performance analysis experiment compares the performance of the EDA-LSHS with the state-of-the-art algorithms and analyzes its actual optimization effect. The low-carbon scheduling analysis experiment contrasts the comprehensive optimization effect and balanced ability of the EDA-LSHS and other algorithms. It also explores in depth the specific optimization capabilities of the EDA-LSHS for different types of energy consumption. In the discussion, the optimization effects of the EDA-LSHS and the traditional dispatcher mode are compared.

5.1. Data Source

The four product instances of an investigated heavy cement equipment manufacturing enterprise referred to in [29] are adopted as the test data in this paper. Since there are multispeed machines and multi-AGV in LCSP-MSFM & MAGVT, the instances need to be extended to fit the updated manufacturing environment. First, there is only a single speed per machine, so a coefficient vector [1,1.3,1.6] (obtained through historical processing data statistics of the investigated enterprise) is multiplied to extend the single speed to three speeds. Then, the expanded machine processing time in different speeds is the original processing time divided by the coefficient vector and rounded up. The number of AGVs is three according to the actual production condition in the investigated enterprise. The no-load and load transportation speeds of AGV are shown in

Table 1. AGV data table.

AGV State	Load Transport	Load Standby	No-Load Transport	No-Load Standby
Power (W)	2500	800	1800	300
Speed (m/s)	0.6	-	1.2	-

. The comprehensive operating power of the four AGV states of load transport, no-load transport, load standby, and no-load standby are shown in Table 1. The processing and standby state power for each speed of the machine are in

Table 2. Machine process/standby power table.

Power (W)	Speed Level 1		Speed Level 2		Speed Level 3
	Process	Standby	Process	Standby	Process	Standby
Machine 1	1120	170	1460	240	1780	310
Machine 2	1340	230	1750	300	2150	370
Machine 3	1050	160	1370	220	1680	280
Machine 4	1210	190	1580	260	1940	330
Machine 5	1170	180	1530	260	1880	320
Machine 6	1290	210	1680	290	2070	360

. Furthermore, the average price of unit processing time (CT) is CNY 21/h and the price of unit energy consumption (CE) is CNY 2.062/kWh.

In Figure 6, the working layout of the workshop of the investigated enterprise is abstracted into a two-dimensional space. The two-dimensional coordinates of the machine are created. The raw material warehouse stores AGVs and the workpieces to be processed. The final warehouse stores the finished workpieces and the AGVs that complete all the tasks on them.

5.2. Performance Analysis

In this section, the performance of the EDA-LSHS is demonstrated with the comparative experiment analysis and the optimization strategy analysis. First, the comparative experiment analysis verifies the convergence efficiency and solution quality and stability of the EDA-LSHS. Then, the optimization strategy analysis explores the actual optimization effect of the LSHS under different complexity instances.

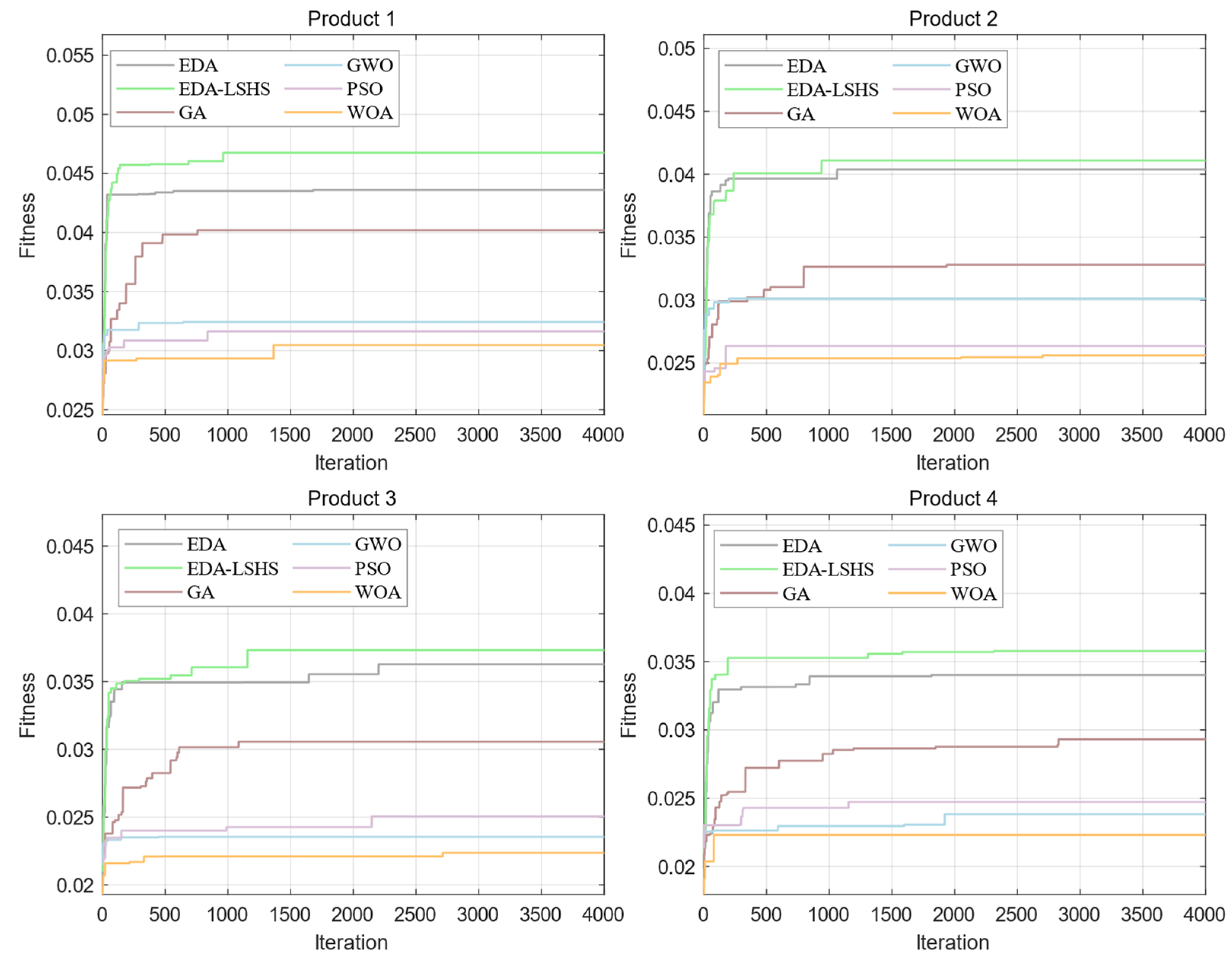
5.2.1. Comparative Experiment Analysis

To analyze the performance of the proposed EDA-LSHS on the LCSP-MSFM & MAGVT, the state-of-the-art algorithms widely used in scheduling problems are used as comparative objects:

(1)

EDA-LSHS: the estimation of distribution algorithm with low-carbon scheduling heuristic strategy.

(2)

EDA: the estimation of distribution algorithm.

(3)

GA: the genetic algorithm.

(4)

PSO: the particle swarm optimization algorithm.

(5)

WOA: the whale optimization algorithm.

(6)

GWO: the grey wolf optimization algorithm.

Since the algorithm parameters significantly impact the performance and stability, the Taguchi method is applied in this paper to obtain the best parameter combination of the compared algorithms [35]. The parameters optimized based on the Taguchi method are as follows: (1) the population size of the above algorithms is defined as 100, and the maximum number of iterations is 4000; (2) the weight coefficient $\mathsf{\lambda }$ in the fitness function is set to 0.6; (3) in EDA-LSHS, dominant individual rate $\eta$ = 0.1, and the learning factors ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, and ${\alpha }_4$ are 0.5, 0.5, 0.5, and 0.5, respectively; (4) the algorithm parameters of EDA are the same as for EDA-LSHS; (5) in GA, crossover rate $Pc$ = 0.8 and mutation rate $Pm$ = 0.1; (6) in PSO, inertia weight $w$ = 0.7, and learning factors $c_1$ and $c_2$ are 0.4 and 0.6, respectively; (7) in WOA, logarithmic spiral shape constant velocity $b$ = 1; (8) in GWO, the adaptive variable $a$ decreases linearly from 2 to 0.

In order to avoid the influence of experimental randomness on the performance evaluation of the algorithms, each group of experiments was run 15 times independently. Figure 7 shows the best convergence curves of the different algorithms for optimizing these four product instances. Figure 8 shows the error analysis results for the compared algorithms. As shown in Figure 7, the WOA performs poorly in these four product instances because it is easy to pre-mature. The convergence speeds of the PSO and the GWO are the fastest among all algorithms, but they have difficulty jumping out of local optimum in the late stage of convergence. The GA achieves relatively good solution quality, but its convergence speed is slow. The EDA describes population evolution macroscopically and has a strong global search ability, and its solution quality is higher than the GA, PSO, GWO, and WOA. because the increased LSHS guides the search direction of the EDA, the EDA-LSHS has stronger search performance and convergence ability than the EDA. Furthermore, it is obvious in Figure 8 that the EDA-LSHS has the best mean and the smallest confidence interval in all four instances, which demonstrates that the EDA-LSHS obtains significant advantages in performance and stability compared with other algorithms.

Consequently, the conclusions of the comparative experiment are summarized as follows:

(1)

The EDA has better search ability than the GA, PSO, GWO, and WOA in the LCSP-MSFM & MAGVT, which provides a basic guarantee for the embedding of heuristic strategies.

(2)

The addition of the LSHS further improves the performance and stability of the EDA in the LCSP-MSFM & MAGVT.

5.2.2. Optimization Strategy Analysis

In the above experiment, the search performance of the EDA and the EDA-LSHS is better than that of other algorithms. Moreover, the EDA-LSHS has better solution quality than the EDA due to the addition of the LSHS. Therefore, this section selects the EDA and the EDA-LSHS for comparison to further analyze the actual optimization effects of the LSHS’s three sub-strategies.

Figure 9 shows the Gantt charts of the optimal scheduling solutions for product 1 and product 4 obtained by the EDA-LSHS and the EDA. As shown in Figure 9a,b, due to the effect of the machine processing energy consumption optimization strategy, the utilization rate of machines is improved, and the makespan is reduced. With the application of the AGV load state energy consumption optimization strategy, the load standby time of AGVs is immensely shortened. Under the action of the AGV no-load transportation energy consumption optimization strategy, the no-load state time of AGVs is well optimized. Then as shown in Figure 9c,d, compared with the EDA, the operations of machines and AGVs are more continuous and the makespan is significant reduced in the EDA-LSHS, which shows that the optimization performance of the EDA-LSHS is not attenuated by the expansion of the solution space. Consequently, by comparing the Gantt charts of the optimal scheduling solutions of the EDA-LSHS and the EDA, the following conclusions can be drawn:

(1)

According to the solution analysis, the three sub-strategies of the LSHS have obvious optimization effects, which not only improves the energy efficiency of machines and AGVs but also shortens the makespan.

(2)

As the complexity of product instances increases, the EDA-LSHS still maintains good optimization performance.

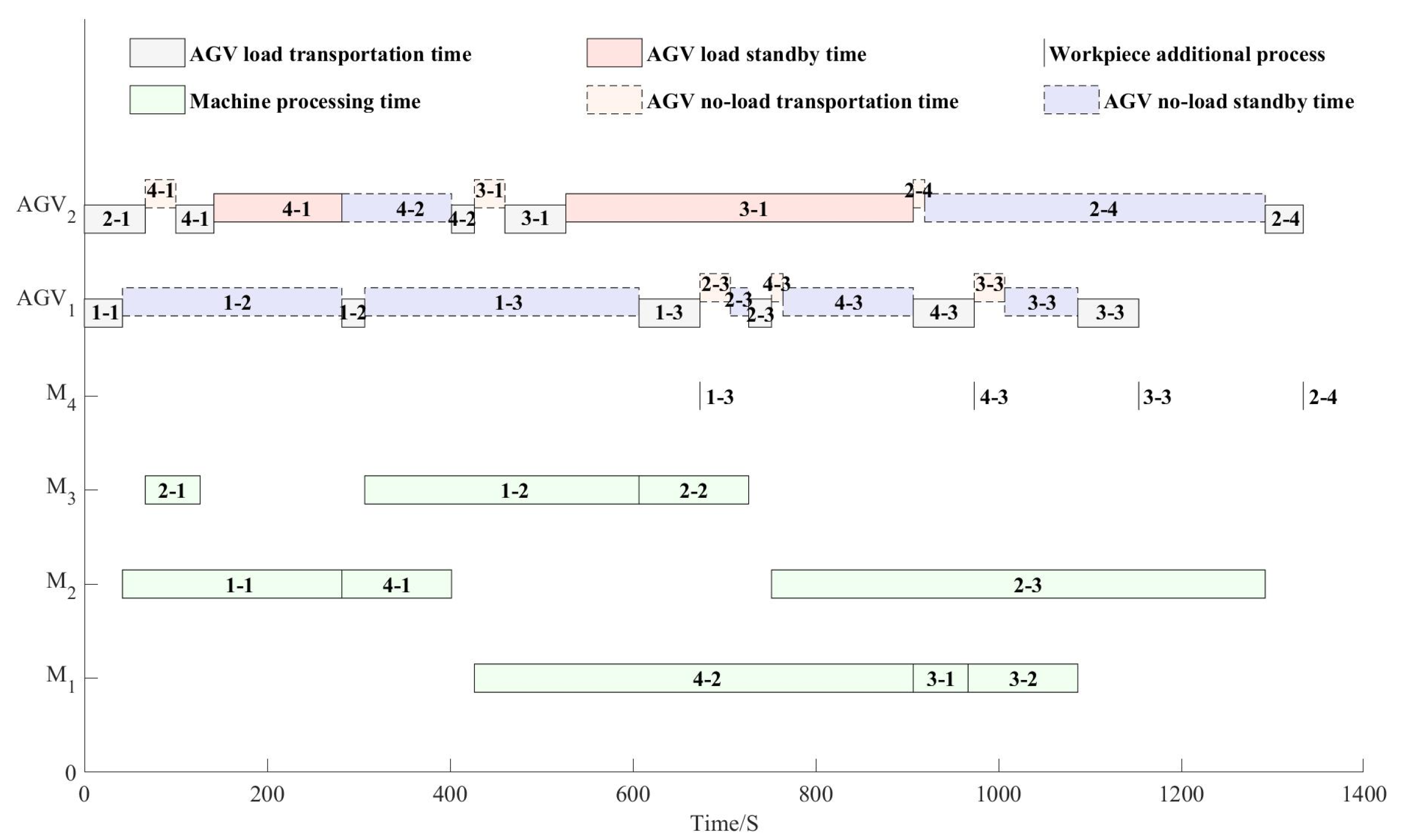
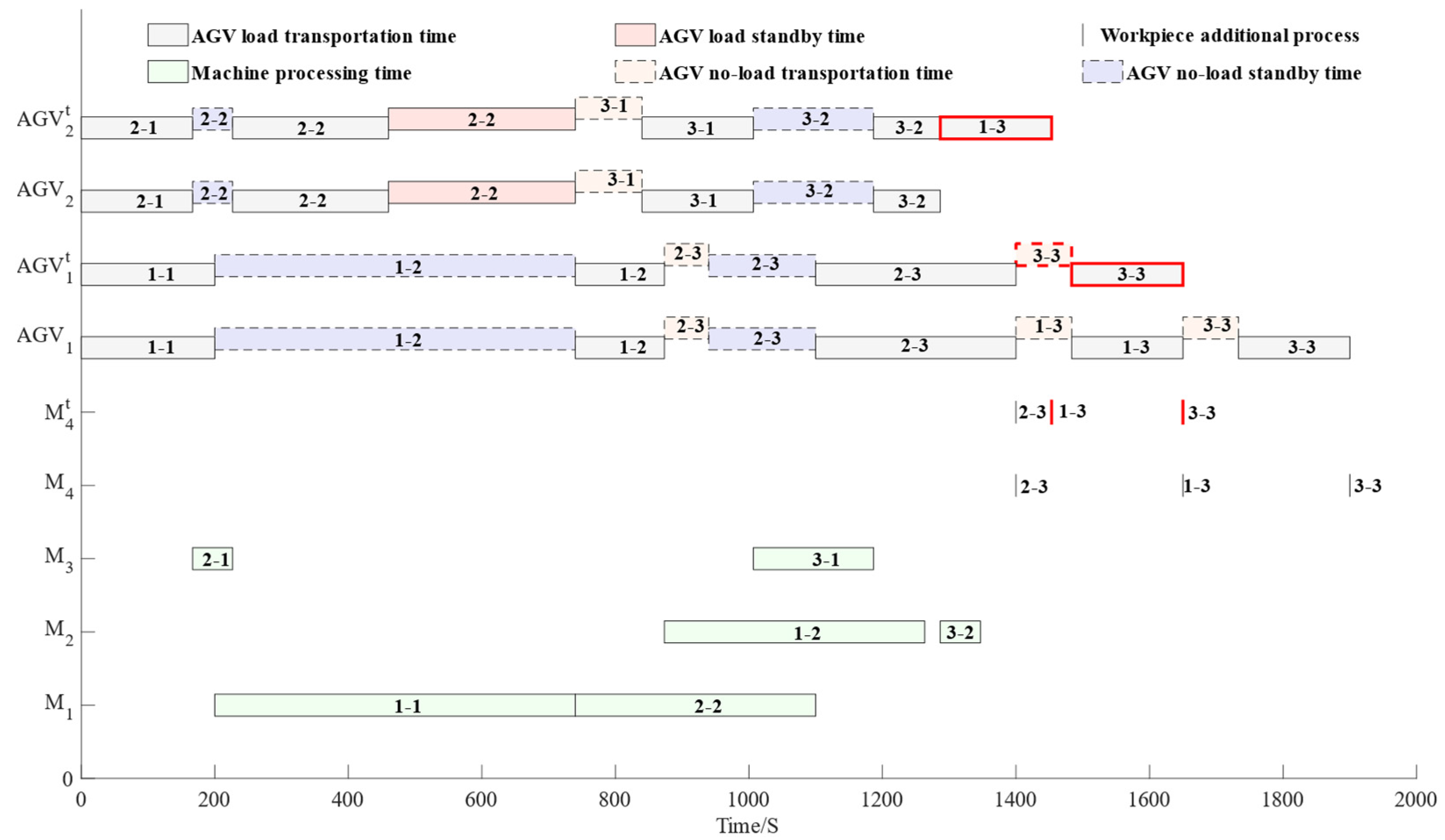
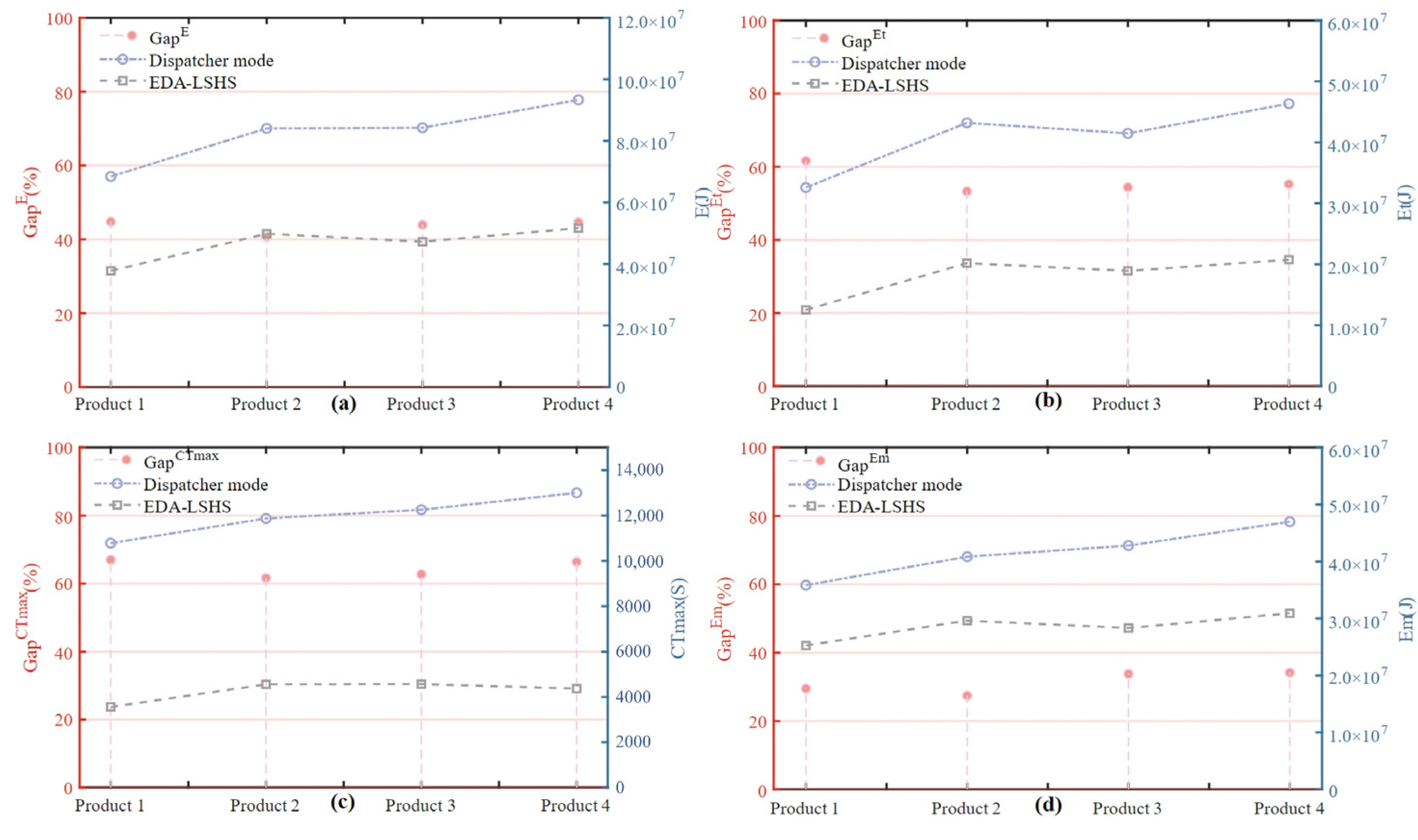
5.3. Low-Carbon Scheduling Analysis

This section mainly analyzes the capability of EDA-LSHS in low-carbon scheduling optimization. A comprehensive optimization analysis contrasts the different algorithms’ comprehensive optimization effects and balanced ability. Then, energy consumption analysis is carried out for different energy consumption types to verify the optimization capability of EDA-LSHS.

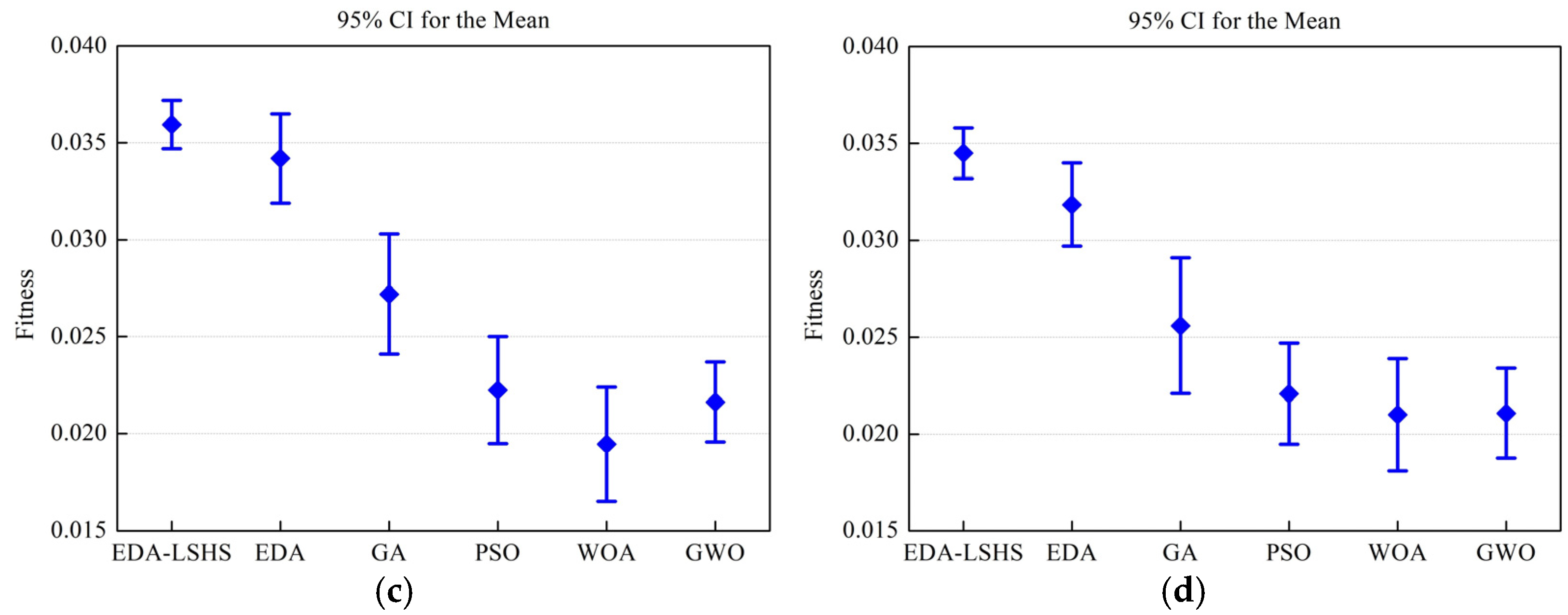
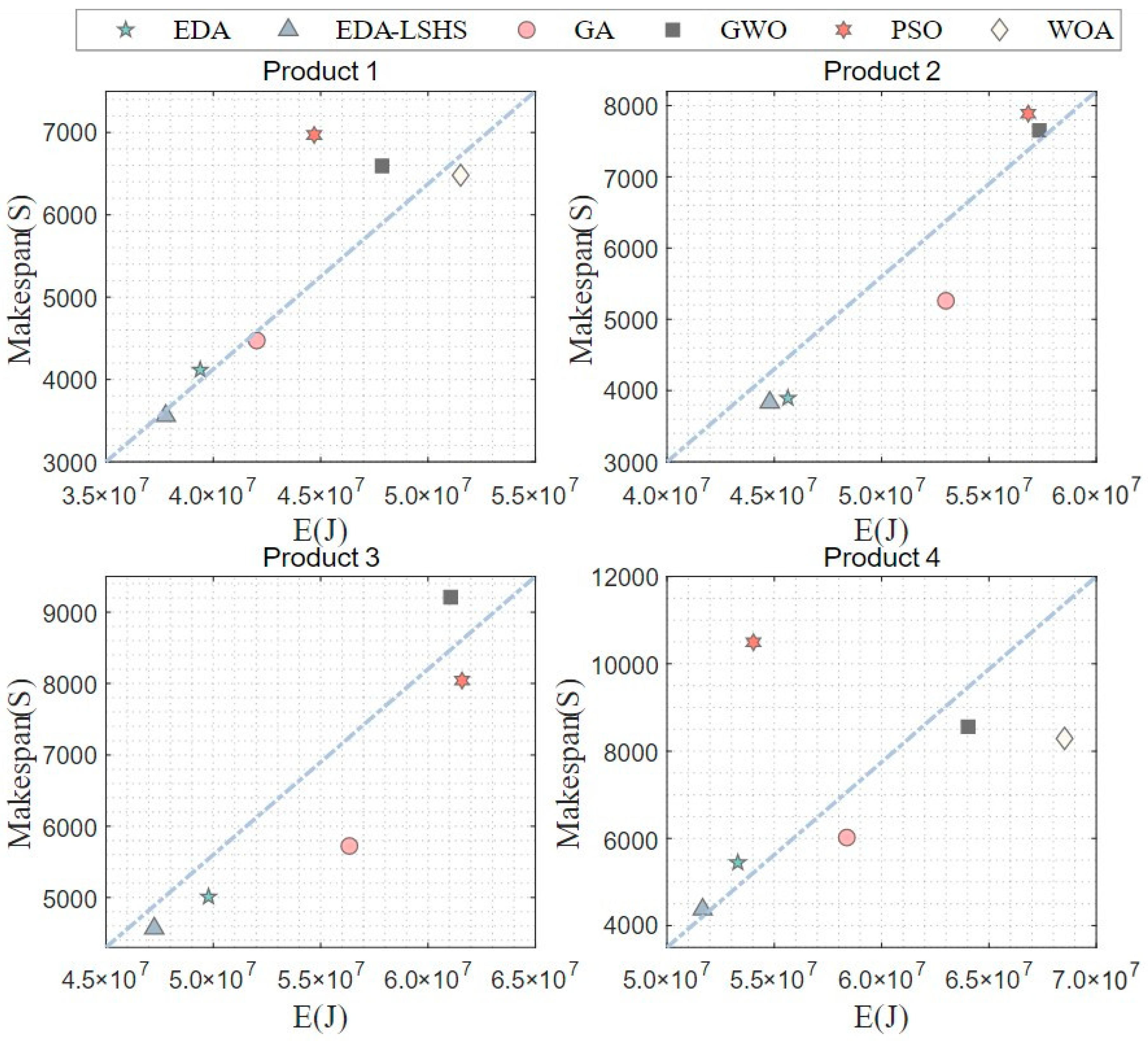
5.3.1. Comprehensive Optimization Analysis

This paper uses energy consumption and makespan as optimization objectives for the proposed MIP model. The comprehensive optimization effect of the two is the fundamental guarantee of low-carbon scheduling. Figure 10 shows the comprehensive optimization effects of different algorithms on the energy consumption and makespans of the four product instances. As shown in Figure 10, the comprehensive optimization effect of each algorithm in product 1 is summarized as follows: (1) the EDA-LSHS is the best and most balanced; (2) the EDA is second; (3) the other algorithms are not ideal and are highly unbalanced. Furthermore, from product 1 to product 4, the EDA-LSHS always maintains the best optimization effect and more balanced optimization ability as the actual complexity continues to increase. Therefore, the conclusions are summarized as follows:

(1)

The EDA-LSHS and EDA have better comprehensive optimization effects and balanced optimization abilities than the other algorithms.

(2)

As the complexity of the products increases, the EDA-LSHS can still maintain favorable low-carbon scheduling optimization ability.

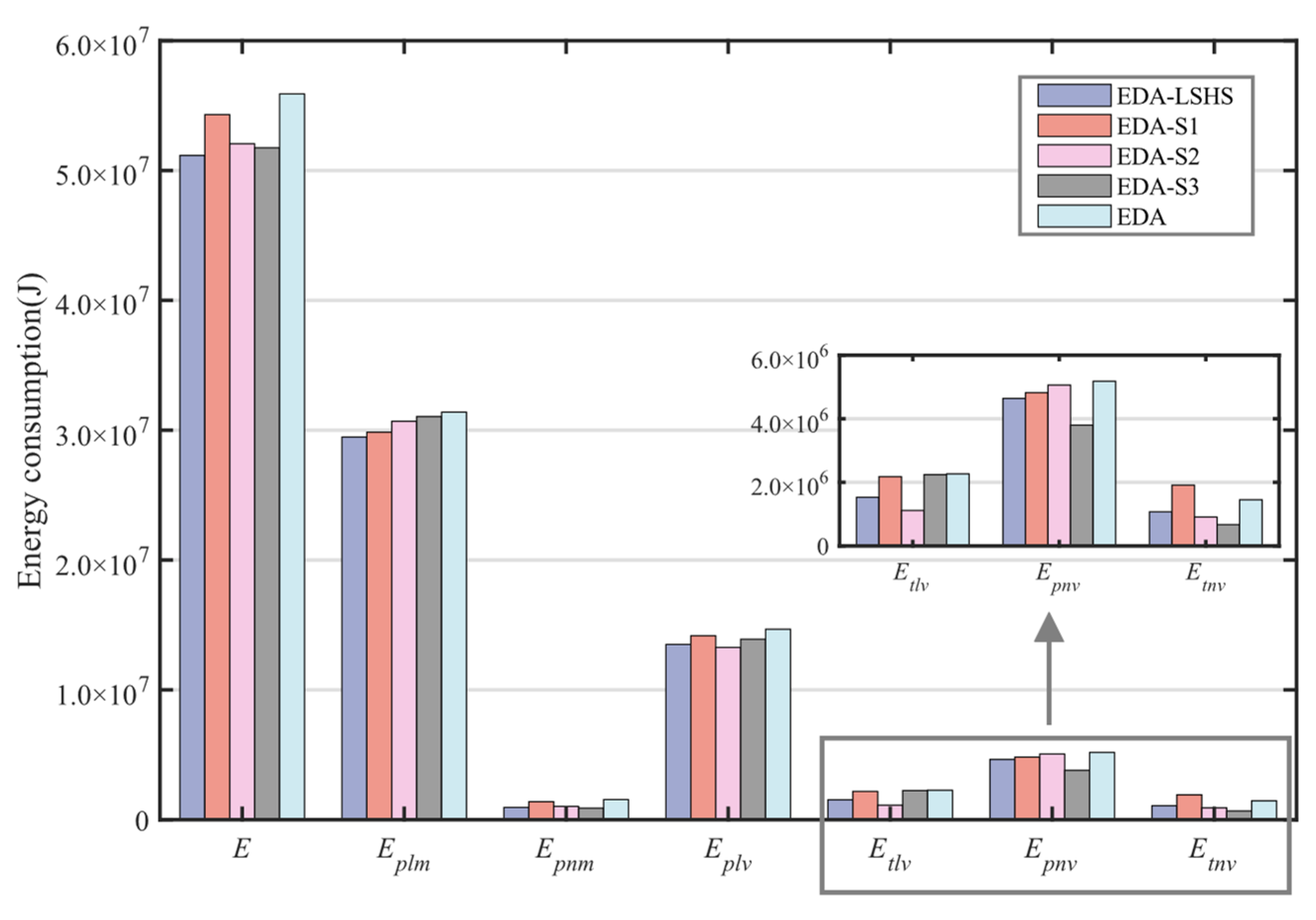
5.3.2. Energy Consumption Analysis

The EDA-LSHS and EDA both have favorable low-carbon scheduling optimization ability, which is proved by the above experiment. Since energy efficiency is a critical factor in low-carbon scheduling optimization, analyzing energy consumption is an effective way to study the above optimization capability of the EDA-LSHS. There are different types of energy consumption during manufacturing operations that have different impacts on low-carbon scheduling. Therefore, it is necessary to further explore the specific optimization effects of the EDA-LSHS on the different types of energy consumption. The EDA-LSHS, the EDA, and the three algorithms based on the sub-strategies of LSHS are adopted for the experiment. These algorithms are defined as follows:

(1)

EDA-LSHS: the estimation of distribution algorithm with the low-carbon scheduling heuristic strategy.

(2)

EDA-S1: the estimation of distribution algorithm with strategy 1, machine processing energy consumption optimization with low-carbon scheduling heuristic strategy.

(3)

EDA-S2: the estimation of distribution algorithm with strategy 2, AGV load state energy consumption optimization with low-carbon scheduling heuristic strategy.

(4)

EDA-S3: the estimation of distribution algorithm with strategy 3, AGV no-load transportation consumption optimization with low-carbon scheduling heuristic strategy.

(5)

EDA: the estimation of distribution algorithm.

Figure 11 shows how the above five algorithms optimize the different types of energy consumption of product 4 during the operation of the machine and the AGV. The optimization effects of the five algorithms for the total energy consumption $E$ are ranked as follows: EDA-LSHS > EDA-S3 > EDA-S2 > EDA-S1 > EDA. Furthermore, these five algorithms have specific characteristics in terms of energy consumption optimization during the operation of the machine and the AGV. First, the EDA-S1 algorithm has a great effect on optimizing machine processing energy consumption $E_{plm}$. However, due to the selection of a lower speed when processing the workpiece, the machine processing time of the workpiece is increased. This can result in large energy consumption in the AGV operation process. Then, the EDA-S2 algorithm has the best optimization effect on AGV load transportation energy consumption $E_{plv}$ and AGV load standby energy consumption $E_{tlv}$ among all algorithms, but it is not ideal in other aspects. Moreover, the EDA-S3 algorithm optimizes AGV no-load transportation energy consumption $E_{pnv}$ better than other algorithms. It is also ideal in the optimization of $E$ and AGV no-load standby energy consumption $E_{tnv}$, but it is not obvious in $E_{plm}$. The EDA is not ideal for the optimization of each energy consumption type. More importantly, the EDA-LSHS has ideal optimization for each type of energy consumption. The EDA-LSHS has the best optimization effect for $E$ and can maintain balanced optimization characteristics. Therefore, the conclusions are summarized as follows:

(1)

The single strategy 1, strategy 2, and strategy 3 in the LSHS have noticeable optimization effects on the energy consumption of machine processing, AGV load state, and AGV no-load transportation process, respectively.

(2)

The EDA-LSHS integrates the advantages of three sub-strategies. It has better optimization effects than the EDA for different types of energy consumption.

6. Discussion

In the investigated heavy cement equipment manufacturing enterprise, the current scheduling mode is manual scheduling by dispatchers. Dispatchers often arrange the next process after the current process is completed based on personal experience. This scheduling mode has many disadvantages. Firstly, the decision-making ability of the scheduler has limitations, resulting in uneven utilization of the machines. Secondly, since each machine can be adjusted to multiple speeds, it is difficult for dispatchers to select an appropriate speed for processing the workpiece. This causes enormous energy waste and a delay in makespan. Thirdly, because the workpieces are transported by multiple AGVs, the dispatcher can only arrange the currently idle AGVs to transport the finished workpieces, ignoring other workpieces waiting to be transported. This reduces transportation efficiency and increases overall energy consumption. This dispatcher mode is widely used in traditional heavy-duty manufacturing enterprises and causes significant energy waste and low efficiency. Therefore, it is necessary to study the gap between the proposed EDA-LSHS and the dispatcher mode.

In the compared experiments between the EDA-LSHS and dispatcher mode, the total energy consumption $E$, AGV operation energy consumption $E_t$, machine operation energy consumption $E_m$, and the makespan $C{T}_{\max }$ are the main research targets. In

Table 3. Results for the EDA-LSHS algorithm and the dispatcher mode.

Product	EDA-LSHS					Dispatcher Mode
	E	Et	Em	CTmax	E	Et	Em	CTmax
1	3.77	1.25	2.53	3.56	6.84	3.27	3.58	10.78
2	4.98	2.01	2.96	4.55	8.40	4.32	4.08	11.87
3	4.72	1.89	2.83	4.57	8.43	4.14	4.27	12.25
4	5.16	2.07	3.09	4.37	9.33	4.63	4.70	13.01

, the experiment results show that EDA-LSHS exceedingly reduces $E$, $E_t$, $E_m$, and $C{T}_{\max }$ compared with the dispatcher mode. Then, ${\mathrm{Gap}}^{\mathrm{E}}$,${\mathrm{Gap}}^{{\mathrm{E}}_{\mathrm{t}}}$,${\mathrm{Gap}}^{{\mathrm{E}}_{\mathrm{m}}}$, and ${\mathrm{Gap}}^{{\mathrm{CT}}_{\max }}$ are calculated with Formulas (57), (58), (59), and (60), respectively, to demonstrate the actual application effect of the EDA-LSHS. The calculation results are shown in Figure 12. In Figure 12, the EDA-LSHS has large gaps in the $E$ and $E_m$ in all four product instances compared with the dispatcher mode. Especially for the $E_t$ and $C{T}_{\max }$ in these four product instances, the EDA-LSHS has great gaps, and the average gaps can be up to 60%. Furthermore,

Table 4. The max gap, average gap, and min gap of four gaps.

$\mathbf{Gap}(\%)$	${\mathbf{Gap}}^{\mathbf{E}}$	${\mathbf{Gap}}^{\mathbf{Et}}$	${\mathbf{Gap}}^{\mathbf{Em}}$	${\mathbf{Gap}}^{{\mathbf{CT}}_{\mathbf{max}}}$
Max gap	44.78	61.60	34.19	66.98
Average gap	43.52	56.12	31.24	64.43
Min gap	40.73	53.27	27.45	61.62

lists the max gap, average gap, and min gap of $E$, $E_t$, $E_m$, and $C{T}_{\max }$ in the four products to further describe the advantage of EDA-LSHS relative to the dispatcher mode. The above results show that the collaborative optimization ability of EDA-LSHS for energy consumption and makespan is significantly better than that of the dispatcher mode.

In summary, the EDA-LSHS effectively improves the disadvantages of the dispatcher mode and promotes the energy efficiency of the investigated heavy cement equipment manufacturing enterprise. More importantly, for a large number of China’s traditional heavy industry manufacturing enterprises, this method can be used as an important reference for improving the level of low-carbon manufacturing:

$${\mathrm{Gap}}^{\mathrm{E}}=\frac{(\mathrm{E}\in \mathrm{Dispatcher}\mathrm{mode})-(\mathrm{E}\in \mathrm{EDA}\text{-}\mathrm{LSHS})}{(\mathrm{E}\in \mathrm{Dispatcher}\mathrm{mode})}\times 100\%$$

(57)

$${\mathrm{Gap}}^{{\mathrm{E}}_{\mathrm{t}}}=\frac{({\mathrm{E}}_{\mathrm{t}}\in \mathrm{Dispatcher}\mathrm{mode})-({\mathrm{E}}_{\mathrm{t}}\in \mathrm{EDA}\text{-}\mathrm{LSHS})}{({\mathrm{E}}_{\mathrm{t}}\in \mathrm{Dispatcher}\mathrm{mode})}\times 100\%$$

(58)

$${\mathrm{Gap}}^{{\mathrm{E}}_{\mathrm{m}}}=\frac{({\mathrm{E}}_{\mathrm{m}}\in \mathrm{Dispatcher}\mathrm{mode})-({\mathrm{E}}_{\mathrm{m}}\in \mathrm{EDA}\text{-}\mathrm{LSHS})}{({\mathrm{E}}_{\mathrm{m}}\in \mathrm{Dispatcher}\mathrm{mode})}\times 100\%$$

(59)

$${\mathrm{Gap}}^{{\mathrm{CT}}_{\max }}=\frac{({\mathrm{CT}}_{\max }\in \mathrm{Dispatcher}\mathrm{mode})-({\mathrm{CT}}_{\max }\in \mathrm{EDA}\text{-}\mathrm{LSHS})}{({\mathrm{CT}}_{\max }\in \mathrm{Dispatcher}\mathrm{mode})}\times 100\%$$

(60)

7. Conclusions

In order to promote the low-carbon and sustainable development of traditional heavy manufacturing enterprises, this paper proposes a novel LCSP-MSFM & MAGVT procedure investigated in a heavy cement equipment manufacturing enterprise. To describe this problem, a MIP model focusing on comprehensive energy consumption and makespan during manufacturing operation is established. In the MIP model, a time-node model is built to describe the completion time per workpiece, and a comprehensive energy consumption model is established to simulate the operation process of the machine and the AGV. Since LCSP-MSFM & MAGVT is an NP-hard problem, the EDA-LSHS is developed to solve the proposed MIP model. Furthermore, a case study is carried out through actual product instances to verify that the EDA-LSHS can obtain better-quality scheduling solutions within a reasonable time range. The proposed method has a wide application background in improving the energy efficiency of manufacturing operations, which provides guiding significance for the low-carbon transformation of China’s traditional heavy industry manufacturing.

As far as the limitations of this paper are concerned, further research prospects are as follows:

(1)

To extend this study to the current major workshop types in manufacturing enterprises.

(2)

To study the impact of co-scheduling between humans and machines.