Development of a Contactless Conductivity Sensor in Flowing Micro Systems for Cerium Nitrate
Abstract
:1. Introduction
2. Basic Theoretical Considerations
3. Materials and Methods
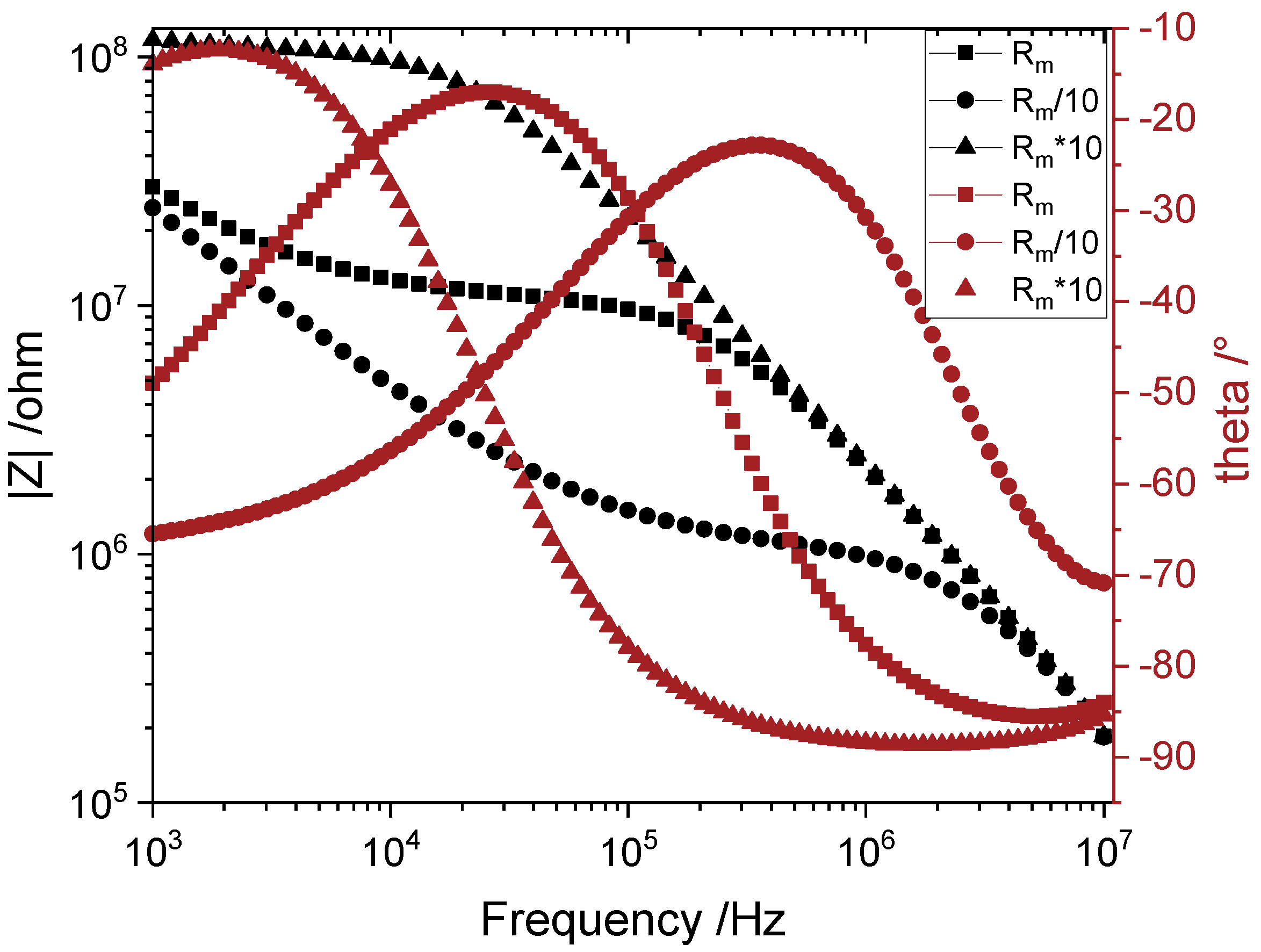
3.1. Principle of Operation
3.2. Fitting Procedure
3.3. Setup and Procedure
4. Results and Discussion
4.1. Fit and Modelling
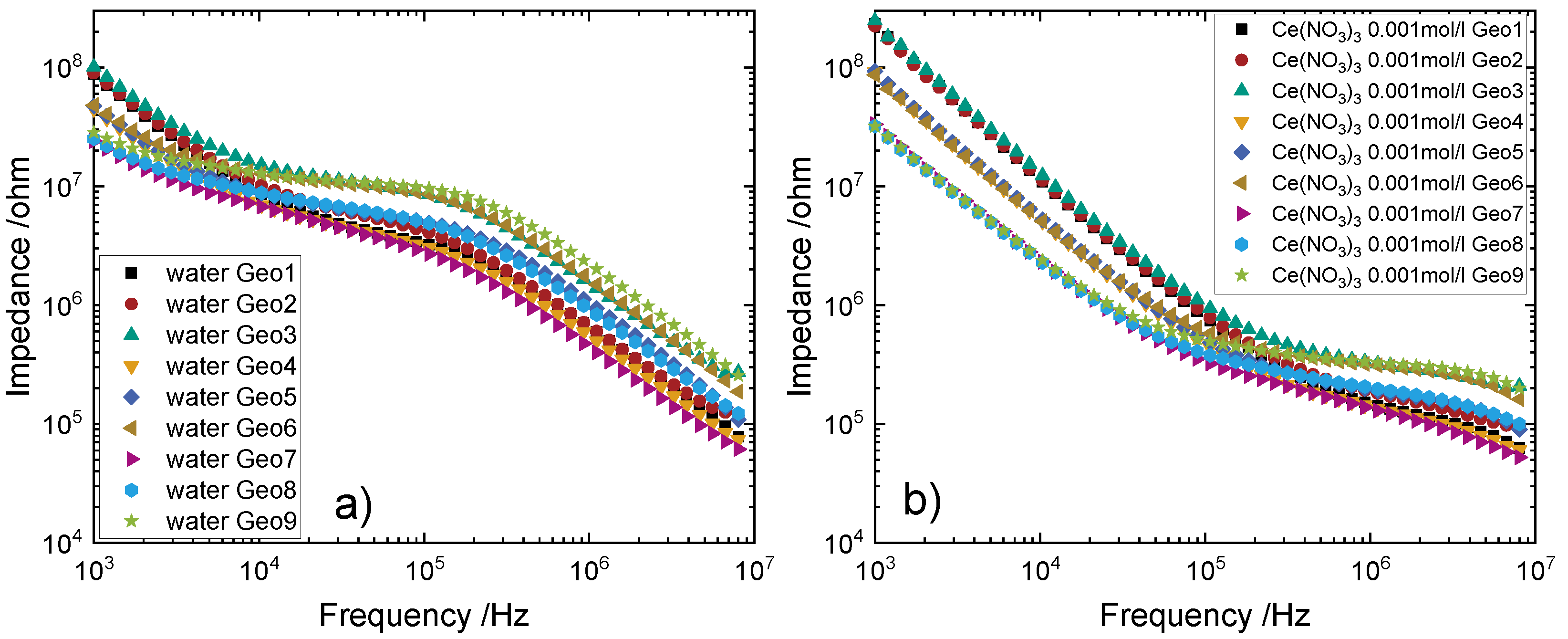
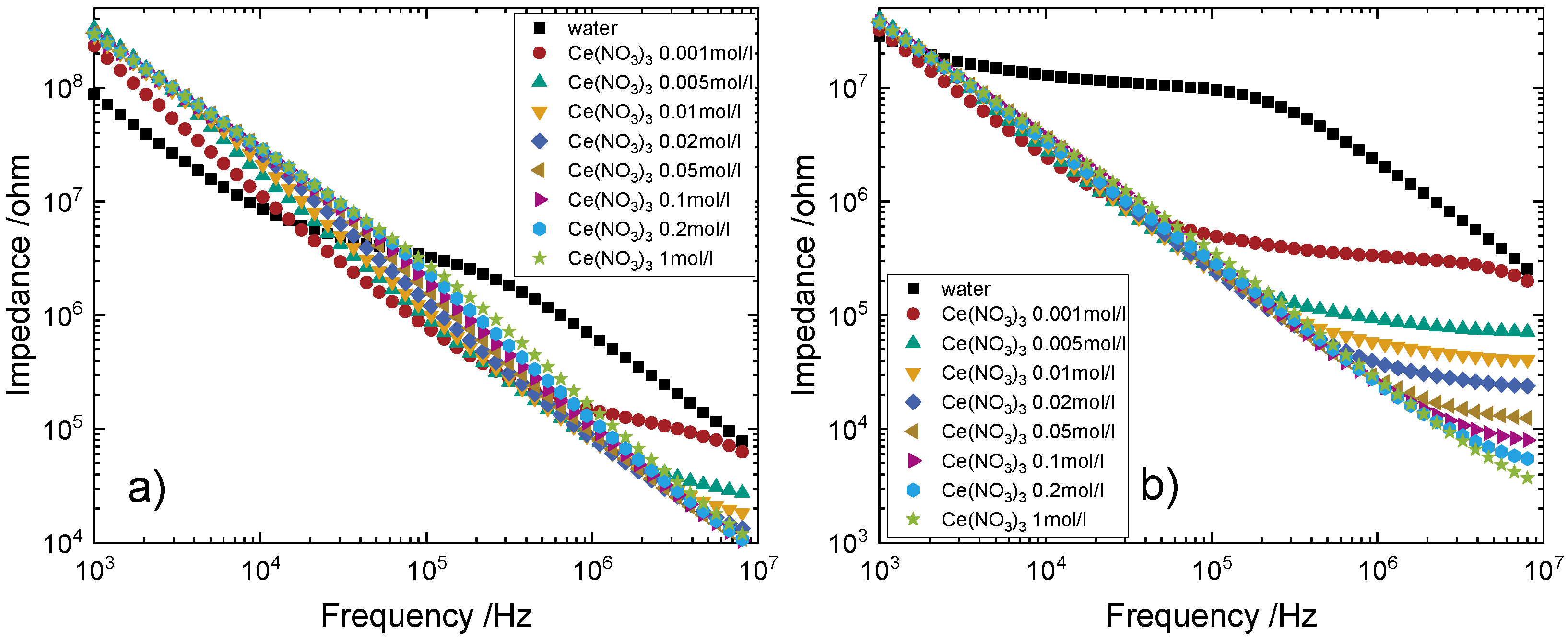
4.2. Measurements with Alumina Tubes as Reactor
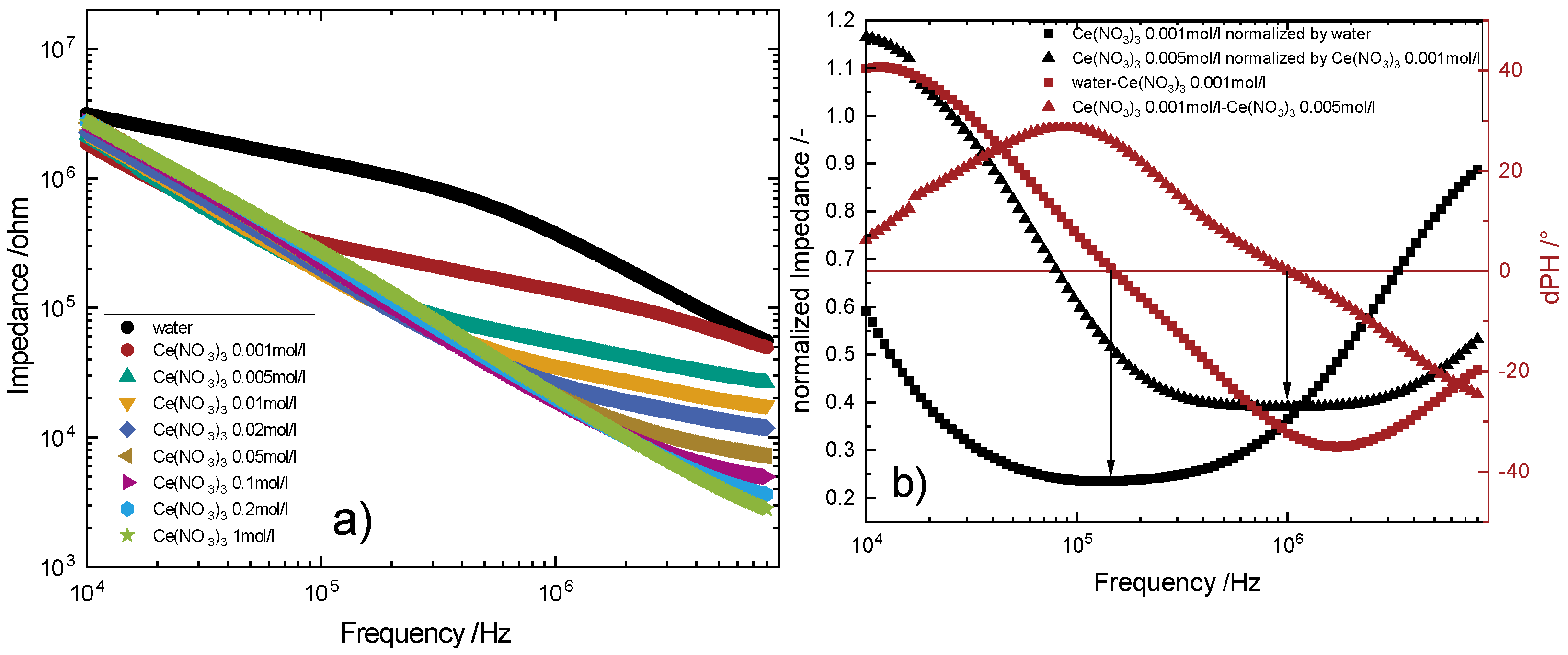
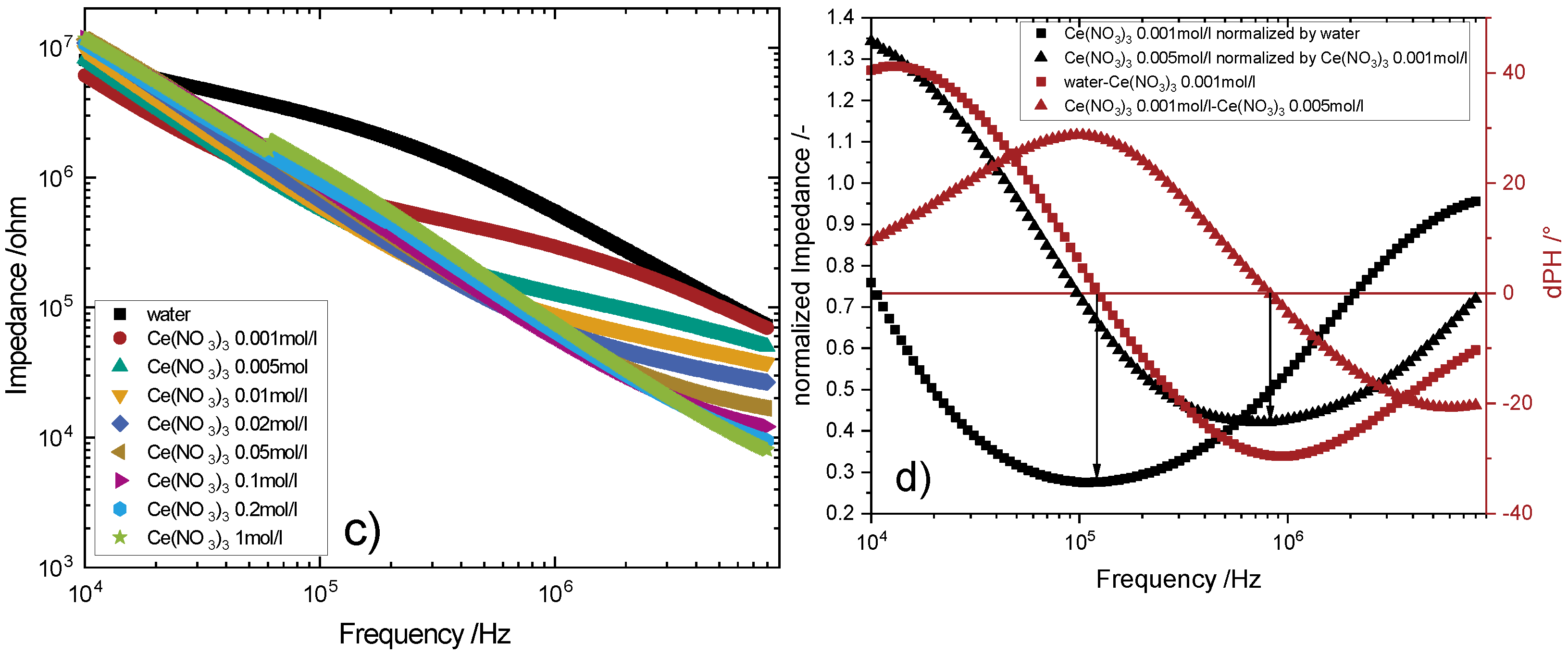
4.2.1. Sweep Measurements
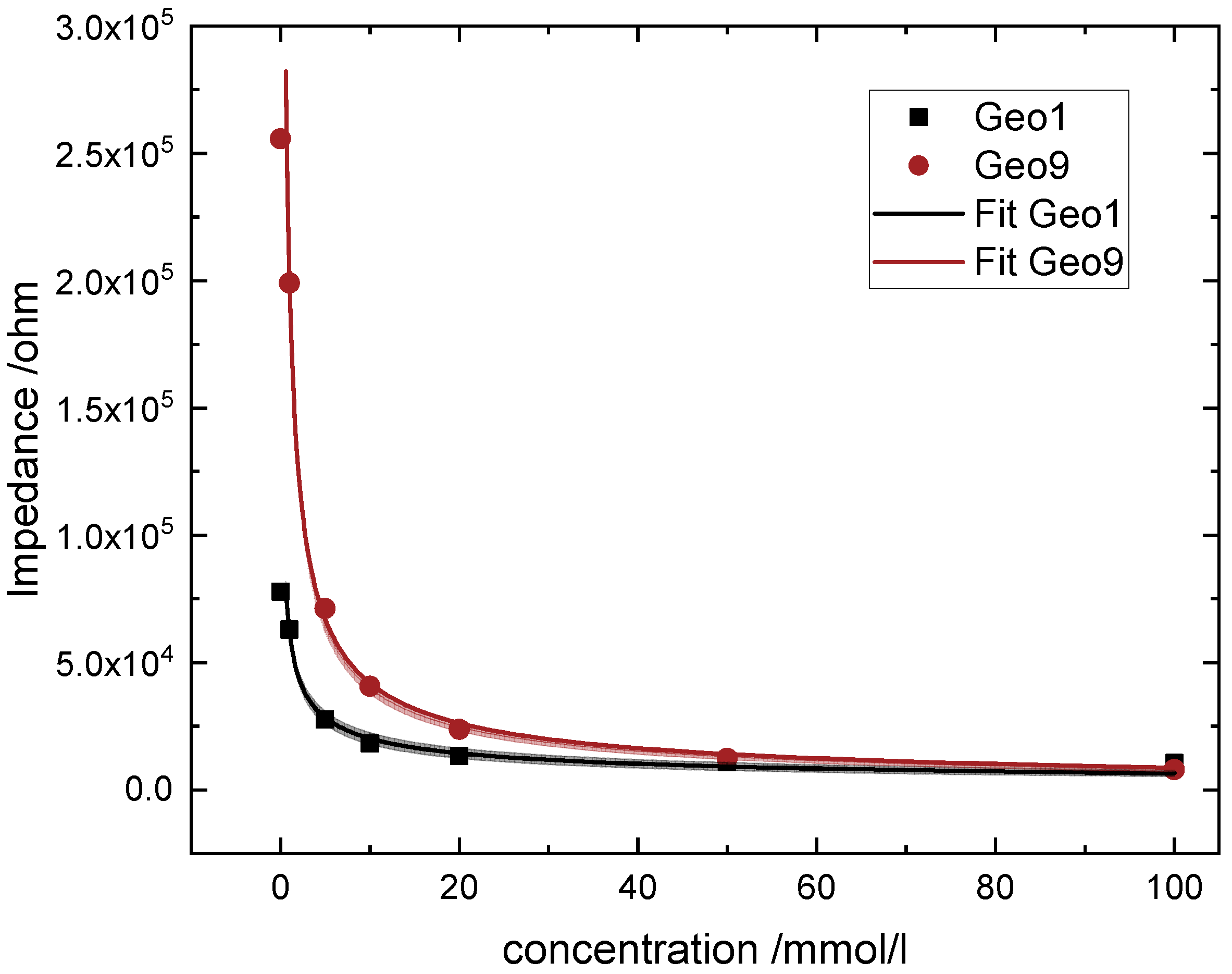
- The larger the electrode width, the more distinguishable is the measurement at lower concentrations for cerium nitrate.
- Higher distances between the electrodes lead to more distinguishable measurements at lower concentrations and till higher concentrations.
4.2.2. Titration Measurements
4.2.3. Ternary Systems
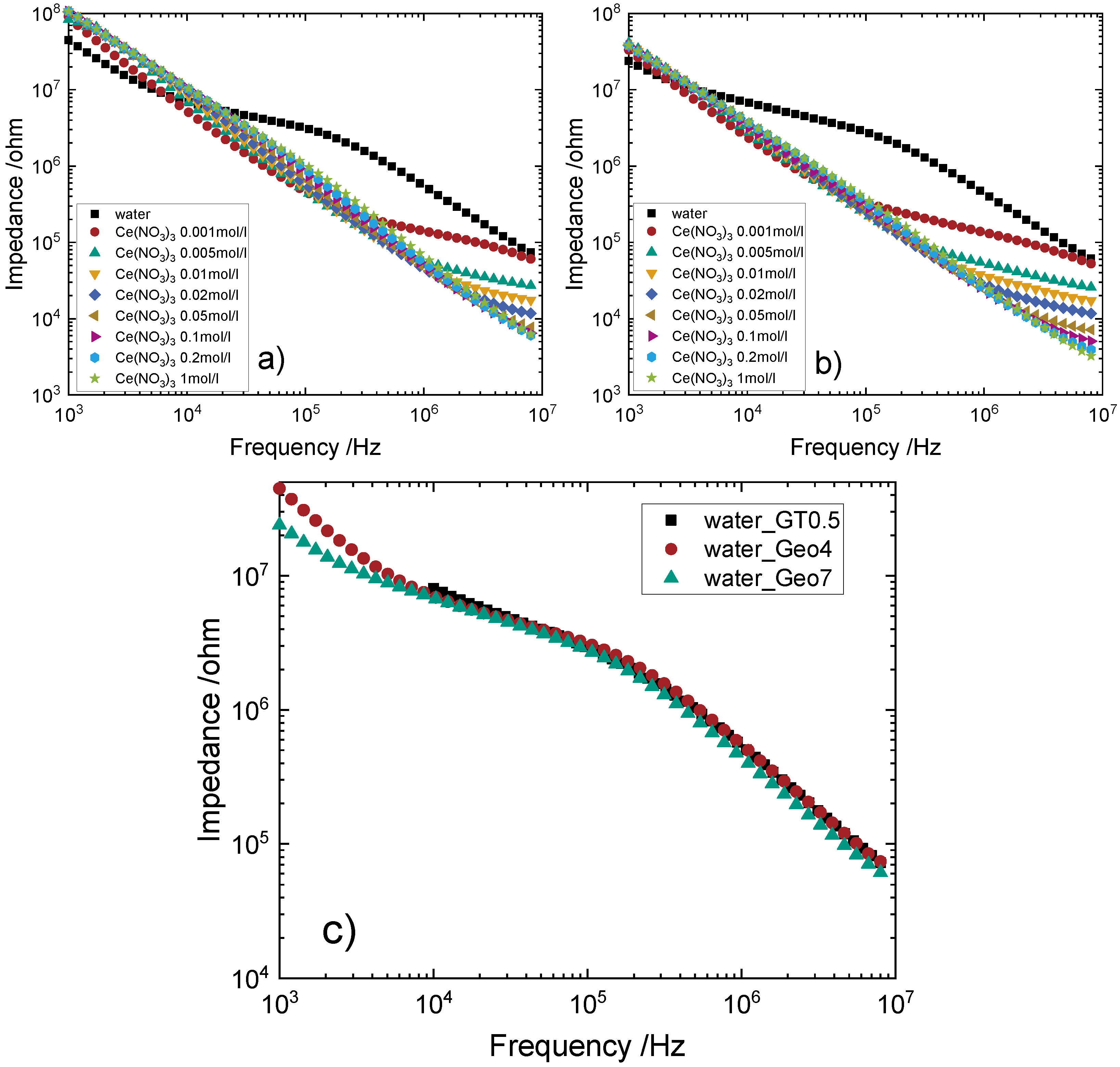
4.3. Measurements with Glass Tubes as Reactor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hall, J.L.; Gibson, J.A. High-Frequency Titration. Anal. Chem. 1951, 23, 966–970. [Google Scholar] [CrossRef]
- Hall, J.L. High-Frequency Titration: Theoretical and Practical Aspects. Anal. Chem. 1952, 24, 1236–1240. [Google Scholar] [CrossRef]
- Zemann, A.J.; Schnell, E.; Volgger, D.; Bonn, G.K. Contactless conductivity detection for capillary electrophoresis. Anal. Chem. 1998, 70, 563–567. [Google Scholar] [CrossRef] [PubMed]
- Kubáň, P.; Hauser, P.C. 20th anniversary of axial capacitively coupled contactless conductivity detection in capillary electrophoresis. TrAC Trends Anal. Chem. 2018, 102, 311–321. [Google Scholar] [CrossRef]
- Kubán, P.; Hauser, P.C. Ten years of axial capacitively coupled contactless conductivity detection for CZE—A review. Electrophoresis 2009, 30, 176–188. [Google Scholar] [CrossRef] [PubMed]
- Kubáň, P.; Hauser, P.C. Contactless Conductivity Detection in Capillary Electrophoresis: A Review. Electroanalysis 2004, 16, 2009–2021. [Google Scholar] [CrossRef]
- Kubán, P.; Hauser, P.C. A review of the recent achievements in capacitively coupled contactless conductivity detection. Anal. Chim. Acta 2008, 607, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Hauser, P.C.; Kubáň, P. Capacitively coupled contactless conductivity detection for analytical techniques—Developments from 2018 to 2020. J. Chromatogr. A 2020, 1632, 461616. [Google Scholar] [CrossRef] [PubMed]
- Cahill, B.P. Optimization of an impedance sensor for droplet-based microfluidic systems. In Smart Sensors, Actuators, and MEMS V; Schmid, U., Sánchez-Rojas, J.L., Leester-Schaedel, M., Eds.; SPIE Proceedings; SPIE: New York, NY, USA, 2011; p. 80660F. [Google Scholar] [CrossRef]
- Tůma, P.; Opekar, F.; Štulík, K. A contactless conductivity detector for capillary electrophoresis: Effects of the detection cell geometry on the detector performance. Electrophoresis 2002, 23, 3718–3724. [Google Scholar] [CrossRef]
- Türk, M. Design metalloxidischer Nanopartikel mittels kontinuierlicher hydrothermaler Synthese. Chem. Ing. Tech. 2018, 90, 436–442. [Google Scholar] [CrossRef]
- Brito-Neto, J.G.A.; Fracassi da Silva, J.A.; Blanes, L.; do Lago, C.L. Understanding Capacitively Coupled Contactless Conductivity Detection in Capillary and Microchip Electrophoresis. Part 2. Peak Shape, Stray Capacitance, Noise, and Actual Electronics. Electroanalysis 2005, 17, 1207–1214. [Google Scholar] [CrossRef]
- Gaš, B.; Zuska, J.; Coufal, P.; van de Goor, T. Optimization of the high-frequency contactless conductivity detector for capillary electrophoresis. Electrophoresis 2002, 23, 3520–3527. [Google Scholar] [CrossRef]
- Opekar, F.; Tůma, P.; Stulík, K. Contactless impedance sensors and their application to flow measurements. Sensors 2013, 13, 2786–2801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novotný, M.; Opekar, F.; Štulík, K. The Effects of the Electrode System Geometry on the Properties of Contactless Conductivity Detectors for Capillary Electrophoresis. Electroanalysis 2005, 17, 1181–1186. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Fracassi da Silva, J.A.; do Lago, C.L. An Oscillometric Detector for Capillary Electrophoresis. Anal. Chem. 1998, 70, 4339–4343. [Google Scholar] [CrossRef]
- Blume, S.O.; Ben-Mrad, R.; Sullivan, P.E. Characterization of coplanar electrode structures for microfluidic-based impedance spectroscopy. Sens. Actuators B Chem. 2015, 218, 261–270. [Google Scholar] [CrossRef]
- Tanyanyiwa, J.; Hauser, P.C. High-voltage capacitively coupled contactless conductivity detection for microchip capillary electrophoresis. Anal. Chem. 2002, 74, 6378–6382. [Google Scholar] [CrossRef] [PubMed]
- Mark, J.J.P.; Coufal, P.; Opekar, F.; Matysik, F.M. Comparison of the performance characteristics of two tubular contactless conductivity detectors with different dimensions and application in conjunction with HPLC. Anal. Bioanal. Chem. 2011, 401, 1669–1676. [Google Scholar] [CrossRef] [PubMed]
- Schüßler, C.; Zürn, M.; Hanemann, T.; Türk, M. Überwachung der kontinuierlichen hydrothermalen Synthese mittels Impedanzspektroskopie. Chem. Ing. Tech. 2021, 38, 242. [Google Scholar] [CrossRef]




| solution number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| concentration /mol/L | 0 | 0.001 | 0.005 | 0.01 | 0.02 | 0.05 | 0.1 | 0.2 | 1 |
| abs. error /mmol/L | 0 | 0.0013 | 0.063 | 0.13 | 0.25 | 0.61 | 1.12 | 2.24 | 5.10 |
| rel. error ± /% | 0 | 0.13 | 1.26 | 1.26 | 1.25 | 1.23 | 1.19 | 1.12 | 0.51 |
| Designation | Tube-Material | Electrode -Material | Distance /mm | Width /mm | L /mm |
|---|---|---|---|---|---|
| Geo1 | alumina | aluminum | 5 | 5 | 15 |
| Geo2 | alumina | aluminum | 10 | 5 | 20 |
| Geo3 | alumina | aluminum | 20 | 5 | 30 |
| Geo4 | alumina | aluminum | 5 | 10 | 25 |
| Geo5 | alumina | aluminum | 10 | 10 | 30 |
| Geo6 | alumina | aluminum | 20 | 10 | 40 |
| Geo7 | alumina | aluminum | 5 | 20 | 45 |
| Geo8 | alumina | aluminum | 10 | 20 | 50 |
| Geo9 | alumina | aluminum | 20 | 20 | 60 |
| Geo10 | alumina | aluminum | 10 | 15 | 40 |
| GT0.2 | glass | aluminum | 5 | 20 | 45 |
| GT0.5 | glass | aluminum | 5 | 20 | 45 |
| Titration Step | Titration Volume /mL | Concentration /mol/L | Abs. Concentration /mol/L | Rel. Error ± /% |
|---|---|---|---|---|
| 0 | 5 | 0 | 0 | 0 |
| 1 | 1 | 0.02 | 0.00333 | 1.48 |
| 2 | 1 | 0.04 | 0.00857 | 1.49 |
| 3 | 1 | 0.04 | 0.0125 | 1.58 |
| 4 | 1 | 0.04 | 0.0156 | 1.66 |
| 5 | 1 | 0.06 | 0.02 | 1.70 |
| 6 | 1 | 0.06 | 0.0236 | 1.75 |
| 7 | 1 | 0.06 | 0.0267 | 1.81 |
| 8 | 1 | 0.06 | 0.0292 | 1.86 |
| 9 | 1 | 0.1 | 0.0343 | 1.87 |
| 10 | 1 | 0.1 | 0.0387 | 1.89 |
| 11 | 1 | 0.1 | 0.0425 | 1.92 |
| 12 | 1 | 0.1 | 0.0459 | 1.94 |
| 13 | 1 | 0.2 | 0.0544 | 1.90 |
| 14 | 1 | 0.2 | 0.0621 | 1.88 |
| 15 | 1 | 0.2 | 0.069 | 1.87 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Label | Equation | a | b | R |
|---|---|---|---|---|
| Geo1 | 62,231.2 ± 2400 | −0.488 ± 0.031 | 0.988 | |
| Geo9 | 199,725.9 ± 2598.7 | −0.678 ± 0.016 | 0.998 |
| Concentration /mol/L | Rel. Error Concentration/% | Rel. Error Impedance/% | Rel. Error Solution/% |
|---|---|---|---|
| 0 | 0 | 2.4 | 0 |
| 0.02 | 0 | 1.5 | 1.7 |
| 0.04 | 3.4 | 2.3 | 1.9 |
| 0.06 | 4.7 | 0.8 | 1.9 |
| 0.08 | 3.4 | 1.3 | 1.9 |
| 0.2 | 0.6 | 4.0 | 1.3 |
| Concentration /mol/L | Rel. Error Concentration/% | Rel. Error Impedance/% | Rel. Error Solution/% |
|---|---|---|---|
| 0 | 0 | 0.3 | 0 |
| 0.02 | 0 | 15.2 | 1.7 |
| 0.04 | 3.4 | 13.4 | 1.9 |
| 0.06 | 5.4 | 5.5 | 1.9 |
| 0.08 | 3.4 | 6.9 | 1.9 |
| 0.1 | 2.8 | 7.6 | 1.6 |
| 0.2 | 1.8 | 7.9 | 1.3 |
| 0.5 | 0.2 | 7.3 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zürn, M.; Hanemann, T. Development of a Contactless Conductivity Sensor in Flowing Micro Systems for Cerium Nitrate. Processes 2022, 10, 2075. https://doi.org/10.3390/pr10102075
Zürn M, Hanemann T. Development of a Contactless Conductivity Sensor in Flowing Micro Systems for Cerium Nitrate. Processes. 2022; 10(10):2075. https://doi.org/10.3390/pr10102075
Chicago/Turabian StyleZürn, Martin, and Thomas Hanemann. 2022. "Development of a Contactless Conductivity Sensor in Flowing Micro Systems for Cerium Nitrate" Processes 10, no. 10: 2075. https://doi.org/10.3390/pr10102075






