Where Reinforcement Learning Meets Process Control: Review and Guidelines
Abstract
:1. Introduction
2. Reinforcement Learning
- (1)
- Definition of the term from animal psychology;
- (2)
- Analysis for optimal control theory and machine learning;
- (3)
- Evolution of training procedures and pattern recognition;
- (4)
- Development of DNN, powerful hardware, data availability and more stable algorithms.
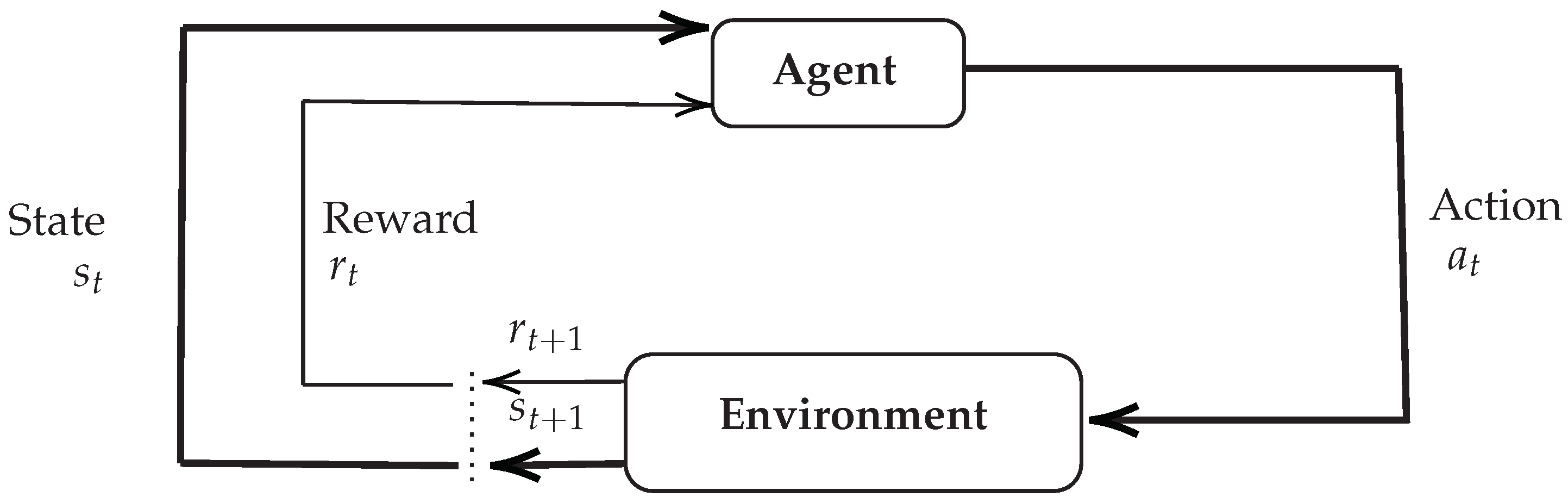
2.1. Basics of RL
2.2. Mathematical Background
2.2.1. Definition
2.2.2. Optimization Objective
2.2.3. Algorithms
2.3. Deep Reinforcement Learning
- Using elements of the mathematical theory of communication in terms of encoding information based on entropy [47];
- Updating DNNs to operate on different dynamic forms of the data distribution in space and time [25];
- Updating gradient descent (GD) and backpropagation algorithms;
- Advances in parallel and distributed computing;
- Open-source software (e.g., Python code).
2.3.1. Deep Q-Learning
- Controlling the exploratory component of the critic model used by the agent (e.g., softmax or -greedy [46])) will contribute to adequately exploring enough transitions of state, avoiding obtaining sub-optimal policies;
- Using experience replay to reduce the effect of temporal correlations between transitions uniformly sampled at random from the buffer, which allows estimating with important dynamic information [10];
- Updating from the target value with delayed (or filtered) copies of the original DNN (i.e., ) [48].
2.3.2. Deep Policy Gradient
2.3.3. Deep Actor–Critic
2.3.4. State-of-the-Art Algorithms
- Deterministic policy gradient (DPG) (i.e., actor–critic and off-policy). According to Silver et al. [48], this is an adaptation to the policy-gradient and Q-learning algorithms, since the stochastic component intrinsic to the policy-gradient algorithms () has a parameterized function in the form of , while depending on the computation of gradients to approximate the optimal values of and , which is guaranteed according to the deterministic-policy-gradient theorem, as shown in Equation (32):
- Deep deterministic policy gradient (DDPG) (i.e., actor–critic and off-policy) [58]. This is an updated version of the DPG algorithm regarding the use of DNN, replay buffer, target networks and batch normalization, in addition to the possibility of handling the exploration problem independent of the learning algorithm used;
- Proximal policy optimization (PPO) [59]. Contrary to the algorithms above (i.e., off-policy), PPO is an algorithm that learns while interacting with the environment over different episodes (i.e., on-policy). Methodologically, this property comes from another similar algorithm considered more complex (trust region policy optimization (TRPO)), addressing the Kullback–Leibler (KL) divergence effect and surrogate objective functions;
- Soft actor–critic (SAC) (i.e., actor–critic and off-policy) [56]. This algorithm is composed of an actor and a critic, and includes a smooth value function, which is responsible for stabilizing the training of the actor and the critic. In addition, it also has similar properties to the DDPG algorithm; however, it adds an entropy value to compose the buffer.
3. Reinforcement Learning for Process Control
3.1. Defining Elements of RL
3.2. Batch Process
- Modeling: processes in batches normally exhibit nonlinear dynamics;
- Measurements: these are typically only available at the end of the batch;
- Uncertainty: present in practically all batch processes, whether resulting from reactant quality, modeling errors, process disturbances and measurement errors;
- Constraints: there is usually the added effect of terminal constraints and the existing security and operational constraints.
3.3. Continuous Process
3.4. Policy Deployment with Transfer Learning
3.5. Conclusions about RL for Process Control
4. Challenges for the Implementation of RL to Process Control
- The MDP design based on the process dynamics;
- The offline training step;
- Policy transfer to the process line;
- Keeping the policy stable against new process changes.
4.1. Overview
- The choice of the algorithm;
- The exploration–exploitation trade-off dilemma;
- Hyperparameter optimization.
4.2. Proposed Learning Structure
5. MDP Design and Agent Training through Imitation Learning
5.1. Imitation Learning Techniques
- Exploration that is outside the scope of the algorithm (Module (2));
- Learning a policy that does something different from the pattern of behavior observed in the dataset E (Module (2));
- Scaling up to complex high-dimensional function approximators, such as DNN, high-dimensional state or observation spaces and temporally extended tasks.
DDPG Algorithm with Adversarial Imitation Learning
5.2. Hyperparameter Optimization
5.2.1. Hyperparameter Optimization Software
- Open-source software (i.e., Python).
- Sequential optimization relies on multiple runs of such a cycle (trials) to obtain credible information about how the parameters influence the value of the cost function. The Bayesian-optimization algorithms use an approximate model for the unknown cost function a priori, being Gaussian processes that maximize expectancy of the cost function concerning the current best solution (e.g., the expected improvement algorithms, such as the tree-structured Parzen estimator (TPE)) [95,96];
- Parallel optimization algorithms are complementary alternatives to sequential algorithms, as they update the information of hyperparameter values based on distributed executions, in contrast to the single-cycle approach used in sequential optimization.
5.3. An Offline RL Control Experiment
- The algorithm is specific to MDP where the sampled state–action pairs are continuous;
- The simplicity of the algorithm, which makes writing the source code easier, the proposed updates to the algorithm (e.g., prioritized buffer replay, inverting gradient) and distributed optimization;
- The algorithm combines RL and adversarial imitation learning to learn from demonstrations.
5.3.1. Case Study: Batch Process
5.3.2. Tree-Structured Parzen Estimator
- It is computationally efficient compared to standard approaches;
- Hyperparameters can belong to any set: integer, ordinal, real (i.e., float) and categorical.
- It optimizes the expected improvement with a Gaussian process and Parzen estimator;
- The default algorithm implemented in Optuna offers an alternative to overcome its main disadvantage, that is, it also models the interactions between hyperparameters, which improves the efficiency and robustness of the algorithm.
5.3.3. Validation of the Control Experiment
6. Conclusions
- State-of-the-art technologies are still embryonic;
- Batch and continuous processes require different learning structures;
- Developing state-of-the-art offline training technologies is essential;
- Transfer learning has a broad meaning in RL, since it can encompass learning from demonstration, reward shaping, policy transfer and inter-task mapping;
- The proposed modified DDPG algorithm with an off-policy discriminator confirmed the hypothesis that information from process demonstrations improves the performance of the standard DDPG algorithm, as detailed in Section 5.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; Volume 95. [Google Scholar]
- Bellman, R. A Markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Hoskins, J.; Himmelblau, D. Process control via artificial neural networks and reinforcement learning. Comput. Chem. Eng. 1992, 16, 241–251. [Google Scholar] [CrossRef]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited On 2012, 14, 2. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Wulfmeier, M.; Posner, I.; Abbeel, P. Mutual alignment transfer learning. In Proceedings of the Conference on Robot Learning (PMLR), Mountain View, CA, USA, 13–15 November 2017; pp. 281–290. [Google Scholar]
- Peng, X.B.; Andrychowicz, M.; Zaremba, W.; Abbeel, P. Sim-to-real transfer of robotic control with dynamics randomization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 3803–3810. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [Green Version]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J.; Choi, D.H.; Powell, R.; Ewalds, T.; Georgiev, P.; et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.; Huang, B. A review on reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Buşoniu, L.; de Bruin, T.; Tolić, D.; Kober, J.; Palunko, I. Reinforcement learning for control: Performance, stability, and deep approximators. Annu. Rev. Control 2018, 46, 8–28. [Google Scholar] [CrossRef]
- Petsagkourakis, P.; Sandoval, I.O.; Bradford, E.; Zhang, D.; del Rio-Chanona, E.A. Reinforcement learning for batch bioprocess optimization. Comput. Chem. Eng. 2020, 133, 106649. [Google Scholar] [CrossRef] [Green Version]
- Petsagkourakis, P.; Sandoval, I.O.; Bradford, E.; Zhang, D.; del Rio-Chanona, E.A. Reinforcement learning for batch-to-batch bioprocess optimisation. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 919–924. [Google Scholar]
- Yoo, H.; Kim, B.; Kim, J.W.; Lee, J.H. Reinforcement learning based optimal control of batch processes using Monte-Carlo deep deterministic policy gradient with phase segmentation. Comput. Chem. Eng. 2021, 144, 107133. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, W.; Benton, M.G.; Romagnoli, J. Continuous control of a polymerization system with deep reinforcement learning. J. Process Control 2019, 75, 40–47. [Google Scholar] [CrossRef]
- Powell, K.M.; Machalek, D.; Quah, T. Real-time optimization using reinforcement learning. Comput. Chem. Eng. 2020, 143, 107077. [Google Scholar] [CrossRef]
- Nikita, S.; Tiwari, A.; Sonawat, D.; Kodamana, H.; Rathore, A.S. Reinforcement learning based optimization of process chromatography for continuous processing of biopharmaceuticals. Chem. Eng. Sci. 2021, 230, 116171. [Google Scholar] [CrossRef]
- Dogru, O.; Wieczorek, N.; Velswamy, K.; Ibrahim, F.; Huang, B. Online reinforcement learning for a continuous space system with experimental validation. J. Process Control 2021, 104, 86–100. [Google Scholar] [CrossRef]
- awryńczuk, M.; Marusak, P.M.; Tatjewski, P. Cooperation of model predictive control with steady-state economic optimisation. Control Cybern. 2008, 37, 133–158. [Google Scholar]
- Skogestad, S. Control structure design for complete chemical plants. Comput. Chem. Eng. 2004, 28, 219–234. [Google Scholar] [CrossRef]
- Backx, T.; Bosgra, O.; Marquardt, W. Integration of model predictive control and optimization of processes: Enabling technology for market driven process operation. IFAC Proc. Vol. 2000, 33, 249–260. [Google Scholar] [CrossRef]
- Adetola, V.; Guay, M. Integration of real-time optimization and model predictive control. J. Process Control 2010, 20, 125–133. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018; Volume 10, pp. 978–983. [Google Scholar]
- Pan, E.; Petsagkourakis, P.; Mowbray, M.; Zhang, D.; del Rio-Chanona, E.A. Constrained model-free reinforcement learning for process optimization. Comput. Chem. Eng. 2021, 154, 107462. [Google Scholar] [CrossRef]
- Mowbray, M.; Smith, R.; Del Rio-Chanona, E.A.; Zhang, D. Using process data to generate an optimal control policy via apprenticeship and reinforcement learning. AIChE J. 2021, 67, e17306. [Google Scholar] [CrossRef]
- Shah, H.; Gopal, M. Model-free predictive control of nonlinear processes based on reinforcement learning. IFAC-PapersOnLine 2016, 49, 89–94. [Google Scholar] [CrossRef]
- Alhazmi, K.; Albalawi, F.; Sarathy, S.M. A reinforcement learning-based economic model predictive control framework for autonomous operation of chemical reactors. Chem. Eng. J. 2022, 428, 130993. [Google Scholar] [CrossRef]
- Kim, J.W.; Park, B.J.; Yoo, H.; Oh, T.H.; Lee, J.H.; Lee, J.M. A model-based deep reinforcement learning method applied to finite-horizon optimal control of nonlinear control-affine system. J. Process Control 2020, 87, 166–178. [Google Scholar] [CrossRef]
- Badgwell, T.A.; Lee, J.H.; Liu, K.H. Reinforcement learning–overview of recent progress and implications for process control. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2018; Volume 44, pp. 71–85. [Google Scholar]
- Görges, D. Relations between model predictive control and reinforcement learning. IFAC-PapersOnLine 2017, 50, 4920–4928. [Google Scholar] [CrossRef]
- Sugiyama, M. Statistical Reinforcement Learning: Modern Machine Learning Approaches; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Howard, R.A. Dynamic Programming and Markov Processes; MITPL: Cambridge, MA, USA, 1960. [Google Scholar]
- Thorndike, E.L. Animal intelligence: An experimental study of the associative processes in animals. Psychol. Rev. Monogr. Suppl. 1898, 2, 1. [Google Scholar]
- Minsky, M. Neural Nets and the Brain-Model Problem. Ph.D. Dissertation, Princeton University, Princeton, NJ, USA, 1954. Unpublished. [Google Scholar]
- Minsky, M. Steps toward artificial intelligence. Proc. IRE 1961, 49, 8–30. [Google Scholar] [CrossRef]
- Barto, A.G.; Sutton, R.S.; Anderson, C.W. Neuronlike adaptive elements that can solve difficult learning control problems. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 834–846. [Google Scholar] [CrossRef]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H. Learning from Delayed Rewards; University of Cambridge: Cambridge, UK, 1989. [Google Scholar]
- Gullapalli, V. A stochastic reinforcement learning algorithm for learning real-valued functions. Neural Netw. 1990, 3, 671–692. [Google Scholar] [CrossRef]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Berry, D.A.; Fristedt, B. Bandit Problems: Sequential Allocation of Experiments (Monographs on Statistics and Applied Probability); Chapman and Hall: London, UK, 1985; Volume 5, pp. 71–87. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; MIT Press Cambridge: Cambridge, MA, USA, 1998; Volume 135. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef] [Green Version]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning (PMLR), Bejing, China, 22–24 June 2014. [Google Scholar]
- Thrun, S.; Schwartz, A. Issues in using function approximation for reinforcement learning. In Proceedings of the 1993 Connectionist Models Summer School; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar]
- Fujimoto, S.; Van Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. arXiv 2018, arXiv:1802.09477. [Google Scholar]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 29 November–4 December 2000; pp. 1057–1063. [Google Scholar]
- Gordon, G.J. Stable function approximation in dynamic programming. In Machine Learning Proceedings 1995; Elsevier: Amsterdam, The Netherlands, 1995; pp. 261–268. [Google Scholar]
- Tsitsiklis, J.N.; Van Roy, B. Feature-based methods for large scale dynamic programming. Mach. Learn. 1996, 22, 59–94. [Google Scholar] [CrossRef]
- Grondman, I.; Busoniu, L.; Lopes, G.A.; Babuska, R. A survey of actor-critic reinforcement learning: Standard and natural policy gradients. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 1291–1307. [Google Scholar] [CrossRef] [Green Version]
- Ramicic, M.; Bonarini, A. Augmented Replay Memory in Reinforcement Learning With Continuous Control. arXiv 2019, arXiv:1912.12719. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning (PMLR), Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Benhamou, E. Variance Reduction in Actor Critic Methods (ACM). arXiv 2019, arXiv:1907.09765. [Google Scholar] [CrossRef] [Green Version]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Cassandra, A.R. Planning and acting in partially observable stochastic domains. Artif. Intell. 1998, 101, 99–134. [Google Scholar] [CrossRef] [Green Version]
- Bonvin, D. Optimal operation of batch reactors—A personal view. J. Process Control 1998, 8, 355–368. [Google Scholar] [CrossRef]
- Bonvin, D.; Srinivasan, B.; Ruppen, D. Dynamic Optimization in the Batch Chemical Industry; Technical Report; NTNU: Trondheim, Norway, 2001. [Google Scholar]
- Arpornwichanop, A.; Kittisupakorn, P.; Mujtaba, I. On-line dynamic optimization and control strategy for improving the performance of batch reactors. Chem. Eng. Process. Process. Intensif. 2005, 44, 101–114. [Google Scholar] [CrossRef]
- Mowbray, M.; Petsagkourakis, P.; Chanona, E.A.d.R.; Smith, R.; Zhang, D. Safe Chance Constrained Reinforcement Learning for Batch Process Control. arXiv 2021, arXiv:2104.11706. [Google Scholar]
- Oh, T.H.; Park, H.M.; Kim, J.W.; Lee, J.M. Integration of reinforcement learning and model predictive control to optimize semi-batch bioreactor. AIChE J. 2022, 68, e17658. [Google Scholar] [CrossRef]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Ramanathan, P.; Mangla, K.K.; Satpathy, S. Smart controller for conical tank system using reinforcement learning algorithm. Measurement 2018, 116, 422–428. [Google Scholar] [CrossRef]
- Hwangbo, S.; Sin, G. Design of control framework based on deep reinforcement learning and Monte-Carlo sampling in downstream separation. Comput. Chem. Eng. 2020, 140, 106910. [Google Scholar] [CrossRef]
- Chen, K.; Wang, H.; Valverde-Pérez, B.; Zhai, S.; Vezzaro, L.; Wang, A. Optimal control towards sustainable wastewater treatment plants based on multi-agent reinforcement learning. Chemosphere 2021, 279, 130498. [Google Scholar] [CrossRef]
- Oh, D.H.; Adams, D.; Vo, N.D.; Gbadago, D.Q.; Lee, C.H.; Oh, M. Actor-critic reinforcement learning to estimate the optimal operating conditions of the hydrocracking process. Comput. Chem. Eng. 2021, 149, 107280. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Tan, C.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A survey on deep transfer learning. In Proceedings of the International Conference on Artificial Neural Networks, Rhodes, Greece, 4–7 October 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 270–279. [Google Scholar]
- Taylor, M.E.; Stone, P. Transfer learning for reinforcement learning domains: A survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Peirelinck, T.; Kazmi, H.; Mbuwir, B.V.; Hermans, C.; Spiessens, F.; Suykens, J.; Deconinck, G. Transfer learning in demand response: A review of algorithms for data-efficient modelling and control. Energy AI 2022, 7, 100126. [Google Scholar] [CrossRef]
- Joshi, G.; Chowdhary, G. Cross-domain transfer in reinforcement learning using target apprentice. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7525–7532. [Google Scholar]
- Zhu, Z.; Lin, K.; Dai, B.; Zhou, J. Learning sparse rewarded tasks from sub-optimal demonstrations. arXiv 2020, arXiv:2004.00530. [Google Scholar]
- Yan, M.; Frosio, I.; Tyree, S.; Kautz, J. Sim-to-real transfer of accurate grasping with eye-in-hand observations and continuous control. arXiv 2017, arXiv:1712.03303. [Google Scholar]
- Christiano, P.; Shah, Z.; Mordatch, I.; Schneider, J.; Blackwell, T.; Tobin, J.; Abbeel, P.; Zaremba, W. Transfer from simulation to real world through learning deep inverse dynamics model. arXiv 2016, arXiv:1610.03518. [Google Scholar]
- Kostrikov, I.; Agrawal, K.K.; Dwibedi, D.; Levine, S.; Tompson, J. Discriminator-actor-critic: Addressing sample inefficiency and reward bias in adversarial imitation learning. arXiv 2018, arXiv:1809.02925. [Google Scholar]
- Spielberg, S.; Tulsyan, A.; Lawrence, N.P.; Loewen, P.D.; Bhushan Gopaluni, R. Toward self-driving processes: A deep reinforcement learning approach to control. AIChE J. 2019, 65, e16689. [Google Scholar] [CrossRef] [Green Version]
- Hausknecht, M.; Stone, P. Deep reinforcement learning in parameterized action space. arXiv 2015, arXiv:1511.04143. [Google Scholar]
- Hou, Y.; Liu, L.; Wei, Q.; Xu, X.; Chen, C. A novel ddpg method with prioritized experience replay. In Proceedings of the 2017 IEEE international conference on systems, man, and cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 316–321. [Google Scholar]
- Wang, X.; Ye, X. Consciousness-driven reinforcement learning: An online learning control framework. Int. J. Intell. Syst. 2022, 37, 770–798. [Google Scholar] [CrossRef]
- Feise, H.J.; Schaer, E. Mastering digitized chemical engineering. Educ. Chem. Eng. 2021, 34, 78–86. [Google Scholar] [CrossRef]
- Hua, J.; Zeng, L.; Li, G.; Ju, Z. Learning for a robot: Deep reinforcement learning, imitation learning, transfer learning. Sensors 2021, 21, 1278. [Google Scholar] [CrossRef]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. (CSUR) 2017, 50, 1–35. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K.; Stützle, T. ParamILS: An automatic algorithm configuration framework. J. Artif. Intell. Res. 2009, 36, 267–306. [Google Scholar] [CrossRef]
- Hutter, F. Automated Configuration of Algorithms for Solving Hard Computational Problems. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2009. [Google Scholar]
- Coates, A.; Ng, A.Y. The importance of encoding versus training with sparse coding and vector quantization. In Proceedings of the 28th International Conference on Machine Learning (ICML), Washington, DC, USA, 28 June–2 July 2011. [Google Scholar]
- Coates, A.; Ng, A.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Rapin, J.; Teytaud, O. Nevergrad—A Gradient-Free Optimization Platform. 2018. Available online: https://GitHub.com/FacebookResearch/Nevergrad (accessed on 10 September 2022).
- Liaw, R.; Liang, E.; Nishihara, R.; Moritz, P.; Gonzalez, J.E.; Stoica, I. Tune: A Research Platform for Distributed Model Selection and Training. arXiv 2018, arXiv:1807.05118. [Google Scholar]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; pp. 2546–2554. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NA, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Li, L.; Jamieson, K.; Rostamizadeh, A.; Gonina, E.; Hardt, M.; Recht, B.; Talwalkar, A. Massively parallel hyperparameter tuning. arXiv 2018, arXiv:1810.05934. [Google Scholar]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K.; et al. Population based training of neural networks. arXiv 2017, arXiv:1711.09846. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Kégl, B.; Bengio, Y. Implementations of algorithms for hyper-parameter optimization. In Proceedings of the NIPS Workshop on Bayesian Optimization, Sierra Nevada, Spain, 16–17 December 2011; p. 29. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Das, L.; Sivaram, A.; Venkatasubramanian, V. Hidden representations in deep neural networks: Part 2. Regression problems. Comput. Chem. Eng. 2020, 139, 106895. [Google Scholar] [CrossRef]

















| Author | Main Topic | Approach |
|---|---|---|
| (Phase 1) | ||
| [35] | Animal psychology | Definition of RL |
| (Phase 2) | ||
| [2,3] | Optimal control | MDP, DP and Bellman’s equation |
| [36] | AI | Discussed RL models |
| [34] | AI | DP algorithm (policy iteration) |
| [37] | AI | Pointed out directions for the evolution of RL |
| (Phase 3) | ||
| [38] | AI | Neuro-like network |
| [39] | AI | Temporal difference (TD) |
| [40] | AI | Q-learning algorithm |
| [41] | AI | Stochastic RL algorithm |
| [42] | AI | REINFORCE algorithm |
| (Phase 4) | ||
| [10] | AI | RL in games (Atari) |
| [9] | AI | AlphaGo |
| Author | Control Algorithm | Learning | Estimator | Process |
|---|---|---|---|---|
| [18] | Deep actor–critic | Off-policy (1) | TD(0) | CSTR |
| [67] | Deep Q-learning | Off-policy (1) | TD(0) | Conical tank systems |
| [68] | Deep Q-learning | Off-policy (1) | TD(0) | Liquid–liquid separation |
| [30] | MPC plus DRL | Online | MC | Nonlinear control-affine system |
| [28] | MPC plus DRL | Online | — | Nonlinear process |
| [69] | MADDPG | Off-policy (1) | TD(0) and TD() | Waste treatment |
| [70] | A2C | Off-policy (1) | TD(0) | Hydrocracking |
| [20] | A3C | Off-policy (1) | TD(0) | Hybrid tank system |
| Author | TL Methodology | Environment |
|---|---|---|
| Wulfmeier et al. [7] | RS and LD | Robot control-oriented |
| Peng et al. [8] | PT | Robot control-oriented |
| Yan et al. [77] | LD with IL | Robot control-oriented |
| Christiano et al. [78] | LD with IRL | Robot control-oriented |
| Joshi and Chowdhary [75] | RS and PT | OpenAIGym |
| Kostrikov et al. [79] | LD with AIL | Robot control-oriented |
| Hyperparameters | Search Space |
|---|---|
| RL | |
| (0.80, 0.99) | |
| (0, 1) | |
| Batch size (K) | (10, 150) |
| Buffer (D) | 500 |
| Expert buffer (E) | 500 |
| Episodes (N) | 2000 |
| (0.005, 0.01) | |
| Actor Network | |
| Activation function | ReLU, Tanh |
| Layers () | (1, 5) |
| Neurons () | (4, 250) |
| Critic Network | |
| Activation function | ReLU, Tanh |
| Layers () | (1, 5) |
| Neurons () | (4, 250) |
| Discriminator | |
| Activation function | Linear, Sigmoid |
| Layers () | (1, 5) |
| Neurons () | (4, 250) |
| NN training algorithm | |
| Optimizer | Adam |
| Actor learning rate () | (, ) |
| Critic learning rate () | (, ) |
| Discriminator learning rate () | (, ) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faria, R.d.R.; Capron, B.D.O.; Secchi, A.R.; de Souza, M.B., Jr. Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes 2022, 10, 2311. https://doi.org/10.3390/pr10112311
Faria RdR, Capron BDO, Secchi AR, de Souza MB Jr. Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes. 2022; 10(11):2311. https://doi.org/10.3390/pr10112311
Chicago/Turabian StyleFaria, Ruan de Rezende, Bruno Didier Olivier Capron, Argimiro Resende Secchi, and Maurício B. de Souza, Jr. 2022. "Where Reinforcement Learning Meets Process Control: Review and Guidelines" Processes 10, no. 11: 2311. https://doi.org/10.3390/pr10112311
APA StyleFaria, R. d. R., Capron, B. D. O., Secchi, A. R., & de Souza, M. B., Jr. (2022). Where Reinforcement Learning Meets Process Control: Review and Guidelines. Processes, 10(11), 2311. https://doi.org/10.3390/pr10112311










