Calibration of Discrete Element Parameters of Maize Root and Its Mixture with Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Materials and Determination of Intrinsic Parameters
2.1.1. Research Materials
2.1.2. Intrinsic Parameters of SMR
2.1.3. Intrinsic Parameters of Soil
2.2. Preliminary DEM Model
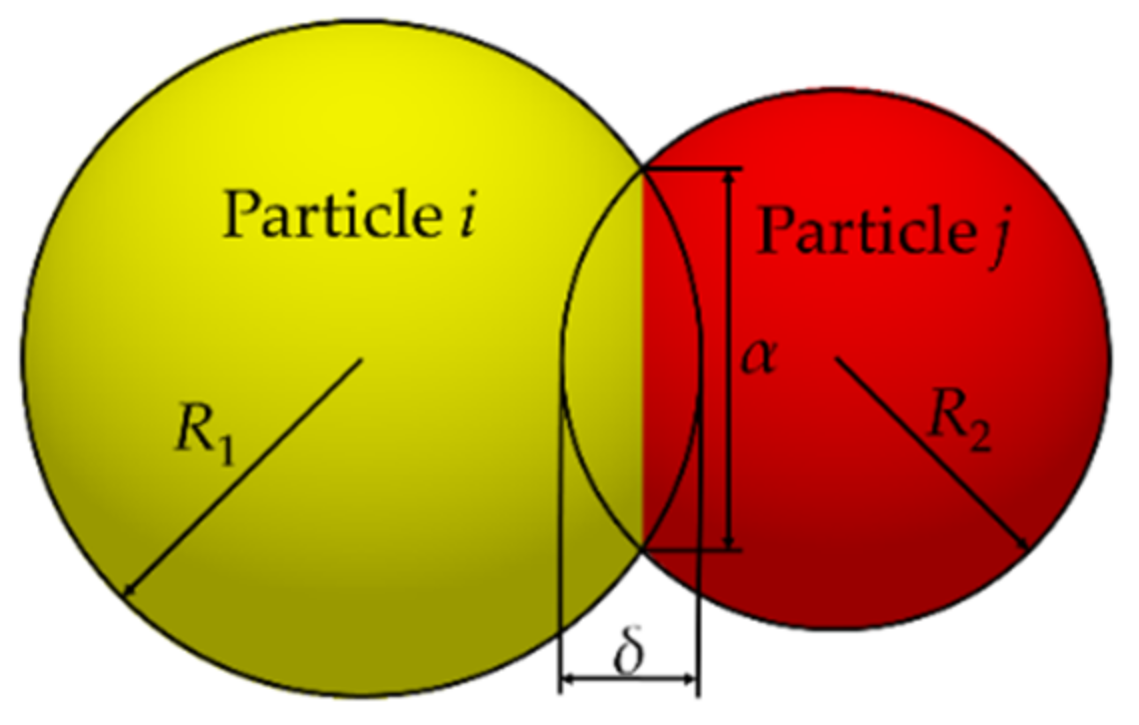
2.2.1. Determine the Contact Model
2.2.2. Single Maize Root Model
2.3. Calibrated Experiments Design
2.3.1. Determine the Restitution Coefficient e
2.3.2. Determine the Coefficient of Friction
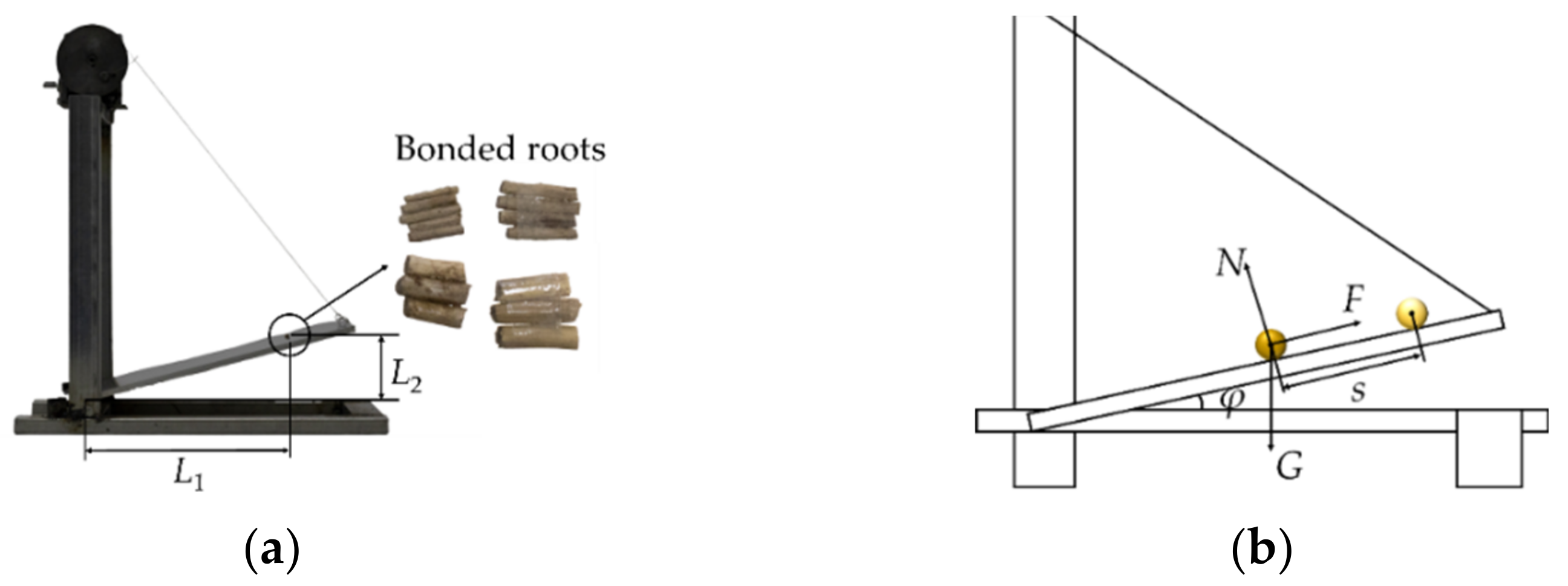
2.3.3. Determination of Actual Natural AOR
2.3.4. Simulation Model of the AOR Test
2.4. Design of AOR Simulation Test
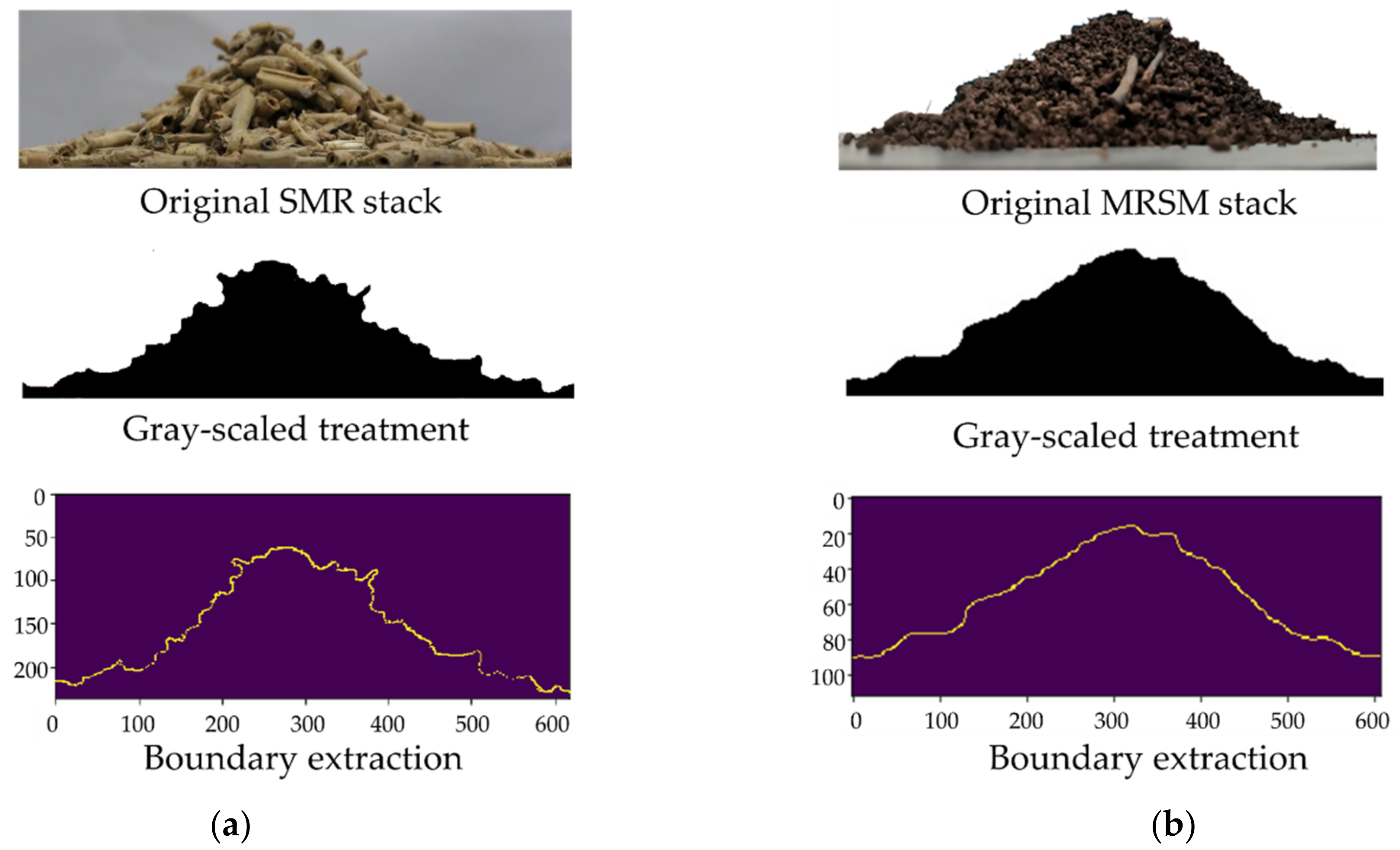
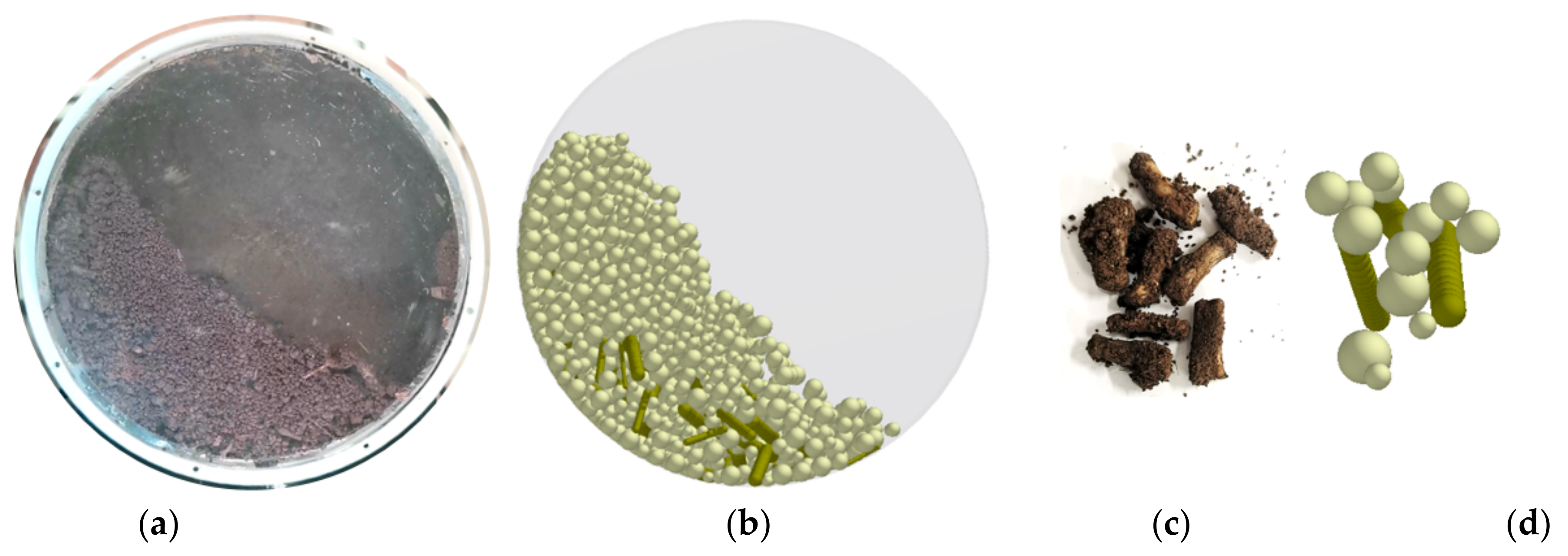
2.4.1. AOR Simulation Test for SMR
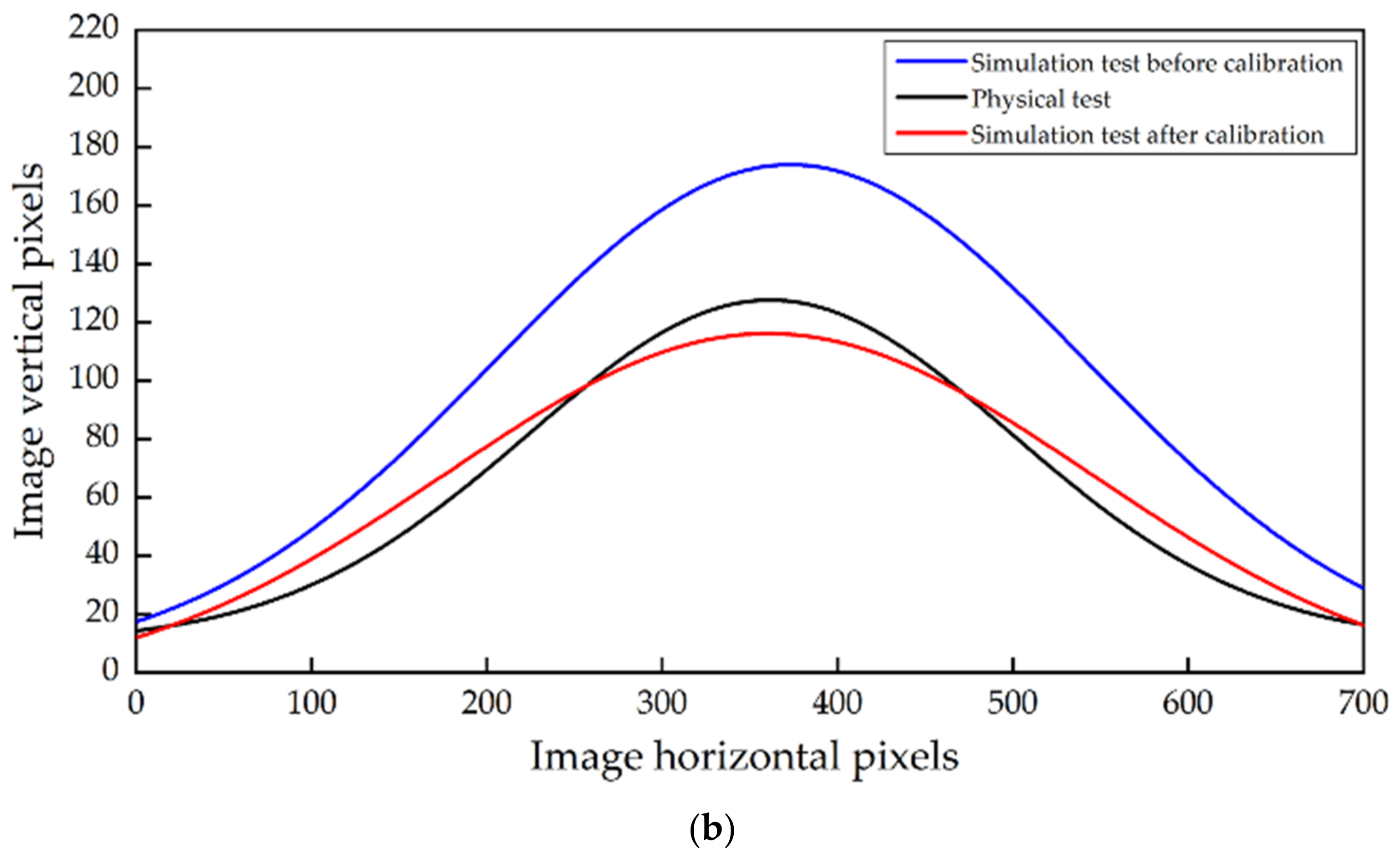
2.4.2. AOR Simulation Test for MRSM
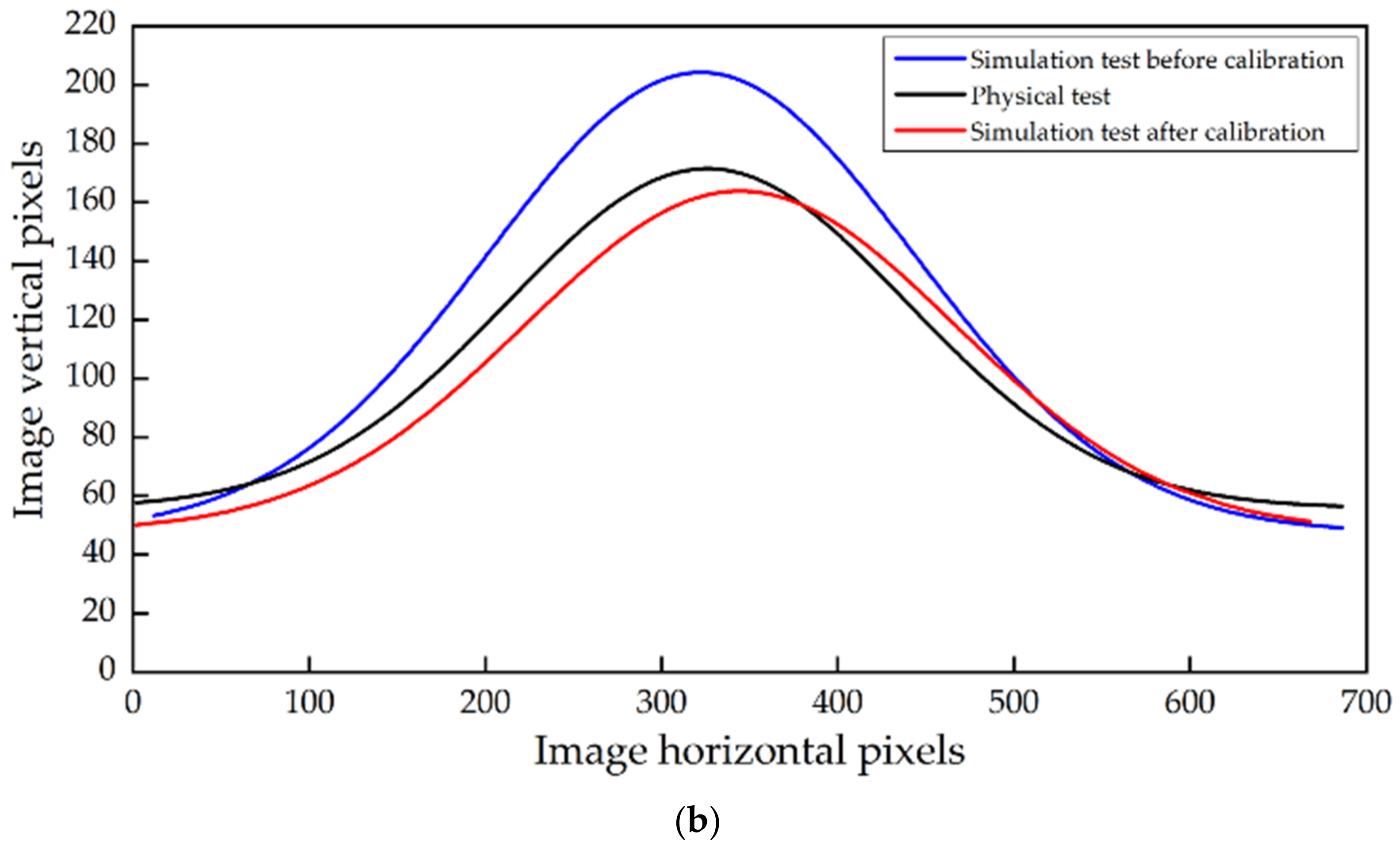
2.5. Validation Test of Dynamic AOR
3. Results and Discussion
3.1. Calibration of Contact Parameters of SMR
3.1.1. The Result of the Plackett–Burman Test
3.1.2. The Result of the Steepest Climbing Test
3.1.3. The Result of BBD Test
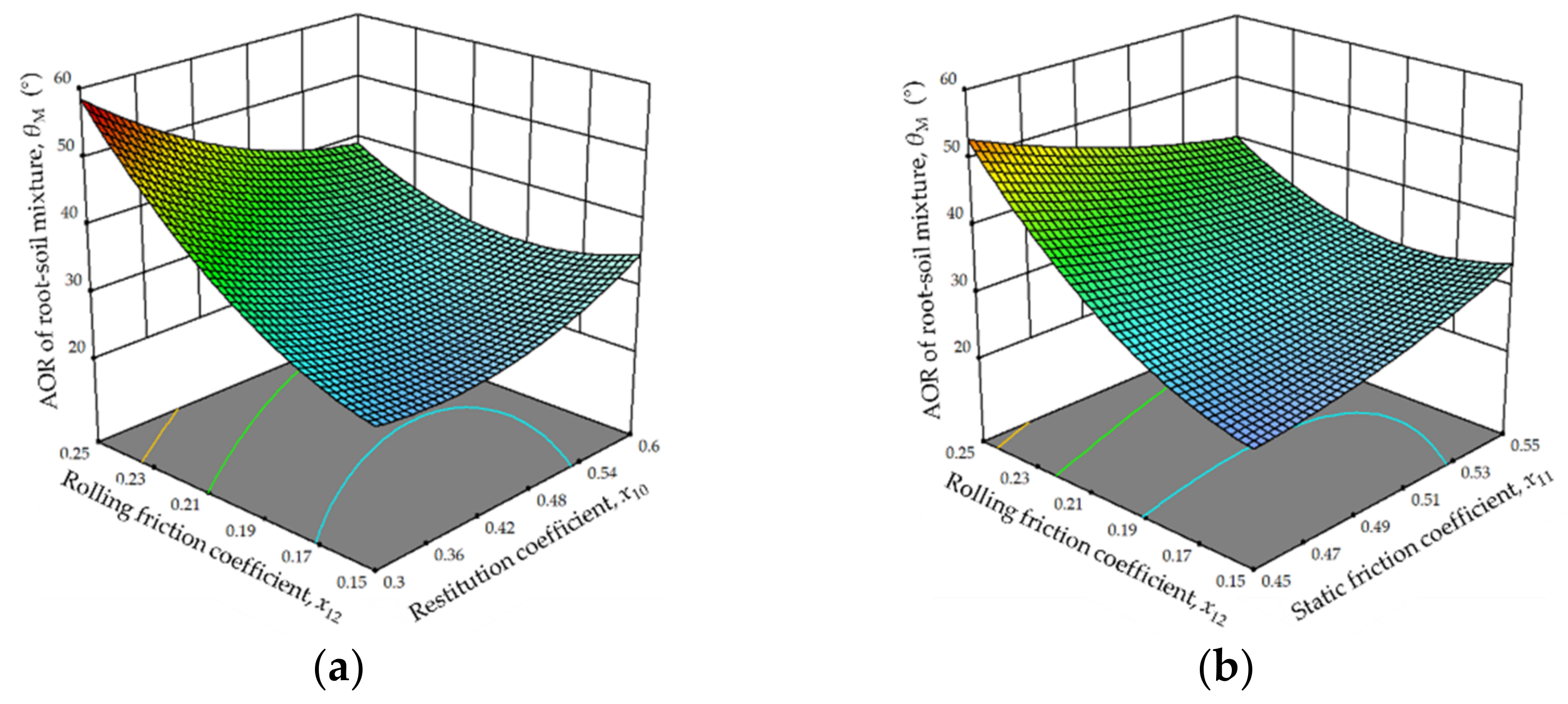
3.2. Calibration of Contact Parameters of MRSM
3.3. Validation Tests
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Niu, M.; Fang, H.; Chandio, F.; Shi, S.; Xue, Y.; Liu, H. Design and experiment of separating-guiding anti-blocking mechanism for no-tillage maize planter. Trans. CSAE 2019, 50, 52–58. [Google Scholar]
- Zeng, Z.W.; Thoms, D.; Chen, Y.; Ma, X. Comparison of soil and corn residue cutting performance of different discs used for vertical tillage. Sci. Rep. 2021, 11, 2537. [Google Scholar] [CrossRef] [PubMed]
- Aikins, K.A.; Ucgul, M.; Barr, J.B.; Jensen, T.A.; Antille, D.L.; Desbiolles, J.M.A. Determination of discrete element model parameters for a cohesive soil and validation through narrow point opener performance analysis. Soil Tillage Res. 2021, 213, 105123. [Google Scholar] [CrossRef]
- Adajar, J.B.; Alfaro, M.; Chen, Y.; Zeng, Z.W. Calibration of discrete element parameters of crop residues and their interfaces with soil. Comput. Electron. Agric. 2021, 188, 11. [Google Scholar] [CrossRef]
- Zhao, H.; Li, H.; Ma, S.; He, J.; Wang, Q.; Lu, C.; Zhang, C. The effect of various edge-curve types of plain-straight blades for strip tillage seeding on torque and soil disturbance using DEM. Soil Tillage Res. 2020, 202, 104674. [Google Scholar] [CrossRef]
- Eden, M.; Bachmann, J.; Cavalaris, C.; Kostopoulou, S.; Kozaiti, M.; Boettcher, J. Soil structure of a clay loam as affected by long-term tillage and residue management. Soil Tillage Res. 2020, 204, 104734. [Google Scholar] [CrossRef]
- Fang, M.; Yu, Z.H.; Zhang, W.J.; Cao, J.; Liu, W.H. Friction coefficient calibration of corn stalk particle mixtures using Plackett-Burman design and response surface methodology. Powder Technol. 2022, 396, 731–742. [Google Scholar] [CrossRef]
- Qin, K.; Cao, C.M.; Liao, Y.; Wang, C.; Fang, L.; Ge, J. Design and optimization of crushing and throwing device for straw returning to field and fertilizing hill-seeding machine. Trans. CSAE 2020, 36, 1–10. [Google Scholar]
- Du, J.; Heng, Y.F.; Zheng, K.; Luo, C.M.; Zhu, Y.H.; Zhang, J.M.; Xia, J.F. Investigation of the burial and mixing performance of a rotary tiller using discrete element method. Soil Tillage Res. 2022, 220, 17. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, F.; Zhao, M.; Liu, Y.; Li, F.; Chen, C.; Zhang, Y. Movement law of maize population in seeds room of seeds metering device based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2016, 32, 27–35. [Google Scholar]
- Wang, X.Z.; Gao, P.Y.; Yue, B.; Shen, H.; Fu, Z.L.; Zheng, Z.Q.; Zhu, R.X.; Huang, Y.X. Optimisation of installation parameters of subsoiler’ wing using the discrete element method. Comput. Electron. Agric. 2019, 162, 523–530. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O. A discrete numerical model for granular assemblies. Géotechnique 2008, 30, 331–336. [Google Scholar] [CrossRef] [Green Version]
- Ucgul, M.; Fielke, J.M.; Saunders, C. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil. Soil Tillage Res. 2014, 144, 220–227. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling of tillage: Determination of a suitable contact model and parameters for a cohesionless soil. Biosyst. Eng. 2014, 121, 105–117. [Google Scholar] [CrossRef]
- Chen, Z.; Wassgren, C.; Veikle, E.; Ambrose, K. Determination of material and interaction properties of maize and wheat kernels for DEM simulation. Biosyst. Eng. 2020, 195, 208–226. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Chen, J. Modeling of flexible wheat straw by discrete element method and its parameters calibration. Int. J. Agric. Biol. Eng. 2018, 11, 42–46. [Google Scholar] [CrossRef] [Green Version]
- Adilet, S.; Zhao, J.; Sayakhat, N.; Chen, J.; Nikolay, Z.; Bu, L.; Sugirbayeva, Z.; Hu, G.; Marat, M.; Wang, Z. Calibration Strategy to Determine the Interaction Properties of Fertilizer Particles Using Two Laboratory Tests and DEM. Agriculture 2021, 11, 592. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Yang, Y.; Zhao, H.; Yang, C.; He, Y.; Xu, H. Discrete element modelling of citrus fruit stalks and its verification. Biosyst. Eng. 2020, 200, 400–414. [Google Scholar] [CrossRef]
- Liao, Y.; Liao, Q.; Zhou, Y.; Wang, Z.; Jiang, Y.; Liang, F. Parameters calibration of discrete element Model of fodder rape crop harvest in bolting Stage. Trans. CSAE 2020, 51, 73–82. [Google Scholar]
- Ren, J.H.; Wu, T.; Mo, W.Y.J.; Li, K.; Hu, P.; Xu, F.Y.; Liu, Q.T. Discrete element simulation modeling method and parameters calibration of sugarcane leaves. Agronomy 2022, 12, 1796. [Google Scholar] [CrossRef]
- Liu, Y.; Mi, G.P.; Zhang, S.L.; Li, P.; Huang, Y.X. Determination of discrete element modeling parameters of adzuki bean seeds. Agriculture 2022, 12, 13. [Google Scholar]
- Peng, C.; Xu, D.; He, X.; Tang, Y.; Sun, S. Parameter calibration of discrete element simulation model for pig manure organic fertilizer treated with Hermetia illucen. Trans. CSAE 2020, 36, 212–218. [Google Scholar]
- Hu, M.J.; Xia, J.F.; Zhou, Y.; Luo, C.M.; Zhou, M.K.; Liu, Z.Y. Measurement and calibration of the discrete element parameters of coated delinted cotton seeds. Agriculture 2022, 12, 286. [Google Scholar] [CrossRef]
- Li, H.C.; Zeng, R.; Niu, Z.Y.; Zhang, J.Q. A calibration method for contact parameters of maize kernels based on the discrete element method. Agriculture 2022, 12, 664. [Google Scholar] [CrossRef]
- Cao, X.L.; Li, H.; Li, H.W.; Wang, X.C.; Ma, X. Measurement and calibration of the parameters for discrete element method modeling of rapeseed. Processes 2021, 9, 605. [Google Scholar] [CrossRef]
- Ma, Y.; Song, C.; Xuan, C.; Wang, H.; Yang, S.; Wu, P. Parameters calibration of discrete element model for alfalfa straw compression simulation. Trans. CSAE 2020, 36, 22–30. [Google Scholar]
- Liao, Y.; Wang, Z.; Liao, Q.; Wan, X.; Zhou, Y.; Liang, F. Calibration of discrete element model parameters of forage rape stalk at early pod stage. Trans. CSAM 2020, 51, 236–243. [Google Scholar]
- Xu, Y.F.; Zhang, X.L.; Sun, X.J.; Wang, J.Z.; Liu, J.Z.; Li, Z.G.; Li, P.P. Tensile mechanical properties of greenhouse cucumber cane. Int. J. Agric. Biol. Eng. 2016, 9, 1–8. [Google Scholar]
- Wang, X.; Zhang, S.; Pan, H.; Zheng, Z.; Huang, Y.; Zhu, R.X. Effect of soil particle size on soil-subsoiler interactions using the discrete element method simulations. Biosyst. Eng. 2019, 182, 138–150. [Google Scholar] [CrossRef]
- EDEM. EDEM Tutorial: Flexible Plane Simulation; DEM Solutions: Edinburgh, UK, 2020. [Google Scholar]
- Guo, Y.; Chen, Q.; Xia, Y.; Westover, T.; Eksioglu, S.; Roni, M. Discrete element modeling of switchgrass particles under compression and rotational shear. Biomass Bioenergy 2020, 141, 105649. [Google Scholar] [CrossRef]
- Guo, J.; Karkee, M.; Yang, Z.; Fu, H.; Li, J.; Jiang, Y.L.; Jiang, T.T.; Liu, E.X.; Duan, J.L. Discrete element modeling and physical experiment research on the biomechanical properties of banana bunch stalk for postharvest machine development. Comput. Electron. Agric. 2021, 188, 31. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Yano, T.; Ohsaki, S.; Nakamura, H.; Watano, S. Numerical study on compression processes of cohesive bimodal particles and their packing structure. Adv. Powder Technol. 2021, 32, 1362–1368. [Google Scholar] [CrossRef]
- Hoshishima, C.; Ohsaki, S.; Nakamura, H.; Watano, S. Parameter calibration of discrete element method modelling for cohesive and non-spherical particles of powder. Powder Technol. 2021, 386, 199–208. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
- Tian, X.L.; Cong, X.; Qi, J.T.; Guo, H.; Li, M.; Fan, X.H. Parameter calibration of discrete element model for corn straw-soil mixture in black soil areas. Trans. CSAE 2021, 52, 100–108+242. [Google Scholar]












| Segment Number | Diameter (mm) | Length (mm) | ||||||
|---|---|---|---|---|---|---|---|---|
| a | b | c | d | a | b | c | d | |
| Average | 1.36 | 2.43 | 3.49 | 4.47 | 40.98 | 48.56 | 46.41 | 32.89 |
| Standard deviation | 0.17 | 0.28 | 0.30 | 0.25 | 7.20 | 4.91 | 4.69 | 7.20 |
| Soil Property | Value |
|---|---|
| Density/(kg·m−3) | 1836.27 |
| Moisture content/(%) | 20.96 |
| Soil particle size/(mm) | 3–7 |
| Parameter | Values |
|---|---|
| ρ of root/(kg·m−3) | 266.33 a |
| ρ of soil/(kg·m−3) | 1836.27 a |
| ρ of steel/(kg·m−3) | 7850 b |
| ν of soil | 0.38 |
| ν of steel | 0.3 b |
| G of soil/(Pa) | 6 × 107 b |
| G of steel/(Pa) | 7.94 × 1010 b |
| γ of soil/(J·m−2) | 0.29 b |
| ν of root x1 | 0.3–0.4 c |
| G of root x2/(Pa) | 1.77 × 107–2.08 × 108 c |
| e of roots x3 | 0.01–0.1 c |
| e of SMR-steel x4 | 0.05–0.2 c |
| μs of SMR-SMR x5 | 0.3–0.6 c |
| μs of SMR-steel x6 | 0.3–0.5 c |
| μr of SMR-SMR x7 | 0.1–0.25 c |
| μr of SMR-steel x8 | 0.1–0.2 c |
| e of root-soil x9 | 0.3–0.6 d |
| μs of root-soil x10 | 0.45–0.65 d |
| μr of root-soil x11 | 0.15–0.25 d |
| γ of root-soil x12/(J·m−2) | 3–5 d |
| Factors | Coded Levels | ||
|---|---|---|---|
| Low (−1) | Middle (0) | High (+1) | |
| x9 | 0.3 | 0.45 | 0.6 |
| x10 | 0.45 | 0.5 | 0.55 |
| x11 | 0.15 | 0.2 | 0.25 |
| x12/(J·m−2) | 3 | 4 | 5 |
| Parameters | Effect | Sum of Squares | F | p | Rank |
|---|---|---|---|---|---|
| x1 | 3.12 | 29.25 | 4.49 | 0.1244 | 5 |
| x2 | −4.20 | 52.97 | 8.12 | 0.0651 | 4 |
| x3 | −0.92 | 2.51 | 0.39 | 0.5786 | 7 |
| x4 | −0.77 | 1.76 | 0.27 | 0.6394 | 8 |
| x5 | 12.42 | 462.47 | 70.92 | 0.0035 * | 1 |
| x6 | 0.99 | 2.96 | 0.45 | 0.5485 | 6 |
| x7 | 4.81 | 69.34 | 10.63 | 0.0471 * | 3 |
| x8 | 5.82 | 101.53 | 15.57 | 0.0290 * | 2 |
| Test Number | x5 | x7 | x8 | θR/(°) | η/(%) |
|---|---|---|---|---|---|
| 1 | 0.30 | 0.10 | 0.10 | 27.63 | 14.43 |
| 2 | 0.36 | 0.13 | 0.14 | 30.93 | 4.20 |
| 3 | 0.42 | 0.16 | 0.18 | 31.81 | 1.49 |
| 4 | 0.48 | 0.19 | 0.22 | 35.32 | 9.38 |
| 5 | 0.54 | 0.22 | 0.26 | 40.75 | 26.19 |
| 6 | 0.60 | 0.25 | 0.30 | 47.64 | 47.53 |
| Test Number | x5 | x7 | x8 | θR/(°) | η/(%) |
|---|---|---|---|---|---|
| 1 | 0.36 | 0.13 | 0.18 | 31.98 | 0.96 |
| 2 | 0.42 | 0.16 | 0.18 | 32.69 | 1.24 |
| 3 | 0.36 | 0.19 | 0.18 | 31.67 | 1.92 |
| 4 | 0.42 | 0.16 | 0.18 | 32.79 | 1.55 |
| 5 | 0.48 | 0.19 | 0.18 | 36.35 | 12.57 |
| 6 | 0.42 | 0.16 | 0.18 | 33.21 | 2.85 |
| 7 | 0.42 | 0.19 | 0.22 | 35.25 | 9.17 |
| 8 | 0.42 | 0.13 | 0.14 | 29.02 | 10.13 |
| 9 | 0.36 | 0.16 | 0.14 | 28.92 | 10.44 |
| 10 | 0.48 | 0.16 | 0.14 | 31.75 | 1.67 |
| 11 | 0.42 | 0.13 | 0.22 | 31.98 | 0.96 |
| 12 | 0.42 | 0.19 | 0.14 | 31.08 | 3.75 |
| 13 | 0.48 | 0.13 | 0.18 | 34.11 | 5.64 |
| 14 | 0.48 | 0.16 | 0.22 | 36.02 | 11.55 |
| 15 | 0.42 | 0.16 | 0.18 | 32.88 | 1.83 |
| 16 | 0.42 | 0.16 | 0.18 | 32.36 | 0.22 |
| 17 | 0.36 | 0.16 | 0.22 | 32.59 | 0.93 |
| Source | df | Mean Square | F | p |
|---|---|---|---|---|
| Model | 9 | 64.68 | 25.88 | 0.0001 * |
| x5 | 1 | 21.35 | 76.88 | <0.0001 * |
| x7 | 1 | 6.59 | 23.72 | 0.0018 * |
| x8 | 1 | 28.39 | 102.21 | <0.0001 * |
| x5x7 | 1 | 1.63 | 5.85 | 0.0461 * |
| x5x8 | 1 | 0.090 | 0.32 | 0.5870 |
| x7x8 | 1 | 0.37 | 1.32 | 0.2887 |
| x52 | 1 | 1.59 | 5.72 | 0.0480 * |
| x72 | 1 | 0.068 | 0.24 | 0.6361 |
| x82 | 1 | 4.92 | 17.70 | 0.0040 * |
| Residual | 7 | 1.94 | ||
| Lack-of-Fit | 3 | 1.56 | 5.5 | 0.0665 |
| Pure Error | 4 | 0.38 | ||
| Cor Total | 16 | 66.63 | ||
| R2 = 0.9708, Adeq Precision = 19.183 | ||||
| Test Number | x9 | x10 | x11 | x12/(J·m−2) | θM/(°) |
|---|---|---|---|---|---|
| 1 | 0.3 | 0.5 | 0.2 | 3 | 32.81 |
| 2 | 0.3 | 0.5 | 0.2 | 5 | 52.52 |
| 3 | 0.6 | 0.5 | 0.2 | 3 | 24.44 |
| 4 | 0.6 | 0.5 | 0.2 | 5 | 47.31 |
| 5 | 0.45 | 0.45 | 0.15 | 4 | 26.09 |
| 6 | 0.45 | 0.55 | 0.15 | 4 | 32.13 |
| 7 | 0.45 | 0.45 | 0.25 | 4 | 55.37 |
| 8 | 0.45 | 0.55 | 0.25 | 4 | 39.58 |
| 9 | 0.45 | 0.5 | 0.15 | 3 | 21.69 |
| 10 | 0.45 | 0.5 | 0.15 | 5 | 43.04 |
| 11 | 0.45 | 0.5 | 0.25 | 3 | 47.26 |
| 12 | 0.45 | 0.5 | 0.25 | 5 | 56.65 |
| 13 | 0.3 | 0.45 | 0.2 | 4 | 44.25 |
| 14 | 0.6 | 0.45 | 0.2 | 4 | 25.25 |
| 15 | 0.3 | 0.55 | 0.2 | 4 | 43.82 |
| 16 | 0.6 | 0.55 | 0.2 | 4 | 38.90 |
| 17 | 0.45 | 0.45 | 0.2 | 3 | 29.09 |
| 18 | 0.45 | 0.45 | 0.2 | 5 | 44.87 |
| 19 | 0.45 | 0.55 | 0.2 | 3 | 25.71 |
| 20 | 0.45 | 0.55 | 0.2 | 5 | 36.16 |
| 21 | 0.3 | 0.5 | 0.15 | 4 | 22.38 |
| 22 | 0.6 | 0.5 | 0.15 | 4 | 37.04 |
| 23 | 0.3 | 0.5 | 0.25 | 4 | 51.37 |
| 24 | 0.6 | 0.5 | 0.25 | 4 | 39.21 |
| 25 | 0.45 | 0.5 | 0.2 | 4 | 27.86 |
| 26 | 0.45 | 0.5 | 0.2 | 4 | 29.26 |
| 27 | 0.45 | 0.5 | 0.2 | 4 | 31.02 |
| 28 | 0.45 | 0.5 | 0.2 | 4 | 32.08 |
| 29 | 0.45 | 0.5 | 0.2 | 4 | 33.74 |
| Source | df | Mean Square | F | p |
|---|---|---|---|---|
| Model | 14 | 183.66 | 7.73 | 0.0002 * |
| x9 | 1 | 825.93 | 34.77 | <0.0001 * |
| x10 | 1 | 101.99 | 4.29 | 0.0572 |
| x11 | 1 | 6.21 | 0.26 | 0.6170 |
| x12 | 1 | 955.13 | 40.21 | <0.0001 * |
| x9x10 | 1 | 2.49 | 0.10 | 0.7507 |
| x9x11 | 1 | 7.11 | 0.30 | 0.5930 |
| x9x12 | 1 | 35.75 | 1.50 | 0.2402 |
| x10x11 | 1 | 49.60 | 2.09 | 0.1705 |
| x10x12 | 1 | 179.89 | 7.57 | 0.0156 * |
| x11x12 | 1 | 119.03 | 5.01 | 0.0420 * |
| x92 | 1 | 108.64 | 4.57 | 0.0506 |
| x102 | 1 | 94.12 | 3.96 | 0.0664 |
| x112 | 1 | 15.59 | 0.66 | 0.4314 |
| x122 | 1 | 187.39 | 7.89 | 0.0139 * |
| Residual | 14 | 23.75 | ||
| Lack-of-Fit | 10 | 31.12 | 5.84 | 0.0519 |
| Pure Error | 4 | 5.33 | ||
| Cor Total | 28 | |||
| R2 = 0.8855, Adeq Precision = 10.974 | ||||
| Time/(s) | Dynamic AOR/(°) | ||
|---|---|---|---|
| Measurement | Simulated | Relative Error/(%) | |
| 4 | 13.75 | 15.02 | 9.24 |
| 5 | 22.35 | 24.37 | 9.04 |
| 6 | 31.33 | 33.29 | 6.26 |
| 7 | 39.59 | 41.63 | 5.15 |
| 8 | 46.72 | 48.15 | 3.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Yang, F.; Dong, J.; Chen, X.; Liu, Y.; Mi, G.; Wang, T.; Jia, X.; Huang, Y.; Wang, X. Calibration of Discrete Element Parameters of Maize Root and Its Mixture with Soil. Processes 2022, 10, 2433. https://doi.org/10.3390/pr10112433
Zhang S, Yang F, Dong J, Chen X, Liu Y, Mi G, Wang T, Jia X, Huang Y, Wang X. Calibration of Discrete Element Parameters of Maize Root and Its Mixture with Soil. Processes. 2022; 10(11):2433. https://doi.org/10.3390/pr10112433
Chicago/Turabian StyleZhang, Shilin, Feifei Yang, Jianxin Dong, Xuhui Chen, Yan Liu, Guopeng Mi, Tao Wang, Xian Jia, Yuxiang Huang, and Xuezhen Wang. 2022. "Calibration of Discrete Element Parameters of Maize Root and Its Mixture with Soil" Processes 10, no. 11: 2433. https://doi.org/10.3390/pr10112433






