Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Simulation Model
2.1.1. Numerical Calculation Model
2.1.2. Motion Parameters and Mechanical Models
2.2. Numerical Method
2.2.1. Control Equation and Turbulence Model
2.2.2. Calculation Method and Boundary Conditions
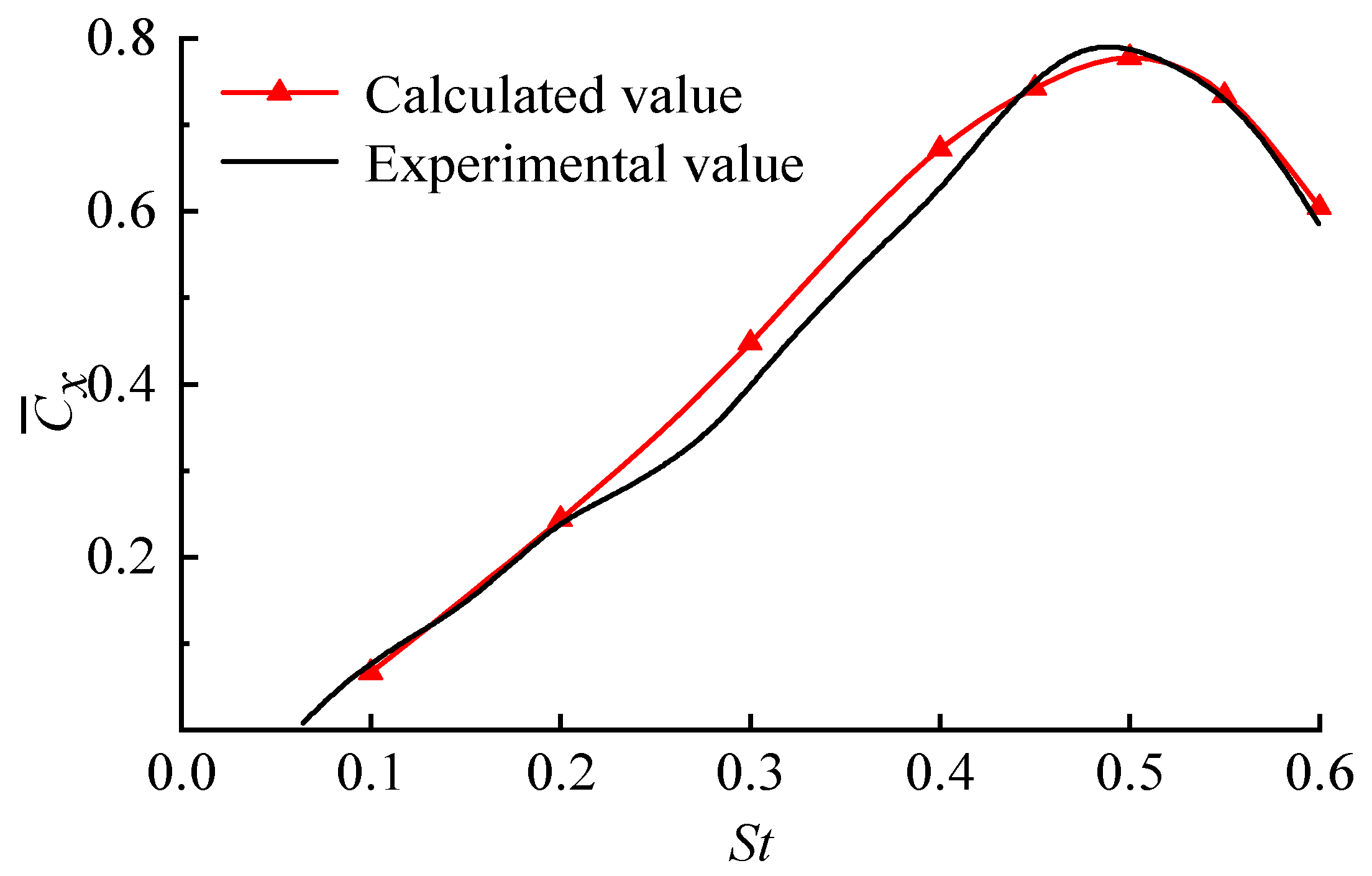
2.2.3. Solver Validation
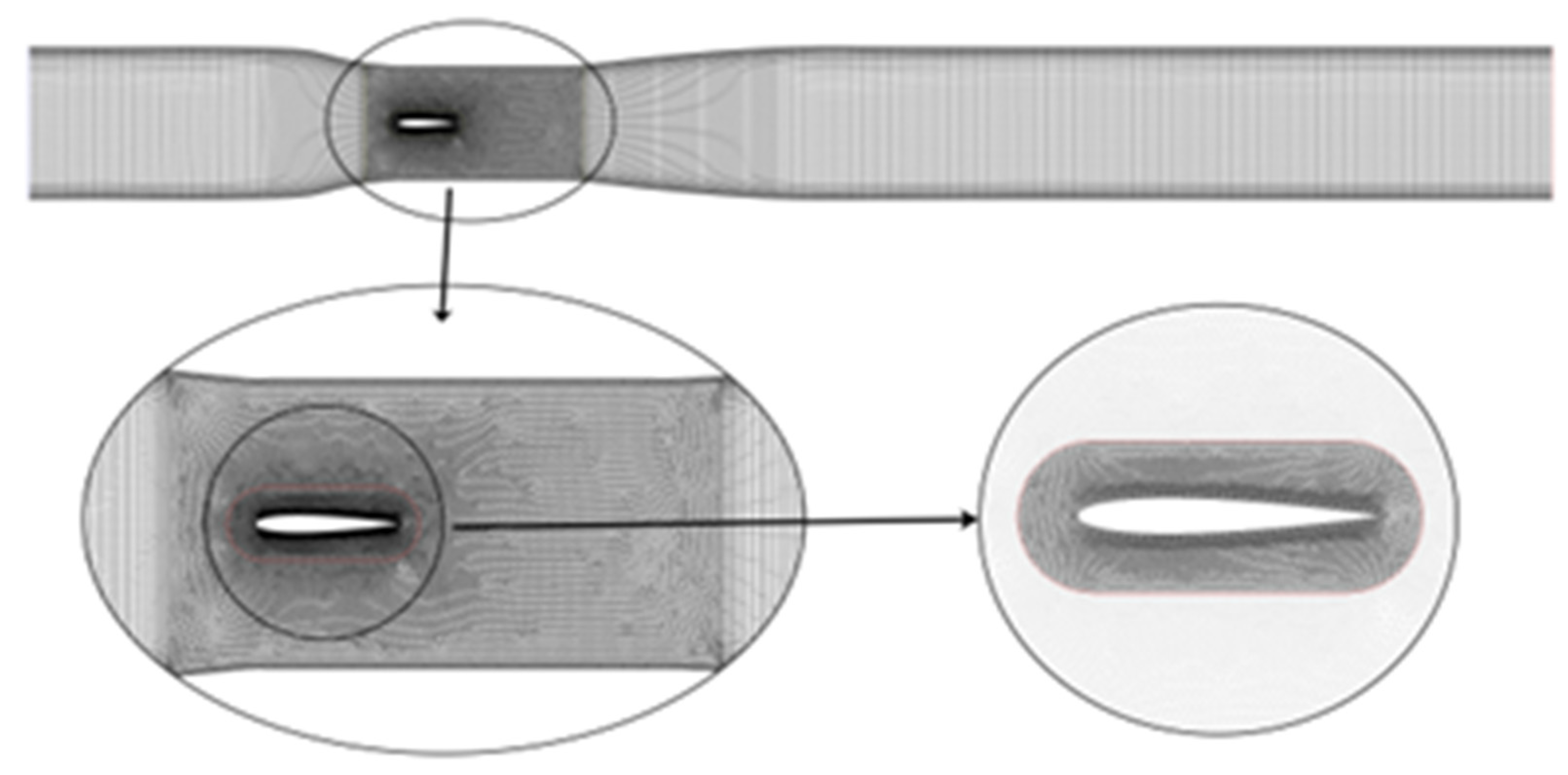
2.2.4. Computational Domain and Grid Generation
2.3. Experimental Setup and Uncertainty Analysis
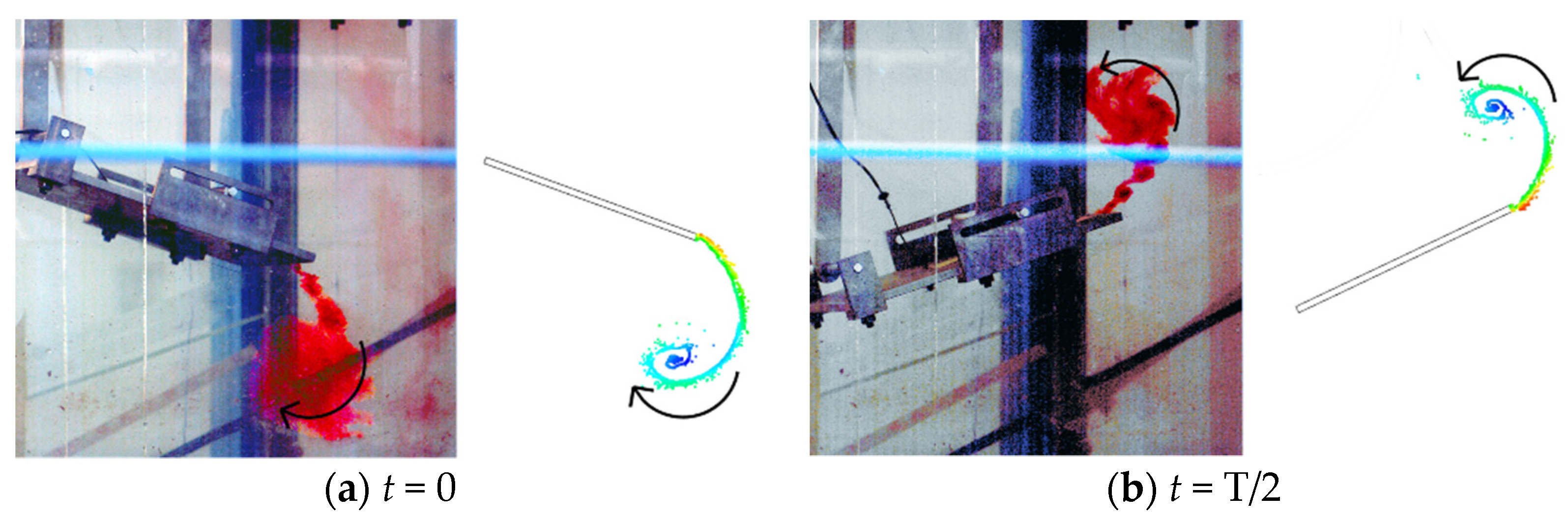
2.3.1. Flapping Hydrofoil Bionic Pump
2.3.2. Uncertainty Analysis of Experiment
3. Results
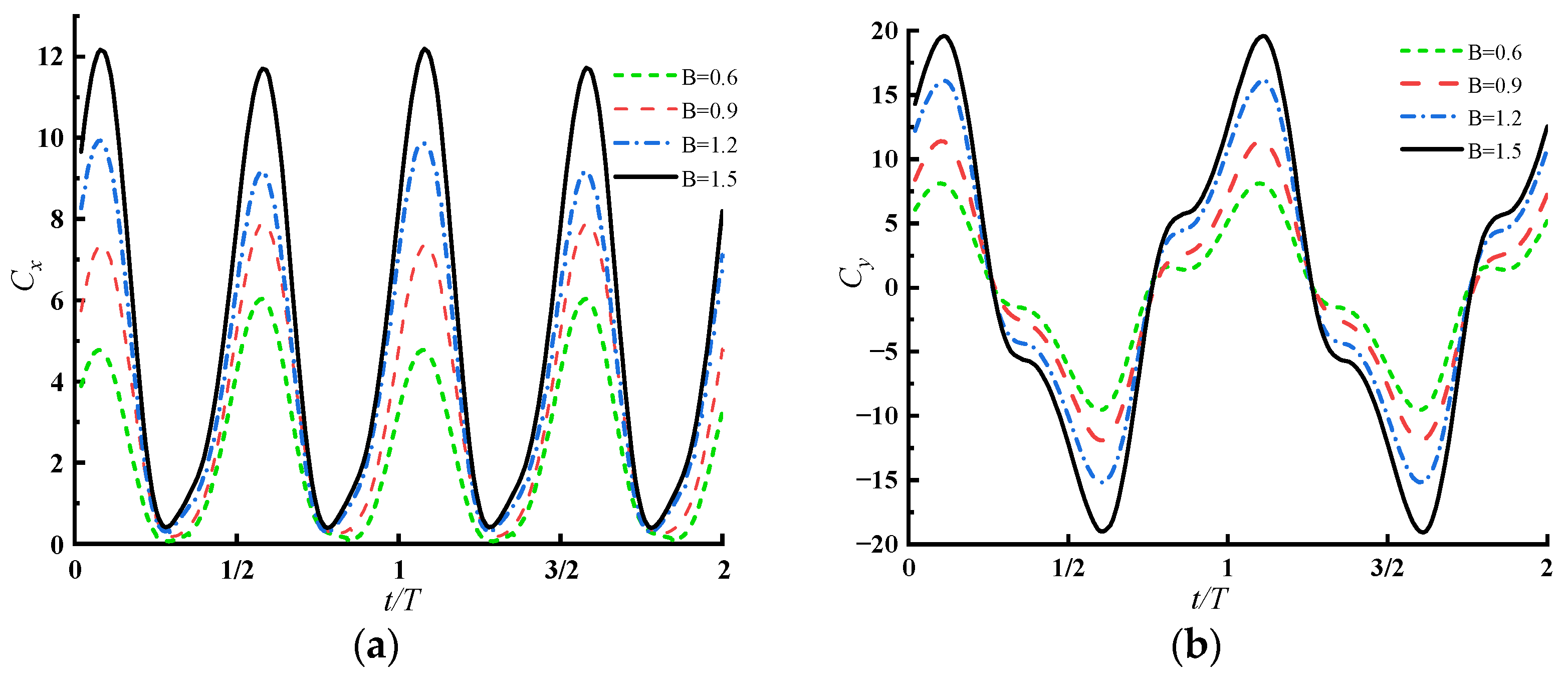
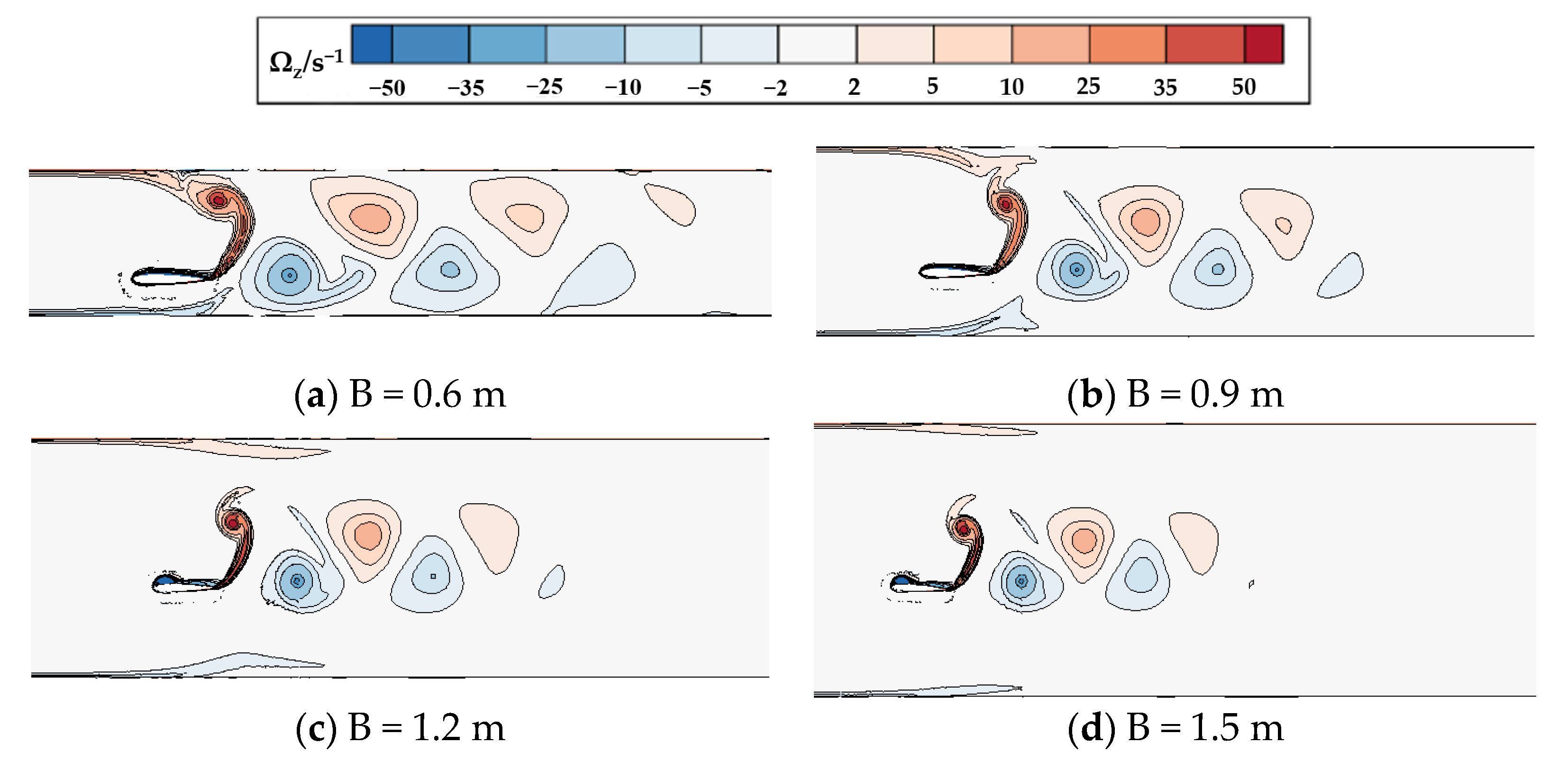
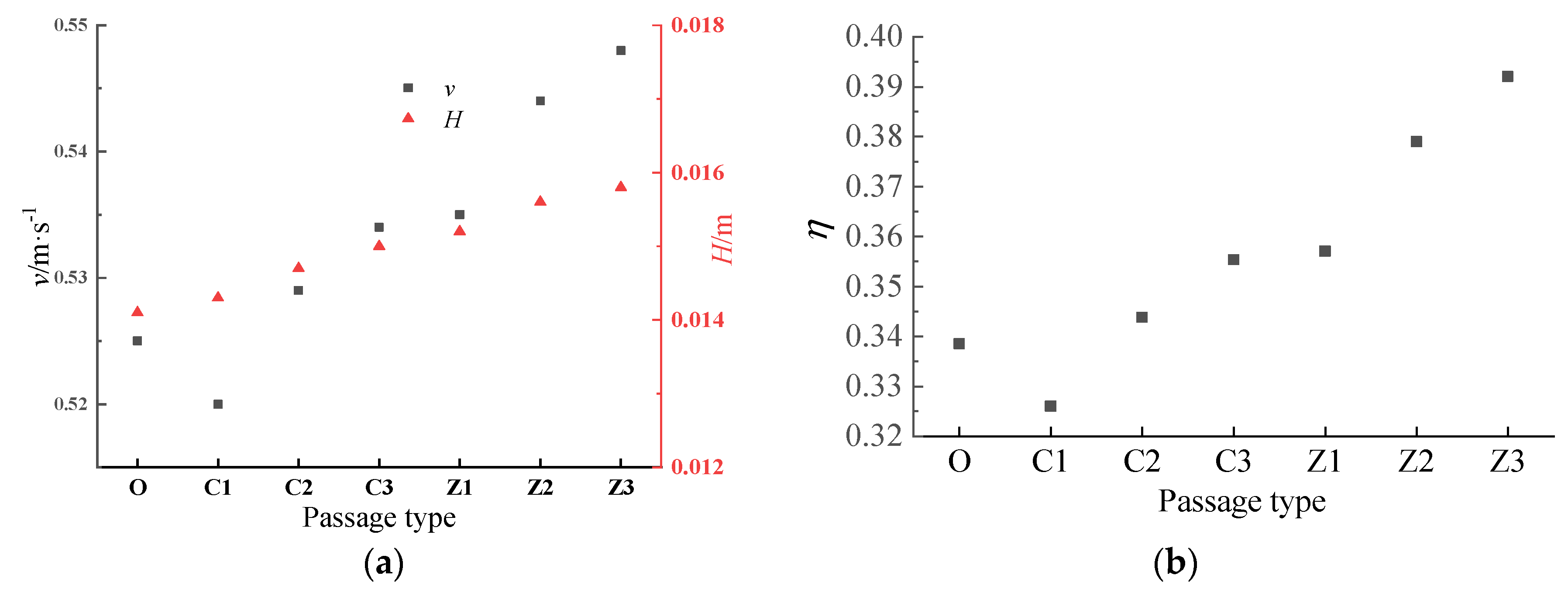
3.1. Influence of Passage on the Dynamic Performance of the Water-Pushing Device
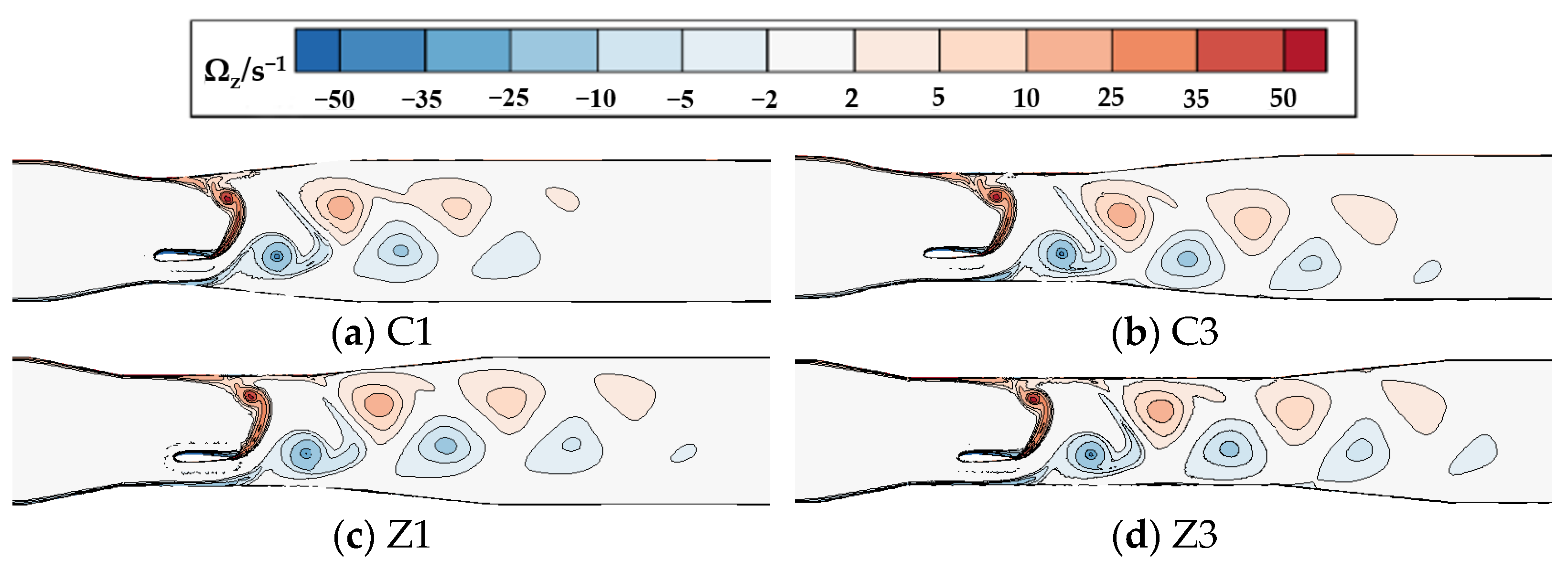
3.2. The Influence of Flow Passage Structure on Hydrofoil Propulsion Characteristics
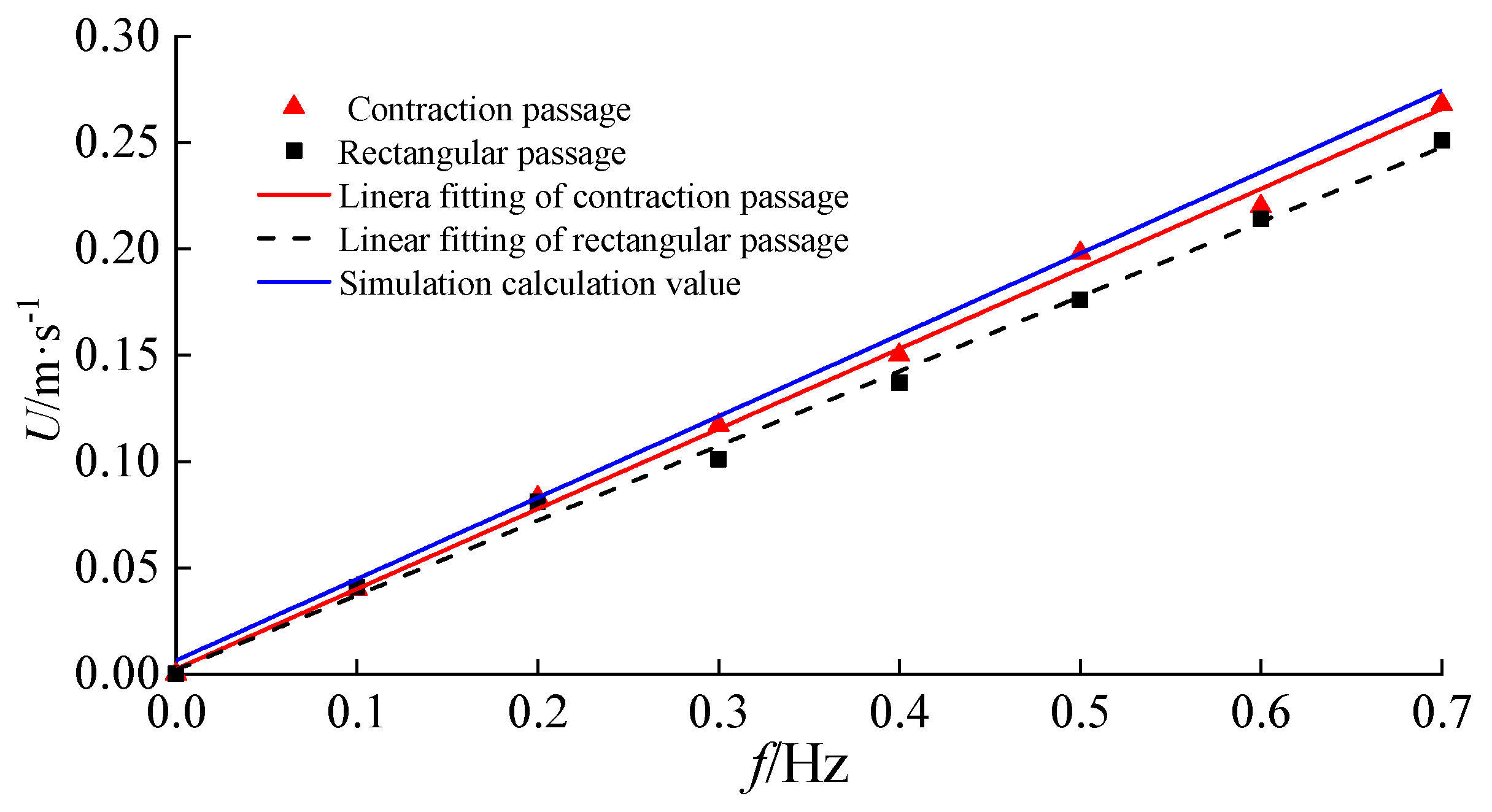
3.3. Performance Test
4. Conclusions
- (1)
- In a certain range, the thrust coefficient of the flapping wing is positively related to the channel width, while the thrust coefficient of the flapping wing will be reduced by using the contraction expansion passage, and the trend is more obvious with the increase of the center contraction length. In addition, on the premise of constraining the center shrinkage length, the thrust coefficient of Z1 group with right angle transition is higher than that of C3 group with fillet transition.
- (2)
- When other parameters are fixed, increasing the passage width can effectively increase the average flow of the flapping wing hydrodynamic device, but its head, flow rate, and pumping efficiency are reduced to a certain extent. When the passage width is 0.6 m, the pumping efficiency of the device is 37.4%, which is 11.2% higher than that when the passage width is 1.5 m, but the flow rate is only 0.375 m3/s, which is far lower than 0.605 m3/s when the passage width is 1.5 m.
- (3)
- Under the same working conditions, the expansion and contraction passages can effectively improve the pumping performance of the flapping wing hydrodynamic device. In addition, the length of the central contraction section in the contraction expansion passage is the main factor affecting the pumping performance of the flapping wing hydrodynamic device. The flow, velocity, and efficiency of the flapping wing hydrodynamic device increase with the length of the central contraction section. When the length of the contraction section is 2 m, the pumping efficiency of the device is as high as 39.2%, and the flow rate is as high as 0.4376 m3/s, and the head is 0.016 m. Compared with the simple narrow flow passage, it also shows obvious improvement, and meets the application design concept of large flow and high efficiency under the ultra-low head condition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Phillips, J.; Slattery, M. Downstream trends in discharge, slope, and stream power in a lower coastal plain river. J. Hydrol. 2007, 334, 290–303. [Google Scholar] [CrossRef]
- Peng, Z.; Hu, W.; Zhang, Y. Modelling the effects of joint operations of water transfer project and lake sluice on circulation and water quality of a large shallow lake. J. Hydrol. 2021, 593, 125881. [Google Scholar] [CrossRef]
- Snedden, G.; Cable, J.; Swarzenski, C.S. ediment discharge into a subsiding Louisiana deltaic estuary through a Mississippi River diversion. J. Estuar. Coast. Shelf Sci. 2007, 71, 181–193. [Google Scholar] [CrossRef]
- Panda, U.; Mahanty, M.; Rao, V. Hydrodynamics and water quality in Chilika Lagoon-A modelling approach. J. Procedia Eng. 2015, 116, 639–646. [Google Scholar] [CrossRef] [Green Version]
- Al-Obaidi, A. Numerical investigation of flow field behaviour and pressure fluctuations within an axial flow pump under transient flow pattern based on CFD analysis method. J. Phys. Conf. Ser. 2019, 1279, 012069. [Google Scholar] [CrossRef] [Green Version]
- Zuo, Z.; Liu, S. Flow-induced instabilities in pump-turbines in China. Engineering 2017, 3, 504–511. [Google Scholar] [CrossRef]
- Feng, J.; Luo, X.; Guo, P. Influence of tip clearance on pressure fluctuations in an axial flow pump. J. Mech. Sci. Technol. 2016, 30, 1603–1610. [Google Scholar] [CrossRef]
- Graf, W. Downstream hydrologic and geomorphic effects of large dams on American rivers. Geomorphology 2006, 79, 336–360. [Google Scholar] [CrossRef]
- Hua, E.; Chen, W.; Tang, S. Water pushing flow characteristics of flapping hydrofoil device in small river. Trans. Chin. Soc. Agric. Mach. 2022, 53, 154–162. [Google Scholar]
- Hua, E.; Tang, S.; Chen, W. Analysis on influence of swimming models of swing hydrofoil on water propulsion. J. Hydroelectr. Eng. 2022, 41, 9–103. [Google Scholar]
- Knoller, R. Die Gesetze des Luftwiderstandes; Flug-und Motortechnik: Wien, Austria, 1909; Volume 3, pp. 1–7. [Google Scholar]
- Von Kaman, T.; Burgers, J.M. General Aerodynamic Theory-Perfect Fluids. M. Division E. Vol. II. In Aerodynamic Theory; Durand, W.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1943. [Google Scholar]
- Liu, W.; Li, N.; Zhao, J. Wake structure and hydrodynamic performance of flapping foils mimicking fish fin kinematics. Saudi J. Biol. Sci. 2017, 24, 1344–1354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Triantafyllou, G.; Triantafyllou, M.; Grosenbaugh, M. Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 1993, 7, 205–224. [Google Scholar] [CrossRef]
- Anderson, J.; Streitlien, K.; Barrett, D. Oscillating foils of high propulsive efficiency. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef] [Green Version]
- Chang, X.; Zhang, L.; He, X. Numerical study of the thunniform mode of fish swimming with different Reynolds number and caudal fin shape. Comput. Fluids 2012, 68, 54–70. [Google Scholar] [CrossRef]
- Boudis, A.; Bayeul-Laine, A.; Oualli, H. Numerical investigation of the effects of nonsinusoidal motion trajectory on the propulsion mechanisms of a flapping airfoil. J. Fluids Eng. 2019, 141, 4. [Google Scholar] [CrossRef] [Green Version]
- Garg, N.; Pearce, B.; Brandner, P. Experimental investigation of a hydrofoil designed via hydrostructural optimization. J. Fluids Struct. 2019, 84, 243–262. [Google Scholar] [CrossRef]
- Tang, F.; Liu, C.; Cheng, L. A new method for low-lift water pump selection. Adv. Sci. Technol. Water Resour. 2001, 21, 41–43. [Google Scholar]
- Xie, R.; Wu, Z.; He, Y. Optimization research on passage of bidirectional shaft tubular pump. Trans. Chin. Soc. Agric. Mach. 2015, 46, 68–74. [Google Scholar]
- Dahmani, F.; Sohn, C. Effect of convergent duct geometry on the energy extraction performance of tandem oscillating hydrofoils system. Sci. China Phys. Mech. Astron. 2020, 95, 102949. [Google Scholar] [CrossRef]
- Dash, S.; Lua, K.; Lim, T. Enhanced thrust performance of a two dimensional elliptic airfoil at high flapping frequency in a forward flight. J. Fluids Struct. 2018, 76, 37–59. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Kheirkhah Gildeh, H. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2019, 19, 543–568. [Google Scholar] [CrossRef]
- Read, D.; Hover, F.; Triantafyllou, G. Forces on oscillating foils for propulsion and maneuvering. J. Fluids Struct. 2003, 17, 163–183. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Yuan, Y. Numerical and experimental investigation of internal flow characteristics and pressure fluctuation in inlet passage of axial flow pump under deflection flow conditions. Energies 2021, 14, 5245. [Google Scholar] [CrossRef]
- Kolář, V.; Moses, P.; Šístek, J. Triple decomposition method for vortex identification in two-dimensional and three-dimensional flows. In Computational Fluid Dynamics 2010; Springer: Berlin/Heidelberg, Germany, 2011; pp. 225–231. [Google Scholar]
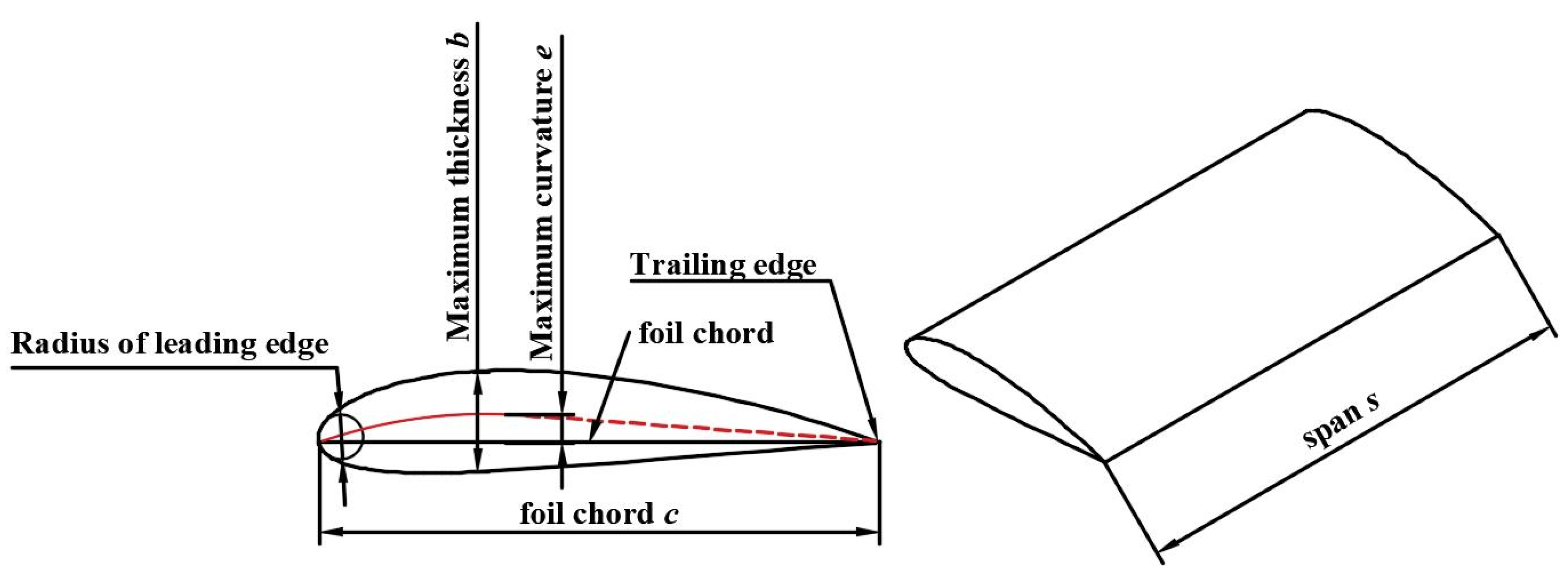

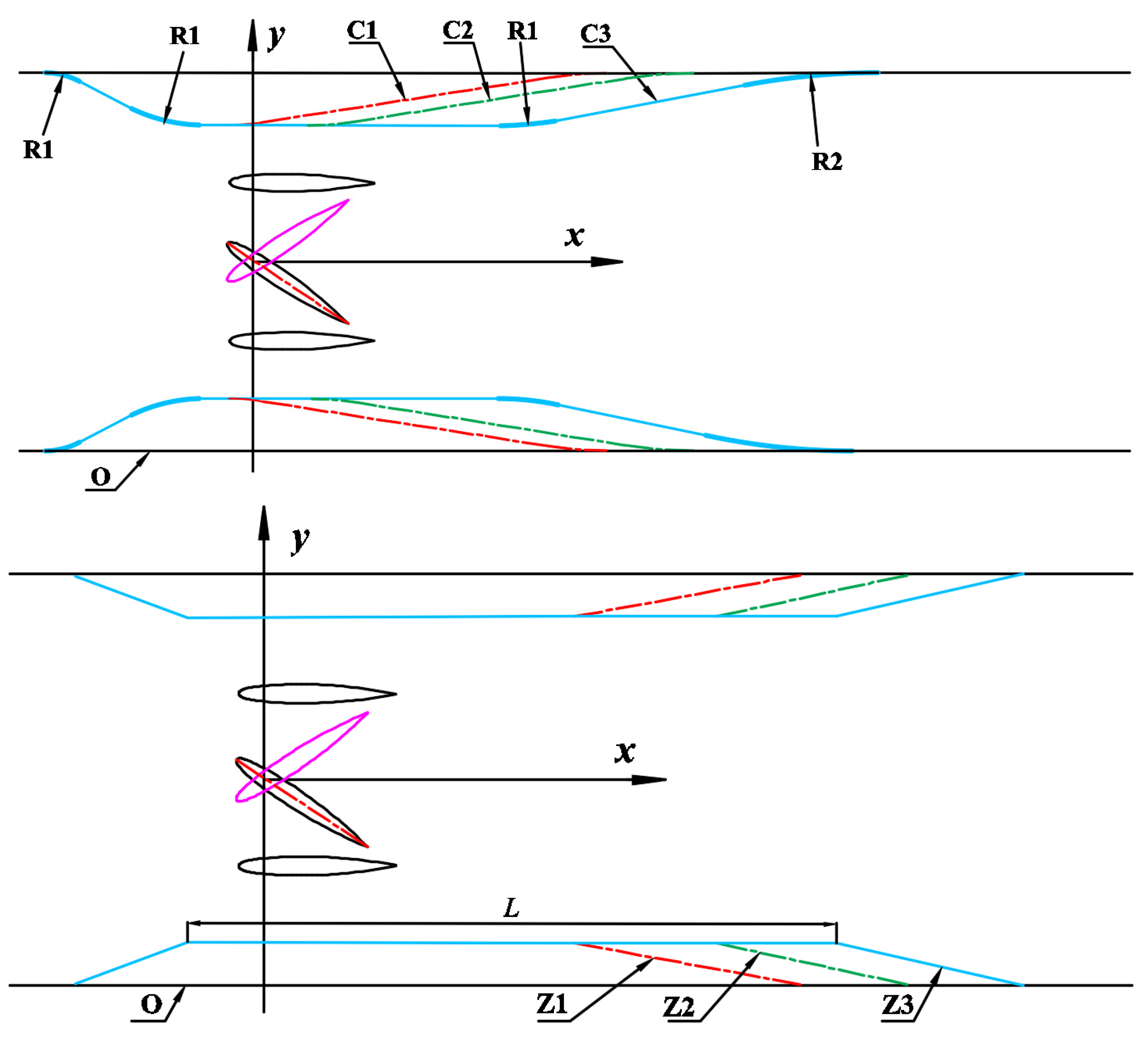
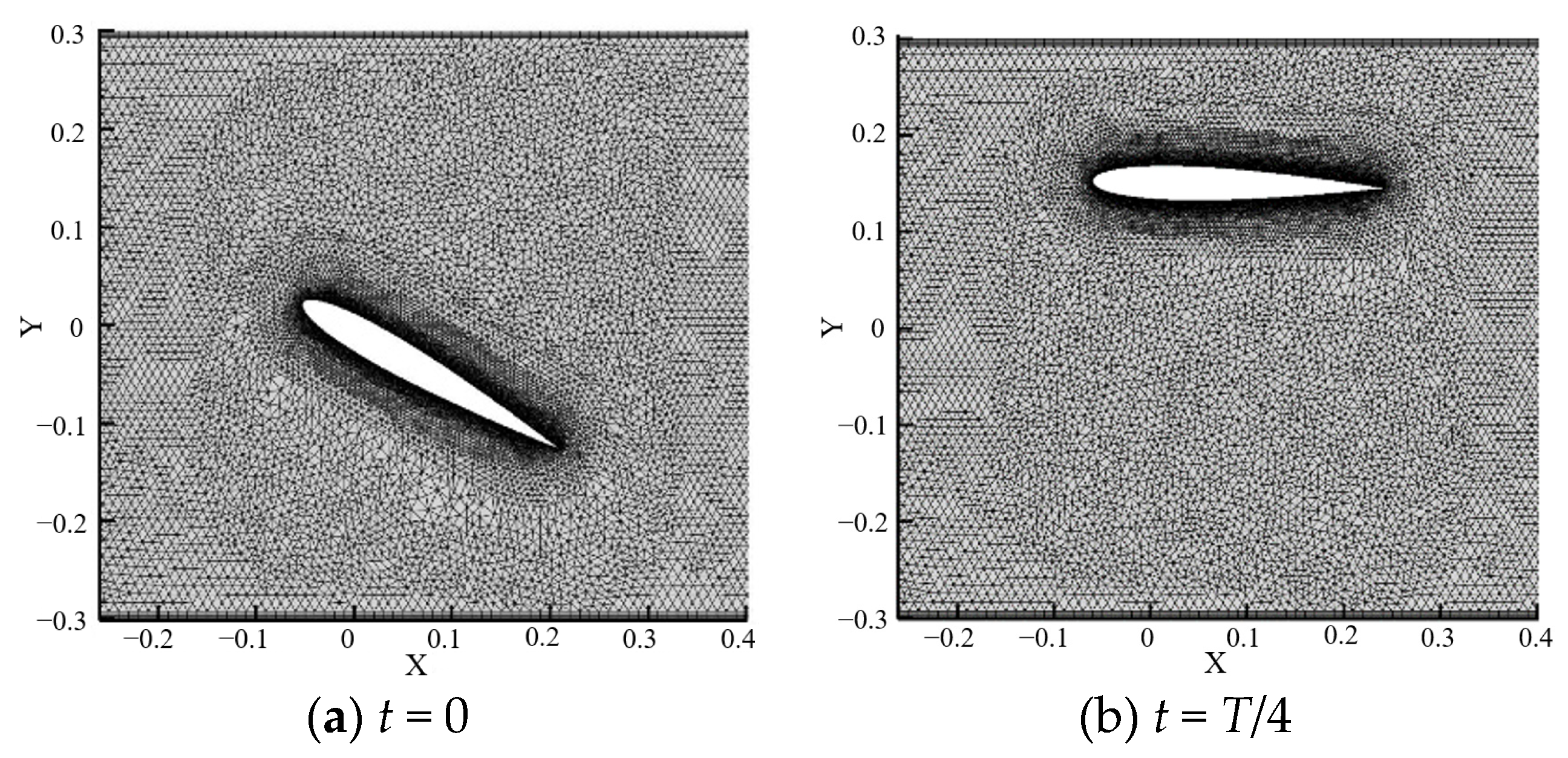
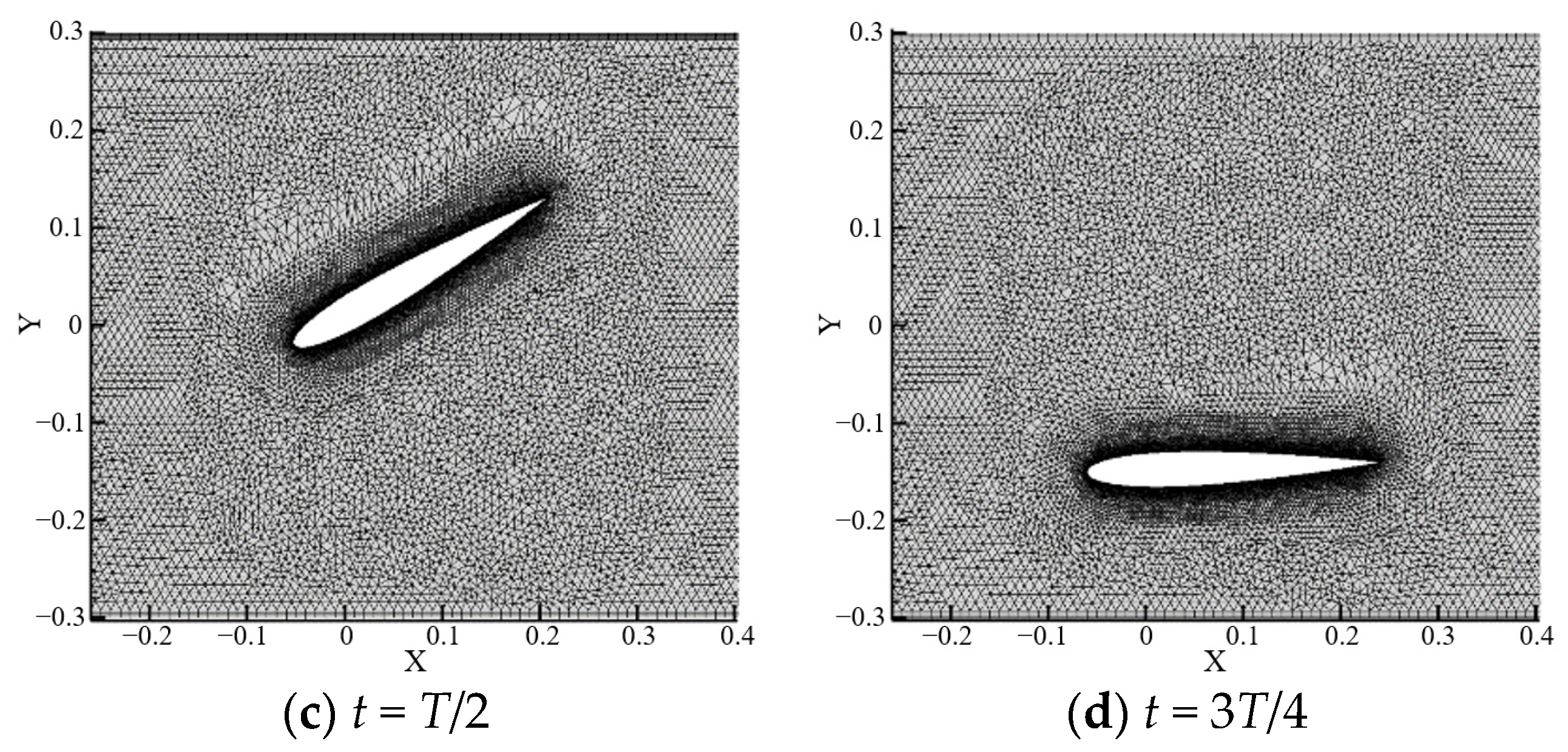




| Passage Type | C1 | C2 | C3 | Z1 | Z2 | Z3 |
|---|---|---|---|---|---|---|
| Length L/m | 0 | 0.5 | 1 | 1 | 1.5 | 2.0 |
| Terms | Equipment | Type | Systematic Error |
|---|---|---|---|
| Flow | Doppler velocimeter | WIM-@ADV | ±1% |
| Head | Differential pressure | 3051 | ±0.2% |
| Current | Clamp power meter | VC6412D | ±2.5% |
| f/Hz | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
|---|---|---|---|---|---|---|---|---|
| Expeiment1 | 0.041 | 0.079 | 0.122 | 0.159 | 0.196 | 0.234 | 0.259 | |
| v/m·s−1 | Expeiment2 | 0.043 | 0.082 | 0.128 | 0.148 | 0.197 | 0.238 | 0.262 |
| Expeiment3 | 0.049 | 0.085 | 0.132 | 0.160 | 0.201 | 0.240 | 0.268 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, E.; Luo, H.; Xie, R.; Chen, W.; Tang, S.; Jin, D. Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps. Processes 2022, 10, 2569. https://doi.org/10.3390/pr10122569
Hua E, Luo H, Xie R, Chen W, Tang S, Jin D. Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps. Processes. 2022; 10(12):2569. https://doi.org/10.3390/pr10122569
Chicago/Turabian StyleHua, Ertian, Haitao Luo, Rongsheng Xie, Wanqian Chen, Shouwei Tang, and Dongyang Jin. 2022. "Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps" Processes 10, no. 12: 2569. https://doi.org/10.3390/pr10122569
APA StyleHua, E., Luo, H., Xie, R., Chen, W., Tang, S., & Jin, D. (2022). Investigation on the Influence of Flow Passage Structure on the Performance of Bionic Pumps. Processes, 10(12), 2569. https://doi.org/10.3390/pr10122569





