Abstract
In recent years, with the rapid development of equipment manufacturing and advances in the research on mine pressure and rock mechanics, large-mining-height comprehensive mechanized coal mining technology has become increasingly widely used in thick-seam mining. On this basis, because the free space extracted is several times that of layered mining, the occurrence of strong ground pressure caused by the violent movement of the basic roof and the low recovery rate of the top coal have become the main problems. In this study, Dong Liang Coal Mine was taken as the engineering background by which to study the three typical movement forms of the basic roof, and the critical fracture conditions of the three forms were obtained through theoretical calculations. The movement result state of the basic roof strata was taken as the different overlying boundary conditions of the top coal to simulate its impact on the recovery rate, to explore the interaction mechanism between the basic roof strata and the top coal, and for use as a theoretical basis to guide engineering practice to improve energy recovery rates and safety efficiency.
1. Background Introduction
Owing to the breakthroughs in and the considerable development of mechanical equipment design and the manufacturing industry, as well as developments in the theory of mine pressure mechanics in recent decades, coal mining equipment is being developed towards a large-scale, heavy, and intelligent design. Thick and extra-thick coal seams that used to rely only on layered mining can now be recovered by using large-mining-height comprehensive mechanized mining or large-mining-height fully mechanized caving mining technology. Compared with the traditional layered mining method, the increase in the mining height has the characteristics of high resource recovery rates and significant reductions in the number of driving and moving operations. Additionally, large-mining-height coal mining technology is also faced with increases in the disturbance range of the roof and floor; the obvious ground pressure appearance and the movement of the roof and the top coal have significantly different movement evolution and interaction relations. Based on the provisions and assumptions of rock fracture mechanics and material mechanics for beam components with one end fixed and one end simply supported, we established a mechanical model of direct roof top coal body boundary interaction, transferred the results of direct roof rock beam movement under the basic roof to the top coal in different areas, and calculated three different types of direct roof top coal interaction relationships: the bench vertical interaction relationship, the rotation action relationship of the short cantilever beam, and the horizontal action relationship of the long cantilever beam.
The movement of the roof structure and the displacement of overburden caused by mining are some of the important factors that lead to the communication of aquifers, the appearance of strong ground pressure in the working face, and the instability of coal pillars in stopes. Since the end of the 20th century, the overlying rock movement caused by mining operation disturbances has mostly used the masonry beam [1,2,3] theory, and the transmission of rock beam theory [4,5] is often used for calculations and solutions. For the integral calculation principle of bearing pressure and the establishment of the beam model, refer to Brauner, G et al. [6], Barczak T.M. et al. [7], and Goodman R. E. et al. [8]. To date, the above achievements have opened up the research field of roof rock pressure control in the field of coal mining engineering, and great progress has been made on this basis by experts and scholars in China and abroad, providing a solid mechanical theoretical basis for large-scale mining equipment, the simultaneous improvement of the recovery rate of thick coal seams and even extra-thick coal seams, the rapid advancement of ultra-long working faces, and the emergence of intelligent roof control systems.
In the past decade, with the gradual entry of mines into the deep mining stage, the increase in the mining height and the gradual enrichment of the research regarding the mechanism of the short-distance coal seam and the steep coal seam groups, mining engineers have frequently faced extremely complex conditions. The calculation results obtained using the traditional empirical calculation formula and the analytical formula obtained under relatively simple hypothetical conditions are difficult to adapt to on-site phenomena. In theoretical and scientific research, because it is difficult to make adaptions between the solid mechanical boundary and the bulk top-coal boundary, the upper boundary is often conditioned by the free surface in the process of similar simulations and numerical simulations of top-coal caving mining, and the influence of the roof fracture movement and pressure change process on the top-coal fracturing movement release process is often ignored. The traditional numerical simulation method is widely based on the “continuum hypothesis” for research of roof fracture movement. In the Flac3D software (HydroChina—ITASCA R&D Center, Hangzhou, China), which uses the finite element method, the elastic–plastic ideal model, the strain-softening plastic model, and the elastic–plastic damage model take the equivalent stress, plastic zone, or damage zone as the criteria for the position of the roof occurrence span. In addition, numerous scholars use the discrete element PFC software to simplify the coal–rock unit into a rectangular block based on the discrete block hypothesis. Spherical blocks are endowed with mechanical properties such as contact stiffness and surface roughness.
The authors of this paper established a fracture mechanical model of roof overburden direct roof top coal with a large mining height based on field investigations; we also studied the mechanical state of the coal–rock interface boundary in depth, and preliminarily designed a similar simulation experimental device to modify the parameters of the numerical simulation experiment to simulate and study the evolutionary law of roof fractures. This research method is of great significance in improving the recovery rate of top coal, controlling the mine pressure, and improving the support conditions.
2. Engineering Background
2.1. Overview of Working Face
Shenmu Dongliang Coal Mine is located 35 km to the north of Shenmu County, Shaanxi Province. It is located in the area bordering the Loess Plateau and the Maowusu Desert in northern Shaanxi Province. It has the geological characteristics of a thick loess layer load and an aeolian sand permeable layer. The Baotou Shenmu Shuozhou Railway runs through the eastern area of the mine field. The transportation is relatively convenient. According to the borehole disclosure and observation data, the Yan’an Formation coal-bearing rock series is a monoclinal structure inclined to the north or northwest, with a flat dip angle of about 1°, aerial photo of the mine field location is shown in Figure 1:
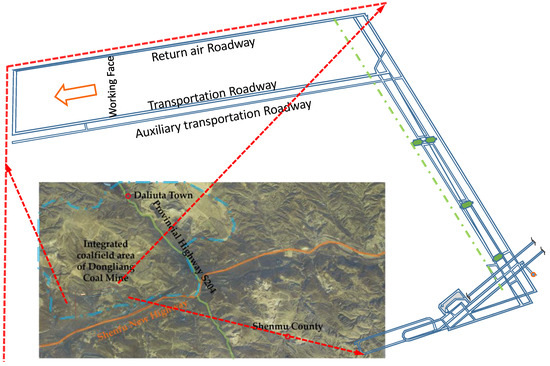
Figure 1.
The relationship between the location of the mine field and the stope layout.
The complexity of the structure is relatively simple. The average thickness of the 2-2 coal seam is 12.0 m, the strike longwall retreating mining method is adopted, the roof is managed by the total caving method, and a shield hydraulic support is used to support the roof of the stope. The direct roof of the 2-2 coal seam is fine-grained sandstone, followed by medium and fine sandstone with a thickness of about 4.3 m. The basic roof is 16.5 m medium-grained sandstone. The floor is dominated by siltstone, followed by mudstone with a thickness of about 2.5 m. The dip length of the working face is 303 m. At present, a 20 m wide coal pillar is reserved in this section. The roadway layout plan and the geological histogram of the working face are shown in Figure 2.
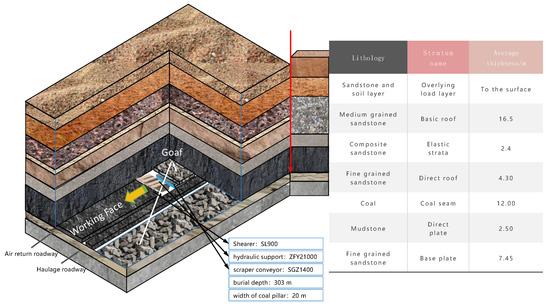
Figure 2.
Comprehensive histogram.
2.2. Establishment of a Mechanical Model of Overburden
It can be seen from the comprehensive histogram of the rock stratum shown in Figure 2 that the overburden of the stope is mainly composed of a relatively brittle direct top of fine sandstone and a basic top of thick-, hard-, and medium-grained sandstone. The combined sandstone in the middle is thin and weak in lithology, which mainly serves as a load transfer and elastic foundation.
An elastic medium-thick plate with zero boundary displacement is separated from the basic roof rock of medium-grained sandstone overlying the stope. Its spatial stress component is shown in Figure 3.
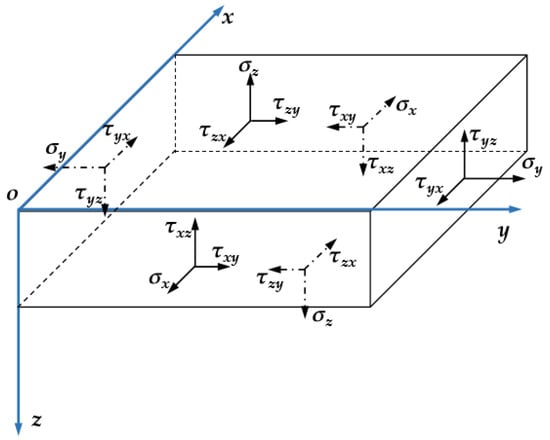
Figure 3.
Schematic diagram of the elastic mechanic model for the basic roof.
The balance equation of the space problem is as follows:
In Equation (1), σx, σy, and σz are the normal stresses in the direction, Mpa; τyx, τzx, and τyz are the shear stresses in the direction, MPa, and Kx, Ky, and Kz are the volume force per unit volume in the direction.
3. Three Typical Characteristics of Basic Roof Movement on Direct Roofs with a Large Mining Height
3.1. Mechanical Model of a Beam Obtained by Dissecting a Medium-Thick Plate
Because the mining height of fully mechanized mining and fully mechanized caving mining technology with a large mining height is multiple times that of an ordinary mining height, the size and cutting depth of the coal drum are different. The width of the front and rear scraper conveyor, the length of the top beam of the hydraulic support, and the effective support distance are also significantly increased, and the mining space is many times larger than that of general fully mechanized top-coal caving. Therefore, the space dimension of the top coal and the free face under the direct roof is also far larger than that of general fully mechanized top-coal caving and fully mechanized top-coal caving.
In view of the above reasons, since the mining disturbance range of the large-mining-height process gradually increases, and the bearing control effect of the direct roof on the transfer of load and movement results in the overlying strata being relatively weaker than that of the non-large-mining-height process, the basic roof of most large-mining-height working faces plays an absolute control role in the rock pressure behavior of the working face and the caving behavior of the top coal; for example, this occurs in Caojiatan coal mine [9], Tongxin coal mine [10], and Hanglaiwan coal mine [11]. According to microseismic event records and field investigations and analyses, it is considered that there are three typical types of the result of the fault movement of the overlying thick and hard basic roof rock after mining disturbances and its influence on the direct roof and intermediate cushion below: I. bench vertical action; Ⅱ. short cantilever beam—rotary action type; and Ⅲ. long cantilever beam—horizontal action type, as shown in Figure 4.
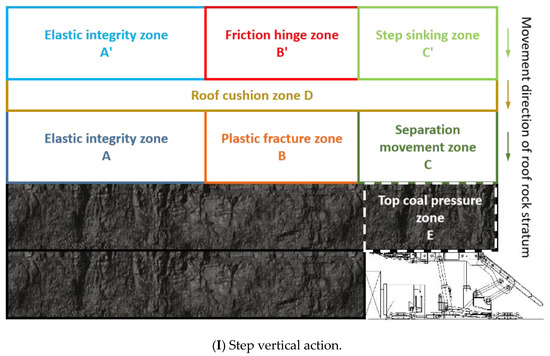
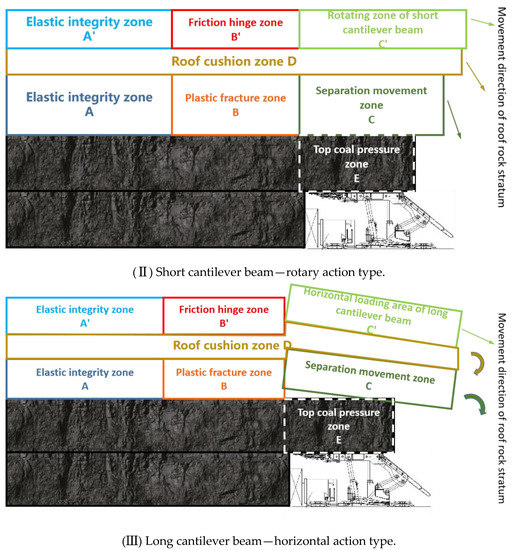
Figure 4.
Typical state of overlying rock movement in a stope with a large mining height.
Li H’s [12] discriminant theoretical formulas for mining overburden failure conditions have been clarified. Because the control effect of the direct roof strata is limited, it is not conducive to supporting working conditions and working face rock pressure control, that is, when the working face is pushed forward from the cutting position, it is assumed that the length of the free surface of the basic roof rock is the same as the pushing distance, and S is the balance judgment formula of the elastic deformation stage of the basic roof rock:
where q is the second root of the ratio of the first and third invariants of the partial stress tensor s; J and the biaxial and uniaxial compressive yield stress σ’ are about [J =(σ’ − 1)/(2σ’ − 1)]; <σ> is the symbol of the Macaulay matrix operation; σt is the tensile stress, MPa, and γ is a parameter related to controlling the cross-sectional shape of the yield surface, according to Li’s research results in 2018 [13], taking 2.991 as the value.
The plastic state equilibrium discrimination is combined in Equation (3):
where G is the judgment formula of the plastic deformation equilibrium of the basic roof stratum; ψ is the shear expansion angle, °, and p is the imaginary part of the conjugate complex of the deviator stress tensor.
Based on the mechanical calculation method of calculating the I/II mixed fracture by the first-principal stress synthesis method, only singular terms are retained in the stress components, and the stress components of high-order small terms are ignored. At this time, the criterion expression of the I/II mixed-fracture tensor formula is as follows:
where is the stress intensity factor of a mode I crack; is the stress intensity factor of a mode II crack; r is the polar diameter around the crack in the polar coordinate system, m, and θ is the polar angle of the crack in the polar coordinate system, rad.
In the actual process of coal mining, due to the geological and stress conditions including too many different influencing factors [14] and due to the changes in the overburden conditions, strata, and rock mechanical properties, it is difficult to determine two stopes with the same roof structure and migration patterns in the field measurements. Therefore, in this study, we only abstractly analyzed three kinds of mechanical models that are common in the roof structure of coal mines from the perspective of rock mechanics, and these were combined with the cognitive laws of traditional research paths; on this basis, in further research, we propose the use of similar physical simulation mechanical experiments to simulate the broken movement form of the coal mine roof along the advancing direction of the working face and the shearing tendency of the coal machine.
3.2. The Boundary Conditions of the Experimental Model Are Set in the Simulation of the Excavation Results
With the continuous increase in the normal stress and stress components in the interface internal stress matrix, the possibility of plastic failure also increased. It is further concluded that with the continuous advancement of the working face, the increase in the exposed length under the basic roof will lead to different forms of failure modes and movement characteristics of the basic roof strata with different thickness-to-span ratios. When the thickness-to-span ratio is less than 0.5, when the rock stratum breaks, the masonry beam structure will be formed, that is, a type III long cantilever beam with a horizontal action structure. When the thickness-to-span ratio is greater than 0.5, the rock stratum will break and form a stepped rock beam structure, i.e., a type I stepped vertical action structure. According to the research results of Zuo et al. [15], it can be considered that the thickness-to-span ratio of a basic roof rock layer of 0.5 is the critical transformation point of the fracture form of the rock layer, and the type II short cantilever beam rotary action structure occurs from time to time as a state near the critical point. In this movement form, the deflection of the overlying rock in the vertical direction is large, and the horizontal force of the rotary lap on the top coal during the movement of the gangue fulcrum in the goaf will also promote the arch articulation of the top coal when it is released [16]. The results of these two actions cause the cracks in the top coal to more fully develop, and cannot easily cause large displacement to the goaf direction leading to coal loss [17,18]. With the intervention of sufficient top-coal pre-cracking strategies, arch articulation can be effectively avoided. Therefore, in a fully mechanized top-coal caving face with a large mining height where the caving property of hard top coal is not ideal, the recovery rate of top coal can be improved by reasonably optimizing the roof fracture migration form to move closer to a type II structure.
Figure 5 shows the geometric model established by the working face and roadway layout and the spatial position relationship between the roof and floor of the coal seam in the numerical simulation experiment.
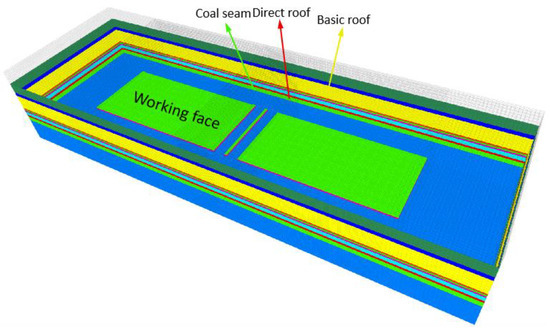
Figure 5.
Numerical simulation model of overburden in a stope.
As shown in Figure 6, as the thickness-to-span ratio of the basic roof gradually reached 0.5 from less than 0.5 and then increased to more than 0.5, the peak displacement of the roof in the working face with a large mining height increased from 0.45 m to 0.5 m when the thickness-to-span ratio was 0.5. When the thickness-to-span ratio exceeded 0.5, the peak displacement of the roof reached 0.55 m. In addition, it is worth noting that when the thickness-to-span ratio of the basic roof rock increased, the displacement and range of the floor also increased, which indicates that the different states of loading and movement of the basic roof rock have a structural impact on the whole stope space.
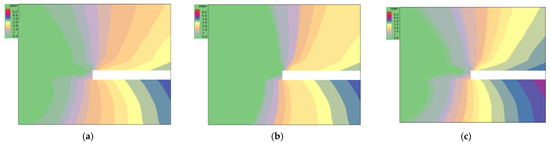
Figure 6.
Evolutionary law of displacement field of surrounding rock with different basic top thickness-to-span ratios in the advancing direction of a stope. (a) Thickness-to-span ratio less than 0.5. (b) Thickness-to-span ratio of 0.5. (c) Thickness-to-span ratio greater than 0.5.
Similarly, from the analysis of the effect of the overlying basic roof thickness-to-span ratio on the stress field of the stope shown in Figure 7, it can be concluded that with the increase in the thickness-to-span ratio, the leading stress peak value and range increased significantly, from 24.8 MPa to 28.62 MPa and, finally, to 32 MPa. The increase in the basic roof thickness of the same lithology led to different modes on the plate failure section of the basic roof stratum. When the rock layer is thin, the failure of the rock plate is mainly due to the normal tensile stress on the interface exceeding the tensile strength of the rock layer under the action of the roof top-coal clamping. When the rock layer is thick, the tensile stress cannot cause the thick and hard basic top rock layer to break. When the shear stress acting in the tangential direction of the breaking section reaches the shear strength of the rock layer at the fixed end edge, the rock layer will be sheared and destroyed and the step will sink. Additionally, the failure of the basic roof rock in the middle scale may only meet the two forms of mixed failure at the same time, that is, there is both vertical pressure and horizontal rotation on the top coal.
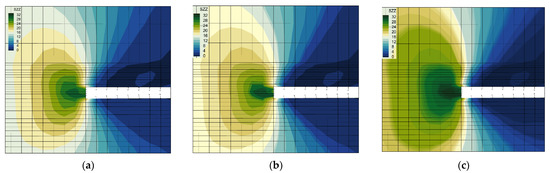
Figure 7.
Evolutionary law of the stress field of surrounding rock with different basic top-coal thickness-to-span ratios in the advancing direction of a stope. (a) Thickness-to-span ratio less than 0.5. (b) Thickness-to-span ratio of 0.5. (c) Thickness-to-span ratio greater than 0.5.
Taking the upper boundary stress conditions of the top coal and the breaking results of the direct roof under the action of the basic roof movement studied above as the upper boundary loads of the coal drawing simulation experiment, it was found that when the bench vertical action occurred when the basic roof thickness-to-span ratio was greater than 0.5, as shown in Figure 8a, the top-coal drawing effect was poor, and there was more coal lost in the goaf. The result of the roof bench sinking was that the top coal fell into the goaf without fully rotating and squeezing. Under the tensile breaking mode with a thickness-to-span ratio less than 0.5, the recovery rate of the top coal was significantly improved, and gangue was observed. However, the interaction between the hinge structure of the roof and the top coal was compressed into an arch, resulting in a surplus of top coal in each round of coal drawing, which could not be released well in the simulation experiment. Obviously, there are more constraints in field applications resulting in some of the top coal being trapped by the hinge structure of the roof and left in the goaf [19]. When the thickness-to-span ratio was equal to about 0.5 in the mixed-fracture mode, the roof was characterized by short cantilever beam rotation. The rotation of the roof gave the top coal a constraint to move to the free surface, and the vertical action stage before the rotation also fractured the top coal to a certain extent, damaged the integrity of the top coal, and made the size of the released coal smaller, the degree of fragmentation higher, and the migration speed faster, so that it could fall onto the rear scraper conveyor at the top of the coal tap in time instead of being left in the goaf, improving the recovery rate of coal resources, as shown in Figure 8c. The typical characteristics of roof rotation cause the top coal to become fully pre-cracked and not obviously hinged in an arch shape during the process of releasing and moving. Only a small amount of boundary coal loss remains behind the goaf. Therefore, when the thickness-to-span ratio reaches about 0.5 and the short cantilever rotation action characteristics appear, these conditions are the most favorable for the recovery of the top coal.

Figure 8.
Evolutionary law of top-coal migration and release under different roof boundary conditions. (a) Law of top-coal release and migration of step vertical action. (b) Law of top-coal release and migration of short cantilever beam—rotary action type. (c) Law of top-coal release and migration of long cantilever beam—horizontal action type.
4. Discussion and Conclusions
4.1. Discussion
Based on the established mechanical model of the top coal–direct roof–follow-up cushion–basic roof structure combined with fracture mechanics and rock mechanics, the coupling boundary conditions of the top coal–roof interface were theoretically deduced, the discrimination formulas of the elastic conditions and plastic conditions were obtained, and the critical conditions were calculated. It is considered that the basic top thickness-to-span ratio has the most significant influence on the different characteristics of rock fracture and movement. Then, numerical simulation experiments were carried out. The evolutionary laws of the stress and strain fields of surrounding rock excavation with different thickness-to-span ratios were analyzed and studied so as to verify the theoretical research results. Finally, the results were substituted into the discrete element simulation software to analyze the influence of the different characteristics of roof failure structure and critical parameters on the difficulty of top-coal caving and the recovery rate.
- The theoretical formula showed that when the thickness-to-span ratio of the basic roof was less than 0.5, the movement of the basic roof belonged to the long cantilever beam horizontal action mode. When the thickness-to-span ratio of the basic roof reached about 0.5, the movement of the basic roof belonged to the short cantilever beam rotation mode. When the thickness-to-span ratio of the basic roof stratum was greater than 0.5, the basic roof movement belonged to the step vertical action mode. These three different migration and fracture modes are significant for determining the state of direct roofs and top coal.
- According to the effect and recovery rate of top-coal caving, it can be judged that the bench subsidence of thick and hard basic top rock is not conducive to top-coal caving, which is somewhat different from the traditional on-site experience of weakening the support pressure by roof pre-cracking in rock pressure control. Therefore, when shortening the roof fracture step and reducing the roof pressure intensity, the thick and hard basic top rock should also be cut in the appropriate horizontal direction of the large-mining-height working face. The thickness-to-span ratio should be about 0.5 to prevent the bench vertical action from causing the top coal to accelerate toward the goaf, thereby causing a large amount of coal loss.
- Under the mining activity of the fully mechanized top-coal caving face with a large mining height, the stress state in the roof rock has a key impact on the roof cutting process. The relationship between the three-dimensional principal stresses directly determines the dominant direction of fracture development during hydraulic fracturing [20,21,22,23]. Therefore, according to the application of the theoretical formula for the ideal thickness-to-span ratio of the basic roof and the boundary conditions of the top coal obtained in this paper, the roof control parameters can be optimized. By improving the geometry of the basic roof and the way in which the rock mechanical properties act on the boundary of the top-coal roof, the purpose of improving the mine pressure and the recovery rate can be achieved.
4.2. Conclusions
- The fracture state of a basic roof with different thickness-to-span ratios has a significant influence on the recovery rate of top-coal caving.
- During coal mining, hydraulic fracturing, blasting roof breaking, ground fracturing, and other means should be used to control the thickness-to-span ratio of the basic roof at about 0.5 so as to reduce the occurrence of ground pressure and to improve the recovery rate of coal resources.
Author Contributions
Conceptualization, L.L. and J.L.; methodology, X.Z.; software, J.L.; validation, L.L. and X.Z.; formal analysis, J.L.; investigation, B.H.; resources, L.L.; data curation, L.L.; writing—original draft preparation, L.L.; writing—review and editing, L.L.; visualization, J.L.; supervision, L.L.; project administration, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study does not require ethical approval.
Informed Consent Statement
The study did not involve humans.
Data Availability Statement
The experimental and analytical calculation result data used to support the findings of this study are included within the article.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
References
- Qian, M.G.; Miao, X.X.; He, F.L. Analysis of the key blocks of the “masonry beam” structure in the stope. Acta Coal Sin. 1994, 6, 557–563. [Google Scholar]
- Miao, X.X.; Qian, M.G. The overall structure of surrounding rock in the stope and the mechanical model of masonry beams. Mine Press. Roof Manag. 1995, 3, 197. [Google Scholar]
- Qian, M.G.; Zhu, D.R.; Wang, Z.T. Fracture type of the main roof rock and its influence on the pressure on the working face. J. China Acad. Min. Technol. 1986, 2, 12–21. [Google Scholar]
- Song, Z.Q.; Liu, Y.X.; Chen, M.B.; Song, Y. Discussion on bearing pressure behavior before and after rock beam fracture and its application. J. Shandong Inst. Min. Technol. 1984, 1, 27–39. [Google Scholar] [CrossRef]
- Song, Z.Q.; Song, Y.; Jiang, Y.J.; Liu, Y.X. Methods and steps of roof control design in mining face. Coal Sci. Technol. 1989, 9, 6–63. [Google Scholar] [CrossRef]
- Bukhoino, G. Rock Pressure and Rockburst; Coal Industry Press: Beijing, China, 1985. [Google Scholar]
- Barczak, T.M.; Oyler, D.C. A Model of Shield Strata Interaction and Its Implications for Active Shield Setting Requirements Missing; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1991.
- Goodman, R.E.; Shi, G.H. Block Theory and Its Application to Rock Engineering; Prentice-Hall: Hoboken, NJ, USA, 1985. [Google Scholar]
- Xu, X.D. Study on the Mechanism of Strong Ground Pressure and Pressure Relief Control along the Goaf in Caojiatan Coal Mine’s Extra Thick Coal Seam; Jilin University: Changchun, China, 2022. [Google Scholar] [CrossRef]
- Chen, Y. Study on the Mining Floor Deformation and Failure Depth of Extra Thick Coal Seam in Datong Mining Area; China University of Mining and Technology: Beijing, China, 2021. [Google Scholar] [CrossRef]
- Dong, Z.Y.; Wang, S.M. Analysis of the impact of coal mining on groundwater resources in Yuxi River Basin in Northern Shaanxi—Taking hanglaiwan coal mining area as an example. Resour. Environ. Arid Areas 2017, 31, 185–190. [Google Scholar] [CrossRef]
- Li, H.; Tang, S.B.; Ma, L.Q.; Bai, H.B.; Kang, Z.Q.; Wu, P.F.; Miao, X.C. Study on continuous discrete coupling simulation of progressive failure of mining overburden. J. Rock Mech. Eng. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Bai, H.B.; Wu, J.J.; Li, Z.Y.; Meng, Q.B.; Guo, J.Q.; Zhu, D.F.; Xiao, M.D.-P. Random damage constitutive model and its application in preventing water inrush of collapse columns. Geotech. Mech. 2018, 39, 4577–4587. [Google Scholar] [CrossRef]
- Zuo, J.P.; Yu, M.L.; Sun, Y.J.; Wu, G.S. Analysis of fracture mode transformation mechanism and mechanical model of rock layers with different thicknesses. Acta Coal Sin. 2022, 1–18. [Google Scholar] [CrossRef]
- Luo, J.; Yan, S.; Yang, T.; Mu, H.; Wei, W.; Shen, Y.; Mu, H. Mechanism of Hydraulic Fracturing Cutting Hard Basic Roof to Prevent Rockburst; Hindawi Limited: London, UK, 2021. [Google Scholar]
- Hubbert, M.K.; Willis, D. Mechanics of hydraulic fracturing. Trans. AIME 1972, 210, 153–168. [Google Scholar] [CrossRef]
- Zhang, P.; Liang, X.; Xian, C.; Liu, B.; Wang, W.; Zhang, C. Geomechanics simulation of stress regime change in hydraulic fracturing: A case study. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 1–18. [Google Scholar] [CrossRef]
- Murthy, M.V.V.S.; Renji, K.; Gopalakrishnan, S. Multi-transform based spectral element to include first order shear deformation in plates. Int. J. Mech. Sci. 2015, 96–97, 110–120. [Google Scholar] [CrossRef]
- Guy, R.; Kent, M.; Russell, F. An assessment of coal pillar system stability criteria based on a mechanistic evaluation of the interaction between coal pillars and the overburden. Int. J. Min. Sci. Technol. 2017, 27, 9–15. [Google Scholar]
- Lv, K.; He, F.; Xu, X.; Zhai, W.; Qin, B. Irregular load—Fracture characteristics and stability analysis of elastic foundation basic roof structure. J. Rock Mech. Eng. 2022, 1–18. [Google Scholar] [CrossRef]
- Xu, X.; He, F.; Lv, K.; Wang, D.; Li, l.; Zhai, W. Study on reasonable roof cutting parameters of thick hard roof cutting and retaining roadway. J. Coal Ind. 2022, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Ren, Y.; Wang, N.; Jin, N.; Ou, X.; Luo, J.; Mei, C. Morphology and evolution characteristics of caving roof in goaf. J. Coal Ind. 2021, 46, 3771–3780. [Google Scholar] [CrossRef]
- Chen, D.; Wu, Y.; Xie, S.; Guo, F.; He, F.; Liu, R. Study on the initial fracture of basic roof slab at the boundary of long side goaf and elastic-plastic softening foundation. J. Coal Ind. 2022, 47, 1473–1489. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).