Multiple Graph Adaptive Regularized Semi-Supervised Nonnegative Matrix Factorization with Sparse Constraint for Data Representation

Abstract

Multiple graph and semi-supervision techniques have been successfully introduced into the nonnegative matrix factorization (NMF) model for taking full advantage of the manifold structure and priori information of data to capture excellent low-dimensional data representation. However, the existing methods do not consider the sparse constraint, which can enhance the local learning ability and improve the performance in practical applications. To overcome this limitation, a novel NMF-based data representation method, namely, the multiple graph adaptive regularized semi-supervised nonnegative matrix factorization with sparse constraint (MSNMFSC) is developed in this paper for obtaining the sparse and discriminative data representation and increasing the quality of decomposition of NMF. Particularly, based on the standard NMF, the proposed MSNMFSC method combines the multiple graph adaptive regularization, the limited supervised information and the sparse constraint together to learn the more discriminative parts-based data representation. Moreover, the convergence analysis of MSNMFSC is studied. Experiments are conducted on several practical image datasets in clustering tasks, and the clustering results have shown that MSNMFSC achieves better performance than several most related NMF-based methods.

1. Introduction

In the era of big data, more and more high-dimensional data have been encountered in various practical application fields. Generally speaking, most of the original data is noisy, and many features in the data are not useful in real-world tasks. In this case, how to discover the low-dimensional data representation in the massive data is critical, since the obtained data representation used in practical applications can efficiently enhance the performance of learning algorithm than the original data. In recent decades, the matrix factorization technique, as one of the popular data representation techniques, has gained much attention because of its advantages for learning superior data representation. The commonly used matrix factorization methods include the singular value decomposition [1], nonnegative matrix factorization [2], independent component analysis (ICA) [3], deterministic column-based matrix decomposition [4], principal component analysis [5] and so on. Among these methods, NMF has shown good performances due to its ability of producing a parts-based representation. Therefore, NMF-based methods have widely used in numerous actual tasks such as document analysis, bioinformatics, information retrieval and so on [6,7,8,9,10,11].

The standard NMF decomposes the nonnegative matrix $\mathbf{X}\in {\mathbb{R}}_{\ge 0}^{M\times N}$ into a nonnegative basis matrix $\mathbf{U}\in {\mathbb{R}}_{\ge 0}^{M\times K}$ and a nonnegative coefficient matrix $\mathbf{V}\in {\mathbb{R}}_{\ge 0}^{N\times K}$, $K\ll min(N,M)$, such that the product of $\mathbf{U}$ and ${\mathbf{V}}^T$ can approximate the original matrix $\mathbf{X}$ as close as possible. During the decomposing procedure one can observe that the nonnegative constraints are enforced into the decomposed factors, NMF often can result in a parts-based data representation [2]. Usually, the advantages of the parts-based representation in NMF have been proved in different fields, and they also have significant improvements for the performance of NMF-based methods in many real-world applications [12,13]. Although the standard NMF model has obtained much attentions in recent decades [14], it still has some critical defects. For instance, it entirely ignores the geometrical structure information, and cannot exploit any supervisory information to increase the quality of decomposition of NMF [12,15,16]. Furthermore, the basic NMF method lacks some extra constraints such as sparse constraint to ensure the sparse parts-based representation, which will have an obvious improvement for the performance of NMF-based algorithms [17].

To enhance the performance of the original NMF method, much new research approaches have been developed in recent years [18,19,20,21,22]. For example, the graph regularization–based NMF methods have been proposed [23,24,25], which consider the intrinsic geometry structure information of data (or feature) space, and incorporate the single (or dual) graph regularization for enhancing the performance. Moreover, the limited supervisory information is used in semi-supervised NMF (SSNMF) methods for further capturing better low-dimensional data representation in practical tasks, since the usage of the prior knowledge can effectively improve performance [16,26,27]. In addition, to ensure the decomposed results are the sparse representation, the sparse and orthogonal NMF methods with different constraints such as sparse constraint and orthogonal constraint, respectively, have also been proposed in [28,29,30,31] for simplifying the computation complexity and ensuring the sparse parts-based representation. However, up to now, the SSNMF method including the multiple graph regularization and the sparse constraint has not been studied yet.

In this paper, a new sparse approach, namely, the multiple graph adaptive regularized SSNMF with sparse constraint (MSNMFSC), is proposed for exploiting good data representation. In particular, MSNMFSC combines together the multiple graph adaptive regularization, the limited supervised information and the dual sparse constraints for the basis and coefficient matrices, to guarantee part-based representation and improve the clustering performance. The multiplicative update algorithm is used to solve the optimization problems of MSNMFSC and obtain the multiplicative update rules of MSNMFSC. The convergence of MSNMFSC is analyzed. Extensive clustering experiments have shown the effectiveness of MSNMFSC on seven real-world image datasets, in comparison to several related NMF methods. The key contributions of our work are:

• This paper proposes the MSNMFSC method, which incorporates the multiple graph adaptive regularization, the limited supervisory information and the sparse constraint into the original NMF model for learning superior low-dimensional data representation.
• The multiplicative update rules of MSNMFSC are derived by solving the optimization problem using the multiplicative update algorithm.
• The convergence of MSNMFSC is analyzed theoretically, and the objective function will monotonically decrease under the update rules of MSNMFSC.

The rest of this paper is organized as follows. Section 2 introduces the preliminaries. Section 3 derives the MSNMFSC method in details. Section 4 analyzes the convergence of the MSNMFSC method. Section 5 gives the clustering experimental results. Finally, Section 6 draws the conclusion of this paper.

2. Preliminaries

2.1. Notations

Notations in this paper are defined as follows: uppercase boldface letters (e.g., $\mathbf{A}$), lowercase boldface letters (e.g., $\mathbf{a}$) represent the matrices and vectors, respectively; ${\mathbf{a}}_i$ and ${\mathbf{a}}_{i*}$ represent the i-the column and row vector of $\mathbf{A}$, respectively; $a_{ij}$ (or ${\mathbf{A}}_{ij}$) is the $(i,j)$-th entry of $\mathbf{A}$. $Tr(·)$ and ${(·)}^T$ are the trace and the transpose operator of a matrix, respectively. ${\parallel ·\parallel }_F$ denotes the Frobebius norm of the matrix.

2.2. Related Works

NMF has become a popular matrix factorization technique, and is widely used in data mining, pattern recognition and so on. Inspired by previous work (i.e., positive matrix factorization in [32]), Lee and Seung firstly proposed the NMF model, and then developed a multiplicative update algorithm to solve the optimization problem of NMF [2]. Owing to its competitiveness and interpretation, the improved NMF methods from different aspects have been presented in recent decades. The following will introduce the most related NMF-based methods.

Cai et al. first proposed the graph regularized nonnegative matrix factorization (GNMF), which constructed an affinity graph to encode the geometrical information and got more discriminating power than orginal NMF [15]. Then Sun et al. developed the sparse dual graph-regularized NMF(SDGNMF) by incorporating the dual graph-regularized and sparse constraints to discover the geometrical information of the data space and feature space [17]. In order to improve the robustness of NMF, Peng et al. proposed the correntropy-based dual graph regularized NMF with local coordinate constraint (LCDNMF) which was robust to the noisy data contaminated by outliers [12]. After that, Peng et al. further proposed the correntropy-based orthogonal nonnegative matrix tri-factorization (CNMTF) algorithm which not only applied correntropy to NMTF to measure the similarity, but also preserved double orthogonality conditions and dual graph regularization [18]. Usually, it is difficult to select a suitable graph model for the single graph regularized NMF methods. Hence, Shu et al. proposed the parameter-less auto-weighted multiple graph regularized NMF (PAMGNMF), which could automatically obtain an optimal weight for each graph and is easily to be applied to practical problems [25].

In recent years, several SSNMF methods have been proposed, since the obtained supervised information has great contribution for gaining the performance in clustering tasks. For instance, Li et al. developed the semi-supervised graph-based discriminative NMF (GDNMF) method, which incorporated the label information of data into the graph-based NMF to enhance the discriminative abilities of clustering representations [33]. Meng et al. proposed the semi-supervised dual graph regularized NMF (SDNMF) method with sparse and orthogonal constraints which added dual-graph model into semi-supervised NMF to improve the clustering performance [23]. Different with the above semi-supervised NMF methods, Wang et al. presented the SSNMF method with pairwise constraints(CPSNMF), which first propagated the constraints from constrained samples to unconstrained samples to obtain the constraint information of the entire dataset. Therefore, CPSNMF can fully utilize the constraint information [26]. After that, Peng et al. proposed the correntropy-based SSNMF (CSNMF) method, which both used the pointwise and pairwise constraints simultaneously to improve the effectiveness of NMF, and also adopted a correntropy-based loss function to improve the robustness [16]. Recently, the MSNMF method was presented in our previous work, which combined the supervised information with multiple graph regularization to obtain better clustering results [34].

In addition, various kinds of constraint conditions, especially the sparse constraint, have been enforced into the standard NMF to improve the performance. For example, Hoyer et al. first incorporated the sparse constraints into NMF to improve the parts-based representations [28]; Alberto et al. proposed the nonsmooth nonnegative matrix factorization (nsNMF), which represented sparseness in the form of nonsmoothness, and got advantages in reconstructing the original data faithfully [29]; and Yang et al. developed the fast NsNMF (FNsNMF), which designed a Lipschitz constant-based proximal function and got a nonlinear convergence rate, which was much faster than the former nonsmooth nonnegative matrix factorization [35].

2.3. Constraint Propagation Algorithm (CPA)

For most of the existing semi-supervised NMF, it is hard to use the supervised information completely. In order to make full use of the limited supervised information, the CPA [26] is presented to obtain a new weight matrix $\tilde{\mathbf{S}}$ with the pairwise constraint supervisory information of all data points, so the limited supervised information can be used effectively. In CPA [26,34], assuming that $l_i$ and $l_j$ are the labels of data ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$, then the initial pairwise constraints matrix $\mathbf{Z}=\left[z_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is defined as follows:

$$z_{ij}=\left\{\begin{array}{c}+1,l_i=l_j\hfill \\ -1,l_i\ne l_j\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(1)

The propagated pairwise constraints matrix is defined as $\mathbf{P}=\left[p_{ij}\right]\in {\mathbb{R}}^{N\times N}$, when $p_{ij}>0$ then $l_i=l_j$, if $p_{ij}<0$, then $l_i\ne l_j$, $|p_{ij}|$ denotes the confidence score of $({\mathbf{x}}_i,{\mathbf{x}}_j)$ for a must-link constraint ($l_i=l_j$) or a cannot-link constraint ($l_i\ne l_j$), similarly, ${\mathbf{P}}_v$ is the vertical propagation of $\mathbf{P}$ and ${\mathbf{P}}_h$ is the horizontal propagation, then the constraint propagation algorithm(CPA) is described as follows [26,34]:

• Construct the pairwise constraints matrix $\mathbf{Z}$ by Formula (1), compute the Laplacian matrix $\mathbf{L}={\mathbf{D}}^{-1/2}\mathbf{S}{\mathbf{D}}^{-1/2}$, in which $\mathbf{D}$ is the diagonal matrix with ${\mathbf{D}}_{ii}={\sum }_{j=1}^N{\mathbf{S}}_{ij}$ and $\mathbf{S}$ is the input weight matrix;
• Make vertical propagating by repeating ${\mathbf{P}}_v(t+1)=\alpha \mathbf{L}{\mathbf{P}}_v\left(t\right)+(1-\alpha )\mathbf{Z}$ until convergence, $\alpha \in (0,1)$ is the balance parameter;
• Make horizontal propagating by repeating ${\mathbf{P}}_h(t+1)=\alpha {\mathbf{P}}_h\left(t\right)\mathbf{L}+(1-\alpha ){\mathbf{P}}_v^{*}$ until convergence, ${\mathbf{P}}_v^{*}$ is the limit of ${\mathbf{P}}_v$;
• Obtain the final propagated pairwise constraints matrix $\mathbf{P}={\mathbf{P}}_h^{*}$, ${\mathbf{P}}_h^{*}$ is the limit of ${\mathbf{P}}_h$;
• Calculate the new weight matrix $\tilde{\mathbf{S}}$ by

  $${\tilde{s}}_{ij}=\left\{\begin{array}{c}1-(1-p_{ij})(1-s_{ij}),p_{ij}\ge 0\hfill \\ (1+p_{ij})s_{ij},p_{ij}<0\hfill \end{array}\right.$$

  (2)

Up to now, there is no technique which combines together multiple graph regularization, supervised information and sparse constraint to solve clustering problems. Therefore, we proposal a novel SSNMF method with multiple graph adaptive regularization and sparse constraint in next section.

3. The Proposed MSNMFSC

Although multiple graph regularization and semi-supervision techniques have been successfully introduced into the NMF model, the existing methods do not consider the sparse constraint which can enhance the parts-based representation and obtain better clustering performance. So in this work, we combine the multiple graph adaptive regularization, the limited supervised information and the sparse constraint together, then propose the MSNMFSC algorithm accordingly.

3.1. Objective Function

Here we give the object function of MSNMFSC step by step. Firstly, the object function of original NMF is given, and the square of Euclidean distance (SED) is used as the similarity measure to calculate the similarity of the original data matrix and the reconstructed matrix. The SED-based object function of original NMF is expressed as follows [34]:

$$\begin{array}{c}\hfill {OBJ}_{SED}={\parallel \mathbf{X}-\mathbf{U}{\mathbf{V}}^T\parallel }_F^2=\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2\end{array}$$

(3)

where $\mathbf{X}\in {\mathbb{R}}_{\ge 0}^{M\times N}$, $\mathbf{U}\in {\mathbb{R}}_{\ge 0}^{M\times K}$, $\mathbf{V}\in {\mathbb{R}}_{\ge 0}^{N\times K}$, $K\ll min(N,M)$.

In order to capture the geometrical structure information of data, the graph regularization [15,34] is given by:

$$\begin{array}{cc}\hfill OB{J}_G& =\frac{1}{2}\beta \sum _{i,j=1}^N{\parallel {\mathbf{v}}_{i*}^T-{\mathbf{v}}_{j*}^T\parallel }_2^2{\left(\mathbf{S}\right)}_{ij}\hfill \\ \hfill & =\beta Tr\left({\mathbf{V}}^T\mathbf{D}\mathbf{V}\right)-\beta Tr\left({\mathbf{V}}^T\mathbf{S}\mathbf{V}\right)\hfill \\ \hfill & =\beta Tr\left({\mathbf{V}}^T\mathbf{L}\mathbf{V}\right)\hfill \end{array}$$

(4)

where $\mathbf{S}$, $\mathbf{D}$ and $\mathbf{L}=\mathbf{D}-\mathbf{S}$ are the edge weight matrix, the diagonal matrix with ${\mathbf{D}}_{ii}={\sum }_{j=1}^N{\mathbf{S}}_{ij}$ and the graph Laplacian of the data graph, respectively. $\beta \ge 0$ is the graph regularization parameter. Previous studies have illustrated that the multiple graph regularized methods usually outperform the single graph regularized method. According to [25], based on (3) and (4), the object function of the NMF method containing multiple graph regularization [34] is as follows:

$$\begin{array}{cc}\hfill OB{J}_{MG}& =\parallel \mathbf{X}-\mathbf{U}{\mathbf{V}}^T{\parallel }_F^2+\frac{1}{2}\beta \sum _{q=1}^Q\sum _{i,j=1}^N{\epsilon }_q{\parallel {\mathbf{v}}_{i*}^T-{\mathbf{v}}_{j*}^T\parallel }_2^2{\left({\mathbf{S}}_q\right)}_{ij}\hfill \\ \hfill & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_q[Tr\left({\mathbf{V}}^T{\mathbf{D}}_q\mathbf{V}\right)-Tr\left({\mathbf{V}}^T{\mathbf{S}}_q\mathbf{V}\right)]\hfill \\ \hfill & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\mathbf{L}}_q\mathbf{V}\right)\hfill \end{array}$$

(5)

where Q is the number of graphs, ${\epsilon }_q$ is the weight value of the qth graph, ${\mathbf{S}}_q$, ${\mathbf{D}}_q$ and ${\mathbf{L}}_q={\mathbf{D}}_q-{\mathbf{S}}_q$ have the same meaning as (4). Supervised information including label information and pairwise constraints is a great help to enhance the performance. Therefore, the CPA [26] described in Section 2.3 is used in our work to reconstruct the new $\tilde{\mathbf{S}}$, so the object function of the semi-supervised NMF with multiple graph regularization  is as follows [34].

$$\begin{array}{cc}\hfill OB{J}_{SMG}& =\parallel \mathbf{X}-\mathbf{U}{\mathbf{V}}^T{\parallel }_F^2+\frac{1}{2}\beta \sum _{q=1}^Q\sum _{i,j=1}^N{\epsilon }_q{\parallel {\mathbf{v}}_{i*}^T-{\mathbf{v}}_{j*}^T\parallel }_2^2{\left({\tilde{\mathbf{S}}}_q\right)}_{ij}\hfill \\ \hfill & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_q[Tr\left({\mathbf{V}}^T{\tilde{\mathbf{D}}}_q\mathbf{V}\right)-Tr\left({\mathbf{V}}^T{\tilde{\mathbf{S}}}_q\mathbf{V}\right)]\hfill \\ \hfill & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)\hfill \end{array}$$

(6)

Here $\widetilde{{\mathbf{L}}_q}=\widetilde{{\mathbf{D}}_q}-\widetilde{{\mathbf{S}}_q}$, in which $\widetilde{{\mathbf{S}}_q}$, $\widetilde{{\mathbf{D}}_q}$ and $\widetilde{{\mathbf{L}}_q}$ have the same meaning as that in (5) but contain supervised information.

Apparently, the object function in (6) fails to consider the sparse constraint which can increase the clustering performance by enhancing parts learning ability [28]. So, here we incorporate the sparse constraint into the object function in (6). L0-norm, L1-norm and Frobenius norm are commonly used to measure the sparseness, however, the optimization procedure under L0-norm has been proved to be a NP-hard problem [36], and the L1-norm-based methods require the original signals to be highly sparse and will be ineffective in some situations [36,37]. In this situation, we choose the Frobenius norm as the measure method due to its advantages such as simplicity and effectiveness, and impose the sparse constraints into the object function in (6), then the object function of MSNMFSC can be derived as follows:    

$$\begin{array}{cc}\hfill OB{J}_{MSNMFSC}& =\parallel \mathbf{X}-\mathbf{U}{\mathbf{V}}^T{\parallel }_F^2+\frac{1}{2}\beta \sum _{q=1}^Q\sum _{i,j=1}^N{\epsilon }_q\parallel {\mathbf{v}}_{i*}^T-{\mathbf{v}}_{j*}^T{\parallel }_2^2{\left({\tilde{\mathbf{S}}}_q\right)}_{ij}+{\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2\hfill \\ \hfill & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)+{\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2\hfill \end{array}$$

(7)

where $\eta$ and $\gamma$ are the sparseness parameters of U and V, respectively, the ranges of $\eta$ and $\gamma$ are both in $(0,1)$.

3.2. Solving Optimization Problem

Although the objective function in (7) is not convex with respect to U and V at the same time, it is convex with respect to single U or single V. So, in most cases, one can have a local minimum of (7). Here, we use the multiplicative update algorithm to obtain the update rules of $\mathbf{U}$ and $\mathbf{V}$ for MSNMFSC, the optimization problem of MSNMFSC in (7) is given as follows:

$$\begin{array}{cc}\hfill & \underset{\mathbf{U},\mathbf{V},\epsilon }{min}OB{J}_{MSNMFSC}\hfill \\ & =\sum _{i=1}^M\sum _{j=1}^N{\left({\mathbf{X}}_{ij}-{\left(\mathbf{U}{\mathbf{V}}^T\right)}_{ij}\right)}^2+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)+{\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2\hfill \\ \hfill =& Tr\left({\mathbf{X}}^T\mathbf{X}-2\mathbf{X}\mathbf{U}{\mathbf{V}}^T+\mathbf{U}{\mathbf{V}}^T\mathbf{V}{\mathbf{U}}^T\right)+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)+{\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2\hfill \end{array}$$

(8)

3.2.1. Updating $\mathbf{U}$

Here, $\mathsf{\Phi }=\left[{\mathsf{\Phi }}_{ik}\right]\in {\mathbb{R}}_{\ge 0}^{M\times K}$ is the Lagrange multiplier for $\mathbf{U}=\left[u_{ik}\right]\in {\mathbb{R}}_{\ge 0}^{M\times K}$, so we have the Lagrange function ${\mathcal{L}}_{\mathbf{U}}$:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathbf{U}}=& Tr\left({\mathbf{X}}^T\mathbf{X}-2\mathbf{X}\mathbf{U}{\mathbf{V}}^T+\mathbf{U}{\mathbf{V}}^T\mathbf{V}{\mathbf{U}}^T\right)+\beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)+\hfill \\ \hfill & {\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2+Tr\left(\mathsf{\Phi }{\mathbf{U}}^T\right)\hfill \end{array}$$

(9)

Then we obtain its partial derivative with respect to $\mathbf{U}$:

$$\begin{array}{cc}\hfill \frac{\mathsf{\partial }{\mathcal{L}}_{\mathbf{U}}}{\mathsf{\partial }\mathbf{U}}=& -2\mathbf{X}\mathbf{V}+2\mathbf{U}{\mathbf{V}}^T\mathbf{V}+2\eta \mathbf{U}+\mathsf{\Phi }\hfill \end{array}$$

(10)

According to the Karush–Kuhn–Tucker (KKT) conditions [38], i.e., ${\mathsf{\Phi }}_{ik}{u}_{ik}=0$, so

$$\begin{array}{c}\hfill -2{\left(\mathbf{X}\mathbf{V}\right)}_{ik}{u}_{ik}+2{\left(\mathbf{U}{\mathbf{V}}^T\mathbf{V}\right)}_{ik}{u}_{ik}+2\eta {\mathbf{U}}_{ik}{u}_{ik}+{\mathsf{\Phi }}_{ik}{u}_{ik}=0\end{array}$$

(11)

Finally, we derive the update rule of U:

$$\begin{array}{c}\hfill u_{ik}\leftarrow u_{ik}\frac{{\left(\mathbf{X}\mathbf{V}\right)}_{ik}}{{\left(\mathbf{U}{\mathbf{V}}^T\mathbf{V}+\eta \mathbf{U}\right)}_{ik}}\end{array}$$

(12)

3.2.2. Updating $\mathbf{V}$

Similarly, we can derive the update rule of V. Assuming that $\mathsf{\Psi }=\left[{\mathsf{\Psi }}_{jk}\right]\in {\mathbb{R}}_{\ge 0}^{N\times K}$ is the Lagrange multiplier for $\mathbf{V}=\left[v_{ik}\right]\in {\mathbb{R}}_{\ge 0}^{N\times K}$, the Lagrange function ${\mathcal{L}}_{\mathbf{V}}$ for $\mathbf{V}$ is as follows:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathbf{V}}=& Tr\left({\mathbf{X}}^T\mathbf{X}-2\mathbf{X}\mathbf{U}{\mathbf{V}}^T+\mathbf{U}{\mathbf{V}}^T\mathbf{V}{\mathbf{U}}^T\right)+\hfill \\ \hfill & \beta \sum _{q=1}^Q{\epsilon }_{q}Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)+{\eta \parallel \mathbf{U}\parallel }_F^2+\gamma {\parallel \mathbf{V}\parallel }_F^2+Tr\left(\mathsf{\Psi }{\mathbf{V}}^T\right)\hfill \end{array}$$

(13)

Then we obtain its partial derivative with respect to $\mathbf{V}$:

$$\begin{array}{c}\hfill \frac{\mathsf{\partial }{\mathcal{L}}_{\mathbf{V}}}{\mathsf{\partial }\mathbf{V}}=-2{\mathbf{X}}^T\mathbf{U}+2\mathbf{V}{\mathbf{U}}^T\mathbf{U}+2\beta \sum _{q=1}^Q{\epsilon }_q{\tilde{\mathbf{L}}}_q\mathbf{V}+2\gamma \mathbf{V}+\mathsf{\Psi }\end{array}$$

(14)

According to the KKT conditions, i.e., ${\mathsf{\Psi }}_{jk}{v}_{jk}=0$, so

$$\begin{array}{c}\hfill -2{\left({\mathbf{X}}^T\mathbf{U}\right)}_{jk}{v}_{jk}+2{\left(\mathbf{V}{\mathbf{U}}^T\mathbf{U}\right)}_{jk}{v}_{jk}+2\beta {\left(\sum _{q=1}^Q{\epsilon }_q{\tilde{\mathbf{L}}}_q\mathbf{V}\right)}_{jk}{v}_{jk}+2\gamma {\mathbf{V}}_{jk}{v}_{jk}+{\mathsf{\Psi }}_{jk}{v}_{jk}=0\end{array}$$

(15)

At last, we derive the update rule for $\mathbf{V}$ as follows:

$$\begin{array}{c}\hfill v_{jk}\leftarrow v_{jk}\frac{{({\mathbf{X}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{S}}}_q\mathbf{V})}_{jk}}{{(\mathbf{V}{\mathbf{U}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{D}}}_q\mathbf{V}+\gamma \mathbf{V})}_{jk}}\end{array}$$

(16)

3.2.3. Computing the Weight Value ${\epsilon }_q$

Inspired by [25,39], in this work, we use the same method in [34] to calculate weight value ${\epsilon }_q$ of the qth graph, which is:

$$\begin{array}{c}\hfill {\epsilon }_q=\frac{1}{2\sqrt{Tr\left({\mathbf{V}}^T{\tilde{\mathbf{L}}}_q\mathbf{V}\right)}}\end{array}$$

(17)

Finally, the proposed MSNMFSC algorithm is summarized in Algorithm 1.

Algorithm 1: MSNMFSC Algorithm.

Input: Data matrix $\mathbf{X}$, label information $l_i$, parameters $\alpha$, p, $\beta$, $\eta$ and $\gamma$. Output: $\mathbf{V}$. 1: Initialize matrices $\mathbf{U}$ and $\mathbf{V}$; 2: Calculate the weight matrix ${\mathbf{S}}_q$, where $q=[1,\dots ,Q]$; 3: Calculate the weight matrix ${\tilde{\mathbf{S}}}_q$ by CPA, where q has the same value as step 2; 4: repeat 5:     Update $\mathbf{U}$ by Formula (12); 6:     Update $\mathbf{V}$ by Formula (16); 7:     Update ${\epsilon }_q$ by Formula (17); 8: until Convergence 9: return $\mathbf{V}$.

4. Convergence of MSNMFSC

Here we use the auxiliary function method [15,34] to analyze the convergence of MSNMFSC. Considering the update rules in (12) and (16), we derive Theorem 1 as follows:

Theorem 1. 

$OB{J}_{MSNMFSC}$ in (7) is monotonically nonincreasing under (12) and (16).

Here, we just give the proof that $OB{J}_{MSNMFSC}$ is nonincreasing under the update rules (16), because the proof procedure of $OB{J}_{MSNMFSC}$ is nonincreasing under (12) is similar; therefore, in this work, we omit it. First, we define the auxiliary function and Lemma 1:

Definition 1 

([34]). If function G satisfies $G(v,v^{\prime })\ge F\left(v\right)$ and $G(v,v)=F\left(v\right)$, then $G(v,v^{\prime })$ is an auxiliary function for $F\left(v\right)$.

Lemma 1 

([34]). F is nonincreasing under the update steps in (18), here G is an auxiliary function of F:

$$\begin{array}{c}\hfill v^{t+1}=arg\underset{v}{min}G(v,v^t)\end{array}$$

(18)

Proof. 

$$\begin{array}{c}\hfill F\left(v^{t+1}\right)\le G(v^{t+1},v^t)\le G(v^t,v^t)=F\left(v^t\right)\end{array}$$

So, Lemma 1 is proved. □

According to Lemma 1, if we can obtain the same update rule as (16) when minimizing the auxiliary function G of $OB{J}_{MSNMFSC}$, we can prove that $OB{J}_{MSNMFSC}$ is nonincreasing under (16). Here, $v_{jk}$ is the corresponding entry of $\mathbf{V}$, and $F_{jk}$ is the part which only involves the $v_{jk}$ term in $OB{J}_{MSNMFSC}$. Then, we derive the following partial derivatives:

$$\begin{array}{c}\hfill F_{jk}^{\prime }={\left(\frac{\mathsf{\partial }OB{J}_{MSNMFSC}}{\mathsf{\partial }\mathbf{V}}\right)}_{jk}={(-2{\mathbf{X}}^T\mathbf{U}+2\mathbf{V}{\mathbf{U}}^T\mathbf{U}+2\beta \sum _{q=1}^Q{\epsilon }_q{\tilde{\mathbf{L}}}_q\mathbf{V}+2\gamma \mathbf{V})}_{jk}\end{array}$$

(19)

$$\begin{array}{c}\hfill F_{jk}^{″}=2{\left({\mathbf{U}}^T\mathbf{U}\right)}_{kk}+2\beta \sum _{q=1}^Q{\epsilon }_q{\left({\tilde{\mathbf{L}}}_q\right)}_{jj}+2\gamma \end{array}$$

(20)

Next, $F_{jk}$ is nonincreasing under (16) needs to be proved.

Lemma 2. 

The function (21) below is an auxiliary function of $F_{jk}$.

$$\begin{array}{cc}\hfill G(v,v_{jk}^t)=& F_{jk}\left(v_{jk}^t\right)+F_{jk}^{\prime }\left(v_{jk}^t\right)(v-v_{jk}^t)+\hfill \\ \hfill & \frac{{\left(\mathbf{V}{\mathbf{U}}^T\mathbf{U}+\beta \sum _{q=1}^Q{\epsilon }_q{\tilde{\mathbf{D}}}_q\mathbf{V}+\gamma \mathbf{V}\right)}_{jk}}{v_{jk}^t}{(v-v_{jk}^t)}^2\hfill \end{array}$$

(21)

Proof. 

Because $G(v,v)=F_{jk}\left(v\right)$, so we just require to prove $G(v,v_{jk}^t)\ge F_{jk}\left(v\right)$. Then we give the Taylor series expansion of $F_{jk}\left(v\right)$ as follows:

$$\begin{array}{cc}\hfill F_{jk}\left(v\right)=& F_{jk}\left(v_{jk}^t\right)+F_{jk}^{\prime }\left(v_{jk}^t\right)(v-v_{jk}^t)+\frac{1}{2}{F}_{jk}^{″}\left(v_{jk}^t\right){(v-v_{jk}^t)}^2\hfill \\ \hfill =& F_{jk}\left(v_{jk}^t\right)+F_{jk}^{\prime }\left(v_{jk}^t\right)(v-v_{jk}^t)+{(v-v_{jk}^t)}^2\times \hfill \\ \hfill & \left({\left({\mathbf{U}}^T\mathbf{U}\right)}_{kk}+\beta \sum _{q=1}^Q{\epsilon }_q{\left({\tilde{\mathbf{L}}}_q\right)}_{jj}+\gamma \right)\hfill \end{array}$$

(22)

According to (21) and (22), if we can prove (23), then $G(v,v_{jk}^t)\ge F_{jk}\left(v\right)$ holds,

$$\begin{array}{c}\hfill \frac{{\left(\mathbf{V}{\mathbf{U}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{D}}}_q\mathbf{V}+\gamma \mathbf{V}\right)}_{jk}}{v_{jk}^t}\ge {\left({\mathbf{U}}^T\mathbf{U}\right)}_{kk}+\beta \sum _{q=1}^Q{\epsilon }_q{\left({\tilde{\mathbf{L}}}_q\right)}_{jj}+\gamma \end{array}$$

(23)

Due to $\beta >0$ and ${\epsilon }_q>0$,

$$\begin{array}{c}\hfill {\left(\mathbf{V}{\mathbf{U}}^T\mathbf{U}\right)}_{jk}=\sum _{l=1}^K{\mathbf{V}}_{jl}{\left({\mathbf{U}}^T\mathbf{U}\right)}_{lk}\ge v_{jk}^t{\left({\mathbf{U}}^T\mathbf{U}\right)}_{kk}\end{array}$$

(24)

and

$$\begin{array}{cc}\hfill {\left({\tilde{\mathbf{D}}}_q\mathbf{V}\right)}_{jk}& =\sum _{l=1}^N{\left({\tilde{\mathbf{D}}}_q\right)}_{jl}{v}_{lk}^t\ge v_{jk}^t{\left({\tilde{\mathbf{D}}}_q\right)}_{jj}\ge v_{jk}^t{\left({\tilde{\mathbf{L}}}_q\right)}_{jj}\hfill \end{array}$$

(25)

and

$$\begin{array}{c}\hfill \gamma {\mathbf{V}}_{jk}^t=\gamma v_{jk}^t\end{array}$$

(26)

So $G(v,v_{jk}^t)\ge F_{jk}\left(v\right)$ is proved. The function (21) is an auxiliary function of $F_{jk}$. □

Next we will prove Theorem 1 on the base of Lemmas 1 and 2.

Proof. 

Based on (21), replacing $G(v,v_{jk}^t)$ in (18), the update rule for $\mathbf{V}$ is:

$$\begin{array}{cc}\hfill v_{jk}^{t+1}=& v_{jk}^t-v_{jk}^t\frac{F_{jk}^{\prime }\left(v_{jk}^t\right)}{2{(\mathbf{V}{\mathbf{U}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{D}}}_q\mathbf{V}+\gamma \mathbf{V})}_{jk}}\hfill \\ \hfill =& v_{jk}^t\frac{{({\mathbf{X}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{S}}}_q\mathbf{V})}_{jk}}{{(\mathbf{V}{\mathbf{U}}^T\mathbf{U}+\beta {\displaystyle \sum _{q=1}^Q}{\epsilon }_q{\tilde{\mathbf{D}}}_q\mathbf{V}+\gamma \mathbf{V})}_{jk}}\hfill \end{array}$$

(27)

Based on Lemmas 1 and 2, under the update rule (16), $F_{jk}$ is nonincreasing, so $OB{J}_{MSNMFSC}$ is monotonically nonincreasing under (16). Theorem 1 is proved. □

5. Experiments Results

Here, we give the experiment results on seven image datasets to illustrate the advantage of MSNMFSC, in comparison to GDNMF [33], SDNMF [23], CPSNMF [26], LCDNMF [12], MGNMF [24], PAMGNMF [25] and MSNMF [34].

5.1. Settings for the Experiments

We choose seven real-world image datasets including two handwritten datasets (Optdigits with 10 classes and MNIST with 10 classes), two object datasets (COIL20 with 20 classes and COIL100 with 100 classes ) and three face datasets (CMU PIE with 68 classes, UMIST with 20 classes and MSRA25 with 12 classes) for the clustering experiments. Particularly, we format every image dataset as a M by N data matrix, in which N is the number of samples, M is the number of dimensions of each sample, which is equal to the product of the sample image’s length and width, so the Optdigits, MNIST, COIL20, COIL100, CMU PIE, UMIST and MSRA25 datasets are formatted as $64\times 5620$, $784\times 6996$, $1024\times 1440$, $1024\times 7200$, $1024\times 2856$, $1024\times 575$ and $256\times 1799$ matrices, respectively. Each column of the data matrix which represents a sample is normalized to have unit Euclidean length. We also use three typical evaluation metrics including accuracy, normalized mutual information (NMI) and purity to evaluate the clustering performance. Here, we omit the detailed definitions of these used metrics since they are described in [16].

The balance parameter $\alpha$, the regularization parameter $\beta$ and the sparseness parameter $\eta$ and $\gamma$ are empirically set to be 0.2, 100, 0.4 and 0.2, respectively. The initial values for $\mathbf{U}$ and $\mathbf{V}$ are randomly selected, ranging from 0 to 1. Here, we adopt three single p-nearest neighbor graphs with $p=5,7,9$, respectively. Furthermore, we select 10% of the data points in each image dataset as the labeled data points, which are used as the supervised information. Particularly for the compared methods, we use best parameters according to their reference papers.

5.2. Clustering Results

The clustering results for all methods on seven datasets are shown in Table 1, and the bold-faced results represent the best result among all the methods. From the table, one can discover that, compared with other state-of-the-art methods, MSNMFSC has the best clustering results on all image datasets in terms of accuracy and NMI, and has better performance on almost all used datasets except CMU PIE and UMIST in term of purity. For example, compared with the MSNMF method, which usually has the second best clustering performance, MSNMFSC has 5.8%, 3.25% and 0.52% improvements on the MNIST dataset, 1.18%, 0.55% and 1.13% improvements on the COIL100 dataset, 3.22%, 1.77% and 0.8% improvements on the MSRA25 dataset, for three evaluation metrics, respectively. The clustering results illustrate that the proposed MSNMFSC outperforms the compared NMF methods in clustering tasks, that’s because MSNMFSC can take full advantage of the multiple graph adaptive regularization, the limited supervised information and the sparse constraint to obtain more discriminative parts-based data representation and improve the clustering performance.

Table 1. Clustering results.

Dataset	Accuracy (%)
	LCDNMF	MGNMF	PAMGNMF	GDNMF	SDNMF	CPSNMF	MSNMF	MSNMFSC
Optdigits	83.95	80.56	81.32	84.18	91.66	98.21	98.39	98.52
MNIST	63.58	59.62	63.49	70.12	72.91	81.48	85.59	90.55
COIL20	80.15	72.51	75.31	81.01	79.76	81.79	82.71	83.87
COIL100	58.93	52.19	55.31	58.16	66.41	66.22	68.45	69.26
CMU PIE	79.83	68.51	72.26	76.03	79.43	82.18	82.91	85.71
UMIST	56.44	49.33	53.35	54.55	64.81	68.86	69.05	70.2
MSRA25	66.22	68.43	72.28	71.11	85.16	88.35	96.18	99.28
Dataset	NMI (%)
	LCDNMF	MGNMF	PAMGNMF	GDNMF	SDNMF	CPSNMF	MSNMF	MSNMFSC
Optdigits	86.78	82.29	84.59	87.18	91.13	95.55	96.01	96.19
MNIST	70.26	56.17	62.35	69.75	74.89	79.59	82.16	84.83
COIL20	90.01	84.17	85.29	88.98	88.66	89.21	90.25	91.08
COIL100	81.43	76.65	77.56	79.26	84.59	85.17	85.97	86.44
CMU PIE	89.88	80.58	84.03	88.14	90.18	91.12	91.49	91.98
UMIST	74.91	67.61	70.93	71.11	78.46	80.12	81.31	81.76
MSRA25	76.23	80.33	84.19	77.29	90.55	92.33	96.79	98.5
Dataset	Purity (%)
	LCDNMF	MGNMF	PAMGNMF	GDNMF	SDNMF	CPSNMF	MSNMF	MSNMFSC
Optdigits	94.57	91.23	92.46	94.69	97.04	98.28	98.46	98.52
MNIST	87.93	66.56	80.86	87.81	90.81	91.57	93.08	93.56
COIL20	90.65	83.91	85.43	90.36	92.34	89.73	92.95	92.99
COIL100	80.05	70.21	73.55	77.68	83.01	84.19	84.75	85.71
CMU PIE	88.86	79.79	84.16	89.38	90.81	90.09	91.66	90.94
UMIST	74.43	66.61	71.51	73.55	80.06	79.57	81.57	79.65
MSRA25	74.18	79.89	84.41	87.39	93.06	98.37	98.49	99.28

5.3. Convergence

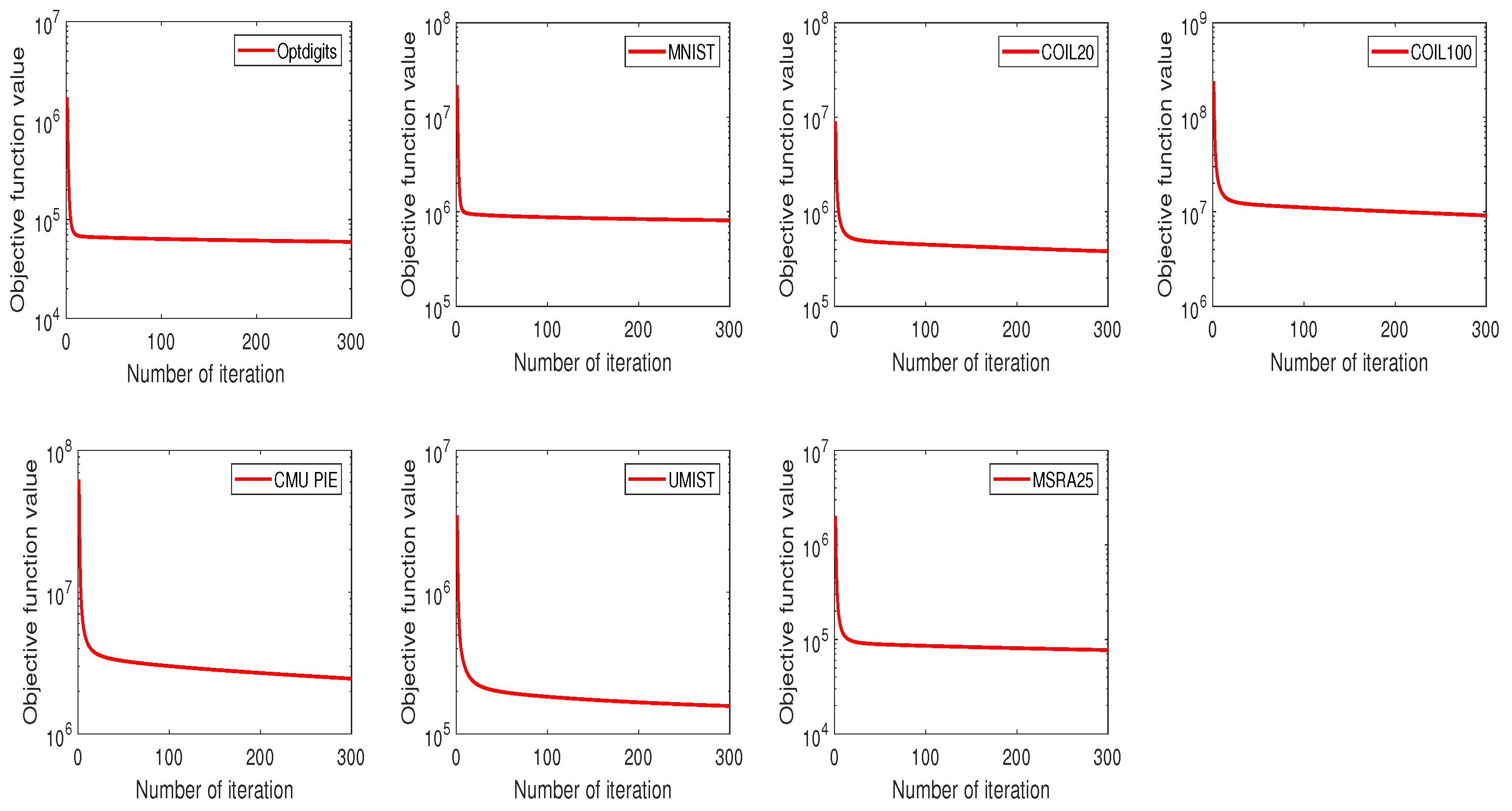
In order to validate that $OB{J}_{MSNMFSC}$ in (7) is monotonically nonincreasing under (12) and (16), we give the convergence curves of MSNMFSC on seven image datasets in Figure 1, in which the number of iteration and the value of $OB{J}_{MSNMFSC}$ are represented by the x-axis and the y-axis, respectively. According to Figure 1, we observe that the value of $OB{J}_{MSNMFSC}$ is monotonically nonincreasing under (12) and (16) for all the datasets used in our experiment, which shows Theorem 1 that have been proved in the convergence analysis section is correct.

Figure 1. Convergence curves of MSNMFSC.

6. Conclusions

In this paper, the multiple graph adaptive regularized SSNMF with sparse constraint (MSNMFSC) is developed, which enforces the multiple graph adaptive regularization, the limited supervised information and the sparse constraints into the NMF model for learning the more discriminative parts-based data representation. We derive the multiplicative update rules of MSNMFSC by solving the optimization problem. Moreover, the convergence of MSNMFSC is also analyzed. The extensive experimental results have shown MSNMFSC outperforms the compared NMF approaches on seven image datasets for clustering tasks.