Experimental Investigation of Non-Linear Seepage Characteristics in Rock Discontinuities and Morphology of the Shear Section in the Shear Process

Abstract

Considering the increasing frequency of geological disasters related to groundwater activities, it is important to study the relationship between geological dislocation and groundwater flow for the safety assessment of engineering rock mass stability. To elucidate the non-linear seepage characteristics at rock discontinuities during shearing, a custom-made device was used to conduct seepage tests at discontinuities that exhibit varying undulation angles and different shear displacements. The results show that as the shear displacement increases, the shear stress at a structural plane involving different undulation angles fluctuates with an increasing trend. Based on an identical shear displacement condition, the shear strengths of the structural planes increase as the undulation angle increases, and this enhances the shear expansion. Concerning an identical fluctuation angle and hydraulic gradient, the seepage flow at a structural plane increases as the shear displacement increases. By contrast, both the linear term coefficient a and non-linear term coefficient b in the Forchheimer fitting equation decrease as the shear displacement increases. In addition, the critical Reynolds number initially increases, followed by stabilisation as the shear displacement increases, and this number varies between 9.65 and 1758.52. The shear fracture morphology of the structural plane exhibits obvious anisotropy. During shearing, the roughness coefficient decreases in all but the vertical direction. The dominant seepage channel is perpendicular to the shear direction. The findings can provide a valuable reference for the stability research and analysis of rock slopes with structural planes.

1. Introduction

Structural planes are common in engineered rock masses, and shear slip along these planes is the main form of failure of these rocks. Groundwater influences the shear mechanical properties of the structural plane, and the change in its shear mechanical properties also affect the seepage channel of groundwater. The shear seepage coupling in structural planes severely affects the stability of engineered rock masses [1,2]. Failures of the Mallpasset (France) and Vajont (Italy) dams and the faceplate dam of the Gouhou Reservoir (Qinghai Province, China) in 1959, 1963, and 1993, respectively, represent typical cases of engineered rock mass problems caused by shear seepage [3]. Therefore, the investigation of stress seepage coupling at the structural planes of rocks is crucial for the evaluation of the stability of engineered rock masses.

Numerous studies have been conducted on the mechanical characteristics of stress seepage coupling in rocks. Lei et al. [4], for example, used experiments to study the seepage characteristics of random surfaces of fractures under varying shear displacements and established a relationship between the shear expansion angle and axial stress at a structural plane. Zhao et al. [5] utilised a numerical simulation approach to construct a random topography discontinuity model, discuss the shear response to seepage characteristics of a rough discontinuity, and establish a relationship with the permeability coefficient of the discontinuity. In addition, Yang et al. [6] investigated mechanisms associated with the effects of the stress loading path and hydraulic gradient on the seepage characteristics of fractures. The seepage characteristics of random single fracture surfaces under shear displacement were discussed, and mechanisms of the impacts of factors, including the confining and seepage pressures, were analysed. Zhang et al. [7] then performed creep tests on a serrated discontinuity based on shearing under pore water pressure, highlighting the effects of the pore water pressure on the deformation, creep rate, and long-term strength of the discontinuity. Conversely, Xu et al. [8] conducted shear seepage coupling tests on coals under different normal stress conditions, followed by 2D and 3D analysis of characteristic parameters of the shear section. Peng et al. [9] and Chen et al. [10] further conducted shear seepage coupling tests on sandstone samples under osmotic water pressure, highlighting the mechanism associated with the shear deformation of sandstones. Based on low-flow saturated seepage tests on structural planes involving different roughness values, Xiong et al. [11] characterised the behaviour of fluids with varying Reynolds numbers during non-linear seepage and then proposed an empirical relationship between the critical Reynolds number and absolute roughness. Following an investigation of the impacts of rock geometric characteristics on discontinuities, such as the mean opening and fractal dimension on parameters of the Forchheimer fitting equation, Zhou et al. [12] proposed a structural model for rough discontinuities. Di et al. [13] carried out stress-percolation coupling tests for fractures of different grain sizes and proposed an equation for the stress-percolation coupled permeability coefficient of a single fracture considering micro-roughness. Zhao et al. [14] studied the mechanical properties of a cataclastic rock in a fracture zone and the evolution of its permeability based on the water pressure, thereby establishing a three-dimensional (3D) model using digital image analysis. Further, Xu et al. [15] investigated the inertial coefficient associated with the non-Darcy flow and proposed mechanisms for the influence of non-linear parameters on the seepage field. Wang et al. [16], Hou et al. [17], and Rong et al. [18] conducted structural planes shear seepage tests using a combination of indoor tests, theoretical analysis, and numerical simulations, focusing on the non-linear seepage motion characteristics in rock structural planes and obtained the relationship between the linear and non-linear parameters of the Forchheimer formula and the critical Reynolds number and the joint surface morphology under shear seepage conditions. Liu et al. [19] carried out a sandstone fracture shear seepage test via a colour tracing image digital processing technique, proposed the loss stage of seepage velocity, and established a model for the coupling of osmotic water pressure and normal stress as a function of flow velocity. Peng et al. [20] analysed the anisotropic characteristics of structural planes produced by different processes using the associated quantitative parameters. These studies provided data that could be used to explain mechanisms through which split and shear structural planes affected the roughness coefficient (JRC).

Wang et al. [21] investigated the anisotropic characteristics of non-linear seepage in rock fractures based on fractal theory and proposed a non-linear fractal model for rough fractures. Li et al. [22] then proposed a method for quantifying the JRC based on shape using the Barton standard roughness grade profile. Further, Ge et al. [23] studied the roughness anisotropy of discontinuities in rocks and suggested that this parameter was controlled by the shear direction, as well as the sampling size and spacing. Xiao et al. [24] and Chen et al. [25] reviewed the mechanical properties of the fractured rocks, highlighting the relationships between the stress seepage coupling characteristics of such rocks and the controlling factors.

Previous studies have provided significant knowledge on stress seepage coupling in rocks. However, only few studies have been conducted on the non-linear seepage characteristics associated with shear seepage coupling and the morphology of the shear section during shearing. Therefore, in the present study, a custom-made device was used to conduct shear seepage coupling tests on prepared samples. The seepage tests were conducted under varying shear displacements at structural planes involving different undulation angles. The impacts of the undulation angle and shear displacement on the mechanical and non-linear seepage properties, as well as the 3D morphology of structural planes, were characterised. The finding of the present study can be used to analyse the stability of rock slopes with structural planes.

2. Materials and Methods

2.1. Samples

Owing to natural factors, obtaining original discontinuities in rocks at different scales is difficult. Discontinuities are usually unidentical, and thus, in the present study, similar materials (cement:river sand:water = 6:4:3; the cement was M32.5 GB/T3183-2017, and the river sand was obtained by filtering through 80 mesh and 120 mesh filters, respectively) were utilised in place of the original rock discontinuities. The physical and mechanical parameters of the prepared samples are presented in

Table 1. Basic mechanical properties that were determined for samples.

σn/MPa	µ	E/MPa	c/MPa	φb/°
15	0.27	3.39	2.84	28

, where σ_n is the uniaxial compressive strength; µ is Poisson’s ratio; E is the elastic modulus; c is cohesion; and φ_b is the internal friction angle.

Structural planes exhibiting varying undulation angles were prepared using the inverted moulding method, representing planes in rocks. The cement mortar was thoroughly mixed and then poured into the mould. A vibrating rod was then used to stir the mixture evenly to eliminate bubbles from the cement mortar to ensure a homogenous distribution of cement mortar in the mould. The prepared samples involving different undulation angles were then kept at room temperature (25 °C) for 3 d to enable demoulding. Subsequently, the samples were placed in a box for 28 d for curing. Following the curing, an 8 mm diameter hole was drilled through the centre of the top half of the structural plane. The sample was then placed in a water column to generate a water channel. Illustrations of the geometric and actual structural plane involved in the present study are displayed in Figure 1a,b, respectively. The undulation angle (i) values from left to right are 15°, 30°, and 45°, and the single tooth length (L) was 5 mm. The saw that was utilised had ten teeth, and the corresponding heights (h) were 0.67, 1.44, and 2.5 mm.

2.2. Test Device

The custom-made shear seepage coupling device [26] that was utilised in the present study is shown in Figure 2. The maximum axial displacement of the servo control loading system is 150 mm, and this involves an accuracy of ±1% FS, whereas the displacement rate ranges from 0.005 to 100 mm/min. The shear compartment and its sealing system were adequate for the desired test conditions. The fluid loading system of the test apparatus could provide a stable water head of up to 5 MPa. The maximum measurement accuracy of the 3D rock section scanning system is 0.01 mm, whereas the average scan interval varies from 0.07 to 0.15 mm. Data for the different parameters measured by the test system can be output in the ASC point cloud file format. The control and data acquisition system enable multi-stage loading and real-time monitoring of the displacement and stress path.

2.3. Shear Tests

2.3.1. Test Program

During the shear test, a constant normal stress of 2.25 MPa was employed, whereas the shear speed was 0.5 mm/min. Fluctuation angles of the regular tooth-shaped structural planes were 15°, 30°, and 45°, and the maximum shear displacement was 25 mm. At different stages of shearing (shear displacements of 0, 5, 10, 15, 20, and 25 mm), seepage tests were conducted via a step-by-step application of water at heads of 0.1, 0.2, 0.3, 0.4, and 0.5 MPa. Tests were performed using three to five subsamples to ensure the reliability of the data, and the specific steps involved in the tests are described subsequently.

2.3.2. Experimental Steps

Preliminary preparation: The measurement and quality of each sample were documented, and the performance of the test equipment was checked before each test. Following the inspection, the sample was placed in a shear box, and the mobile base was adjusted to ensure that the box was directly beneath the normal indenter of the loading system. The tangential indenter and the reaction bar were jointly used to fix the position of the shear box, and the normal indenter was set in position using the servo control system.

Connection of the water source: The water inlet valve, water pressure gauge, shear box, and water tank were attached to a flow pipe using a tapered ferrule joint, whereas the outlet of the water tank was connected to a flowmeter.

Testing: Normal loading was initiated, and after the predetermined value was attained, the shear load was introduced using a rate of 0.5 mm/min. The normal load remained constant throughout the test. Following the attainment of each shear displacement, the fluid source was opened, and the system was loaded to perform seepage tests sequentially at 0.1, 0.2, 0.3, 0.4, and 0.5 MPa. During each test, the pressure at the water inlet pressure was kept constant for 120 s whilst flow data through the water outlet was stored by the acquisition system. At the set shear displacement, the water supply was switched off at the end of the permeation water pressure test. The water flow was discharged through the guide pipe to the structural plane of the test piece. The water flow indication from the data acquisition system was observed to drop and remain stable before the next test operation was carried out. A flow diagram for the test system is shown in Figure 3.

Post-processing: At the end of each test, the sample was removed from the shear box, and its structural plane was cleaned using a brush two days later. The cleaned sample was then weighed, and both the test sample and debris were photographed. Subsequently, the test sample was subjected to 3D scanning, and the generated data were analysed.

3. Results

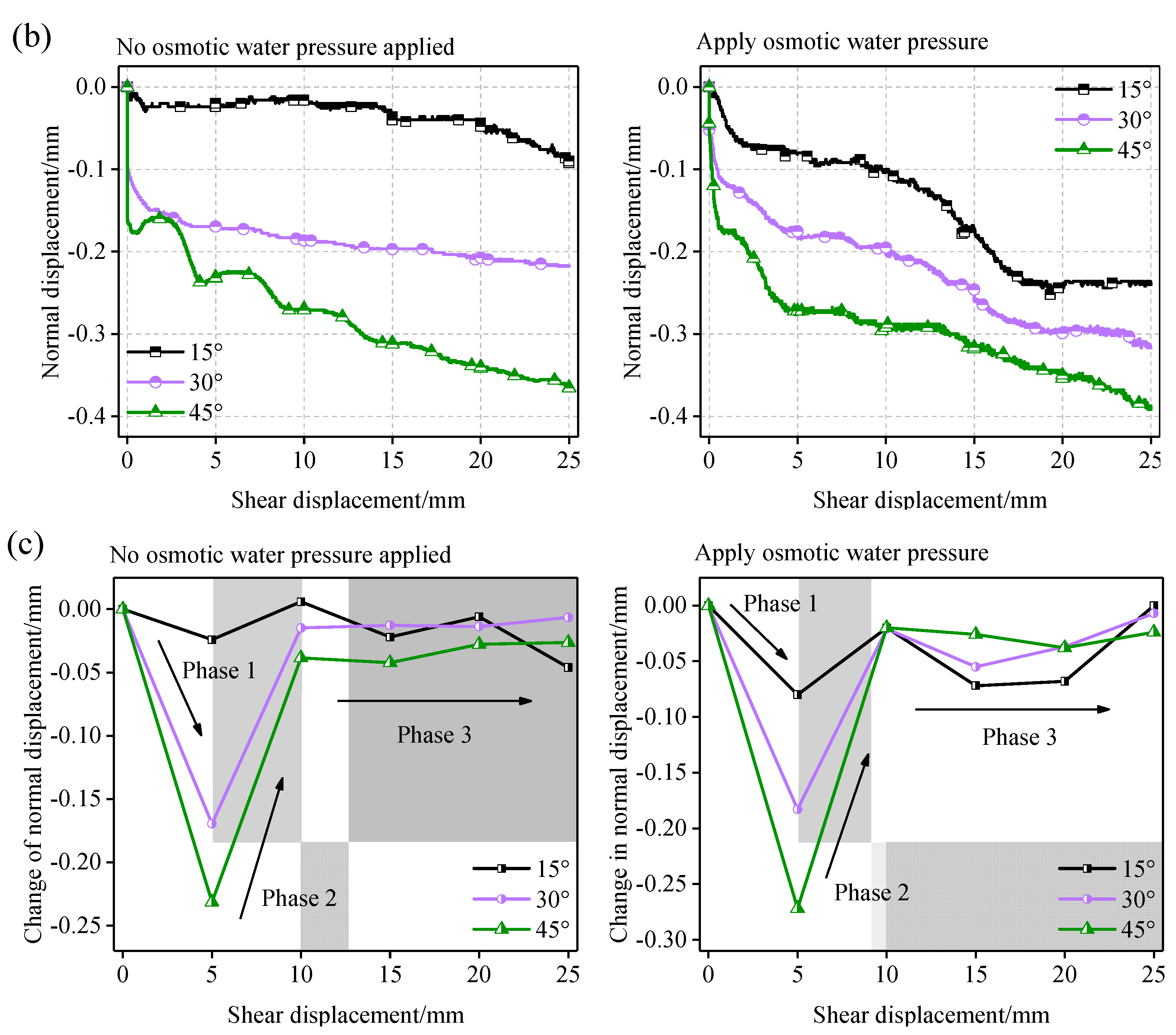
3.1. Shear Mechanical Properties of Structural Planes

Figure 4 shows a typical shear stress–strain curve under the normal stress of 2.25 MPa for a sample. Figure 4a reveals that the application of osmotic water pressure to the structural plane at a shear displacement of 0 mm resulted in different shear strengths after shear misalignment. The shear strength of the structural plane under the applied osmotic water was weaker during the test period. The shear stress increases rapidly as the shear displacement increases without the osmotic pressure from the water. Once the peak shear stress is attained, the shear stress data exhibits a fluctuating downward trend, and then it gradually stabilises. However, under the application of osmotic water pressure, the shear stress increases faster as the shear displacement increases, but the shear stress exhibits fluctuations. This difference is because, without osmotic water pressure, the shear stress is primarily affected by the undulation of the structural plane. As the shear displacement increases, the shear stress reaches the peak shear strength of the protrusions, and thus, the structural plane is damaged via cutting. The shear stress then decreases rapidly, gradually transforming to slip, thereby stabilising the shear stress. Upon the application of seepage water, because of the scouring and seepage pressure, the locations of the shear debris between the structural planes were altered, and the roughness between the structural planes increased in complexity. During each test, the shear stress gradually increased because of residual bulges between the upper and lower parts of the structural planes, friction between the structural plane and shear debris, and friction between shear debris. At the set shear displacement, the shear stress was observed to fluctuate significantly up and down around this value; this is due to the servo-controlled stopping of the shear box movement. The structural plane is in a process from “moving-static”; at this time, the structural plane, using the shear box thrust, is reduced, and the maximum static friction force under constant normal stress is greater than the inertia force. The upper and lower structural planes stop moving relative to the shear displacement and the shear stress is reduced according to the law of conservation of energy. At the cessation of shear displacement, due to the longer relative resting time of the surface, the pressure at the contact points on the structural plane is higher and the structural plane is elastoplastically pressed into each other, so the plastic change of the structural plane produces a larger contact area and a greater depth of mutual indentation. After the increase in shear displacement, the structural plane is in a “static-motion” process and needs to overcome greater static friction, so the shear stress appears to surge in a short period of time.

Figure 4b shows that the normal displacement of the structural plane gradually increases in the negative direction as the shear displacement increases both with and without the osmotic water pressure. The shear expansion is obvious, and as the fluctuation angle increases, the expansion is enhanced. Following data in Figure 4c, changes in the normal displacement for successive shear steps exhibit three stages. In Stage I, changes in the normal displacement for each shear step reach a maximum, and these are associated with prominent shear expansions in the structural plane. By contrast, during Stage II, because the structural plane remains in a state of dilatancy, changes in the normal displacement for successive shear steps decrease, and the speed at which failure of the structural plane occurs decreases. Finally, in Stage III, changes in the normal displacement for different shear steps stabilise. A comparison of the normal displacement changes for the structural plane produces the following order: Stages I > Stage II > Stage III. These differences are attributed to the prominent shear stress increase at the beginning of the test and the significant decrease in the height of the structural plane after shear failure in its lower half because of the cut tooth. However, as the shear displacement increases, the failure of the structural plane changes from shear to slip. Therefore, the extent of damage to the structural plane gradually diminishes, and thus, the change in the normal displacement also declines.

3.2. Non-Linear Seepage Characteristics of the Structural Plane

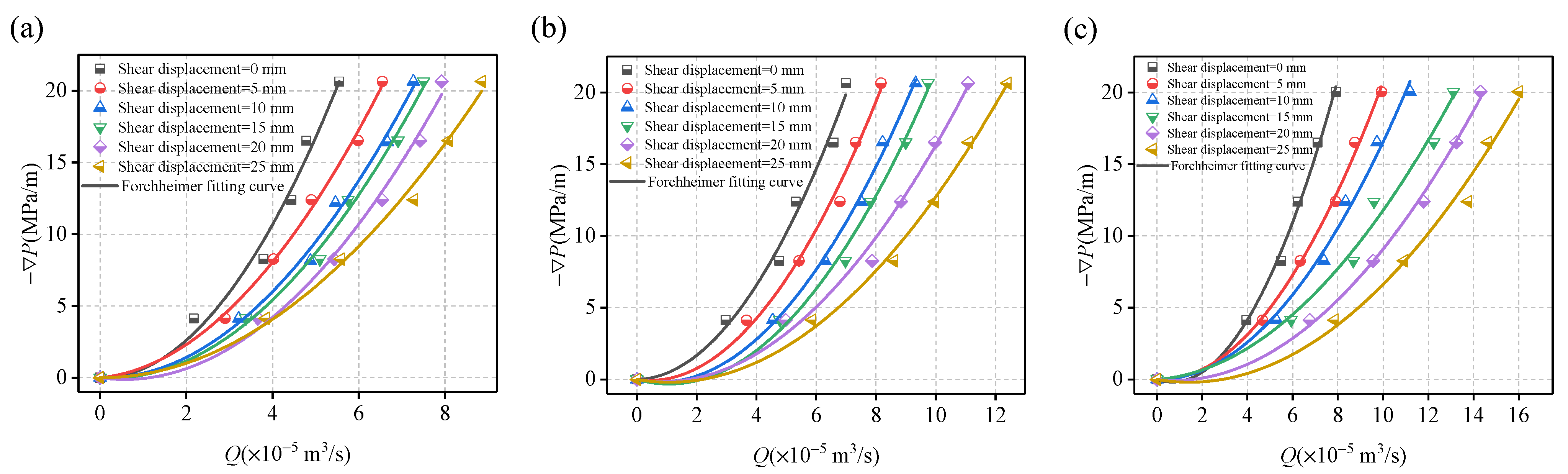
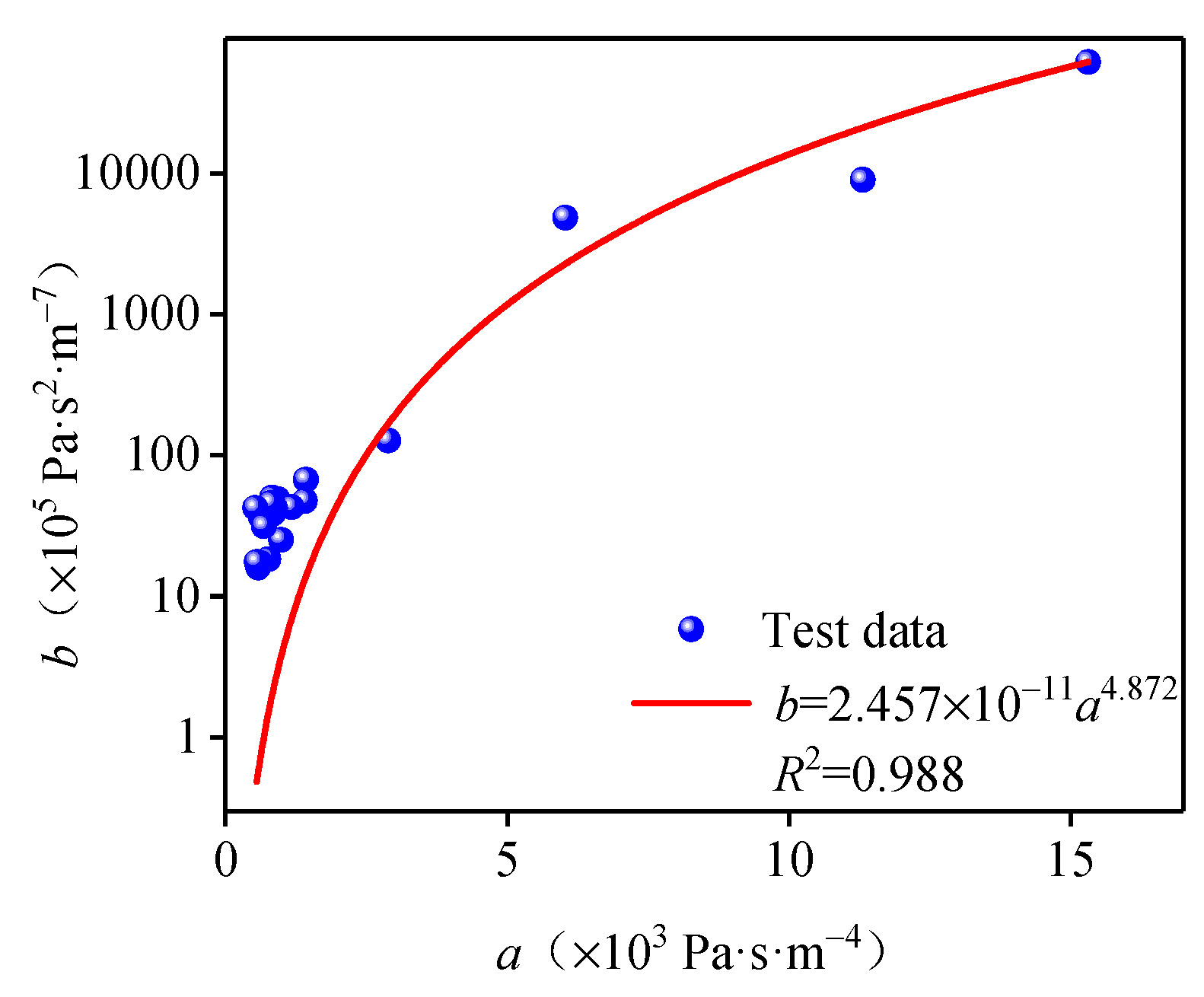
3.2.1. Non-Linear Seepage Characteristics

Many studies have been carried out by scholars at home and abroad on the seepage pattern of rock structural planes under compression-shear loading. The results of these studies show that as the water flow increases, the loss of inertia force becomes non-negligible and the seepage characteristics of the structural planes have non-linear characteristics. The Forchheimer equation has been used in national and international studies for nonlinear seepage with fruitful results [27,28,29,30,31,32,33,34].

The relationship curve between the hydraulic gradient (−▽P) and flow (Q) in the regular tooth-shaped structural plane under different shear displacements is shown in Figure 5. The data points in Figure were obtained from measurements, whereas the solid line represents the result of fitting the measured data using the Forchheimer equation (See

Table 2. Fitting results associated with the Forchheimer equation for the hydraulic gradient and discharge of the regular tooth-shaped structural plane.

Fluctuation Angle	Shear Displacement/mm	Fitting Equation	Fitting of Poisonous R2
15°	0	$-\nabla P=6.029\times {10}^{3}Q+4.827\times {10}^8{Q}^2$	0.979
	5	$-\nabla P=9.845\times {10}^{2}Q+2.512\times {10}^6{Q}^2$	0.995
	10	$-\nabla P=7.551\times {10}^{2}Q+1.828\times {10}^6{Q}^2$	0.991
	15	$-\nabla P=6.385\times {10}^{2}Q+1.762\times {10}^6{Q}^2$	0.993
	20	$-\nabla P=5.882\times {10}^{2}Q+1.673\times {10}^6{Q}^2$	0.991
	25	$-\nabla P=5.123\times {10}^{2}Q+1.607\times {10}^6{Q}^2$	0.992
30°	0	$-\nabla P=1.113\times {10}^{4}Q+8.208\times {10}^8{Q}^2$	0.983
	5	$-\nabla P=1.589\times {10}^{3}Q+5.194\times {10}^6{Q}^2$	0.989
	10	$-\nabla P=1.132\times {10}^{3}Q+3.868\times {10}^6{Q}^2$	0.996
	15	$-\nabla P=9.846\times {10}^{2}Q+3.693\times {10}^6{Q}^2$	0.992
	20	$-\nabla P=7.981\times {10}^{2}Q+3.336\times {10}^6{Q}^2$	0.988
	25	$-\nabla P=6.215\times {10}^{2}Q+2.808\times {10}^6{Q}^2$	0.995
45°	0	$-\nabla P=1.531\times {10}^{4}Q+6.125\times {10}^9{Q}^2$	0.995
	5	$-\nabla P=2.885\times {10}^{3}Q+1.227\times {10}^7{Q}^2$	0.996
	10	$-\nabla P=1.704\times {10}^{3}Q+7.524\times {10}^6{Q}^2$	0.987
	15	$-\nabla P=1.213\times {10}^{3}Q+5.915\times {10}^6{Q}^2$	0.984
	20	$-\nabla P=1.083\times {10}^{3}Q+5.378\times {10}^6{Q}^2$	0.997
	25	$-\nabla P=8.569\times {10}^{2}Q+4.502\times {10}^6{Q}^2$	0.986

for details). The Forchheimer equation can be expressed as follows [35]:

$$-\nabla P=\frac{P_{out}-P_{in}}{l}=aQ+b{Q}^2$$

(1)

$$\begin{array}{l}a=\frac{\mu }{k{A}_h}=\frac{12\mu }{w{\mathrm{e}}_h^3}\\ \end{array}$$

(2)

$$b=\frac{\beta \rho }{w^2{\mathrm{e}}_h^2}$$

(3)

where −▽P is the hydraulic gradient (MPa/m); P_in and P_out are the inlet and outlet pressures, respectively (MPa); l represents the vertical distance between the water inlet and outlet (m); Q denotes the inlet flow (m³/s); a is the coefficient of the linear term, which highlights losses in the viscous force (Pa·s·m⁻⁴); b denotes the coefficient of the non-linear term, which represents losses in the inertial force (Pa·s²·m⁻⁷); µ is the dynamic viscosity coefficient (0.89 × 10⁻³ Pa·s); k denotes the permeability (m²); A_h is the overcurrent area (m²); w represents the width of the fracture along the pressure gradient (m); e_h is the inherent hydraulic opening (m); ß denotes the inertial resistance coefficient (Pa·s²·kg⁻¹); and ρ is the density of water (0.997 × 10³ kg/m³).

Figure 5 reveals that under an identical shear displacement, the flow in the structural plane increases as the hydraulic gradient increases. Relatedly, at an identical hydraulic gradient, the flow in the structural plane also increases as the shear displacement increases. This response is attributed mainly to the enlargement of the crack in the structural plane as the shear displacement increases, where a wider crack requires a higher flow to maintain the hydraulic gradient. A comparison of the relationship between the hydraulic gradient (−▽P) and flow (Q) in the structural planes involving different fluctuation angles shows that as the fluctuation angle increases, the difference between the flow in adjacent shear steps under the same hydraulic gradient increases.

The results of fitting the hydraulic gradient (−▽P) and flow (Q) data for the regular tooth-shaped structural plane using the Forchheimer equation (Table 2) produced an average goodness of fit value (R²) of 0.991. Therefore, the Forchheimer equation is suitable for adequately fitting the test results. These results indicate that as the hydraulic gradient increases, the non-linear term associated with flow in the rough structural plane deserves consideration. This partially explains the non-linear relationship between the hydraulic gradient and flow.

To further understand the impact of shear displacement on changes in the non-linear seepage, the linear term coefficient a and non-linear term coefficient b of the Forchheimer equation were calculated using the data presented in Table 2. The relationships between these coefficients and shear displacement are displayed in Figure 6.

Following data shown in Figure 6, as the shear displacement increases, both the a and b values for the structural plane involving an identical fluctuation angle decrease. These variation patterns are linked to changes in the hydraulic fracture within structural planes during the shearing. As the shear displacement increases, the hydraulic fracture widens, and this expansion of the seepage channel enhances the flow velocity. The cumulative erosion of shear debris in the structural plane causes the water flow channel to increase, and thus, the flow gradually stabilises. Consequently, a and b also decrease and eventually stabilise.

Furthermore, under an identical shear displacement, a comparison of a and b values for a structural plane with different undulation angles reveals that as the undulation angle increases, losses in the inertial and viscous forces also increase. These responses are attributed to the higher tortuosity involved in water flow through the structural plane as the fluctuation angle increases.

The data for a and b for a structural plane under different shear displacements and fluctuation angles are plotted in Figure 7. Based on a fitting analysis, the following relationship was obtained between these coefficients:

$$b=2.457\times {10}^{-11}{a}^{4.872}$$

(4)

The average R² value obtained from the normalisation analysis was 0.988. Following Equation (4), b is adequately predicted from the a value of the shear seepage in the structural plane. The equation is applicable to seepage tests where the roughness of the structural plane is large. When applied to other seepage conditions, the correction of the equation is subject to further verification.

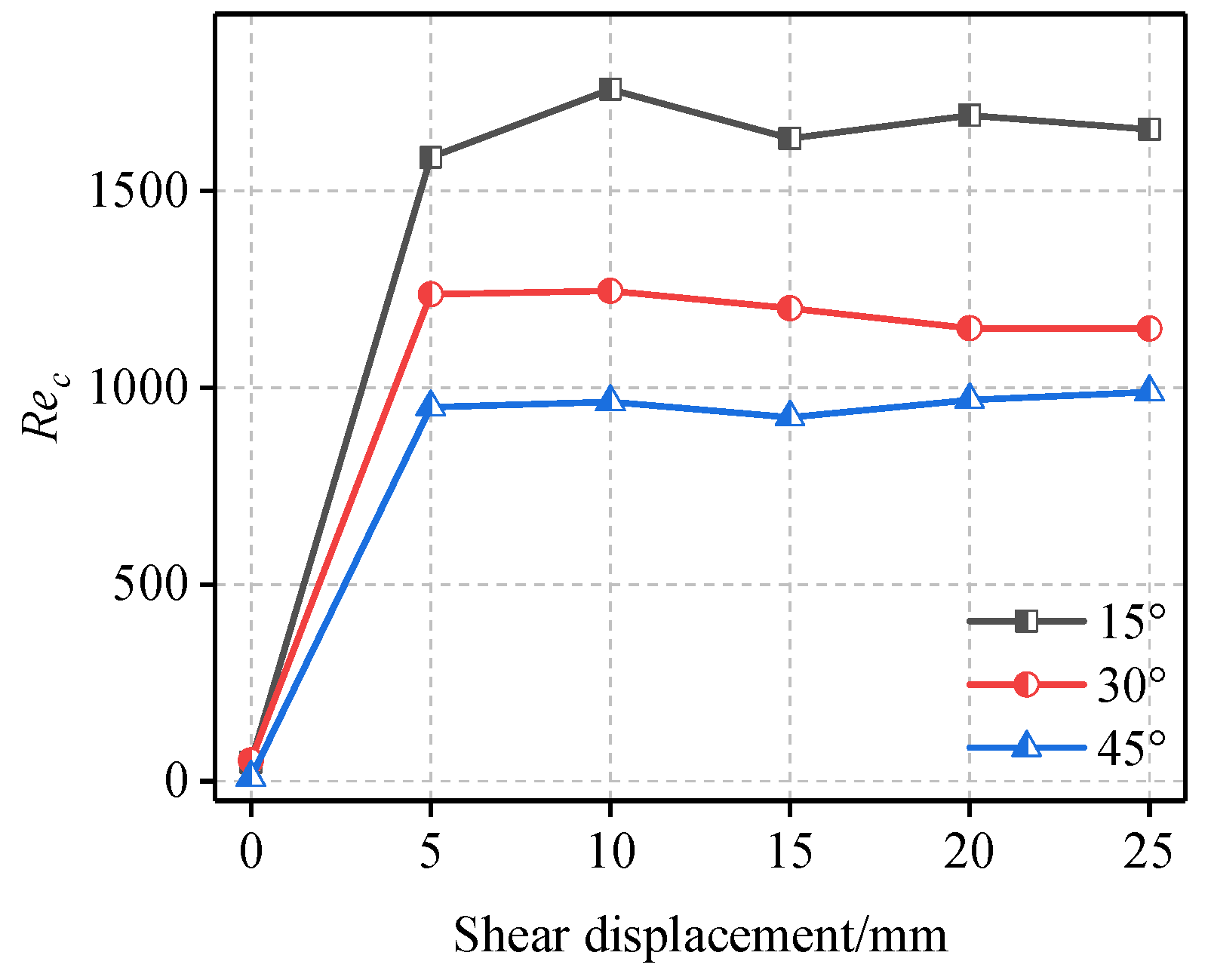
3.2.2. Critical Reynolds Number Criterion

The Forchheimer equation shows that as the water flow increases, the impact of the inertial force on work done by the flow of water requires consideration. To quantify the effect of the non-linear term on the hydraulic gradient, a non-linear factor E [36] was introduced, and this can be expressed as follows:

$$E=\frac{b{Q}^2}{aQ+b{Q}^2}$$

(5)

In practical engineering, if E ≥ 0.1, the non-linear term cannot be neglected regarding work associated with the flow of water. An E value of 0.1 is the critical point of the transition between the linear and non-linear seepage. The Reynolds number, Re, was then introduced to characterise the influence of the inertial force on the viscous force during non-linear seepage, and this can be expressed as follows [37,38]:

$$Re=\frac{\rho uh}{\mu }=\frac{\rho Q}{\mu w}$$

(6)

$$w=r_0+r_1$$

(7)

$$r_1=\sqrt{\frac{L_1\times L_2}{\pi }}$$

(8)

where ρ is the density of water (0.997 × 10³ kg/m³), u denotes the average flow velocity (m/s), h represents the average fracture between structural planes (m), µ is the dynamic viscosity coefficient (0.89 × 10⁻³ Pa·s), Q denotes the inlet flow (m³/s), and w is the width of the fracture along the direction of the increasing pressure gradient. In radial flow, w is obtained using the inner radius, r₀, and outer radius, r₁, of the structural plane [39,40]. The parameter r₀ is the radius of the water injection hole, whereas r₁ is the equivalent radius of the structural plane outlet, which is expressed using Equation (8). The L₁ and L₂ are respective to the length and width of the seepage structural plane (m).

If E = 0.1, the critical Reynolds number, Re_c [41], is obtained by substituting Equation (5) into Equation (6):

$$R{e}_{\mathrm{c}}=\frac{a\rho E}{b\mu w\left(1-E\right)}=\frac{a\rho }{9b\mu w}$$

(9)

The relationship between Re_c and the shear displacement of the structural plane is shown in Figure 8. Moreover, as the shear displacement increases during the shearing, the Re_c initially increases and then stabilises, and its values vary between 9.65 and 1758.52. During the initial stage of shearing, the structural plane is compact under normal stress. Therefore, cracks begin to sprout and expand, and the flow of water in the sample is weak. This flow is mainly linear, and the Re_c is low. As the shear displacement increases, the convex structural plane is sheared, and the cracks widen. A channel for the flow of water is gradually developed, and the momentum associated with the fluid changes. Therefore, the Re_c initially increases, and then it stabilises.

In addition, as the fluctuation angle of the structural plane increases, the Re_c decreases. This is because a structural plane involving a higher fluctuation angle is sheared under the same conditions. Therefore, the longer the water flow path formed within the structural plane after the tooth cut, the stronger the inertial fluid flow effect. This condition facilitates non-linear seepage within the structural plane, and thus, the Re_c is lower.

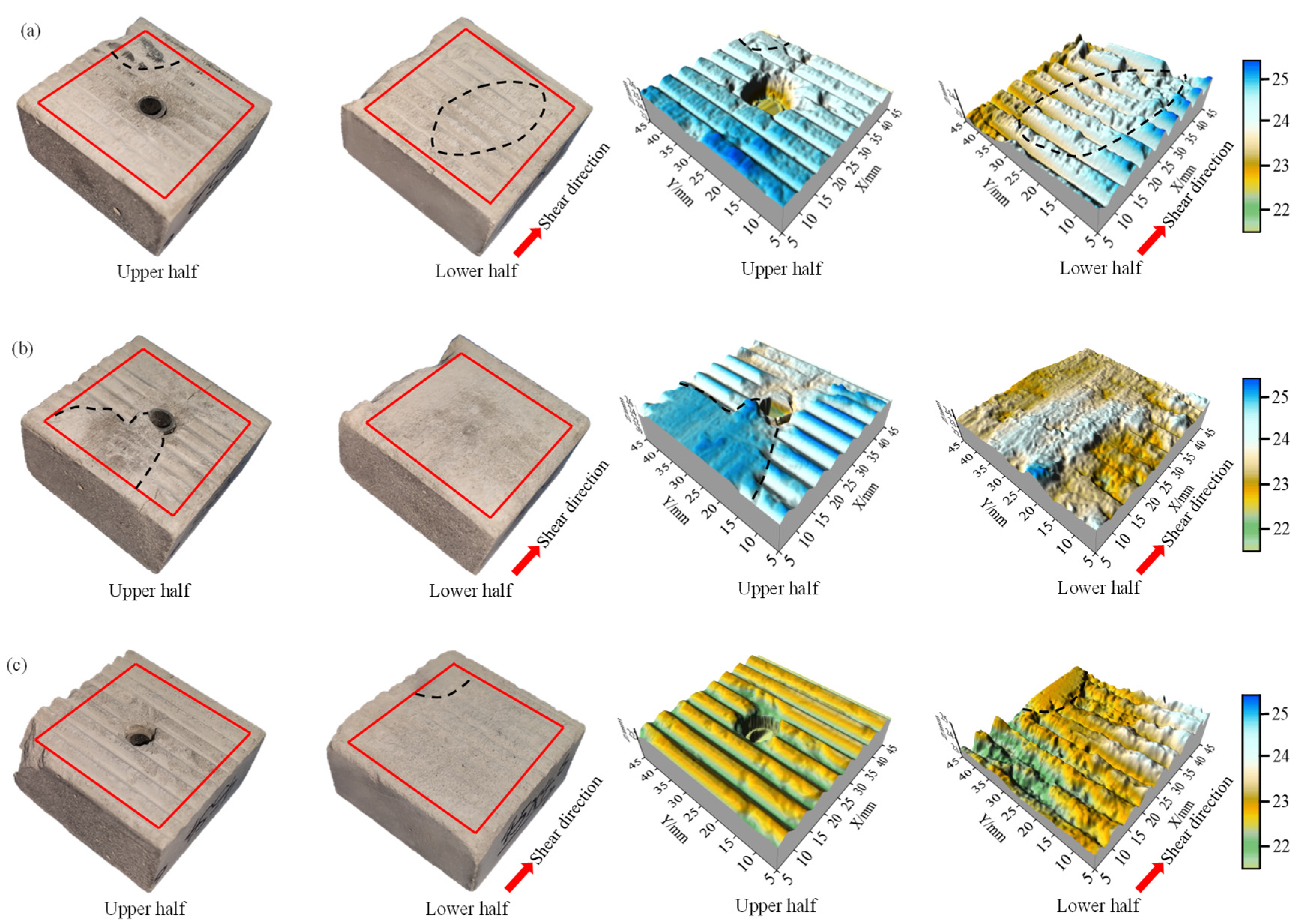
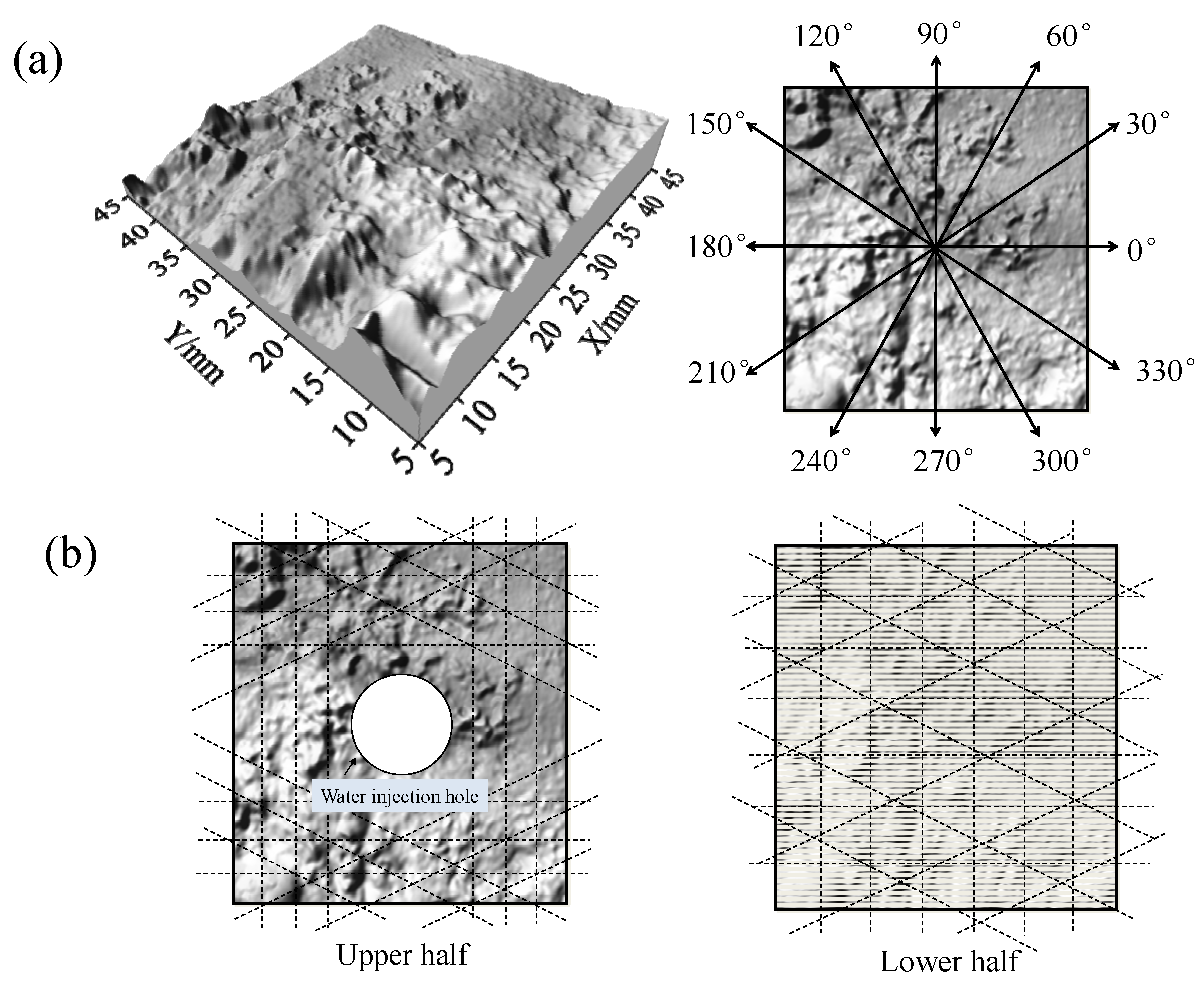
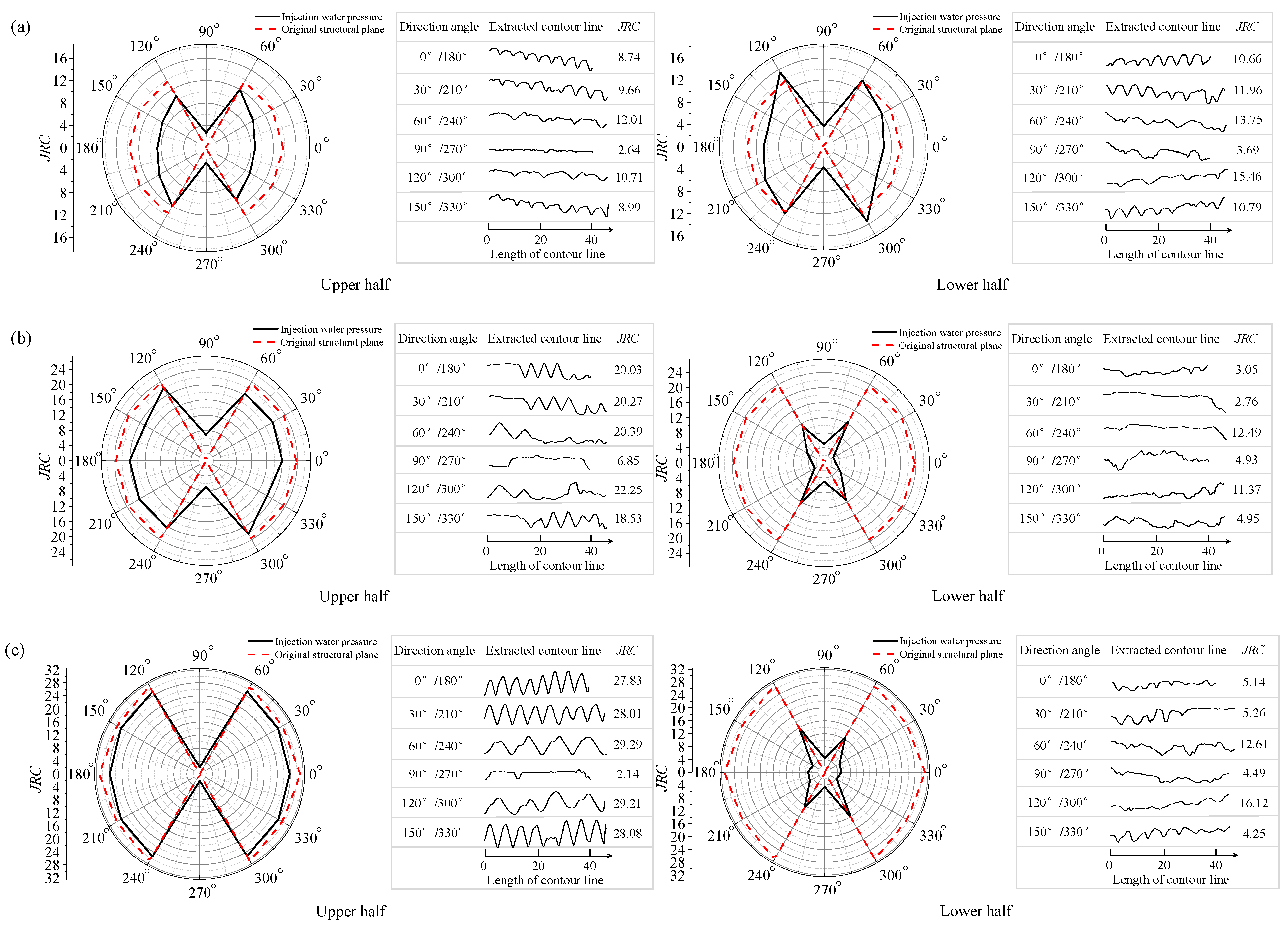
3.3. Three-Dimensional Morphological Characteristics of Structural Planes

The visual topography and 3D scans of a structural plane involving different relief angles for a shearing displacement of 25 mm are shown in Figure 9. The 3D scan represents just 40 mm of the structural plane, and the area was magnified × 40 mm (i.e., X and Y are 5 and 45 mm, respectively, and the area is enclosed in the frame in red). The arrow in red in the lower portion of the structural plane indicates the direction of cutting.

In Figure 9, the black dotted line area reveals an obvious tooth-cut failure in the structural plane. The wear direction is along that of shearing in the structural plane.

To further evaluate the influence of the morphology of the surface structure on seepage characteristics, the anisotropy of the surface roughness of the structure was analysed as point cloud data using a 3D scanner. These data improved our understanding of the formation of water flow channels between structural planes.

To obtain roughness parameters that represent the entire structural plane, the roughness of the structural plane was calculated by dividing it into 30° segments. The JRC was calculated using six equally spaced contour lines in the selected calculation direction of the structural plane. Further, the JRC of the entire structural plane was obtained by averaging the results associated with the six contour lines. A scheme that can be utilised to calculate the JRC of a structural plane is shown in Figure 10. The JRC value of each contour line was calculated using the following empirical formula [42]:

$$JR{C}_i=32.20+32.47\log \left(Z_2\right)$$

(10)

$$JRC=\frac{1}{6}{\displaystyle \sum _{i=1}^{6}JR{C}_i}$$

(11)

$$Z_2=\sqrt{\frac{1}{m}{\displaystyle {\sum }_{i-1}^{m-1}{\left(\frac{z_{i+1}-z_i}{\Delta }\right)}^2}}$$

(12)

where i is the plot of the ith contour, Z₂ denotes the root mean square of the slope of the structural plane profile, m represents the number of acquisition points on the profile, Z_{i + 1} and Z_i are heights of adjacent points, and Δ is the lateral distance between adjacent points.

Figure 11 shows polar charts of the JRC for the upper and lower sections of structural planes involving different relief angles. The values that were calculated for the contour lines in different directions are based on a shear displacement of 25 mm. Figure 11 reveals that the JRC of the structural plane varies following the direction, and this suggests that the failure of the structural plane is characterised by anisotropy. The polar charts reveal that the roughness of the structural plane perpendicular to the shear direction increased during the shearing, and thus, the shear failure induced roughness changes in this direction. By contrast, the JRC exhibits decreasing trends in other directions. In addition, because the highest effective shear dip angle [43] is parallel to the shear direction, the damage associated with cutting the structural plane in this direction is also the highest. Consequently, the ranges of variations in the JRC before and after are also the highest. A comparison of changes in the JRC in the upper and lower portions of structural planes that involve different undulation angles reveals that the range of JRC variations increases as the undulation angle increases. In addition, the range of variation for the lower portion of the structural plane is higher than that of the upper portion.

Programming the 3D scanning data of the upper and lower portions of the structural planes using MATLAB enabled the creation of a hydraulic fracture development diagram of the structural planes. Figure 12 shows a schematic diagram of the hydraulic fractures in the structural planes. The associated formula is expressed as follows:

$${\Delta }_i={\mathrm{z}}_2-{\mathrm{z}}_1$$

(13)

where Δ_i is the crack opening at point i₁ in the lower portion of the structural plane; z₁ represents the height at point i₁ (x₁, y₁, z₁) in the lower portion of the structural plane; and z₂ denotes the height at the point i₂ (x₂, y₂, z₂) in the upper section of the structural plane, and x₂ = x₁ + 25, y₂ = y₁, x₁ ∈ [5, 25].

Figure 13 shows the development of hydraulic fractures in a structural plane for a shear displacement of 25 mm. Moreover, hydraulic fracturing of the structural plane increases as the fluctuation angle increases. If the undulation angle is 15°, the structural plane is characterised by a low hydraulic fracturing, and water flows mainly along the area associated with considerable damage from the cut tooth of the structural plane; that is, the vertical shear direction. Conversely, if the fluctuation angle is 30°, the tendency for hydraulic fracturing of the structural plane is low within the area enclosed by dotted lines in black. Therefore, if water flows through this area, it will encounter obstacles, and thus, it will flow into the area involving the large crack. Consequently, the area involving the major hydraulic fracture is the main channel for the diversion of water; that is, the dominant seepage channel [44]. Finally, if the fluctuation angle is 45°, the potential for hydraulic fracturing of the structural plane is relatively high. The dominant seepage channel is perpendicular to the shear direction.

4. Conclusions

In the present study, we conducted seepage tests at structural planes involving varying undulation angles and shear displacement conditions. The shear mechanical and non-linear seepage properties, as well as the 3D morphological characteristics of the shear sections in the structural planes, were analysed. The main findings can be summarised as follows:

(1)

The shear stresses at structural planes involving different undulation angles fluctuated and showed an increasing trend as the shear displacement increased. The normal displacement associated with an adjacent shear step initially increased and then decreased before stabilising. The shear strength at a structural plane and variation in the normal displacement increased as the undulation angle increased, and the associated shear expansion was enhanced.

(2)

Under an identical hydraulic gradient, the seepage flow associated with structural planes of equal undulating angles increased as the shear displacement increased. By contrast, both the linear term coefficient a and non-linear term coefficient b in the Forchheimer fitting equation decreased as the shear displacement increased. Fitting of the data generated produced the following empirical relationship between a and b: b = 2.457 × 10⁻¹¹ a^4.872.

(3)

An analysis of the effects of losses in the non-linear inertial force on the hydraulic gradient enabled the establishment of the variation pattern and range of the critical Reynolds number. During shearing at a structural plane, as the shear displacement increased, the critical Reynolds number initially increased and subsequently stabilised. Critical Reynolds numbers that were obtained in the present study varied from 9.65 to 1758.52.

(4)

An evaluation of the JRC and hydraulic fracture data of the structural planes revealed anisotropy of the fracture morphology associated with the hydraulic and mechanical coupling. The JRC varied significantly perpendicular to the shear direction, and its range for a structural plane increased as the fluctuation angle increased. The dominant seepage channel was perpendicular to the shear direction.

We aimed to provide insight into the mechanisms affecting the non-linear seepage characteristics of rough structural planes and the morphological characteristics of shear surfaces caused by shear seepage action. The research results complement the accurate evaluation of seepage characteristics of fractured rock masses and provide theoretical guidance for the study and analysis of the slope stability of structural plane rock projects.