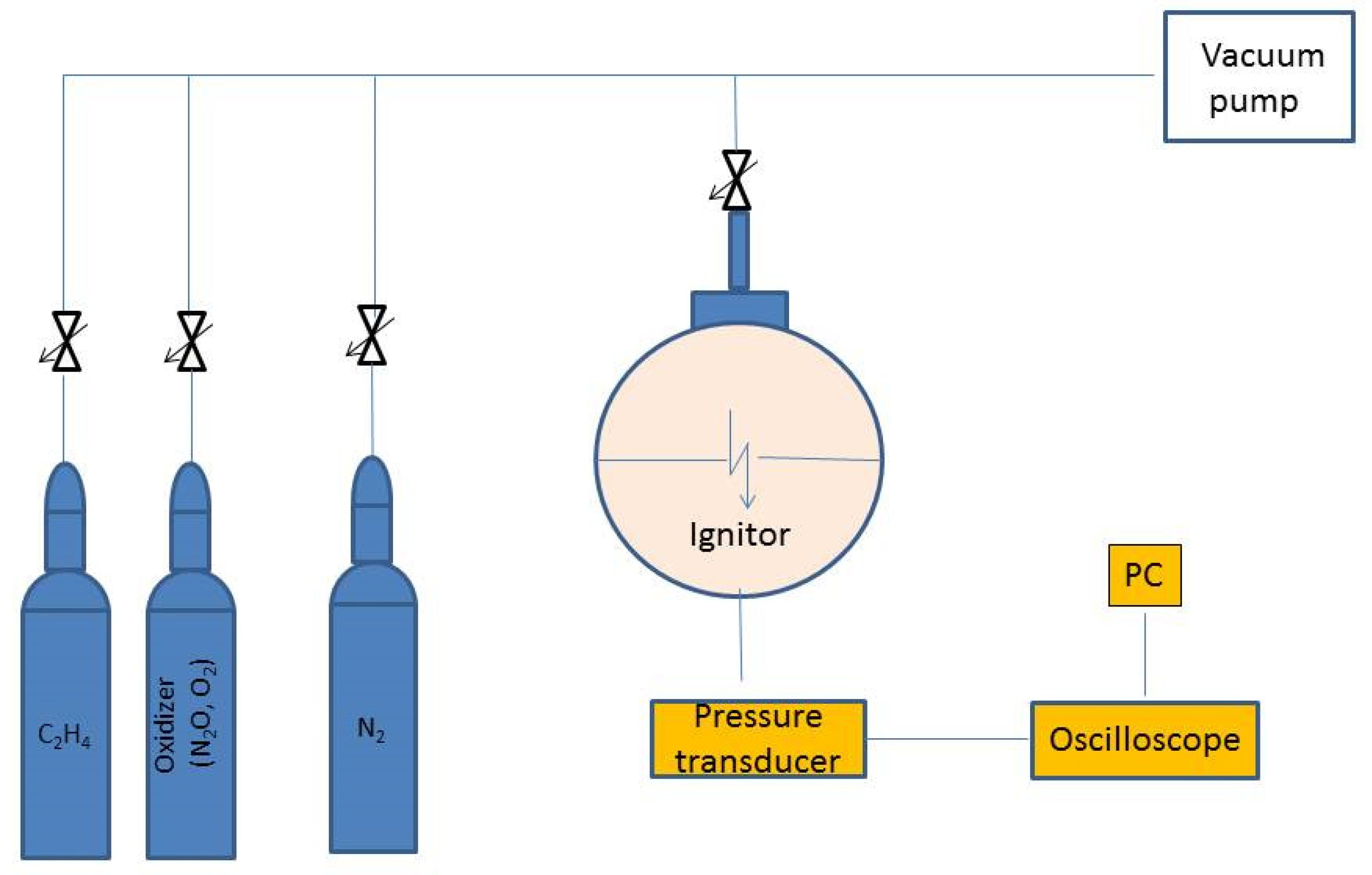
1. Introduction
Combustion is the major energy production process, so the study of flammability features of gaseous combustible mixtures at various initial conditions still represents a major challenge for researchers. Fuel–air combustion has been intensively studied, but in recent years an important concern has been raised: not only to find alternative fuels to substitute the conventional fuels, but also to find alternative oxidizers to replace oxygen. Nitrous oxide (N
2O, also known as laughing gas) is a strong oxidizing agent, roughly equivalent to hydrogen peroxide, and much stronger than oxygen gas. It was used as oxidizer in the semiconductors industry and as a rocket propulsion system [
1,
2,
3]. On the other hand, N
2O is highly exothermic and during its decomposition a supplementary heat amount is released, so its handling is critical.
As an oxidizer, N
2O can easily decompose to oxygen and nitrogen at elevated pressures and temperatures [
2,
4]. Numerous studies were published on fuel-N
2O mixtures in terms of flammability parameters such as flammability limits, ignition energy, flame speeds, etc. The explosion ignition and propagation in H
2-CH
4-NH
3-N
2O-O
2-N
2 mixtures was studied by Pfahl et al. [
5]. They reported flammability limits, ignition energies and flame speeds in combustion vessels at initial pressure of 1 bar and initial temperature of 295 K. Some investigations on N
2O flames focused on the flammability domain of different fuel-N
2O mixtures (flammability limits) in the presence of inert gases [
6,
7].
The explosion parameters of toluene/N
2O at initial pressure of 1 or 6 bar and initial temperature of 343 K from measurements in an 8 L spherical vessel were reported by Vandebroek et al. [
6]. The explosion features of volatile organic vapours, such as n-pentane, diethyl ether and diethyl amine, and of C
1-C
8 n-alkanes in N
2O atmosphere in a cylindrical explosion vessel were studied by Koshiba et al. [
2,
8] and compared with those of mixtures containing O
2.
Vandooren et al. [
9] conducted a study on the flame structure of stoichiometric methane-N
2O-Ar and methane-O
2-Ar by means of the molecular beam sampling and mass spectroscopy methods. The propagation parameters and laminar burning velocities of CH
4-N
2O in the presence of various inert gases (e.g., He, Ar, N
2 and CO
2) obtained from experiments in a 0.52 L spherical vessel, at initial pressures from 0.3 to 1.8 bar were recently investigated by Razus et al. [
10,
11]. The authors reported that the maximum explosion pressure as well as the maximum rates of pressure rise present a linear dependence on the initial pressure. The additive efficiency on the explosion parameters decreased starting with CO
2, followed by N
2, Ar and He. The overall activation energy of methane oxidation by N
2O, which is lower than the overall activation energy when O
2 from air is used as an oxidant, can be due to N
2O dissociation.
Ethylene-N
2O flame was less studied despite the safety concerns raised from handling and storage of nuclear waste, where these mixtures can form, as well as due to their use in aerospace applications. Ethylene is a high-reactivity fuel used in the chemical industry, but previous investigations focused on explosion of ethylene-air (oxygen) mixtures [
12,
13,
14,
15,
16]. However, ethylene–N
2O mixtures have recently been proposed as a promising propellant for hydrazine replacement [
17,
18] due to their advantages: similar vapor pressures, which allow a good miscibility, and high vapor pressure, which allows a self-pressurizing without an external pressure supply. Additionally, ethylene–N
2O mixtures are not carcinogenic, have a relatively low cost and a low toxicity and after their combustion, no ammonia results in comparison with hydrazine. Therefore, ethylene–N
2O mixtures represent a green propellant and thus, the studies related to these mixtures are always necessary.
Shen et al. [
19] experimentally investigated the explosion dynamics of inert-diluted C
2H
4-N
2O explosions in a standard 20-L spherical vessel at sub-atmospheric pressure (inerts: N
2 and CO
2). For inert concentrations lower than 30% they found a correspondence between the maximum explosion pressure experimentally measured and the corresponding Chapman–Jouguet (CJ) detonation pressure, meaning the activation of a DDT (Deflagration-to-Detonation) mechanism during the explosion process, also demonstrated by Bane et al. [
20] for nitrogen-diluted hydrogen–nitrous oxide flames. The explosion characteristics of C
2H
4-N
2O-N
2 mixtures measured in various cylinders (0.17 L, 1.18 L and 2.0 L), at different initial pressures, were reported by Movileanu et al. [
21]. They found a linear dependence of the maximum explosion pressure (as well as of the maximum rise of pressure rise) on the initial pressure, similar to that reported for fuel-air mixtures [
16]. In smaller volume explosion vessels, no DDT occurred. The DDT in long tubes, the explosion limits, and the ignition delay times of explosions in C
2H
4-N
2O and C
2H
4-O
2 mixtures were also investigated in the previous studies [
22,
23,
24,
25,
26].
From the above literature review it can be concluded that researchers have focused their interest mostly on studying the explosion characteristics of other fuel–N2O flames rather than that of ethylene-N2O flames. Therefore, these latter flames must be studied in detail to cover the gap that exists regarding them in literature.
In the present study, the dynamics of closed-vessel explosion of nitrogen-diluted C2H4/N2O mixtures is examined by means of the maximum (peak) explosion pressures, explosion times, maximum rate of pressure rise and severity factors. Lean and stoichiometric C2H4/N2O mixtures diluted with various nitrogen amounts were examined using a 0.52 L vessel with spherical aspect and central ignition at different initial pressures. The nitrogen was chosen as diluent because it is frequently used as an inert gas in the case of explosion inhibition. The data and conclusions from the present research could contribute to a better understanding of explosions occurring in N2O atmosphere, providing new insights of these processes.
4. Results
An example of pressure-time record for stoichiometric C
2H
4-N
2O-N
2 mixture explosion in spherical vessel with central ignition at 1 bar initial pressure and ambient initial temperature is presented in
Figure 2 and compared with that obtained for stoichiometric C
2H
4-air explosion registered under the same initial conditions [
30]. The comparison can be performed since the examined mixtures have close flame temperatures.
It can be observed that for equivalent initial conditions the use of N2O for replacing O2 as oxidizer entails the increase of the maximum explosion pressure and the decrease of the explosion time. This shows us that the fuel–N2O mixtures are more reactive when compared with the mixtures with air with the same flame temperature. This behaviour is due to the additional heat amount released from the exothermal decomposition of N2O when N2O is used as oxidizer instead of air (O2).
For all pressure–time trajectories, the pressure first increases progressively, and then decreases once the maximum values are reached, this fact indicating that a complete combustion has taken place.
The pressure evolutions of C
2H
4-N
2O-N
2 explosions at initial pressure of 1 bar and various amounts of nitrogen are presented in
Figure 3 as examples. The comparison presented in this figure shows that, for the same initial pressure, temperature and fuel:oxidizer ratio, the explosion pressure decreases when the inert concentration increases. It can be seen that, starting with 40 vol.% dilution, the pressure inside the explosion vessel rises up smoothly after mixture ignition. This behaviour has been widely reported by other researchers [
16,
31,
32].
The initial pressure is one of the parameters that influence the maximum (peak) explosion pressure. An example of maximum (peak) explosion pressures’ variation against initial pressures for stoichiometric C
2H
4-N
2O-N
2 mixtures is presented in
Figure 4 for various N
2 dilution ratios and ambient initial temperature. Such variations were also observed for lean C
2H
4-N
2O-N
2 mixtures. As expected, the maximum explosion pressure during the explosion of C
2H
4-N
2O-N
2 mixtures increases as the initial pressure increases.
Due to the lack of experimental data reported in literature for explosions of C
2H
4-N
2O-N
2 mixtures in spherical vessels at initial pressures
p0 ≥ 1 bar, we can only compare our data with those reported at sub-atmospheric pressures. Our data registered at
p0 = 0.5 bar are:
pmax = 6.50 bar for stoichiometric C
2H
4-N
2O mixture diluted with 40 vol.% N
2 and
pmax = 5.70 bar for stoichiometric C
2H
4-N
2O mixture diluted with 50 vol.% N
2. These results are higher than those reported by Shen et al. [
19] for mixtures with the same composition and initial pressure obtained from experiments in a 20 L spherical vessel (
pmax = 5.70 bar for the stoichiometric C
2H
4-N
2O mixture diluted with 40 vol.% N
2 and
pmax = 5.00 bar for stoichiometric C
2H
4-N
2O mixture diluted with 50 vol.% N
2). These discrepancies might be due to the differences in vessel volumes, which can affect the heat losses and through them, the explosion pressures.
Linear correlations of maximum explosion pressures with initial pressures of the mixture were found for all examined systems. The correlation could be described using the following equation:
The coefficients
a and
b from Equation (1) are necessary to find the unknown values of the explosion pressures at a certain value of the initial pressure in the studied pressure range without experimental measurements, as long as the combustion is propagating as a deflagration. They depend on a series of parameters such as: initial temperature, nature of the mixture, vessel shape, and aspect ratio. The coefficients of linear regressions for stoichiometric and lean C
2H
4-N
2O-N
2 mixtures are presented in
Table 1.
Such linear correlations between explosion pressures and initial pressures were observed not only for fuel–air mixtures [
16], but also when other fuel–N
2O inert mixtures were examined [
10].
Besides the initial pressure, the shape and size of the explosion vessel influence the explosion pressure. Thus, in cylindrical vessels, the explosion pressures are smaller in comparison with those registered in spherical vessels due to higher heat losses that occur in these cylindrical enclosures. On the other hand, the higher vessel size is, the smaller the explosion pressure is. The influence of the size and aspect of the explosion vessels on this parameter can be observed from
Table 2, where data referring to stoichiometric C
2H
4-N
2O-N
2 diluted with 60 vol.% N
2 measured in a cylinder with L/D = 1.0 and in a cylinder with L/D = 1.5 measured at initial pressures between 0.50 and 1.50 bar collected from [
21] are given along with the present data. All data from
Table 2 refer to experiments with central ignition.
The presence of an inert diluent affects the maximum explosion pressures as can be seen in
Figure 5, where data referring to both studied mixtures (lean and stoichiometric) at ambient initial conditions are given. As expected, the higher the nitrogen amount is, the smaller the explosion pressure is. Adding an inert (such as nitrogen) to a gaseous flammable mixture leads to an alteration of both thermodynamics and kinetics of the combustion process, so that a higher inert concentration leads to a small explosion pressure.
The kinetic effect due to N
2 addition on C
2H
4-N
2O mixtures can be assigned mainly to N
2 participation in the following reaction:
The study undertaken by Shen et al. [
19] pointed out that, at high initial pressures, nitrogen acts as both as a reactant and a third body, and thus reaction (R1) becomes important. Therefore, although the N
2O undergoes an energetic decomposition through the reaction (R2) written below, nitrogen can effectively inhibit N
2O decomposition, as described in [
19].
Furthermore, the nitrogen addition can lead to a decrease in the branching ratio of the following reaction (R3) over reaction (R1), by its third-body collisional effect [
19]:
Besides the kinetic effect, nitrogen addition contributes to the reduction of the flame temperature and flame speed, acting as a heat sink.
For all studied mixtures, a linear dependency of explosion pressure on inert concentration was observed. This dependency can be described using a correlation proposed by Oancea et al. [
33,
34] based on heat balance of the isochoric combustion of a fuel–air mixture in non-adiabatic conditions:
where
pmax represents the maximum explosion pressure attained at pressure
p0;
ξ =
ne/
n0 is the ratio between the final (
ne) and initial (
n0) mole numbers;
rl=
nl/
n0 represents the ratio between the number of moles corresponding to the limiting component of the mixture and the total initial number of moles;
νl represents the stoichiometric coefficient of the limiting component in the mixture; Δ
cU’ represents the heat of combustion (at temperature
T0 and constant volume) corrected by taking into account the accompanying secondary reactions;
represents the molar heat capacity of the end gaseous mixture, averaged for the end components and for the temperature range
T0 to
Te,V;
qtr represents the amount of heat transferred by the gas to the vessel before the end of combustion; and
γe represents the adiabatic coefficient of the burned gas, at the end of combustion.
For the isochoric combustion of a gaseous fuel-oxidizer mixture, Equation (2) holds as long as it is assumed that the studied gas behaves like an ideal gas and that pmax is approximately equal to the pressure at the combustion end. However, in the real cases, the gaseous fuels are made up from polyatomic molecules, having many degrees of freedom, and their heat capacities are high and depend on temperature, which leads to explosion pressures which differ from those obtained with this equation. Keeping constant the initial temperature, the maximum explosion pressures of N2-diluted C2H4-N2O mixtures depend on initial pressures (influencing the molar heat capacity of the end gaseous mixture and the adiabatic coefficient of the burned gas, at the end of combustion) and on the amount of heat transferred by the gas to the vessel before the end of combustion. Therefore, we can observe that N2 addition to C2H4-N2O mixtures influences both the slope and intercepts of pmax versus p0 plots.
Over a well-defined initial pressure domain, we can assume that
ξ, Δ
cU’and
do not depend on
p0 (or that their variations compensate each other) and therefore, the amount of heat transferred from the burned gas to the explosion vessel before the combustion ends, can be obtained using the intercepts of the linear correlations
pmax vs.
p0, whose values are presented in
Table 1. Representative results regarding the amount of heat transferred by the stoichiometric and lean ethylene-N
2O-N
2 flames to the vessel’s walls are presented in
Table 3. In the present case,
qtr was calculated following [
16], as:
From
Table 3 it is seen that an increase of the nitrogen concentration leads to larger amounts of heat being lost to the vessel’s wall due to the longer explosion times and lower propagation speeds for both lean and stoichiometric ethylene-N
2O-N
2 mixtures.
Another important parameter that describes the heat transferred during explosions in closed vessels is the fraction (
F) of the heat transferred (lost) from the total released heat. This property depends, on one hand, on the corrected heat of combustion and the average heat capacity of burned gas (factors influenced by the composition of fuel and oxidizer) and, on the other hand, on the initial pressure of the studied mixture. In this study, the fractions
F of transferred heat were calculated using the following equation [
35], derived also from Equation (2):
Their values calculated at
p0 = 1 bar are also presented in
Table 3. At constant inert composition, lower
F values were obtained for the stoichiometric C
2H
4-N
2O flames compared to the lean flames. This is due to the fact that the stoichiometric mixtures have shorter explosion times and higher burning velocities when compared to the lean mixtures.
When a certain amount of inert (molar fraction:
xi) is added to a fuel-air mixture, it is expected that the heat transferred from the burned gas to the vessel, before the combustion ends, to be a function of mixture composition. Therefore, the term
qtr from Equation (2) becomes
= f(rl, xi) and Equation (2) is rewritten as:
When the composition of fuel-oxidizer mixture as well as the initial pressure
p0 are constant, we can assume that the coefficients
m and
n (characterized by
ξ, rl and
νl) are constant. This is true only for a restricted domain of inert gas concentrations. Only when these conditions are fulfilled, the explosion pressure present a linearly dependence on the molar fraction of added inert gas. In this case, a linear dependence of explosion pressure on the molar fraction of added inert gas is observed, as shown by the data from
Figure 5.
Even if explosions occur in a spherical vessel, where the explosion is considered to propagate as close as possible to the ideal case, the differences between experimental and ideal adiabatic explosion pressures are significant, as it can be seen from
Figure 5. This behaviour shows once more that in the real case, the heat transferred (by convection, conduction or radiation) from the flame front to the vessel walls influences the explosion’s propagation. In the present research, the flame was monitored by means of an ionization probe. The ionization probe signal, reaching its peak value at the same time with the peak of the pressure rise rate, can be seen in
Figure 6. The observed differences between the experimental and adiabatic values of the explosion pressures can be attributed not only to the heat losses during experiments, but also to the aspect and volume of the explosion vessel, the position of the ignition source or the appearance of turbulences in the gaseous mixture before ignition, which may lead to a decrease in explosion pressure. In the case of an adiabatic process when there are no heat losses, the explosion pressures are influenced only by the initial pressure and temperature and by the composition and the nature of the studied mixture. The differences between the experimental and calculated (adiabatic) explosion pressure are useful to obtain with approximation the amount of lost energy in the course of the combustion process. This was already noted by Kunz in his study on combustion characteristics of H
2- and hydrocarbon–air mixtures in closed vessels [
36]. Kunz concluded that the larger the differences between the calculated and experimental explosion pressures are, the higher the thermal losses are that occur during the explosion.
The adiabatic explosion pressures have the same behaviour as the experimental explosion pressures does. At a constant amount of nitrogen, higher values of the adiabatic explosion pressures were observed for stoichiometric C2H4-N2O mixture compared to lean C2H4-N2O mixture. Keeping the equivalence ratio constant, the adiabatic explosion pressures decreased with an increase in initial pressure.
Set as the zero point (0 s) on an X-axis the moment of ignition. Considering this, the explosion time,
θmax, which represents another important combustion parameter, is defined as the explosion duration between the ignition and the moment when the maximum explosion pressure is reached. Adding an inert to a gaseous fuel–oxidizer mixture influences not only the maximum explosion pressure, but also the explosion times. Obviously, with increasing N
2 dilution, the explosion duration
θmax increases, as it can be observed from
Table 4.
It was found that for stoichiometric ethylene-air mixture at p0 = 1 bar, the maximum time to reach pmax is θmax = 14.6 ms, higher that for an ethylene-N2O-N2 mixture with the same flame temperature (θmax = 10.7 ms). Lower values of characteristic parameters θmax were obtained for a stoichiometric C2H4-N2O-N2 mixture compared to the lean mixture. This behaviour is in accordance with their burning velocities.
The maximum rate of pressure rise represents a safety parameter important for assessing the hazard of a process and, together with the explosion pressure, is used for design of enclosures able to withstand explosions, or of vents used as relief devices for these vessels to avoid the damages caused by explosions occurring in the gaseous phase [
37,
38,
39]. For explosions of nitrogen-diluted ethylene-N
2O mixtures linear dependences of the form:
were obtained from the graphic representation of the maximum rates of pressure rise versus initial pressures, as can be observed in
Figure 7a,b. The coefficients
α and
β depend, on one hand, on the equivalence ratio of studied mixture, and, on the other hand, on the nature and of amount of inert added to the gaseous mixture.
Similar dependences as those given in
Figure 7 were reported earlier for fuel–air mixtures such as propane–air [
40], LPG–air [
41] or propylene–air [
42] and for fuel–air–diluent mixtures (e.g., H
2–air–steam [
43,
44], CH
4–air–N
2, CH
4–air–CO
2 [
45], natural gas–air–CO
2 [
46]) obtained at sub-atmospheric initial pressures or at initial pressures above 1 bar (with the obvious limitation to deflagrative combustions).
Such diagrams as those depicted in
Figure 7 are useful to calculate the maximum rates of pressure rises at any initial pressures different from the ambient one, but within the studied pressure range. This is valid only as long as the explosion propagates as deflagration.
At
p0 = 0.5 bar and stoichiometric equivalence ratio of C
2H
4-N
2O-N
2 mixtures, Shen et al. [
19] reported
(dp/dt)max = 20 bar/s for a nitrogen amount of 40 vol.% and
(dp/dt)max = 10 bar/s for a nitrogen amount of 50 vol.%. As a comparison, the present data are:
(dp/dt)max = 21.0 bar/s for a nitrogen amount of 40 vol.% and
(dp/dt)max = 14.8 bar/s for a nitrogen amount of 50 vol.%.
As shown by the above data, the presence of an inert influences the rates of pressure rise. From
Figure 7 it is observed that, for constant equivalence ratio, the higher the amount of inert added is, the lower the pressure rise rates are, for both lean and stoichiometric ethylene-N
2O flames. When the amount of N
2 is kept constant, it is noticed that the pressure rise rates of lean ethylene-N
2O mixtures are lower compared to the pressure rise rates of stoichiometric mixture. This behaviour was already reported for CH
4-N
2O-N
2 flames [
10].
The severity factor is an efficient scaling parameter able to predict the failure effect of enclosures where an explosion occurs. In this study, the severity factors (
KG) of C
2H
4-N
2O-N
2 flames were determined by means of the rates of pressure rise obtained from measurements in the spherical vessel with central ignition and are given in
Figure 8 versus the initial pressure. The greater the amount of inert is, the lower the severity factors are, a fact observed for both stoichiometric and lean C
2H
4-N
2O mixtures when the equivalence ratio is kept constant. As expected, when the inert concentration is kept constant, the higher values of the severity factors are observed for the stoichiometric C
2H
4-N
2O mixture compared to lean C
2H
4-N
2O mixture.
As already reported for CH
4-air mixture [
47], and as seen from
Figure 8, the severity factors are strongly affected by the initial pressure. As expected, the severity factors present the same linear dependence on the initial pressure as previously observed for the maximum explosion pressures and the rates of pressure rise.
Therefore, the severity of an explosion in fuel–oxidizer mixtures can be reduced by using inert additives which have the role of taking over some of the heat released from the combustion reaction and thereby lowering the temperature in the flame front. The decrease of the flame temperature has as a major effect the decrease of the explosion pressure, accompanied by the decrease of the reaction rate resulting in the decrease of maximum rates of pressure rise and thus of the severity factors.
The maximum explosion pressures and maximum rates of pressure rise of stoichiometric C
2H
4-N
2O mixtures diluted with various amounts of N
2 or CO
2 were studied at various initial pressures using a standard-volume vessel [
19]. The authors of this paper concluded that, in the case of the aerospace applications where the dilution degree is small, a N
2 dilution contributes better to safety and power efficiency when compared to CO
2. On the other hand, in the case of nuclear or other hazardous waste which contains N
2O, the nitrogen presents almost the same dilution effect as CO
2 due to its presence in large quantities. Therefore, for a better use of these mixtures that present a high explosive risk, specialized scientific studies are always necessary.