Interaction between Iron Fluoride and Molten FLiBe
Abstract
1. Introduction
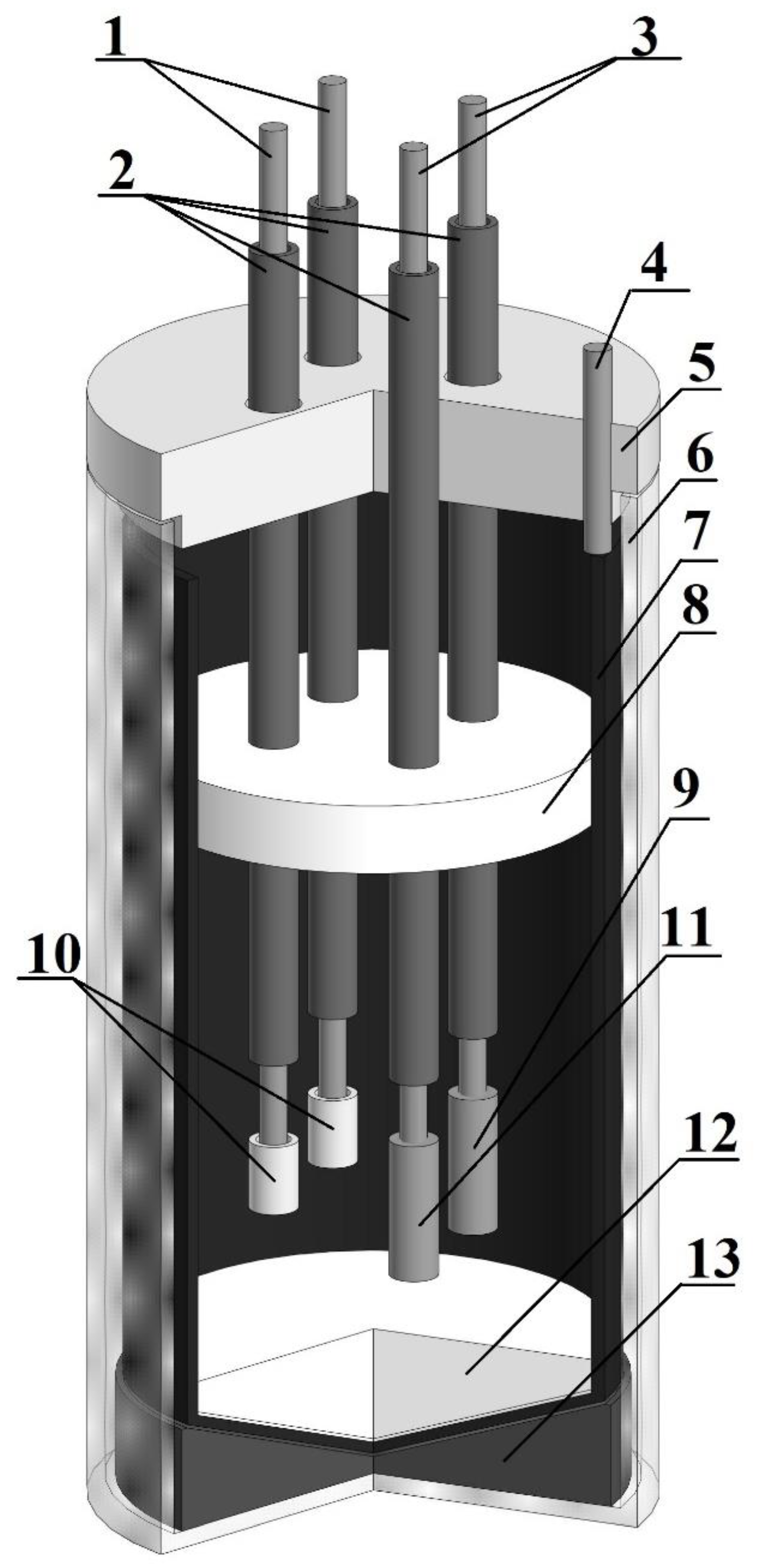
2. Materials and Methods
2.1. Reagents Preparation
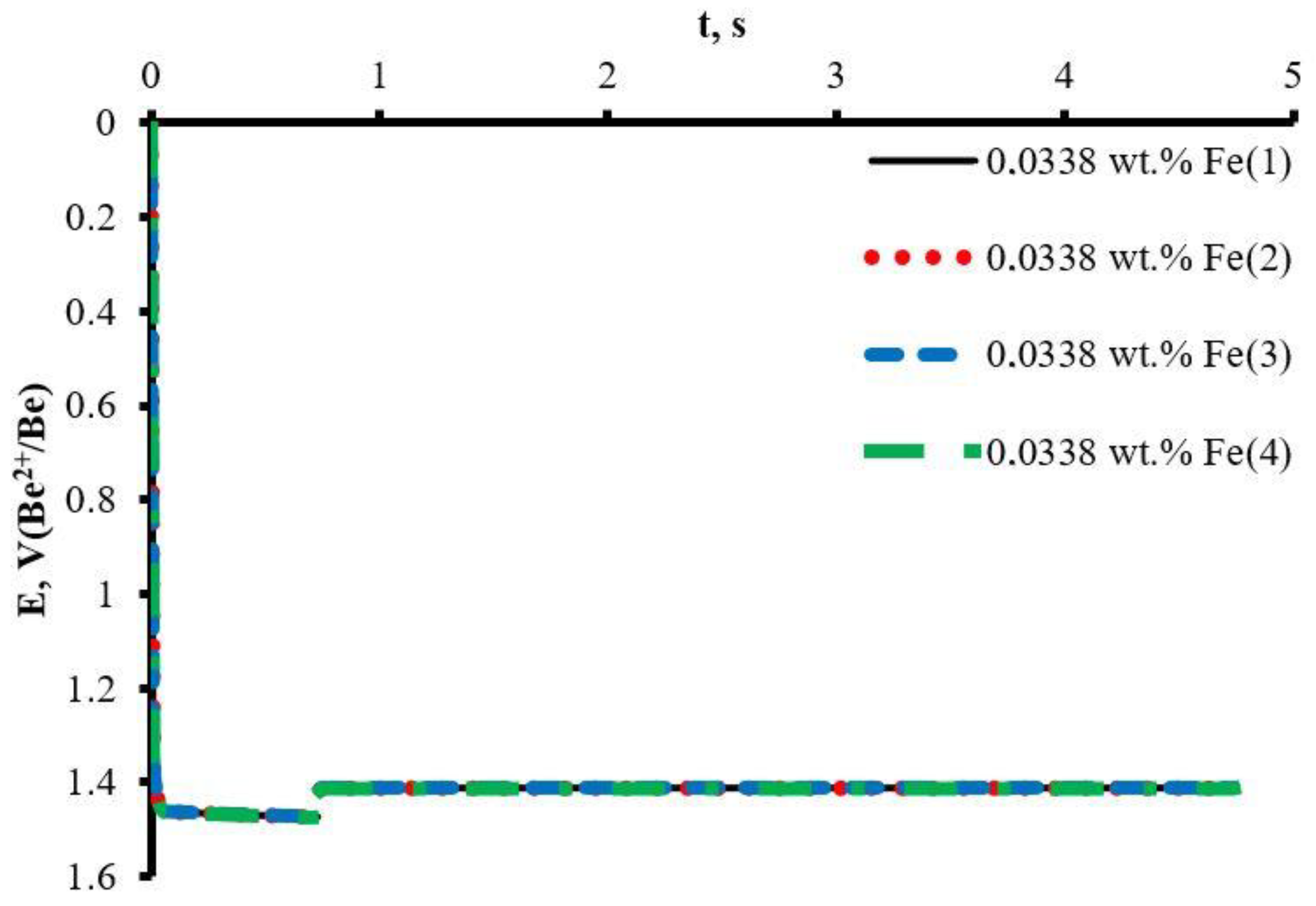
2.2. Equilibrium Potentials Measurement
2.3. Mass Spectroscopy with Inductively Coupled Plasma
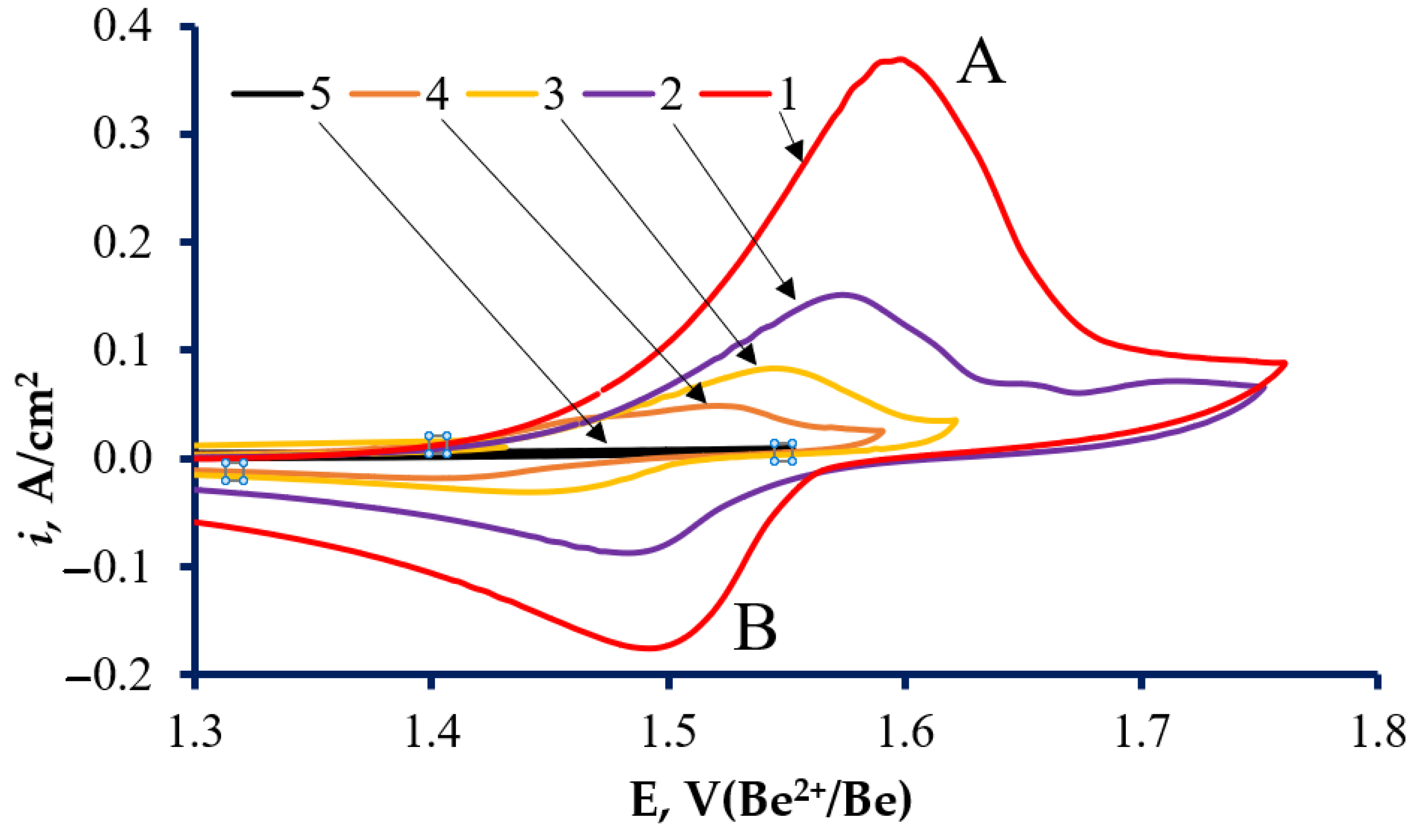
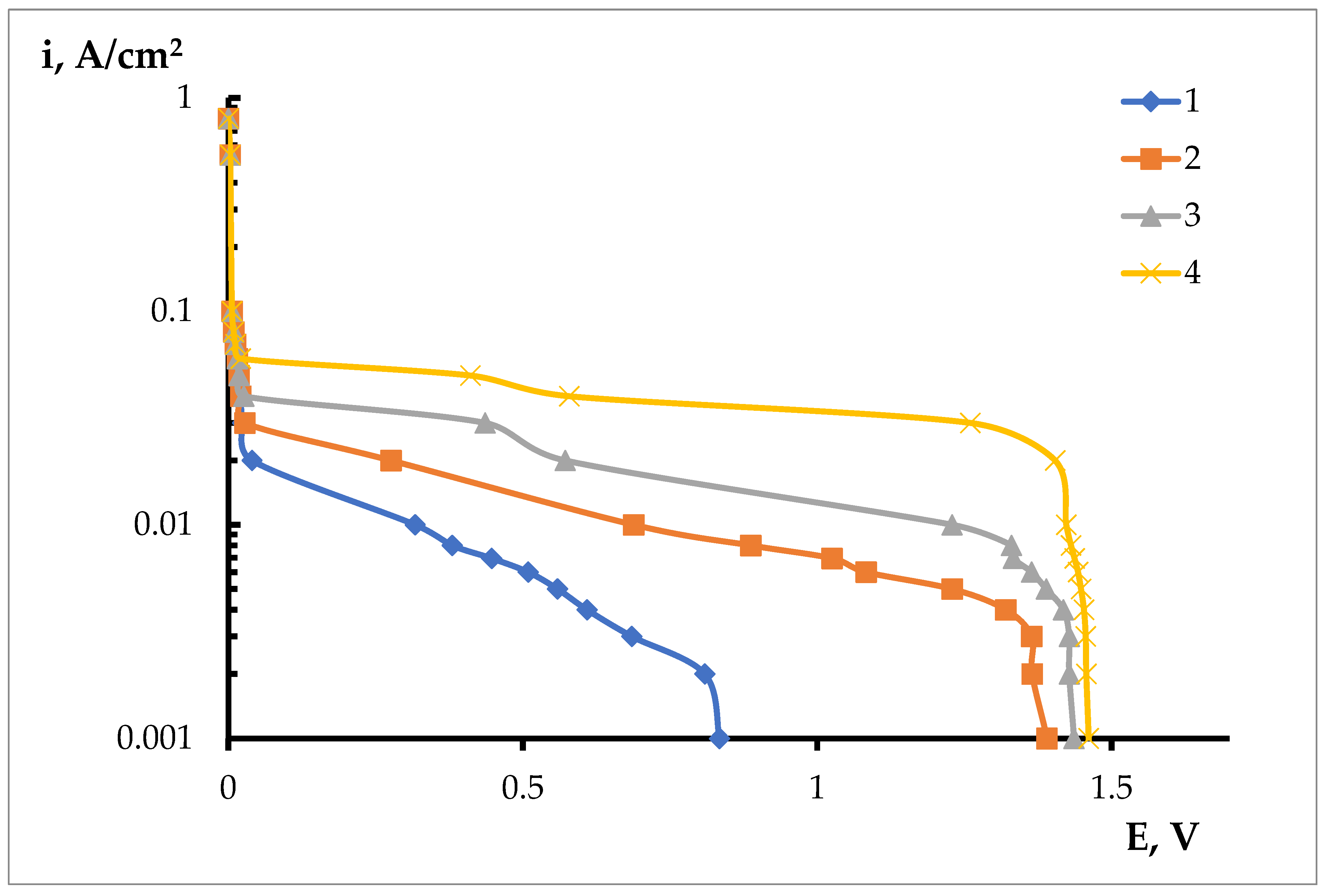
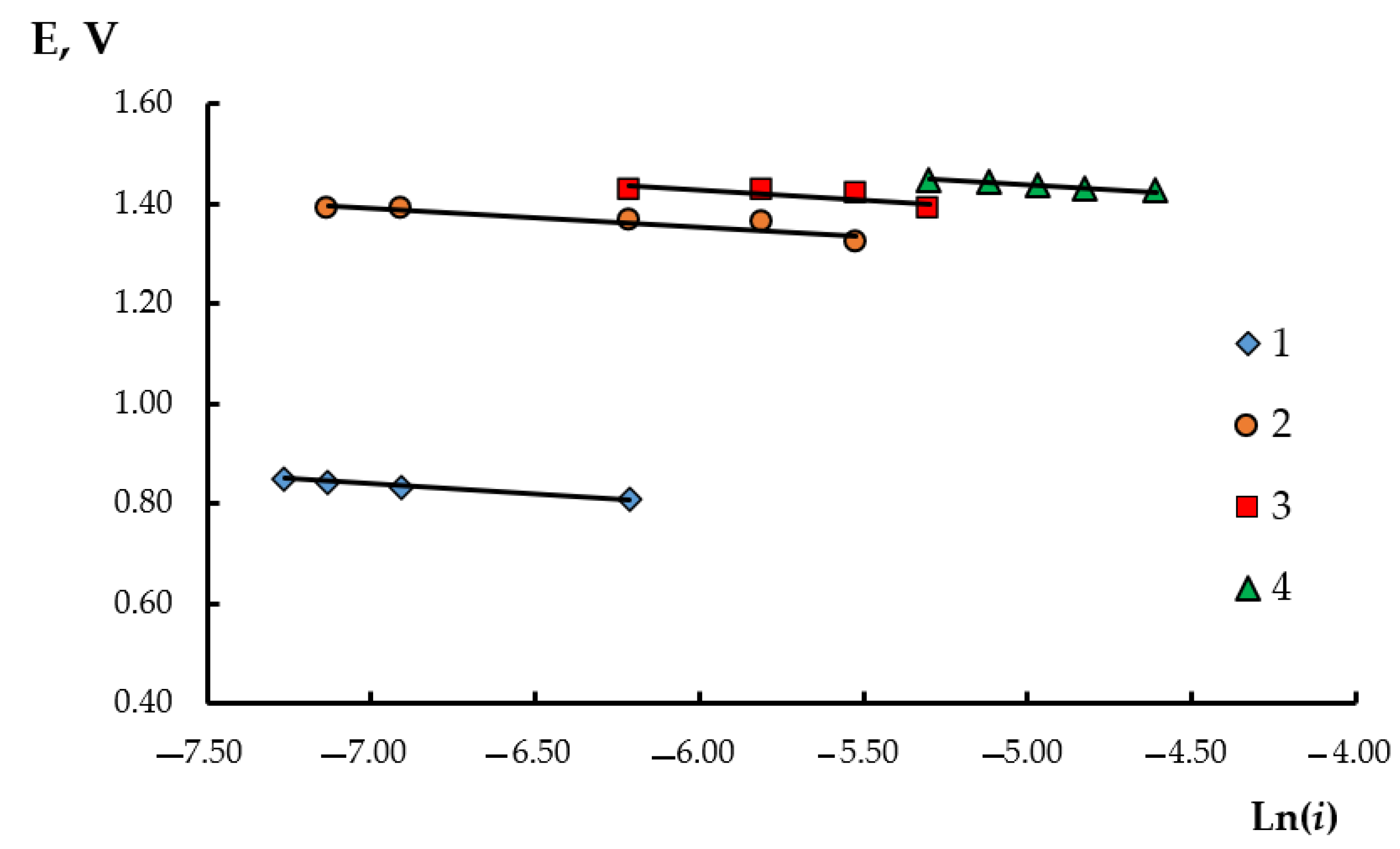
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beneš, O.; Konings, R.J.M. Thermodynamic properties and phase diagrams of fluoride salts for nuclear applications. J. Fluor. Chem. 2009, 130, 22–29. [Google Scholar] [CrossRef]
- Zaikov, Y.P.; Khokhlov, V.A.; Afonichkin, V.K.; Volkov, S.V.; Omelchuk, A.A. Nekotoriye problemy khimii zhidkosolevykh yadernykh reactorov novogo pokoleniya (Some problems of chemistry of new generation molten salt reactors). In Proceedings of the XVI Russian Conference on Physical Chemistry and Electrochemistry of Molten and Solid Electrolytes (with International Participation), Ekaterinburg, Russia, 16–20 September 2013; pp. 87–88. [Google Scholar]
- Bromley, B.P. Initial Exploratory Reactor Physics Assessment of Nonconventional Fuel Concepts for Very Compact Small Modular Reactors Using Hydroxides as Coolants and/or Moderators. Nucl. Technol. 2022, 208, 160–191. [Google Scholar] [CrossRef]
- Ignatiev, V.V.; Abalin, S.S.; Gurov, M.Y.; Zakirov, R.Y.; Konakov, S.A.; Merzlyakov, A.V.; Surenkov, A.I.; Feynberg, O.S. Reactor with Circulating Fuel Based on Molten Metal Fluorides for Np, Am, Cm Incineration. Sov. At. Energy 2021, 129, 122–126. [Google Scholar] [CrossRef]
- Ignat’ev, V.V.; Subbotin, S.A.; Feinberg, O.S. Accident Resistance of Molten-Salt Nuclear Reactor. Sov. At. Energy 2018, 124, 371–378. [Google Scholar] [CrossRef]
- Lizin, A.A.; Ponomarev, L.I.; Tomilin, S.V. Vybor nesyshey soli dly zhidkosolevogo reactora s bystrym spectrum neitronov (Selection of the bearing salt for molten salt reactor with fast neutron spectra. Vopr. At. Nauk. Tech. Seriya Materialoved. Noviye Mater. 2016, 3, 80–99. [Google Scholar]
- Consiglio, A.N.; Carotti, F.; Liu, E.; Williams, H.; Scarlat, R.O. Design and operation of a molten salt electrochemical cell. MethodsX 2022, 9, 101626. [Google Scholar] [CrossRef]
- Ponomarev, L.I.; Seregin, M.B.; Parshin, A.P.; Mel’nikov, S.A.; Mikhalichenko, A.A.L.; Zagorets, L.P.; Manuilov, R.N.; Rzheutskii, A.A. Fuel Salt for the Molten-Salt Reactor. Energy 2013, 115, 5–10. [Google Scholar] [CrossRef]
- Nikitina, E.V.; Karfidov, E.A.; Zaikov, Y.P. Corrosion of advanced metal materials in fluoride melts for liquid salt reactors. Russ. Met. 2021, 1, 21–45. [Google Scholar]
- Surenkov, A.I.; Ignat’ev, V.V.; Abalin, S.S.; Konakov, S.A.; Uglov, V.S. Corrosion Resistance and Mechanical Stability of Nickel Alloys in Molten-Salt Nuclear Reactors. Energy 2018, 124, 43–49. [Google Scholar] [CrossRef]
- Sandhi, K.K.; Szpunar, J. Analysis of Corrosion of Hastelloy-N, Alloy X750, SS316 and SS304 in Molten Salt High-Temperature Environment. Energies 2021, 14, 543. [Google Scholar] [CrossRef]
- Karfidov, E.A.; Nikitina, E.V. Corrosion Electrochemical Behavior of Nickel in Molten Lithium and Potassium Chlorides Containing Additives of Substances of Various Chemical Origins. Russ. Met. 2022, 978–983. [Google Scholar] [CrossRef]
- Keiser, J.R.; Singh, P.M.; Lance, M.J.; Meyer, H.M.; Myhre, K.G.; Lowe, T.M.; Sulejmanovic, D.; Cakmak, E.; Cox, V.A.; Hawkins, C.S.; et al. Interaction of beryllium with 316H stainless steel in molten Li2BeF4 (FLiBe). J. Nucl. Mater. 2022, 565, 153698. [Google Scholar] [CrossRef]
- Raiman, S.S.; Kurley, J.M.; Sulejmanovic, D.; Willoughby, A.; Nelson, S.; Mao, K.; Parish, C.M.; Greenwood, M.S.; Pint, B.A. Corrosion of 316H stainless steel in flowing FLiNaK salt. J. Nucl. Mater. 2022, 561, 153551. [Google Scholar] [CrossRef]
- Olson, L.C.; Ambrosek, J.; Sridharan, K.; Anderson, M.H.; Allen, A.R. Materials corrosion in molten LiF–NaF–KF salt. J. Fluor. Chem. 2009, 130, 67–73. [Google Scholar] [CrossRef]
- Zhang, G.; Kelleher, B.; He, H.; Cao, G.; Anderson, A.; Allen, T.; Sridharan, K. High-temperature corrosion of UNS N10003 in molten Li2BeF4 (FLiBe) salt. Corrosion 2015, 71, 1257–1266. [Google Scholar] [CrossRef]
- Karfidov, E.A.; Zaikov, Y.P.; Nikitina, E.V.; Seliverstov, K.E.; Dub, A.V. High-Temperature Passivation of the Surface of Candidate Materials for MSR by Adding Oxygen Ions to FLiNaK Salt. Materials 2022, 15, 5174. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Yu, G.; Hou, J.; Zeng, C. Electrochemical study of the corrosion of a Ni-based alloy GH3535 in molten (Li, Na, K) F at 700 °C. J. Fluor. Chem. 2015, 178, 14–22. [Google Scholar] [CrossRef]
- Kondo, M.; Nagasaka, T.; Xu, Q.; Muroga, T.; Sagara, A.; Noda, N.; Ninomiya, D.; Nagura, M.; Suzuki, A.; Terai, T.; et al. Corrosion characteristics of reduced activation ferritic steel, JLF-1 (8.92Cr–2W) in molten salts Flibe and Flinak. Fusion Eng. Des. 2009, 84, 1081–1085. [Google Scholar] [CrossRef]
- Koger, J.W. Chromium Depletion and Void Formation in Fe—Ni—Cr Alloys during Molten Salt Corrosion and Related Processes. In Book Advances in Corrosion Science and Technology; Fontana, M.G., Staehle, R.W., Eds.; Springer: Boston, MA, USA, 1974; Volume 4, pp. 245–318. [Google Scholar]
- Wang, Y.L.; Wang, Q.; Liu, H.J.; Zeng, C.L. Effects of the oxidants H2O and CrF3 on the corrosion of pure metals in molten (Li, Na, K) F. Corros. Sci 2016, 103, 268–282. [Google Scholar] [CrossRef]
- Kondo, M.; Nagasaka, T.; Tsisar, V.; Sagara, A.; Muroga, T.; Watanabe, T.; Oshima, T.; Yokoyama, Y.; Miyamoto, H.; Nakamura, E.; et al. Corrosion of reduced activation ferritic martensitic steel JLF-1 in purified Flinak at static and flowing conditions. Fusion Eng. Des. 2010, 85, 1430–1436. [Google Scholar] [CrossRef]
- Pavlik, V.; Kontrik, M.; Boča, M. Corrosion behavior of Incoloy 800H/HT in the fluoride molten salt FLiNaK + MF x (MF x = CrF3, FeF2, FeF3 and NiF2). N. J. Chem. 2015, 39, 9841–9847. [Google Scholar] [CrossRef]
- Guo, S.; Shay, N.; Wang, Y.; Zhou, W.; Zhang, J. Measurement of europium (III)/europium (II) couple in fluoride molten salt for redox control in a molten salt reactor concept. J. Nucl. Mater. 2017, 496, 197–206. [Google Scholar] [CrossRef]
- Doniger, W.H.; Sridharan, K. Application of voltammetry for quantitative analysis of chromium in molten 2LiF-BeF2 (FLiBe) salt. J. Electroanal. Chem. 2019, 838, 73–81. [Google Scholar] [CrossRef]
- Blood, C.M. Solubility and Stability of Structural Metal Difluorides in Molten Fluoride Mixtures; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1964; No. ORNL-TM-760.
- Cho, S.K.; Lee, S.-K.; Choi, E.-Y.; Hur, J.-M. The evaluation of polarized dynamic reference electrode (p-Dyn RE) for LiCl-1 wt% Li2O molten salt at 650 °C: Li+/Li p-Dyn RE versus O2/O2- p-Dyn RE. J. Electrochem. Soc. 2016, 163, E308–E312. [Google Scholar] [CrossRef]
- Suzdaltsev, A.V.; Khramov, A.P.; Zaikov, Y.P.; Pankratov, A.A.; Vovkotrub, E.G.; Antonov, B.D. Reduction of the solid A12O3 at the electrolysis of the CaC12 based melt. J. Electrochem. Soc. 2017, 164, H5183–H5188. [Google Scholar] [CrossRef]
- Duran-Klie, G.; Rodrigues, D.; Delpech, S. Dynamic Reference Electrode Development for Redox Potential Measurements in Fluoride Molten Salt at High Temperature. Electrochim. Acta 2016, 195, 19. [Google Scholar] [CrossRef]
- Keiser, J.R.; Devan, J.H.; Manning, D.L. The Corrosion Resistance of Type 316 Stainless Steel to Li2BeF4; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1977; ORNL/TM-5782.
- Afonichkin, V.K.; Bovet, A.L.; Ignatiev, V.V.; Panov, A.V.; Subbotin, V.G.; Surenkov, A.I.; Toropov, A.D.; Zherebtsov, A.L. Dynamic reference electrode for investigation of fluoride melts containing beryllium difluoride. J. Fluor. Chem. 2009, 130, 83–88. [Google Scholar] [CrossRef]
- Baes, C.F., Jr. The Chemistry and Thermodynamics of Molten-Salt-Reactor Fluoride Solutions; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1966.
- Wicks, C.E.; Block, F. Thermodynamic Properties of 65 Elements: Their Oxides, Halides, Carbides and Nitrides; Bureau of Mines: Pittsburgh, AR, USA, 1961; p. 239.

| Concentration, wt.% | ||||||||
|---|---|---|---|---|---|---|---|---|
| Li | Be | Fe | Cr | Ni | Mo | Al | B | |
| 1 | 13.8391 | 9.2494 | 0.0031 | 0.0003 | 0.0008 | 0.0002 | 0.0021 | 0.0006 |
| 2 | 13.8385 | 9.2183 | 0.0338 | 0.0002 | 0.0004 | <0.0001 | 0.0022 | 0.0004 |
| 3 | 13.8345 | 9.1976 | 0.0559 | 0.0001 | 0.0006 | <0.0001 | 0.0021 | 0.0001 |
| 4 | 13.8356 | 9.1871 | 0.0651 | 0.0002 | 0.0008 | <0.0001 | 0.0027 | 0.0005 |
| 5 | 13.8387 | 9.1534 | 0.0992 | 0.0003 | 0.0005 | <0.0001 | 0.0024 | 0.0006 |
| T, K | EMF (1), V CFe = 0.0031 wt.% | EMF (1), V CFe = 0.0338 wt.% | EMF (1), V CFe = 0.0559 wt.% | EMF (1), V CFe = 0.0651 wt.% | EMF (1), V CFe = 0.0992 wt.% |
|---|---|---|---|---|---|
| 923 | 0.837 | 1.394 | 1.412 | 1.422 | 1.441 |
| 0.838 | 1.395 | 1.412 | 1.421 | 1.439 | |
| 0.836 | 1.394 | 1.415 | 1.419 | 1.441 | |
| 0.837 | 1.396 | 1.412 | 1.422 | 1.442 | |
| 973 | 0.785 | 1.366 | 1.386 | 1.395 | 1.415 |
| 0.786 | 1.364 | 1.385 | 1.394 | 1.416 | |
| 0.785 | 1.366 | 1.386 | 1.395 | 1.415 | |
| 0.784 | 1.365 | 1.386 | 1.395 | 1.413 | |
| 1023 | 0.738 | 1.340 | 1.364 | 1.373 | 1.391 |
| 0.739 | 1.341 | 1.363 | 1.374 | 1.392 | |
| 0.736 | 1.340 | 1.364 | 1.372 | 1.391 | |
| 0.738 | 1.342 | 1.365 | 1.374 | 1.391 |
| T, K | −a, V | b, V | R2 | n |
|---|---|---|---|---|
| 923 | 2.953 | 0.0406 | 0.99 | 1.96 |
| 973 | 2.931 | 0.0421 | 0.99 | 1.99 |
| 1023 | 2.905 | 0.0440 | 0.99 | 2.00 |
| № | Concentration Fe, wt.% | , B | R2 | N |
|---|---|---|---|---|
| 1 | 0.0031 | 0.0389 | 0.99 | 2.04 |
| 2 | 0.0338 | 0.0373 | 0.82 | 2.13 |
| 3 | 0.0651 | 0.0383 | 0.68 | 2.08 |
| 4 | 0.0992 | 0.0370 | 0.99 | 2.15 |
| T, K | ΔG*(l,melt), kJ/mol | ΔH(l,melt), kJ/mol | ΔS*(l,melt), J/(mol·K) | ΔG*(mix), kJ/mol | ΔH(mix), kJ/mol | ΔS*(mix), J/(mol·K) |
|---|---|---|---|---|---|---|
| 923 | −561.5 | −654.2 | 100 | 46.0 | 87.21 | −45 |
| 973 | −557.1 | −654.2 | 100 | 43.2 | 87.21 | −45 |
| 1023 | −551.5 | −654.2 | 100 | 41.5 | 87.21 | −45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arkhipov, S.P.; Zaikov, Y.P.; Arkhipov, P.A.; Mullabaev, A.R. Interaction between Iron Fluoride and Molten FLiBe. Processes 2022, 10, 2742. https://doi.org/10.3390/pr10122742
Arkhipov SP, Zaikov YP, Arkhipov PA, Mullabaev AR. Interaction between Iron Fluoride and Molten FLiBe. Processes. 2022; 10(12):2742. https://doi.org/10.3390/pr10122742
Chicago/Turabian StyleArkhipov, Stepan P., Yury P. Zaikov, Pavel A. Arkhipov, and Albert R. Mullabaev. 2022. "Interaction between Iron Fluoride and Molten FLiBe" Processes 10, no. 12: 2742. https://doi.org/10.3390/pr10122742
APA StyleArkhipov, S. P., Zaikov, Y. P., Arkhipov, P. A., & Mullabaev, A. R. (2022). Interaction between Iron Fluoride and Molten FLiBe. Processes, 10(12), 2742. https://doi.org/10.3390/pr10122742








