A New Thermal Damage-Controlled Protocol for Thermal Ablation Modeled with Modified Porous Media-Based Bioheat Equation with Variable Porosity
Abstract
:1. Introduction
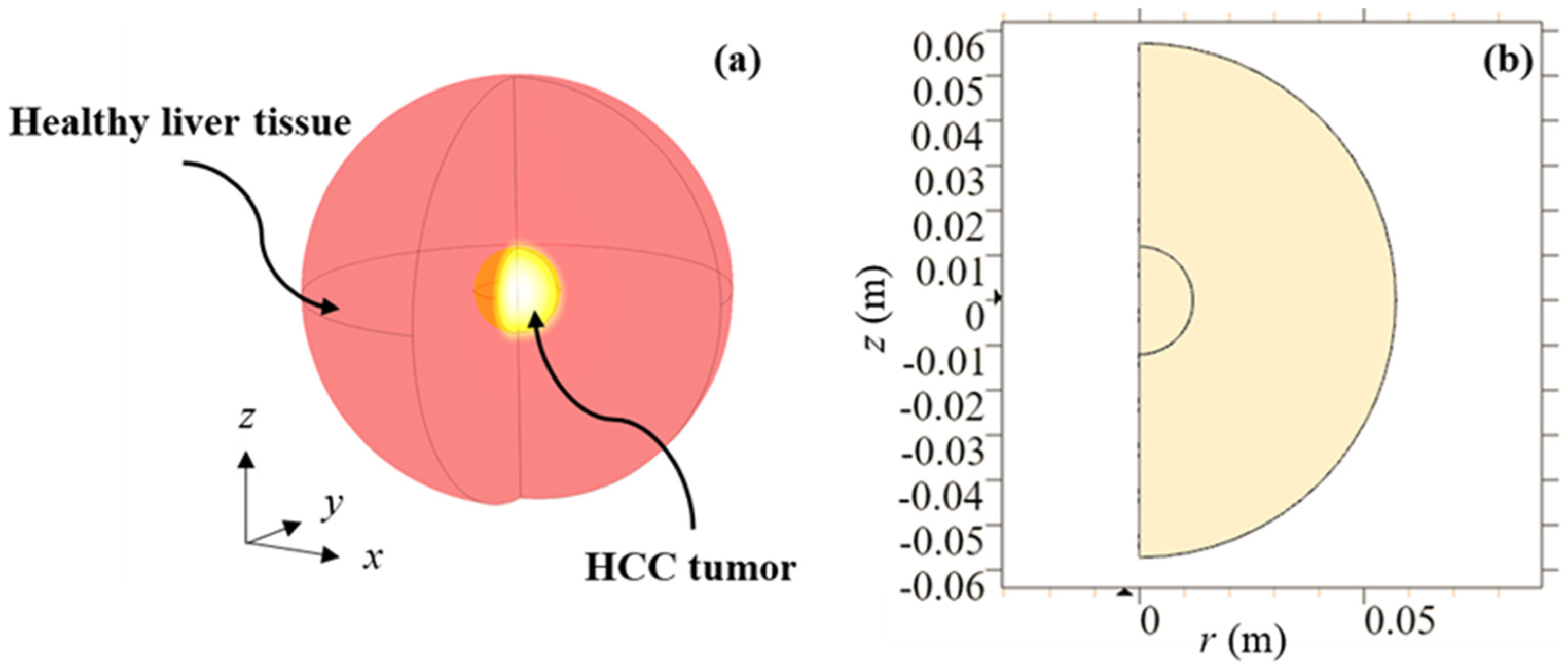
2. Materials and Methods
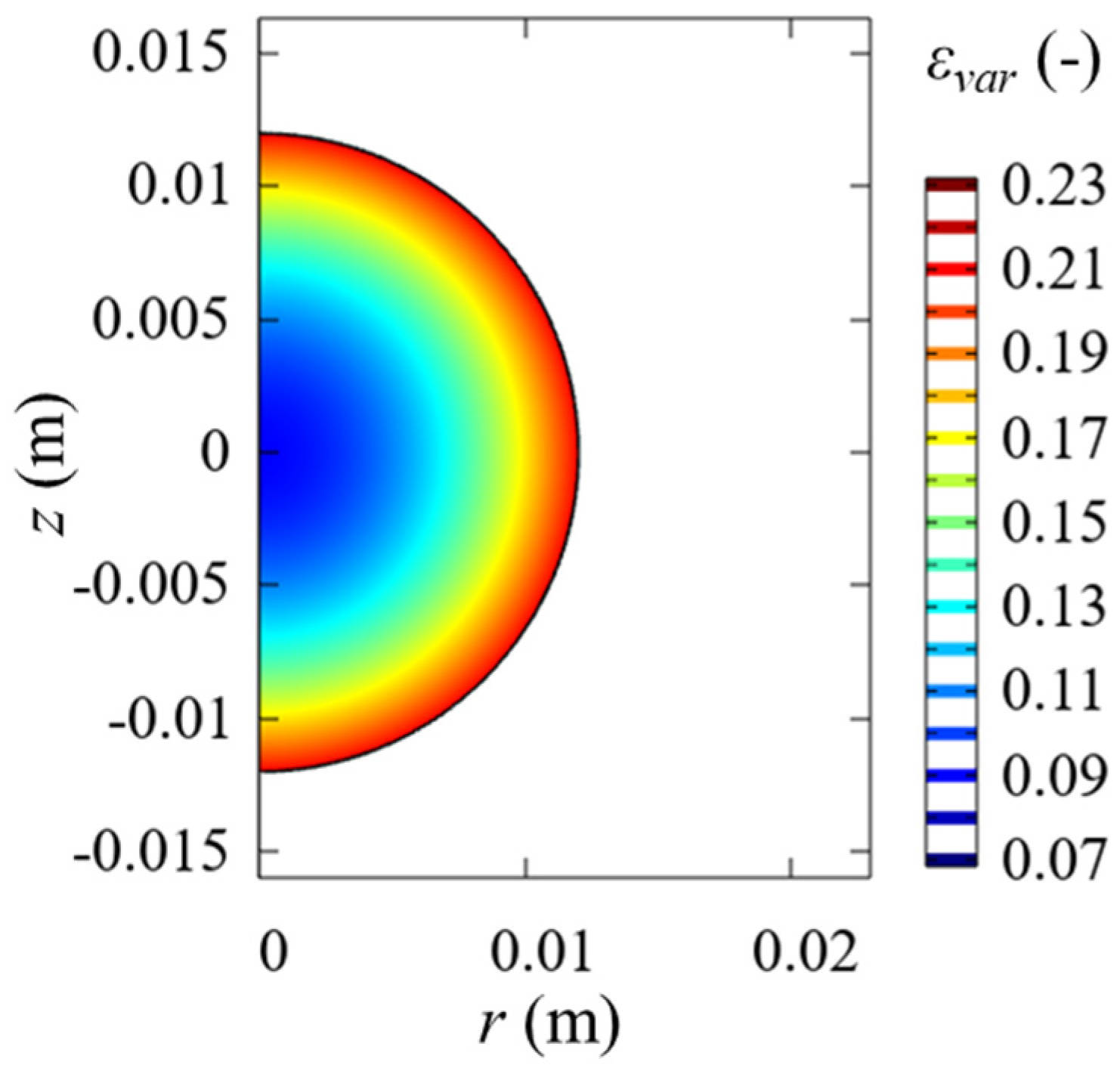
2.1. Mathematical Model
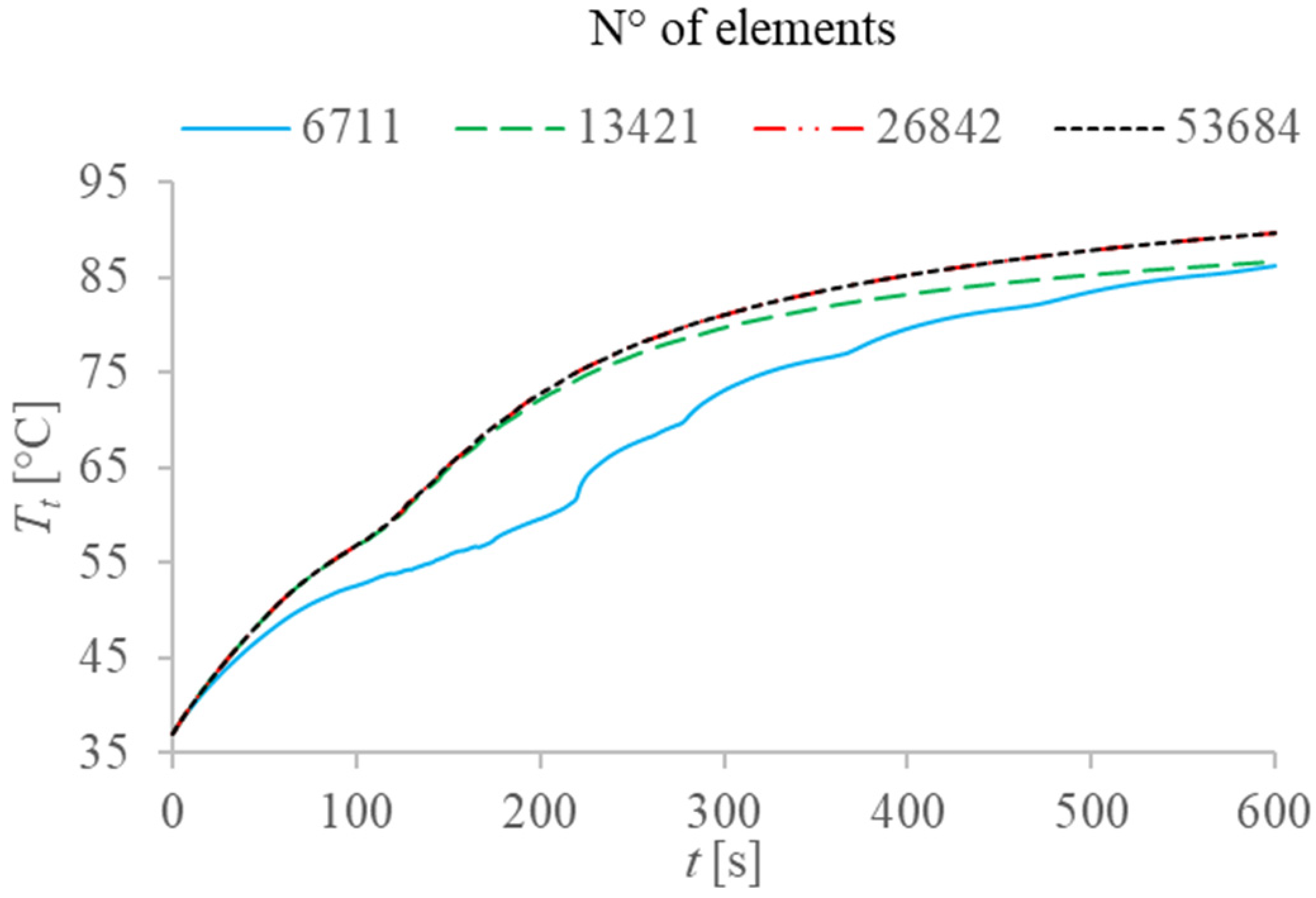
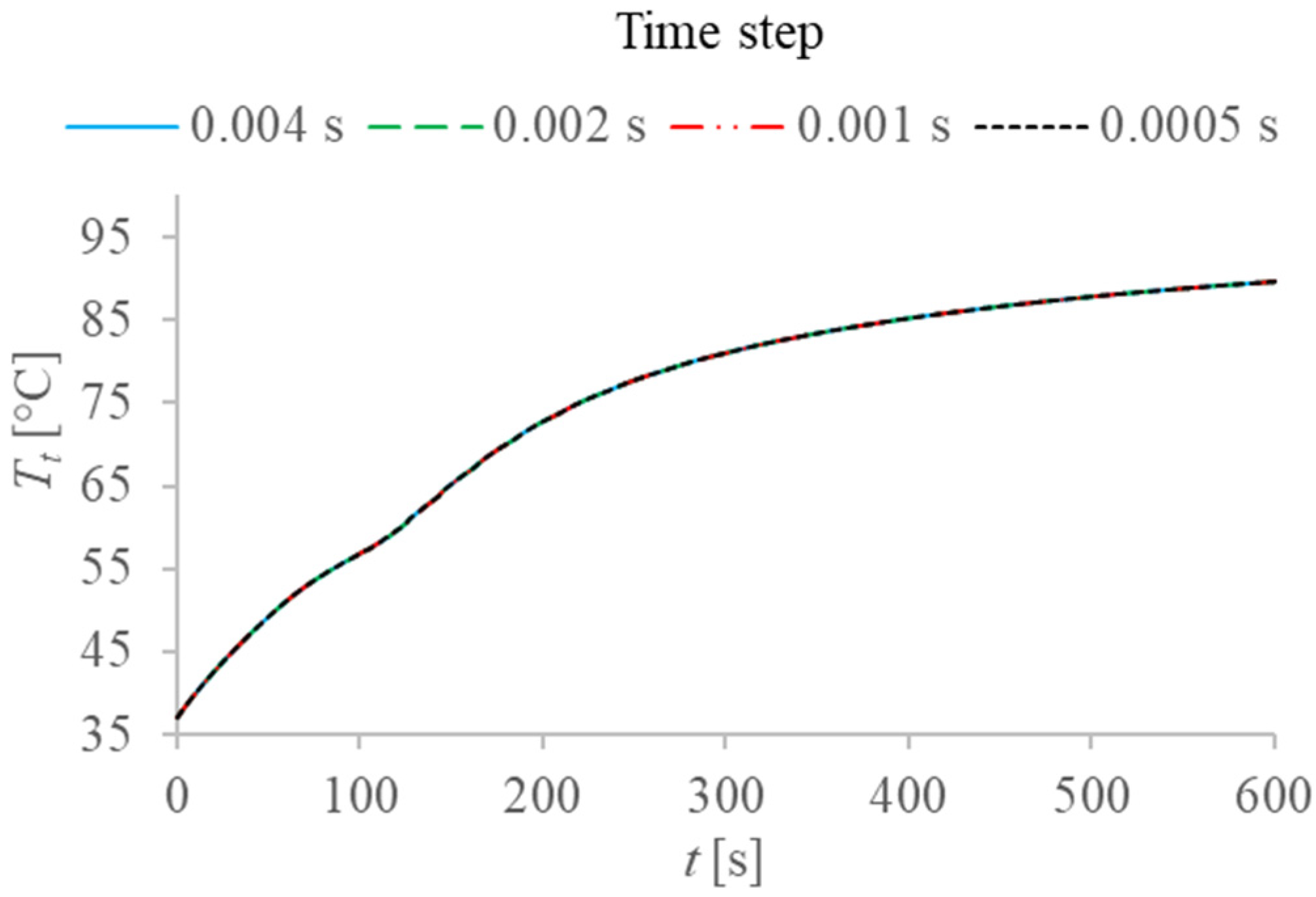
2.2. Numerical Solution and Validation
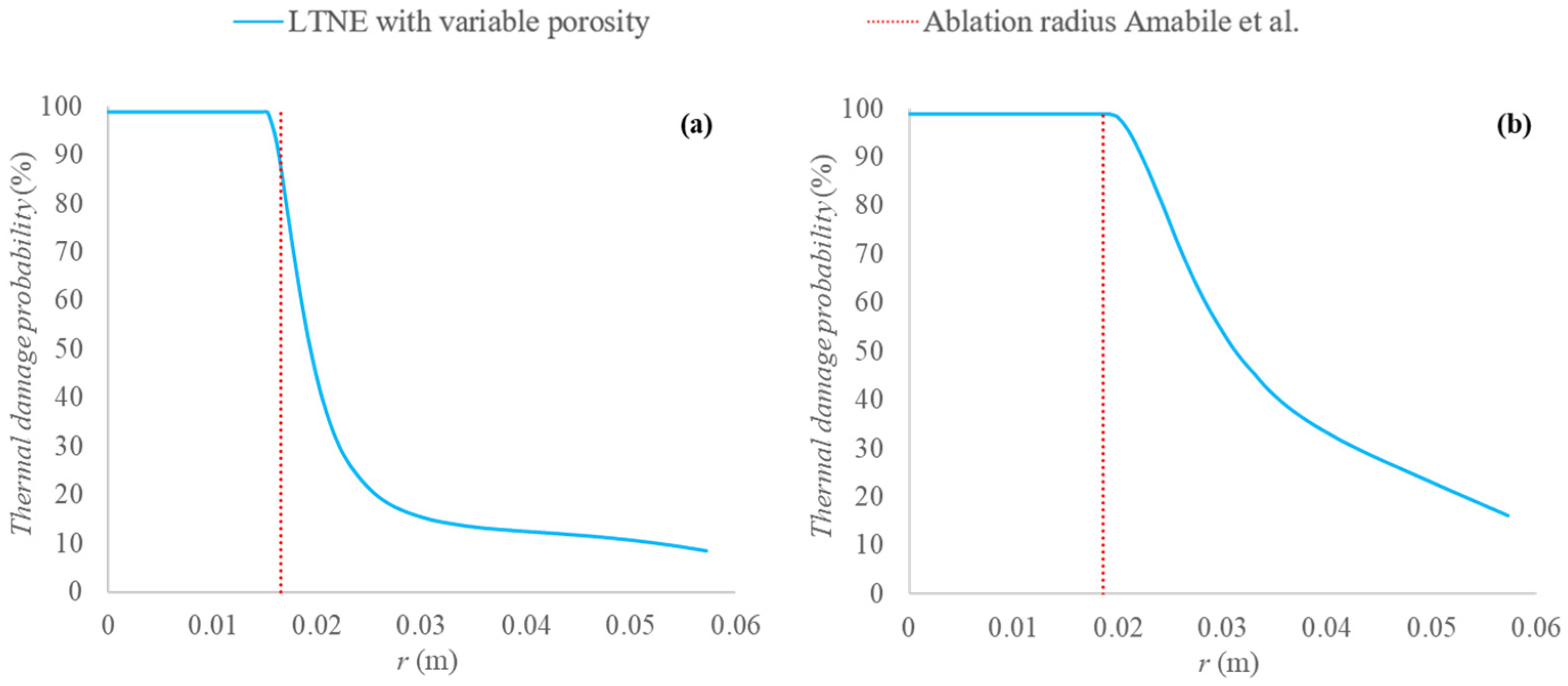
2.3. Validation of the Model
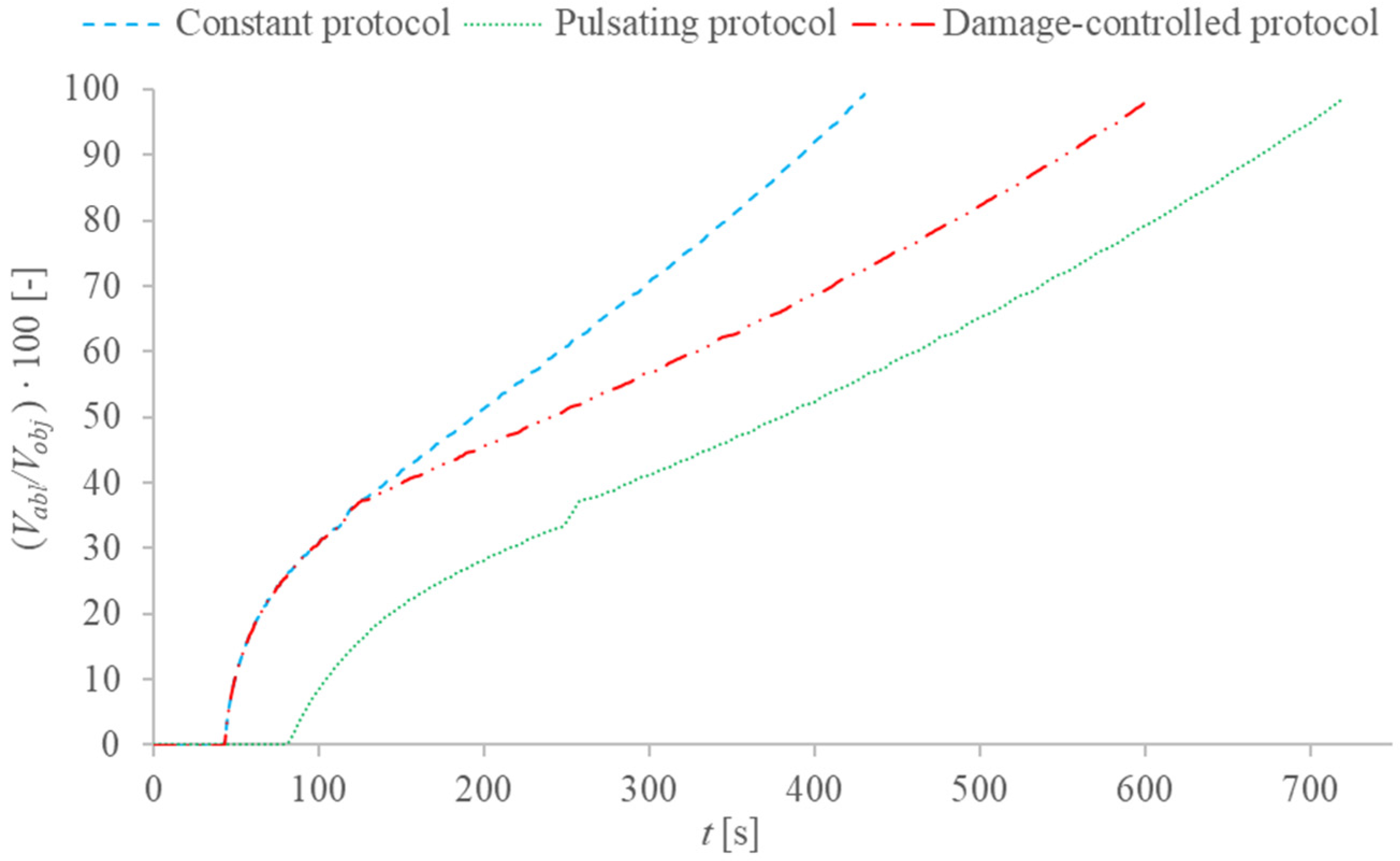
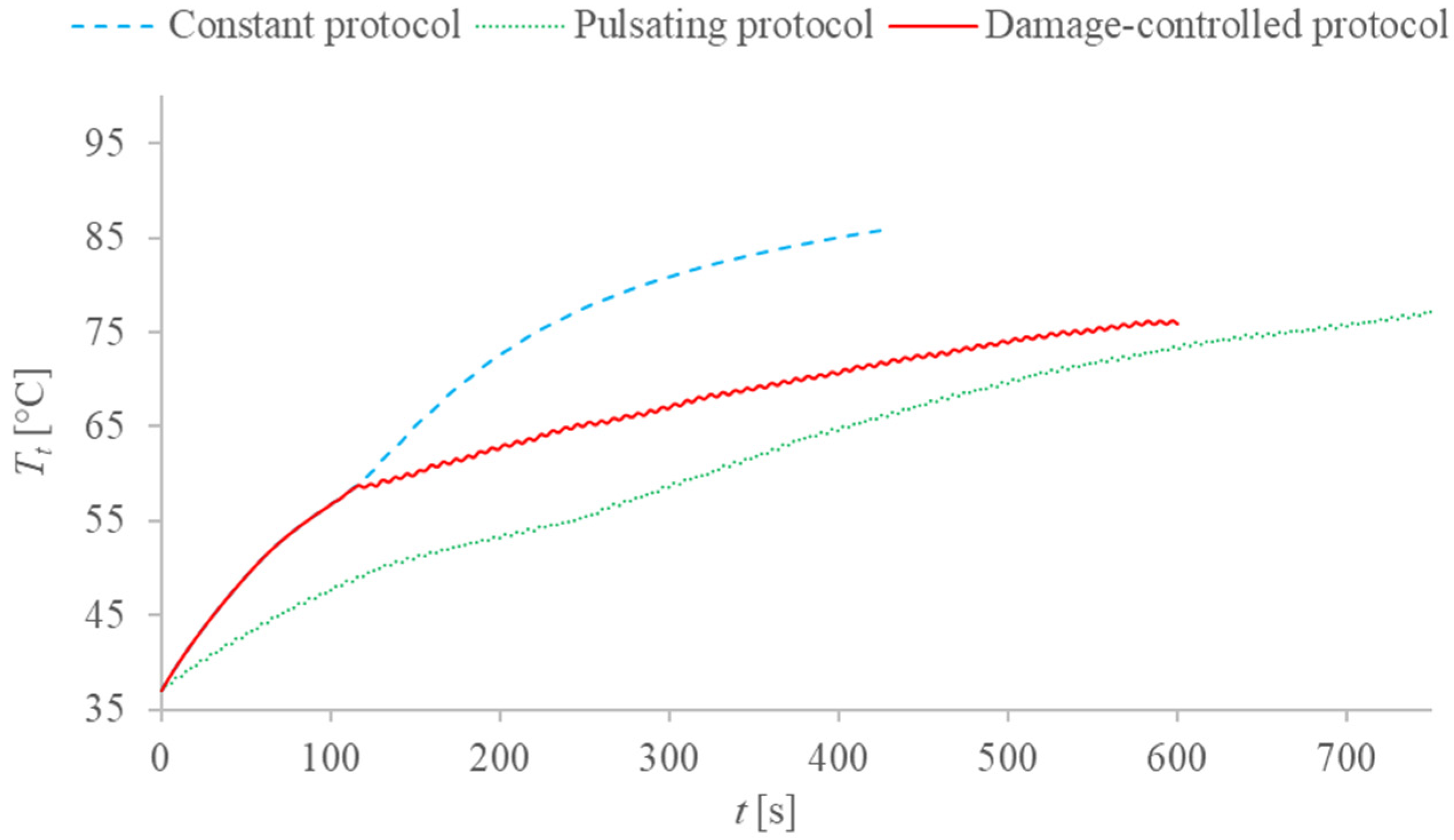
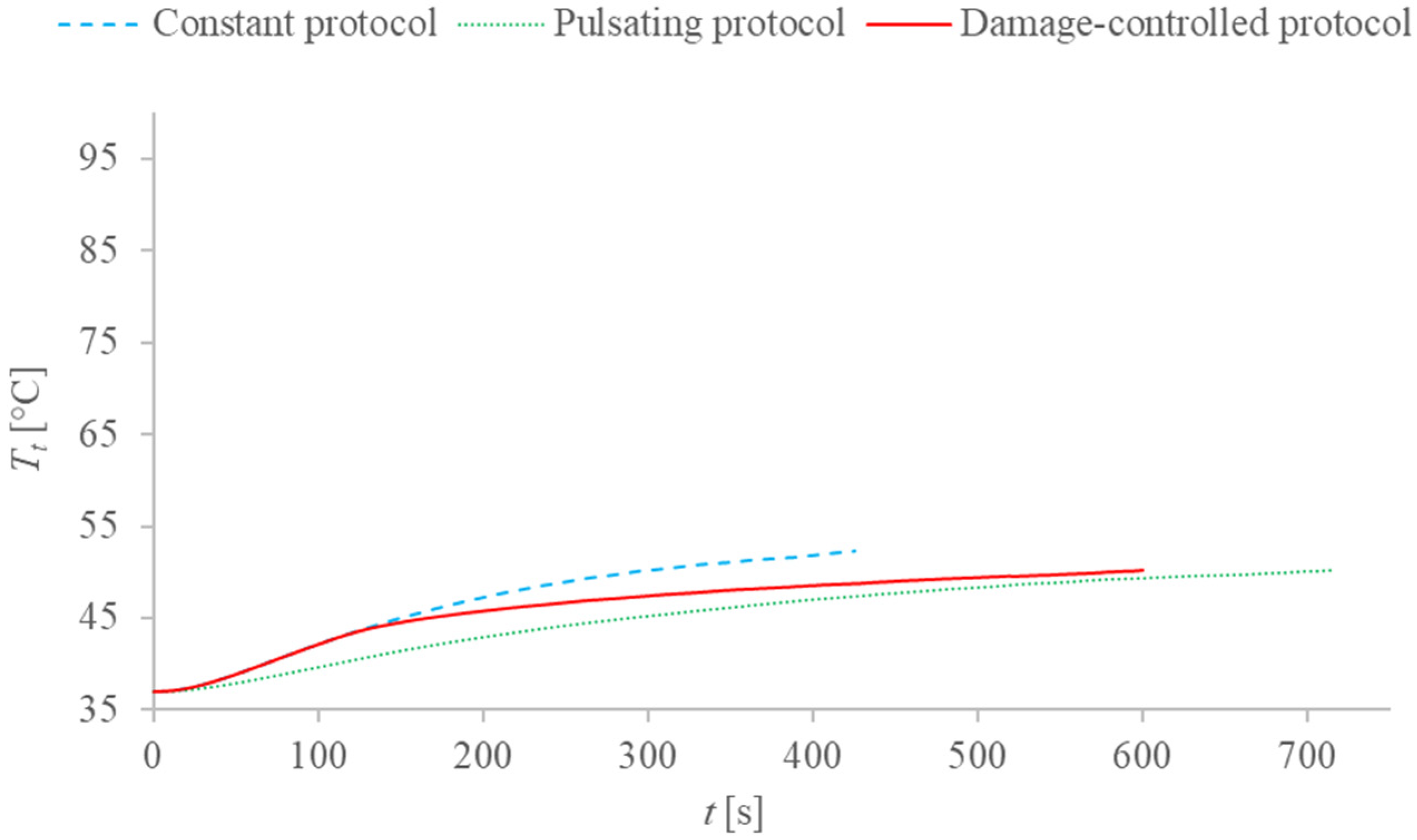
2.4. Description of the Different Applied Protocols
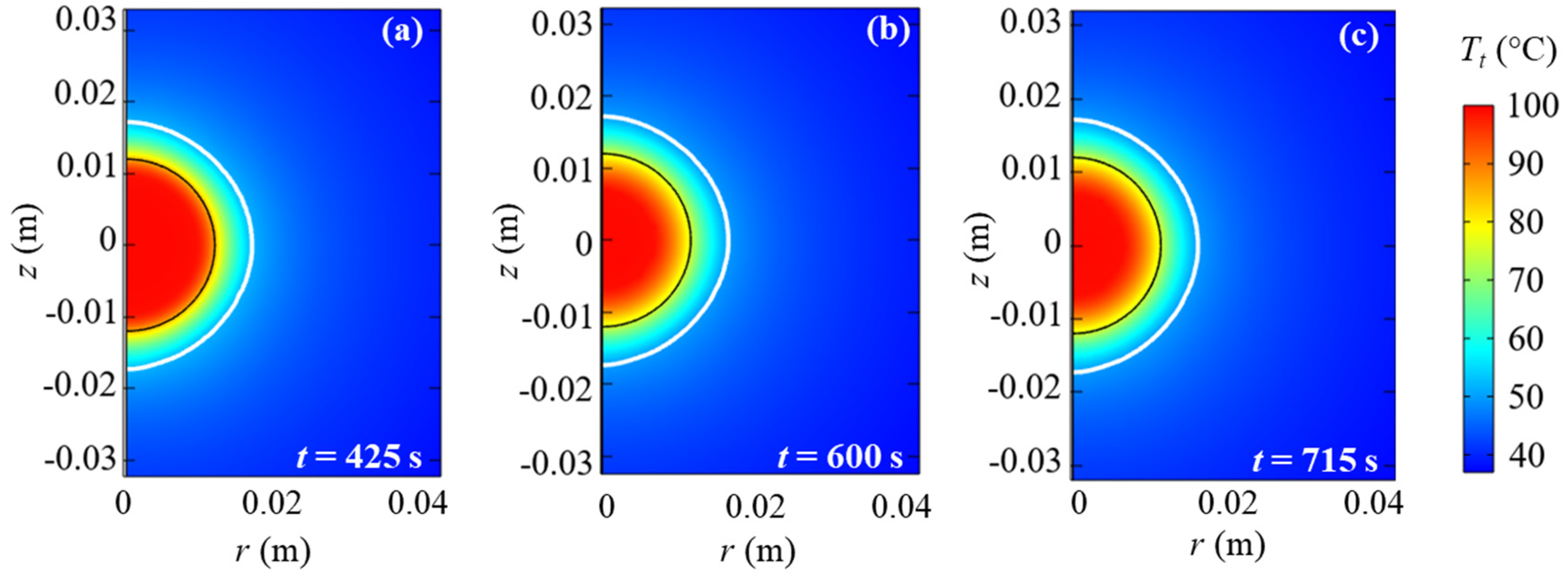
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Volumetric transfer area (m−1) |
| a1 | Coefficient (m−2) |
| A | Frequency factor (s−1) |
| b1 | Coefficient (m−1) |
| c | Specific heat (J kg−1 K−1) |
| c1 | Coefficient (-) |
| Cw | Water content (%) |
| d | Diameter of blood vessel (m) |
| da | Diameter of the ablation zone (m) |
| E | Electric field vector (V m−1) |
| hc | Convective interfacial heat transfer coefficient (W m−2 K−1) |
| hfg | Product of water latent heat of vaporization and water density at 100 °C (J m−3) |
| k | Thermal conductivity (W m−1 K−1) |
| P | Cell death probability (%) |
| Qext | External power density (W m−3) |
| r | Spatial coordinate (m) |
| r1 | Radius of tumor (m) |
| R | Universal gas constant (J mol−1 K−1) |
| t | Time (s) |
| T | Temperature (K) |
| u | Velocity vector (m s−1) |
| V | Volume (m3) |
| x, y, z | Spatial coordinates (m) |
| Greek symbols | |
| β | Coefficient (-) |
| ΔE | Activation energy (J mol−1) |
| ε | Porosity (-) |
| ρ | Density (kg m−3) |
| σe | Effective electric conductivity (S m−1) |
| τ | Time integration variable (s) |
| ω | Pulsation (s−1) |
| Ω | Thermal damage (-) |
| Subscripts | |
| abl | Ablated |
| b | Blood |
| fin | Final |
| g | Referred to temperatures above 100 °C |
| int | Intermediate |
| l | Referred to temperatures below 100 °C |
| max | Maximum |
| min | Minimum |
| obj | Objective |
| prot | Referred to damage-controlled protocol |
| puls | Pulsating |
| t | Tissue |
| var | Variable |
References
- Chu, K.F.; Dupuy, D.E. Thermal ablation of tumours: Biological mechanisms and advances in therapy. Nat. Rev. Cancer 2014, 14, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Brace, C. Thermal Tumor Ablation in Clinical Use. IEEE Pulse 2011, 2, 28–38. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diederich, C.J. Thermal ablation and high-temperature thermal therapy: Overview of technology and clinical implementation. Int. J. Hyperth. 2005, 21, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Markezana, A.; Ahmed, M.; Kumar, G.; Zorde-Khvalevsky, E.; Rozenblum, N.; Galun, E.; Goldberg, S.N. Moderate hyperthermic heating encountered during thermal ablation increases tumor cell activity. Int. J. Hyperth. 2020, 37, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Prakash, P.; Faridi, P.; Radosevic, A.; Curto, S.; Burdio, F.; Berjano, E. How large is the periablational zone after radiofrequency and microwave ablation? Computer-based comparative study of two currently used clinical de-vices. Int. J. Hyperth. 2020, 37, 1131–1138. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of ther-mal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef] [PubMed]
- Berjano, E.J. Theoretical modeling for radiofrequency ablation: State-of-the-art and challenges for the future. Biomed. Eng. Online 2006, 5, 24. [Google Scholar] [CrossRef] [Green Version]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Bioheat equation of the human thermal system. Chem. Eng. Technol. 1997, 20, 268–276. [Google Scholar] [CrossRef]
- Vafai, K. (Ed.) Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Bioheat transfer in a spherical biological tissue: A comparison among various models. J. Phys. Conf. Ser. 2019, 1224, 012001. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef] [PubMed]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Mathematical modeling of microwave liver ablation with a variable-porosity medium approach. Comput. Methods Programs Biomed. 2021, 214, 106569. [Google Scholar] [CrossRef] [PubMed]
- Cuenod, C.; Balvay, D. Perfusion and vascular permeability: Basic concepts and measurement in DCE-CT and DCE-MRI. Diagn. Interv. Imaging 2013, 94, 1187–1204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Effros, R.M.; Lowenstein, J.; Baldwin, D.S.; Chinard, F.P. Vascular and Extravascular Volumes of the Kidney of Man. Circ. Res. 1967, 20, 162–173. [Google Scholar] [CrossRef] [Green Version]
- Stewart, E.E.; Chen, X.; Hadway, J.; Lee, T.-Y. Correlation between Hepatic Tumor Blood Flow and Glucose Utilization in a Rabbit Liver Tumor Model. Radiology 2006, 239, 740–750. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Numerical Investigation of a Thermal Ablation Porous Media-Based Model for Tumoral Tissue with Variable Porosity. Computation 2021, 9, 50. [Google Scholar] [CrossRef]
- Andreozzi, A.; Iasiello, M.; Tucci, C. An overview of mathematical models and modulated-heating protocols for thermal ablation. Adv. Heat Transf. 2020, 52, 489–541. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Numerical analysis of the pulsating heat source ef-fects in a tumor tissue. Comput. Methods Programs Biomed. 2021, 200, 105887. [Google Scholar] [CrossRef]
- Goldberg, S.N.; Stein, M.C.; Gazelle, G.S.; Sheiman, R.G.; Kruskal, J.B.; Clouse, M.E. Percutaneous radiofre-quency tissue ablation: Optimization of pulsed-radiofrequency technique to increase coagulation necrosis. J. Vasc. Interv. Radiol. 1999, 10, 907–916. [Google Scholar] [CrossRef]
- Khanafer, K.; Bull, J.L.; Pop, I.; Berguer, R. Influence of pulsatile blood flow and heating scheme on the tempera-ture distribution during hyperthermia treatment. Int. J. Heat Mass Transf. 2007, 50, 4883–4890. [Google Scholar] [CrossRef]
- Molina JA, L.; Rivera, M.J.; Trujillo, M.; Berjano, E.J. Thermal modeling for pulsed radiofrequency ablation: Ana-lytical study based on hyperbolic heat conduction. Med. Phys. 2009, 36, 1112–1119. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, M.; Bon, J.; Rivera, M.J.; Burdio, F.; Berjano, E. Computer modelling of an impedance-controlled pulsing protocol for RF tumour ablation with a cooled electrode. Int. J. Hyperth. 2016, 32, 931–939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedoya, M.; del Rio, A.M.; Chiang, J.; Brace, C.L. Microwave ablationenergy delivery: Influence of power pulsing on ablation results in an ex vivo and in vivo liver model. Med. Phys. 2014, 41, 123301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gentili, G.B.; Ignesti, C. Dual applicator thermal ablation at 2.45 GHz: A numerical comparison and experiments on synchronous versus asynchronous and switched-mode feeding. Int. J. Hyperth. 2015, 31, 528–537. [Google Scholar] [CrossRef] [PubMed]
- Amabile, C.; Ahmed, M.; Solbiati, L.; Meloni, M.F.; Solbiati, M.; Cassarino, S.; Tosoratti, N.; Nissenbaum, Y.; Ierace, T.; Goldberg, S.N. Microwave ablation of primary and secondary liver tumours: Ex vivo, in vivo, and clinical characterisation. Int. J. Hyperth. 2016, 33, 34–42. [Google Scholar] [CrossRef] [Green Version]
- Radjenović, B.; Sabo, M.; Šoltes, L.; Prnova, M.; Čičak, P.; Radmilović-Radjenović, M. On Efficacy of Microwave Ablation in the Thermal Treatment of an Early-Stage Hepatocellular Carcinoma. Cancers 2021, 13, 5784. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. A novel local thermal non-equilibrium model for bi-ological tissue applied to multiple-antennas configurations for thermal ablation. Numer. Heat Transf. Part A Appl. 2020, 79, 111–121. [Google Scholar] [CrossRef]
- Yuan, P. Numerical analysis of temperature and thermal dose response of biological tissues to thermal non-equilibrium during hyperthermia therapy. Med. Eng. Phys. 2008, 30, 135–143. [Google Scholar] [CrossRef]
- Crezee, J.; Lagendijk, J.J.W. Temperature uniformity during hyperthermia: The impact of large vessels. Phys. Med. Biol. 1992, 37, 1321–1337. [Google Scholar] [CrossRef]
- Chen, M.M.; Holmes, K.R. Microvascular contributions in tissue heat transfer. Ann. N. Y. Acad. Sci. 1980, 335, 137–150. [Google Scholar] [CrossRef]
- Chang, I.A. Considerations for thermal injury analysis for RF ablation devices. Open Biomed. Eng. J. 2010, 4, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Moser, M.A.; Zhang, E.M.; Luo, Y.; Zhang, W. Numerical analysis of the relationship between the area of target tissue necrosis and the size of target tissue in liver tumours with pulsed radiofrequency ablation. Int. J. Hyperth. 2015, 31, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.; Sparrow, E. A thermal-ablation bioheat model including liquid-to-vapor phase change, pressure- and necrosis-dependent perfusion, and moisture-dependent properties. Int. J. Heat Mass Transf. 2007, 50, 2537–2544. [Google Scholar] [CrossRef]
- Smith, S.R.; Foster, K.R.; Wolf, G.L. Dielectric Properties of VX-2 Carcinoma versus Normal Liver Tissue. IEEE Trans. Biomed. Eng. 1986, 33, 522–524. [Google Scholar] [CrossRef] [PubMed]
- Woodard, H.Q.; White, D.R. The composition of body tissues. Br. J. Radiol. 1986, 59, 1209–1218. [Google Scholar] [CrossRef]
- Lim, H.; Namgung, B.; Woo, D.G.; Choi, J.S.; Kim, H.S.; Tack, G.R. Effect of Input Waveform Pattern and Large Blood Vessel Existence on Destruction of Liver Tumor Using Radiofrequency Ablation: Finite Element Analysis. J. Biomech. Eng. 2010, 132, 061003. [Google Scholar] [CrossRef]
| ρ (kg·m−3) | c (J·kg−1·K−1) | k (W·m−1·K−1) | |
|---|---|---|---|
| Healthy liver | 1080 | 3455 | 0.502 |
| Tumor | 1045 | 3760 | 0.600 |
| Blood | 1000 | 3639 | 0.502 |
| da [cm] | da Deviation from [26] in % | |||
|---|---|---|---|---|
| 60 W, 300 s | 60 W, 600 s | 60 W, 300 s | 60 W, 600 s | |
| Modified LTNE | 3.0 | 3.8 | −9.1% | +2.7% |
| Clinical study [26] | 3.3 ± 0.5 | 3.7 ± 0.3 | ||
| Protocol | tfin [s] |
|---|---|
| Constant heat source | 425 |
| Damage-controlled heat source | 600 |
| Pulsating heat source | 715 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. A New Thermal Damage-Controlled Protocol for Thermal Ablation Modeled with Modified Porous Media-Based Bioheat Equation with Variable Porosity. Processes 2022, 10, 236. https://doi.org/10.3390/pr10020236
Andreozzi A, Brunese L, Iasiello M, Tucci C, Vanoli GP. A New Thermal Damage-Controlled Protocol for Thermal Ablation Modeled with Modified Porous Media-Based Bioheat Equation with Variable Porosity. Processes. 2022; 10(2):236. https://doi.org/10.3390/pr10020236
Chicago/Turabian StyleAndreozzi, Assunta, Luca Brunese, Marcello Iasiello, Claudio Tucci, and Giuseppe Peter Vanoli. 2022. "A New Thermal Damage-Controlled Protocol for Thermal Ablation Modeled with Modified Porous Media-Based Bioheat Equation with Variable Porosity" Processes 10, no. 2: 236. https://doi.org/10.3390/pr10020236
APA StyleAndreozzi, A., Brunese, L., Iasiello, M., Tucci, C., & Vanoli, G. P. (2022). A New Thermal Damage-Controlled Protocol for Thermal Ablation Modeled with Modified Porous Media-Based Bioheat Equation with Variable Porosity. Processes, 10(2), 236. https://doi.org/10.3390/pr10020236







