Comparison of Two CFD Approaches Using Constant and Temperature Dependent Heat Capacities during the Phase Transition in PCMs with Experimental and Analytical Results
Abstract
:1. Introduction
2. Theoretical Background
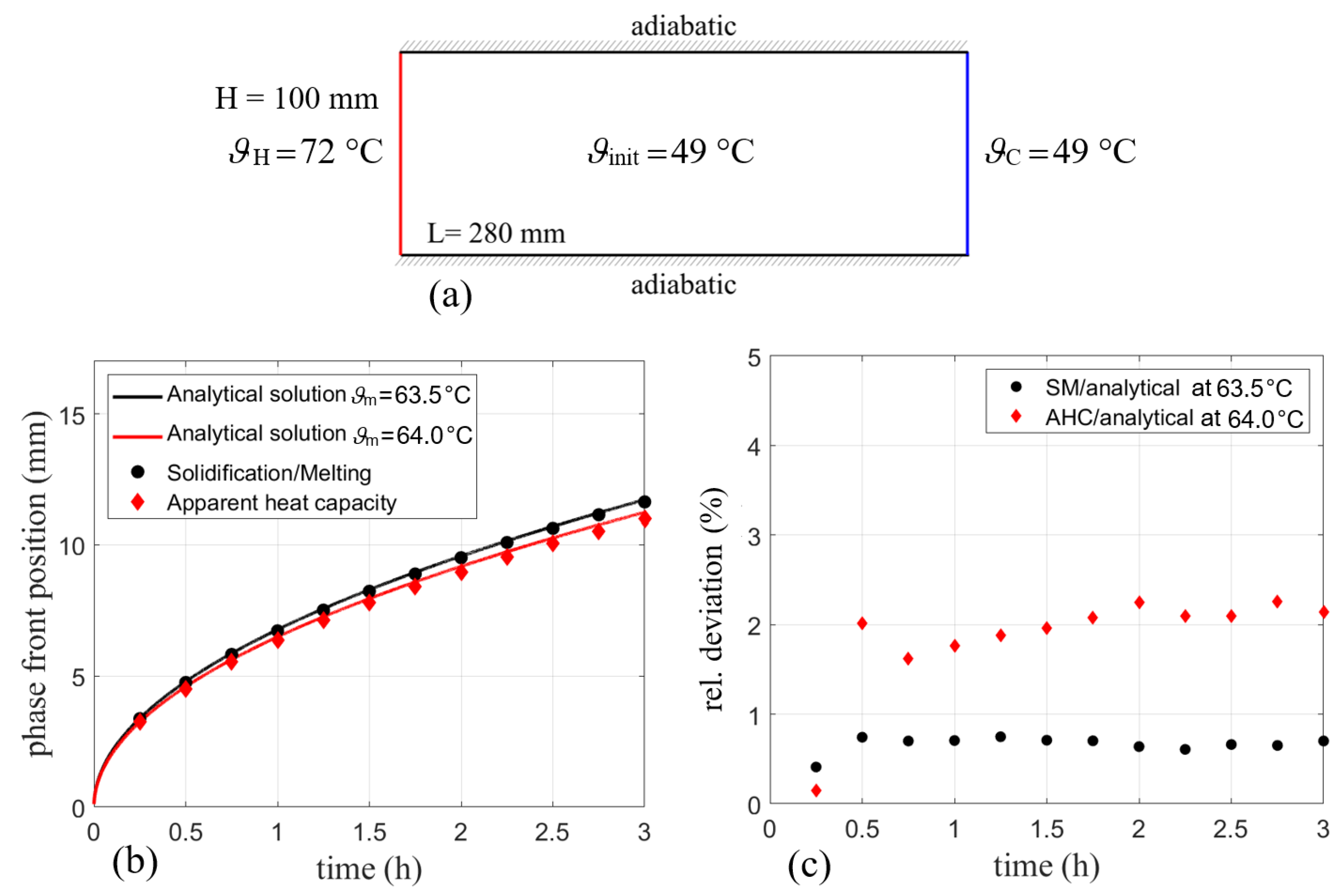
2.1. Analytical Solution of the Two-Phase Stefan Problem
2.2. Numerical Treatment
2.2.1. Enthalpy-Porosity Technique
2.2.2. Apparent Heat Capacity Method
3. Model and Materials
3.1. Thermophysical Properties
3.1.1. Heat Capacity
3.1.2. Dynamic Viscosity
3.2. Density
Thermal Conductivity
3.3. Model Summary
- Solidification/Melting (SM): Heat capacities and phase transition enthalpies are considered constant. Viscosity change over phase transition is included in the mushy zone constant of .
- Apparent heat capacity (AHC): Phase transition enthalpy is include in the apparent heat capacity curves presented in Figure 1. Viscosity change is considered by a very large viscosity in the solid phase transition and a small viscosity over phase change. Regarding density, two approaches are compared.
- (a)
- Variable density: A temperature-dependent density is used while neglecting volume change upon phase change;
- (b)
- Constant density: The Boussinesq approximation with the liquid density given in the data sheet as operating density and the melting temperature as operating temperature.
4. Results & Discussion
4.1. Comparison of SM and AHC with Variable Density
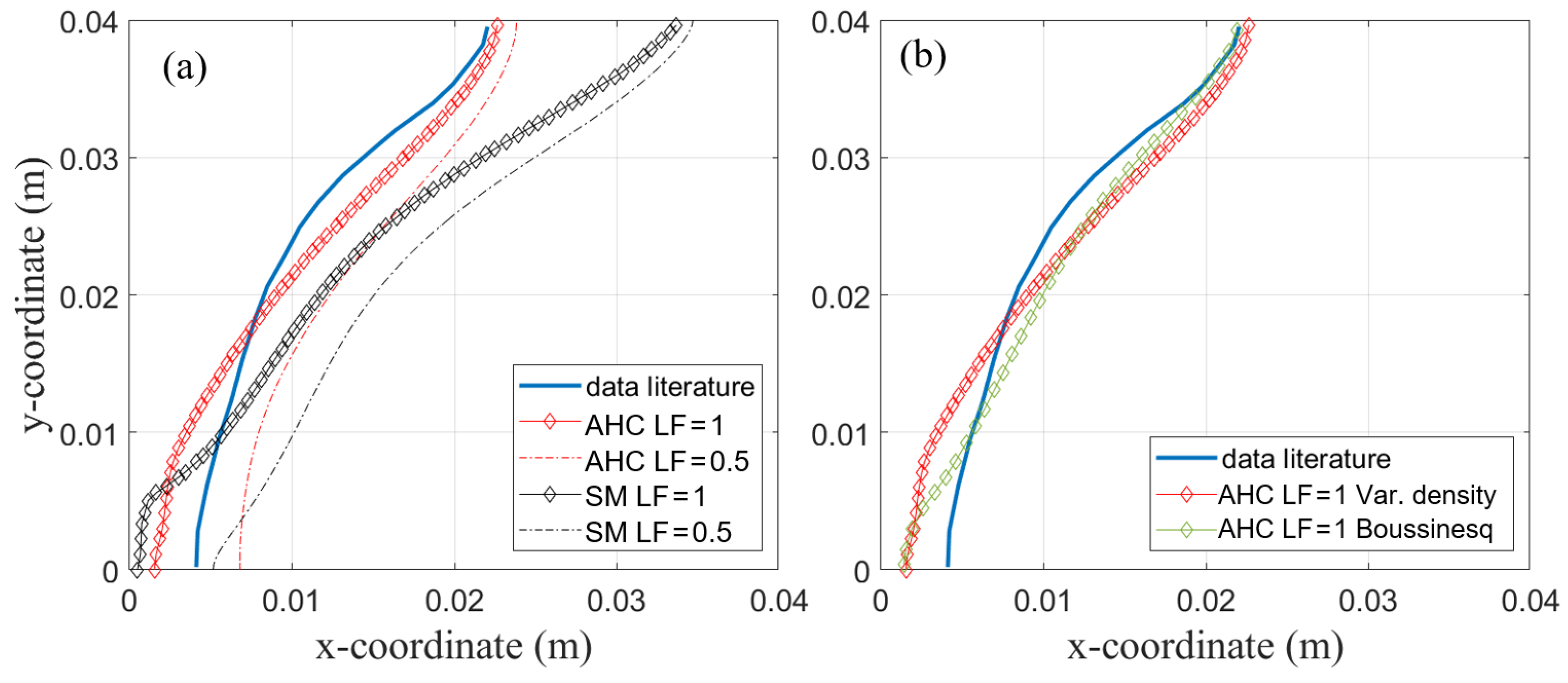
4.1.1. Comparison to the Analytical Solution
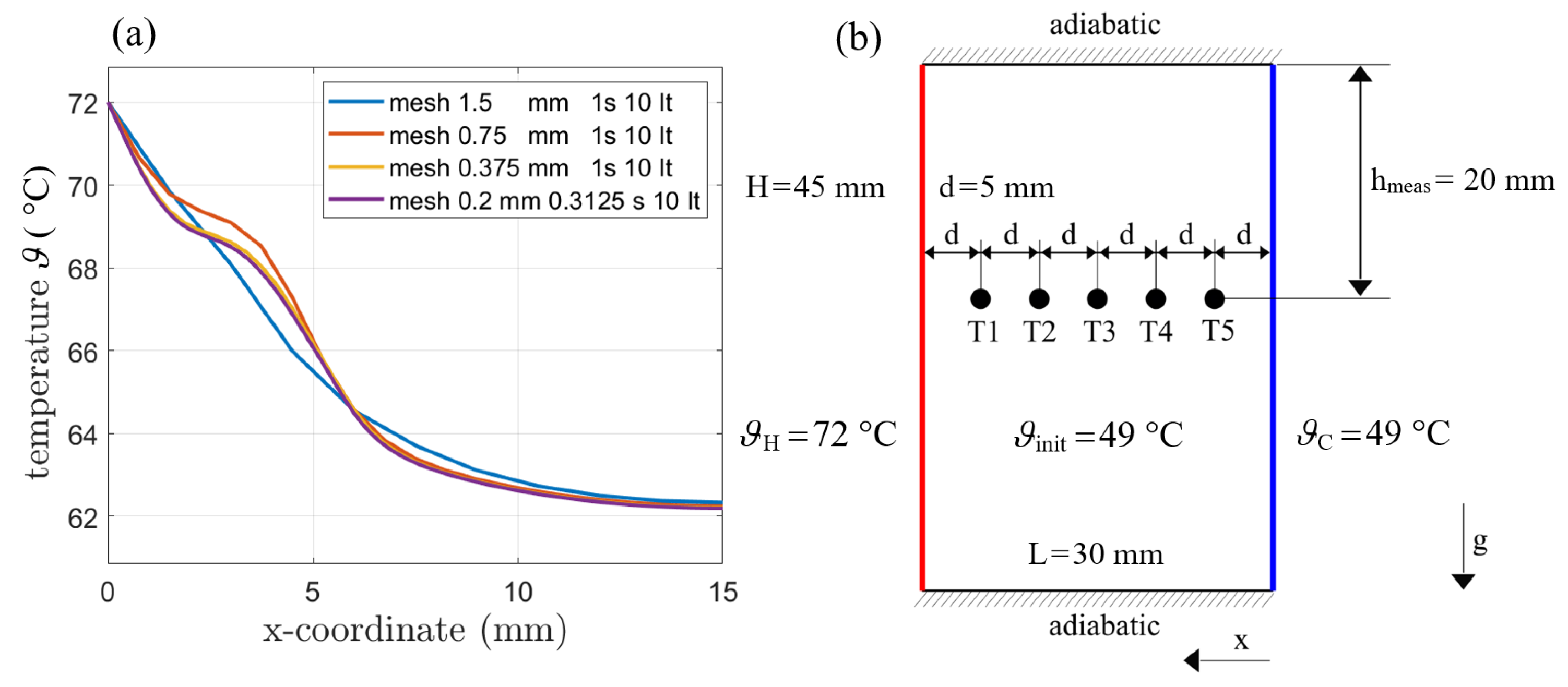
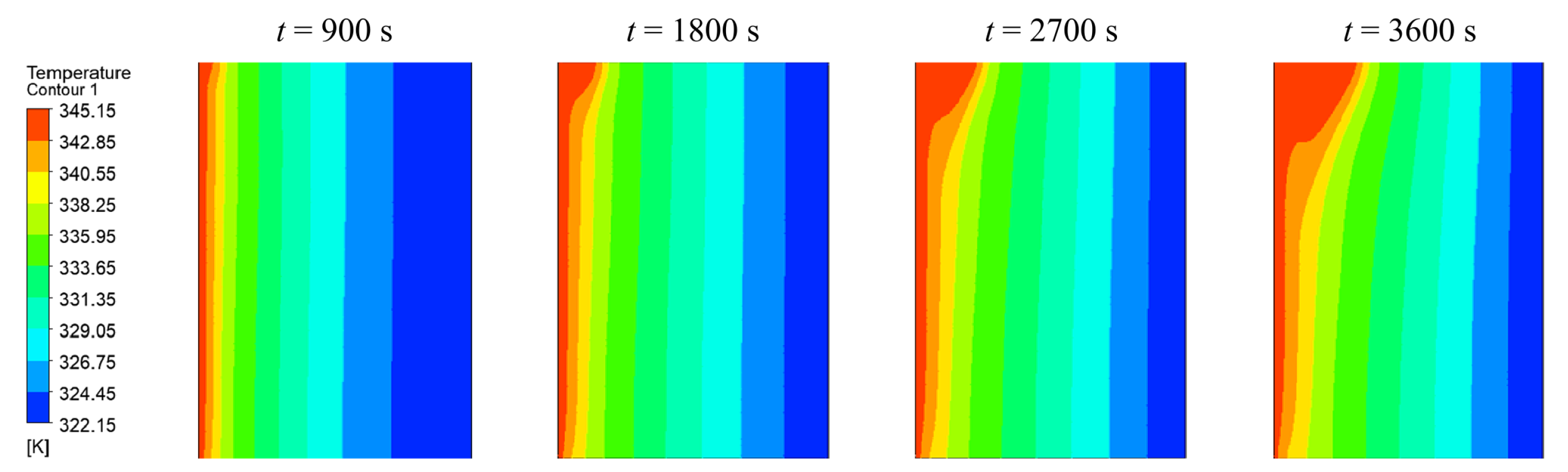
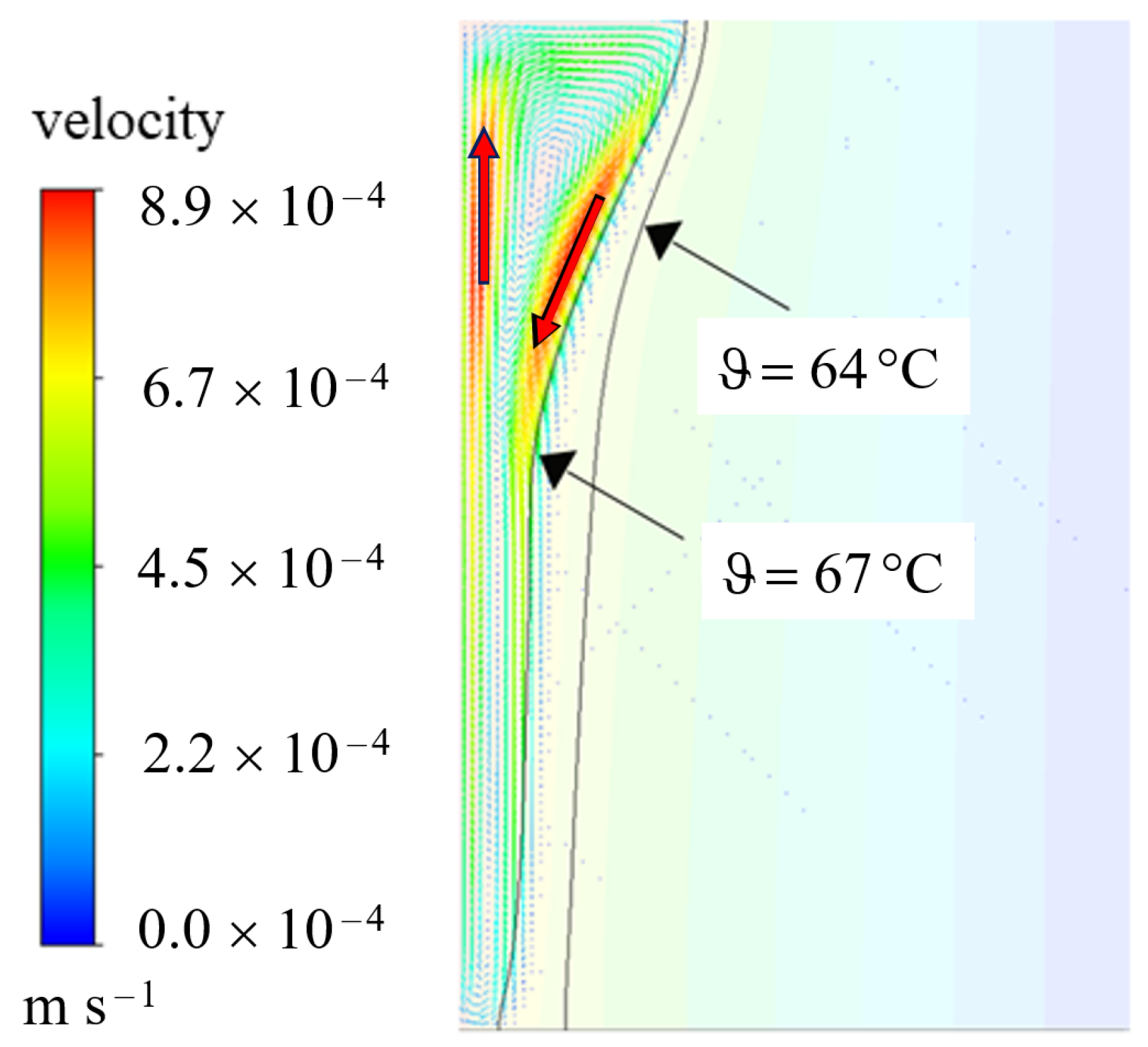
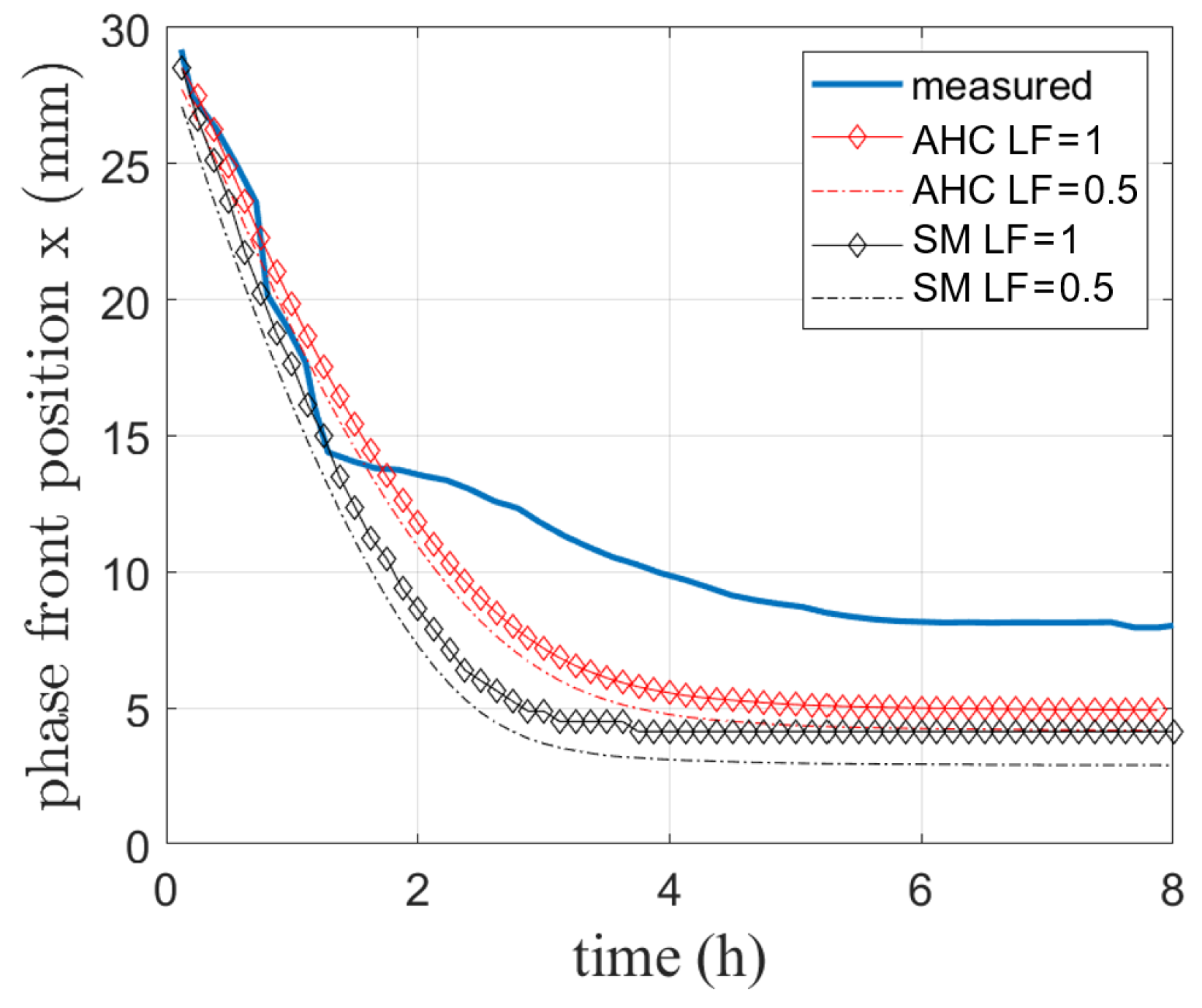
4.1.2. Comparison to Experimental Data with Gravity and Natural Convection
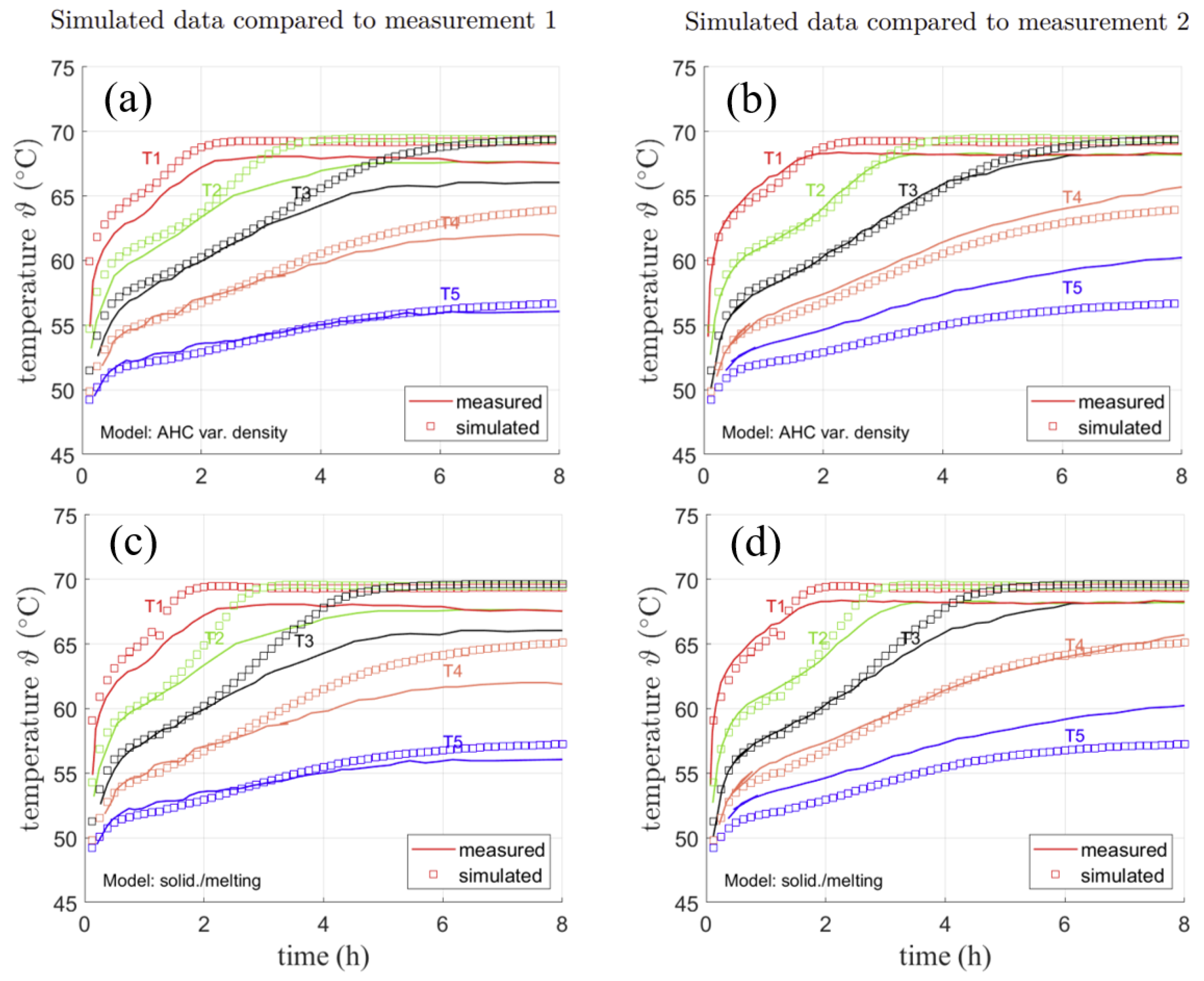
4.1.3. Comparison with RT64HC Data from AIT measurements
- ;
- ;
- .
4.1.4. Comparison with RT35HC Data from Literature
4.1.5. Comparison of AHC with Variable Density and Boussinesq Approximation
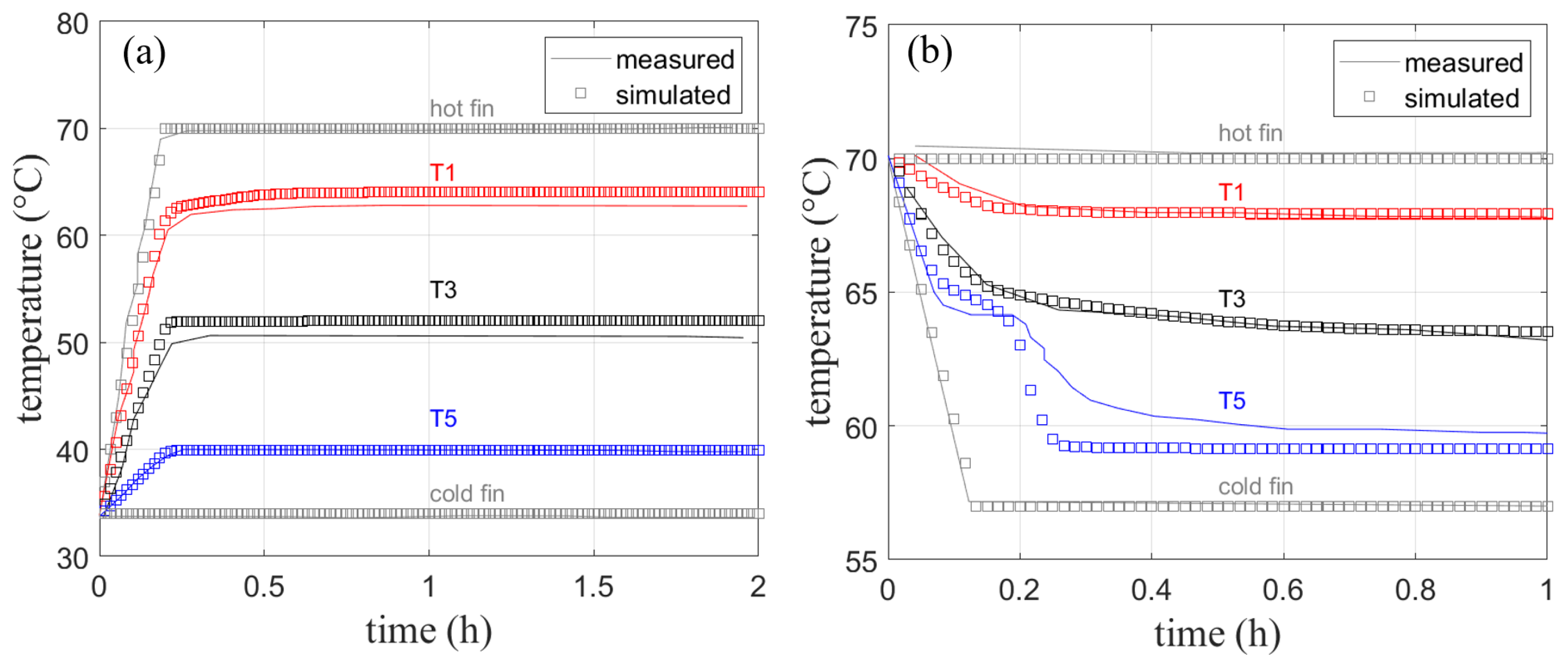
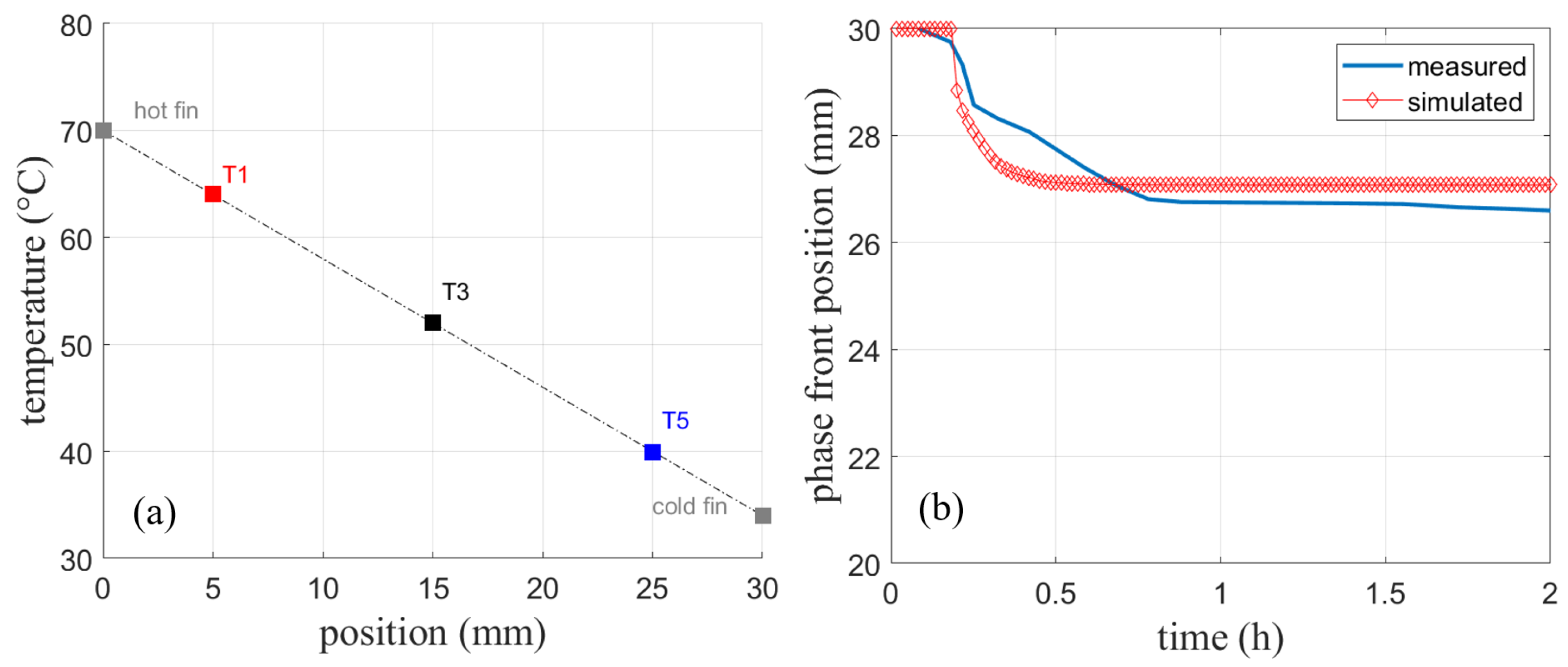
4.2. Validation of the PCM Model with Fins
4.2.1. Melting
- heating from 34 °C to 70 °C (hot fin) in 12 min;
- constant temperature of 34 °C (cold fin);
- Initial temperature 34 °C.
4.2.2. Solidification
- 70 °C;
- 70 °C to 57 °C in 8 min;
- Initial temperature 70 °C.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Latin letters | Unit | |
| a | Temperature diffusivity | m s |
| C | Mushy zone constant | kgs m |
| Specific heat capacity | Jkg K | |
| Liquid fraction | - | |
| Grashof number | - | |
| Enthalpy (specific) | J (Jkg) | |
| L | Latent heat | Jkg |
| Characteristic length | m | |
| m | Mass | kg |
| Rayleigh number | - | |
| Reynolds number | - | |
| Stefan number | - | |
| T | Temperature | K |
| x | Vapor quality | - |
| X | Phase front position | m |
| Greek letters | Unit | |
| Heat transfer coefficient | Wm K | |
| Thermal expansion coefficient | K | |
| Temperature | ||
| Thermal conductivity | Wm K | |
| Dynamic viscosity | kgm s | |
| Kinematic viscosity | m s | |
| Density | kgm | |
| Sub-scripts | ||
| c | cold | |
| g | gaseous | |
| H | hot | |
| in | inlet | |
| init | initial | |
| L | low | |
| l | liquid | |
| liq | liquidus | |
| m | melting | |
| m | mass | |
| o | operating | |
| s | solid | |
| sol | solidus | |
| v | volume | |
| w | wall | |
| Abbreviations | ||
| AHC | Apparent heat capacity model | |
| DSC | Differential scanning calorimetry | |
| LF | Liquid fraction | |
| PCM | Phase change material | |
| SM | Solidification and melting model |
References
- Iten, M.; Liu, S.; Shukla, A. Experimental validation of an air-PCM storage unit comparing the effective heat capacity and enthalpy methods through CFD simulations. Energy 2018, 155, 495–503. [Google Scholar] [CrossRef]
- Kasibhatla, R.R.; König-Haagen, A.; Rösler, F.; Brüggemann, D. Numerical modelling of melting and settling of an encapsulated PCM using variable viscosity. Heat Mass Transf. 2017, 53, 1735–1744. [Google Scholar] [CrossRef] [Green Version]
- Barz, T.; Emhofer, J. Paraffins as phase change material in a compact plate-fin heat exchanger—Part I: Experimental analysis and modeling of complete phase transitions. J. Energy Storage 2021, 33, 102128. [Google Scholar] [CrossRef]
- Mascherbauer, P. Experimental Analysis of a Compression Heat Pump with an Integrated Latent Storage. Diploma Thesis, Technical University of Vienna, Vienna, Austria, 2020. [Google Scholar]
- Kheirabadi, A.C.; Groulx, D. The effect of the mushy-zone constant on simulated phase change heat transfer. In Proceedings of the CHT-15. 6th International Symposium on Advances in Computational Heat Transfer, New Brunswick, NJ, USA, 25–29 May 2015; Begellhouse: Danbury, CT, USA, 2015; p. 22. [Google Scholar]
- Mallya, N.; Haussener, S. Buoyancy-driven melting and solidification heat transfer analysis in encapsulated phase change materials. Int. J. Heat Mass Transf. 2021, 164, 120525. [Google Scholar] [CrossRef]
- Jmal, I.; Baccar, M. Numerical investigation of PCM solidification in a finned rectangular heat exchanger including natural convection. Int. J. Heat Mass Transf. 2018, 127, 714–727. [Google Scholar] [CrossRef]
- Gürtürk, M.; Kok, B. A new approach in the design of heat transfer fin for melting and solidification of PCM. Int. J. Heat Mass Transf. 2020, 153, 119671. [Google Scholar] [CrossRef]
- Buonomo, B.; Ercole, D.; Manca, O.; Nardini, S. Numerical investigation on thermal behaviors of two-dimensional latent thermal energy storage with PCM and aluminum foam. J. Phys. Conf. Ser. 2017, 796, 012031. [Google Scholar] [CrossRef] [Green Version]
- ANSYS. ANSYS Fluent-CFD Software|ANSYS 2020. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 22 December 2021).
- Vikas, A.Y.; Soni, S. Simulation of melting process of a phase change material (PCM) using ANSYS (Fluent). Int. Res. J. Eng. Technol. 2017, 4. Available online: https://www.irjet.net/archives/V4/i5/IRJET-V4I5807.pdf" (accessed on 22 December 2021).
- Huang, B.; Tian, L.L.; Yu, Q.H.; Liu, X.; Shen, Z.G. Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations. Energies 2021, 14, 4091. [Google Scholar] [CrossRef]
- Barz, T.; Krämer, J.; Emhofer, J. Identification of Phase Fraction–Temperature Curves from Heat Capacity Data for Numerical Modeling of Heat Transfer in Commercial Paraffin Waxes. Energies 2020, 13, 5149. [Google Scholar] [CrossRef]
- Joybari, M.M.; Haghighat, F.; Seddegh, S.; Al-abidi, A.A. Heat transfer enhancement of phase change materials by fins under simultaneous charging and discharging. Energy Convers. Manag. 2017, 152, 136–156. [Google Scholar] [CrossRef]
- Kumar, M.; Krishna, D.J. Influence of Mushy Zone Constant on Thermohydraulics of a PCM. Energy Procedia 2017, 109, 314–321. [Google Scholar] [CrossRef]
- Koller, M.; Walter, H.; Hameter, M. Transient Numerical Simulation of the Melting and Solidification Behavior of NaNO3 Using a Wire Matrix for Enhancing the Heat Transfer. Energies 2016, 9, 205. [Google Scholar] [CrossRef]
- Walter, H.; Beck, A.; Hameter, M. Influence of the Fin Design on the Melting and Solidification Process of NaNO3 in a Thermal Energy Storage System. J. Energy Power Eng. 2015, 9, 913–928. [Google Scholar] [CrossRef] [Green Version]
- Tenpierik, M.; Wattez, Y.; Turrin, M.; Cosmatu, T.; Tsafou, S. Temperature Control in (Translucent) Phase Change Materials Applied in Facades: A Numerical Study. Energies 2019, 12, 3286. [Google Scholar] [CrossRef] [Green Version]
- Cornejo, I.; Cornejo, G.; Ramírez, C.; Almonacid, S.; Simpson, R. Inverse method for the simultaneous estimation of the thermophysical properties of foods at freezing temperatures. J. Food Eng. 2016, 191, 37–47. [Google Scholar] [CrossRef]
- Mariani, V.C.; Do Amarante, Á.C.C.; Dos Santos Coelho, L. Estimation of apparent thermal conductivity of carrot purée during freezing using inverse problem. Int. J. Food Sci. Technol. 2009, 44, 1292–1303. [Google Scholar] [CrossRef]
- Tubini, N.; Gruber, S.; Rigon, R. A method for solving heat transfer with phase change in ice or soil that allows for large time steps while guaranteeing energy conservation. Cryosphere 2021, 15, 2541–2568. [Google Scholar] [CrossRef]
- Khattari, Y.; Rhafiki, T.; Choab, N.; Kousksou, T.; Alaphilippe, M.; Zeraouli, Y. Apparent heat capacity method to investigate heat transfer in a composite phase change material. J. Energy Storage 2020, 28, 101239. [Google Scholar] [CrossRef]
- Baehr, H.D.; Stephan, K. Wärme- und Stoffübertragung; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- CRC Press (Ed.) Handbook of Thermal Science and Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Dutil, Y.; Rousse, D.R.; Salah, N.B.; Lassue, S.; Zalewski, L. A review on phase-change materials: Mathematical modeling and simulations. Renew. Sustain. Energy Rev. 2011, 15, 112–130. [Google Scholar] [CrossRef]
- Hu, H.; Argyropoulos, S.A. Mathematical modelling of solidification and melting: A review. Model. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef] [Green Version]
- AL-Saadi, S.N.; Zhai, Z. Modeling phase change materials embedded in building enclosure: A review. Renew. Sustain. Energy Rev. 2013, 21, 659–673. [Google Scholar] [CrossRef]
- Voller, V.R.; Cross, M.; Markatos, N.C. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Voller, V.R.; Brent, A.D.; Prakash, C. Modelling the mushy region in a binary alloy. Appl. Math. Model. 1990, 14, 320–326. [Google Scholar] [CrossRef]
- Caggiano, A.; Mankel, C.; Koenders, E. Reviewing Theoretical and Numerical Models for PCM-embedded Cementitious Composites. Buildings 2019, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; He, Y. Solving heat transfer problems with phase change via smoothed effective heat capacity and element-free Galerkin methods. Int. Commun. Heat Mass Transf. 2010, 37, 385–392. [Google Scholar] [CrossRef]
- Iten, M.; Liu, S.; Shukla, A.; Silva, P.D. Investigating the impact of C p -T values determined by DSC on the PCM-CFD model. Appl. Therm. Eng. 2017, 117, 65–75. [Google Scholar] [CrossRef]
- Li, Z.; Gariboldi, E. Review on the temperature-dependent thermophysical properties of liquid paraffins and composite phase change materials with metallic porous structures. Mater. Today Energy 2021, 20, 100642. [Google Scholar] [CrossRef]
- Ukrainczyk, N.; Kurajica, S.; Šipušic, J. Thermophysical Comparison of Five Commerical Paraffin Waxes. Chem. Biochem. Eng. 2010, 24, 129–137. [Google Scholar] [CrossRef]
- Leal, L.G. Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes; Cambridge Series in Chemical Engineering; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Peyret, R. Handbook of Computational Fluid Mechanics; Academic Press: London, UK, 1996. [Google Scholar]
- Chakraborty, P.R. Enthalpy porosity model for melting and solidification of pure-substances with large difference in phase specific heats. Int. Commun. Heat Mass Transf. 2017, 81, 183–189. [Google Scholar] [CrossRef]
- Nogueira, R.M.; Martins, M.A.; Ampessan, F. Natural convection in rectangular cavities with different aspect ratios. Rev. Eng. Térmica 2011, 10, 44. [Google Scholar] [CrossRef] [Green Version]
- Laurien, E.; Oertel, H. Numerische Strömungsmechanik; Springer: Wiesbaden, Germany, 2018. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Incropera’s Principles of Heat and Mass Transfer, 1st ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]

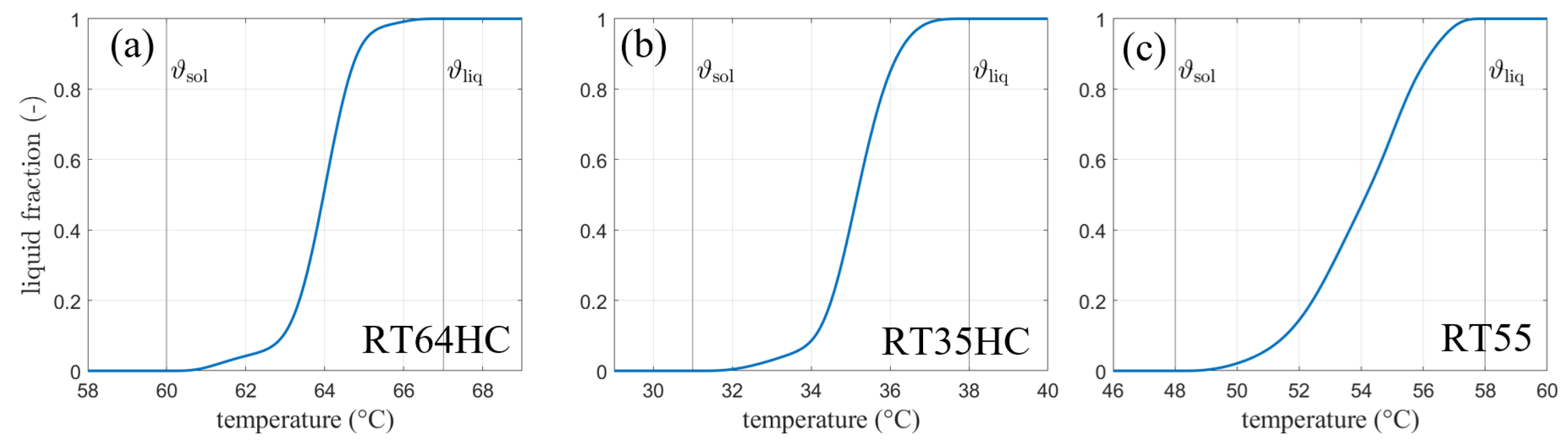
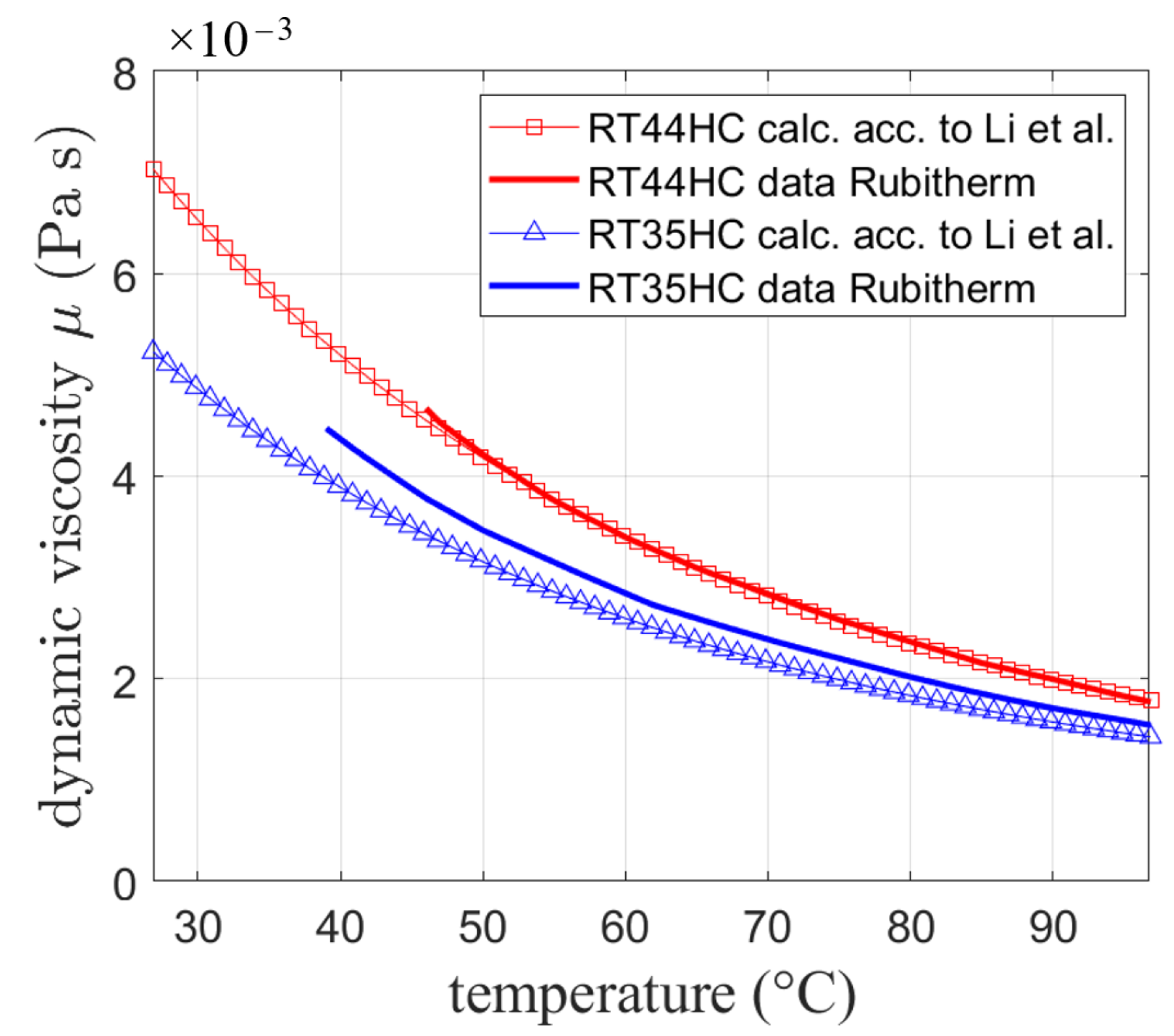
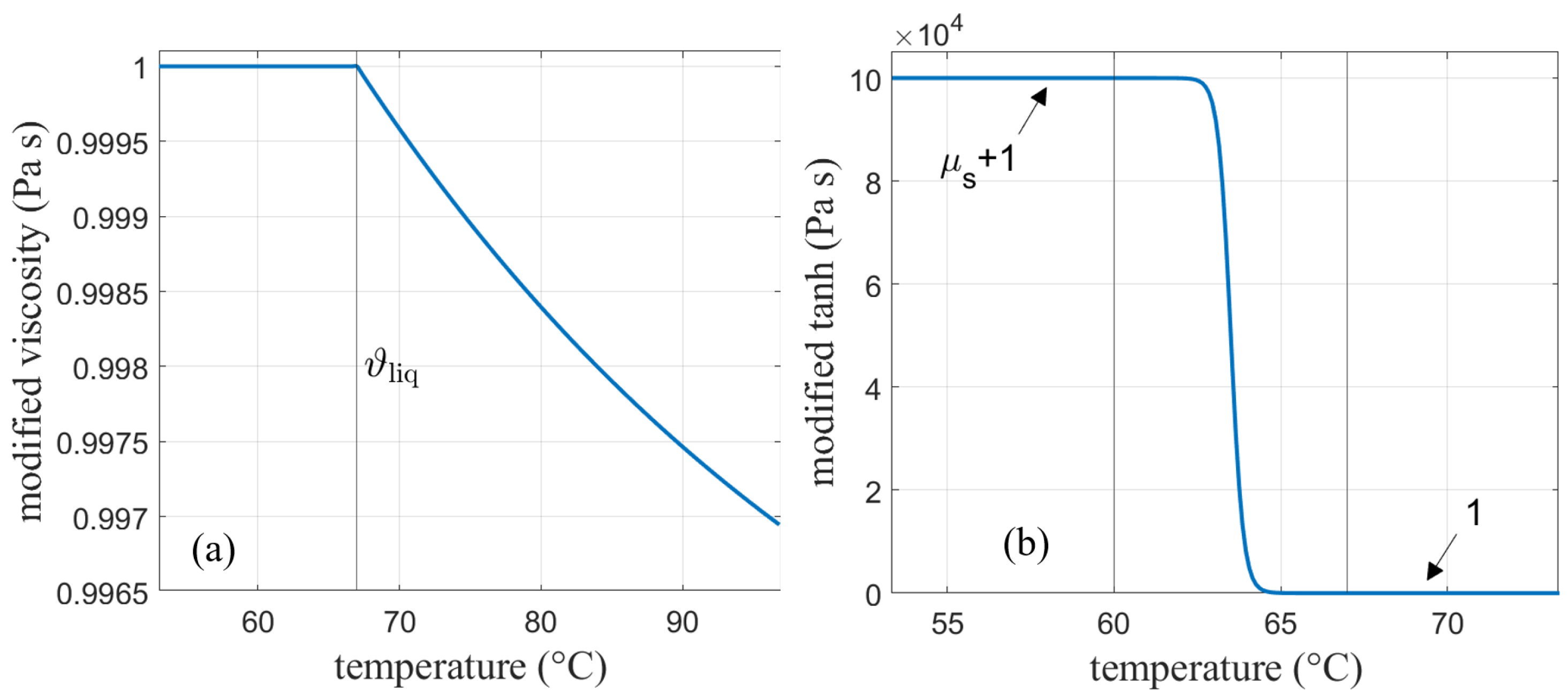
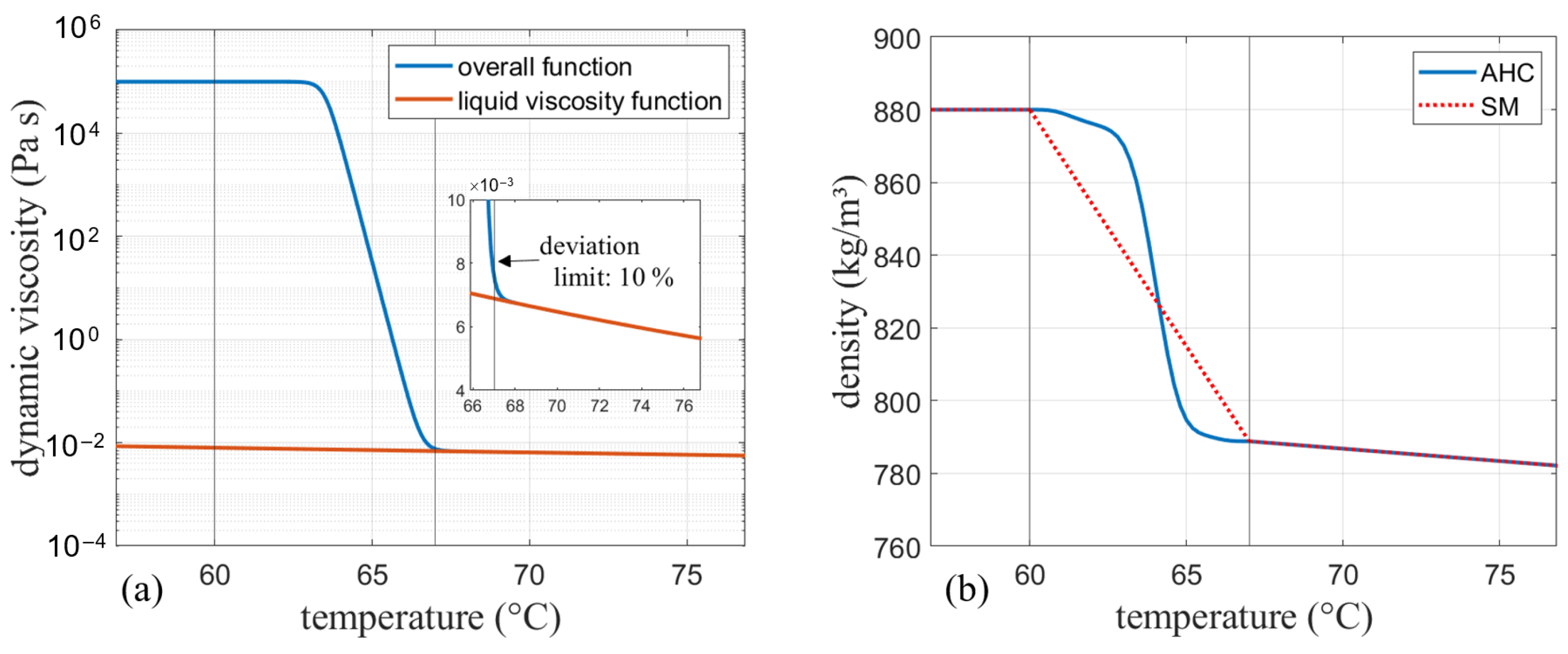


| Quantity | Unit | RT64HC | RT35HC | RT55 |
|---|---|---|---|---|
| kJ kg K | 2 | 2 | 2 | |
| kJ kg K | 2 | 2 | 2 | |
| °C | 60 | 31 | 48 | |
| °C | 67 | 38 | 58 | |
| L | kJ kg | 220 | 210 | 140 |
| PCM | Slope | ||||
|---|---|---|---|---|---|
| kgm | kgm | kgm K | kgm | K | |
| RT64HC | 880 | 788.84 | −0.68 | 780 at 64 °C | 0.00087179 |
| RT35HC | 880 | 771.36 | −0.68 | 770 at 35.1 °C | 0.00088312 |
| RT55 | 880 | 771.36 | −0.68 | 770 at 54.2 °C | 0.00088312 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reichl, C.; Both, S.; Mascherbauer, P.; Emhofer, J. Comparison of Two CFD Approaches Using Constant and Temperature Dependent Heat Capacities during the Phase Transition in PCMs with Experimental and Analytical Results. Processes 2022, 10, 302. https://doi.org/10.3390/pr10020302
Reichl C, Both S, Mascherbauer P, Emhofer J. Comparison of Two CFD Approaches Using Constant and Temperature Dependent Heat Capacities during the Phase Transition in PCMs with Experimental and Analytical Results. Processes. 2022; 10(2):302. https://doi.org/10.3390/pr10020302
Chicago/Turabian StyleReichl, Christoph, Svenja Both, Philipp Mascherbauer, and Johann Emhofer. 2022. "Comparison of Two CFD Approaches Using Constant and Temperature Dependent Heat Capacities during the Phase Transition in PCMs with Experimental and Analytical Results" Processes 10, no. 2: 302. https://doi.org/10.3390/pr10020302
APA StyleReichl, C., Both, S., Mascherbauer, P., & Emhofer, J. (2022). Comparison of Two CFD Approaches Using Constant and Temperature Dependent Heat Capacities during the Phase Transition in PCMs with Experimental and Analytical Results. Processes, 10(2), 302. https://doi.org/10.3390/pr10020302







