Tuning of Model Predictive Controllers Based on Hybrid Optimization ^†

Abstract

A tuning procedure for a model predictive controller (MPC) is presented for multi-input multi-output systems. The approach consists of two steps based on a hybrid method: the goal attainment method and a variable neighborhood search. In the first step, the weights of the MPC objective function are obtained, minimizing the square error between the closed-loop response of the internal controller model and a predefined desired reference trajectory. In the second step, the integer variables of the problem (prediction and control horizons) are obtained, minimizing the square error between the closed-loop response and an optimal trajectory, aiming a controller with low computational cost and good performance. The proposed method was tested in two benchmark processes using different MPC formulations, showing satisfactory results.

1. Introduction

Model predictive control (MPC) is an advanced control structure that uses an open-loop model to predict future process behavior over a predefined horizon by solving an optimization algorithm at each time step [1]. The MPC is a versatile controller, which is effective in obtaining optimized control actions in constrained systems. For this reason, several MPC algorithms have been generated, differing in regard to the kind of model, the noise, disturbance model, and objective function.

The successful implementation of MPC requires the proper tuning of its parameters, which is a challenging problem for multivariable systems, in which the number of these parameters increases proportionally to the system’s size. MPC tuning parameters include the prediction and control horizons and the weight matrices used in the cost function [2]. The classical MPC cost function incorporates two diagonal and positive semidefinite weighting matrices, $\mathbf{Q}$ and $\mathbf{W}$. The first matrix penalizes the output reference tracking, and the second matrix penalizes the manipulated variable move suppression. The tuning of all these parameters is directly related to the closed-loop performance of the control system [3].

According to Garriga and Soroush [4], two categories—(i) ad hoc methods and (ii) self-tuning methods—have been used as MPC tuning strategies. The first one uses mathematical expressions, approximation or simulation error bounds or process dynamics parameters to adjust the MPC specifications. The second one uses optimization algorithms to find the tuning parameters of the MPC.

Different proposals to set the prediction and control horizons and the weighting matrices of the objective function can be found in the literature. Some of these works are presented in a review by Rani and Unbehauen [5], which addressed tuning methods for dynamic matrix control (DMC) and generalized predictive control (GPC) during 1984–1995. Next, in Garriga and Soroush [4], a review of the heuristic and theoretical tunings of the MPC method is presented up to the year 2009 and, in Alhajeri and Soroush [6], a review is presented covering research up to the year 2019.

There is still no consensus as to which methodology provides the best tuning in terms of the controller’s performance and the computational cost. For instance, in Shridhar and Cooper [7,8], Ad hoc systematic expressions were employed for tuning of the parameters of an MPC based on DMC in both single-input single-output (SISO) and multi-input multi-output (MIMO) systems. Their tuning method was based on a first-order plus dead time (FOPDT) model approximation of the process with zero-order retention. Based on the FOPDT approximation, they obtained an equation to calculate the suppression weights of the controller. The prediction horizon was calculated using an equation based on the condition number of the matrix A of the process and the control horizon was based on the time constant of the model. Trierweiler and Farina [9] proposed a robust performance number index to tune the MPC parameters, which reflected both the directionality of the system and its attainable performance to determine the weight matrices.

In Tran and Özkan [10], a tuning procedure for GPC was divided into two steps. The first step matched the GPC gain to an arbitrary linear-time-invariant controller (the favorite controller) using the transfer function of the control law. Then, the weight matrices in the cost function were found, resulting in the GPC gain obtained in the first step. A methodology of tuning the control parameters of GPC with long time-delay plants was proposed in the work of García and Albertos [11]. Their methodology used an equivalent representation of the Smith predictor structure. A tuning parameter was provided to reach an intuitive tradeoff between performance and robust stability using sensitivity transfer functions without delay.

Different self-tuning procedures have also been reported in the literature. For instance, in Al-Ghazzawi et al. [12] expresseda relationship between the MPC controller’s parameters and the process outputs through a linear approximation algorithm to analytically obtain the sensitivity functions of $\mathbf{Q}$ and $\mathbf{W}$ in constrained problems. Using these functions, the authors guided the MPC feedback response within predefined performance specifications. In Van der Lee et al. [13], fuzzy goal programming using the integral square error (ISE) criterion was used to find the MPC tuning parameters through a metaheuristic.

Some contributions focus specifically on characterizing the set of solutions in the Pareto front, defining different objectives regarding the required specifications of the process and solving a multi-objective problem to obtain the tuning parameters of the MPC [14,15]. A recursive multi-objective optimization algorithm was presented in Liu and Wang [16], who minimized the sensitivity function between the tuning parameters and the closed-loop performance as the goals of a mixed-integer nonlinear optimization problem. In Vega et al. [17], an MPC tuning method was proposed, using constrained mixed-integer nonlinear programming. In their work, a particle swarm optimization approach was implemented to solve the tuning problem for the worst-case model mismatch scenario, employing a comprehensive combination of the condition number and the Morari resiliency index. In Yamashita et al. [3], two optimization algorithms, lexicographic optimization tuning and compromised tuning were used to obtain the weighting matrices of the MPC control law.

In Lozano and Gómez [18], a general tuning algorithm for nonlinear model predictive control (NMPC) was presented. The method was based on the utopia tracking concept in a multi-objective optimization problem to adjust the weights of the objective function. Then, closed-loop performance index optimization was applied to find the horizon lengths. In the work of De Schutter and Zanon [19], an open-source software framework was introduced for the tuning of an economic nonlinear model predictive control (ENMPC) process. This tool calculates the optimal stable states or periodic trajectories for constrained nonlinear systems with an economic objective, returning the corresponding positive-definite stage cost matrices for a tracking (N)MPC problem.

In general, the prediction and control horizons are set following several rules [4,9], which have shown satisfactory performance. In the academic literature, it is common to select single values for control and prediction horizons. However, in commercial packages for MPC the prediction horizon is usually the same for all outputs, although a different control horizon is defined for each input variable. In general, this policy has been employed in input blocking design, which was described in [20], and has been extensively used in industry to reduce computation costs [21]. With this strategy, the control input determined by the optimization stage cannot vary freely at each sampling time of the prediction horizon but only in predefined patterns.

The works found in the literature have focused mainly on adjusting the MPC weights using optimization algorithms. In the present paper, we propose a different tuning strategy that can be applied to any MPC algorithm, capable of dealing with model uncertainty in its formulation and selecting the controller parameters to ensure that the given performance requirements or desirable control behavior are attained. This work proposes a tuning method for MPC which is not restricted to a specific type of prediction model or MPC algorithm. The method is based on the use of two optimization algorithms, forming a hybrid approach: (i) the goal attainment method (GAM) and (ii) a variable neighborhood search (VNS). The motivation of the present work is to propose a methodology to combine two optimization methods to address the problem regarding the nature of the integer variables and the competitive objectives in the formulation of MPC control, which is advantageous if compared with a mixed-integer dynamic optimization methodology in terms of computational complexity. Furthermore, a tuning method using hybrid optimization to address this problem has not yet been reported in the literature.

In this approach, the VNS optimization algorithm finds the adequate sizes of the control horizons in reference to each manipulated variable of the process and a single prediction horizon for the entire system. This approach is advantageous since the dynamics in chemical processes can present differences, showing fast, slow, non-minimal, or unstable behavior, and different actions and speeds may be required for each manipulated variable along the control horizon. Therefore, adequate lengths of horizons are searched for each manipulated variable of the system. This flexibility also allows one to obtain a reduced number of control actions for the MPC compared with the fixed control horizon approach, reducing the computational cost of the MPC controller.

An initial version of this algorithm for a linear GPC was presented by Giraldo et al. [22], and this is now extended with the formal theoretical background and new contributions, namely:

• this paper shows that the algorithm can be applied to any formulation of MPC control;
• the tuning algorithm is capable of dealing with model mismatch and system noise by adjusting parameters based on the worst-case scenario from the family models of the process, using a robust MPC formulation in the MPC tuner, or via the predefined desired trajectory in the system;
• according to the performance criteria, which are pre-established by the user, the tuning algorithm can provide a quick parameter adjustment, presenting a low computational cost;
• the algorithm works in conjunction with the internal MPC optimizer to obtain adequate system performance and robustness;
• improvement of the objective function for obtaining the adequate length of prediction and control horizons, using the VNS algorithm to reach the desired closed-loop dynamic;
• reduction of the computational cost of the algorithm by removing an optimization stage in the calculation of the utopia point of the goal attainment method algorithm; and
• since this work proposes a sequential optimization method, better results were attained by executing the GAM algorithm first, followed by the VNS algorithm.

The remaining sections of this manuscript are organized as follows. Section 2 presents a brief review of the MPC algorithm and an explanation of the optimization methods presented herein. Section 3 provides the proposed approach of MPC tuning. In Section 4, algorithm testing results are presented and discussed, followed by the main conclusions, which are provided in Section 5.

2. Background

2.1. Model Predictive Control

An MPC is an advanced control strategy that solves an optimal control problem at every sampling time. The control uses an explicit model to predict the outputs of the system at a future time by calculating the future control sequences to minimize a cost function. However, only the first value of the control sequences is applied to the process, and the rest of the predicted future actions are used as initial guesses for the next optimization cycle. The predictions are adjusted based on new measurements and estimates of the state variables at the next sampling instant, at which point the optimal control problem is solved again.

The MPC optimization problem can be described in the classical formulation as:

$$\begin{array}{cc}\hfill \underset{\mathbf{u}}{\min }\{J=& \sum _{i=1}^{n_y}\sum _{n=1}^p\left\{Q_{ii}{\left[{\widehat{y}}_i(k+n|k)-w_i(k+n)\right]}^2\right\}+\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j=1}^{n_u}}{\displaystyle \sum _{n=1}^{m_j}}\left\{W_{jj}{\left[{\Delta u}_j(k+n-1)\right]}^2\right\}\},\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill & x(k+n)=f(k,x(k+n-1),u(k+n),\mathit{\mu }),n=1,\dots ,p\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill & g(k,y(k+n),x(k+n),u(k+n),\mathit{\mu })=\mathbf{0},n=1,\dots ,p\hfill \end{array}$$

(1c)

$$\begin{array}{cc}\hfill & x\left(k\right)=\widehat{x}\left(k\right)\hfill \end{array}$$

(1d)

$$\begin{array}{cc}\hfill & u_{j_{min}}\le u_j(k+n-1)\le u_{j_{max}},j=1,\dots ,n_u\mathrm{and}n=1,\dots ,m_j\hfill \\ \hfill & \Delta u_{j_{min}}\le u_j(k+n-1)-u_j(k+n-2)\le \Delta u_{j_{max}},\hfill \end{array}$$

(1e)

$$\begin{array}{cc}\hfill & j=1,\dots ,n_u\mathrm{and}n=1,\dots ,m_j\hfill \end{array}$$

(1f)

$$\begin{array}{cc}\hfill & y_{i_{min}}\le {\widehat{y}}_i(k+n)\le y_{i_{max}},i=1,\dots ,n_y\mathrm{and}n=1,\dots ,p,\hfill \end{array}$$

(1g)

where J is the cost function; $\mathbf{y}$, $\mathbf{x}$ and $\mathbf{u}$ are vectors of the controlled, state and manipulated variables, respectively; and $\mathit{\mu }$ is the vector of the model parameters, which can include disturbances. Equation (1b,c) describe the process model, Equation (1d) is the initial condition of the prediction horizon, and Equation (1e–g) are the lower and upper bounds on the manipulated variables and their rate of variation and the lower and upper bounds on the controlled variables. $n_y$ and $n_u$ are the numbers of controlled and manipulated variables, respectively, of the MIMO system. p is the prediction horizon value and $m_j$ is the control horizon value of j-th plant input. All control horizons are condensed in a vector $\mathbf{m}$. $\mathbf{Q}$ and $\mathbf{W}$ are positive semidefinite weight matrices. The future reference trajectory for the i-th plant output at the n-th prediction horizon step is given by $w_i(k+n)$ and the predicted value of the i-th plant output at the n-th prediction horizon step is given by ${\widehat{y}}_i(k+n|k)$, where k is the current control interval.

In Equation (Section 2.1), p, $\mathbf{m}$, $\mathbf{Q}$ and $\mathbf{W}$ are the MPC tuning parameters. These parameters have a direct relationship with the size of the control system structure, as the greater the system is, the more parameters will have to be tuned and the problem becomes more complex. A poor tuning of the MPC parameters contributes to an ill-posed optimization control problem, which can cause undesired oscillations in the controlled variables. Therefore, each MPC tuning parameter has an influence on the system dynamics  [9]. A good selection of the sampling period, control and prediction horizons allows a good estimate of the system behavior to be obtained, as well as avoiding a high computational cost in the calculation of the control action. The weight matrices guarantee the performance and robustness of the system, providing priorities and scaling among the considered process variables.

2.2. Optimization Methods

The MPC tuning method used in this work is achieved through the synergy of the GAM and VNS algorithms, which results in a hybrid approach that allows one to estimate the controller parameters based on the desired performance of the system. These two optimization methods are described in detail below.

2.2.1. Goal Attainment Method

The operation of a chemical process usually involves the fulfilment of different requirements or specifications in order to reach an optimal point. For instance, low cost, low operating risks, low pollution, high reliability, high quality, and high productivity are reasonable objectives to be achieved in this process [22]. Nevertheless, most of these goals are often in conflict with each other. Thus, for that reason, a compromise solution must be obtained between them. This is known as a multi-objective optimization problem.

When there are multiple objectives, usually there is not only a single solution but a set of them, each satisfying one objective to the detriment of the others. This is known as the Pareto set, where the ideal solution is adopted based on the optimization problem’s decisions [23]. Figure 1 shows a geometric representation of the compromise solution, considering a bi-objective problem.

The major problem in multi-objective optimization can be inferred from Figure 1, i.e., the conflict between the objective functions, where the improvement in one of the objective functions may cause the degradation of others. Therefore, the choice of the optimal point in the Pareto curve will depend on a decision for the planned operation of the process.

The GAM formulation, proposed by Gembicki [24], involves expressing a set of utopian goals, ${\mathbf{f}}^{*}=[f_1^{*},f_2^{*},\dots ,f_n^{*}]$, which is associated with a set of objectives, $\mathbf{f}=[f_1\left(x\right),f_2\left(x\right),\dots ,f_n\left(x\right)]$. ${\mathbf{f}}^{*}$ is an unreachable point when minimizing all the objectives simultaneously. The problem’s formulation is given by:

$$\begin{array}{cc}\hfill \underset{\mathbf{x},\gamma }{\min }& \gamma ,\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \mathbf{h}\left(\mathbf{x}\right)=0\hfill \\ \hfill & \mathbf{g}\left(\mathbf{x}\right)\le 0\hfill \\ \hfill & f_i\left(\mathbf{x}\right)-{\omega }_i\gamma -f_i^{*}\le 0,i=1,\cdots ,n\hfill \\ \hfill & {\mathbf{L}}_{\mathbf{B}}\le \mathbf{x}\le {\mathbf{U}}_{\mathbf{B}},\hfill \end{array}$$

(2)

where $\mathbf{h}\left(x\right)$ and $\mathbf{g}\left(x\right)$ are equality and inequality constraints, respectively, and ${\omega }_i$ is the relative weight for the i-th objective function $f_i\left(x\right)$. ${\mathbf{L}}_{\mathbf{B}}$ and ${\mathbf{U}}_{\mathbf{B}}$ are the lower and upper bounds of the decision variables.

The weight vector, $\omega$, measures the relative tradeoffs among the objectives and, in order to eliminate the rigid constraints of the problem, the term ${\omega }_i\gamma$ is used as a slackness variable.

Equation (2) is a convenient way of expressing the commitments among the objective functions, giving greater flexibility to the optimization algorithm to find the best solution. The schematic evolution of this method in the direction of the solution in two dimensions is presented in Figure 2 [25], where ${\mathbf{f}}^{*}$ is the goal and ${\mathbf{f}}_{\mathbf{o}}$ is the optimal point obtained for a given weight vector, $\mathit{\omega }$, which defines the search direction. The feasible function space, $\Lambda \left(\gamma \right)$, shrinks as $\gamma$ is reduced.

2.2.2. Variable Neighborhood Search

The VNS algorithm is a metaheuristic used to solve combinatorial optimization problems, with its operation based on the idea of neighborhood change to find local minima and escape the valleys which contain them [26]. Initially proposed in Mladenović and Hansen [27], this metaheuristic has been developed in terms of its methods and successfully applied to solve several application problems [28,29].

The VNS formulation is given by:

$$\min \left[f_v\left(x\right)|x\in X,X\subseteq S\right],$$

(3)

where S is the solution space, X is the feasible set, x is the feasible solution, and $f_v$ is the real-valued objective function. If S is a finite set, then a combinatorial optimization is established in the VNS algorithm. Otherwise, when $S={\mathbb{R}}^n$, the VNS is a continuous optimization. The optimal solution of $x^{*}$ is given if

$$f_v\left(x^{*}\right)\le f_v\left(x\right),\forall x\in X.$$

(4)

The VNS algorithm works in the following way. First, an initial condition is established in x, from which a descending direction is found that minimizes $f_v\left(x\right)$ within a neighborhood denoted as $N_e\left(x\right)$. The metaheuristic iterates the algorithm as long as there is a decent direction; otherwise, it stops. The best improvement or the first descent are the two descent directions of the VNS algorithm. In the first one, the VNS checks all the neighborhoods in $N_e\left(x\right)$ and selects the neighborhood with the minimum goal. In the second one, the first neighborhood that minimizes $f_v\left(x\right)$ is selected. The first descent direction can find an improvement quickly if the neighborhood is searched in an orderly fashion. When the steps most likely to result in an improvement are prioritized, the total search time tends to decrease. However, this is not guaranteed, and the worst-case performance remains the same as the best improvement. The best improvement strategy will produce improvements in the short term, but it has no long-term guarantees. Figure 3 illustrates the VNS method.

The VNS algorithm applies random steps in neighborhoods with growing size to diversify the search into combinatorial problems; this is known as shaking [26]. The VNS systematically changes the neighborhood elements to find the optimal one. When the algorithm changes a single neighborhood component, this is known as a first-order search. If the algorithm changes two neighborhood components, this is known as a second-order search and so on.

3. Model Predictive Control Tuning Approach (MPCT)

The MPC controller tuning strategy proposed in this work will be called MPCT, and is described in this section. Once the MPC is based on a process model, a good tuning is also dependent on the quality of this model. In most MPC applications, models are derived by applying experiment design, data collection and system identification methods. At this stage, the correct selection of the sampling time ($T_s$) and the scaling of the multivariable model need to be highlighted, as detailed in Appendix A, because these selections have strong effects on the tuning performance.

As the MPCT uses a hybrid optimization formulation, it is able to find the integer and real variables of the tuning problem. The decision variables of the algorithm are ${\mathbf{x}}_{dv}=[p,\mathbf{m},\mathrm{diag}\left(\mathbf{Q}\right),\mathrm{diag}\left(\mathbf{W}\right)]$, where integer variables p and $\mathbf{m}$ are determined by means of the VNS method, and $\mathbf{Q}$ and $\mathbf{W}$ are real-valued diagonal matrices to be found by the GAM algorithm. The lower and upper bounds of the ${\mathbf{x}}_{dv}$ are ${\mathbf{L}}_{\mathbf{B}}=[1,{\mathbf{1}}_{n_u},{\mathbf{1}}_{n_y+n_u}\times {10}^{-5}]$ and ${\mathbf{U}}_{\mathbf{B}}=[2^{H_p},{\mathbf{1}}_{n_u}\left(2^{H_c}\right),and {\mathbf{1}}_{n_y+n_u}(\infty )]$, respectively, where ${\mathbf{1}}_n$ is a row vector of ones of size n, and $H_p$ and $H_c$ are given values such that $2^{H_p}$ and $2^{H_c}$ are the upper bounds of p and $\mathbf{m}$.

The MPCT algorithm executes the hybrid optimization (i.e., GAM and VNS algorithms) sequentially. For this purpose, GAM is the first algorithm to be executed. Minimizing the square error between the closed-loop responses and the pre-established reference trajectories is a common tuning objective, reported in diverse MPC tuning procedures [3,12,30]. This strategy is employed in the GAM algorithm, where the reference trajectory is set as a tuning parameter. This reference trajectory defines the desirable closed-loop dynamics, represented as a first- or second-order transfer function system with dead-time. Therefore, the multi-objective GAM formulation is giving by:

$$\begin{array}{c}\hfill f_i\left({\mathbf{x}}_{dv}\right)=\sum _{k=1}^{\varphi }{\left[y_i^R\left(k\right)-y_i(k,{\mathbf{x}}_{dv})\right]}^2,i=1,\cdots ,n_y,\end{array}$$

(5)

where $y_i^R\left(k\right)$ is the discretized reference trajectory of the MIMO output, defined by the user for performance requirements or desirable control behavior; $y_i(k,{\mathbf{x}}_{dv})$ is the MPC closed-loop trajectory of output i; and $\varphi$ is a predefined tuning horizon, which is large enough to capture the system dynamics.

One may note that the reference trajectory, ${\mathbf{y}}^R\left(k\right)$, is different from the reference tracking signal, $\mathbf{w}\left(k\right)$. The reference tracking signal is necessary to obtain the closed-loop trajectory when Equation (1a–g) is solved. Due to the MIMO system features, the interactions between the plant variables affect the desired performance for each pre-established variable in the reference trajectory. Therefore, in the GAM algorithm it is recommended to establish a similar reference tracking signal to that established in the real plant in both the reference trajectory and the closed-loop trajectory becausethe algorithm manages to minimize the effect of the MIMO system interactions by minimizing Equation (5).

The utopian solution was initially proposed in [22] by solving the optimization problems defined as:

$$\begin{array}{cc}\hfill f_i^{*}\left({\mathbf{x}}_{dv}\right)=& \underset{{\mathbf{x}}_{dv}}{\min }{f}_i\left({\mathbf{x}}_{dv}\right),i=1,\cdots ,n_y\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & {\mathbf{L}}_{\mathbf{B}}\le {\mathbf{x}}_{dv}\le {\mathbf{U}}_{\mathbf{B}}.\hfill \end{array}$$

(6)

Nevertheless, as a utopian solution is an infeasible point because not all the tuning objectives have the same optimal point. We propose here to remove this optimization stage to improve the computational cost of the GAM algorithm. In this case, a reasonable selection of the utopia point is to select it as zero because the set of objectives, shown in Equation (5), are positive functions and because it meets the criteria of being a utopia point. Note that the only way Equation (5) can be zero is a case in which each objective perfectly follows the reference trajectory. Thus, the GAM algorithm, shown in Equation (2), is solved by means of sequential quadratic programming to find the tuning parameters. Once GAM predetermines the weight matrices, the MPCT proceeds to search the prediction and control horizons using VNS.

p and $\mathbf{m}$ are integer parameters of the objective function J, Equation (1a–g). These parameters are converted into binary numbers of which the maximum sizes in bits are $H_p$ and $H_c$, respectively; for instance, if p is a $H_p=4$-bit variable, then it has a maximum prediction horizon size of 15.

The MPCT finds only one prediction horizon for the system and different control horizons for each manipulated variable. In this context, the algorithm takes the slowest dynamics to define the prediction horizon. If a linear transformation of the system is made and then diagonalized, slow eigenvalues will dominate the system’s dynamic modes. Moreover, since the process is a MIMO system with interactions between variables, the algorithm needs to simulate the system until the slowest dynamics are captured; therefore, only one prediction horizon is defined. Now, for each manipulated variable, it is possible to define a different control horizon to manipulate the process, minimize the computational cost, and improve the system’s dynamic response.

The selection of the control and prediction horizons within an MPC strategy depends largely on the dynamics of the system to be controlled; that is, it depends on whether the system is stable, unstable, oscillatory, non-minimal phase, etc. Intuitively, it can be noted that the design of an MPC controller in an unconstrained way must show a good performance. Therefore, if the desired performance is not achieved, this controller tuning will most likely not control the system with the active constraints.

To obtain a good selection of the MPC horizons, one should ask what is a well-posed optimization problem. To answer this question, one may start from the fundamental concept of an MPC controller, where the controller uses the system model (linear or nonlinear) to solve the objective function (with or without constraints) shown in Equation (1a–g). In this context, the MPC, in a given Pareto front, finds an optimal trajectory (open loop) to be applied in the control law. However, as stated before, only the first action is applied to the process because, in the next sampling time, there will be updated process measures that allow the correction of the trajectory, solving Equation (1a–g) again. This is known as the receding horizon [1]. However, if one only considers this first calculation, in $k=1$, and if the prediction and control horizons are poorly selected, the prediction of this first trajectory will differ significantly from the closed-loop behavior of the system when the receding horizon concept is applied, then the predictions do not make sense because the optimization does not represent what is really going to happen in the future.

Optimizing the objective function J, as shown in Equation (1a–g), will be especially useful if the trajectories are close to the response of the closed-loop system, both of which are calculated with the internal model of the controller. For this, the internal model of the MPC is taken, with the VNS algorithm establising a step reference, ${\mathbf{w}}_s\left(k\right)$, for the internal model. Finally, the controller algorithm is solved. With this solution it is possible to obtain the output response and the control action in a closed loop, $\mathbf{y}\left(k\right)$ and $\mathbf{u}\left(k\right)$, respectively, using the receding horizon concept and remembering that $\mathbf{u}\left(k\right)=\Delta \mathbf{u}\left(k\right)+\mathbf{u}(k-1)$. However, it is also possible to calculate the trajectories of the outputs and inputs of the system (open-loop responses) ${\mathbf{y}}_o\left(k\right|1)$ and ${\mathbf{u}}_o\left(k\right|1)$, respectively, which is the first optimization that the MPC made at the first sampling time.

These signals are shown in Figure 4 for a stable SISO system in three different scenarios with (a) $p=3$, $m=1$; (b) $p=5$, $m=2$; and (c) $p=20$, $m=15$, which compares the closed-loop behavior of the MPC controller, with a receding horizon, with the trajectory calculated at the first sampling time. One may note that ${\mathbf{u}}_o\left(k\right|1)$ is an $n_u\times m$ vector, so the last value is repeated to complete the simulation time, as one can see in the projection of ${\mathbf{u}}_o\left(k\right|1)$. In scenario (a), the output trajectory, ${\mathbf{y}}_o\left(k\right|1)$, is far from the closed-loop response, $\mathbf{y}\left(k\right)$, meaning that with only one control action and a small prediction horizon, the controller has a bad estimate trajectory at the first optimization step. It needs to correct the direction in the next sampling times. In scenario (b), ${\mathbf{y}}_o\left(k\right|1)$ is close to $\mathbf{y}\left(k\right)$, meaning that, with only two control actions and a small prediction horizon, the controller forecasts the correct trajectory in the first optimization step. It only needs to make a few corrections to achieve the setpoint reference in the subsequent sampling times. Finally, in scenario (c), ${\mathbf{y}}_o\left(k\right|1)$ matches to $\mathbf{y}\left(k\right)$ using a large prediction and control horizons, where the controller achieves a perfect prediction of the future behavior of the system. However, the optimization algorithm calculates a similar control action, ${\mathbf{u}}_o\left(k\right|1)$, from time 7 to 15. This means that the rate of change of the manipulated variable, $\Delta \mathbf{u}\left(k\right)$, tends to be zero, providing little information and increasing the computational cost of the MPC. Therefore, the best alternative is scenario (b), which presents a compromise between computational cost and a good prediction. This analysis is not valid for unstable open-loop systems.

The VNS algorithm must find the appropriate sizes for the prediction and control horizons to match both trajectories. The algorithm uses the first-descent direction with a first-order search, that is, modifying a single bit from the initial condition and solving Equation (7). When the algorithm does not find other solutions, a second-order and then third-order search are applied to escape from local minima. If the third-order search is executed and the algorithm does not find another solution, then the VNS method selects the horizons with the lowest cost found in its search.

$$\begin{array}{cc}\hfill \underset{p,\mathbf{m}}{\min }\{f_v\left({\mathbf{x}}_{dv}\right)=& \sum _{i=1}^{n_y}\left[\sum _{k=1}^{\varphi }\left({\left\{y_i\left(k\right)-y_{o_i}\left(k\right|1)\right\}}^2+{\left\{y_i^R\left(k\right)-y_i\left(k\right)\right\}}^2\right)\right]\hfill \\ \hfill & +p+\sum _{j=1}^{n_u}\sum _{k=1}^{m_j}{\displaystyle \frac{|u_{o_j}\left(1\right|1)|}{|u_{o_j}(k+1|1)-u_{o_j}\left(k\right|1)|}}\}\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \mathrm{Equation}\left(1\mathrm{a}\text{–}\mathrm{g}\right)\hfill \\ \hfill & u_{o_j}(k+1|1)\ne u_{o_j}\left(k\right|1)\hfill \\ \hfill & \mathbf{m}<p,\hfill \end{array}$$

(7)

where the first term of the objective function seeks to minimize the distance between the closed-loop, $y_i\left(k\right)$, and the $y_{oi}\left(k\right|1)$ trajectory of the output i. This term is used to establish the performance criteria desired by the user and can be used to ensure the robustness of the controller against model uncertainties by establishing more conservative dynamics. The second term seeks to minimize the distance between the reference trajectory, $y_i^R\left(k\right)$, and the closed-loop response, $y_i\left(k\right)$, and the last two terms of the function avoid the selection of large p and $\mathbf{m}$, respectively. One may note that this method seeks to avoid selecting a large control horizon in the last term as long as the rate of change in the denominator is significant. For instance, if the rate of change is close to zero, as in scenario (c) in Figure 4, this term is penalized. An illustrative algorithm of the VNS is presented in Algorithm 1 where $\dot{\mathbf{x}}$ is the process model (state-space representation), and ${\dot{\mathbf{x}}}^R$ is the state-space model for the reference trajectory.

Algorithm 1: VNS algorithm

Once the VNS algorithm is terminated, the MPCT executes the whole procedure again in an iteration loop, trying to improve the solution set. If the algorithm does not improve, it stops; otherwise, it continues until reaching the stopping criterion.

An illustrative algorithm of the MPCT is presented in Algorithm 2.

Algorithm 2: MPCT algorithm

Robust Stability Analysis

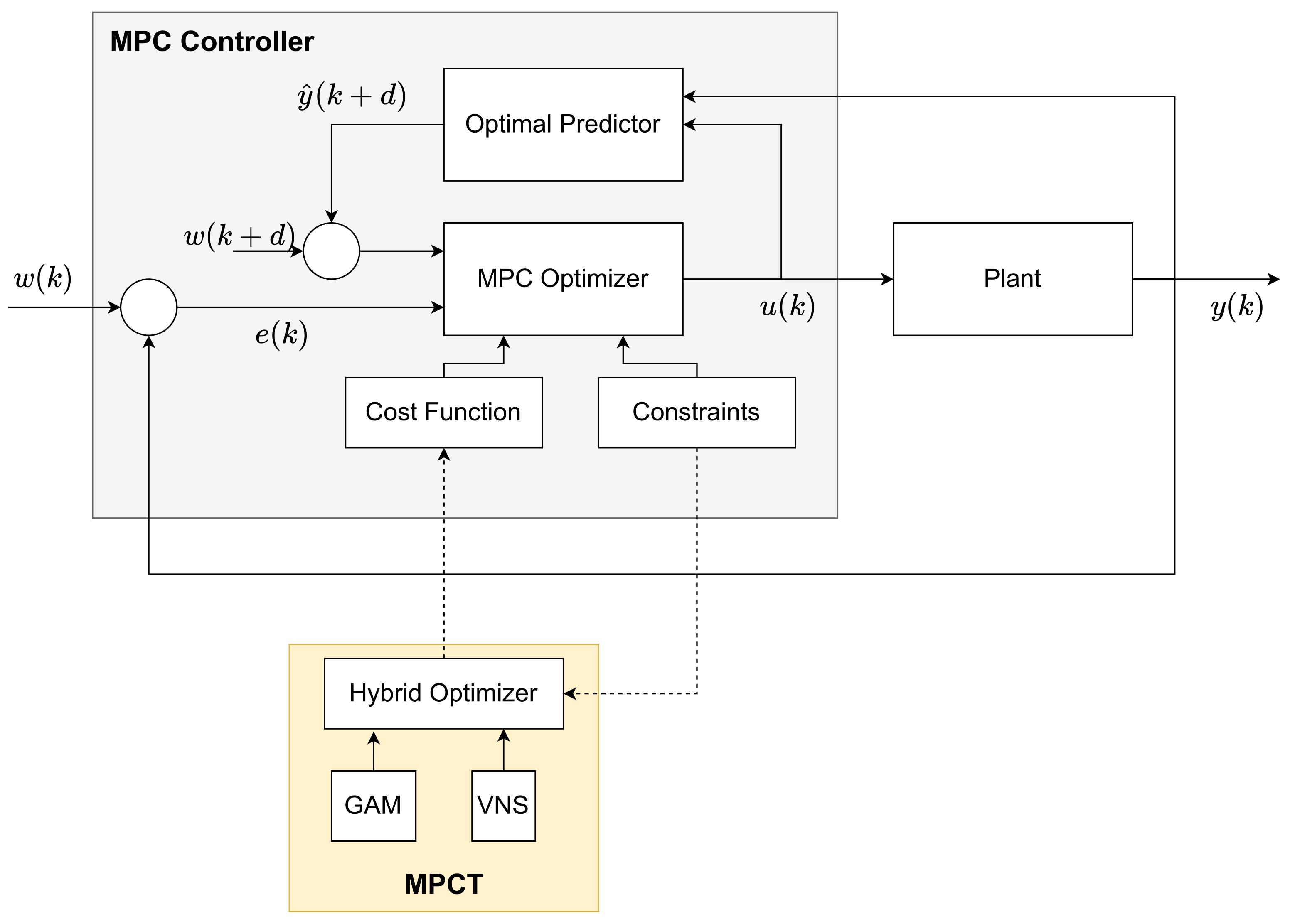
An important point in relation to tuning methods is performance/robustness requirements. Heuristic methods generally have pre-set adjustment criteria, whereas self-tuning methods are based on the desired response information [31]. Since two optimizers are working together, as shown in Figure 5, this implies that robustness is not an exclusive task of the tuning algorithm. The MPCT works in conjunction with the MPC controller, where the primarily responsible for dealing with the problem’s robustness is the optimizer of the MPC controller. In this context, if a fast tuning is required, the robustness project must be considered in the MPC formulation. However, to meet either the robustness or the performance criteria on the MPCT, the robustness in the tuning method will be explicitly considered.

To assure a robust method, the tuning parameters in this work can be adjusted in different ways since GAM and VNS algorithms use the internal model of the MPC: (i) it is possible to use the same robust formulation of the MPC in the MPCT to find the tuning parameters, e.g., through minimax optimization formulations in both algorithms; (ii) it is possible to estimate the tuning parameters under a worst-case control problem using a family of models that represent the dynamic behavior of the process, and finally; (iii) robustness can be considered through the result of a conservative performance since the MPCT algorithm employs a reference trajectory defined by the user.

Problem constraints are also considered by the tuning algorithm, limiting the search region of the controller parameters. In general, the same optimizer used in the controller is used within the optimization of the MPC tuning algorithm to include the problem constraints and guarantee robustness in the modeling of errors.

4. Simulation Case Studies

4.1. The Shell Heavy Oil Fractionator

A $3\times 3$ subsystem MIMO subsystem of the Shell Heavy Oil Fractionator (HOF) benchmark system presented in Maciejowski [32] was tuned to demonstrate the performance of the MPCT algorithm. For this case study, we selected a linear formulation of MPC, known as generalized predictive control (GPC). Naturally, any other linear formulation for this problem is possible.

The three inputs of the system, $u_1$, $u_2$, and $u_3$, are the top draw flow rate, the side draw flow rate, and the bottom reboiler heat duty, respectively. The three controlled outputs, $y_1$, $y_2$, and $y_3$, are the top end point composition, the side end point composition, and the bottom reboiler temperature, respectively. This system is represented by the following transfer functions:

$$\mathbf{G}\left(s\right)=\left[\begin{array}{ccc}{\displaystyle \frac{4.05+2.11{ϵ}_1}{50s+1}}{e}^{-27s}& {\displaystyle \frac{1.77+0.39{ϵ}_2}{60s+1}}{e}^{-28s}& {\displaystyle \frac{5.88+0.59{ϵ}_3}{50s+1}}{e}^{-27s}\\ \\ {\displaystyle \frac{5.396+3.29{ϵ}_1}{50s+1}}{e}^{-18s}& {\displaystyle \frac{5.72+0.57{ϵ}_2}{60s+1}}{e}^{-14s}& {\displaystyle \frac{6.90+0.89{ϵ}_3}{40s+1}}{e}^{-15s}\\ \\ {\displaystyle \frac{4.38+3.11{ϵ}_1}{33s+1}}{e}^{-20s}& {\displaystyle \frac{4.42+0.73{ϵ}_2}{44s+1}}{e}^{-22s}& {\displaystyle \frac{7.20+1.33{ϵ}_3}{19s+1}}\end{array}\right],$$

(8)

where ${ϵ}_i$ are the uncertainties in the gain model and the time constants are given in minutes.

The first step of the algorithm is to scale the process model using the following diagonal matrices: $\mathbf{L}=\mathrm{diag}[0.617;0.595;0.840]$ and $\mathbf{R}=\mathrm{diag}[1.0;0.416;0.622]$, which are found through the solution of Equation (A1). The scaled gain matrix for the nominal case is given by:

$$\mathbf{K}=\left[\begin{array}{ccc}2.4983& 0.4546& 2.2563\\ 3.2087& 1.4179& 2.5552\\ 3.6784& 1.5457& 3.7614\end{array}\right].$$

(9)

A zero-order hold discretization of the scaled process transfer function is used with a sampling period of $T_s=4$ min.

The MPCT parameters are set as: $p=255$ (8-bits), $\mathbf{m}=[15,15,15]$ (4-bits each), and $\varphi =400$.

The relative gain array (RGA) is used to select the input/output pairs of the HOF as $u_1:y_1$, $u_2:y_2$, and $u_3:y_3$. RGA is a classical method for determining the best input-output pairings for MIMO process control systems. Two reference trajectories for the HOF are established to demonstrate the desired performance and robustness of the MPC tuning parameters. Therefore, the two reference trajectories are commanded by first-order plus dead-time systems with static gain ${\mathbf{k}}^R=[1.0,1.0,1.0]$ and dead-time ${\theta }^R=[27.0,14.0,0.0]$. The difference between the two references is in the time constant. The first one, named case 1, has an aggressive dynamics with the time constant ${\tau }_{\mathbf{a}}^R=[5.0,9.0,5.7]$. The second one, named case 2, has a conservative dynamics with the time constant ${\tau }_{\mathbf{c}}^R=[30.0,30.0,30.0]$.

A Matlab routine fgoalattain was used for the GAM optimization problem. The termination tolerance for the function value, the constraint violation, and the first-order optimality were set to ${10}^{-6}$. The relative weight for GAM was set as $\omega =[0.40,0.05,0.55]$. The problem described here was solved using an Intel^® Core i7 8750H 2.2GHz, 16 GB RAM computer.

Table 1. Tuning parameters.

MPCT Scenario	${\mathit{x}}_{\mathbf{dv}}$
case 1	$[\underset{p}{\underbrace{34}},\underset{\mathbf{m}}{\underbrace{2,2,3}},\underset{\mathrm{diag}\left(\mathbf{Q}\right)}{\underbrace{0.38,0.08,0.12}},\underset{\mathrm{diag}\left(\mathbf{W}\right)}{\underbrace{0.075,0.00036,0.61}}]$
case 2	$[\underset{p}{\underbrace{8}},\underset{\mathbf{m}}{\underbrace{2,2,3}},\underset{\mathrm{diag}\left(\mathbf{Q}\right)}{\underbrace{0.29,0.10,0.08}},\underset{\mathrm{diag}\left(\mathbf{W}\right)}{\underbrace{0.27,0.02,2.28}}]$

presents the solution of the MPCT tuning procedure for the two scenarios.

The required computational time was 35 min for case 1 and 40 min for case 2. Tuning the MPC controller for the HOF benchmark was reported in [3,14], in which the computational time required for the lexicographic tuning technique optimization method was 4.27 h, for the compromise tuning technique it was 53 min, and for the normal boundary intersection it was 20.1 h.

Figure 6, Figure 7 and Figure 8 show the resulting trajectories for the MPCT, where one may notice that the VNS algorithm estimated an adequate size for prediction and control horizons since the closed-loop response, $\mathbf{y}\left(k\right)$, is as close as possible to the output trajectory at the first optimization, ${\mathbf{y}}_o\left(k\right|1)$, in both scenarios obtaining small values for both horizons.

The same setpoint has been configured for the GAM algorithm and the plant to consider the internal interaction between the variables of the MIMO system. The lower and upper bounds of the input and the minimum and maximum input increments of the MPC controller are ${\mathbf{u}}_{\mathbf{min}}=[-0.5,-0.5,-0.5]$, ${\mathbf{u}}_{\mathbf{max}}=[0.5,0.5,0.5]$, $\Delta {\mathbf{u}}_{\mathbf{min}}=[-0.05,-0.05,-0.05]$, and $\Delta {\mathbf{u}}_{\mathbf{max}}=[0.05,0.05,0.05]$. The setpoints are changed to $\mathbf{w}=[0.2,0.2,0.2]$ at 70 min, then to $\mathbf{w}=[0.0,0.4,0.1]$ at 315 min, then to $\mathbf{w}=[0.1,0.3,0.0]$ at 800 min, and finally to $\mathbf{w}=[0.0,0.0,0.0]$ at 1600 min, with unknown pulse disturbances of intensity −0.05 on input $u_1$ from 1100 min to 1120 min, and intensity 0.1 on input $u_2$ from time 1400 min to 1420 min. Figure 9, Figure 10, Figure 11 and Figure 12 show the behavior of the MPC with tuning parameters shown in Table 1 for both cases. Two scenarios are considered for every case: (i) the nominal case with ${ϵ}_1={ϵ}_2={ϵ}_3=0$ and (ii) the modelling error case with ${ϵ}_1={ϵ}_2=0.2$, and ${ϵ}_3=0.3$.

Both tunings seek to adjust the response with the reference trajectory to attend to the performance established by the user in the nominal case, as exhibited in Figure 9 and Figure 11. These dynamics are especially evident in the first change of the setpoint at 70 min, at which point the response complies with the established accommodation time. However, it is also fulfilled at other simulation points, such as at 800 min. In this case study, the setpoint changes were intentionally set in opposite directions, as shown in Figure 9 and Figure 11 at 315 min, to increase the influence of the interaction between variables. At the points where the interaction is strong, the response cannot adjust to the reference trajectory; however, it manages to track the setpoint without an offset. Moreover, the MPC controller rejects the load of unknown pulse disturbances on the three manipulated variables faster than the tracking accommodation time. Additionally, it is observed that $y_3$, which has the minimal effective time delay, is the variable that suffers most with the effect of the interactions of the MIMO system caused by $y_1$ and $y_2$. Therefore, this variable presents the highest overshoot in the reference changes, mainly if these changes are also applied to the other two variables simultaneously.

It is also possible to observe the robustness of the tuning parameters, which are directly related to the performance desired by the user. The robustness is guaranteed only for case 2 because it establishes a conservative desired dynamics compared to case 1. The MPCT algorithm maintains robustness in case 2 because it searches for the weighting matrices of the objective function using the GAM optimization algorithm for a conservative dynamic that presents a slow change and a moderate control action. This concept can be extended to a practical level, where a family of models can represent the real process, so the tuning parameters can be calculated using the worst case.

It is important to remember that robustness is not the exclusive task of the MPCT optimization algorithm. Rather, it can work together with the MPC control algorithm to obtain better results in a robust configuration. To demonstrate this, Figure 13, Figure 14, Figure 15 and Figure 16 show the dynamic behavior of the two cases, further increasing the modeling error for ${ϵ}_1={ϵ}_2={ϵ}_3=1$, using a robust version of the GPC control. This robust version can be achieved by using a T filter in the controlled auto-regressive integrated moving average model or using a low-pass filter in the optimal predictor stage, known as DTC-GPC [33,34]. For this case, DTC-GPC is implemented with a discrete second-order low-pass filter, as shown in Equation (10), using $\alpha =0.85$ for case 1 and $\alpha =0.5$ for case 2:

$$F_{r_i}\left(z\right)={\displaystyle \frac{{(1-\alpha )}^2}{{(z-\alpha )}^2}}.$$

(10)

The implementation of a robust control method allows the stabilization of both cases, even with a greater modelling error. The user must establish a compromise between performance and robustness. For case 1, the desired dynamics are very aggressive; therefore, it is impossible to meet this specification in the robust control project without sacrificing the system’s stability. In case 2, the accommodation time is close to the desired trajectory, excluding the high interaction sections of the MIMO system; however, the high degradation of the model prevents a similar behavior to that shown in the nominal case.

In the cases presented above, the tuning parameters of the MPCT are evaluated under scenarios of model uncertainty, which contribute to the robustness of the proposed method.

In

Table 2. Performance indices for the Shell Heavy Oil Fractionator.

	${\mathit{y}}_1$	${\mathit{y}}_2$	${\mathit{y}}_3$	Total
ITAE
Nominal case 1	28,941.40	39,052.69	15,736.18	83,730.28
Nominal case 2	16,616.41	20,049.39	20,999.08	57,664.88
Robust case 1	53,558.08	72,581.68	48,516.48	17,4656.25
Robust case 2	22,603.27	30,625.79	17,230.78	70,459.85
IAE
Nominal case 1	32.24	43.03	17.82	93.10
Nominal case 2	17.86	23.98	21.91	63.76
Robust case 1	64.13	95.81	68.32	228.27
Robust case 2	31.91	45.44	27.27	104.63

, the closed-loop responses are compared with the desired reference trajectories, defined by the user for both cases using two performance indices: the integral time-weighted absolute error (ITAE) and the integral absolute error (IAE). For this comparison, we selected the nominal and robust control cases. Small values indicate better performance concerning the dynamics desired by the user. A general analysis, observing the total values, shows that case 2 has better performance than case 1 because the ITAE and IAE criteria present smaller values in case 2 than in case 1. For the nominal case, this is true in every single variable except in $y_3$ in the ITAE criterion, where the closed-loop was close to the fast reference trajectory. For the robust control, case 2 shows better performance in both ITAE and IAE criteria. This is because case 2 was designed to deal with uncertainties, so the desired trajectory is reasonable. The algorithm can match the closed-loop response with the desired trajectory given by the user and reject the load disturbances.

4.2. The Van de Vusse Reactor

A nonlinear continuously stirred tank reactor conducting the well-known Van de Vusse reactions was chosen to test the behavior of the MPC controller using the tuning proposed in this work. In this case, we selected a nonlinear formulation of MPC (NMPC) to control the system.

The Van de Vusse scheme ($A\stackrel{k_1}{\to }B\stackrel{k_2}{\to }C$ and $2A\stackrel{k_3}{\to }D$) comprises two reactions of the reactant A, producing the desired product B and to the undesired byproducts C and D [35].

The reaction rates parameters $k_i$, $i=1,2,3$ depend on the temperature, T, and they are represented by the Arrhenius equation:

$$\begin{array}{c}\hfill k_i\left(T\right)=k_{i0}exp\left({\displaystyle \frac{-E_i/R}{T{(}^{\circ }\mathrm{C})+273.15}}\right),\end{array}$$

(11)

where $E_i$, $i=1,2,3$, are the activation energies of the three reactions and R is the universal gas constant.

The process is described by the non-adiabatic model, represented by the following mass and energy balance equations in the reactor:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{C}_A}{dt}}={\displaystyle \frac{F}{V}}(C_{Af}-C_A)-k_1\left(T\right)C_A-k_3\left(T\right)C_A^2,\end{array}$$

(12)

$$\begin{array}{c}\hfill {\displaystyle \frac{d{C}_B}{dt}}=-{\displaystyle \frac{F}{V}}{C}_B+k_1\left(T\right)C_A-k_2\left(T\right)C_B,\end{array}$$

(13)

$$\begin{array}{cc}\hfill \frac{dT}{dt}=& {\displaystyle \frac{1}{\rho C_p}}\left[k_1\left(T\right)C_A(-\Delta H_{RAB})+k_2\left(T\right)C_B(-\Delta H_{RBC})+\right.\hfill \\ \hfill & \left.k_3\left(T\right)C_A^2(-\Delta H_{RAD})\right]+{\displaystyle \frac{F}{V}}(T_0-T)+{\displaystyle \frac{K_w{A}_R}{\rho C_{p}V}}(T_k-T),\hfill \end{array}$$

(14)

where the concentration of A in the reactor and in the feed are, respectively, $C_A$ and $C_{Af}$; $C_B$ is the desired output of the concentration of B; the manipulated inputs are the dilution rate, $F/V$, and the reactor jacket temperature, $T_k$; V is the constant reactor volume; $T_0$ is the feed temperature; $\rho$ is the liquid density; $C_p$ is the heat capacity. $Q=K_w{A}_R(T-T_k)$ is the heat transferred from the reactor to the jacket, where $K_w$ is the heat transfer coefficient and $A_R$ is the surface area for heat transfer; reaction enthalpies are given by $(-\Delta H_{RAB}),(-\Delta H_{RBC}),(-\Delta H_{RAD})$.

The parameter values of the system were obtained from Trierweiler [36] and are presented in

Table 3. Van de Vusse parameters.

Parameters	Value	Unit
$k_{10}$	$1.287\times {10}^{12}$	${\mathrm{h}}^{-1}$
$k_{20}$	$1.287\times {10}^{12}$	${\mathrm{h}}^{-1}$
$k_{30}$	$9.043\times {10}^9$	$\mathrm{L}/\left(\mathrm{mol}\mathrm{h}\right)$
$-E_1/R$	$-9758.3$	$\mathrm{K}$
$-E_2/R$	$-9758.3$	$\mathrm{K}$
$-E_3/R$	$-8560.0$	$\mathrm{K}$
$(-\Delta H_{RAB})$	$-4.20$	$\mathrm{kJ}/\mathrm{mol}$
$(-\Delta H_{RBC})$	$11.00$	$\mathrm{kJ}/\mathrm{mol}$
$(-\Delta H_{RAD})$	$41.85$	$\mathrm{kJ}/\mathrm{mol}$
$\rho$	$0.9342$	$\mathrm{kg}/\mathrm{L}$
$C_p$	$3.01$	$\mathrm{kJ}/\left(\mathrm{kg}\mathrm{K}\right)$
$K_w$	$4032.0$	$\mathrm{kJ}/\left(\mathrm{h}\mathrm{K}{\mathrm{m}}^2\right)$
$A_R$	$0.215$	${\mathrm{m}}^2$
V	10	$\mathrm{L}$
$T_k$	$128.95$	${}^{\circ }\mathrm{C}$
$T_0$	$130.0$	${}^{\circ }\mathrm{C}$
$C_{Af}$	$5.10$	$\mathrm{mol}/\mathrm{L}$

.

The two system inputs, $u_1$ and $u_2$, are the dilution rate $F/V$ and the reactor jacket temperature $T_k$, respectively. The two controlled outputs, $y_1$ and $y_2$, are the concentration in $C_B$ and the reactor temperature T, respectively. The input/output variable pairs of the Van de Vusse reactor were established as $u_1$:$y_1$ and $u_2$:$y_2$. The NMPC sampling period is set to $T_s=0.05$ h. The prediction horizon was set as $p=32$ (5-bits), the control horizon was set as $\mathbf{m}=[7,7]$ (3-bits each) and the tuning horizon was set as $\varphi =60$.

To show the competitive objectives of the GAM formulation presented in Equation (5), Figure 17 depicts the compromise optimization results in the Pareto frontier for the Van de Vusse problem.

Two cases for the reference trajectory are also considered here, governed by first-order systems, where the static gains are ${\mathbf{k}}^R=[1,1]$ and the two time constants are ${\tau }_{\mathbf{a}}^R=[0.05,0.0875]$ hours and ${\tau }_{\mathbf{c}}^R=[0.3,0.4]$ hours for the aggressive and conservative dynamics, respectively.

One may note that the orders of magnitude between the concentration and the temperature are different; therefore, Equation (A2) is used to scale the variables between 0 and 1. The relative weight for the GAM was set as $\mathit{\omega }=[1,1]$. The step references for the VNS algorithm are set as ${\mathbf{w}}_s=[0.1,4]$ from the steady-state.

Table 4. Tuning parameters for Van de Vusse reactor.

MPCT Scenario	${\mathit{x}}_{\mathbf{dv}}$
case 1	$[\underset{p}{\underbrace{15}},\underset{\mathbf{m}}{\underbrace{2,2}},\underset{\mathrm{diag}\left(\mathbf{Q}\right)}{\underbrace{1,1}},\underset{\mathrm{diag}\left(\mathbf{W}\right)}{\underbrace{1\times {10}^{-5},1\times {10}^{-5}}}]$
case 2	$[\underset{p}{\underbrace{14}},\underset{\mathbf{m}}{\underbrace{3,2}},\underset{\mathrm{diag}\left(\mathbf{Q}\right)}{\underbrace{0.484,1.220}},\underset{\mathrm{diag}\left(\mathbf{W}\right)}{\underbrace{6.050,1.44\times {10}^{-4}}}]$

presents the solution of the tuning procedure for both cases.

The required computational time was 7 min for case 1 and 140 min for case 2. In Figure 18 and Figure 19, it is possible to see the approximation of the closed-loop response, $\mathbf{y}\left(k\right)$, with the output trajectory at the first optimization, ${\mathbf{y}}_o\left(k\right|1)$, resulting in a suitable horizon size.

In this case study, the controlled variables are affected by measurement noise and unknown pulse disturbances with an intensity of $-5{}^{\circ }\mathrm{C}$ on input $u_2$ from 6 h to 6.25 h. The response of the tuning of the MPCT on the NMPC can be seen in Figure 20, Figure 21, Figure 22 and Figure 23. The reference for $y_1$ changes from $0.9052\mathrm{mol}/\mathrm{L}$ to $1.0\mathrm{mol}/\mathrm{L}$ at 0.3 h and $y_2$ changes from $134.95{}^{\circ }\mathrm{C}$ to $140{}^{\circ }\mathrm{C}$ at 1.85 h. Additionally, constraints on the process inputs of $0.1{\mathrm{h}}^{-1}\le {\mathrm{u}}_1\le 140{\mathrm{h}}^{-1}$ and $90{}^{\circ }\mathrm{C}\le {\mathrm{u}}_2\le 200{}^{\circ }\mathrm{C}$ are established.

Both tunings have close dynamics to the desired reference trajectory established by the user. In both cases, the control is capable of dealing with the noise present in the controlled variables and the load disturbance. An analysis of the performance indices presented in

Table 5. The performance indices for the Van de Vusse reactor.

	${\mathit{y}}_1$	${\mathit{y}}_2$	Total
ITAE
Case 1	0.05470	5.4129	5.4676
Case 2	0.1724	14.6038	14.7762
IAE
Case 1	0.01656	1.2382	1.2548
Case 2	0.05818	4.347	4.4052

shows that the tuning in case 1 exhibits better performance than that in case 2, reaching the setpoint quickly and guaranteeing the proper regulation of the variables. As the disturbance rejection dynamics of the NMPC in case 1 are faster, the indices associated to it are generally better.

5. Conclusions

A tuning method for an MPC based on a hybrid optimization approach was proposed. The main idea of the method was to match the closed-loop behavior and a predefined reference trajectory using a sequential optimization algorithm to determine the weight matrices and the prediction and control horizons of the MPC objective function. This procedure demonstrated desirable behavior, presenting a satisfactory closed-loop performance and guaranteeing a robust tuning against modeling errors or measurement noise.

One of the principal characteristics of the MPCT tuning method is to consider a single prediction horizon and all the control horizons of the manipulated variables in the optimization algorithm. The cost function uses the concept of the receding horizon of the MPC controller. In this case, we aimed for the controller optimizations to be as close as possible to the real trajectory of the controlled variables. This helps to obtain a better estimate of the horizon sizes, allowing the controller to move in the best direction to obtain the control law within each given period of time.

Three different MPC formulations were employed in case studies to illustrate the effectiveness of the tuning algorithm. It was shown that the algorithm has a low computational cost in finding the MPC tuning parameters and presents versatility, enabling it to adapt to the desired trajectory defined by the user. Structured parametric mismatches were included in the case studies, and tuning results acquired using the MPC showed satisfactory results according to the users’ specifications.