Research on Fault Tree Reconstruction Based on Contingency
Abstract
1. Introduction
2. Analysis of the Construction Process of a Probability Accident Tree
2.1. Problems in the Existing Fault Tree
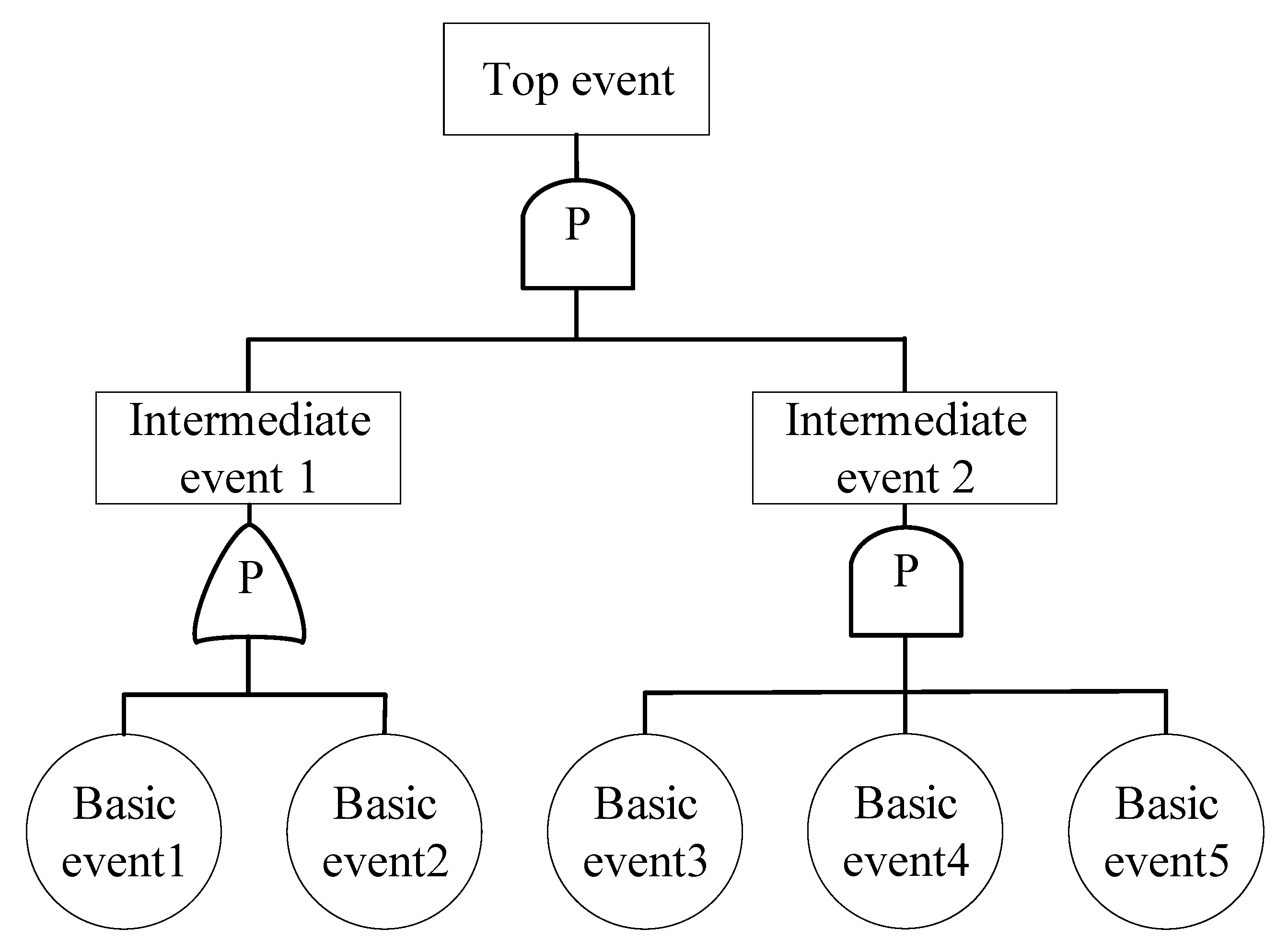
2.2. Fault Tree Reconstruction
2.2.1. Probability AND Gate
2.2.2. Probability OR Gate
2.2.3. Probability Accident Tree
3. Improvement of the Quantitative Calculation Method of Fault Trees
3.1. Improvement of the Quantitative Calculation Method
3.2. Application of the Probability Fault Tree
4. Conclusions
- (1)
- Through the analysis of typical collision accidents, the shortcomings of the existing FTA are analyzed, and the concept of a probabilistic FTA is innovatively proposed to enrich accident tree analysis. The concepts of probability AND and OR gates are presented and applied to the accident tree.
- (2)
- The quantitative calculation method of traditional FTA essentially exaggerates the probability of an accident. Therefore, the traditional FTA has been reformed and the probability accident tree is compiled, and the quantitative calculation method of probability FTA is proposed.
- (3)
- The proposal of probabilistic FTA has important practical significance and theoretical value for guiding safety management. It provides a new idea for the study of top event probability in traditional FTA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xin, S.; Zhang, L.; Jin, X.; Zhang, Q. Reconstruction of the Fault Tree Based on Accident Evolution. Process Saf. Environ. Prot. 2019, 121, 307–311. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.; Liang, W. An Accident Causation Analysis and Taxonomy (ACAT) Model of Complex Industrial System from both System Safety and Control Theory Perspectives. Saf. Sci. 2017, 92, 94–103. [Google Scholar] [CrossRef]
- Liu, P.; Yang, L.; Gao, Z.; Li, S.; Gao, Y. Fault Tree Analysis Combined with Quantitative Analysis for High-Speed Railway Accidents. Saf. Sci. 2015, 79, 344–357. [Google Scholar] [CrossRef]
- Lippiello, D.; Degan, G.A.; Pinzari, M. A Novel Fault Tree Analysis Approach to Investigate Uncommon Accidents in Quarries: A Case Study. Int. J. Saf. Secur. Eng. 2018, 8, 451–462. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Li, S.G.; He, X. Fault Tree Analysis of “Mistakes, Forgetfulness, and Negligence” Accidents in ATC. Appl. Mech. Mater. 2011, 1280, 924–929. [Google Scholar] [CrossRef]
- Jafari, M.J.; Pouyakian, M.; Khanteymoori, A.; Hanifi, S.M. Reliability Evaluation of Fire Alarm Systems Using Dynamic Bayesian Networks and Fuzzy Fault Tree Analysis. J. Loss Prev. Process Ind. 2020, 67, 104229. [Google Scholar] [CrossRef]
- Lee, W.S.; Grosh, D.L.; Tillman, F.A.; Lie, C.H. Fault Tree Analysis, Methods, and Applications-A Review. IEEE Trans. Reliab. 2009, R-34, 194–203. [Google Scholar] [CrossRef]
- Khan, F.I.; Iqbal, A.; Ramesh, N.; Abbasi, S.A. SCAP: A New Methodology for Safety Management Based on Feedback from Credible Accident-Probabilistic Fault Tree Analysis System. J. Hazard. Mater. 2001, 87, 23–56. [Google Scholar] [CrossRef]
- Nicolae, F.; Cotorcea, A.; Ristea, M.; Atodiresei, D. Human Reliability Using the Fault Tree Analysis. A Case Study of a Military Accident Investigation. Int. Conf. Knowl.-Based Organ. 2016, 22, 215–219. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, X.; Xia, S.; Cao, Q. Incident Tree Model and Incident Tree Analysis Method for Quantified Risk Assessment: An In-Depth Accident Study in Traffic Operation. Saf. Sci. 2010, 48, 1248–1262. [Google Scholar] [CrossRef]
- Hua, W.; Chen, J.; Qin, Q.; Wan, Z.; Song, L. Causation Analysis and Governance Strategy for Hazardous Cargo Accidents at Ports: Case Study of Tianjin Port’s Hazardous Cargo Explosion Accident. Mar. Pollut. Bull. 2021, 30, 542–555. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Tang, S.; Li, Z.; Fang, X. Dynamic Study of Critical Factors of Explosion Accident in Laboratory Based on FTA. Saf. Sci. 2020, 130, 104877. [Google Scholar] [CrossRef]
- Jafarian, E.; Rezvani, M.A. Application of fuzzy fault tree analysis for evaluation of railway safety risks: An evaluation of root causes for passenger train derailment. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2012, 226, 14–25. [Google Scholar] [CrossRef]
- Chu, Z.; Yang, Z.; Peng, M.; Sun, W. Research of Security Analysis Based on Subjective Bayesian Networks; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- My, A.; Skb, C.; Mw, B. Uncertainty handling in fault tree based risk assessment: State of the art and future perspectives. Process Saf. Environ. Prot. 2019, 131, 89–104. [Google Scholar]
- Cao, Q. Safety System Engineering; China Coal Industry Press: Beijing, China, 2010. [Google Scholar]
- Khare, V.; Nema, S.; Baredar, P. Reliability analysis of hybrid renewable energy system by fault tree analysis. Energy Environ. 2019, 30, 542–555. [Google Scholar] [CrossRef]
- Cho, B.H.; Yum, B.; Kim, S. Calculation of Top Event Probability of Fault Tree using BDD. J. Korea Inst. Inf. Commun. Eng. 2016, 20, 654–662. [Google Scholar] [CrossRef][Green Version]
- Fei, P.; Nali, S. Fire Hazard Analysis of Student Dormitory in a University Based on Accident Tree. J. Jilin Univ. Chem. Technol. 2019, 36, 46–50. [Google Scholar]
- Zhang, X. Exploration and Prevention of University Student Dormitory Fire Laws Based on Accident Tree Analysis. Smart City 2019, 5, 3. [Google Scholar]

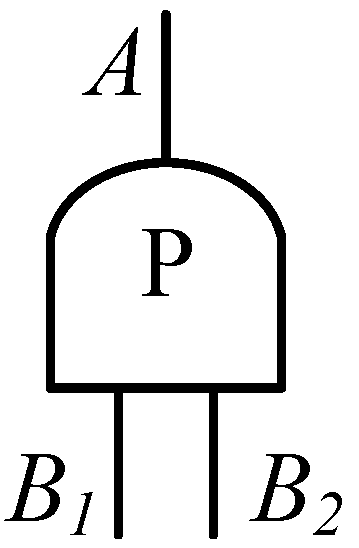

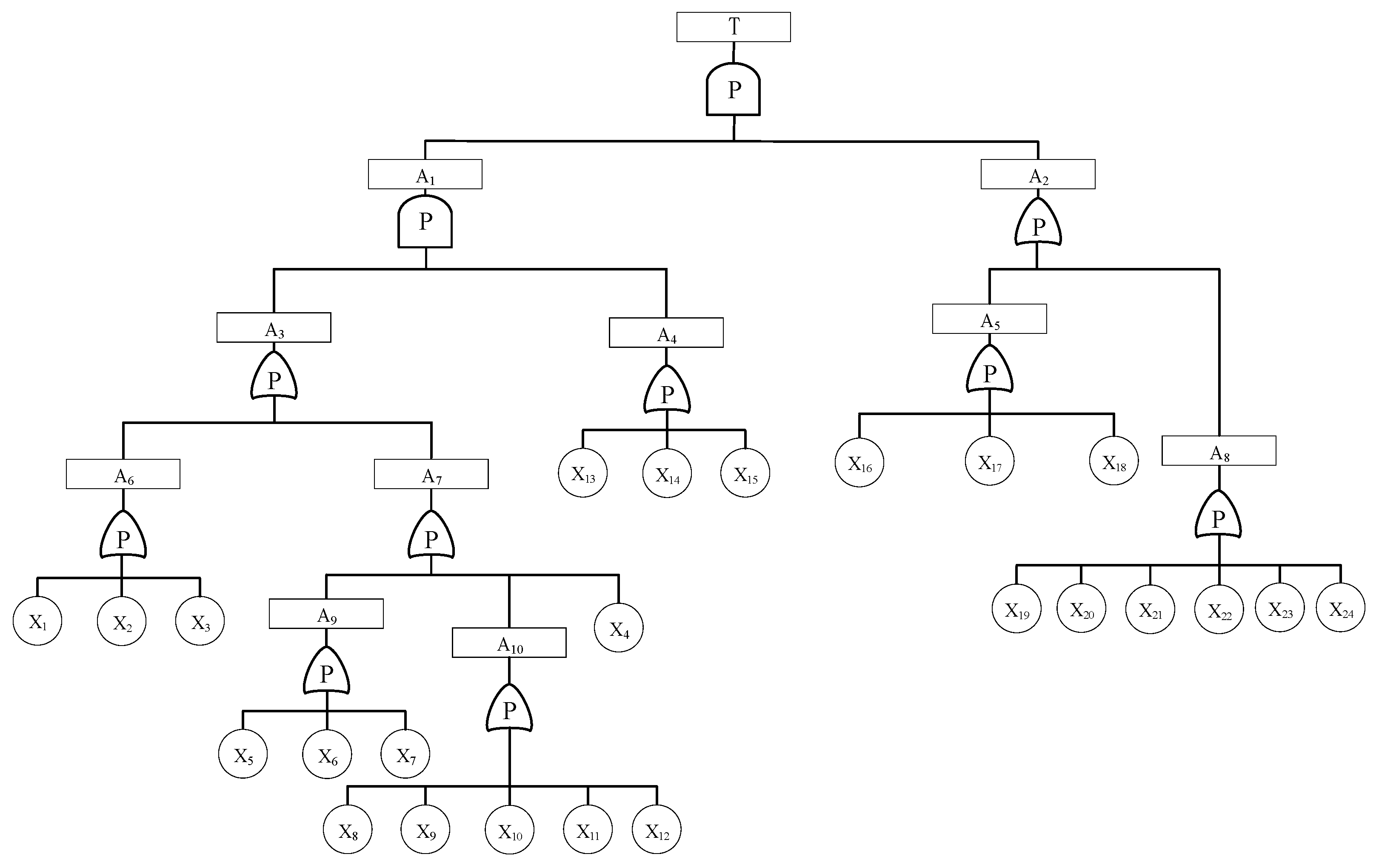
| Symbol | Event Name | Symbol | Event Name | Symbol | Event Name |
|---|---|---|---|---|---|
| T | Collision accident | X1 | Inability to dodge | X12 | Poor lighting for driving at night |
| A1 | Insufficient vertical spacing | X2 | Illegal turn | X13 | Bad mood |
| A2 | Speed too fast | X3 | Violation of giving way to an oncoming vehicle | X14 | Drive after drinking |
| A3 | Misjudgment | X4 | Overtaking in violation of regulations | X15 | Poor health |
| A4 | Observation error | X5 | Illegal parking | X16 | Poor road traffic conditions |
| A5 | Operation error | X6 | Pursuit of stimulation | X17 | Bad brake performance or too much wear |
| A6 | Braking problem | X7 | Lack of knowledge and experience | X18 | Lack of sleep |
| A7 | Poor sight | X8 | Not enough sight distance | X19 | Driving too long |
| A8 | Inattention | X9 | Limited driving skills | X20 | Poor temperature ventilation |
| A9 | Poor braking | X10 | Brake failure | ||
| A10 | Fatigue driving | X11 | Impact of rain, snow, and fog |
| Symbol | Event Name | Probability Value | Symbol | Event Name | Probability Value |
|---|---|---|---|---|---|
| T | Dormitory fire accident | A6 | Open fire source | ||
| A1 | On fire | A7 | Electric fire source | ||
| A2 | Out of control | A8 | Firefighting facilities not working | ||
| A3 | Fire source | A9 | Line | ||
| A4 | Combustible | A10 | Electrical appliances | ||
| A5 | Rescue not timely | ||||
| X1 | Smoking | 0.02 | X13 | Clothes, quilt | 0.02 |
| X2 | Alcohol stove | 0.05 | X14 | Textbook, desk | 0.03 |
| X3 | Burning mosquito repellent incense | 0.02 | X15 | Other flammable materials | 0.02 |
| X4 | Thunder | 0.03 | X16 | Alarm system not working | 0.05 |
| X5 | Connecting wires without permission | 0.05 | X17 | Not found in time | 0.03 |
| X6 | Wires short-circuited | 0.02 | X18 | At a loss | 0.03 |
| X7 | Line aging | 0.03 | X19 | Fire extinguishers in short supply | 0.05 |
| X8 | Use of illegal electrical appliances | 0.06 | X20 | Insufficient input in fire hydrants | 0.01 |
| X9 | Use of inferior electrical appliances | 0.05 | X21 | Unreasonable configuration of the automatic sprinkler system | 0.02 |
| X10 | Use of an electric heater | 0.03 | X22 | Lack of knowledge of how to use a fire extinguisher | 0.03 |
| X11 | Use of an electric blanket | 0.03 | X23 | Insufficient water supply for fire hydrants | 0.03 |
| X12 | Use of hand warmers | 0.02 | X24 | Failure of the automatic sprinkler system | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, S.; Zhu, X.; Liu, S.; Guo, J. Research on Fault Tree Reconstruction Based on Contingency. Processes 2022, 10, 427. https://doi.org/10.3390/pr10020427
Xin S, Zhu X, Liu S, Guo J. Research on Fault Tree Reconstruction Based on Contingency. Processes. 2022; 10(2):427. https://doi.org/10.3390/pr10020427
Chicago/Turabian StyleXin, Song, Xiaozhen Zhu, Shangxiao Liu, and Jianghui Guo. 2022. "Research on Fault Tree Reconstruction Based on Contingency" Processes 10, no. 2: 427. https://doi.org/10.3390/pr10020427
APA StyleXin, S., Zhu, X., Liu, S., & Guo, J. (2022). Research on Fault Tree Reconstruction Based on Contingency. Processes, 10(2), 427. https://doi.org/10.3390/pr10020427






