Influence of Sparger Type on Mass Transfer in a Pilot-Scale Internal Loop Airlift Reactor
Abstract
:1. Introduction
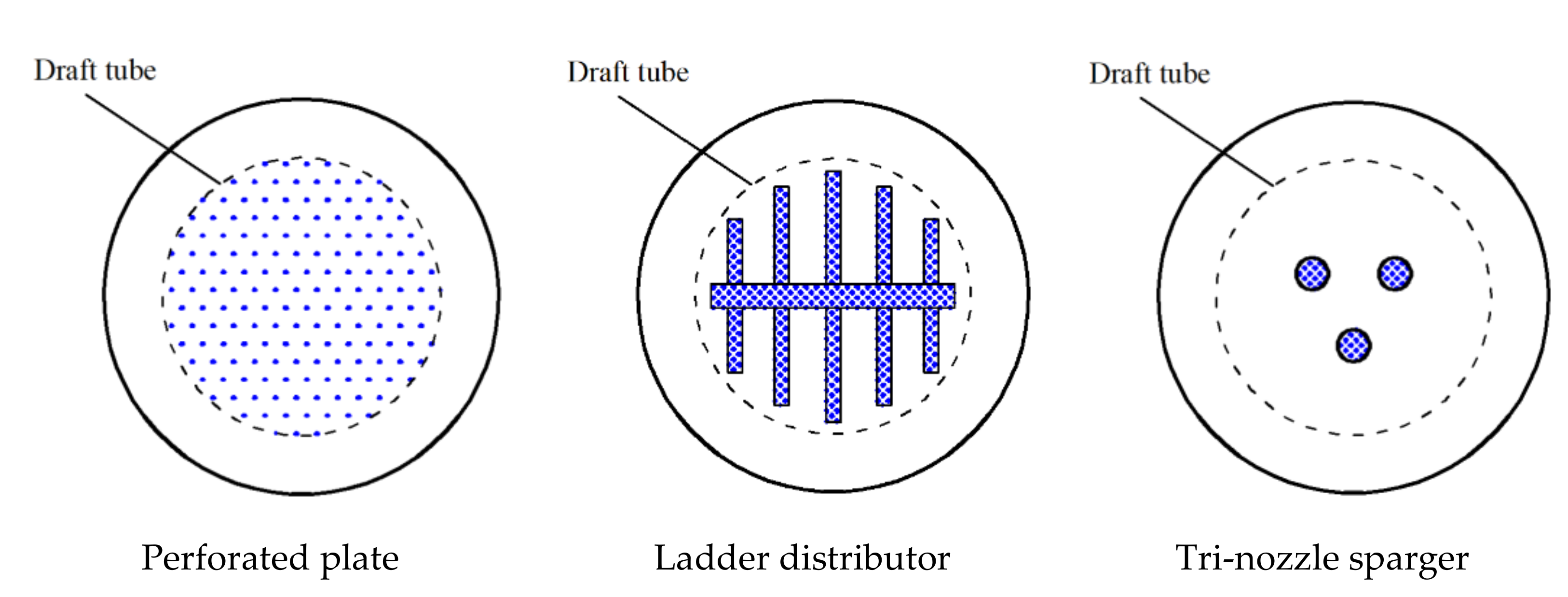
2. Experimental Apparatus and Methods
3. Results and Discussion
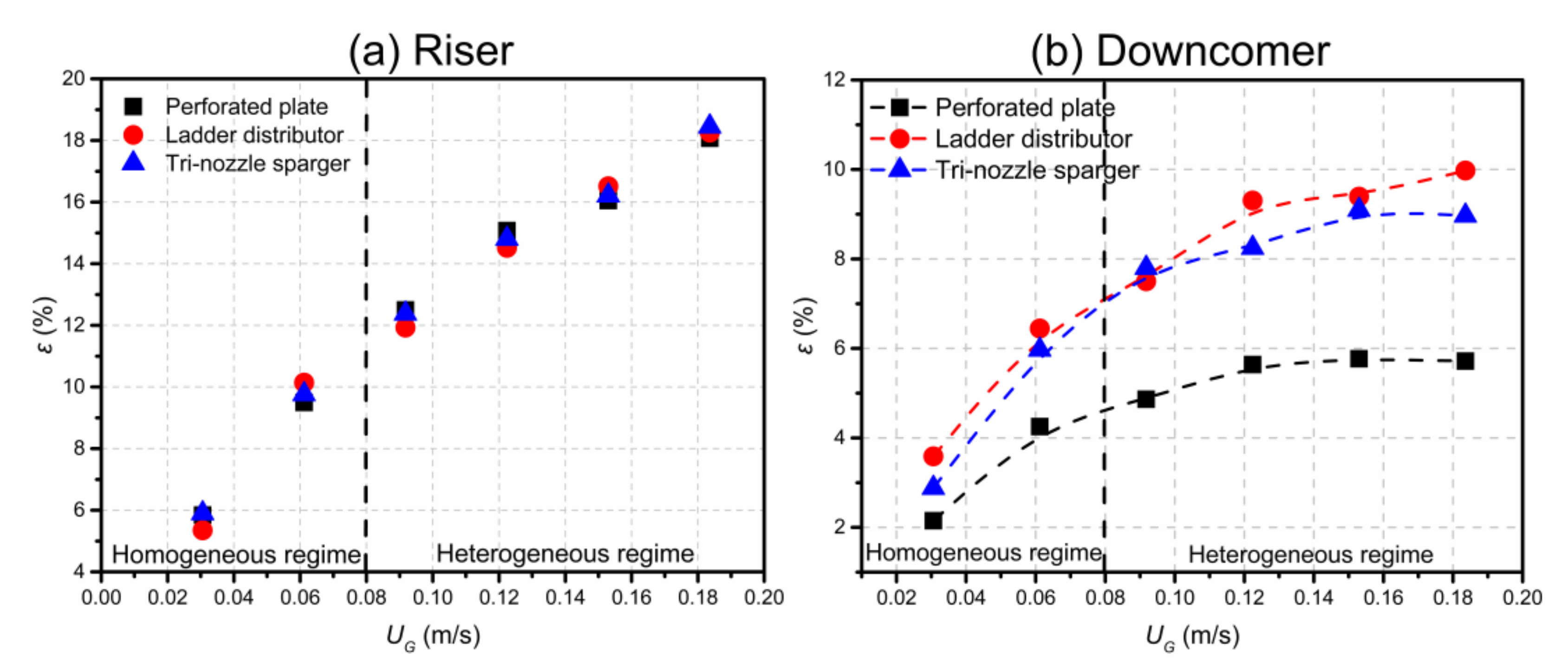
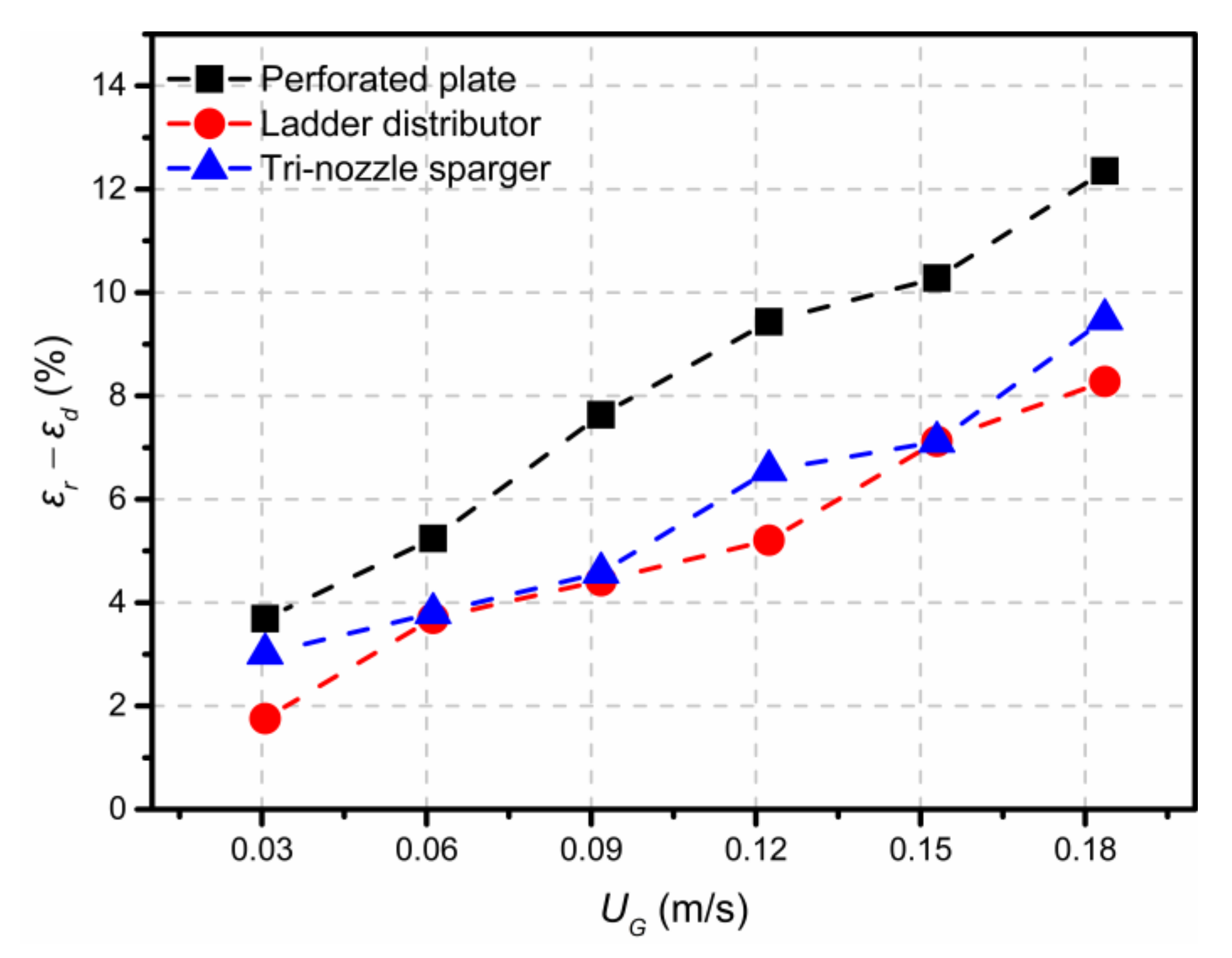
3.1. Gas Holdup
3.2. Circulating Liquid Velocity
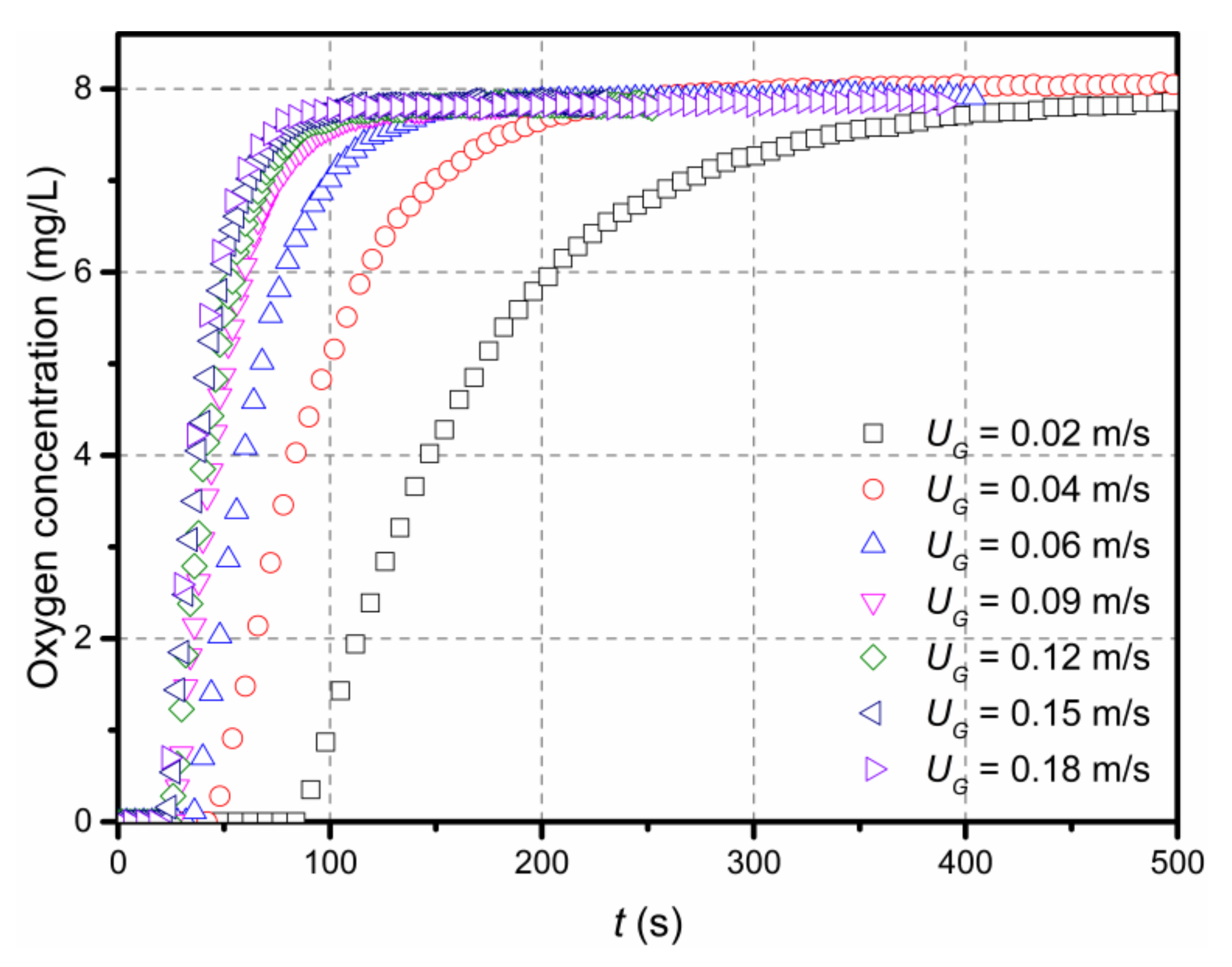
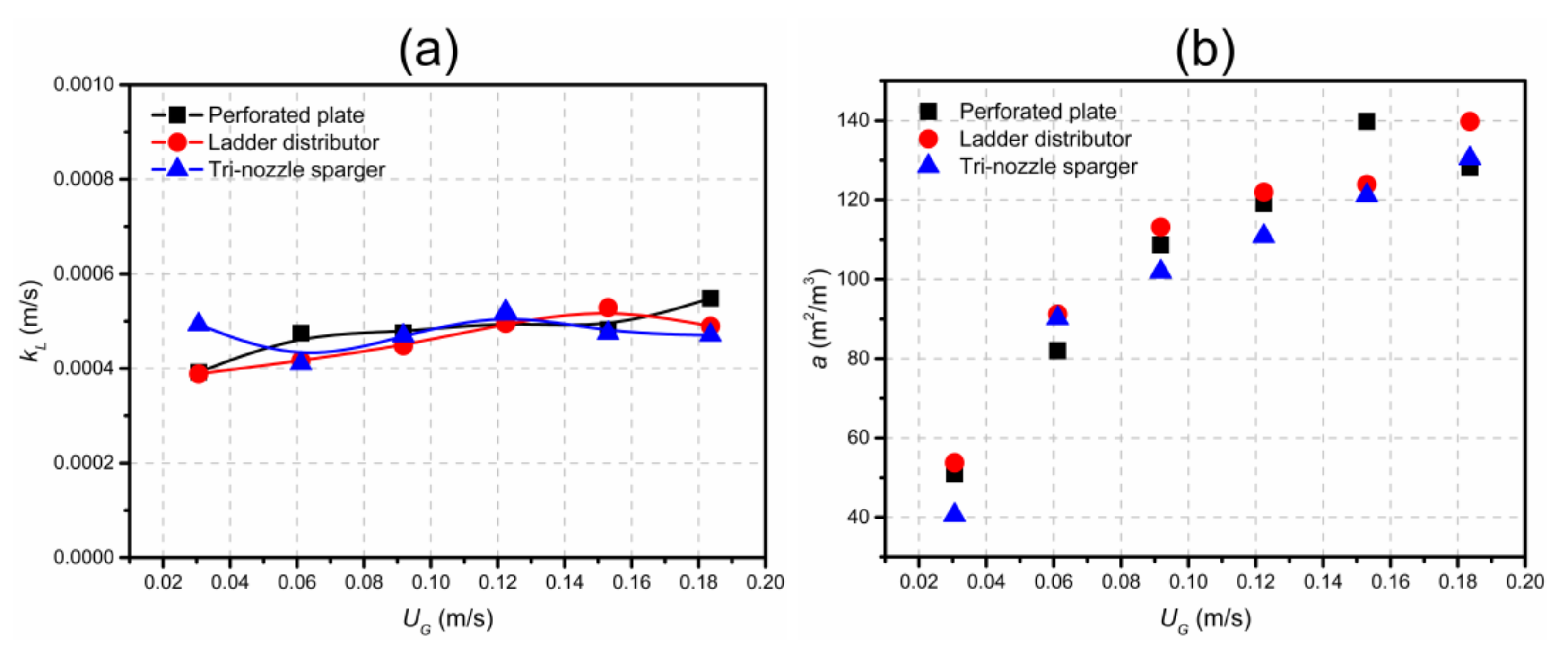
3.3. Mass Transfer Coefficient
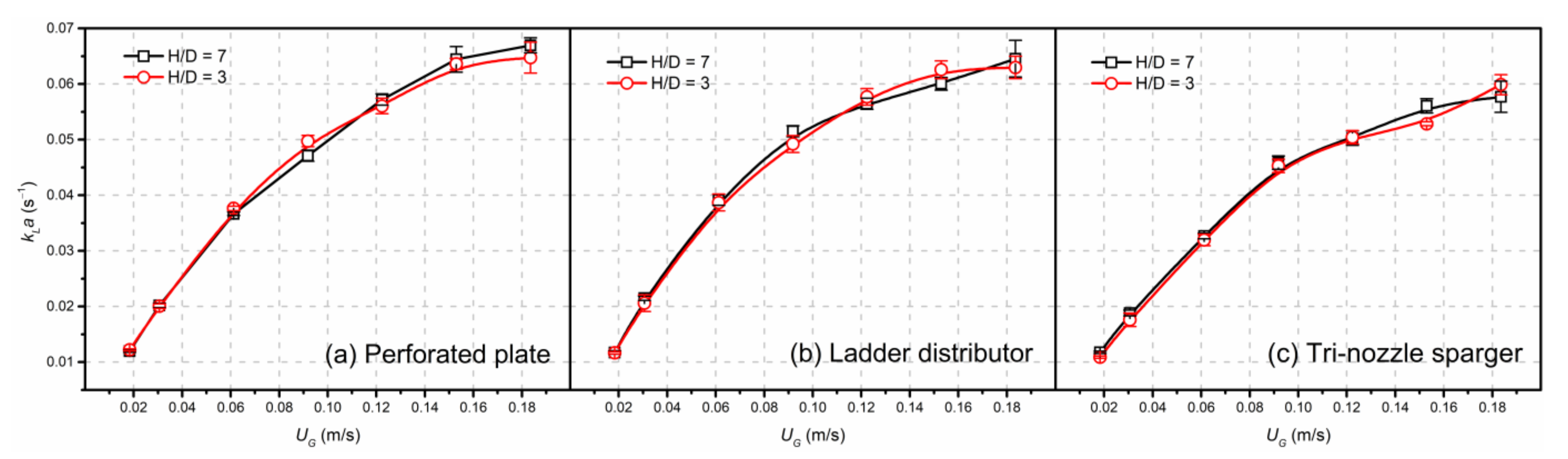
3.3.1. Influence of Gas Velocity
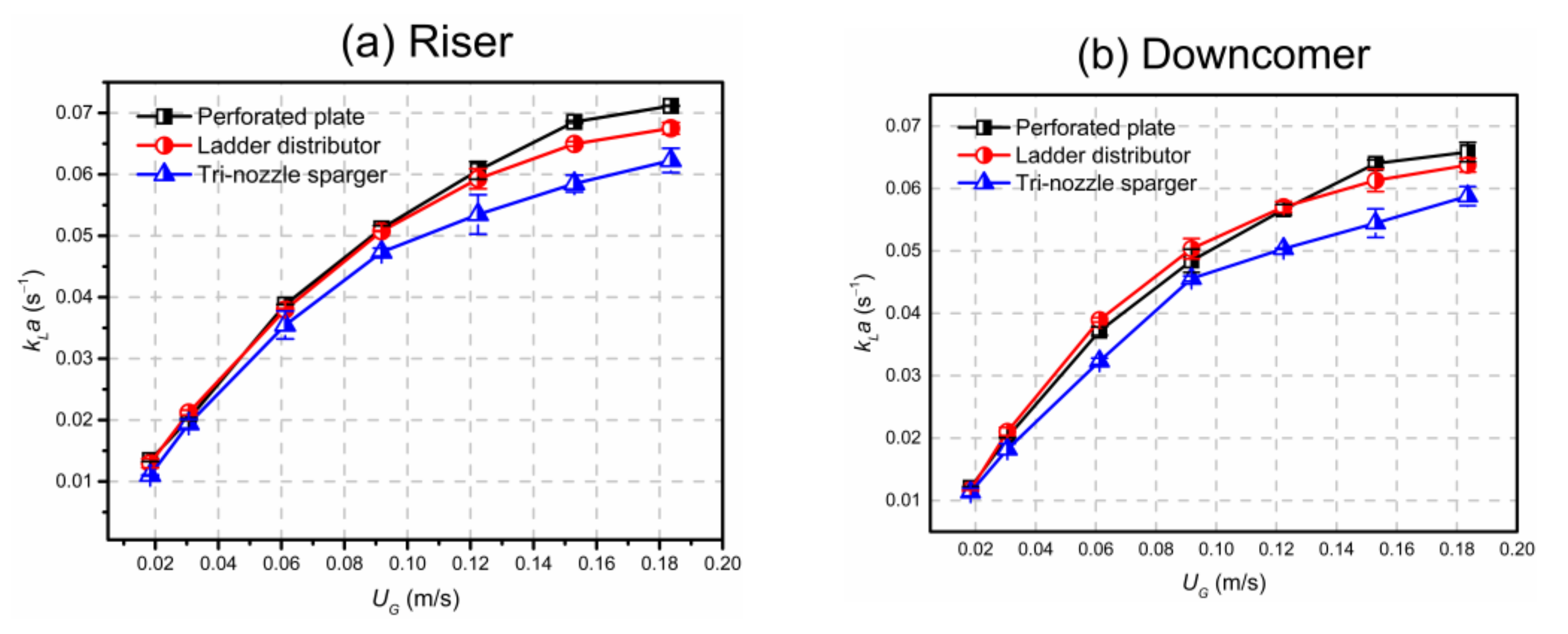
3.3.2. Influence of Axial and Radial Positions
3.3.3. Influence of Sparger Structure
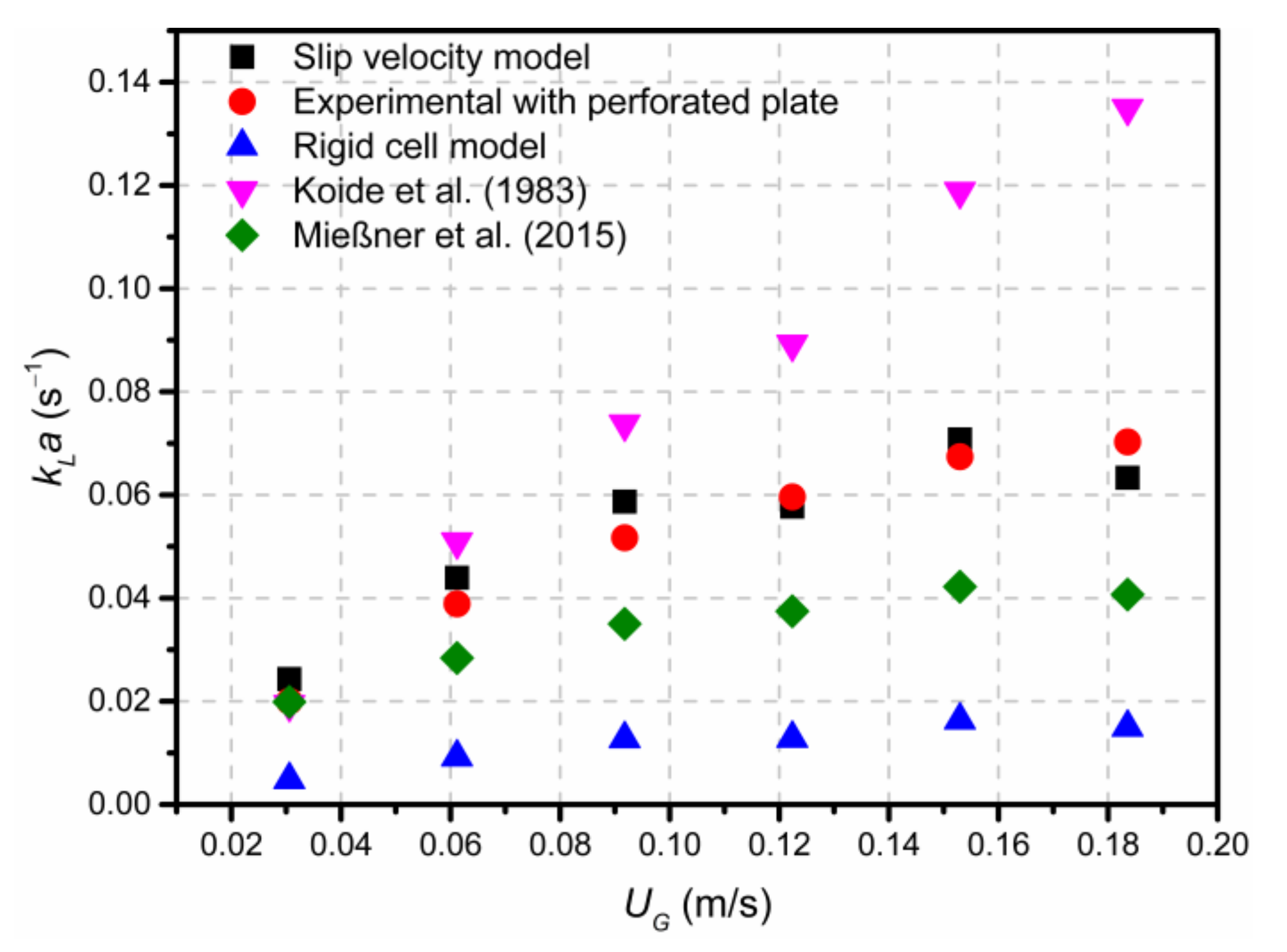
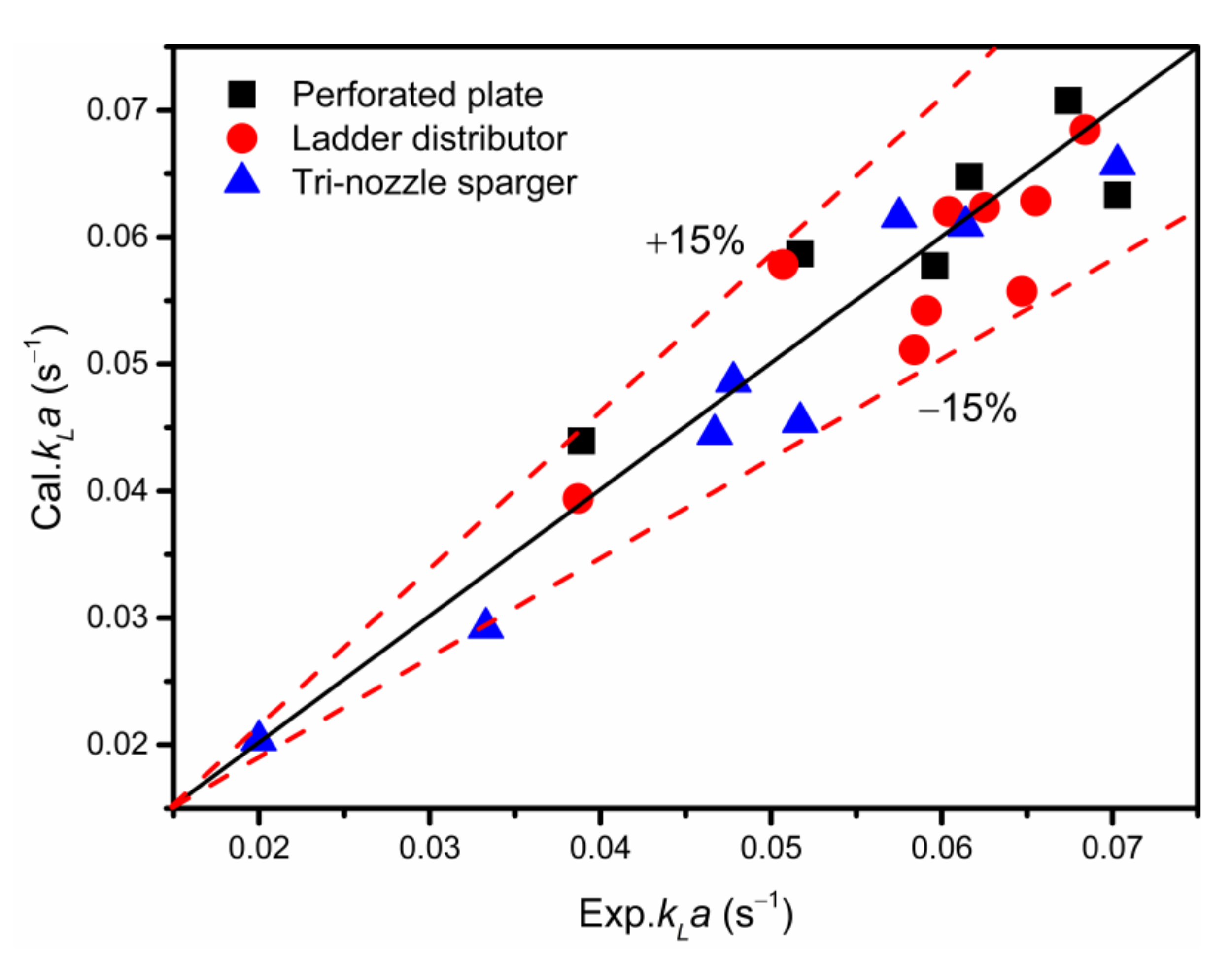
3.3.4. Modeling for kLa
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| symbol | description |
| a | mass transfer area, m−1 |
| Ad | downcomer cross-sectional area, m2 |
| Ar | riser cross-sectional area, m2 |
| C | liquid oxygen concentration, kg m−3 |
| C* | saturation dissolved oxygen concentration, kg m−3 |
| CA | concentration of alcohol, wt.% |
| Csensor | oxygen concentration indicated by sensor, kg m−3 |
| D | inner diameter of column, m |
| d32 | Sauter mean bubble diameter, m |
| dB | mean bubble diameter, m |
| Di | riser diameter, m |
| DL | liquid-phase diffusivity of dissolved oxygen, m2 s−1 |
| g | gravitational constant, m s−2 |
| H | height, m |
| kL | liquid film mass transfer coefficient, m s−1 |
| kLa | volumetric mass transfer coefficient, s−1 |
| ksensor | sensor response constant, s−1 |
| n | total number of data points collected |
| P | pressure, Pa |
| t | time, s |
| UB | bubble velocity, m s−1 |
| UG | superficial gas velocity, m s−1 |
| UL | circulating liquid velocity, m s−1 |
| Ur | relative velocity of bubbles and liquid, m s−1 |
| Greek letters | |
| vL | kinematic liquid viscosity, m2 s−1 |
| ε | gas holdup, dimensionless |
| μL | liquid viscosity, Pa s |
| ρL | liquid density, kg m−3 |
| σ | surface tension, N m−1 |
| Subscripts | |
| d | downcomer |
| G | gas |
| L | liquid |
| r | riser |
References
- Geng, S.; Mao, Z.-S.; Huang, Q.; Yang, C. Process intensification in pneumatically agitated slurry reactors. Engineering 2021, 7, 304–325. [Google Scholar] [CrossRef]
- Zhang, T.; We, C.H.; Ren, Y.; Feng, C.H.; Wu, H.Z. Advances in airlift reactors: Modified design and optimization of operation conditions. Rev. Chem. Eng. 2017, 33, 163–182. [Google Scholar] [CrossRef]
- Chisti, M.Y.; Moo-Young, M. Airlift reactors: Characteristics, applications and design considerations. Chem. Eng. Commun. 1987, 60, 195–242. [Google Scholar] [CrossRef]
- Götz, M.; Lefebvre, J.; Mörs, F.; Ortloff, F.; Reimert, R.; Bajohr, S.; Kolb, T. Novel gas holdup correlation for slurry bubble column reactors operated in the homogeneous regime. Chem. Eng. J. 2017, 308, 1209–1224. [Google Scholar] [CrossRef]
- Rubio, F.C.; Garcia, J.L.; Molina, E.; Chisti, Y. Axial inhomogeneities in steady-state dissolved oxygen in airlift bioreactors: Predictive models. Chem. Eng. J. 2001, 84, 43–55. [Google Scholar] [CrossRef] [Green Version]
- Naidoo, N.; Pauck, W.J.; Carsky, M. Effects of sparger design on the gas holdup and mass transfer in a pilot scale external loop airlift reactor. S. Afr. J. Chem. Eng. 2021, 37, 127–134. [Google Scholar] [CrossRef]
- Wei, C.; Wu, B.; Li, G.; Chen, K.; Jiang, M.; Ouyang, P. Comparison of the hydrodynamics and mass transfer characteristics in internal-loop airlift bioreactors utilizing either a novel membrane-tube sparger or perforated plate sparger. Bioprocess Biosyst. Eng. 2014, 37, 2289–2304. [Google Scholar] [CrossRef]
- Šijački, I.M.; Tokić, M.S.; Kojić, P.S.; Petrović, D.L.; Tekić, M.N.; Lukić, N.L. Sparger type influence on the volumetric mass transfer coefficient in the draft tube airlift reactor with diluted alcohol solutions. Ind. Eng. Chem. Res. 2013, 52, 6812–6821. [Google Scholar] [CrossRef]
- Luo, L.; Liu, F.; Xu, Y.; Yuan, J. Hydrodynamics and mass transfer characteristics in an internal loop airlift reactor with different spargers. Chem. Eng. J. 2011, 175, 494–504. [Google Scholar] [CrossRef]
- Ham, P.; Bun, S.; Painmanakul, P.; Wongwailikhit, K. Effective analysis of different gas diffusers on bubble hydrodynamics in bubble column and airlift reactors towards mass transfer enhancement. Processes 2021, 9, 1765. [Google Scholar] [CrossRef]
- Kojić, P.S.; Tokić, M.S.; Šijački, I.M.; Lukić, N.L.; Petrović, D.L.; Jovičević, D.Z.; Popović, S.S. Influence of the sparger type and added alcohol on the gas holdup of an external-loop airlift reactor. Chem. Eng. Technol. 2015, 38, 701–708. [Google Scholar] [CrossRef]
- Kojić, P.S.; Šijački, I.M.; Lukić, N.L.; Jovičević, D.Z.; Popović, S.S.; Petrović, D.L. Volumetric gas-liquid mass transfer coefficient in an external-loop airlift reactor with inserted membrane. Chem. Ind. Chem. Eng. Q. 2016, 22, 275–284. [Google Scholar] [CrossRef]
- Cao, C.; Dong, S.; Geng, Q.; Guo, Q. Hydrodynamics and axial dispersion in a gas-liquid-(solid) EL-ALR with different sparger designs. Ind. Eng. Chem. Res. 2008, 47, 4008–4017. [Google Scholar] [CrossRef]
- Snape, J.B.; Fialova, M.; Zahradnik, J.; Thomas, N.H. Hydrodynamic studies in an external loop airlift reactor containing aqueous electrolyte and sugar solutions. Chem. Eng. Sci. 1992, 47, 3387–3394. [Google Scholar] [CrossRef]
- Merchuk, J.C.; Contreras, A.; García, F.; Molina, E. Studies of mixing in a concentric tube airlift bioreactor with different spargers. Chem. Eng. Sci. 1998, 53, 709–719. [Google Scholar] [CrossRef]
- McClure, D.D.; Liu, Z.; Barton, G.W.; Fletcher, D.F.; Kavanagh, J.M. Oxygen transfer in pilot-scale contactors: An experimental and computational investigation into the effect of contactor design. Chem. Eng. J. 2018, 344, 173–183. [Google Scholar] [CrossRef]
- Koide, K.; Kurematsu, K.; Iwamoto, S.; Iwata, Y.; Horibe, K. Gas holdup and volumetric liquid-phase mass transfer coefficient in bubble column with draught tube and with gas dispersion into tube. J. Chem. Eng. Jpn. 1983, 16, 413–419. [Google Scholar] [CrossRef] [Green Version]
- Bello, R.A.; Robinson, C.W.; Moo-Young, M. Prediction of the volumetric mass transfer coefficient in pneumatic contactors. Chem. Eng. Sci. 1985, 40, 53–58. [Google Scholar] [CrossRef]
- Freitas, C.; Teixeira, J.A. Oxygen mass transfer in a high solids loading three-phase internal-loop airlift reactor. Chem. Eng. J. 2001, 84, 57–61. [Google Scholar] [CrossRef] [Green Version]
- Albijanić, B.; Havran, V.; Petrović, D.L.; Đurić, M.; Tekić, M.N. Hydrodynamics and mass transfer in a draft tube airlift reactor with dilute alcohol solutions. AIChE J. 2007, 53, 2897–2904. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, H.; Zhang, H.; Ying, W.; Fang, D. Oxygen mass transfer coefficient in bubble column slurry reactor with ultrafine suspended particles and neural network prediction. Can. J. Chem. Eng. 2013, 91, 532–541. [Google Scholar] [CrossRef]
- Mießner, U.; Kück, U.D.; Dujardin, V.; Heithoff, S.; Räbiger, N. Correlation for kLa prediction of airlift loop reactors including the gas phase residence time effect. Chem. Eng. Technol. 2015, 38, 2002–2010. [Google Scholar] [CrossRef]
- Huang, Z.; Cheng, Z. Liquid circulation hydrodynamics in an external loop airlift reactor. Can. J. Chem. Eng. 2013, 91, 223–230. [Google Scholar] [CrossRef]
- Painmanakul, P.; Loubiere, K.; Hebrard, G.; Mietton-Peuchot, M.; Roustan, M. Effect of surfactants on liquid-side mass transfer coefficients. Chem. Eng. Sci. 2005, 60, 6480–6491. [Google Scholar] [CrossRef] [Green Version]
- Fadili, A.; Essadki, A.H. Flow pattern study, gas hold-up and gas liquid mass transfer correlations in a bubble column: Effect of non-coalescing water-organic mixtures. Korean J. Chem. Eng. 2021, 38, 924–937. [Google Scholar] [CrossRef]
- Letzel, H.M.; Schouten, J.C.; Krishna, R.; van den Bleek, C.M. Gas holdup and mass transfer in bubble column reactors operated at elevated pressure. Chem. Eng. Sci. 1999, 54, 2237–2246. [Google Scholar] [CrossRef]
- Lu, X.; Zheng, X.; Ding, Y.; Lin, W.; Wang, W.; Yu, J. Experimental study on the influence of the orifice size on hydrodynamic characteristics and bubble size distribution of an external loop airlift reactor. Can. J. Chem. Eng. 2020, 98, 1593–1606. [Google Scholar] [CrossRef]
- Yang, T.; Geng, S.; Yang, C.; Huang, Q. Hydrodynamics and mass transfer in an internal airlift slurry reactor for process intensification. Chem. Eng. Sci. 2018, 184, 126–133. [Google Scholar] [CrossRef]
- Han, M.; Laari, A.; Koiranen, T. Effect of aeration mode on the performance of center-and annulus-rising internal-loop airlift bioreactors. Can. J. Chem. Eng. 2018, 96, 367–376. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, C.; Yu, G.; Mao, Z.-S. CFD simulation of hydrodynamics and mass transfer in an internal airlift loop reactor using a steady two-fluid model. Chem. Eng. Sci. 2010, 65, 5527–5536. [Google Scholar] [CrossRef]
- Fadavi, A.; Chisti, Y. Gas-liquid mass transfer in a novel forced circulation loop reactor. Chem. Eng. J. 2005, 112, 73–80. [Google Scholar] [CrossRef]
- Shimizu, K.; Takada, S.; Takahashi, T.; Kawase, Y. Phenomenological simulation model for gas hold-ups and volumetric mass transfer coefficients in external-loop airlift reactors. Chem. Eng. J. 2001, 84, 599–603. [Google Scholar] [CrossRef]
- Choi, K.H. Hydrodynamic and mass transfer characteristics of external-loop airlift reactors without an extension tube above the downcomer. Korean J. Chem. Eng. 2001, 18, 240–246. [Google Scholar] [CrossRef]
- Teli, S.M.; Mathpati, C.S. Experimental and numerical study of gas-liquid flow in a sectionalized external-loop airlift reactor. Chin. J. Chem. Eng. 2021, 32, 39–60. [Google Scholar] [CrossRef]




| Reference | Equation | Range of Application |
|---|---|---|
| Koide et al. [17] | Water; 3.69 × 102 ≤ (μ/ρDL) ≤ 5.68 × 104, 1.36 × 103 ≤ (gD2ρ/σ) ≤ 1.22 × 104, 2.27 × 108 ≤ (gD3ρ2/μ2) ≤ 3.32 × 1011, 0.471 ≤ (Di/D) ≤ 0.743, 0.037 ≤ ε ≤ 0.21,0 ≤ (Crk2/σ) ≤ 67.3; Airlift loop reactor | |
| Bello et al. [18] | Water; aqueous salt solution (0.15 mol/L NaCl); ILAR: Ad/Ar = 0.13, 0.35, 0.56; ELAR: Ad/Ar = 0.11~0.69; Bubble column | |
| Chisti et al. [3] | Water; aqueous salt solution; 0.026 m/s < UG < 0.21 m/s; ELAR: Ad/Ar = 0.25, 0.44; | |
| Freitas et al. [19] | ILAR, Water/low density solids 0 m/s < UG < 0. 5 m/s 0 < CS < 0.3 | |
| Albijanic’ et al. [20] | ILAR, aqueous alcohol solution | |
| Chen et al. [21] | 0.01 m/s < UG < 0.085 m/s, 0 < Cs < 0.3, 1 < H/D < 12; Bubble column | |
| Mießner et al. [22] | Airlift loop reactor |
| Sparger Type | Correlation | Correlation Coefficient |
|---|---|---|
| Perforated plate | R2 = 0.97 | |
| Ladder distributor | R2 = 0.99 | |
| Tri-nozzle sparger | R2 = 0.97 |
| Sparger Type | Correlation | Correlation Coefficient |
|---|---|---|
| Perforated plate | R2 = 0.97 | |
| Ladder distributor | R2 = 0.96 | |
| Tri-nozzle sparger | R2 = 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Guo, H.; Zhou, T.; Cheng, Z.; Huang, Z. Influence of Sparger Type on Mass Transfer in a Pilot-Scale Internal Loop Airlift Reactor. Processes 2022, 10, 429. https://doi.org/10.3390/pr10020429
Wang Z, Guo H, Zhou T, Cheng Z, Huang Z. Influence of Sparger Type on Mass Transfer in a Pilot-Scale Internal Loop Airlift Reactor. Processes. 2022; 10(2):429. https://doi.org/10.3390/pr10020429
Chicago/Turabian StyleWang, Zongliang, Hongshan Guo, Tong Zhou, Zhenmin Cheng, and Zibin Huang. 2022. "Influence of Sparger Type on Mass Transfer in a Pilot-Scale Internal Loop Airlift Reactor" Processes 10, no. 2: 429. https://doi.org/10.3390/pr10020429
APA StyleWang, Z., Guo, H., Zhou, T., Cheng, Z., & Huang, Z. (2022). Influence of Sparger Type on Mass Transfer in a Pilot-Scale Internal Loop Airlift Reactor. Processes, 10(2), 429. https://doi.org/10.3390/pr10020429







